Как найти площадь многоугольника 4 класс формула пример: Урок математики по теме:»Площадь многоугольника»

Урок математики по теме:»Площадь многоугольника»

Цели:

• обучающие: научить учащихся находить площадь многоугольника, используя выбранные ими способы, сформировать начальные представления 
• многоугольнике, графические и измерительные навыки;
• развивающие: развитие способов умственной деятельности учащихся при выполнении заданий от наблюдения, расчетов до выяснения закономерностей вычисления площади многоугольника;
• воспитывающие: раскрытие субъективного опыта учащихся, поощрение действий, стремлений учащихся как основы воспитания положительных качеств личности;
• методическая: создание условий для проявления познавательной активности учащихся.

Оснащение урока:

1. Оформление доски: слева — фигуры многоугольника, справа — чистое полотно доски для записи на уроке, в центре – многоугольник-прямоугольник.
2. Листок “К исследованию”.
3. Инструментарии учителя и учащихся (мел, указка, линейка, листок исследования, фигуры, ватман, маркер).

Метод урока:

• По взаимодействию учителя и учащихся – диалог-общение;
• По способу решения задач – частично-поисковый;
• По способу умственной деятельности — (СУД) развивающее обучение.

Форма урока — фронтальная, в парах, индивидуальная.

Тип урока — урок усвоения новых знаний, умений и навыков.

Структура урока — постепенное углубление в тему, гибкая, диалогическая.

Ход урока

Приветствие.

Урок прекрасен и приносит радость, когда мы мыслим, дружно работаем. Сегодня мы будем рассматривать фигуры, определять их названия, думать, искать и находить решения. Пожелаем друг другу успешной работы.

Актуализация знаний.

Рассмотрите фигуры (на доске многоугольники).

Они все вместе. Почему? Какой у них общий признак? (Многоугольники).

Назовите этот многоугольник (5-угольник, 6-угольник…)

Может быть, вы знаете, что такое площадь многоугольника?

Тогда покажите на одной из фигур.

(Обобщение учителем: площадь — часть плоскости внутри замкнутой геометрической фигуры.)

В русском языке это слово имеет несколько значений.

(Ученик по словарю знакомит со значениями.)

1. Часть плоскости внутри замкнутой геометрической фигуры.
2. Большое незастроенное и ровное место.
3. Помещение для какой-либо цели.

Какое из значений используется в математике?

В математике используется первое значение.

(На доске фигура).

Это многоугольник? Да.

Назовите фигуру по-другому. Прямоугольник.

Покажи длину, ширину.

Как найти площадь многоугольника?

Запишите при помощи букв и знаков формулу.

S = а * в

Если длина нашего прямоугольника 20 см, ширина 10см. Чему равна площадь?

Площадь равна 200 см²

Подумайте, как приложить линейку, чтобы фигура разделилась на:

1. Два треугольника
2. Два четырехугольника
3. Треугольник и четырехугольник
4. Треугольник и пятиугольник

Увидели, из каких частей состоит фигура? А теперь, наоборот, по частям соберем целое.

( Части фигуры лежат на партах. Дети собирают из них прямоугольник ).

Сделайте вывод по наблюдениям.

Целую фигуру можно разделить на части и из частей составить целую.

Дома на основе треугольников и четырехугольников составляли фигуры, силуэты. Вот какие они получились.

(Демонстрация рисунков, выполненных дома учащимися. Одна из работ анализируется).

Какие фигуры использовал? У тебя получился сложный многоугольник.

Постановка учебной задачи.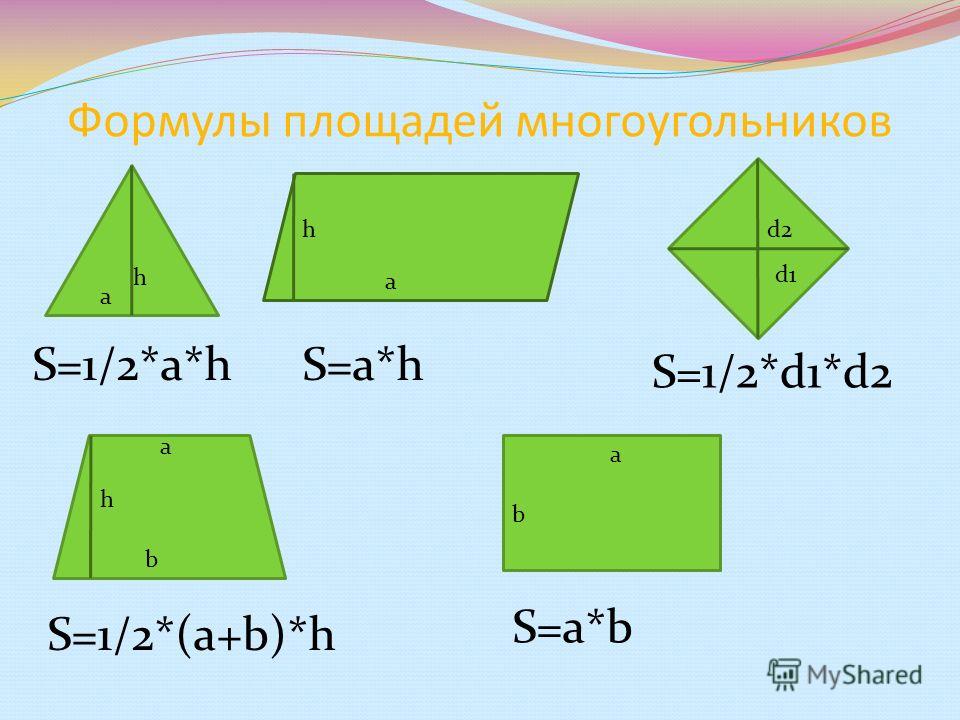

На уроке мы должны ответить на вопрос: как найти площадь сложного многоугольника?

Для чего человеку нужно находить площадь?

(Ответы детей и обобщение учителем).

Задача определения площади возникла из практики.

(Показывается план школьного участка).

Для того чтобы построить школу, сначала создали план. Потом разбивалась территория на участки определенной площади, размещались строения, клумбы, стадион. При этом участок имеет определенную форму — форму многоугольника.

Решение учебной задачи.

(Раздаются листы для исследования).

 

Перед вами фигура. Назовите ее.

Многоугольник, шестиугольник.

Найдем площадь многоугольника. Что для этого надо делать?

Разделить на прямоугольники.

(При затруднении будет другой вопрос: “Из каких фигур состоит многоугольник?”).

Из двух прямоугольников.

С помощью линейки и карандаша разделите фигуру на прямоугольники. Обозначьте цифрами 1 и 2 полученные части.

Проведем измерения.

Найдем площадь первой фигуры.

(Учащиеся предлагают следующие варианты решений и записывают их на доске).

1способ:

• S₁ = 5 ? 2 = 10 см²
• S₂ = 5 ? 1 = 5 см²

Зная площадь частей, как найти площадь целой фигуры?

S = 10 + 5 = 15 см²

2 способ:

• S₁ = 6 ? 2 = 12 см²
• S₂ = 3 ? 1 = 3 см²
• S = 12 + 3 = 15 см².

Сравните результаты и сделайте вывод.

Проследим наши действия

Как находили площадь многоугольника?

Составляется и записывается на плакате алгоритм:?

1. Делим фигуру на части

2. Находим площади частей этих многоугольников ( S₁, S₂ ).

3. Находим площадь целого многоугольника ( S₁ + S ₂ ).

Проговорить алгоритм.

( Несколько учащихся проговаривают алгоритм).

Мы нашли два способа, а может, есть еще?

А можно фигуру достроить.

Сколько прямоугольников получилось?

Два.

Обозначим части 1 и 2. Проведем измерения.

Найдите площадь каждой части многоугольника.

• S₁₌6? 5=30см²
• S₂= 5 ? 3 = 15 см²

Как найти площадь нашего шестиугольника?

S = 30 – 15 = 15 см²

Составим алгоритм:

Достроили фигуру до прямоугольника

Нашли S₁ и S₂.

Нашли разность S₁ – S₂.

Сравните два алгоритма. Сделайте вывод. Какие действия одинаковые? Где разошлись наши действия?

Закройте глазки, опустите головки. Мысленно повторите алгоритм.

Мы провели исследовательскую работу, рассмотрели разные способы и теперь можем находить площадь любого многоугольника.

Проверка результативности.

Проверьте себя.

Перед вами многоугольники.

Найти площадь одной фигуры по выбору, при этом можете пользоваться разными способами.

Работа выполняется самостоятельно. Дети выбирают фигуру. Находят площадь одним из способов. Проверка – ключ на доске.

Что можно сказать о форме? ( Форма разная)

А какова площадь этих многоугольников? ( Площади этих многоугольников равны)

Оценивают результаты.

У кого правильно – поставь “+”.

У кого сомнения, затруднения – “?”

Консультанты оказывают помощь ребятам, ищут ошибки, помогают исправить.

Домашнее задание:

Составить свои листки исследования, вычислить площадь многоугольника разными способами.

Итог урока.

Итак, ребята, что вы расскажите родителям, о том как найти площадь геометрической фигуры – многоугольника.

Площадь многоугольника

Бизнес с Oriflame — рост и РАЗВИТИЕ!

ЗАМУЧИЛИ БОЛИ В СПИНЕ?

Александр | 2016-11-10

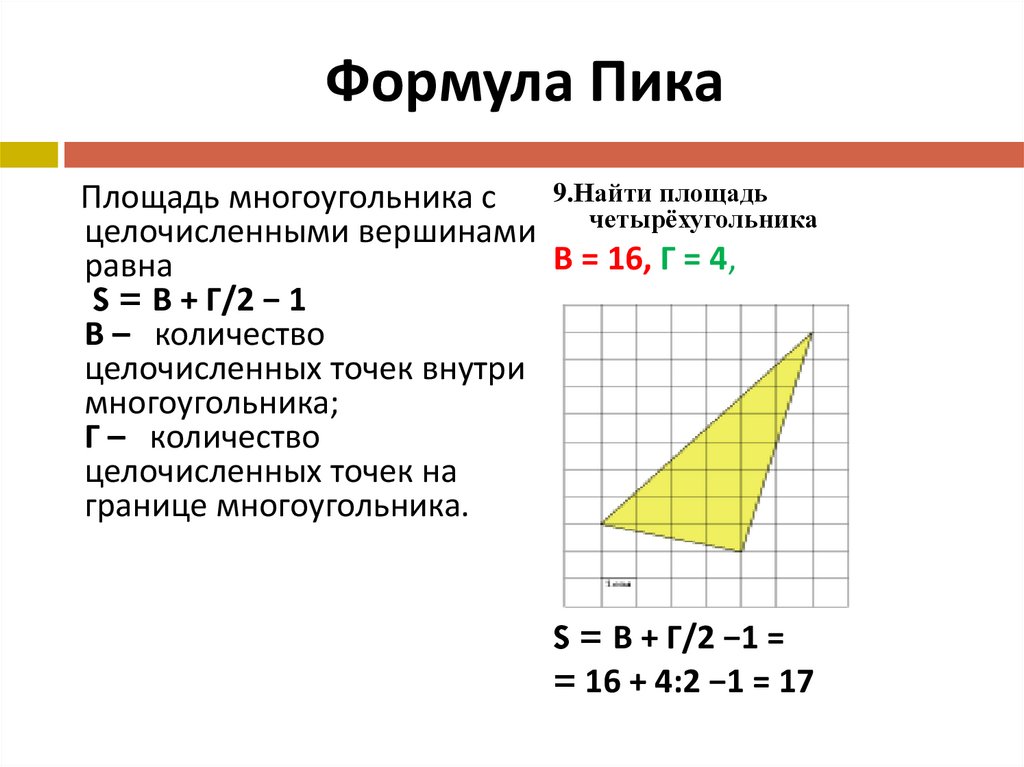
Площадь многоугольника. Друзья!  К вашему вниманию пару задачек с многоугольником и вписанной в него окружностью. Существует формула, которой связывается радиус указанной окружности и периметр с площадью такого многоугольника. Вот она:

Как выводится эта формула? Просто!

Имеем многоугольник и вписанную окружность. *Рассмотрим вывод на примере пятиугольника. Разобьём его на треугольники (соединим центр окружности и вершины отрезками). Получается, что у каждого треугольника основание является стороной многоугольника, а высоты образованных треугольников равны радиусу вписанной окружности:

Используя формулу площади треугольника можем записать:

Вынесем общие множители:

Уверен, сам принцип вам понятен.

*При выводе формулы количество сторон взятого многоугольника не имеет значения. В общем виде вывод формулы выглядел бы так:

*Дополнительная информация!

Известна формула радиуса окружности вписанной в треугольник

Не трудно заметить, что она исходит из полученной нами формулы, посмотрите (a,b,c – это стороны треугольника):

 

27640. Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь.

Вычисляем:

Ответ: 30

Ещё пара задач с многоугольниками.

27930. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 54⁰. Найдите n.

Если угол между радиусом окружности и стороной многоугольника равен 54⁰, то угол между сторонами многоугольника будет равен 108⁰. Тут необходимо вспомнить формулу угла правильного многоугольника:

Остаётся подставить в формулу значение угла и вычислить n:

Ответ: 5

27595. Периметры двух подобных многоугольников относятся как 2:7. Площадь меньшего многоугольника равна 28. Найдите площадь большего многоугольника.

Здесь нужно вспомнить о том, что если линейные размеры фигуры увеличивается в k раз, то площадь фигуры увеличивается в k² раз. *Свойство подобия фигур.

Периметр большего многоугольника больше периметра меньшего в 7/2 раза, значит площадь увеличилась в (7/2)² раза.  Таким образом, площадь большего многоугольника равна:

Ответ: 343

27639. Около окружности, радиус которой равен 3, описан многоугольник, площадь которого равна 33. Найдите его периметр.

Посмотреть решение

27641. Около окружности описан многоугольник, площадь которого равна 5. Его периметр равен 10. Найдите радиус этой окружности.

Посмотреть решение

27595. Периметры двух подобных многоугольников относятся как 3:5. Площадь меньшего многоугольника равна 18. Найдите площадь большего многоугольника.

Ответ: 50

Всего доброго! Учитесь с удовольствием!

С уважением, Александр.

Категория: Площади фигур | ЕГЭ-№1Формулы

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Замучили боль и скованность в мышцах спины?

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

Площадь многоугольников – формула, площадь правильных многоугольников Примеры

Площадь многоугольника определяется как площадь, ограниченная границей многоугольника. Другими словами, мы говорим, что область, занимаемая любым многоугольником, дает его площадь. В этом уроке мы научимся определять площадь многоугольников и детально находить разницу между периметром и площадью многоугольников.

1.	Какова площадь многоугольника?
2.	Разница между периметром и площадью полигонов
3.	Формулы площади многоугольника
4.	Площадь полигонов с координатами
5.	Часто задаваемые вопросы о площади полигонов

Какова площадь многоугольника?

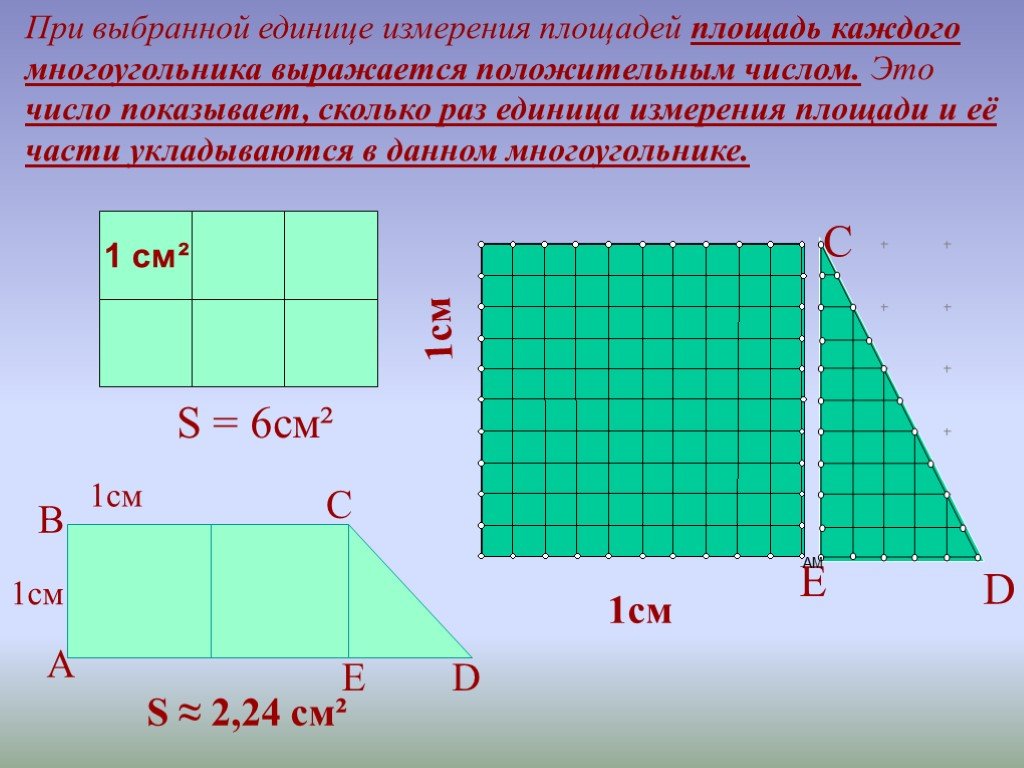
Определение площади многоугольника — это мера площади, заключенной в него. Поскольку многоугольники представляют собой замкнутые плоские формы, то площадь многоугольника — это пространство, которое он занимает в двумерной плоскости. Единица площади любого многоугольника всегда выражается в квадратных единицах. Обратите внимание на следующий рисунок, на котором показана площадь многоугольника на двумерной плоскости.

Разница между периметром и площадью полигонов

Периметр и площадь многоугольников являются измеримыми величинами, которые зависят от длины сторон многоугольника. Чтобы различать их обоих, необходимо понять основную разницу между периметром и площадью. Обратите внимание на приведенную ниже таблицу, чтобы лучше понять эту разницу.

Критерии отличия	Периметр Полигона	Площадь полигона
Определение	Определяется как общая длина границы многоугольника, которую можно получить, сложив длины всех его сторон.	Определяется как область или пространство, окруженное любым многоугольником.
Формула	Периметр многоугольника = длина стороны 1 + длина стороны 2 + …+ длина стороны N (для N-стороннего многоугольника)	Площадь многоугольника можно найти по разным формулам в зависимости от того, является ли многоугольник правильным или неправильным многоугольником.
Блок	Единица измерения периметра многоугольника выражается в метрах, сантиметрах, дюймах, футах и ​​т. д.	Единица площади многоугольников выражается в (метрах) 2 , (сантиметрах) 2 , (дюймах) 2 , (футах) 2 и т. д.

Сходство между вычислением периметра и площади многоугольника заключается в том, что оба они зависят от длины сторон формы, а не от внутренних или внешних углов многоугольника.

Формулы площади многоугольника

Многоугольник может быть классифицирован как правильный или неправильный многоугольник в зависимости от длины его сторон.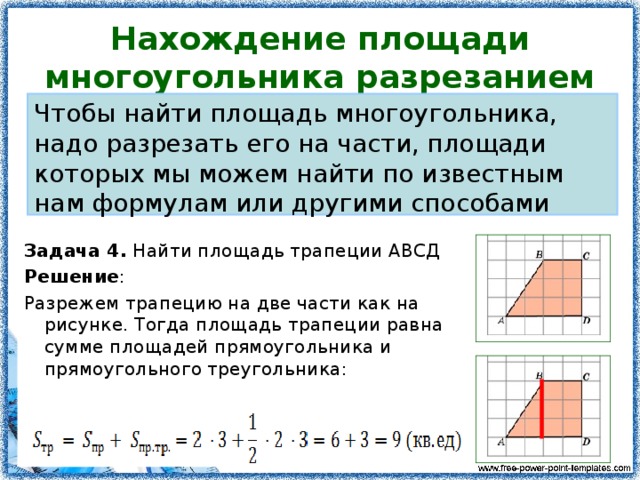 Таким образом, эта дифференциация также вносит различие в вычисление площади многоугольников. Площадь некоторых общеизвестных многоугольников определяется как:

• Площадь треугольника = (1/2) × основание × высота
  Мы также можем найти площадь треугольника, если известна длина его сторон, используя формулу Герона, которая выглядит следующим образом: Площадь = \(\sqrt{s(s-a)(s-b)(s-c)}\), где s = периметр/ 2 = (a + b + c)/2, a, b и c — длины его сторон.
• Площадь прямоугольника = длина × ширина
• Площадь параллелограмма = основание × высота
• Площадь трапеции = (1/2) × (сумма длин ее параллельных сторон или оснований) × высота
• Площадь ромба = (1/2) × (произведение диагоналей)

Чтобы вычислить площадь многоугольника, необходимо сначала узнать, является ли данный многоугольник правильным или неправильным многоугольником.

Площадь правильных многоугольников

Правильный многоугольник — это многоугольник с равными сторонами и равными углами.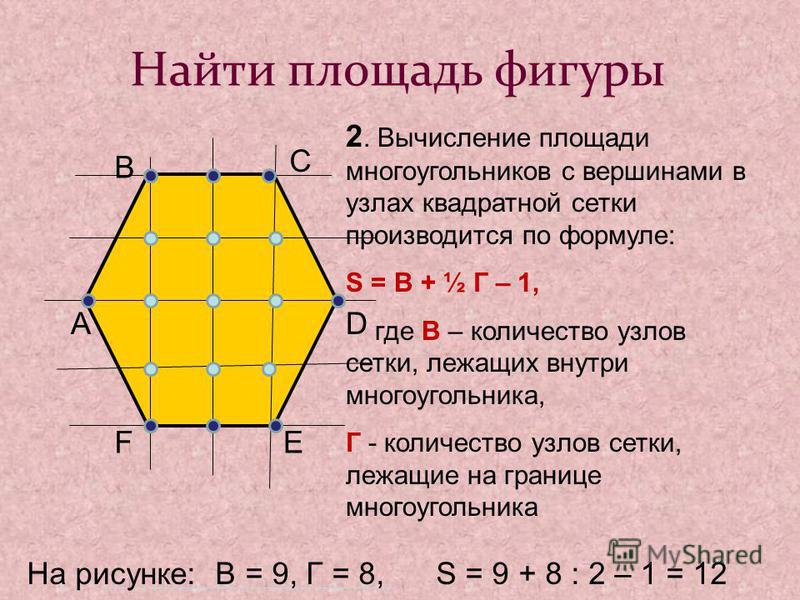 Таким образом, метод расчета площади правильных многоугольников основан на формулах, связанных с каждым многоугольником. Давайте посмотрим на формулы некоторых часто используемых правильных многоугольников:

Названия правильных многоугольников	Площадь правильного многоугольника
Равносторонний треугольник	Площадь = (√3 ×(длина стороны) 2 )/4
Квадрат	Площадь = (длина) 2
Обычный пятиугольник	Площадь = 5/2 × длина стороны × длина апофемы 92\)
Обычный шестигранник	Площадь = [3√3 × (длина стороны) 2 ]/2

Для определения площади правильного многоугольника, если известно число его сторон, дается формула:

• Площадь правильного многоугольника = (число сторон × длина одной стороны × апофема)/2 , где длина апофемы задается как \(\dfrac{l}{2\tan(\dfrac{180}{n})}\), где l — длина стороны, а n — количество сторон правильный многоугольник. 92\)
  ⇒ A = 84,3 квадратных дюйма

  Таким образом, площадь правильного пятиугольника равна 84,3 квадратных дюйма.

  Площадь неправильных многоугольников

  Неправильный многоугольник представляет собой плоскую замкнутую форму, не имеющую равных сторон и равных углов. Таким образом, чтобы вычислить площадь неправильного многоугольника, мы разобьем неправильный многоугольник на множество правильных многоугольников так, что известны формулы их площадей. Рассмотрим пример, приведенный ниже.

  Многоугольник ABCD является неправильным многоугольником. Таким образом, мы можем разделить многоугольник ABCD на два треугольника ABC и ADC. Площадь треугольника можно получить: 92 }\)

• Шаг 2: Зная размеры многоугольников, определите, является ли данный многоугольник правильным многоугольником или нет.
• Шаг 3: Если многоугольник является правильным многоугольником, мы используем формулу площадь правильного многоугольника = (количество сторон × длина одной стороны × апофема)/2, где длина апофемы определяется как (длина одной стороны )/(2 ×(tan(180°/количество сторон))). 2}\) = 2 единицы 92}\) = 2 единицы

  Теперь, когда мы знаем, что длина всех сторон данного многоугольника одинакова, это показывает, что это квадрат. Таким образом, площадь многоугольника ABCD определяется как A = (длина) ² = (2) ² = 4 квадратных единицы.

  Следовательно, площадь многоугольника с координатами (0,0), (0, 2), (2, 2) и (2, 0) равна 4 квадратным единицам.

  Важные примечания

  • Если известна длина одной стороны, можно найти площадь правильного многоугольника, найдя апофему.
  • Апофема падает на середину стороны под прямым углом, разделяя ее на две равные части.
  • Равносторонний треугольник — это правильный многоугольник с 3 сторонами, а квадрат — правильный многоугольник с 4 сторонами. Следовательно, они не имеют обычного префикса перед именем формы.

  Часто задаваемые вопросы о площади полигонов

  Что такое определение площади многоугольника?

  Пространство, ограниченное любым многоугольником на двумерной плоскости, определяется как площадь многоугольника. Запишем единицу площади многоугольника в квадратных единицах ^{, где единицей измерения могут быть единицы СИ, такие как метры или сантиметры и т. д., или единицы USCS (дюймы или футы и т. д.).}

  Как найти площадь многоугольника?

  Площадь многоугольника можно рассчитать, поняв, является ли данный многоугольник правильным или неправильным многоугольником. Шаги для вычисления площади многоугольников:

  • Шаг 1: Определите, является ли данный многоугольник правильным многоугольником или нет.
  • Шаг 2: Если это правильный многоугольник или имеет стандартную формулу расчета, используйте ее для определения значения при всех заданных размерах многоугольника, в противном случае площадь многоугольника можно вычислить, разделив его на множество правильные многоугольники, площадь которых можно сложить, чтобы получить площадь требуемого многоугольника.

  Какова площадь многоугольника с n сторонами?

  Если задано количество сторон многоугольника, площадь многоугольника можно рассчитать по формуле Площадь = [(L ² n)/4 tan(180/n)]; где L — длина его стороны, а «n» — количество сторон многоугольника.

  В чем разница между периметром и площадью многоугольников?

  Периметр многоугольника — это общая длина его границы, тогда как площадь многоугольника — это занимаемая им область. Периметр многоугольника получается путем сложения длин всех его сторон, а площадь многоугольника получается с помощью требуемой формулы в зависимости от того, является ли данный многоугольник правильным многоугольником или нет. Единица периметра многоугольника всегда дается в линейных единицах, поскольку она одномерна, в то время как единица площади многоугольника всегда дается в квадратных единицах, поскольку площадь является двумерным понятием. 92 }\)

• Шаг 2: Как только нам известны размеры многоугольников, мы определяем, является ли данный многоугольник правильным многоугольником или нет.
• Шаг 3: Если вывод из шага 2 показывает, что многоугольник является правильным многоугольником, мы используем формулу площадь правильного многоугольника = (количество сторон × длина одной стороны × апофема)/2, где длина апофемы определяется как , Апофема = [(длина одной стороны)/{2 ×(tan(180/количество сторон))}]. С другой стороны, если многоугольник является неправильным многоугольником, его делят на несколько меньших правильных многоугольников, находя размерность диагоналей по формуле расстояния.

Как найти площадь правильного многоугольника?

Площадь правильного многоугольника можно найти по формуле Площадь = (количество сторон × длина одной стороны × апофема)/2. Соблюдайте следующие шаги для всей процедуры:

• Шаг 1: Найдите количество сторон многоугольника.
• Шаг 2: Если для заданного правильного многоугольника существует стандартная формула, примените ее. Если нет, обратитесь к шагам, приведенным ниже.
• Шаг 3: Проверьте измерение длины одной стороны.
• Шаг 4: Используйте значения, полученные на шагах 1 и 2, для определения значения апофемы по формуле Апофема = [(длина одной стороны)/{2 ×(тангенс(180/количество сторон))}].
• Шаг 5: Теперь найдите площадь правильного многоугольника по формуле Площадь = (количество сторон × длина одной стороны × апофема)/2.

Как найти площадь неправильного многоугольника?

Чтобы вычислить значение площади неправильного многоугольника, мы используем следующие шаги:

• Шаг 1: Разделите заданный многоугольник на меньшие части, образуя различные правильные или известные многоугольники.
• Шаг 2: Найдите площадь каждой секции по отдельности.
• Шаг 3: Добавьте площадь каждой секции, чтобы получить площадь заданного неправильного многоугольника.

Как найти площадь многоугольника с периметром?

Если периметр многоугольника задан, то его площадь можно рассчитать по формуле: Площадь = (Периметр × апофема)/2. В этой формуле также должна быть известна апофема или ее можно вычислить с помощью формулы Апофема = [(длина одной стороны)/{2 ×(tan(180/число сторон))}]. Подставляя значение апофемы и периметра, можно вычислить площадь многоугольника.

Какая формула используется для вычисления площади правильных многоугольников?

Формула для вычисления площади правильного многоугольника: Площадь = (количество сторон × длина одной стороны × апофема)/2, где значение апофемы можно рассчитать по формуле Апофема = [(длина одного сторона)/{2 ×(tan(180/количество сторон))}].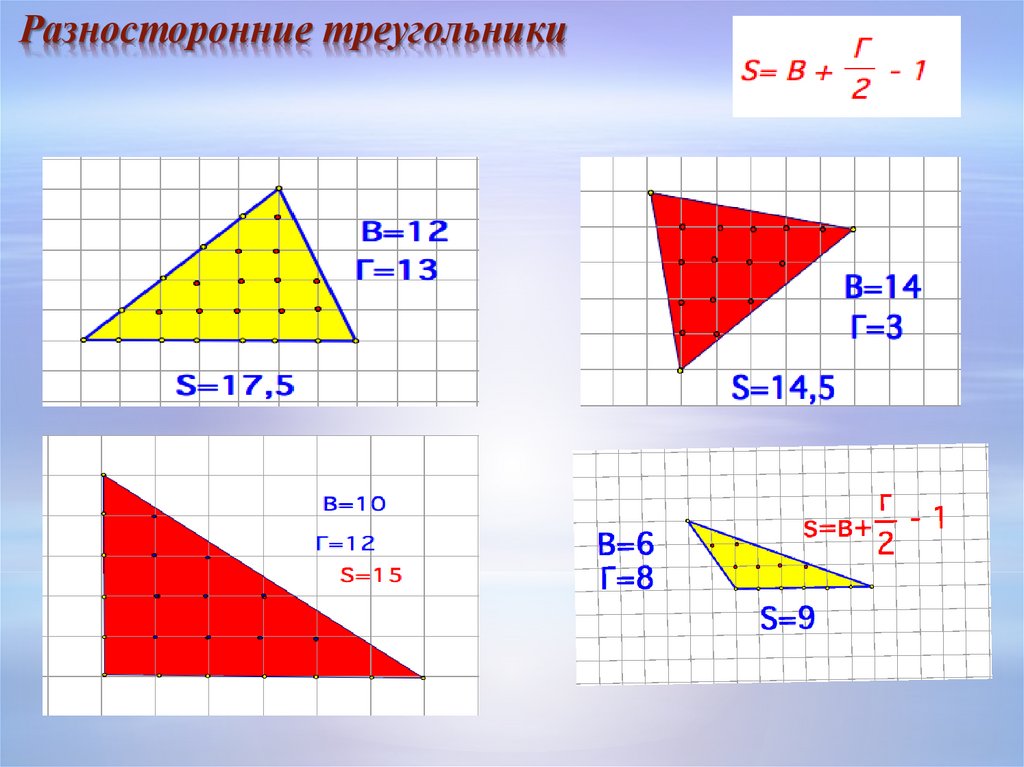

Площадь многоугольника – формулы, примеры

Площадь многоугольника – это общее пространство, заключенное внутри фигуры. Измерение производится в квадратных единицах.

Как известно, многоугольник может быть правильным или неправильным. Стороны правильных многоугольников имеют определенный размер, поэтому их площадь легко вычислить по сравнению с неправильными многоугольниками, стороны которых не имеют фиксированного размера. Давайте изучим основной подход к определению площади обоих типов по отдельности.

Как найти площадь правильного многоугольника

Чтобы определить площадь поверхности правильного многоугольника с n сторон (где каждая сторона представлена ​​как «s»), мы используем формулу, приведенную ниже:

Площадь правильного многоугольника

Найдите площадь правильного многоугольника с периметром 44 см и длиной апофемы 10 см.

Решение:

Как мы знаем,
Площадь (A) = ½ x p x a, здесь p = 44 см и a = 10 см
 = ½ x 44 x 10 см ²
 = 22 0 см ²

Нахождение площади правильного многоугольника, когда известны СТОРОНА и АПОТЕМ .

Вычислите площадь правильного пятиугольника со стороной 12 см и апофемой 7,5 см.

Решение:

Поскольку многоугольник представляет собой пятиугольник с пятью сторонами, где каждая сторона (s) имеет размер 12 см, его периметр (p) равен (5 x s) = (5 x 12) = 60 см
Теперь , как мы знаем,
 Площадь (A) = ½ x p x a, здесь p = 60 см и a = 7,5 см
= ½ x 60 x 7,5 см ²
= 225 см Неправильный многоугольник

Для неправильных многоугольников мы делим многоугольник на два или более правильных многоугольника, находим индивидуальную площадь каждого такого многоугольника, а затем складываем их, чтобы получить площадь общей фигуры.

Площадь неправильного многоугольника

Давайте рассмотрим пример, чтобы лучше понять концепцию.

Найдите площадь неправильного многоугольника ABCDE с данными размерами сторон. (Прием: Разделите многоугольник на два прямоугольника)

Решение:

Чтобы решить данную задачу, разделим данную фигуру на два прямоугольника ABFE и GFDC.