Как найти площадь треугольника через медианы: Нахождение площади через медианы

Медиана равностороннего треугольника – формула

4.6

Средняя оценка: 4.6

Всего получено оценок: 126.

4.6

Средняя оценка: 4.6

Всего получено оценок: 126.

Равносторонний треугольник стоит особняком среди всех фигур: в нем легко можно найти значение всех сторон и углов, так как все углы известны заранее, а найдя одну сторону, можно найти сразу все три. Но именно из-за этих свойств, составители задач любят писать каверзные условия, в которых не всегда можно разобраться с первого раза, например, не всегда можно понять, что такое медиана, потому что человеку проще воспринимать понятие высоты, нежели медианы. Рассмотрим же понятие медианы в равностороннем треугольнике подробно.

Определения

Равносторонний треугольник – это треугольник, все стороны которого равны, а углы по 60 градусов.

Равносторонний треугольник это частный случай равнобедренного, но в равностороннем любую сторону можно считать основанием.

Рис. 1. Равносторонний треугольник.

Из этого следует, что любая высота равностороннего треугольника является медианой и биссектрисой, так как любая высота проводится к стороне, которую можно считать основанием.

Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположно стороны. Медиана также имеет ряд свойств, которые можно использовать в решении задач.

Медианы в треугольнике пересекаются в одной точке и делят эту точку в отношении 2:3, считая от вершины. При этом медианы разбивают треугольник на 6 разновеликих треугольников. Если посмотреть на рисунок, то можно увидеть, что в равностороннем треугольнике каждый из 6 этих треугольников будет прямоугольным.

Формула медианы равностороннего треугольника

Выведем формулу медианы равностороннего треугольника. В равностороннем треугольнике АВС проведем высоту АН. Она же будет являться медианой и высотой. Медиана разобьет треугольник на два прямоугольных: АНС и АНВ. Рассмотрим треугольник АНС.

Рис. 2\over4}}$$

Это и есть формула медианы равностороннего треугольника. С другой стороны, можно воспользоваться тригонометрическими тождествами и вывести еще одну формулу:

$$sin(ACH)={AH\over AC}$$

При этом угол АСН равен 60 градусам. Значит, можно определить синус угла: $$sin(ACH)={\sqrt{3}\over 2}$$

Выразим значение медианы АН

$$АН=sin(ACH)*AC={\sqrt{3}\over2}*AC={\sqrt{3}\over2}*a$$

Вот еще одна формула, характерная для равностороннего треугольника.

Задача

Для закрепления темы решим простую задачу на обратное использование формулы медианы.

В равностороннем треугольнике медиана равна $$20\over{\sqrt{3}}$$. Найти площадь треугольника.

Для нахождения площади воспользуемся классической формулой.

Классическую формулу можно использовать для нахождения площади любого треугольника.

Для нее нам нужно значение стороны и высоты. Высота в равностороннем треугольнике совпадает с медианой, поэтому нужно найти только сторону.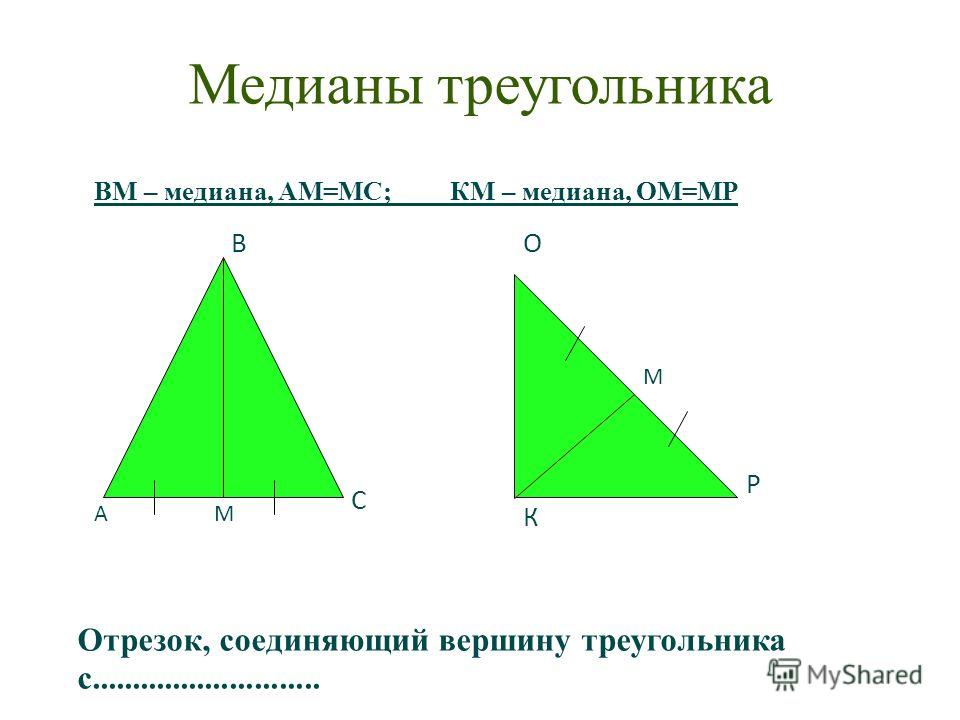

Выразим ее через формулу медианы равностороннего треугольника.

Рис. 3. Рисунок к задаче.

$$m={\sqrt{3}\over2}*a$$

$$a={m\over{\sqrt{3}\over2}}=m*{2\over\sqrt{3}}$$

Подставим в формулу значение медианы:

$$a={20\over\sqrt{3}}*{2\over\sqrt{3}}={40\over3}$$

Посчитаем площадь:

$$S={1\over2}*a*m={1\over2}*{40\over3}*{20 \over\sqrt{3}}={400\over{3\sqrt{3}}}$$

Что мы узнали?

Мы вывели две формулы медианы равностороннего треугольника, дали определения, необходимые для решения задач и решили небольшую задачу для закрепления знаний.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Александр Рудаков

  5/5

Оценка статьи

4.6

Средняя оценка: 4.6

Всего получено оценок: 126.

---

А какая ваша оценка?

Как найти площадь треугольника: прямоугольного, равнобедренного и тд

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel. ru Математика Геометрия Нахождение площади треугольника: формула и примеры

Треугольник – это геометрическая фигура, которая состоит из трех сторон, образованных путем соединения трех точек на плоскости, не принадлежащих одной прямой.

• Общие формулы расчета площади треугольника
  • По основанию и высоте
  • Формула Герона
  • Через две стороны и угол между ними
• Площадь прямоугольного треугольника
• Площадь равнобедренного треугольника
• Площадь равностороннего треугольника
  • Через длину стороны
  • Через высоту
• Примеры задач

Общие формулы расчета площади треугольника

По основанию и высоте

Площадь (S) треугольника равняется половине произведения его основания и высоты, проведенной к нему.

Формула Герона

Для нахождения площади (S) треугольника необходимо знать длины всех его сторон. Считается она следующим образом:

p – полупериметр треугольника:

Через две стороны и угол между ними

Площадь треугольника (S) равняется половине произведения двух его сторон и синуса угла между ними.

Площадь прямоугольного треугольника

Площадь (S) фигуры равняется половине произведения его катетов.

Площадь равнобедренного треугольника

Площадь (S) рассчитывается по следующей формуле:

Площадь равностороннего треугольника

Чтобы найти площадь правильного треугольника (все стороны фигуры равны), необходимо воспользоваться одной из формул ниже:

Через длину стороны

Через высоту

Примеры задач

Задание 1
Найдите площадь треугольника, если одна из его сторон равна 7 см, а высота, проведенная к ней – 5 см.

Решение:
Используем формулу, в которой участвуют длина стороны и высота:
S = 1/2 ⋅ 7 см ⋅ 5 см = 17,5 см².

Задание 2
Найдите площадь треугольника, стороны которого равны 3, 4 и 5 см.

Решение 1:
Воспользуемся формулой Герона:
Полупериметр (p) = (3 + 4 + 5) / 2 = 6 см.

Следовательно, S = √6(6-3)(6-4)(6-5) = 6 см².

Решение 2:

Т.к. треугольник со сторонами 3, 4 и 5 – прямоугольный, его площадь можно посчитать по соответствующей формуле:
S = 1/2 ⋅ 3 см ⋅ 4 см = 6 см².

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

геометрия — Нахождение площади треугольника по длинам медиан

спросил 10 лет, 5 месяцев назад

Изменено 7 лет, 5 месяцев назад

Просмотрено 24к раз

$\begingroup$

Мой вопрос:

В треугольнике ABC длина медианы из вершины A равна $13$, длина медиана из вершины B равна $14$, длина медианы из вершины C равна $15$. Вычислите площадь треугольника ABC.

• геометрия
• треугольники

$\endgroup$

1

$\begingroup$

Одна стратегия, вероятно, не оптимальная, состоит в том, чтобы найти длины сторон, а затем использовать формулу Герона.

Возьмем треугольник $XYZ$ со сторонами $x$, $y$, $z$, как обычно, и пусть $m$ — длина медианы от $Z$ до стороны $XY$, длина которой $з$.

92$.

Теперь, когда у нас есть стороны, мы можем использовать формулу Герона.

$\endgroup$

$\begingroup$

Используйте формулу:

$$A = \frac{4}{3} \sqrt{s \cdot (s_m — m_1) \cdot (s_m — m_2) \cdot (s_m — m_3)} $$

где $m_1$ = 1-я медиана, $m_2$ = 2-я медиана, $m_3$ = 3-я медиана, $s_m = (m_1+m_2+m_3)/2$

Это один из самых простых методов

С уважением Джей Шарма

$\endgroup$

$\begingroup$

Площадь: $$\Delta=\dfrac 43\sqrt {s(s-a)(s-b)(s-c)}$$ Где $a,b$ и $c$ — средние длины, а $s$ — полупериметр.

$\endgroup$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

геометрия — отношение площади треугольника к площади, образованной его медианами

спросил 8 лет, 7 месяцев назад

Изменено 2 года, 6 месяцев назад

Просмотрено 2к раз

$\begingroup$

Каково отношение площади треугольника $ABC$ к площади треугольника, длины сторон которого равны медианам треугольника $ABC$?

Я вижу очевидный метод грубой силы, в котором я могу наложить на фигуру систему координат. Но есть ли лучшее решение?

• геометрия
• конкурс-математика

$\endgroup$

2

$\begingroup$

Пусть $X$, $Y$ и $Z$ — середины сторон. Постройте параллелограмм PYBZ и подключите PC.

По построению PY = BZ = AZ, PY || AZ, а затем PYZA также являются параллелограммом, что приводит к AP || ЗЫ || XC и AP = XC, и, в свою очередь, параллелограмм APCX. Таким образом, PC = AX и стороны треугольника PCZ являются медианами треугольника ABC.

Параллелограмм PYZA также дает AQ = QY = $\frac14$AC и затем

$$\frac{Area_{PCZ}}{Area_{ABC}}=\frac{Area_{QCZ}}{Area_{AZC} }=\frac{QC}{AC} = \frac34 $$

$\endgroup$

$\begingroup$

Площадь треугольника с учетом его медиан равна $(4/3)\sqrt{m(m-m_a)(m-m_b)(m-m_b)}$ а площадь треугольника, образованного медианами первого треугольника, по формуле Герона равна $\sqrt{m(m-m_a)(m-m_b)(m-m_b)}$.