Как найти по графику множество значений функции: Как найти множество значений функции по графику. Тема урока «Множество значений функции в задачах ЕГЭ

График линии с использованием таблицы значений

Поиск

Наиболее фундаментальной стратегией построения графика является использование таблицы значений . Цель состоит в том, чтобы выбрать любые значения x и подставить эти значения в данное уравнение, чтобы получить соответствующие значения y. Не существует правильного или неправильного способа выбора этих значений x. По мере развития своих навыков вы научитесь выбирать подходящие значения x в зависимости от того, как вы хотите отобразить график.

Как это выглядит? Есть два способа настроить таблицу значений. Если таблица представлена ​​горизонтально, верхняя строка будет содержать все значения x, а нижняя строка будет содержать соответствующее значение y для каждого x. С другой стороны, когда таблица отображается вертикально, левый столбец содержит значения x, а правый столбец — значения y.

---

Примеры построения графика с помощью таблицы значений

Давайте рассмотрим несколько примеров, чтобы понять, как это работает.

Пример 1:

Нарисуйте уравнение линии ниже, используя таблицу значений.

Неважно, какую таблицу значений использовать. Для этого мы будем использовать горизонтальный формат. Следующим шагом является выбор значений x.

Нет неправильного выбора значений x. Имейте в виду, что нам нужно как минимум две точки для построения линии. Это означает, что можно превысить минимальные требования для повышения точности. Что касается меня, я всегда рисую три точки или больше. Причина в том, что если линия не проходит через три точки, это говорит мне, что я допустил ошибку в своих вычислениях. Это дает мне возможность перепроверить свою работу.

Чтобы решить, какие значения x выбрать, я предлагаю вам посмотреть на размер нашей оси xy. В частности, посмотрите на доступные числа по горизонтальной оси.

Предположим, ваш учитель дает вам эту ось xy на вашем рабочем листе.

Если мы хотим, чтобы график отображался в пределах этой оси xy, имеет смысл выбрать значения x между {- 4} и { + 4}.

Всегда старайтесь включать ноль в одно из ваших значений x, потому что это упростит ваши вычисления. Итак, мы выбрали следующие x-координаты и соответственно поместили их в таблицу.

Следующим очевидным шагом является вычисление значения y для каждого x в таблице. Для этого мы будем использовать данное уравнение прямой, потому что это формула, которая дает нам прямую информацию о том, как получить значение y при заданном значении x. Мы собираемся использовать формулу три раза, так как у нас есть три значения x.

• x = — 1

• x = 0

• x = 1

Давайте соберем эти выходные значения и поместим их в строку, где расположены значения y.

Нанесите три точки на оси xy.

С помощью линейки (линейки) соедините точки, чтобы увидеть график линии. Вот и все!

---

Пример 2: Нарисуйте уравнение линии ниже, используя таблицу значений.

Первое, что бросается в глаза в этой задаче, это то, что коэффициент при «х-члене» является дробным.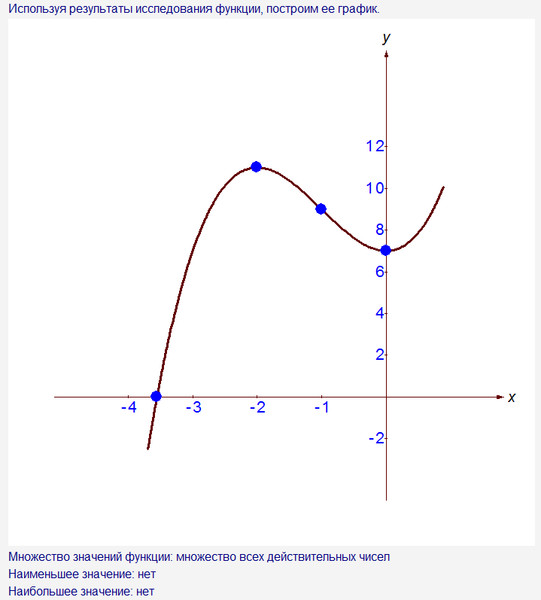 Здесь нам нужно быть немного осторожными, так как мы можем легко получить дробные значения y. Точки с дробными координатами могут быть сложными при построении их на оси.

В этой задаче мы хотим, чтобы значения x при умножении на коэффициент — {1 \over 2} давали нам положительные или отрицательные целых числа . Поскольку знаменатель дроби равен 2, значения x должны быть кратны 2. Верно? Опять же, не забывайте всегда включать ноль в качестве одного из ваших входных значений.

В этом примере мы будем использовать вертикальный формат значений таблицы. Для большей практики давайте возьмем пять входных значений x.

Найдите значение y для каждого x, используя уравнение.

• x = — 4

• x = — 2

• x = 0

• x = 2

• x = 4

. в соответствующем месте в таблице значений.

Теперь пришло время нанести каждую точку на оси координат и соединить их, чтобы показать график линии. Готово!

---

Пример 3: Нарисуйте уравнение линии ниже, используя таблицу значений.

Я вижу, что у нас есть дробный коэффициент x со знаменателем 3. Это означает, что наш выбор координат x будет включать ноль (как всегда!) и несколько кратных 3.

Вот выбранные значения x для нашего таблица значений.

Найдем значение y для каждого x, используя данное уравнение y = {2 \over 3}x + 1.

• x = — 6

• x = — 3

• x3 = 1 0

• х = 3

• x = 6

Поместите эти значения y вместе со значениями x в таблицу.

Нанесите точки на декартовой плоскости и соедините точки, чтобы показать график линии.

---

Вас также могут заинтересовать:

Три способа построения графика линии
График линии с использованием наклона и точки пересечения по оси Y
График линии с использованием точек пересечения по осям X и Y

3.

6 Графики функций — средний уровень алгебры 2e

Цели обучения

К концу этого раздела вы сможете:

• Используйте тест вертикальной линии
• Определение графиков основных функций
• Чтение информации с графика функции

Приготовься 3.16

Прежде чем приступить к работе, пройдите этот тест на готовность.

Оценка: ⓐ 2323 ⓑ 32,32.
Если вы пропустили эту проблему, просмотрите пример 1.5.

Приготовься 3.17

Оценка: ⓐ |7||7| ⓑ |−3|.|−3|.
Если вы пропустили эту проблему, просмотрите пример 1.14.

Приготовься 3.18

Оценка: ⓐ 44 ⓑ 16.16.
Если вы пропустили эту проблему, просмотрите пример 1.41.

Используйте тест вертикальной линии

В предыдущем разделе мы узнали, как определить, является ли отношение функцией. Отношения, которые мы рассматривали, выражались в виде набора упорядоченных пар, отображения или уравнения.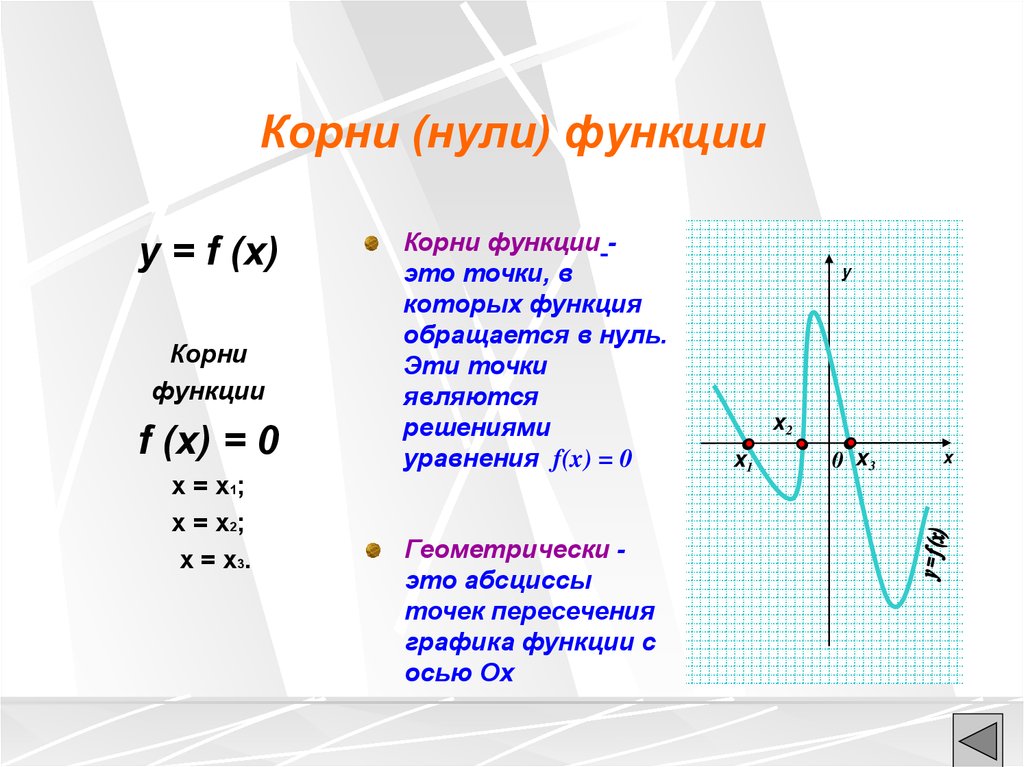 Теперь мы рассмотрим, как определить, является ли график графиком функции.

Упорядоченная пара (x,y)(x,y) является решением линейного уравнения, если уравнение является истинным утверждением, когда x — и y -значения упорядоченной пары подставляются в уравнение.

График линейного уравнения представляет собой прямую линию, каждая точка на которой является решением уравнения, а каждое решение этого уравнения является точкой на этой прямой.

На рисунке 3.14 мы видим, что на графике уравнения y=2x−3,y=2x−3 для каждого значения x имеется только одно значение y , как показано в прилагаемой таблице. .

Рисунок 3,14

Отношение является функцией, если каждый элемент домена имеет ровно одно значение в диапазоне. Таким образом, отношение, определяемое уравнением y=2x−3y=2x−3, является функцией.

Если мы посмотрим на график, то увидим, что каждая вертикальная пунктирная линия пересекает линию только в одной точке.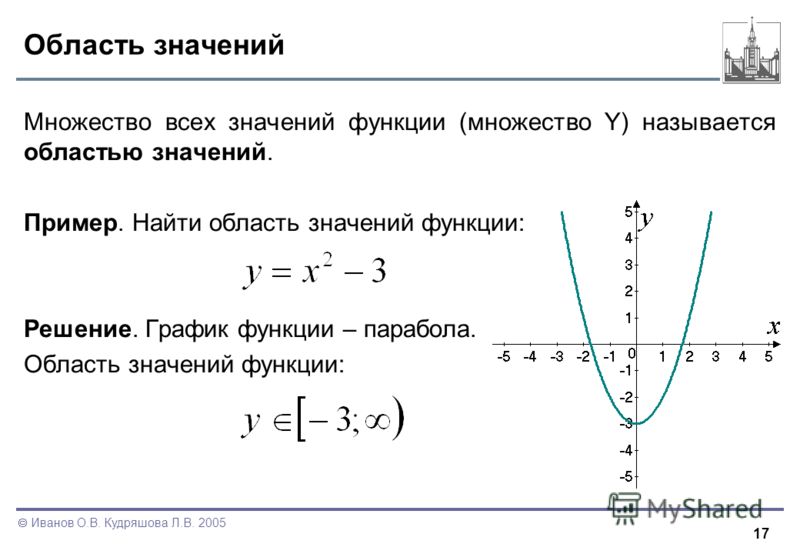 Это имеет смысл, поскольку в функции для каждого значения x существует только одно значение y .

Если вертикальная линия коснется графика дважды, значение x будет сопоставлено с двумя значениями

y , и поэтому график не будет представлять функцию.

Это приводит нас к тесту вертикальной линии. Набор точек в прямоугольной системе координат называется графиком функции, если каждая вертикальная линия пересекает график не более чем в одной точке. Если любая вертикальная линия пересекает график более чем в одной точке, график не представляет функцию.

Проверка вертикальной линии

Набор точек в прямоугольной системе координат является графиком функции, если каждая вертикальная линия пересекает график не более чем в одной точке.

Если любая вертикальная линия пересекает график более чем в одной точке, график не представляет функцию.

Пример 3,51

Определить, является ли каждый график графиком функции.

Решение

ⓐ Поскольку любая вертикальная линия пересекает график не более чем в одной точке, график является графиком функции.

ⓑ Одна из вертикальных линий, показанных на графике, пересекает его в двух точках. Этот график не представляет функцию.

Попробуй 3.101

Определить, является ли каждый график графиком функции.

Попробуй 3.102

Определить, является ли каждый график графиком функции.

Определение графиков основных функций

Мы использовали уравнение y=2x−3y=2x−3 и его график при разработке теста вертикальной линии. Мы сказали, что отношение, определяемое уравнением y=2x−3y=2x−3, является функцией.

Мы можем записать это как в обозначении функций как f(x)=2x−3.f(x)=2x−3. Это по-прежнему означает то же самое. График функции — это график всех упорядоченных пар (x,y)(x,y), где y=f(x).

y=f(x). Таким образом, мы можем записать упорядоченные пары как (x,f(x)).(x,f(x)). Это выглядит иначе, но график будет таким же.

Сравните график y=2x−3y=2x−3, ранее показанный на рис. 3.14, с графиком f(x)=2x−3f(x)=2x−3, показанным на рис. 3.15. Ничего не изменилось, кроме обозначения.

Рисунок 3.15

График функции

График функции – это график всех ее упорядоченных пар (x,y)(x,y) или, используя функциональную запись, (x,f(x))(x,f(x)), где y= е (х). у = е (х).

fимя функцииxx-координата упорядоченной парыf(x)y-координата упорядоченной парыfимя функцииxx-координата упорядоченной парыf(x)y-координата упорядоченной пары

По мере того, как мы продвигаемся вперед в нашем исследовании, полезно ознакомиться с графиками нескольких основных функций и уметь их идентифицировать.

Благодаря нашей предыдущей работе мы знакомы с графиками линейных уравнений. Процесс, который мы использовали, чтобы решить, является ли y=2x−3y=2x−3 функцией, применим ко всем линейным уравнениям.

Все невертикальные линейные уравнения являются функциями. Вертикальные линии не являются функциями, поскольку значение x имеет бесконечно много значений y .

Мы записали линейные уравнения в нескольких формах, но здесь нам будет наиболее полезно использовать форму линейного уравнения, основанную на пересечении наклона. Форма линейного уравнения с пересечением наклона имеет вид y=mx+b.y=mx+b. В функциональном обозначении эта линейная функция принимает вид f(x)=mx+bf(x)=mx+b, где m — наклон линии, а b — точка пересечения y .

Домен — это множество всех действительных чисел, а диапазон — это также множество всех действительных чисел.

Линейная функция

Мы будем использовать методы построения графиков, которые мы использовали ранее, для построения графиков основных функций.

Пример 3,52

График: f(x)=−2x−4.f(x)=−2x−4.

Решение

	f(x)=−2x−4f(x)=−2x−4
Мы признаем это как линейную функцию.
Найти наклон и у -пересечение.	м=-2м=-2 б=-4б=-4
График с использованием точки пересечения наклона.

Попробуй 3.103

График: f(x)=−3x−1f(x)=−3x−1

Попробуй 3.104

График: f(x)=−4x−5f(x)=−4x−5

Следующая функция, график которой мы рассмотрим, называется постоянной функцией, и ее уравнение имеет вид f(x)=b,f(x)=b, где b — любое действительное число. Если мы заменим f(x)f(x) на y, мы получим y=b.y=b. Мы узнаем это как горизонтальную линию, y — точка пересечения которой равна б . График функции f(x)=b,f(x)=b также представляет собой горизонтальную линию, точка пересечения y которой равна b .

Обратите внимание, что для любого действительного числа, которое мы вводим в функцию, значение функции будет b . Это говорит нам, что диапазон имеет только одно значение, b .

Постоянная функция

Пример 3,53

График: f(x)=4.f(x)=4.

Решение

	f(x)=4f(x)=4
Мы признаем это постоянной функцией.
График будет представлять собой горизонтальную линию, проходящую через (0,4).(0,4).

Попробуй 3.105

График: f(x)=−2.f(x)=−2.

Попробуй 3.106

График: f(x)=3.f(x)=3.

Функция тождества f(x)=xf(x)=x является частным случаем линейной функции. Если мы запишем это в виде линейной функции, f(x)=1x+0,f(x)=1x+0, мы увидим, что наклон равен 1, а г — перехват равен 0.

Идентификационная функция

Следующая функция, которую мы рассмотрим, не является линейной функцией. Таким образом, график не будет линией. Единственный метод, который у нас есть, — это построение графика этой функции. Поскольку это незнакомая функция, мы обязательно выбираем несколько положительных и отрицательных значений, а также 0 для наших значений x.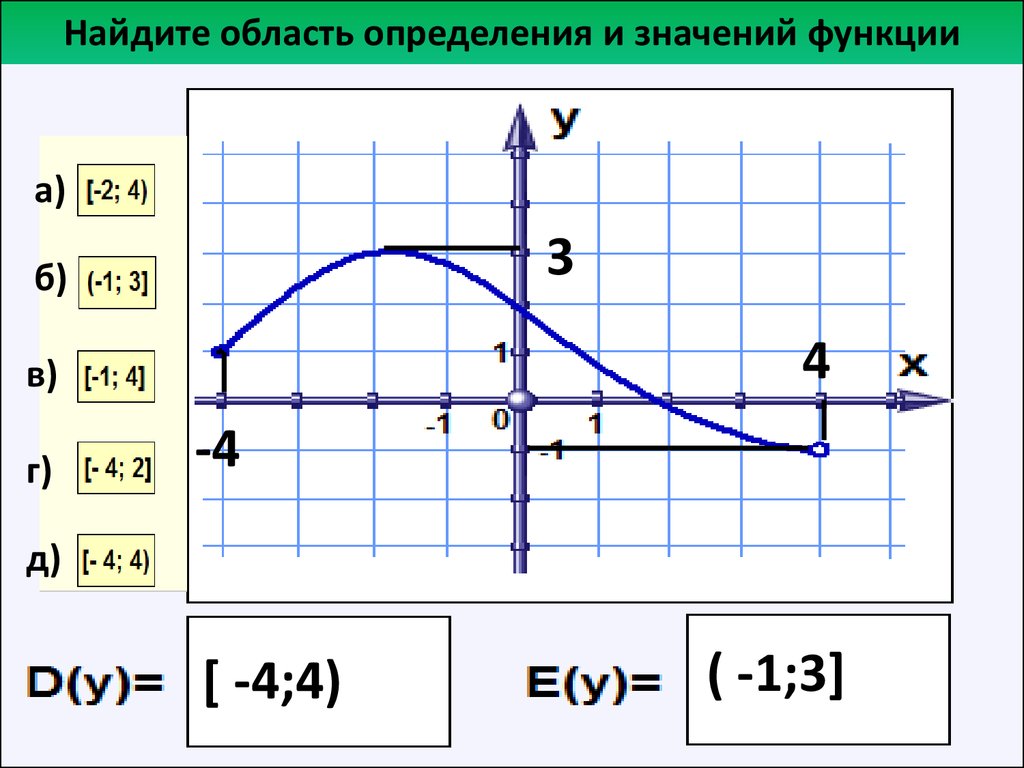

Пример 3,54

График: f(x)=x2.f(x)=x2.

Решение

Выбираем x -значения. Мы подставляем их и затем создаем диаграмму, как показано на рисунке.

Попробуй 3.107

График: f(x)=x2.f(x)=x2.

Попробуй 3.108

f(x)=−x2f(x)=−x2

Глядя на результат в примере 3.54, мы можем обобщить особенности функции квадрата. Назовем этот график параболой. Поскольку мы рассматриваем домен, обратите внимание, что любое действительное число может использоваться как значение x . Домен состоит из всех действительных чисел.

Диапазон не все действительные числа. Обратите внимание, что график состоит из значений и , которые никогда не опускаются ниже нуля. Это имеет смысл, так как квадрат любого числа не может быть отрицательным. Итак, диапазон функции квадрата — это все неотрицательные действительные числа.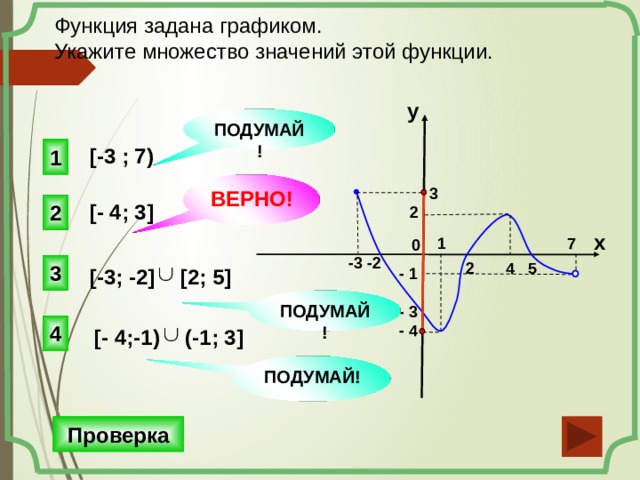

Квадратная функция

Следующая функция, которую мы рассмотрим, также не является линейной функцией, поэтому график не будет линией. Мы снова будем использовать точечный график и обязательно выберем несколько положительных и отрицательных значений, а также 0 для наших x -значения.

Пример 3,55

График: f(x)=x3.f(x)=x3.

Решение

Мы выбираем x -значений. Мы подставляем их и затем создаем диаграмму.

Попробуй 3.109

График: f(x)=x3.f(x)=x3.

Попробуй 3.110

График: f(x)=−x3.f(x)=−x3.

Глядя на результат в примере 3.55, мы можем обобщить особенности функции куба. Поскольку мы рассматриваем домен, обратите внимание, что любое действительное число может использоваться как 9.0166 x -значение. Домен состоит из всех действительных чисел.

Диапазон состоит из действительных чисел. Это имеет смысл, поскольку куб любого ненулевого числа может быть положительным или отрицательным. Итак, диапазон функции куба — это все действительные числа.

Функция куба

Следующая функция, которую мы рассмотрим, не возводит входные значения в квадрат или куб, а извлекает квадратный корень из этих значений.

Давайте построим график функции f(x)=xf(x)=x, а затем суммируем особенности функции. Помните, что мы можем извлечь квадратный корень только из неотрицательных действительных чисел, поэтому нашей областью определения будут неотрицательные действительные числа.

Пример 3,56

е(х)=хf(х)=х

Решение

Мы выбираем x -значений. Поскольку мы будем извлекать квадратный корень, мы выбираем числа, которые являются полными квадратами, чтобы упростить нашу работу. Мы подставляем их и затем создаем диаграмму.

Попробуй 3.111

График: f(x)=x.f(x)=x.

Попробуй 3.112

График: f(x)=−x.f(x)=−x.

Функция квадратного корня

Наша последняя базовая функция — функция абсолютного значения, f(x)=|x|.f(x)=|x|. Имейте в виду, что абсолютное значение числа — это его расстояние от нуля. Поскольку мы никогда не измеряем расстояние как отрицательное число, мы никогда не получим отрицательное число в диапазоне.

Пример 3,57

График: f(x)=|x|.f(x)=|x|.

Решение

Мы выбираем x -значений. Мы подставляем их и затем создаем диаграмму.

Попробуй 3.113

График: f(x)=|x|.f(x)=|x|.

Попробуй 3.114

График: f(x)=−|x|.f(x)=−|x|.

Функция абсолютного значения

Чтение информации из графика функции

В науке и бизнесе данные часто собираются, а затем отображаются в виде графиков.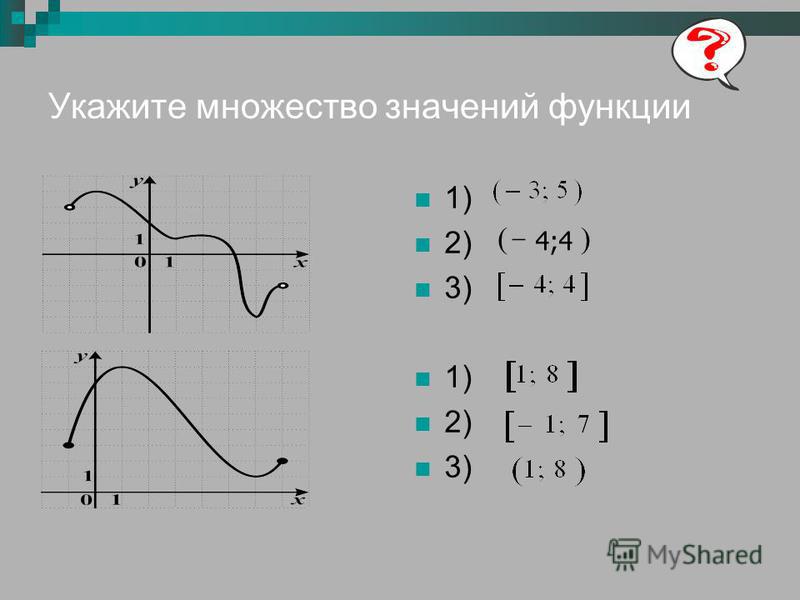 График анализируется, из него извлекается информация, а затем часто из данных делаются прогнозы.

Мы начнем с чтения домена и диапазона функции с ее графика.

Помните, что домен — это набор всех значений x в упорядоченных парах в функции. Чтобы найти домен, мы смотрим на график и находим все значения x , которые имеют соответствующее значение на графике. Следуйте за значением x вверх или вниз по вертикали. Если вы нажмете на график функции, то x находится в домене.

Помните, что диапазон — это набор всех значений y в упорядоченных парах в функции. Чтобы найти диапазон, мы смотрим на график и находим все значения и , которые имеют соответствующее значение на графике. Следуйте за значением y влево или вправо по горизонтали. Если вы нажмете на график функции, то y находятся в диапазоне.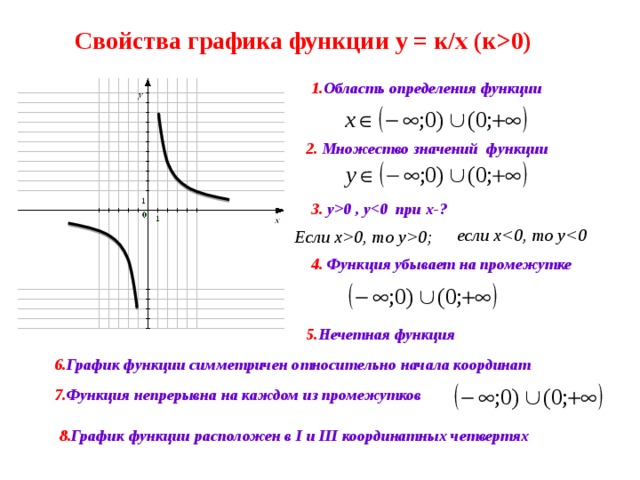

Пример 3,58

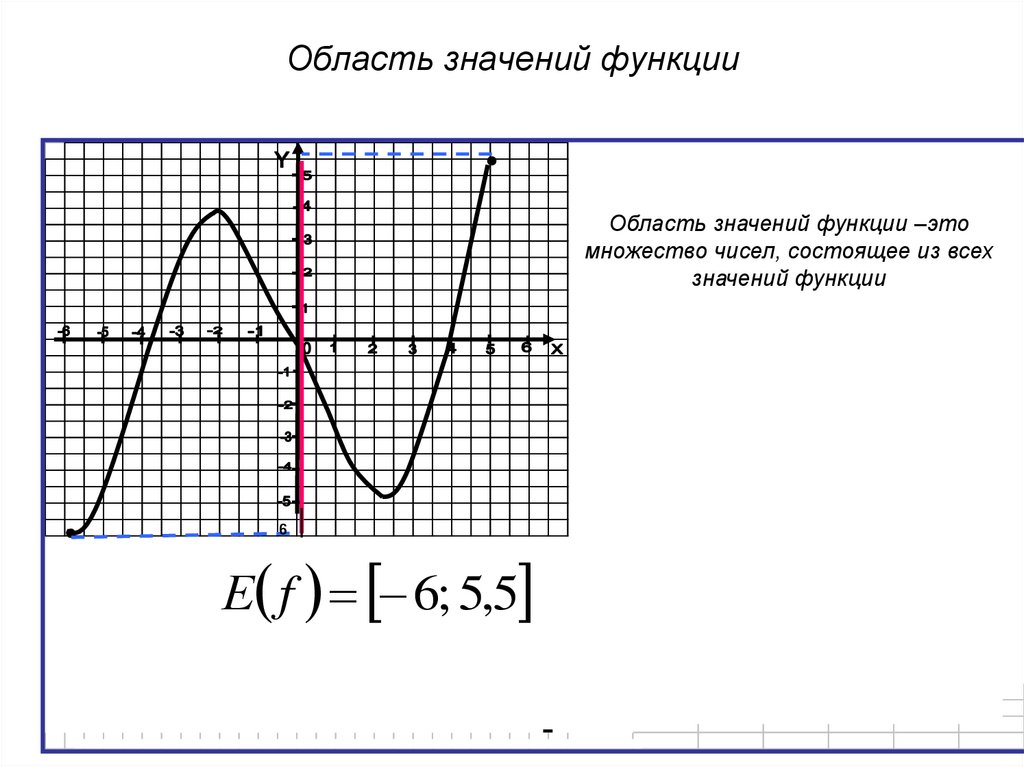
Используйте график функции, чтобы найти ее домен и диапазон. Запишите домен и диапазон в интервальной нотации.

Решение

Чтобы найти домен, мы смотрим на график и находим все значения x , которые соответствуют точке на графике. Домен выделен красным цветом на графике. Домен [−3,3].[−3,3].

Чтобы найти диапазон, мы смотрим на график и находим все значения y , которые соответствуют точке на графике. Диапазон выделен синим цветом на графике. Диапазон: [−1,3].[−1,3].

Попробуй 3.115

Используйте график функции, чтобы найти ее домен и диапазон. Запишите домен и диапазон в интервальной нотации.

Попробуй 3.116

Используйте график функции, чтобы найти ее домен и диапазон. Запишите домен и диапазон в интервальной нотации.

Сейчас мы прочитаем информацию с графика, который вы можете увидеть на будущих уроках математики.

Пример 3,59

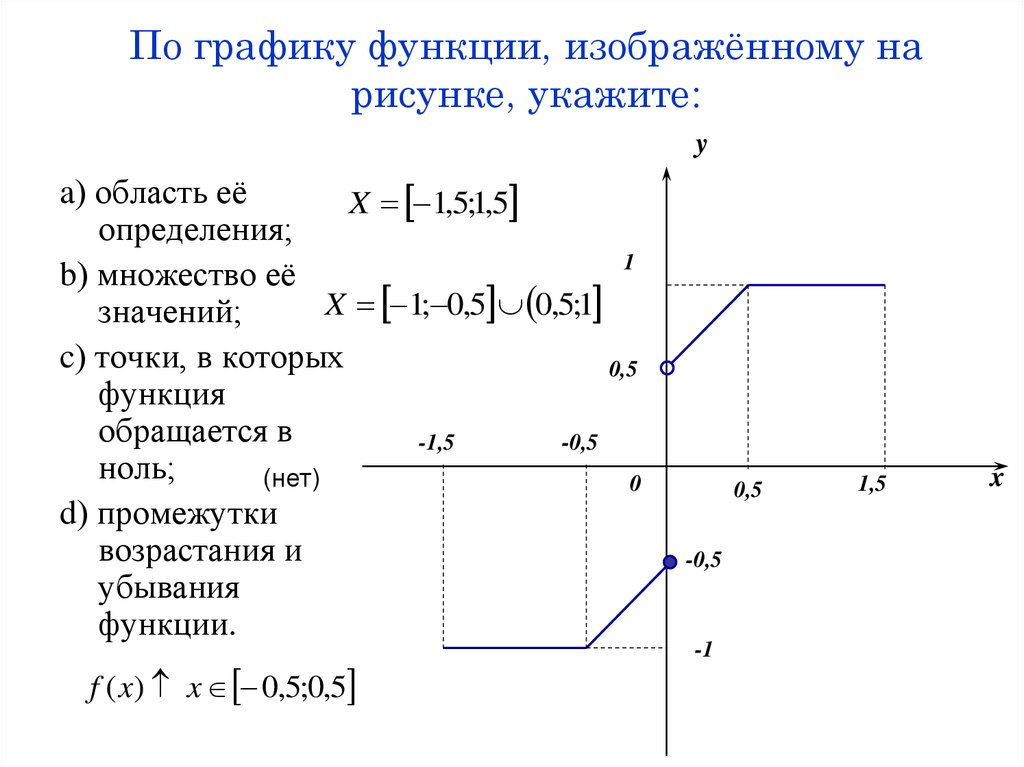
Используйте график функции, чтобы найти указанные значения.

ⓐ Найти: f(0).f(0).
ⓑ Найти: f(32π).f(32π).
ⓒ Найти: f(−12π).f(−12π).
ⓓ Найдите значения для x , когда f(x)=0.f(x)=0.
ⓔ Найдите x -перехватов.
ⓕ Найдите y -перехваты.
ⓖ Найдите домен. Запишите его в интервальной записи.
ⓗ Найдите диапазон. Запишите его в интервальной записи.

Решение

ⓐ Когда x=0,x=0, функция пересекает ось y в точке 0. Таким образом, f(0)=0.f(0)=0.
ⓑ Когда x=32π,x=32π, y -значение функции равно −1,−1. Итак, f(32π)=−1.f(32π)=−1.
ⓒ Когда x=−12π,x=−12π, y -значение функции равно −1,−1. Итак, f(−12π)=−1.f(−12π)=−1.
ⓓ Функция равна 0 в точках (−2π,0),(−π,0),(0,0),(π,0),(2π,0). (−2π,0),( −π,0),(0,0),(π,0),(2π,0). x -значений, когда f(x)=0f(x)=0 равны −2π,−π,0,π,2π.−2π,−π,0,π,2π.
ⓔ Перехваты x происходят, когда y=0.y=0. Таким образом, перехваты x происходят, когда f(x)=0.f(x)=0. x -перехватов: (−2π,0),(−π,0),(0,0),(π,0),(2π,0).(−2π,0),(−π, 0),(0,0),(π,0),(2π,0).
ⓕ Перехваты y происходят, когда x=0.x=0. Таким образом, y -перехватов происходят в точке f(0).f(0). Перехват y равен (0,0).(0,0).
ⓖ Эта функция имеет значение для всех значений х . Таким образом, область в интервальной записи равна (−∞,∞)(−∞,∞)
ⓗ Значения этой функции, или y -значений идут от −1−1 до 1. Следовательно, диапазон в интервальной записи равно [−1,1].[−1,1].

Попробуй 3.

117

Используйте график функции, чтобы найти указанные значения.

ⓐ Найти: f(0).f(0).
ⓑ Найти: f(12π).f(12π).
ⓒ Найти: f(−32π).f(−32π).
ⓓ Найдите значения для x , когда f(x)=0.f(x)=0.
ⓔ Найдите x -перехваты.
ⓕ Найдите y -перехваты.
ⓖ Найдите домен. Запишите его в интервальной записи.
ⓗ Найдите диапазон. Запишите его в интервальной записи.

Попробуй 3.118

Используйте график функции, чтобы найти указанные значения.

ⓐ Найти: f(0).f(0).
ⓑ Найти: f(π).f(π).
ⓒ Найти: f(−π).f(−π).
ⓓ Найдите значения для x , когда f(x)=0.f(x)=0.
ⓔ Найдите x -перехватов.
ⓕ Найдите y -перехваты.
ⓖ Найдите домен. Запишите его в интервальной записи.
ⓗ Найдите диапазон. Запишите его в интервальной записи.

СМИ

Получите доступ к этому онлайн-ресурсу для получения дополнительных инструкций и практики с графиками функций.

• Найти домен и диапазон

Раздел 3.6 Упражнения

Практика ведет к совершенству

Использовать тест вертикальной линии

В следующих упражнениях определите, является ли каждый график графиком функции.

337.

ⓐ

ⓑ

338.

ⓐ

ⓑ

339.

ⓐ

ⓑ

340.

ⓐ

ⓑ

Определение графиков основных функций

В следующих упражнениях ⓐ нарисуйте график каждой функции ⓑ укажите ее область определения и диапазон. Запишите домен и диапазон в интервальной нотации.

341.

f(x)=3x+4f(x)=3x+4

342.

f(x)=2x+5f(x)=2x+5

343.

f(x)=−x−2f(x)=−x−2

344.

f(x)=−4x−3f(x)=−4x−3

345.

f(x)=−2x+2f(x)=−2x+2

346.

f(x)=−3x+3f(x)=−3x+3

347.

f(x)=12x+1f(x)=12x+1

348.

f(x)=23x−2f(x)=23x−2

349.

f(x)=5f(x)=5

350.

f(x)=2f(x)=2

351.

f(x)=−3f(x)=−3

352.

f(x)=−1f(x)=−1

353.

f(x)=2xf(x)=2x

354.

f(x)=3xf(x)=3x

355.

f(x)=−2xf(x)=−2x

356.

f(x)=−3xf(x)=−3x

357.

f(x)=3x2f(x)=3×2

358.

f(x)=2x2f(x)=2×2

359.

f(x)=−3x2f(x)=−3×2

360.

f(x)=−2x2f(x)=−2×2

361.

f(x)=12x2f(x)=12×2

362.

f(x)=13x2f(x)=13×2

363.

f(x)=x2−1f(x)=x2−1

364.

f(x)=x2+1f(x)=x2+1

365.

f(x)=−2x3f(x)=−2×3

366.

f(x)=2x3f(x)=2×3

367.

f(x)=x3+2f(x)=x3+2

368.

f(x)=x3−2f(x)=x3−2

369.

f(x)=2xf(x)=2x

370.

f(x)=−2xf(x)=−2x

371.

f(x)=x−1f(x)=x−1

372.

f(x)=x+1f(x)=x+1

373.

е (х) = 3 | х | е (х) = 3 | х |

374.

f(x)=−2|x|f(x)=−2|x|

375.

f(x)=|x|+1f(x)=|x|+1

376.

f(x)=|x|−1f(x)=|x|−1

Чтение информации из графика функции

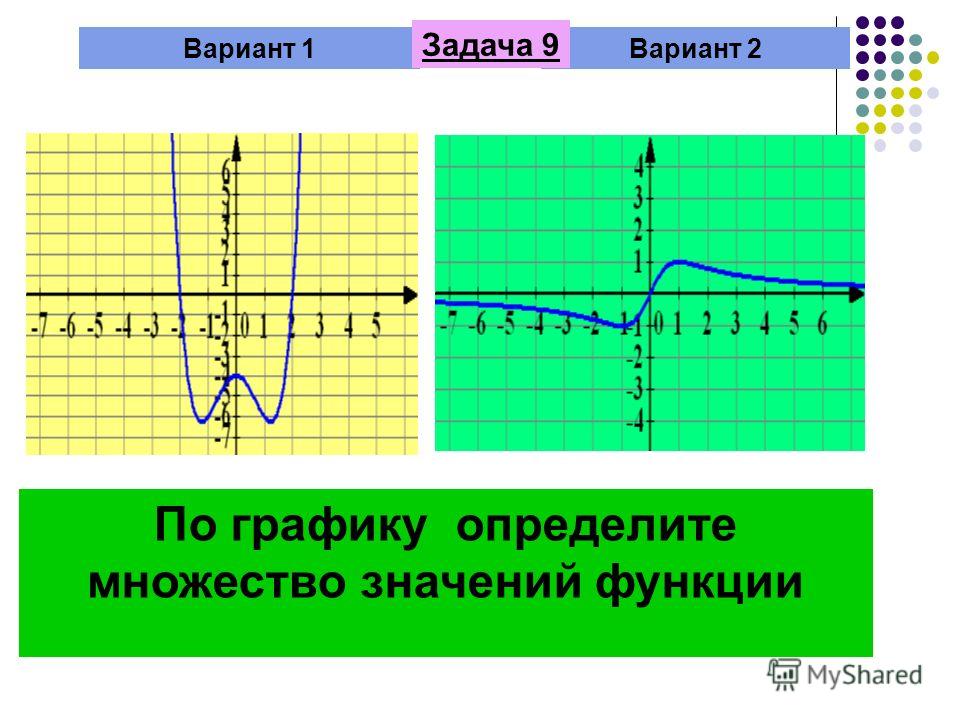
В следующих упражнениях используйте график функции, чтобы найти ее область определения и диапазон. Запишите домен и диапазон в интервальной нотации.

377.

378.

379.

380.

381.

382.

В следующих упражнениях используйте график функции, чтобы найти указанные значения.

383.

ⓐ Найти: f(0).f(0).
ⓑ Найти: f(12π).f(12π).
ⓒ Найти: f(−32π).f(−32π).
ⓓ Найдите значения для x , когда f(x)=0.f(x)=0.
ⓔ Найдите x -перехватов.
ⓕ Найдите y -перехваты.
ⓖ Найдите домен. Запишите его в интервальной записи.
ⓗ Найдите диапазон. Запишите его в интервальной записи.

384.

ⓐ Найти: f(0).f(0).
ⓑ Найти: f(π).f(π).
ⓒ Найти: f(−π).f(−π).
ⓓ Найдите значения для x , когда f(x)=0. f(x)=0.
ⓔ Найди x — перехваты.
ⓕ Найдите y -перехваты.
ⓖ Найдите домен. Запишите его в интервальной записи.
ⓗ Найдите диапазон. Запишите его в интервальной нотации

.

385.

ⓐ Найти: f(0).f(0).
ⓑ Найти: f(−3).f(−3).
ⓒ Найти: f(3).f(3).
ⓓ Найдите значения для x , когда f(x)=0.f(x)=0.
ⓔ Найдите x -перехватов.
ⓕ Найдите y -перехваты.
ⓖ Найдите домен. Запишите его в интервальной записи.
ⓗ Найдите диапазон. Запишите его в интервальной записи.

386.

ⓐ Найти: f(0).f(0).
ⓑ Найдите значения для x , когда f(x)=0.f(x)=0.
ⓒ Найдите x -перехватов.
ⓓ Найдите и -перехваты.