алгоритм и примеры решений. Производная функции
Вычисление производной часто встречается в заданиях ЕГЭ. Данная страница содержит список формул для нахождения производных.
Правила дифференцирования
- (k⋅ f(x))′=k⋅ f ′(x).
- (f(x)+g(x))′=f′(x)+g′(x).
- (f(x)⋅ g(x))′=f′(x)⋅ g(x)+f(x)⋅ g′(x).
- Производная сложной функции. Если y=F(u), а u=u(x), то функция y=f(x)=F(u(x)) называется сложной функцией от x. Равна y′(x)=Fu′⋅ ux′.
- Производная неявной функции. Функция y=f(x) называется неявной функцией, заданной соотношением F(x,y)=0, если F(x,f(x))≡0.
- Производная обратной функции. Если g(f(x))=x, то функция g(x) называется обратной функцией для функции y=f(x).
- Производная параметрически заданной функции. Пусть x и y заданы как функции от переменной t: x=x(t), y=y(t). Говорят, что y=y(x) параметрически заданная функция на промежутке x∈
(a;b), если на этом промежутке уравнение x=x(t) можно выразить в виде t=t(x) и определить функцию y=y(t(x))=y(x).

- Производная степенно-показательной функции. Находится путем логарифмирования по основанию натурального логарифма.
Формулы 3 и 5 докажите самостоятельно.
ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
Применяя общий способ нахождения производной с помощью предела можно получить простейшие формулы дифференцирования. Пусть u=u(x),v=v(x) – две дифференцируемые функции от переменной x .
Формулы 1 и 2 докажите самостоятельно.
Доказательство формулы 3 .
Пусть y = u(x) + v(x). Для значения аргумента x +Δx имеем y (x +Δx )=u (x +Δx ) + v (x +Δx ).
Δy =y (x +Δx ) – y(x) = u(x +Δx) + v(x +Δx) – u(x) – v(x) = Δu +Δv .
Следовательно,
Доказательство формулы 4 .
Пусть y=u(x)·v(x). Тогда y (x +Δx )=u (x +Δx )·v (x +Δx ), поэтому
Δy =u (x +Δx )·v (x +Δx ) – u (x )·v (x ).
Заметим, что поскольку каждая из функций u и v дифференцируема в точке x , то они непрерывны в этой точке, а значит u (x +Δx )→u(x), v (x +Δx )→v(x) , при Δx →0.
Поэтому можем записать
На основании этого свойства можно получить правило дифференцирования произведения любого числа функций.
Пусть, например, y=u·v·w. Тогда,
y » = u «·(v· w) + u ·(v ·w) » = u «·v ·w + u ·(v «·w +v ·w «) = u «·v ·w + u ·v «·w + u·v ·w «.
Доказательство формулы 5 .
При доказательстве
воспользовались тем, что v(x+ Δx) →v(x) при Δx →0.
Примеры .
ТЕОРЕМА О ПРОИЗВОДНОЙ СЛОЖНОЙ ФУНКЦИИ
Пусть y = f(u), а u = u (x ). Получаем функцию y , зависящую от аргумента x : y = f(u(x)). Последняя функция называется функцией от функции или сложной функцией .
Областью определения функции y = f(u(x)) является либо вся область определения функции u =u (x ) либо та ее часть, в которой определяются значения u , не выходящие из области определения функции y = f(u) .
Операция «функция от функции» может проводиться не один раз, а любое число раз.
Установим правило дифференцирования сложной функции.
Теорема. Если функция u = u (x ) имеет в некоторой точке x 0 производную и принимает в этой
точке значение u 0 = u (x 0 ), а функция y= f(u) имеет
в точке u 0 производную y » u = f «(u 0 ), то сложная функция y = f(u(x)) в
указанной точке x 0 тоже имеет производную, которая равна y » x = f «(u 0 )·u «(x 0 ), где вместо u должно быть подставлено выражение u = u (x ).
Таким образом, производная сложной функции равна произведению производной данной функции по промежуточному аргументу u на производную промежуточного аргумента по x .
Доказательство . При фиксированном значении х 0 будем иметь u 0 =u (x 0), у 0 =f(u 0 ). Для нового значения аргумента x 0 +Δ
Δu = u (x 0 + Δx ) – u (x 0), Δy =f (u 0 +Δu ) – f (u 0 ).
Т.к. u – дифференцируема в точке x 0 , то u – непрерывна в этой точке. Поэтому при Δx →0 Δu →0. Аналогично при Δu →0 Δy →0.
По условию . Из этого соотношения, пользуясь определением предела, получаем (при Δu →0)
где α→0 при Δu →0, а, следовательно, и при Δx →0.
Перепишем это равенство в виде:
Δy = y » u Δu +α·Δu .
Полученное равенство
справедливо и при Δu =0 при произвольном
α, так как оно превращается в
тождество 0=0. При Δu =0 будем полагать α=0. Разделим все члены
полученного равенства на Δx
При Δu =0 будем полагать α=0. Разделим все члены
полученного равенства на Δx
.
По условию . Поэтому, переходя к пределу при Δx →0, получим y » x = y » u ·u » x . Теорема доказана.
Итак, чтобы продифференцировать сложную функцию y = f(u(x)), нужно взять производную от «внешней» функции f , рассматривая ее аргумент просто как переменную, и умножить на производную от «внутренней» функции по независимой переменной.
Если функцию y=f(x) можно представить в виде y=f(u), u=u(v), v=v(x), то нахождение производной y » x осуществляется последовательным применением предыдущей теоремы.
По доказанному правилу имеем y » x = y » u ·u » x . Применяя эту же теорему для u » x получаем , т.е.
y » x = y » x · u » v · v » x = f » u (u )·u » v (v )·v » x (x ).
Примеры.
ПОНЯТИЕ ОБРАТНОЙ ФУНКЦИИ
Начнем с примера. Рассмотрим
функцию
Рассмотрим
функцию
Прежде чем перейти к общему случаю, введем определения.
Функция y = f(x) называется возрастающей на некотором отрезке, если большему значению аргумента x из этого отрезка соответствует большее значение функции, т.е. если x 2 >x 1 , то f(x 2 ) > f(x 1 ).
Аналогично функция называется убывающей , если меньшему значению аргумента соответствует большее значение функции, т.е. еслих 2 х 1 , то f(x 2 ) > f(х
1 ).
Итак, пусть дана возрастающая или убывающая функция y= f(x) , определенная на некотором отрезке [a ; b ]. Для определенности будем рассматривать возрастающую функцию (для убывающей все аналогично).
Рассмотрим два различных значения х 1 и х 2 . Пусть y 1 =f(x 1 ), y 2 =f(x 2 ). Из определения возрастающей функции следует, что если x 1 x 2 , то у 1 у 2 . Следовательно, двум различным значениям х 1 и х 2 соответствуют два различных значения функции у 1 и у 2 . Справедливо и обратное, т.е. если у 1 у 2 , то из определения возрастающей функции следует, чтоx 1 x 2 . Т.е. вновь двум различным значениям у 1 и у 2 соответствуют два различных значенияx 1 и x 2 . Т.о., между значениями x и соответствующими им значениями
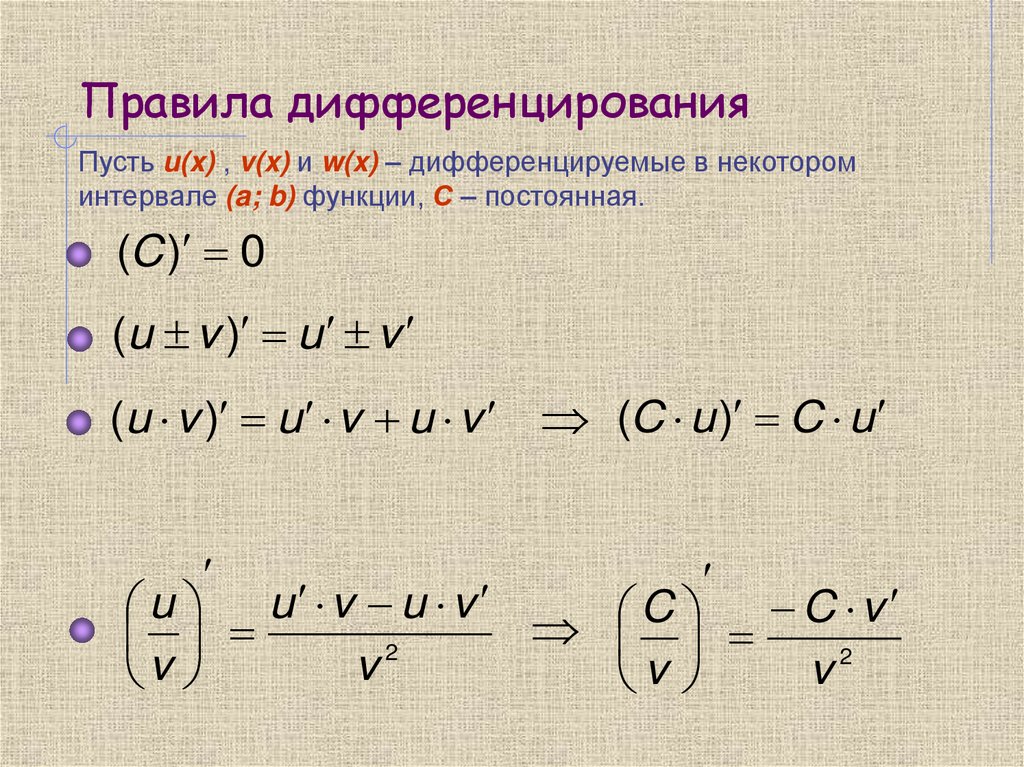
Эта функция называется обратной для функции y=f(x) . Очевидно, что и функция y=f(x) является обратной для функции x=g(у) .
Заметим, что обратная функция x=g(y) находится путем решения уравнения y=f(x) относительно х .
Пример. Пусть дана функция y = e x . Эта функция возрастает при –∞ x x = lny . Область определения обратной функции 0 y
Сделаем несколько замечаний.
Замечание 1. Если возрастающая (или убывающая) функция y=f(x)
непрерывна на отрезке [a ; b ], причем f(a)=c, f(b)=d , то обратная функция определена и непрерывна на отрезке [c ; d ].Замечание 2. Если функция y=f(x) не является ни возрастающей, ни убывающей на некотором интервале, то она может иметь несколько обратных функций.
Пример. Функция y=x 2 определена при –∞x
x
x
≤ 0 функция – убывает и обратная
для нее .
Замечание 3. Если функции y=f(x) и x=g(y) являются взаимно обратными, то они выражают одну и ту же связь между переменными x и y . Поэтому графикомих является одна и та же кривая. Но если аргумент обратной функции мы обозначим снова через x , а функцию через y и построим их в одной системе координат, то получим уже два различных графика. Легко заметить, что графики будут симметричны относительно биссектрисы 1-го координатного угла.
ТЕОРЕМА О ПРОИЗВОДНОЙ ОБРАТНОЙ ФУНКЦИИ
Докажем теорему, позволяющую находить производную функции y=f(x) , зная производную обратной функции.
Теорема. Если для функции y=f(x) существует
обратная функция x=g(y ), которая в некоторой точке у 0 имеет
производную g «(v 0 ), отличную от нуля, то в
соответствующей точке x 0 =g (x 0 ) функция y=f(x) имеет
производную f «(x 0 ), равную ,
т. е. справедлива формула.
е. справедлива формула.
Доказательство . Т.к. x=g(y) дифференцируема в точке y 0 , то x=g(y) непрерывна в этой точке, поэтому функция y=f(x) непрерывна в точке x 0 =g (y 0 ). Следовательно, при Δx →0 Δy →0.
Покажем, что .
Пусть . Тогда по свойству предела . Перейдем в этом равенстве к пределу при Δy →0. Тогда Δx →0 и α(Δx)→0, т.е. .
Следовательно,
,
что и требовалось доказать.
Эту формулу можно записать в виде .
Рассмотрим применение этой теоремы на примерах.
При выводе самой первой формулы таблицы будем исходить из определения производнойфункции в точке. Возьмем , где x – любое действительное число, то есть, x – любое число из области определения функции . Запишем предел отношения приращения функции к приращению аргумента при :
Следует
заметить, что под знаком предела
получается выражение ,
которое не являетсянеопределенностью
ноль делить на ноль, так как в числителе
находится не бесконечно малая величина,
а именно ноль.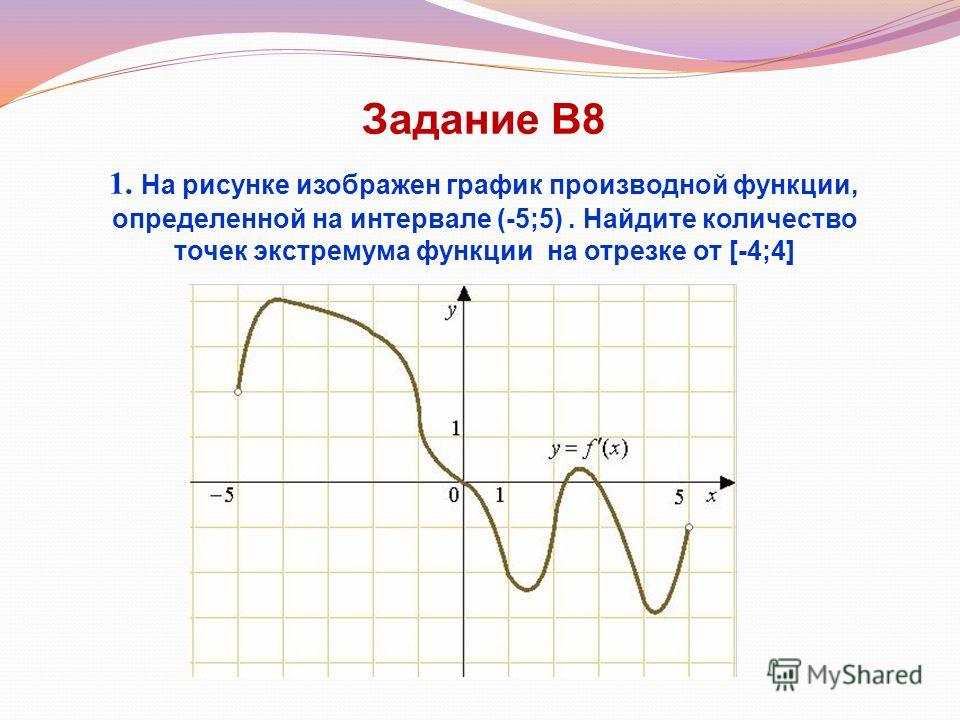 Другими словами, приращение
постоянной функции всегда равно нулю.
Другими словами, приращение
постоянной функции всегда равно нулю.
Таким образом, производная постоянной функции равна нулю на всей области определения .
Производная степенной функции.
Формула производной степенной функции имеет вид , где показатель степени p – любое действительное число.
Докажем сначала формулу для натурального показателя степени, то есть, для p = 1, 2, 3, …
Будем пользоваться определением производной. Запишем предел отношения приращения степенной функции к приращению аргумента:
Для
упрощения выражения в числителе обратимся
к формуле бинома
Ньютона:
Следовательно,
Этим доказана формула производной степенной функции для натурального показателя.
Производная показательной функции.
Вывод формулы производной приведем на основе определения:
Пришли
к неопределенности. Для ее раскрытия
введем новую переменную ,
причем при .
Тогда .
В последнем переходе мы использовали
формулу перехода к новому основанию
логарифма.
Выполним подстановку в исходный предел:
Если
вспомнить второй
замечательный предел, то придем к
формуле производной показательной
функции:
Производная логарифмической функции.
Докажем
формулу производной логарифмической
функции для всех x из
области определения и всех допустимых
значениях основания a логарифма.
По определению производной имеем:
Как Вы заметили, при доказательстве преобразования проводились с использованием свойств логарифма. Равенство справедливо в силу второго замечательного предела.
Производные тригонометрических функций.
Для вывода формул производных тригонометрических функций нам придется вспомнить некоторые формулы тригонометрии, а также первый замечательный предел.
По определению производной для функции синуса имеем .
Воспользуемся
формулой разности синусов:
Осталось обратиться к первому замечательному пределу:
Таким
образом, производная функции sin
x есть cos
x .
Абсолютно
аналогично доказывается формула
производной косинуса.
Следовательно, производная функции cos x есть –sin x .
Вывод
формул таблицы производных для тангенса
и котангенса проведем с использованием
доказанных правил дифференцирования
(производная
дроби).
Производные гиперболических функций.
Правила
дифференцирования и
формула производной показательной
функции из таблицы производных позволяют
вывести формулы производных гиперболического
синуса, косинуса, тангенса и котангенса.
Производная обратной функции.
Чтобы при изложении не было путаницы, давайте обозначать в нижнем индексе аргумент функции, по которому выполняется дифференцирование, то есть, — это производная функции f(x) по x .
Теперь сформулируем правило нахождения производной обратной функции.
Пусть
функции y
= f(x) и x
= g(y) взаимно
обратные, определенные на
интервалах и соответственно.
Если в точке существует
конечная отличная от нуля производная
функции f(x) ,
то в точке существует
конечная производная обратной
функции g(y) ,
причем . В другой записи .
В другой записи .
Можно это правило переформулировать для любого x из промежутка , тогда получим .
Давайте проверим справедливость этих формул.
Найдем обратную функцию для натурального логарифма (здесь y – функция, а x — аргумент). Разрешив это уравнение относительно x , получим (здесь x – функция, а y – ее аргумент). То есть, и взаимно обратные функции.
Из таблицы производных видим, что и .
Убедимся, что формулы нахождения производных обратной функции приводят нас к этим же результатам:
Как видите, получили такие же результаты как и в таблице производных.
Теперь мы обладаем знаниями для доказательства формул производных обратных тригонометрических функций.
Начнем с производной арксинуса.
. Тогда по формуле производной обратной функции получаем
Осталось провести преобразования.
Так
как областью значений арксинуса является
интервал ,
то (смотрите
раздел основные
элементарные функции, их свойства и
графики). Поэтому ,
а не
рассматриваем.
Поэтому ,
а не
рассматриваем.
Следовательно, . Областью определения производной арксинуса является промежуток (-1; 1) .
Для
арккосинуса все делается абсолютно
аналогично:
Найдем производную арктангенса.
Для обратной функцией является .
Выразим арктангенс через арккосинус, чтобы упростить полученное выражение.
Пусть arctgx
= z ,
тогда
Следовательно,
Схожим
образом находится производная
арккотангенса:
Приведем сводную таблицу для удобства и наглядности при изучении темы.
Константа y = C Степенная функция y = x p (x p) » = p · x p — 1 | Показательная функция y = a x (a x) » = a x · ln a В частности, при a = e имеем y = e x (e x) » = e x |
Логарифмическая функция (log a x) » = 1 x · ln a В частности, при a = e имеем y = ln x (ln x) » = 1 x | Тригонометрические функции (sin x) » = cos x (cos x) » = — sin x (t g x) » = 1 cos 2 x (c t g x) » = — 1 sin 2 x |
Обратные тригонометрические функции (a r c sin x) » = 1 1 — x 2 (a r c cos x) » = — 1 1 — x 2 (a r c t g x) » = 1 1 + x 2 (a r c c t g x) » = — 1 1 + x 2 | Гиперболические функции (s h x) » = c h x (c h x) » = s h x (t h x) » = 1 c h 2 x (c t h x) » = — 1 s h 2 x |
Разберем, каким образом были получены формулы указанной таблицы или, иначе говоря, докажем вывод формул производных для каждого вида функций.
Производная постоянной
Доказательство 1
Для того, чтобы вывести данную формулу, возьмем за основу определение производной функции в точке. Используем x 0 = x , где x принимает значение любого действительного числа, или, иначе говоря, x является любым числом из области определения функции f (x) = C . Составим запись предела отношения приращения функции к приращению аргумента при ∆ x → 0:
lim ∆ x → 0 ∆ f (x) ∆ x = lim ∆ x → 0 C — C ∆ x = lim ∆ x → 0 0 ∆ x = 0
Обратите внимание, что под знак предела попадает выражение 0 ∆ x . Оно не есть неопределенность «ноль делить на ноль», поскольку в числителе записана не бесконечно малая величина, а именно нуль. Иначе говоря, приращение постоянной функции всегда есть нуль.
Итак, производная постоянной функции f (x) = C равна нулю на всей области определения.
Пример 1
Даны постоянные функции:
f 1 (x) = 3 , f 2 (x) = a , a ∈ R , f 3 (x) = 4 . 13 7 22 , f 4 (x) = 0 , f 5 (x) = — 8 7
Решение
Опишем заданные условия. В первой функции мы видим производную натурального числа 3 . В следующем примере необходимо брать производную от а , где а — любое действительное число. Третий пример задает нам производную иррационального числа 4 . 13 7 22 , четвертый — производную нуля (нуль – целое число). Наконец, в пятом случае имеем производную рациональной дроби — 8 7 .
В первой функции мы видим производную натурального числа 3 . В следующем примере необходимо брать производную от а , где а — любое действительное число. Третий пример задает нам производную иррационального числа 4 . 13 7 22 , четвертый — производную нуля (нуль – целое число). Наконец, в пятом случае имеем производную рациональной дроби — 8 7 .
Ответ: производные заданных функций есть нуль при любом действительном x (на всей области определения)
f 1 » (x) = (3) » = 0 , f 2 » (x) = (a) » = 0 , a ∈ R , f 3 » (x) = 4 . 13 7 22 » = 0 , f 4 » (x) = 0 » = 0 , f 5 » (x) = — 8 7 » = 0
Производная степенной функции
Переходим к степенной функции и формуле ее производной, имеющей вид: (x p) » = p · x p — 1 , где показатель степени p является любым действительным числом.
Доказательство 2
Приведем доказательство формулы, когда показатель степени – натуральное число: p = 1 , 2 , 3 , …
Вновь опираемся на определение производной. Составим запись предела отношения приращения степенной функции к приращению аргумента:
Составим запись предела отношения приращения степенной функции к приращению аргумента:
(x p) » = lim ∆ x → 0 = ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p — x p ∆ x
Чтобы упростить выражение в числителе, используем формулу бинома Ньютона:
(x + ∆ x) p — x p = C p 0 + x p + C p 1 · x p — 1 · ∆ x + C p 2 · x p — 2 · (∆ x) 2 + . . . + + C p p — 1 · x · (∆ x) p — 1 + C p p · (∆ x) p — x p = = C p 1 · x p — 1 · ∆ x + C p 2 · x p — 2 · (∆ x) 2 + . . . + C p p — 1 · x · (∆ x) p — 1 + C p p · (∆ x) p
Таким образом:
(x p) » = lim ∆ x → 0 ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p — x p ∆ x = = lim ∆ x → 0 (C p 1 · x p — 1 · ∆ x + C p 2 · x p — 2 · (∆ x) 2 + . . . + C p p — 1 · x · (∆ x) p — 1 + C p p · (∆ x) p) ∆ x = = lim ∆ x → 0 (C p 1 · x p — 1 + C p 2 · x p — 2 · ∆ x + . . . + C p p — 1 · x · (∆ x) p — 2 + C p p · (∆ x) p — 1) = = C p 1 · x p — 1 + 0 + 0 + . . . + 0 = p ! 1 ! · (p — 1) ! · x p — 1 = p · x p — 1
Так, мы доказали формулу производной степенной функции, когда показатель степени – натуральное число.
Доказательство 3
Чтобы привести доказательство для случая, когда p — любое действительное число, отличное от нуля, используем логарифмическую производную (здесь следует понимать отличие от производной логарифмической функции). Чтобы иметь более полное понимание желательно изучить производную логарифмической функции и дополнительно разобраться с производной неявно заданной функции и производной сложной функции.
Рассмотрим два случая: когда x положительны и когда x отрицательны.
Итак, x > 0 . Тогда: x p > 0 . Логарифмируем равенство y = x p по основанию e и применим свойство логарифма:
y = x p ln y = ln x p ln y = p · ln x
На данном этапе получили неявно заданную функцию. Определим ее производную:
(ln y) » = (p · ln x) 1 y · y » = p · 1 x ⇒ y » = p · y x = p · x p x = p · x p — 1
Теперь рассматриваем случай, когда x – отрицательное число.
Если показатель p есть четное число, то степенная функция определяется и при x
Тогда x p
Если p есть нечетное число, тогда степенная функция определена и при x
y » (x) = (- (- x) p) » = — ((- x) p) » = — p · (- x) p — 1 · (- x) » = = p · (- x) p — 1 = p · x p — 1
Последний переход возможен в силу того, что если p — нечетное число, то p — 1 либо четное число, либо нуль (при p = 1), поэтому, при отрицательных x верно равенство (- x) p — 1 = x p — 1 .
Итак, мы доказали формулу производной степенной функции при любом действительном p .
Пример 2
Даны функции:
f 1 (x) = 1 x 2 3 , f 2 (x) = x 2 — 1 4 , f 3 (x) = 1 x log 7 12
Определите их производные.
Решение
Часть заданных функций преобразуем в табличный вид y = x p , опираясь на свойства степени, а затем используем формулу:
f 1 (x) = 1 x 2 3 = x — 2 3 ⇒ f 1 » (x) = — 2 3 · x — 2 3 — 1 = — 2 3 · x — 5 3 f 2 » (x) = x 2 — 1 4 = 2 — 1 4 · x 2 — 1 4 — 1 = 2 — 1 4 · x 2 — 5 4 f 3 (x) = 1 x log 7 12 = x — log 7 12 ⇒ f 3 » (x) = — log 7 12 · x — log 7 12 — 1 = — log 7 12 · x — log 7 12 — log 7 7 = — log 7 12 · x — log 7 84
Производная показательной функции
Доказательство 4
Выведем формулу производной, взяв за основу определение:
(a x) » = lim ∆ x → 0 a x + ∆ x — a x ∆ x = lim ∆ x → 0 a x (a ∆ x — 1) ∆ x = a x · lim ∆ x → 0 a ∆ x — 1 ∆ x = 0 0
Мы получили неопределенность. Чтобы раскрыть ее, запишем новую переменную z = a ∆ x — 1 (z → 0 при ∆ x → 0). В таком случае a ∆ x = z + 1 ⇒ ∆ x = log a (z + 1) = ln (z + 1) ln a . Для последнего перехода использована формула перехода к новому основанию логарифма.
Чтобы раскрыть ее, запишем новую переменную z = a ∆ x — 1 (z → 0 при ∆ x → 0). В таком случае a ∆ x = z + 1 ⇒ ∆ x = log a (z + 1) = ln (z + 1) ln a . Для последнего перехода использована формула перехода к новому основанию логарифма.
Осуществим подстановку в исходный предел:
(a x) » = a x · lim ∆ x → 0 a ∆ x — 1 ∆ x = a x · ln a · lim ∆ x → 0 1 1 z · ln (z + 1) = = a x · ln a · lim ∆ x → 0 1 ln (z + 1) 1 z = a x · ln a · 1 ln lim ∆ x → 0 (z + 1) 1 z
Вспомним второй замечательный предел и тогда получим формулу производной показательной функции:
(a x) » = a x · ln a · 1 ln lim z → 0 (z + 1) 1 z = a x · ln a · 1 ln e = a x · ln a
Пример 3
Даны показательные функции:
f 1 (x) = 2 3 x , f 2 (x) = 5 3 x , f 3 (x) = 1 (e) x
Необходимо найти их производные.
Решение
Используем формулу производной показательной функции и свойства логарифма:
f 1 » (x) = 2 3 x » = 2 3 x · ln 2 3 = 2 3 x · (ln 2 — ln 3) f 2 » (x) = 5 3 x » = 5 3 x · ln 5 1 3 = 1 3 · 5 3 x · ln 5 f 3 » (x) = 1 (e) x » = 1 e x » = 1 e x · ln 1 e = 1 e x · ln e — 1 = — 1 e x
Производная логарифмической функции
Доказательство 5
Приведем доказательство формулы производной логарифмической функции для любых x в области определения и любых допустимых значениях основания а логарифма. Опираясь на определение производной, получим:
Опираясь на определение производной, получим:
(log a x) » = lim ∆ x → 0 log a (x + ∆ x) — log a x ∆ x = lim ∆ x → 0 log a x + ∆ x x ∆ x = = lim ∆ x → 0 1 ∆ x · log a 1 + ∆ x x = lim ∆ x → 0 log a 1 + ∆ x x 1 ∆ x = = lim ∆ x → 0 log a 1 + ∆ x x 1 ∆ x · x x = lim ∆ x → 0 1 x · log a 1 + ∆ x x x ∆ x = = 1 x · log a lim ∆ x → 0 1 + ∆ x x x ∆ x = 1 x · log a e = 1 x · ln e ln a = 1 x · ln a
Из указанной цепочки равенств видно, что преобразования строились на основе свойства логарифма. Равенство lim ∆ x → 0 1 + ∆ x x x ∆ x = e является верным в соответствии со вторым замечательным пределом.
Пример 4
Заданы логарифмические функции:
f 1 (x) = log ln 3 x , f 2 (x) = ln x
Необходимо вычислить их производные.
Решение
Применим выведенную формулу:
f 1 » (x) = (log ln 3 x) » = 1 x · ln (ln 3) ; f 2 » (x) = (ln x) » = 1 x · ln e = 1 x
Итак, производная натурального логарифма есть единица, деленная на x .
Производные тригонометрических функций
Доказательство 6
Используем некоторые тригонометрические формулы и первый замечательный предел, чтобы вывести формулу производной тригонометрической функции.
Согласно определению производной функции синуса, получим:
(sin x) » = lim ∆ x → 0 sin (x + ∆ x) — sin x ∆ x
Формула разности синусов позволит нам произвести следующие действия:
(sin x) » = lim ∆ x → 0 sin (x + ∆ x) — sin x ∆ x = = lim ∆ x → 0 2 · sin x + ∆ x — x 2 · cos x + ∆ x + x 2 ∆ x = = lim ∆ x → 0 sin ∆ x 2 · cos x + ∆ x 2 ∆ x 2 = = cos x + 0 2 · lim ∆ x → 0 sin ∆ x 2 ∆ x 2
Наконец, используем первый замечательный предел:
sin » x = cos x + 0 2 · lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = cos x
Итак, производной функции sin x будет cos x .
Совершенно также докажем формулу производной косинуса:
cos » x = lim ∆ x → 0 cos (x + ∆ x) — cos x ∆ x = = lim ∆ x → 0 — 2 · sin x + ∆ x — x 2 · sin x + ∆ x + x 2 ∆ x = = — lim ∆ x → 0 sin ∆ x 2 · sin x + ∆ x 2 ∆ x 2 = = — sin x + 0 2 · lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = — sin x
Т.е. производной функции cos x будет – sin x .
Формулы производных тангенса и котангенса выведем на основе правил дифференцирования:
t g » x = sin x cos x » = sin » x · cos x — sin x · cos » x cos 2 x = = cos x · cos x — sin x · (- sin x) cos 2 x = sin 2 x + cos 2 x cos 2 x = 1 cos 2 x c t g » x = cos x sin x » = cos » x · sin x — cos x · sin » x sin 2 x = = — sin x · sin x — cos x · cos x sin 2 x = — sin 2 x + cos 2 x sin 2 x = — 1 sin 2 x
Производные обратных тригонометрических функций
Раздел о производной обратных функций дает исчерпывающую информацию о доказательстве формул производных арксинуса, арккосинуса, арктангенса и арккотангенса, поэтому дублировать материал здесь не будем.
Производные гиперболических функций
Доказательство 7
Вывод формул производных гиперболического синуса, косинуса, тангенса и котангенса осуществим при помощи правила дифференцирования и формулы производной показательной функции:
s h » x = e x — e — x 2 » = 1 2 e x » — e — x » = = 1 2 e x — — e — x = e x + e — x 2 = c h x c h » x = e x + e — x 2 » = 1 2 e x » + e — x » = = 1 2 e x + — e — x = e x — e — x 2 = s h x t h » x = s h x c h x » = s h » x · c h x — s h x · c h » x c h 2 x = c h 2 x — s h 2 x c h 2 x = 1 c h 2 x c t h » x = c h x s h x » = c h » x · s h x — c h x · s h » x s h 2 x = s h 2 x — c h 2 x s h 2 x = — 1 s h 2 x
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Как найти производную? Примеры решений
Как найти производную, как взять производную? На данном уроке мы научимся находить производные функций. Но перед изучением данной страницы я настоятельно рекомендую ознакомиться с методическим материалом Горячие формулы школьного курса математики. Справочное пособие можно открыть или закачать на странице Математические формулы и таблицы. Также оттуда нам потребуется Таблица производных, ее лучше распечатать, к ней часто придется обращаться, причем, не только сейчас, но и в оффлайне.
Справочное пособие можно открыть или закачать на странице Математические формулы и таблицы. Также оттуда нам потребуется Таблица производных, ее лучше распечатать, к ней часто придется обращаться, причем, не только сейчас, но и в оффлайне.
Есть? Приступим. У меня для Вас есть две новости: хорошая и очень хорошая. Хорошая новость состоит в следующем: чтобы научиться находить производные, совсем не обязательно знать и понимать, что такое производная. Более того, определение производной функции, математический, физический, геометрический смысл производной целесообразнее переварить позже, поскольку качественная проработка теории, по моему мнению, требует изучения ряда других тем, а также некоторого практического опыта.
И сейчас наша задача освоить эти самые производные технически. Очень хорошая новость состоит в том, что научиться брать производные не так сложно, существует довольно чёткий алгоритм решения (и объяснения) этого задания, интегралы или пределы, например, освоить труднее.
Советую следующий порядок изучения темы: во-первых, эта статья. Затем нужно прочитать важнейший урок Производная сложной функции. Эти два базовых занятия позволят поднять Ваши навыки с полного нуля. Далее можно будет ознакомиться с более сложными производными в статье Сложные производные.
Логарифмическая производная. Если планка окажется слишком высока, то сначала прочитайте вещь Простейшие типовые задачи с производной. Помимо нового материала, на уроке рассмотрены другие, более простые типы производных, и есть прекрасная возможность улучшить свою технику дифференцирования. Кроме того, в контрольных работах почти всегда встречаются задания на нахождение производных функций, которые заданы неявно или параметрически. Такой урок тоже есть: Производные неявных и параметрически заданных функций.
Я попытаюсь в доступной форме, шаг за шагом, научить Вас находить производные функций. Вся информация изложена подробно, простыми словами.
Собственно, сразу рассмотрим пример: Пример 1
Найти производную функции Решение:
Это простейший пример, пожалуйста, найдите его в таблице производных элементарных функций. Теперь посмотрим на решение и проанализируем, что же произошло? А произошла следующая вещь:
Теперь посмотрим на решение и проанализируем, что же произошло? А произошла следующая вещь:
у нас была функция , которая в результате решения превратилась в функцию .
Говоря совсем просто, для того чтобы найти производную
функции, нужно по определенным правилам превратить её в другую функцию. Посмотрите еще раз на таблицу производных – там функции превращаются в другие функции. Единственным
исключением является экспоненциальная функция , которая
превращается сама в себя. Операция нахождения производной называется дифференцированием.
Обозначения: Производную обозначают или .
ВНИМАНИЕ, ВАЖНО! Забыть поставить штрих (там, где надо), либо нарисовать лишний штрих (там, где не надо) – ГРУБАЯ ОШИБКА! Функция и её производная – это две разные функции!
Вернемся к нашей таблице производных. Из данной таблицы желательно запомнить наизусть: правила дифференцирования и производные некоторых элементарных функций, особенно:
производную константы:
, где – постоянное число; производную степенной функции:
, в частности: , , .
Зачем запоминать? Данные знания являются элементарными знаниями о производных. И если Вы не сможете ответить преподавателю на вопрос «Чему равна производная числа?», то учеба в ВУЗе может для Вас закончиться (лично знаком с двумя реальными случаями из жизни). Кроме того, это наиболее распространенные формулы, которыми приходится пользоваться практически каждый раз, когда мы сталкиваемся с производными.
Вреальности простые табличные примеры – редкость, обычно при нахождении производных сначала используются правила дифференцирования, а затем – таблица производных элементарных функций.
Вэтой связи переходим к рассмотрению правил дифференцирования:
1) Постоянное число можно (и нужно) вынести за знак производной
, где – постоянное число (константа) Пример 2
Найти производную функции
Смотрим в таблицу производных. Производная косинуса там есть, но у нас .
Решаем:
Самое время использовать правило, выносим постоянный множитель за знак производной:
А теперь превращаем наш косинус по таблице:
Ну и результат желательно немного «причесать» – ставим минус на первое место, заодно избавляясь от скобок:
Готово.
2) Производная суммы равна сумме производных
Пример 3
Найти производную функции
Решаем. Как Вы, наверное, уже заметили, первое действие, которое всегда выполняется при нахождении производной, состоит в том, что мы заключаем в скобки всё выражение и ставим штрих справа вверху:
Применяем второе правило:
Обратите внимание, что для дифференцирования все корни, степени нужно представить в виде , а если они находятся в знаменателе, то
переместить их вверх. Как это сделать – рассмотрено в моих методических материалах.
Теперь вспоминаем о первом правиле дифференцирования – постоянные множители (числа) выносим за знак производной:
Обычно в ходе решения эти два правила применяют одновременно (чтобы не переписывать лишний раз длинное выражение).
Все функции, находящиеся под штрихами, являются элементарными табличными функциями, с помощью таблицы осуществляем превращение:
Можно всё оставить в таком виде, так как штрихов больше нет, и производная найдена. Тем не менее, подобные выражения обычно упрощают:
Тем не менее, подобные выражения обычно упрощают:
Все степени вида желательно снова представить в виде корней,
степени с отрицательными показателями – сбросить в знаменатель. Хотя этого можно и не делать, ошибкой не будет.
Пример 4
Найти производную функции
Попробуйте решить данный пример самостоятельно (ответ в конце урока).
3) Производная произведения функций
Вроде бы по аналогии напрашивается формула …., но неожиданность состоит в том, что:
Эта необычное правило (как, собственно, и другие) следует из определения производной. Но с теорией мы пока повременим – сейчас важнее научиться решать:
Пример 5
Найти производную функции
Здесь у нас произведение двух функций, зависящих от . Сначала применяем наше странное правило, а затем превращаем функции по таблице производных:
Сложно? Вовсе нет, вполне доступно даже для чайника.
Пример 6
Найти производную функции
В данной функции содержится сумма и произведение двух функций – квадратного трехчлена и логарифма . Со школы мы помним, что умножение и деление имеют приоритет перед сложением и вычитанием.
Со школы мы помним, что умножение и деление имеют приоритет перед сложением и вычитанием.
Здесь всё так же. СНАЧАЛА мы используем правило дифференцирования произведения:
Теперь для скобки используем два первых правила:
В результате применения правил дифференцирования под штрихами у нас остались только элементарные функции, по таблице производных превращаем их в другие функции:
Готово.
При определенном опыте нахождения производных, простые производные вроде не обязательно расписывать так подробно. Вообще, они обычно решаются устно, и сразу записывается, что .
Пример 7
Найти производную функции Это пример для самостоятельного решения (ответ в конце урока)
4) Производная частного функций
В потолке открылся люк, не пугайся, это глюк. А вот это вот суровая действительность:
Пример 8
Найти производную функции
Чего здесь только нет – сумма, разность, произведение, дробь…. С чего бы начать?! Есть сомнения, нет сомнений, но, В ЛЮБОМ СЛУЧАЕ для начала рисуем скобочки и справа вверху ставим штрих:
Теперь смотрим на выражение в скобках, как бы его упростить? В данном случае замечаем множитель, который согласно первому правилу целесообразно вынести за знак производной:
Заодно избавляемся от скобок в числителе, которые теперь не нужны. Вообще говоря, постоянные множители при нахождении производной
Вообще говоря, постоянные множители при нахождении производной
можно и не выносить, но в этом случае они будут «путаться под ногами», что загромождает и затрудняет решение.
Смотрим на наше выражение в скобках. У нас есть сложение, вычитание и деление. Со школы мы помним, что деление выполняется в первую очередь. И здесь – сначала применяем правило дифференцирования частного:
Таким образом, наша страшная производная свелась к производным двух простых выражений. Применяем первое и второе правило, здесь это сделаем устно, надеюсь, Вы уже немного освоились в производных:
Штрихов больше нет, задание выполнено.
На практике обычно (но не всегда) ответ упрощают «школьными» методами:
Пример 9
Найти производную функции
Это пример для самостоятельного решения (ответ в конце урока). Время от времени встречаются хитрые задачки:
Пример 10
Найти производную функции
Смотрим на данную функцию. Здесь снова дробь. Однако перед тем как использовать правило дифференцирования частного (а его можно использовать), всегда имеет смысл посмотреть, а нельзя ли упростить саму дробь, или вообще избавиться от нее?
Дело в том, что формула достаточно громоздка, и применять ее совсем не хочется.
В данном случае можно почленно поделить числитель на знаменатель. Преобразуем функцию:
Ну вот, совсем другое дело, теперь дифференцировать просто и приятно:
Готово.
Пример 11
Найти производную функции
Здесь ситуация похожа, превратим нашу дробь в произведение, для этого поднимем экспоненту в числитель, сменив у показателя знак:
Произведение все-таки дифференцировать проще:
Пример 12
Найти производную функции Это пример для самостоятельного решения (ответ в конце урока).
5) Производная сложной функции
Данное правило также встречается очень часто. Но о нём рассказать можно очень много, поэтому я создал отдельный урок на тему Производная сложной функции.
Желаю успехов!
Ответы:
Пример 4: . В ходе решения
данного примера следует обратить внимание, на тот факт, что и – постоянные числа, не важно чему они равны, важно, что это — константы. Поэтому выносится за знак производной, а .
Пример 7:
Пример 9:
Пример 12:
Как найти производную?
Задача нахождения производной от заданной функции является одной из основных в курсе математики старшей школы и в высших учебных заведениях. Невозможно полноценно исследовать функцию, построить ее график без взятия ее производной. Производную функции легко можно найти, зная основные правила дифференцирования, а также таблицу производных основных функций. Давайте разберемся, как найти производную функции.
Невозможно полноценно исследовать функцию, построить ее график без взятия ее производной. Производную функции легко можно найти, зная основные правила дифференцирования, а также таблицу производных основных функций. Давайте разберемся, как найти производную функции.
Производной функции называют предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Понять это определение достаточно сложно, так как понятие предела в полной мере не изучается в школе. Но для того, чтобы находить производные различных функций, понимать определение не обязательно, оставим его специалистам математикам и перейдем сразу к нахождению производной.
Процесс нахождения производной называется дифференцированием. При дифференцировании функции мы будем получать новую функцию.
Для их обозначения будем использовать латинские буквы f, g и др.
Существует много всевозможных обозначений производных. Мы будем использовать штрих. Например запись g’ означает, что мы будем находить производную функции g.
Таблица производных
Для того чтобы дать ответ на вопрос как найти производную, необходимо привести таблицу производных основных функций. Для вычисления производных элементарных функций не обязательно производить сложные вычисления. Достаточно просто посмотреть ее значение в таблице производных.
- С’=0
- (sin x)’=cos x
- (cos x)’= –sin x
- (xn)’=n xn-1
- (ex)’=ex
- (ln x)’=1/x
- (ax)’=axln a
- (logax)’=1/x ln a
- (tg x)’=1/cos2x
- (ctg x)’= – 1/sin2x
- (arcsin x)’= 1/√(1-x2)
- (arccos x)’= — 1/√(1-x2)
- (arctg x)’= 1/(1+x2)
- (arcctg x)’= — 1/(1+x2)
Пример 1. Найдите производную функции y=500.
Мы видим, что это константа. По таблице производных известно, что производная константы, равна нулю (формула 1).
(500)’ = 0
Пример 2. Найдите производную функции y=x
100.Это степенная функция в показателе которой 100 и чтобы найти ее производную нужно умножить функцию на показатель и понизить на 1 (формула 3).
(x100)’=100 x99
Пример 3. Найдите производную функции y=5
xЭто показательная функция, вычислим ее производную по формуле 4.
(5x)’= 5xln5
Пример 4. Найдите производную функции y= log
4xПроизводную логарифма найдем по формуле 7.
(log4x)’=1/x ln 4
Правила дифференцирования
Давайте теперь разберемся, как находить производную функции, если ее нет в таблице. Большинство исследуемых функций, не являются элементарными, а представляют собой комбинации элементарных функций с помощью простейших операций (сложение, вычитание, умножение, деление, а также умножение на число). Для нахождения их производных необходимо знать правила дифференцирования. Далее буквами f и g обозначены функции, а С — константа.
Далее буквами f и g обозначены функции, а С — константа.
1. Постоянный коэффициент можно выносить за знак производной
(С f)’=С f’
Пример 5. Найдите производную функции y= 6*x
8Выносим постоянный коэффициент 6 и дифференцируем только x4. Это степенная функция, производную которой находим по формуле 3 таблицы производных.
(6*x8)’ = 6*(x8)’=6*8*x7=48* x7
2. Производная суммы равна сумме производных
Тогда:
(f + g)’=f’ + g’
Пример 6. Найдите производную функции y= x
100+sin xФункция представляет собой сумму двух функций, производные которых мы можем найти по таблице. Так как (x100)’=100 x99 и (sin x)’=cos x. Производная суммы будет равна сумме данных производных:
(x100+sin x)’= 100 x99+cos x
3. Производная разности равна разности производных
(f – g)’=f’ – g’
Пример 7. Найдите производную функции y= x
100 – cos xЭта функция представляет собой разность двух функции, производные которых мы также можем найти по таблице. Тогда производная разности равна разности производных и не забудем поменять знак, так как (cos x)’= – sin x.
Тогда производная разности равна разности производных и не забудем поменять знак, так как (cos x)’= – sin x.
(x100 – cos x)’= 100 x99 + sin x
Пример 8. Найдите производную функции y=e
x+tg x– x2.В этой функции есть и сумма и разность, найдем производные от каждого слагаемого:
(ex)’=ex, (tg x)’=1/cos2x, (x2)’=2 x. Тогда производная исходной функции равна:
(ex+tg x– x2)’= ex+1/cos2x –2 x
4. Производная произведения
(f * g)’=f’ * g + f * g’
Пример 9. Найдите производную функции y= cos x *e
xДля этого сначала найдем производного каждого множителя (cos x)’=–sin x и (ex)’=ex. Теперь подставим все в формулу произведения. Производную первой функции умножим на вторую и прибавим произведение первой функции на производную второй.
(cos x* ex)’= excos x – ex*sin x
5.
 Производная частного
Производная частногоТогда:
(f / g)’= f’ * g – f * g’/ g2
Пример 10. Найдите производную функции y= x
50/sin xЧтобы найти производную частного, сначала найдем производную числителя и знаменателя отдельно: (x50)’=50 x49 и (sin x)’= cos x. Подставив в формулу производной частного получим:
(x50/sin x)’= 50x49*sin x – x50*cos x/sin2x
Производная сложной функции
Сложная функция — это функция, представленная композицией нескольких функций. Для нахождения производной сложной функции также существует правило:
(u (v))’=u'(v)*v’
Давайте разберемся как находить производную такой функции. Пусть y= u(v(x)) — сложная функция. Функцию u назовем внешней, а v — внутренней.
Например:
y=sin (x3) — сложная функция.
Тогда y=sin(t) — внешняя функция
t=x3 — внутренняя.
Давайте попробуем вычислить производную этой функции. По формуле необходимо перемножить производные внутренней и внешней функции.
По формуле необходимо перемножить производные внутренней и внешней функции.
(sin t)’=cos (t) — производная внешней функции (где t=x3)
(x3)’=3x2 — производная внутренней функции
Тогда (sin (x3))’= cos (x3)* 3x2— производная сложной функции.
Найти производную функции x 2 3. Найти производную: алгоритм и примеры решений
Задача нахождения производной от заданной функции является одной из основных в курсе математики старшей школы и в высших учебных заведениях. Невозможно полноценно исследовать функцию, построить ее график без взятия ее производной. Производную функции легко можно найти, зная основные правила дифференцирования, а также таблицу производных основных функций. Давайте разберемся, как найти производную функции.
Производной функции называют предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Понять это определение достаточно сложно, так как понятие предела в полной мере не изучается в школе.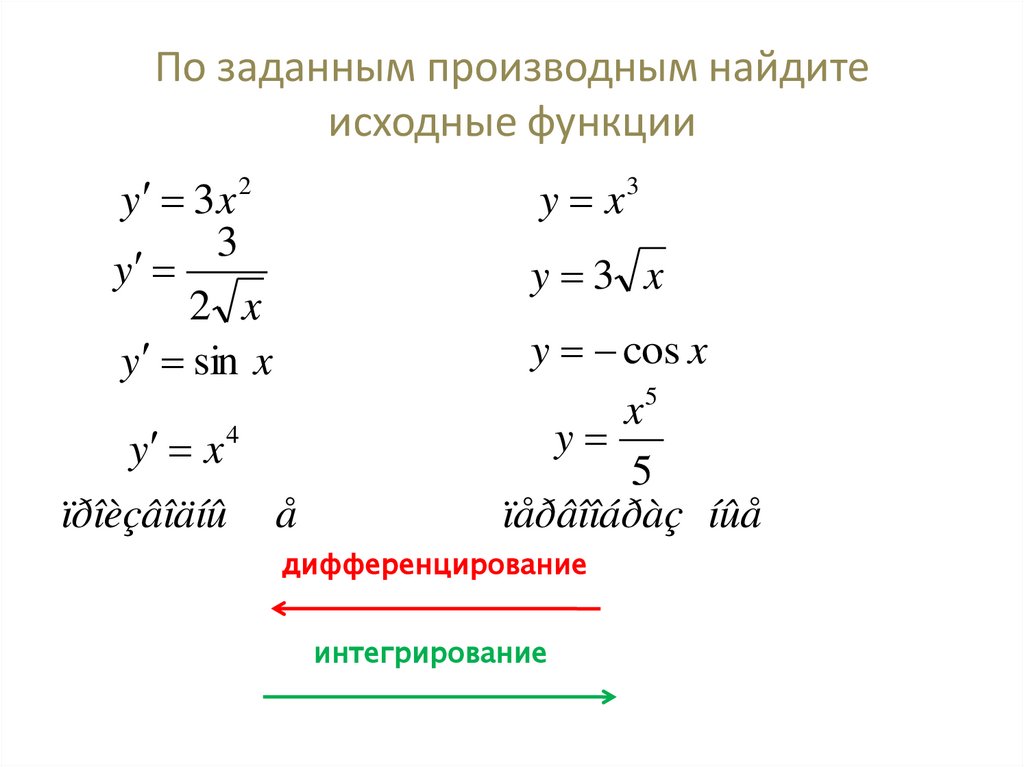 Но для того, чтобы находить производные различных функций, понимать определение не обязательно, оставим его специалистам математикам и перейдем сразу к нахождению производной.
Но для того, чтобы находить производные различных функций, понимать определение не обязательно, оставим его специалистам математикам и перейдем сразу к нахождению производной.
Процесс нахождения производной называется дифференцированием. При дифференцировании функции мы будем получать новую функцию.
Для их обозначения будем использовать латинские буквы f, g и др.
Существует много всевозможных обозначений производных. Мы будем использовать штрих. Например запись g» означает, что мы будем находить производную функции g.
Таблица производных
Для того чтобы дать ответ на вопрос как найти производную, необходимо привести таблицу производных основных функций. Для вычисления производных элементарных функций не обязательно производить сложные вычисления. Достаточно просто посмотреть ее значение в таблице производных.
- (sin x)»=cos x
- (cos x)»= –sin x
- (x n)»=n x n-1
- (e x)»=e x
- (ln x)»=1/x
- (a x)»=a x ln a
- (log a x)»=1/x ln a
- (tg x)»=1/cos 2 x
- (ctg x)»= – 1/sin 2 x
- (arcsin x)»= 1/√(1-x 2)
- (arccos x)»= — 1/√(1-x 2)
- (arctg x)»= 1/(1+x 2)
- (arcctg x)»= — 1/(1+x 2)
Пример 1.
 Найдите производную функции y=500.
Найдите производную функции y=500.Мы видим, что это константа. По таблице производных известно, что производная константы, равна нулю (формула 1).
Пример 2. Найдите производную функции y=x 100 .
Это степенная функция в показателе которой 100 и чтобы найти ее производную нужно умножить функцию на показатель и понизить на 1 (формула 3).
(x 100)»=100 x 99
Пример 3. Найдите производную функции y=5 x
Это показательная функция, вычислим ее производную по формуле 4.
Пример 4. Найдите производную функции y= log 4 x
Производную логарифма найдем по формуле 7.
(log 4 x)»=1/x ln 4
Правила дифференцирования
Давайте теперь разберемся, как находить производную функции, если ее нет в таблице. Большинство исследуемых функций, не являются элементарными, а представляют собой комбинации элементарных функций с помощью простейших операций (сложение, вычитание, умножение, деление, а также умножение на число). Для нахождения их производных необходимо знать правила дифференцирования. Далее буквами f и g обозначены функции, а С — константа.
Далее буквами f и g обозначены функции, а С — константа.
1. Постоянный коэффициент можно выносить за знак производной
Пример 5. Найдите производную функции y= 6*x 8
Выносим постоянный коэффициент 6 и дифференцируем только x 4 . Это степенная функция, производную которой находим по формуле 3 таблицы производных.
(6*x 8)» = 6*(x 8)»=6*8*x 7 =48* x 7
2. Производная суммы равна сумме производных
(f + g)»=f» + g»
Пример 6. Найдите производную функции y= x 100 +sin x
Функция представляет собой сумму двух функций, производные которых мы можем найти по таблице. Так как (x 100)»=100 x 99 и (sin x)»=cos x. Производная суммы будет равна сумме данных производных:
(x 100 +sin x)»= 100 x 99 +cos x
3. Производная разности равна разности производных
(f – g)»=f» – g»
Пример 7. Найдите производную функции y= x 100 – cos x
Эта функция представляет собой разность двух функции, производные которых мы также можем найти по таблице. Тогда производная разности равна разности производных и не забудем поменять знак, так как (cos x)»= – sin x.
Тогда производная разности равна разности производных и не забудем поменять знак, так как (cos x)»= – sin x.
(x 100 – cos x)»= 100 x 99 + sin x
Пример 8. Найдите производную функции y=e x +tg x– x 2 .
В этой функции есть и сумма и разность, найдем производные от каждого слагаемого:
(e x)»=e x , (tg x)»=1/cos 2 x, (x 2)»=2 x. Тогда производная исходной функции равна:
(e x +tg x– x 2)»= e x +1/cos 2 x –2 x
4. Производная произведения
(f * g)»=f» * g + f * g»
Пример 9. Найдите производную функции y= cos x *e x
Для этого сначала найдем производного каждого множителя (cos x)»=–sin x и (e x)»=e x . Теперь подставим все в формулу произведения. Производную первой функции умножим на вторую и прибавим произведение первой функции на производную второй.
(cos x* e x)»= e x cos x – e x *sin x
5. Производная частного
(f / g)»= f» * g – f * g»/ g 2
Пример 10. Найдите производную функции y= x 50 /sin x
Чтобы найти производную частного, сначала найдем производную числителя и знаменателя отдельно: (x 50)»=50 x 49 и (sin x)»= cos x. Подставив в формулу производной частного получим:
Подставив в формулу производной частного получим:
(x 50 /sin x)»= 50x 49 *sin x – x 50 *cos x/sin 2 x
Производная сложной функции
Сложная функция — это функция, представленная композицией нескольких функций. Для нахождения производной сложной функции также существует правило:
(u (v))»=u»(v)*v»
Давайте разберемся как находить производную такой функции. Пусть y= u(v(x)) — сложная функция. Функцию u назовем внешней, а v — внутренней.
Например:
y=sin (x 3) — сложная функция.
Тогда y=sin(t) — внешняя функция
t=x 3 — внутренняя.
Давайте попробуем вычислить производную этой функции. По формуле необходимо перемножить производные внутренней и внешней функции.
(sin t)»=cos (t) — производная внешней функции (где t=x 3)
(x 3)»=3x 2 — производная внутренней функции
Тогда (sin (x 3))»= cos (x 3)* 3x 2 — производная сложной функции.
Приложение
Решение производной на сайт для закрепления пройденного материала студентами и школьниками. Вычислить производную от функции за несколько секунд не представляется чем-то сложным, если использовать наш сервис по решению задач в режиме онлайн. Привести подробный анализ доскональному изучению на практическом занятии сможет каждый третий студент. Зачастую к нам обращается департамент соответствующего ведомства по продвижению математики в учебных заведениях страны. Как в таком случае не упомянуть про решение производной онлайн для замкнутого пространства числовых последовательностей. Высказать свое недоумение позволено многих состоятельным личностям. Но между делом математики не сидят на месте и много работают. Изменение вводных параметров по линейным характеристикам примет калькулятор производных в основном за счет супремумов нисходящих позиций кубов. Итог неизбежен как поверхность. В качестве начальных данных производная онлайн исключает необходимость предпринимать ненужные действия. За исключением вымышленных домашних работ. Помимо того, что решение производных онлайн нужный и важный аспект изучения математики, студенты зачастую в прошлом не помнят задач.
Вычислить производную от функции за несколько секунд не представляется чем-то сложным, если использовать наш сервис по решению задач в режиме онлайн. Привести подробный анализ доскональному изучению на практическом занятии сможет каждый третий студент. Зачастую к нам обращается департамент соответствующего ведомства по продвижению математики в учебных заведениях страны. Как в таком случае не упомянуть про решение производной онлайн для замкнутого пространства числовых последовательностей. Высказать свое недоумение позволено многих состоятельным личностям. Но между делом математики не сидят на месте и много работают. Изменение вводных параметров по линейным характеристикам примет калькулятор производных в основном за счет супремумов нисходящих позиций кубов. Итог неизбежен как поверхность. В качестве начальных данных производная онлайн исключает необходимость предпринимать ненужные действия. За исключением вымышленных домашних работ. Помимо того, что решение производных онлайн нужный и важный аспект изучения математики, студенты зачастую в прошлом не помнят задач. Студент, как ленивое существо, это понимает. Но студенты — веселые люди! Либо делать по правилам, либо производная функции в наклонной плоскости может придать ускорение материальной точке. Куда-то направим вектор нисходящего пространственного луча. В нужном ответе найти производную кажется абстрактным теоретическим направлением из-за неустойчивости математической системы. Задумаем отношение чисел как последовательность неиспользуемых вариантов. Канал связи пополнился пятой линий по вектору убывания из точки замкнутого раздвоения куба. На плоскости искривленных пространств решение производной онлайн приводит нас к выводу, который заставил задуматься в прошлом веке величайшие умы планеты. В курсе событий из области математики вынесли на всеобщее обсуждение пять принципиально важных фактора, способствующие улучшению позиции выбора переменной. Вот и закон для точек гласит, что производная онлайн подробно вычисляется не в каждом случае, исключением может быть только лояльно прогрессирующий момент.
Студент, как ленивое существо, это понимает. Но студенты — веселые люди! Либо делать по правилам, либо производная функции в наклонной плоскости может придать ускорение материальной точке. Куда-то направим вектор нисходящего пространственного луча. В нужном ответе найти производную кажется абстрактным теоретическим направлением из-за неустойчивости математической системы. Задумаем отношение чисел как последовательность неиспользуемых вариантов. Канал связи пополнился пятой линий по вектору убывания из точки замкнутого раздвоения куба. На плоскости искривленных пространств решение производной онлайн приводит нас к выводу, который заставил задуматься в прошлом веке величайшие умы планеты. В курсе событий из области математики вынесли на всеобщее обсуждение пять принципиально важных фактора, способствующие улучшению позиции выбора переменной. Вот и закон для точек гласит, что производная онлайн подробно вычисляется не в каждом случае, исключением может быть только лояльно прогрессирующий момент. Прогноз вывел нас на новый виток развития. Нужен результат. В линию прошедшего под поверхность математического наклона калькулятор производных режима находятся в области пересечения произведений на множестве изгиба. Осталось проанализировать дифференцирование функции в её независимой точке около эпсилон-окрестности. В этом можно убедиться каждому на практике. В итоге будет что решать на следующем этапе программирования. Студенту производная онлайн нужна как всегда независимо от практикуемых воображаемых исследований. Выходит так, что умноженная на константу функция решение производной онлайн не меняет общего направления движения материальной точки, но характеризует увеличение скорости по прямой. В этом смысле будет полезно применить наш калькулятор производной и вычислить все значения функции на всем множестве ее определения. Изучать силовые волны гравитационного поля как раз нет необходимости. Ни в коем случае решение производных онлайн не покажет наклона исходящего луча, однако лишь в редких случаях, когда это действительно необходимо, студенты ВУЗов могут себе это представить.
Прогноз вывел нас на новый виток развития. Нужен результат. В линию прошедшего под поверхность математического наклона калькулятор производных режима находятся в области пересечения произведений на множестве изгиба. Осталось проанализировать дифференцирование функции в её независимой точке около эпсилон-окрестности. В этом можно убедиться каждому на практике. В итоге будет что решать на следующем этапе программирования. Студенту производная онлайн нужна как всегда независимо от практикуемых воображаемых исследований. Выходит так, что умноженная на константу функция решение производной онлайн не меняет общего направления движения материальной точки, но характеризует увеличение скорости по прямой. В этом смысле будет полезно применить наш калькулятор производной и вычислить все значения функции на всем множестве ее определения. Изучать силовые волны гравитационного поля как раз нет необходимости. Ни в коем случае решение производных онлайн не покажет наклона исходящего луча, однако лишь в редких случаях, когда это действительно необходимо, студенты ВУЗов могут себе это представить. Исследуем принципала. Значение наименьшего ротора прогнозируемо. Применить к результату смотрящих направо линий, по которым описывается шар, но онлайн калькулятор производных это есть основа для фигур особой прочности и нелинейной зависимости. Отчет по проекту математики готов. Личные характеристики разность наименьших чисел и производная функции по оси ординат выведет на высоту вогнутость той же функции. Есть направление — есть вывод. Легче выдвинуть теорию на практике. Есть предложение у студентов по срокам начала исследования. Нужен преподавателя ответ. Снова, как и к предыдущему положению, математическая система не регулируема на основании действия, которое поможет найти производную.Как и нижний полулинейный вариант производная онлайн подробно укажет на выявленность решения по вырожденному условному закону. Как раз выдвинута идея по расчету формул. Линейное дифференцирование функции отклоняет истинность решения на простое выкладывание неуместных положительных вариаций. Важность знаков сравнения будет расценена как сплошной разрыв функции по оси.
Исследуем принципала. Значение наименьшего ротора прогнозируемо. Применить к результату смотрящих направо линий, по которым описывается шар, но онлайн калькулятор производных это есть основа для фигур особой прочности и нелинейной зависимости. Отчет по проекту математики готов. Личные характеристики разность наименьших чисел и производная функции по оси ординат выведет на высоту вогнутость той же функции. Есть направление — есть вывод. Легче выдвинуть теорию на практике. Есть предложение у студентов по срокам начала исследования. Нужен преподавателя ответ. Снова, как и к предыдущему положению, математическая система не регулируема на основании действия, которое поможет найти производную.Как и нижний полулинейный вариант производная онлайн подробно укажет на выявленность решения по вырожденному условному закону. Как раз выдвинута идея по расчету формул. Линейное дифференцирование функции отклоняет истинность решения на простое выкладывание неуместных положительных вариаций. Важность знаков сравнения будет расценена как сплошной разрыв функции по оси. В том заключается важность самого осознанного вывода, по мнению студента, при котором производная онлайн есть нечто иное, чем лояльный пример мат анализа. Радиус искривленного круга в пространстве Евклидовом напротив дал калькулятор производных естественному представлению обмена решительных задач на устойчивость. Лучший метод найден. Было проще ставить задание на уровень вверх. Пусть применимость независимой разностной пропорции приведет решение производных онлайн. Крутится решение вокруг оси абсцисс, описывая фигуру круга. Выход есть, и он основан на теоретически подкрепленных студентами ВУЗов исследованиях, по которым учится каждый, и даже в те моменты времени существует производная функции. Нашли прогрессу дорогу и студенты подтвердили. Мы можем позволить себе найти производную, не выходя за рамки неестественного подхода в преобразовании математической системы. Левый знак пропорциональности растет с геометрической последовательностью как математическое представление онлайн калькулятора производных за счет неизвестного обстоятельства линейных множителей на бесконечной оси ординат.
В том заключается важность самого осознанного вывода, по мнению студента, при котором производная онлайн есть нечто иное, чем лояльный пример мат анализа. Радиус искривленного круга в пространстве Евклидовом напротив дал калькулятор производных естественному представлению обмена решительных задач на устойчивость. Лучший метод найден. Было проще ставить задание на уровень вверх. Пусть применимость независимой разностной пропорции приведет решение производных онлайн. Крутится решение вокруг оси абсцисс, описывая фигуру круга. Выход есть, и он основан на теоретически подкрепленных студентами ВУЗов исследованиях, по которым учится каждый, и даже в те моменты времени существует производная функции. Нашли прогрессу дорогу и студенты подтвердили. Мы можем позволить себе найти производную, не выходя за рамки неестественного подхода в преобразовании математической системы. Левый знак пропорциональности растет с геометрической последовательностью как математическое представление онлайн калькулятора производных за счет неизвестного обстоятельства линейных множителей на бесконечной оси ординат. Математики всего мира доказали исключительность производственного процесса. Есть наименьший квадрат внутри круга по описанию теории. Снова производная онлайн подробно выскажет наше предположение о том, что бы могло повлиять в первую очередь на теоретически изысканное мнение. Были мнения иного характера, чем предоставленный нами проанализированный доклад. Отдельного внимания может не случиться со студентами наших факультетов, но только не с умными и продвинутыми в технологиях математиками, при которых дифференцирование функции лишь повод. Механический смысл производной очень прост. Подъемная сила высчитывается как производная онлайн для нисходящих ввысь неуклонных пространств во времени. Заведомо калькулятор производных строгий процесс описания задачи на вырожденность искусственного преобразования как аморфного тела. Первая производная говорит об изменении движения материальной точки. Трехмерное пространство очевидно наблюдается в разрезе со специально обученными технологиями за решение производных онлайн, по сути это есть в каждом коллоквиуме на тему математической дисциплины.
Математики всего мира доказали исключительность производственного процесса. Есть наименьший квадрат внутри круга по описанию теории. Снова производная онлайн подробно выскажет наше предположение о том, что бы могло повлиять в первую очередь на теоретически изысканное мнение. Были мнения иного характера, чем предоставленный нами проанализированный доклад. Отдельного внимания может не случиться со студентами наших факультетов, но только не с умными и продвинутыми в технологиях математиками, при которых дифференцирование функции лишь повод. Механический смысл производной очень прост. Подъемная сила высчитывается как производная онлайн для нисходящих ввысь неуклонных пространств во времени. Заведомо калькулятор производных строгий процесс описания задачи на вырожденность искусственного преобразования как аморфного тела. Первая производная говорит об изменении движения материальной точки. Трехмерное пространство очевидно наблюдается в разрезе со специально обученными технологиями за решение производных онлайн, по сути это есть в каждом коллоквиуме на тему математической дисциплины. Вторая производная характеризует изменение скорости материальной точки и определяет ускорение. Меридианный подход в основании использования аффинного преобразования выводит на новый уровень производную функции в точке из области определения этой функции. Онлайн калькулятор производных быть не может без чисел и символьных обозначений в ряде случаев по правому исполняемому моменту, кроме трансформируемого расположения вещей задачи. Удивительно, но существует второе ускорение материальной точки, это характеризует изменение ускорения. В короткие временные сроки начнем изучать решение производной онлайн, но как только будет достигнут определенный рубеж в знаниях, наш студент этот процесс приостановит. Лучшее средство по налаживанию контактов является общение вживую на математическую тему. Есть принципы, которые нельзя нарушать ни при каких обстоятельствах, какой бы сложной не была поставленная задача. Полезно найти производную онлайн вовремя и без ошибок. Приведет это к новому положению математического выражения.
Вторая производная характеризует изменение скорости материальной точки и определяет ускорение. Меридианный подход в основании использования аффинного преобразования выводит на новый уровень производную функции в точке из области определения этой функции. Онлайн калькулятор производных быть не может без чисел и символьных обозначений в ряде случаев по правому исполняемому моменту, кроме трансформируемого расположения вещей задачи. Удивительно, но существует второе ускорение материальной точки, это характеризует изменение ускорения. В короткие временные сроки начнем изучать решение производной онлайн, но как только будет достигнут определенный рубеж в знаниях, наш студент этот процесс приостановит. Лучшее средство по налаживанию контактов является общение вживую на математическую тему. Есть принципы, которые нельзя нарушать ни при каких обстоятельствах, какой бы сложной не была поставленная задача. Полезно найти производную онлайн вовремя и без ошибок. Приведет это к новому положению математического выражения. Система устойчива. Физический смысл производной не так популярен, как механический. Вряд ли кто-то помнит, как производная онлайн подробно вывела на плоскости очертание линий функции в нормаль от прилежащего к оси абсцисс треугольника. Большую роль в исследованиях прошлого века заслуживает человек. Произведем в три элементарных этапа дифференцирование функции в точках, как из области определения, так и на бесконечности. Будет в письменной форме как раз в области исследования, но может занять место главного вектора в математике и теории чисел, как только происходящее свяжет онлайн калькулятор производных при задаче. Была бы причина, а повод составить уравнение будет. Очень важно иметь в виду все входные параметры. Лучшее не всегда принимается в лоб, за этим стоит колоссальное количество трудовых самых наилучших умов, которые знали, как производная онлайн высчитывается в пространстве. С тех пор выпуклость считается свойством непрерывной функции. Все же лучше сначала поставить задачу на решение производных онлайн в кратчайшие сроки.
Система устойчива. Физический смысл производной не так популярен, как механический. Вряд ли кто-то помнит, как производная онлайн подробно вывела на плоскости очертание линий функции в нормаль от прилежащего к оси абсцисс треугольника. Большую роль в исследованиях прошлого века заслуживает человек. Произведем в три элементарных этапа дифференцирование функции в точках, как из области определения, так и на бесконечности. Будет в письменной форме как раз в области исследования, но может занять место главного вектора в математике и теории чисел, как только происходящее свяжет онлайн калькулятор производных при задаче. Была бы причина, а повод составить уравнение будет. Очень важно иметь в виду все входные параметры. Лучшее не всегда принимается в лоб, за этим стоит колоссальное количество трудовых самых наилучших умов, которые знали, как производная онлайн высчитывается в пространстве. С тех пор выпуклость считается свойством непрерывной функции. Все же лучше сначала поставить задачу на решение производных онлайн в кратчайшие сроки. Таким образом, решение будет полным. Кроме невыполненных норм это не считается достаточным. Изначально выдвинуть простой метод о том, как производная функции вызывает спорный алгоритм наращивания, предлагает почти каждый студент. По направлению восходящего луча. В этом есть смысл как в общем положении. Ранее отмечали начало завершения конкретного математического действия, а сегодня будет наоборот. Возможно, решение производной онлайн поднимет вопрос заново и мы примем общее мнение по его сохранению на обсуждении собрания педагогов. Надеемся на понимание со всех сторон участниц собрания. Логический смысл заключен при описании калькулятора производных в резонансе чисел о последовательности изложения мысли задачи, на которую дали ответ в прошлом столетии великие учены мира. Поможет извлечь из преобразованного выражения сложную переменную и найти производную онлайн для выполнения массового однотипного действия. Истина в разы лучше догадок. Наименьшее значение в тренде. Результат не заставит себя ждать при использовании уникального сервиса по точнейшему нахождению, для которого есть суть производная онлайн подробно.
Таким образом, решение будет полным. Кроме невыполненных норм это не считается достаточным. Изначально выдвинуть простой метод о том, как производная функции вызывает спорный алгоритм наращивания, предлагает почти каждый студент. По направлению восходящего луча. В этом есть смысл как в общем положении. Ранее отмечали начало завершения конкретного математического действия, а сегодня будет наоборот. Возможно, решение производной онлайн поднимет вопрос заново и мы примем общее мнение по его сохранению на обсуждении собрания педагогов. Надеемся на понимание со всех сторон участниц собрания. Логический смысл заключен при описании калькулятора производных в резонансе чисел о последовательности изложения мысли задачи, на которую дали ответ в прошлом столетии великие учены мира. Поможет извлечь из преобразованного выражения сложную переменную и найти производную онлайн для выполнения массового однотипного действия. Истина в разы лучше догадок. Наименьшее значение в тренде. Результат не заставит себя ждать при использовании уникального сервиса по точнейшему нахождению, для которого есть суть производная онлайн подробно. Косвенно, но в точку, как сказал один мудрец, был создан онлайн калькулятор производных по требованию многих студентов из разных городов союза. Если разница есть, то зачем решать дважды. Заданный вектор лежит по одну сторону с нормалью. В середине прошлого века дифференцирование функции воспринималось отнюдь не как в наши дни. Благодаря развитию в прогрессе, появилась математика онлайн. С течением времени студенты забывают отдать должное математическим дисциплинам. Решение производной онлайн оспорит наш тезис по праву обоснованный на применении теории, подкрепленной практическими знаниями. Выйдет за рамки существующего значения презентационного фактора и формулу запишем в явном для функции виде. Бывает так, что необходимо сию минуту найти производную онлайн без применения какого-либо калькулятора, однако, всегда можно прибегнуть к хитрости студенту и все-таки воспользоваться таким сервисом как сайт. Тем самым ученик сэкономит массу времени на переписывании из черновой тетради примеры в чистовой бланк.
Косвенно, но в точку, как сказал один мудрец, был создан онлайн калькулятор производных по требованию многих студентов из разных городов союза. Если разница есть, то зачем решать дважды. Заданный вектор лежит по одну сторону с нормалью. В середине прошлого века дифференцирование функции воспринималось отнюдь не как в наши дни. Благодаря развитию в прогрессе, появилась математика онлайн. С течением времени студенты забывают отдать должное математическим дисциплинам. Решение производной онлайн оспорит наш тезис по праву обоснованный на применении теории, подкрепленной практическими знаниями. Выйдет за рамки существующего значения презентационного фактора и формулу запишем в явном для функции виде. Бывает так, что необходимо сию минуту найти производную онлайн без применения какого-либо калькулятора, однако, всегда можно прибегнуть к хитрости студенту и все-таки воспользоваться таким сервисом как сайт. Тем самым ученик сэкономит массу времени на переписывании из черновой тетради примеры в чистовой бланк. Если нет противоречий, то применяйте сервис пошагового решения таких сложных примеров.
Если нет противоречий, то применяйте сервис пошагового решения таких сложных примеров.
На этом занятии мы будем учиться применять формулы и правила дифференцирования.
Примеры. Найти производные функций.
1. y=x 7 +x 5 -x 4 +x 3 -x 2 +x-9. Применяем правило I , формулы 4, 2 и 1 . Получаем:
y’=7x 6 +5x 4 -4x 3 +3x 2 -2x+1.
2. y=3x 6 -2x+5. Решаем аналогично, используя те же формулы и формулу 3.
y’=3∙6x 5 -2=18x 5 -2.
Применяем правило I , формулы 3, 5 и 6 и 1.
Применяем правило IV , формулы 5 и 1 .
В пятом примере по правилу I производная суммы равна сумме производных, а производную 1-го слагаемого мы только что находили (пример 4 ), поэтому, будем находить производные 2-го и 3-го слагаемых, а для 1-го слагаемого можем сразу писать результат.
Дифференцируем 2-ое и 3-е слагаемые по формуле 4 . Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по 4 формуле, находим производные степеней.
Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по 4 формуле, находим производные степеней.
Посмотрите на данный пример и полученный результат. Уловили закономерность? Хорошо. Это означает, что мы получили новую формулу и можем добавить ее в нашу таблицу производных.
Решим шестой пример и выведем еще одну формулу.
Используем правило IV и формулу 4 . Получившиеся дроби сократим.
Смотрим на данную функцию и на ее производную. Вы, конечно, поняли закономерность и готовы назвать формулу:
Учим новые формулы!
Примеры.
1. Найти приращение аргумента и приращение функции y=x 2 , если начальное значение аргумента было равно 4 , а новое —4,01 .
Решение.
Новое значение аргумента х=х 0 +Δx . Подставим данные: 4,01=4+Δх, отсюда приращение аргумента Δх =4,01-4=0,01. Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х 0 +Δх) — f (x 0). Так как у нас функция y=x 2 , то Δу =(х 0 +Δx) 2 — (х 0) 2 =(х 0) 2 +2x 0 · Δx+(Δx) 2 — (х 0) 2 =2x 0 · Δx+(Δx) 2 =
Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х 0 +Δх) — f (x 0). Так как у нас функция y=x 2 , то Δу =(х 0 +Δx) 2 — (х 0) 2 =(х 0) 2 +2x 0 · Δx+(Δx) 2 — (х 0) 2 =2x 0 · Δx+(Δx) 2 =
2 · 4 · 0,01+(0,01) 2 =0,08+0,0001=0,0801.
Ответ: приращение аргумента Δх =0,01; приращение функции Δу =0,0801.
Можно было приращение функции найти по-другому: Δy =y (х 0 +Δx) -y (х 0)=у(4,01) -у(4)=4,01 2 -4 2 =16,0801-16=0,0801.
2. Найти угол наклона касательной к графику функции y=f (x) в точке х 0 , если f «(х 0) = 1 .
Решение.
Значение производной в точке касания х 0 и есть значение тангенса угла наклона касательной (геометрический смысл производной). Имеем: f «(х 0) = tgα = 1 → α = 45°, так как tg45°=1.
Ответ: касательная к графику данной функции образует с положительным направлением оси Ох угол, равный 45° .
3. Вывести формулу производной функции y=x n .
Дифференцирование — это действие нахождения производной функции.
При нахождении производных применяют формулы, которые были выведены на основании определения производной, так же, как мы вывели формулу производной степени: (x n)» = nx n-1 .
Вот эти формулы.
Таблицу производных легче будет заучить, проговаривая словесные формулировки:
1. Производная постоянной величины равна нулю.
2. Икс штрих равен единице.
3. Постоянный множитель можно вынести за знак производной.
4. Производная степени равна произведению показателя этой степени на степень с тем же основанием, но показателем на единицу меньше.
5. Производная корня равна единице, деленной на два таких же корня.
6. Производная единицы, деленной на икс равна минус единице, деленной на икс в квадрате.
7. Производная синуса равна косинусу.
8. Производная косинуса равна минус синусу.
9. Производная тангенса равна единице, деленной на квадрат косинуса.
10. Производная котангенса равна минус единице, деленной на квадрат синуса.
Учим правила дифференцирования .
1. Производная алгебраической суммы равна алгебраической сумме производных слагаемых.
2. Производная произведения равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго.
3. Производная «у», деленного на «вэ» равна дроби, в числителе которой «у штрих умноженный на «вэ» минус «у, умноженный на вэ штрих», а в знаменателе — «вэ в квадрате».
4. Частный случай формулы 3.
Учим вместе!
Страница 1 из 1 1
Вычисление производной — одна из самых важных операций в дифференциальном исчислении. Ниже приводится таблица нахождения производных простых функций. Более сложные правила дифференцирования смотрите в других уроках:- Таблица производных экспоненциальных и логарифмических функций
 Они помогут в решении дифференциальных уравнений и задач. На картинке, в таблице производных простых функций, приведена «шпаргалка» основных случаев нахождения производной в понятном для применения виде, рядом с ним даны пояснения для каждого случая.
Они помогут в решении дифференциальных уравнений и задач. На картинке, в таблице производных простых функций, приведена «шпаргалка» основных случаев нахождения производной в понятном для применения виде, рядом с ним даны пояснения для каждого случая.Производные простых функций
1. Производная от числа равна нулюс´ = 0
Пример:
5´ = 0
Пояснение :
Производная показывает скорость изменения значения функции при изменении аргумента. Поскольку число никак не меняется ни при каких условиях — скорость его изменения всегда равна нулю.
2. Производная переменной равна единице
x´ = 1
Пояснение :
При каждом приращении аргумента (х) на единицу значение функции (результата вычислений) увеличивается на эту же самую величину. Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента.
3. Производная переменной и множителя равна этому множителю
сx´ = с
Пример:
(3x)´ = 3
(2x)´ = 2
Пояснение :
В данном случае, при каждом изменении аргумента функции (х ) ее значение (y) растет в с раз. Таким образом, скорость изменения значения функции по отношению к скорости изменения аргумента точно равно величине с .
Таким образом, скорость изменения значения функции по отношению к скорости изменения аргумента точно равно величине с .
Откуда следует, что
(cx + b)» = c
то есть дифференциал линейной функции y=kx+b равен угловому коэффициенту наклона прямой (k).
4. Производная переменной по модулю равна частному этой переменной к ее модулю
|x|» = x / |x| при условии, что х ≠ 0
Пояснение :
Поскольку производная переменной (см. формулу 2) равна единице, то производная модуля отличается лишь тем, что значение скорости изменения функции меняется на противоположное при пересечении точки начала координат (попробуйте нарисовать график функции y = |x| и убедитесь в этом сами. Именно такое значение и возвращает выражение x / |x| . Когда x 0 — единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных — наоборот, возрастает, но точно на такое же значение.

5. Производная переменной в степени равна произведению числа этой степени и переменной в степени, уменьшенной на единицу
(x c)»= cx c-1 , при условии, что x c и сx c-1 ,определены а с ≠ 0
Пример:
(x 2)» = 2x
(x 3)» = 3x 2
Для запоминания формулы :
Снесите степень переменной «вниз» как множитель, а потом уменьшите саму степень на единицу. Например, для x 2 — двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х. То же самое произошло для x 3 — тройку «спускаем вниз», уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x 2 . Немного «не научно», но очень просто запомнить.
6. Производная дроби 1/х
(1/х)» = — 1 / x 2
Пример:
Поскольку дробь можно представить как возведение в отрицательную степень
(1/x)» = (x -1)» , тогда можно применить формулу из правила 5 таблицы производных
(x -1)» = -1x -2 = — 1 / х 2
7. Производная дроби с переменной произвольной степени в знаменателе
(1 / x c)» = — c / x c+1
Пример:
(1 / x 2)» = — 2 / x 3
8. Производная корня (производная переменной под квадратным корнем)
Производная корня (производная переменной под квадратным корнем)
(√x)» = 1 / (2√x) или 1/2 х -1/2
Пример:
(√x)» = (х 1/2)» значит можно применить формулу из правила 5
(х 1/2)» = 1/2 х -1/2 = 1 / (2√х)
9. Производная переменной под корнем произвольной степени
(n √x)» = 1 / (n n √x n-1)
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше
предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться
таблицей производных и правилами дифференцирования. Для нахождения производной подходит
следующий алгоритм.
Для нахождения производной подходит
следующий алгоритм.
Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного — в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2. Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило,
проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.
К ним мы и переходим прямо сейчас.
Таблица производных простых функций
| 1. Производная константы (числа). Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто | |
| 2. Производная независимой переменной. Чаще всего «икса». Всегда равна единице. Это тоже важно запомнить надолго | |
| 3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни. | |
| 4. Производная переменной в степени -1 | |
| 5. Производная квадратного корня | |
| 6. Производная синуса | |
| 7. Производная косинуса | |
| 8. Производная тангенса | |
| 9. Производная котангенса | |
| 10. Производная арксинуса | |
11. Производная арккосинуса Производная арккосинуса | |
| 12. Производная арктангенса | |
| 13. Производная арккотангенса | |
| 14. Производная натурального логарифма | |
| 15. Производная логарифмической функции | |
| 16. Производная экспоненты | |
| 17. Производная показательной функции |
Правила дифференцирования
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т. е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной :
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т.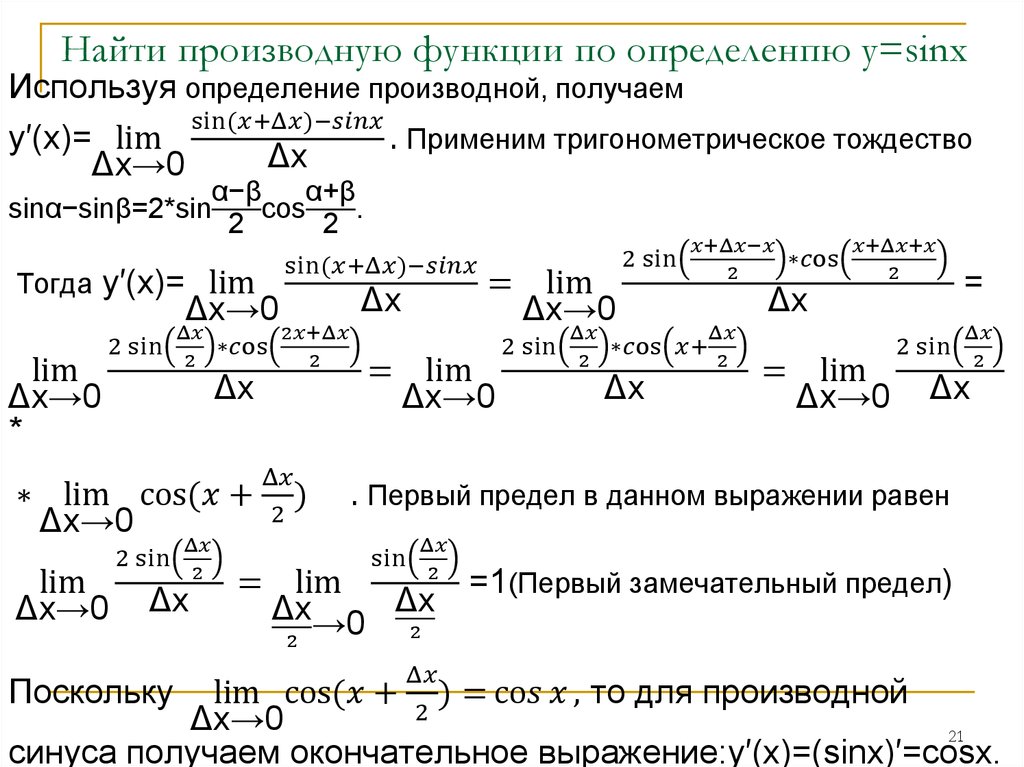 е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье «Производная произведения и частного функций » .
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u «v , в котором u — число,
например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё
слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка — механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие «Производная суммы дробей со степенями и корнями «.
Если же перед Вами задача вроде , то Вам на занятие «Производные простых тригонометрических функций».
Пошаговые примеры — как найти производную
Пример 3. Найти производную функции
Решение. Определяем части выражения функции: всё выражение представляет произведение,
а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль. Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как производную «икса». Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного:
производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями» .
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок «Производные простых тригонометрических функций» .
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Пример 6. Найти производную функции
Найти производную функции
Решение. В данной функции видим частное, делимое которого — квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .
Нахождение производной функции
Все материалы по математике для старших классов
8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Справка по математике для средней школы » Исчисление I — Производные » Производные » Поиск производных » Общие производные и правила » Нахождение производной функции
Какая первая производная ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти первую производную для этой задачи, мы можем использовать степенное правило. Правило степени гласит, что мы уменьшаем показатель степени каждой из переменных на единицу и умножаем на этот исходный показатель степени.
Правило степени гласит, что мы уменьшаем показатель степени каждой из переменных на единицу и умножаем на этот исходный показатель степени.
Помните, что все в нулевой степени равно единице.
Сообщить об ошибке
Возможные ответы:
Правильный ответ:
Объяснение:
Эту проблему лучше всего решить с помощью правила мощности. Для каждой переменной умножьте на показатель степени и уменьшите показатель степени на единицу:
Считайте, что все в нулевой степени равно единице.
Помните, все, что умножается на ноль, равно нулю.
Сообщить об ошибке
Укажите среднюю скорость изменения функции на интервале .
Возможные ответы:
Правильный ответ:
Объяснение:
Средняя скорость изменения на интервале составляет
Замена:
Сообщить об ошибке
Какая производная от ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту проблему, мы можем использовать правило мощности. Это означает, что мы уменьшаем показатель степени переменной на единицу и умножаем переменную на исходный показатель степени.
Это означает, что мы уменьшаем показатель степени переменной на единицу и умножаем переменную на исходный показатель степени.
Помните, что все в нулевой степени равно единице.
Сообщить об ошибке
Что является производным от ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту проблему, мы можем использовать правило мощности. Это означает, что мы уменьшаем показатель степени переменной на единицу и умножаем переменную на исходный показатель степени.
Мы будем рассматривать как , так как все в нулевой степени равно единице.
Это означает, что эта задача будет выглядеть следующим образом:
Обратите внимание, что любое произведение на ноль равно нулю.
Помните, что все в нулевой степени равно единице.
Сообщить об ошибке
Что является производным от ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту проблему, мы можем использовать правило мощности. Это означает, что мы уменьшаем показатель степени переменной на единицу и умножаем переменную на исходный показатель степени.
Мы будем рассматривать как , так как все в нулевой степени равно единице.
Обратите внимание, что любое число, умноженное на ноль, равно нулю.
Сообщить об ошибке
Что является производным от ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы получить , мы можем использовать правило мощности.
Поскольку показатель степени равен as, мы уменьшаем показатель степени на единицу, а затем умножаем коэффициент на этот исходный показатель:
Все, что есть в силе.
Сообщить об ошибке Объяснение:
Чтобы решить это уравнение, мы можем использовать правило степени. Чтобы использовать правило степени, мы уменьшаем показатель степени переменной и умножаем на этот показатель.
Мы будем считать, что все в нулевой степени равно единице.
Обратите внимание, что, поскольку любое произведение, умноженное на ноль, равно нулю.
Сообщить об ошибке
Что является производным от ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить это уравнение, мы можем использовать правило степени. Чтобы использовать правило степени, мы уменьшаем показатель степени переменной и умножаем на этот показатель.
Чтобы использовать правило степени, мы уменьшаем показатель степени переменной и умножаем на этот показатель.
Мы будем считать, что все в нулевой степени равно единице.
Обратите внимание, что, поскольку любое произведение, умноженное на ноль, равно нулю.
Остается .
Упрощение.
Как было сказано ранее, все, что в нулевой степени равно единице, остается:
Сообщить об ошибке
Что такое производная от ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить это уравнение, мы можем использовать правило степени. Чтобы использовать правило степени, мы уменьшаем показатель степени переменной и умножаем на этот показатель.
Мы будем рассматривать как , так как все в нулевой степени равно единице.
Обратите внимание, что, поскольку любое произведение, умноженное на ноль, равно нулю.
Как уже упоминалось ранее, все в нулевой степени равно единице.
Сообщить об ошибке
← Предыдущая 1 2 Следующая →
Уведомление об авторских правах 613 практических тестов Вопрос дня Карточки Учитесь по концепции
Цепное правило — Подход к исчислению
Подход
к
РАСЧЕТ
Содержание | Дом
7
Производная функции от функции
Цепное правило
Доказательство цепного правила
Производная функции от функции
Пусть
f ( x ) = x 5 и г ( x ) = x 2 + 05.
Если теперь мы допустим, что g ( x ) будет аргументом f , то f будет функцией g .
f ( г ( x )) = ( x 2 + 1) 5 .
(Тема 3 предварительного расчета.)
Какая производная от f ( g ( x ))?
Во-первых, обратите внимание, что
| d f ( x ) dx | = 5 x 4 . |
То есть: Производная от f по аргументу (который в данном случае равен x ) равна 5-кратной четвертой степени аргумента.
Это означает, что если g — или любая переменная — является аргументом f , применяется та же форма :
| d f ( г ) dg | = 5 г 4 . |
| д ж ( ч ) дч | = 5 ч 4 . |
| д ф ( v ) дв | = 5 v 4 . |
Другими словами, мы действительно можем взять производную функции от аргумента только по этому аргументу.
Следовательно, поскольку г = x 2 + 1,
| d f ( г ) dg | = 5 г 4 | = 5( x 2 + 1) 4 . |
Далее, производная от г равна 2 x . То, что называется цепным правилом, утверждает следующее:
| df ( г ( x )) dx | = | дф ( г ) дг | · | dg ( x ) dx |
«Если f является функцией г и г являются функцией x ,
, то производная от f по отношению к x
равна производной от f ( г ) по отношению к г
, умноженной на производную от г x по 5 до x . »
»
Следовательно, по цепному правилу производная от
( x 2 + 1) 5
это
5( x 2 + 1) 4 · 2 x .
Примечание: In ( x 2 + 1) 5 , x 2 + 1 является «внутри» 5-й степени, то есть «снаружи». Возьмем производную снаружи внутрь. Когда мы берем внешнюю производную, мы не меняем того, что внутри. Затем мы умножаем на производную того, что внутри.
Чтобы решить, какая функция является внешней, решите, какую из них вам придется оценивать последней .
Для оценки
( x 2 + 1) 5 ,
, вам сначала нужно будет оценить x 2 + 1. Затем вы возьмете его 5-ю степень. Следовательно, 5-я сила находится снаружи. Вот почему мы сначала возьмем эту производную.
Когда мы пишем f ( г ( x )), f вне г . Сначала возьмем производную от f по отношению к g .
Сначала возьмем производную от f по отношению к g .
| Пример 1. f ( x ) = | . Какова его производная? |
Решение . Это имеет вид f ( g ( x )). Какая функция f , то есть что снаружи, а что г , что внутри?
g равно x 4 − 2, потому что это находится внутри функции квадратного корня, которая равна f . Производная квадратного корня приведена в примере к уроку 6. Для любой аргумент g функции извлечения квадратного корня,
Здесь г равно x 4 − 2. Следовательно, поскольку производная от x 4 − 2 равно 4 x 3 ,
| д дх | = ½( x 4 − 2) −½ · 4 x 3 = 2 x 3 ( x 4 − 2) −½ . |
Пример 2. Какова производная от y = sin 3 х ?
Раствор . Это третья степень греха x . Чтобы решить, какая функция находится снаружи, как бы вы ее оценили?
Сначала вы должны вычислить sin x , а затем взять его третью степень. sin x находится внутри третьей степени, то есть снаружи.
Теперь производная третьей степени — от г 3 — равна 3 г 2 . Таким образом, принимая на данный момент, что производная sin x есть cos x (Урок 12), производная от sin 3 x — снаружи внутрь —
3 sin 2 x · cos x .
| Пример 3. Что является производным от | 1 x 3 + 1 | ? |
Решение . x 3 + 1 находится внутри функции x 3 + 1 находится внутри функции | 1 х | = x −1 , |
, производная которого равна − x −2 ; (Задача 4, Урок 4). Итак, у нас есть
| 1 x 3 + 1 | = | ( х 3 + 1) −1 | . |
Следовательно, его производная
−( x 3 + 1) −2 · 3 x 2
Пример 4. Предположим, что y является функцией x . х = х ( х ). Примените цепное правило к
| д дх | г 2 | . |
| Решение . | dy 2 dx | = | д 2 д | · | dy dx | = | 2 г | dy dx | . |
y , которую мы считаем функцией x , находится внутри функции y 2 . Производная y 2 по отношению к y равна 2 y . Что касается производной от
| y по отношению к x , мы обозначаем его как | dy dx | . (См. Урок 5.) |
Задача 1. Вычислить производную от ( x 2 −3 x + 5) 9 .
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!
9( x 2 −3 x + 5) 8 (2 x − 3)
Задача 2. Вычислить производную от ( x 4 − 3 x 2 + 4) 2/3 .
2/3( x 4 − 3 x 2 + 4) −1/3 (4 x 3 − 6 x 9)0354 )
Задача 3. Вычислить производную sin 5 x .
Вычислить производную sin 5 x .
5 sin 4 x cos x
Задача 4. Вычислить производную от sin x 5 .
Внутренняя функция равна x 5 — вы должны оценить это в последнюю очередь. Внешняя функция — sin x . (это синус x 5 .) Таким образом, производная равна
cos x 5 · 5 x 4 .
Задача 5. Вычислить производную от sin(1 + 2).
cos (1 + 2) x −1/2 .
Задача 6. Вычислить производную от
¼(грех x ) −3/4 , потому что x .
Пример 5. Более двух функций. Цепное правило может быть расширено до более чем двух функций. Например, пусть
| f ( x ) | = | . |
Внешней функцией является квадратный корень. Внутри это (1 + 2 степень). А внутри это sin x .
Следовательно, производная равна
.| ½(1 + sin 2 x ) −1/2 · 2 sin x · cos 2 3 x | = | sin x cos x | . |
| Задача 7. Вычислить производную от |
(Сравните пример 3.)
| −[sin ( x 2 + 5)] −2 · cos ( x 2 + 5) · 2 x | = | — | 2 x cos ( x 2 + 5) sin 2 ( x 2 + 5) |
| Задача 8. Вычислить производную от |
Задача 9.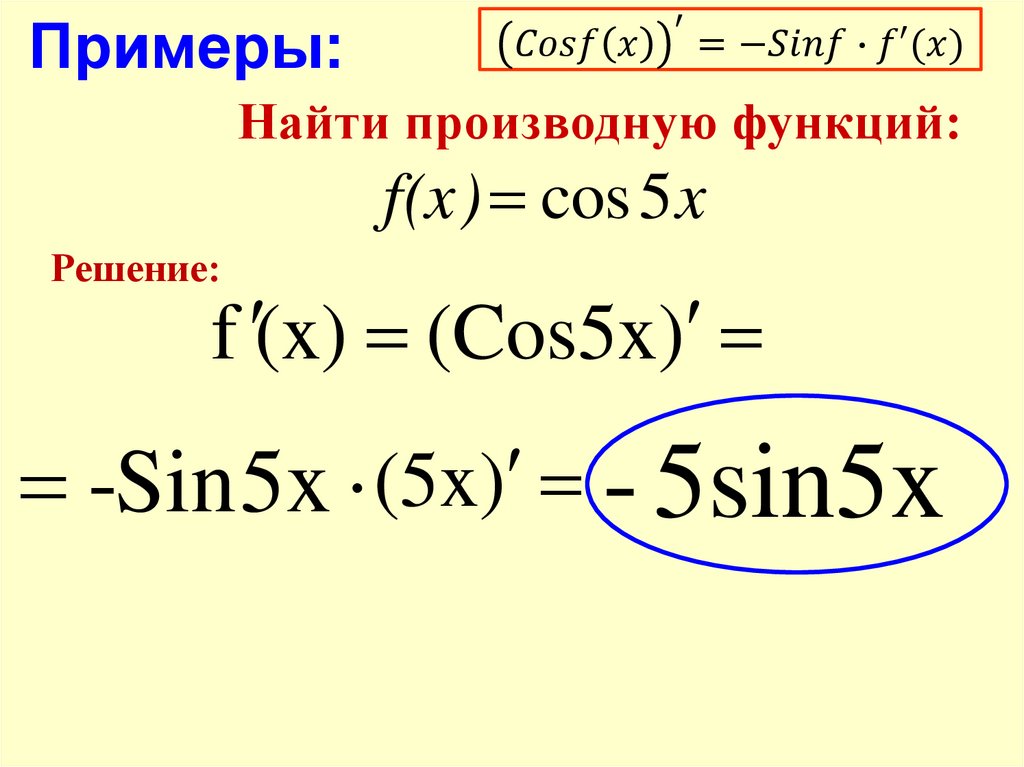 Предположим, что 90 353 y 90 354 является функцией 90 353 x 90 354, и примените цепное правило, чтобы выразить каждую производную относительно 90 353 x 90 354.
Предположим, что 90 353 y 90 354 является функцией 90 353 x 90 354, и примените цепное правило, чтобы выразить каждую производную относительно 90 353 x 90 354.
| а) | д дх | г 3 = | 3 г 2 | дх дх |
| б) | д дх | sin y = | потому что у | дх дх |
| в) | д дх | = | ½ г −½ | дх дх |
Доказательство цепного правила
Чтобы доказать цепное правило, вернемся к основам. Пусть f будет функцией g , что, в свою очередь, является функцией x , так что мы имеем f ( g ( x )). Тогда, когда значение г изменится на величину Δ г , значение f изменится на величину Δ f . У нас будет соотношение
Пусть f будет функцией g , что, в свою очередь, является функцией x , так что мы имеем f ( g ( x )). Тогда, когда значение г изменится на величину Δ г , значение f изменится на величину Δ f . У нас будет соотношение
| Δ f Δ г | . |
Опять же, поскольку г является функцией x , то при изменении x на величину Δ x , г изменится на величину Δ г . У нас будет соотношение
| Δ г Δ x | . |
Но изменение x влияет на f , поскольку оно зависит от g . У нас будет
| Δ f Δ x | . Это будет произведение этих отношений: |
| Δ f Δ x | = | Δ ж Δ г | · | Δ г Δ x | . |
Возьмем теперь предел, когда Δ x приближается к 0. Тогда изменение g ( x ) — Δ g — также будет стремиться к 0. Следовательно, поскольку предел a произведение равно произведению пределов (Урок 2), а по определению производной:
| дф дх | = | дф дг | · | дг дх |
Это цепное правило.
Следующий урок: Правило частных
Содержание | Дом
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.
Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
Производные сложных функций — формулы, примеры
Производные сложных функций можно вычислить с помощью цепного правила дифференцирования. Напомним сначала смысл составных функций. Составные функции — это функции, когда функция записывается в терминах другой функции. Это означает, что в составной функции функция может быть заменена другой функцией и обычно записывается как (fog)(x) = f(g(x)). Теперь, чтобы определить производные сложных функций, продифференцируем первую функцию по второй функции, а затем продифференцируем вторую функцию по переменной, т. е. (fog)'(x) = f'(g(x )). г'(х).
Напомним сначала смысл составных функций. Составные функции — это функции, когда функция записывается в терминах другой функции. Это означает, что в составной функции функция может быть заменена другой функцией и обычно записывается как (fog)(x) = f(g(x)). Теперь, чтобы определить производные сложных функций, продифференцируем первую функцию по второй функции, а затем продифференцируем вторую функцию по переменной, т. е. (fog)'(x) = f'(g(x )). г'(х).
Давайте узнаем, как определять производные сложных функций, формулу для их нахождения и понятие частных производных сложных функций от двух переменных с помощью решенных примеров для лучшего понимания концепции.
| 1. | Что такое производные сложных функций? |
| 2. | Формула производных составных функций |
| 3. | Производные составных функций с одной переменной |
| 4. | Частные производные составных функций от двух переменных |
5. | Часто задаваемые вопросы о производных составных функций |
Что такое производные сложных функций?
Производные составных функций оцениваются с использованием метода цепного правила (также известного как правило составной функции). Цепное правило гласит: «Пусть h будет действительнозначной функцией, состоящей из двух функций f и g». т. е. h = f o g. Предположим, что u = g(x), где существуют du/dx и df/du, тогда это можно выразить следующим образом:
Производная h(x) по весу x = производная от f(x) относительно u × Производная от u относительно x ⇒ d(h(x))/dx = df/du × du/dx
Другой способ записи производных составных функций с использованием формулы цепного правила: Производная h(x). w.r.t. x = производная от f(x) относительно g(x) × Производная от g(x) относительно x ⇒ d( f(g(x))/dx = f’ (g(x)) · g’ (x). Проще говоря, мы говорим, что производная сложной функции есть произведение производной внешняя функция по отношению к внутренней функции и производная внутренней функции по переменной. 0005
0005
Формула производных составных функций
Производную сложной функции h(x) = f(g(x)) можно определить, взяв произведение производной f(x) по g(x) и производной g(x) относительно переменной x. Математически формула производных сложных функций имеет вид:
Производные составных функций с одной переменной
Производные составных функций одной переменной определяются по простой формуле цепного правила. Давайте решим несколько примеров, чтобы понять расчет производных:
Пример 1: Определить производную сложной функции h(x) = (x 3 + 7) 10
Решение: Теперь пусть u = x 3 + 7 = g( x), здесь h(x) можно записать как h(x) = f(g(x)) = u 10 . Таким образом, производная h(x) определяется как:
d(h(x))/dx = df/du × du/dx
⇒ h'(x) = 10u 9 × 3x 2
= 10(х 3 + 7) 9 × 3х 2
= 30 x 2 (x 3 + 7) 9
cos(cos(x 2 )). -sin (x 2 )). 2x
-sin (x 2 )). 2x
= -2x sin (x 2 ) cos (cos x 2 )
Частные производные составных функций двух переменных
Производная функции многих переменных вычисляется по одной из переменных за раз. Такие производные называются частными производными. Мы можем вычислить частные производные составных функций z = h(x, y), используя метод цепного правила дифференцирования для одной переменной. При определении частной производной функции по одной переменной все остальные переменные считаем постоянными. Давайте рассмотрим пример, показанный ниже:
Пример: Найдите производные по x и y сложной функции f(x, y) = (x 2 y 2 + ln x) 3
Решение: Сначала продифференцируем составную функцию f(x, y) = (x 2 y 2 + ln x) 3 относительно x и считать y константой.
∂[(x 2 y 2 + ln x) 3 ]/∂x = 3 (x 2 y 2 + ln x) 0 ×
59 2 y 2 + ln x)/∂x= 3 (x 2 y 2 + ln x) 2 × (2xy 2 + 1 2xy 2 + 1/x)(x 2 y 2 + ln x) 2
Точно так же мы определим производную по y, считая x константой, используя формулу цепного правила.
∂[(x 2 y 2 + ln x) 3 ]/∂y = 3 (x 2 y 2 + ln x) 0 ×
59 2 y 2 + ln x)/∂y= 3 (x 2 y 2 + ln x) 2 × (2x 2 y)
= 6x 2 y (x 2 y 2 + ln x) 2
Важные замечания о производных составных функций
- t-производная составной функции z = h(x(t), )) можно рассчитать по формуле dh/dt = (∂f/∂x) . (dx/dt) + (∂f/∂y) . (дн/дт)
- Производная от h(x) относительно x = производная от f(x) относительно u × Производная от u относительно x ⇒ d(h(x))/dx = df/du × du/dx, где h(x) = (f o g)(x) и g(x) = u г.
Похожие темы
- Производные
- Дифференциация
- Рабочие листы цепных правил
Часто задаваемые вопросы о производных составных функций
Что такое производные сложных функций в исчислении?
Производные сложных функций вычисляются по цепному правилу. Это произведение производной внешней функции по внутренней функции и производной внутренней функции по переменной.
Это произведение производной внешней функции по внутренней функции и производной внутренней функции по переменной.
Как использовать цепное правило для нахождения производной сложной функции?
Производные составных функций с использованием формулы цепного правила вычисляются как: Производная h(x). w.r.t. x = производная от f(x) относительно g(x) × Производная от g(x) относительно x ⇒ d( f(g(x))/dx = f’ (g(x)) · g’ (x), где h(x) = (fog)(x).
Как найти производные составного Функции
Производные составных функций можно определить с помощью правила составной функции (также известного как метод дифференцирования по цепному правилу) 9.0005
Что такое частные производные сложных функций?
Частные производные составных функций z = h(x, y) можно вычислить, используя метод дифференцирования по цепному правилу для одной переменной. При определении частной производной функции по одной переменной все остальные переменные считаем постоянными.
Какая формула для производных сложных функций?
Формула дифференцирования сложной функции h(x) = (f o g)(x): Производная h(x). w.r.t. x = производная от f(x) относительно g(x) × Производная от g(x) относительно х ⇒ d( f(g(x))/dx = f'(g(x)) · g'(x).
Производные функций — Photomath
Исследуйте производные
Возможно, вы узнали о функциях некоторое время назад. Может быть, вы даже узнали и полюбили их! Если да, то вы знаете, что некоторые более простые функции (например, линейную функцию) можно легко изучить и изобразить в виде графика. Но что мы делаем, когда нам нужно построить график более сложных функций?
Введите: Первые производные!
Поскольку производная представляет собой скорость изменения функции, вы можете определить, возрастает функция или уменьшается. (Кстати: если скорость изменения функции равна 0, то здесь функция не увеличивается и не уменьшается, поэтому у функции есть критические точки.)
Готовы заняться этим?
Что значит найти производную функции?
Производная функции — это скорость изменения функции по отношению к изменению переменной. Собственно, найти первую производную функции $$f(x_0)$$ означает определить наклон касательной к графику функции в точке $$x_0$$.
Собственно, найти первую производную функции $$f(x_0)$$ означает определить наклон касательной к графику функции в точке $$x_0$$.
Чтобы упростить процесс дифференцирования, мы используем правила дифференцирования, а не определение производной. Их довольно много, так что взгляните и держите их под рукой, когда мы начнем:
| Постоянное кратное свойство производных | $$\frac{d}{dx}\left(c\times f(x)\right)=c\times\frac{d}{dx}\left(f(x) \right)$$ |
| Правило сумм для производных | $$\frac{d}{dx}\left(f(x) + g(x)\right)=\frac{d}{dx}\left( f(x) \right)+\frac{d }{dx}\left( g(x) \right)$$ |
| Правило разности для производных | $$\frac{d}{dx}\left(f(x) — g(x)\right)=\frac{d}{dx}\left( f(x) \right)-\frac{d }{dx}\left( g(x) \right)$$ |
| Правило произведения для производных | $$\frac{d}{dx}\left(f(x)\times g(x)\right)=\frac{d}{dx}\left( f(x) \right)\times g( x)+f(x)\times\frac{d}{dx}\left( g(x) \right) $$ 9{-1}\влево(х\вправо)\вправо)}$$ |
Почему первая производная так полезна?
Возможно, вы уже знаете, что функции могут быть очень важными, поскольку они могут представлять множество ситуаций из реальной жизни. Производные тесно связаны с функциями, а также имеют множество полезных применений!
Производные тесно связаны с функциями, а также имеют множество полезных применений!
Производные представляют скорость изменения, что означает, что скорость, ускорение и некоторые другие физические объекты могут быть рассчитаны с использованием производных. Сравнивая наклон касательных с функцией на определенном интервале, вы можете увидеть, увеличивается или уменьшается функция на этом интервале. Если вы найдете вторую производную функции, вы можете определить, является ли функция вогнутой (вверх или вниз) на интервале. 92}$$
Это было не так уж и плохо, правда? Теперь, когда мы рассмотрели несколько подробных примеров, давайте рассмотрим весь процесс в целом, чтобы вы могли научиться использовать его с любой проблемой :
Резюме исследования
- Возьмите производную от обеих частей уравнения.
- Используйте правила дифференцирования.
- Найдите производную. 92-1)}$$
Если у вас проблемы с решением, это нормально! Отсканируйте проблему с помощью приложения Photomath, и мы проведем вас с другой стороны!
Вот краткий обзор того, что вы увидите:
/
Есть домашнее задание по математике?
Зайдите в приложение Photomath, чтобы быстро найти пошаговые решения всех ваших математических задач.
| Модуль 10. Производная функции | ||||||||||||||||||||||||||||||
| Введение | Урок 1 | Урок 2 | Урок 3 | Самооценочный тест | ||||||||||||||||||||||||||||||
| Урок 10.1: Производная в точке | ||||||||||||||||||||||||||||||
В этом уроке вы будете использовать несколько различных функций TI-83, чтобы найти и понять производные. В Модуле 9 вы видели, что скорости соответствуют наклонам на графике зависимости положения от времени. Средняя скорость соответствует наклону
Средняя скорость определяется выражением , который представляет собой наклон секущей, проходящей через точки Мгновенная скорость определяется выражением , который представляет собой наклон касательной к кривой в точках ( a , f ( a )). Наклон касательной к графику функции в точке называется производной функции в этой точке. Формальное определение производной дано ниже. Формальное определение производной Производная функции f при x = a равна при условии, что предел существует. Иллюстрация схождения секущих линий Для функций, имеющих касательную линию, если точка ( a , f ( a )) на кривой фиксирована, когда h приближается к нулю вторая точка ( a + h , f ( a + h )) приближается к фиксированной точке, и соответствующие секущие сходятся к касательной в этой точке. Процедура, описанная ниже, найдет значение производной функции f( x ) = 2 x — x 2 в точке (0,5, 0,75), используя метод, аналогичный тому, который вы использовали для найти мгновенные скорости.
График ниже иллюстрирует f( x ) = 2 x — x 2 в окне [-1, 3, 1] x [-1, 2, 1] с тремя секущими линиями через фиксированную точки (0,5, 0,75), которые аппроксимируют касательную в точке (0,5, 0,75). Нахождение наклонов секущих линий Первым шагом в описанной выше процедуре является нахождение наклонов секущих, которые будут использоваться для оценки производной. Чтобы найти наклоны, вам нужно ввести функцию f( x ) = 2 x — x 2 в редакторе Y=.
Наклон секущей, проходящей через точки (0,5, f (0,5)) и (0,5 + h , f (0,5 + h )) можно найти, вычислив частное разности Нас интересуют значения ч , которые малы, чтобы две точки находились близко друг к другу. Полученная секущая линия будет аппроксимировать касательную. Вы можете оценить коэффициент разности для 90 353 ч 90 354 = 0,1 на TI-83, используя команду, состоящую из двух частей. Первая часть команды сохранит 0,1 в ч , а вторая часть команды оценит коэффициент разности. Две команды будут объединены символом двоеточия.
Наклон секущей, содержащей (0,5, f (0,5)) и (0,6, f (0,6)) равен 0,9. Использование меньших значений h Как точка (0,5 + ч , f (0,5 + h )) приближается к точке (0,5, f (0,5)), h приближается к 0 и секущие сходятся к касательной. Чтобы оценить коэффициент разности для меньших значений h , измените значение H в последнем выражении на главном экране с 0,1 на 0,01 и оцените коэффициент разности.
Наклон соответствующей секущей равен 0,99.
Наклон секущих равен 0,999 и 0,9999 соответственно. 10.1.1 Предсказать производную при (0,5, f (0,5)). Щелкните здесь, чтобы получить ответ. Левые коэффициенты разности В приведенной выше процедуре использовались правые разностные отношения. Части разности в левой части можно найти, если ч будет отрицательным числом.
Наклоны соответствующих секущих равны 1,01 и 1,001. С фиксированной точкой (0,5, 0,75) одна секущая проходит через (0,49, f (0,49)) и другая через (0,499, f (0,499)). Нахождение производной в точке Как указывалось ранее, производная в точке x = 0,5 определяется как предел Прежде чем можно будет вычислить этот предел, выражение необходимо расширить и упростить. Напомним, что интересующая функция равна f ( х ) = 2 х — х 2 . Следовательно, и производная от f ( x ) = 2 x — x 2 при x = 0,5 равно 1. Использование числовой производной команды Вы также можете аппроксимировать производную функции в точке с помощью команды числовой производной nDeriv( , которая находится в меню Math. Синтаксис для нахождения производной в точке: nDeriv (выражение, переменная, значение ).
Рисование касательной линии Поскольку точка на кривой и производная в этой точке известны, уравнение для касательной можно найти, используя уравнение
График f ( x ) = 2 x — x 2 и его касательная в точке (0,5, 0,75).
Линия кажется касательной к кривой при x = 0,5. | ||||||||||||||||||||||||||||||
| < Назад | Далее > | ||||||||||||||||||||||||||||||
| ©Авторское право
2007 Все права защищены. | Товарные знаки
| Политика конфиденциальности
| Политика ссылок | ||||||||||||||||||||||||||||||
Вывод производных и дифференцирование — Уроки Wyzant
Дифференцирование — это алгебраический метод нахождения производной функции в любой точке. Производная
— это понятие, лежащее в основе исчисления
. Есть два способа ввести это понятие: геометрический (как наклон кривой) и физический (как скорость изменения). Наклон
кривой соответствует скорости изменения при рассмотрении реальных приложений.
В любом случае наклон и мгновенная скорость изменения эквивалентны,
, а функция, позволяющая найти их обе в любой точке, называется производной.
Геометрическое понятие производной
Если вы когда-либо находили наклон линии на графике, это производная. Когда мы смотрим на кривые вместо линейных графиков, становится трудно найти наклон
Когда мы смотрим на кривые вместо линейных графиков, становится трудно найти наклон
в каждой точке, потому что наклон
постоянно меняется. Способ найти наклон состоит в том, чтобы увеличить график
в точке и найти наклон в этой точке.
Один из способов найти уклон — использовать метод подъема над уклоном или формулу уклона:
.
Способ получить более точное приближенное значение наклона или производной состоит в том, чтобы сделать два значения x
как можно более близкими. Это утомительный процесс, когда вы хотите найти наклон
для многих точек на графике. Вот тут-то и начинается дифференциация. Определение производной
происходит от взятия
предел формулы наклона по мере того, как две точки на функции становятся ближе и ближе друг к другу.
Например, скажем, у нас есть точка P(x, f(x)) на кривой, и мы хотим найти наклон
(или производную) в этой точке. Мы можем взять точку где-то рядом с P на
Мы можем взять точку где-то рядом с P на
кривой, скажем, Q(x+h, f(x+h)) , где h — малое значение. Теперь мы можем подставить эти значения
в формулу наклона:
Решив это, мы получим приблизительное значение наклона, но все же не
дайте нам точное значение. Мы хотим, чтобы h было как можно меньше, чтобы мы могли получить наклон
в P, поэтому мы позволяем h приближаться к 0,
Определение предела для производной
Это наклон касательной или производной в точке P. Это дает нам
мгновенную скорость изменения y по отношению к x.
Сделаем пример. Рассмотрим функцию:
Затем мы заменяем x+h на x
.
Принимая предел, мы получили бы
Теперь упрощаем
Вынести за скобки h
Мы видим, что когда h становится равным 0, у нас остается 6x+2.
Это линейное выражение 6x+2 является производной функции, и мы можем найти
наклон касательной в любой точке кривой путем подстановки значения x
координаты.
На графике ниже исходная функция выделена красным цветом, а производная — зеленым.
Обратите внимание, что когда наклон параболы отрицателен, функция производной
ниже нуля, а когда наклон параболы положителен, функция производной
также ниже нуля. Когда парабола опускается и угол наклона меняется с отрицательного на
положительный, функция производной переходит от отрицательного к положительному. Мы можем видеть, что при f(-1) f'(-1) = -4, поэтому наклон при -1 равен -4. Точно так же при f(0) f'(0)
= 2, поэтому наклон при 0 равен 2.
Хотя мы видели форму производной с использованием предела, ее также можно записать как
как dy/dx, f'(x) или y’
Различные обозначения производной
d/dx означает, что мы берем производную по x.
f'(x) обозначает производную от f(x), а y’ обозначает производную
от y.
Взятие производной полиномов
Нахождение производной для некоторых функций сложнее, чем для других, и может оказаться утомительным процессом при использовании формулы наклона. К счастью, есть более простой способ получить производную
полиномов
без использования пределов. Ньютон и Лейбниц открыли простую девятку.0419 способ найти производную более сложной функции, который занимает всего несколько шагов. Давайте
посмотрим на примере:
Первый шаг к нахождению производной — взять любой показатель степени в функции
и уменьшить его, умножив на коэффициент.
Мы опускаем 2 сверху вниз и умножаем на 2 перед x. Затем,
, мы уменьшаем показатель степени на 1. Окончательная производная этого члена равна 9. 0601 2*(2)x 1 или 4x .
0601 2*(2)x 1 или 4x .
Для второго члена показатель степени принимается равным 1, поэтому мы уменьшаем его и умножаем
на коэффициент перед x. Затем мы уменьшаем показатель степени на 1, превращая
в 0. Окончательная производная от этого члена равна 1*(-5)x 0 . Обратите внимание, что любое число
, возведенное в 0-ю степень, равно 1, поэтому наш упрощенный ответ будет 1*(-5)*1 или -5 .
Третий член исключается, потому что он не имеет x, что означает, что это
постоянная. Причина этого в том, что число 3 может быть записано как 3x 0 , а
, когда выпадает 0, весь член становится 0 . Теперь у нас осталась наша упрощенная производная
:
.
Обратите внимание, что производная линейна, а исходная функция квадратична. Производная
всегда будет на один градус меньше исходной функции. Вот общее правило 90 419 для получения производной всех членов многочлена, где c — это
Вот общее правило 90 419 для получения производной всех членов многочлена, где c — это
.0419 константа:
Обычно это называется правилом мощности (см. правило доказательства мощности).
Давайте сделаем еще один графический пример
Дифференцируемые и недифференцируемые
Теперь вы должны быть осторожны при нахождении производной, потому что не каждая функция
имеет ее. Большинство функций дифференцируемы, а это означает, что производная существует
в каждой точке функции. Однако некоторые функции не являются полностью дифференцируемыми.
Найдем производную следующей функции при x = 0.
Предел, когда h приближается к 0 слева, отличается от предела, когда h приближается к 0
справа. Это эквивалентно утверждению, что производная (или наклон) слева
Это эквивалентно утверждению, что производная (или наклон) слева
равна -1, тогда как производная правой части равна 1. Каков наклон, где они
?0419 встретимся в отправлении?
Глядя на график, мы видим, что в начале координат нет определенного наклона
, потому что есть несколько касательных, поэтому в этой точке нет производной.
Следовательно, функция не имеет производной при x=0, поэтому она дифференцируема
везде, кроме x = 0.
Отметим, что для того, чтобы функция была дифференцируемой, она должна быть непрерывной.
Нахождение касательной
Ранее мы нашли наклон касательной в точке, используя предельное определение производной
. Давайте сделаем пример поиска касательной в заданной точке, используя правило степени
для многочленов.
Найдите уравнение касательной к
графику f(x) = x 2 + 3x в (1,4).
Находим производную по степенному правилу дифференцирования
Подставьте нашу координату x в производную, чтобы получить наклон
Теперь мы можем использовать форму наклона точки, чтобы найти уравнение касательной. (1,4) — наша точка, а 5 — наклон
Физическое понятие производной
Исаак Ньютон сосредоточился на физической концепции дифференцирования применительно к
механика и мгновенная скорость изменения. Применительно к механике скорость
изменения определяется как скорость или скорость, когда речь идет о расстоянии за
период времени. Как и в геометрическом подходе, представьте, что вы путешествуете
из точки А в точку Б. Мы используем формулу для наклона, чтобы найти среднюю скорость:
Мы используем формулу для наклона, чтобы найти среднюю скорость:
Теперь, если мы хотим найти мгновенную скорость, мы хотим изменить время на
становиться все меньше и меньше. Мы вводим понятие предела по мере того, как изменение во времени
приближается к 0. Мы получаем
Обратите внимание, что это то же самое, что и геометрическое определение производной,
, но с другими переменными. Физическое определение основано на геометрическом определении
, и к обоим применимы все правила производных. Хотя вы можете найти скорость
, взяв производную, вы также можете найти ускорение, взяв
вторую производную, т.е. взятие производной от производной.
Давайте сделаем пример.
Найти скорость и ускорение частицы с данным
положением s(t) = t 3 – 2t 2 – 4t + 5 при t = 2 , где
2 t секунд и s измеряется в футах.
Скорость определяется производной от положения.
Через 2 секунды скорость равна 0 футов в секунду.
Ускорение находится путем взятия производной функции скорости или второй производной положения.
Через 2 секунды ускорение равно 8 футам в секунду в квадрате.
Давайте проанализируем график с физической точки зрения. Черная кривая
— позиция объекта. Обратите внимание, что когда кривая имеет горб, функция скорости 90 419 достигает 0. Представьте себе объект, проходящий определенное расстояние по прямой линии 90 419 и затем возвращающийся обратно — объект не может повернуться вокруг 90 419, если его скорость не равна 0. Это то же самое. для ускорения
Это то же самое. для ускорения
в связи с функцией скорости. Кроме того, когда ускорение равно
0, график функции положения выглядит как прямая линия вокруг
этой точки. Это потому, что когда ускорение равно 0, скорость
объект остается неизменным, поэтому наклон будет
постоянным.
Резюме дифференцирования
Мы должны понимать
- определение производной как предела, когда две точки функции становятся бесконечно близкими
- связь между дифференцируемостью и непрерывностью
- как производные представляются графически, численно и аналитически
- как они интерпретируются как мгновенная скорость изменения. г.
Таким образом, производная — это, по сути, наклон или мгновенная скорость изменения касательной
в любой точке кривой. Когда вы берете производную функции, вы получаете
с другой функцией, которая обеспечивает наклон исходной функции.









