2. Дифференциальные уравнения первого порядка. Задача Коши
Общий вид дифференциального уравнения первого порядка
. | (4) |
Если это уравнение разрешимо относительно , то
. | (5) |
Следовательно, общим решением дифференциального уравнения (4) называется функция
,
зависящая от х и произвольной постоянной С, обращающая это уравнение в тождество.
Общее решение, заданное в неявном виде
,
называется общим интегралом.
Геометрически общее решение представляет собой семейство интегральных кривых на плоскости, зависящих от одного параметра
Частное решение и частный интеграл
имеют соответственно вид:; .
Уравнение имеет бесконечное число решений. Чтобы из этого множества решений выделить одно, т. е. частное решение, надо задать некоторые дополнительные условия. Таким условием, определяющим частное решение, является начальное условие, или условие Коши:
, | (6) |
где х0 – заданный элемент из области определения.
Задача отыскания частного решения уравнения (5), удовлетворяющего начальному условию (6), называется задачей Коши для этого уравнения.
Рассмотрим простейшее дифференциальное уравнение первого порядка
, | (7) |
где – непрерывная на некотором промежутке функция.
Решение ОДУ (7) находится интегрированием левой и правой частей (7):
.
ПРИМЕР 1
Решить уравнение и построить семейство интегральных кривых.
Решение
– общее решение данного уравнения, где С = const.
Задавая конкретные значения постоянной С, будем иметь частные решения исходного уравнения.
Таким образом, интегральные кривые – это множество парабол. Построим их:
Если для данного уравнения задана задача Коши, т. е. необходимо найти решение исходного уравнения, удовлетворяющего начальному условию, например:
,
то для ее решения необходимо в общее решение задачи вместо х и у подставить , и найти конкретное значение произвольной постоянной С. Так как , то .
Следовательно, решением данной задачи Коши будет функция
.
Заметим, что график этой функции проходит через точку . С геометрической точки зрения, решить задачу Коши – значит, из бесконечного множества интегральных кривых найти ту, которая проходит через точку с координатами .
ПРИМЕР 2
Решить задачу Коши
, .
Решение
,
– общее решение данного уравнения.
Для решения задачи Коши найдем константу С. Подставим в общее решение , :
.
Таким образом, решением задачи Коши будет функция
.
Следовательно, интегральная кривая имеет вид
Дифференциальным уравнением с разделяющимися переменными называется уравнение вида
, | (8) |
или уравнение вида
. | (9) |
Заметим, что уравнение (8) можно привести к виду (9), и наоборот. Действительно, так как , то, умножив обе части уравнения на , будем иметь:
– уравнение вида (9).
Далее будем рассматривать уравнение вида (9). Для его решения необходимо добиться того, чтобы при дифференциале стояли только функции, зависящие от переменной х, а при дифференциале – функции, зависящие от переменной у, а затем получившееся уравнение с разделенными переменными можно будет почленно интегрировать. Заметим, что это необходимо сделать обязательно, так как непосредственно уравнение вида (9) интегрировать крайне сложно.
Пусть ни одна из функций не равна тождественно нулю. Тогда, разделив уравнение (9) на произведение , получим уравнение с разделенными переменными:
, . | (10) |
Интегрируя (10) почленно, получаем общий интеграл исходного уравнения (9):
. | (11) |
Заметим, что мы делили уравнение (9) на произведение , предполагая, что , . При этом мы могли не учесть другие решения исходного уравнения. Непосредственной подстановкой или необходимо проверить, будут ли еще решения уравнения (9) помимо решения (11).
ПРИМЕР 3
Решить уравнение .
Решение
.
Таким образом, мы получили уравнение с разделенными переменными. Интегрируя его, получим
– общее решение данного уравнения. Заметим:
1) мы взяли константу С в виде , учитывая вид интегралов;
2) мы делили на
.
Пусть теперь
.
Непосредственной подстановкой убеждаемся,
что – решение исходного уравнения. Но оно
не будет особым решением, так как оно
получается из общего при
.
ПРИМЕР 4
Решить задачу Коши
, .
Решение
Данное уравнение есть уравнение вида (9), т. е. уравнение с разделяющимися переменными. Непосредственно его интегрировать нельзя, так как при стоит функция от у, а при – функция от х. Умножив данное уравнение на , получим
. | (12) |
Уравнение (12) – уравнение с разделенными переменными. Следовательно, его можно почленно интегрировать (обратите внимание на выбор вида константы С):
– общее решение
исходного ОДУ.
Интегральными кривыми
будут окружности радиуса с центром в начале координат:
Для решения задачи Коши необходимо из бесконечного множества интегральных кривых найти ту, которая проходит через точку . Для нахождения конкретного значения С подставим в общее решение:
.
Таким образом, решением задачи Коши будет функция , а соответствующая интегральная кривая – это окружность радиуса с центром в начале координат.
ПРИМЕР 5
Решить уравнение
.
Решение
Данное уравнение не является уравнением с разделяющимися переменными (9), так как при дифференциале стоит функция , которую нельзя представить в виде произведения , поэтому это уравнение нельзя решить способом, описанным выше. Способ решения подобных уравнений будет описан в следующей лекции.
Заметим, что ОДУ
с разделяющимися переменными играют
очень важную роль в теории дифференциальных
уравнений.
Как правило, основные виды
ОДУ первого порядка путем различных
подстановок будут приводиться к данному
типу уравнений.
Лекция 2. ОДНОРОДНЫЕ И ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
План:
1. Однородные дифференциальные уравнения.
2. Линейные дифференциальные уравнения.3. Уравнения в полных дифференциалах.
Дифференциальные уравнения с разделяющимися переменными и их интегрирование: определение, задача Коши
- Понятие дифференциального уравнения с разделяющимися переменными
- Задача Коши
- Закон радиоактивного распада
- Зарядка конденсатора
- Примеры
п.1. Понятие дифференциального уравнения с разделяющимися переменными
Дифференциальное уравнение – это уравнение, в которое входят производные некоторой функции, а также может входить сама функция, независимая переменная и параметры.
2=19\) – ДУ первого порядка третьей степени
\(\sqrt{y+1}=y’x\) — ДУ первого порядка первой степени
Самыми простыми для решения будут такие уравнения, у которых можно разделить переменные, т.е. собрать всё, что связано с функцией \(y\), по одну сторону знака равенства, и всё, что связано с независимой переменной \(x\), — по другую сторону.
Дифференциальное уравнение первого порядка \(y’=f(x,y)\) называется уравнением с разделяющимися переменными, если функцию \(f(x,y)\) можно представить в виде произведения двух функций \(f(x,y)=g(x)\cdot h(y)\), по отдельности зависящих только от независимой переменной \(x\) и только от функции \(y\).
Например:
Уравнение \(\sqrt{y+1}=y’x\) является уравнением с разделяющимися переменными, т.к. $$ y’=\frac{\sqrt{y+1}}{x}=g(x)\cdot h(y),\ \ \text{где}\ g(x)=\frac1x,\ h(y)=\sqrt{y+1} $$
Алгоритм решения ДУ с разделяющимися переменными
На входе: уравнение первого порядка \(y’=f(x,y)\), для которого \(f(x,y)=g(x)\cdot h(y)\)
Шаг 1.
{\frac23}-1,\ x\geq 1\)
п.3. Закон радиоактивного распада
В многочисленных экспериментах по определению радиоактивности вещества был установлен следующий факт:
| Число распадов ΔN, которые произошли за интервал времени Δt, пропорционально числу атомов N в образце. |
Перейдем к бесконечно малым \(dN\) и \(dt\) и запишем соответствующее этому факту дифференциальное уравнение: $$ \frac{dN}{td}=-\lambda N $$ где знак «-» учитывает уменьшение числа атомов N со временем.
Полученное ДУ является уравнением с разделяющимися переменными.
Найдем его общее решение: $$ \frac{dN}{N}=-\lambda dt\Rightarrow\int\frac{dN}{N}=-\lambda\int dt\Rightarrow \ln N=-\lambda t+C $$ Пусть в начальный момент времени \(t=0\) в образце было \(N_0\) атомов.
Подставляем найденное C в общее решение. Получаем: $$ \ln N=-\lambda N+\ln N_0\Rightarrow \ln N-\ln N_0=-\lambda t\Rightarrow\ln\frac{N}{N_0}=-\lambda t\Rightarrow\frac{N}{N_0}=e^{-\lambda t} $$
Закон радиоактивного распада
Количество атомов радиоактивного вещества убывает по экспоненциальному закону: $$ N(t)=N_0e^{-\lambda t} $$ где \(N_0\) — начальное количество атомов вещества, \(\lambda\) – постоянная распада, характеризующая вероятность распада в единицу времени.
За время \(\tau=\frac 1\lambda\) число атомов радиоактивного вещества уменьшается в e раз.
За время \(T_{1/2}=\frac{\ln 2}{\lambda}\) (время полураспада) число атомов радиоактивного вещества уменьшается в 2 раза.
п.4. Зарядка конденсатора
| Соберем цепь, состоящую из конденсатора C, резистора R, источника ЭДС E и ключа K. Пусть в начальный момент времени конденсатор разряжен, напряжение на обкладках: \(U(0)=0\) Замкнем ключ и начнем зарядку конденсатора. |
По закону Ома для замкнутой цепи можем записать: $$ I(R+r_0)+U=\varepsilon $$ где \(I\) — ток в цепи, \(I(R+r_0)\) – падение напряжения на резисторе и источнике, \(U\) — напряжение на конденсаторе, \(\varepsilon\) – ЭДС источника.
Ток в цепи равен производной от заряда по времени: $$ I=\frac{dq}{dt}=\frac{d(CU)}{dt}=C\frac{dU}{dt} $$ Подставляем: $$ C\frac{dU}{dt}\cdot (R+r_0)=\varepsilon-U $$ Получили ДУ с разделяющимися переменными: $$ \frac{dU}{\varepsilon-U}=\frac{dt}{C(R+r_0)} $$ Интегрируем (не забываем про минус перед U в знаменателе): $$ \int\frac{dU}{\varepsilon-U}=-\ln(\varepsilon-U),\ \ \int\frac{td}{C(R+r_0)} = \frac{t}{C(R+r_0)} $$ Общее решение: $$ \ln(\varepsilon-U)=-\frac{t}{C(R+r_0)}+B $$ где \(B\) константа, которую мы обозначили так, чтобы не путать с емкостью.
4=\frac{1}{16} $$ в 16 раз.
Получаем: $$ m\left(4T_{\frac12}\right)=\frac{m_0}{16},\ \ m\left(4T_{\frac12}\right)=\frac{64}{16}=4\ \text{(г)} $$ Ответ: 4 г
Пример 4. Выведите зависимость \(U(t)\) на обкладках конденсатора при его разрядке в RC-цепи.
| Разрядка конденсатора происходит в цепи без источника ЭДС. Пусть в начальный момент заряд на обкладках \(U(0)=U_0.\) Замкнем ключ и начнем разрядку конденсатора. |
По закону Ома для замкнутой цепи: $$ IR+U=0 $$ Ток в цепи равен производной от заряда по времени: $$ I=\frac{dq}{dt}=\frac{d(CU)}{dt}=C\frac{dU}{dt} $$ Подставляем: $$ RC\frac{dU}{dt}=-U $$ Получили ДУ с разделяющимися переменными: $$ \frac{dU}{U}=-\frac{dt}{RC} $$ Интегрируем: $$ \int\frac{dU}{U}=\ln U,\ \ \int{dt}{RC}=\frac{t}{RC} $$ Общее решение: $$ \ln U=-\frac{t}{RC}+B $$ где \(B\) константа, которую мы обозначили так, чтобы не путать с емкостью.
Начальное условие \(U(0)=0\). Подставляем: $$ \ln U_0=-\frac{0}{RC}+B\Rightarrow B=\ln U_0 $$ Решение задачи Коши: \begin{gather*} \ln U=-\frac{t}{RC}+\ln U_0\Rightarrow\ln U-\ln U_0=-\frac{t}{RC}\Rightarrow \ln\frac{U}{U_0}=-\frac{t}{RC}\\ \frac{U}{U_0}=e^{-\frac{t}{RC}} \end{gather*}
| Изменение напряжение на обкладках конденсатора при разрядке: $$ U(t)=U_0 e^{-\frac{t}{RC}} $$ |
Например, \(при U_0=5В,\ RC=0,01 с\) график разрядки конденсатора имеет вид:
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья… Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда… Интересное: Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей… Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления. Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 3 из 8Следующая ⇒ Обыкновенным дифференциальным уравнением называется уравнение, которое содержит производные от искомой функции y(x): (2. где x — независимая переменная, (n) — порядок производной. Наивысший порядок n, входящий в уравнение (2.1) называется порядком дифференциального уравнения. Общее решение дифференциального уравнения имеет вид: (2.2) где c1,c2,…,cn — произвольные постоянные. Их количество определяется порядком уравнения. Если значения c1,c2,…,cn известны и соответственно равны , то из (2.2) получаем частное решение: Значения определяются из условий, которые называются дополнительными условиями для уравнения (2.1). Графики частных решений называются интегральными кривыми для данного дифференциального уравнения. Общее решение можно представить в виде семейства интегральных кривых. Если дополнительные условия задаются в одной точке, то такая задача называется задачей Коши. Дополнительные условия в задачи Коши называются начальными условиями, а точка x=x0, в которой они задаются — начальной точкой. Если дополнительные условия задаются в двух точках a и b — “краях” отрезка [a,b], где ищется решение, то такая задача называется краевой задачей. Дифференциальное уравнение первого порядка: (2.4) при заданных начальных условиях y(x0)=y0 называется задачей Коши для дифференциального уравнения первого порядка. Если мы имеем систему дифференциальных уравнений первого порядка, то задачу Коши удобно записать в векторной форме:
Теорема существования решения задачи Коши Интегральные кривые
Экзаменационный билет № 10 Корректность вычислительных алгоритмов. Три условия корректности вычислительного алгоритма. Обусловленность вычислительного алгоритма Корректность вычислительных алгоритмов 1. Результат получен после конечного числа шагов 2. Результат устойчив к малым возмущения входных данных 3. Результат обладает вычислительной устойчивостью. 4. Метод Монте-Карло для задач вычисления кратных интегралов Формула (5.33) непосредственно обобщается на кратные интегралы
,
где – объем области интегрирования. Например, для двукратного интеграла с прямоугольной областью интегрирования имеем
. Модификации метода Эйлера второго порядка точности для дифференциального уравнения первого порядка Метод трапеции. В этом методе решение имеет вид: (2.9) Этот метод неявный, т.к. для определения значений yi+1 необходимо решать нелинейное уравнение (2.9). Метод трапеций имеет второй порядок точности по h.
метод Эйлера-Коши. Данный метод является прямым методом второго порядка точности: (2.10)
Экзаменационный билет № 11 Требования, предъявляемые к вычислительным алгоритмам. Требования к вычислительным алгоритмам 1. Экономичность(число элементарных операций) 2. Надлежащая точность(решение задачи с заданной или приемлемой точностью) 3. Экономия памяти(-) 4. Простота Требования к программным реализациям алгоритмов 1. Надежность(без ошибок) 2. Работоспособность 3. Переносимость 4. Поддерживаемость 5. Простота ⇐ Предыдущая12345678Следующая ⇒ Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни. |
Теорема существования решения задачи Коши. Интегральные кривые — КиберПедия
..
1)
Требования к программным реализациям вычислительной задачи
..П.1. Постановка задачи Коши
Известно, что обыкновенное дифференциальное уравнение первого порядка имеет вид:
y’ (x) = f(x, y(x)).
Решением уравнения является дифференцируемая функция y(x), которая при подстановке в уравнение обращает его в тождество. График решения дифференциального уравнения называется интегральной кривой.
Производную y’(x) в каждой точке (x, y) можно геометрически интерпретировать как тангенс угла наклона касательной к графику решения, проходящего через эту точку, т е.
k = tg = f (x, y).
Уравнение y’ (x) = f(x, y(x)) определяет целое семейство решений. Чтобы выделить одно решение, задают начальное условие: y ( ) = , где – начальное значение аргумента x, а – начальное значение функции.
Задача Коши заключается в отыскании функции y = y(x), удовлетворяющей уравнению и начальному условию. Обычно определяют решение задачи Коши на отрезке, расположенном справа от начального значения , т. е. для .
Даже для простых дифференциальных уравнений первого порядка не всегда удается получить аналитическое решение. Поэтому большое значение имеют численные методы решения. Численные методы позволяют определить приближенные значения искомого решения y(x) на некоторой выбранной сетке значений аргумента , i = 0, 1, …n. Точки называются узлами сетки, а величина – шагом сетки. Часто рассматривают равномерные сетки, для которых шаг постоянен, = h = . При этом решение получается в виде таблицы, в которой каждому узлу сетки соответствуют приближенные значения функции y(x) в узлах сетки .
Численные методы не позволяют найти решение в общем виде, зато они применимы к широкому классу дифференциальных уравнений.
Сходимость численных методов решения задачи Коши.
Пусть y(x) – решение задачи Коши. Назовем глобальной погрешностью (или просто погрешностью) численного метода функцию = – , заданную в узлах сетки . В качестве абсолютной погрешности примем величину R = | y – |.
Численный метод решения задачи Коши называется сходящимся, если для него R→0 при h→0. Говорят, что метод имеет p-ый порядок точности, если для погрешности справедлива оценка R ≤ C , p > 0, C – константа, C ≠ 0.
П.2. Метод Эйлера
Простейшим методом решения задачи Коши является метод Эйлера. Будем решать задачу Коши
на отрезке . Выберем шаг и построим сетку с системой узлов , вычислим приближенные значения функции y(x) в узлах сетки Заменив производную y’ (x) конечными разностями на отрезках [ ], i = 0, 1, …, n —1, получим приближенное равенство , i = 0, 1, …, n —1, которое можно переписать так:
, i = 0, 1, …, n — 1.
Данные формулы и начальное условие являются расчетными формулами метода Эйлера.
Геометрическая интерпретация одного шага метода Эйлера заключается в том, что решение на отрезке [ ] заменяется касательной
y — = y’ ( )( x – ),
проведенной в точке ( , y( )) к интегральной кривой, проходящей через эту точку. После выполнения n шагов неизвестная интегральная кривая заменяется ломаной линией (ломаной Эйлера).
Оценка погрешности. Для оценки погрешности используется правило Рунге, которое заключается в следующем. Пусть — приближения, полученные с шагом , а — приближения, полученные с шагом h. Тогда справедливо приближенное равенство:
Таким образом, чтобы оценить погрешность одношагового метода с шагом h, нужно найти то же решение с шагом h и вычислить величину, стоящую справа в формуле, т. е.
где p – порядок точности.
Так как метод Эйлера имеет первый порядок точности, т. е. p = 1, то приближенное равенство примет вид:
Используя правило Рунге, можно построить процедуру приближенного вычисления решения задачи Коши с заданной точностью . Нужно, начав вычисления с некоторого значения шага h, последовательно уменьшать это значение в два раза, каждый раз вычисляя приближенное значение , i = 0, 1, …, n. Вычисления прекращаются тогда, когда будет выполнено условие: Для метода Эйлера это условие имеет вид: Приближенным решением будут значения , i = 0, 1, …, n.
Пример.
Найдем решение на отрезке следующей задачи Коши:
Решение.
Возьмем шаг h = 0.2. Тогда
В соответствии с формулами получим расчетную формулу Эйлера:
,
Решение представим в виде таблицы:
| i | ||||||
0. 2
| 0.4 | 0.6 | 0.8 | 1.0 | ||
| 1.0000 | 1.2000 | 1.3733 | 1.5294 | 1.6786 | 1.8237 |
Исходное уравнение есть уравнение Бернулли. Его решение можно найти в явном виде:
Для сравнения точного и приближенного решения представим точное решение в виде таблицы:
| i | ||||||
| 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | ||
| 1.0000 | 1.1832 | 1.3416 | 1.4832 | 1.6124 | 1.7320 |
Из таблицы видно, что погрешность составляет:
Дата добавления: 2016-06-15; просмотров: 3085; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Дифференциальные уравнения первого порядка.
Задача Коши. Общее, частное и особое решения дифференциального уравнения — МегаобучалкаСвойства общего решения.
1) Т.к. постоянная С – произвольная величина, то вообще говоря дифференциальное уравнение имеет бесконечное множество решений.
2) При каких- либо начальных условиях х = х0, у(х0) = у0 существует такое значение С = С0, при котором решением дифференциального уравнения является функция у = j(х, С0).
Определение. Решение вида у = j(х, С0) называется частным решениемдифференциального уравнения.
Определение. Задачей Коши(Огюстен Луи Коши (1789-1857)- французский математик) называется нахождение любого частного решения дифференциального уравнения вида у = j(х, С0), удовлетворяющего начальным условиям у(х0) = у0.
Теорема Коши. (теорема о существовании и единственности решения дифференциального уравнения 1- го порядка)
Если функция f(x, y) непрерывна в некоторой области D в плоскости XOY и имеет в этой области непрерывную частную производную , то какова бы не была точка (х0, у0) в области D, существует единственное решение уравнения , определенное в некотором интервале, содержащем точку х0, принимающее при х = х0 значение j(х0) = у0, т.
е. существует единственное решение дифференциального уравнения.
Определение. Интеграломдифференциального уравнения называется любое уравнение, не содержащее производных, для которого данное дифференциальное уравнение является следствием.
Пример. Найти общее решение дифференциального уравнения .
Общее решение дифференциального уравнения ищется с помощью интегрирования левой и правой частей уравнения, которое предварительно преобразовано следующим образом:
Теперь интегрируем:
— это общее решение исходного дифференциального уравнения.
Допустим, заданы некоторые начальные условия: x0 = 1; y0 = 2, тогда имеем
При подстановке полученного значения постоянной в общее решение получаем частное решение при заданных начальных условиях (решение задачи Коши).
Определение. Интегральной кривойназывается график y = j(x) решения дифференциального уравнения на плоскости ХОY.
Определение. Особым решениемдифференциального уравнения называется такое решение, во всех точках которого условие единственности Коши (см. Теорема Коши. ) не выполняется, т.е. в окрестности некоторой точки (х, у) существует не менее двух интегральных кривых.
Особые решения не зависят от постоянной С.
Особые решения нельзя получить из общего решения ни при каких значениях постоянной С. Если построить семейство интегральных кривых дифференциального уравнения, то особое решение будет изображаться линией, которая в каждой своей точке касается по крайней мере одной интегральной кривой.
Отметим, что не каждое дифференциальное уравнение имеет особые решения.
Дифференциальные уравнения первого порядка.
Определение. Дифференциальным уравнением первого порядканазывается соотношение, связывающее функцию, ее первую производную и независимую переменную, т.е. соотношение вида:
Если такое соотношение преобразовать к виду то это дифференциальное уравнение первого порядка будет называться уравнением, разрешенным относительно производной.
Преобразуем такое выражение далее:
Функцию f(x,y) представим в виде: тогда при подстановке в полученное выше уравнение имеем:
— это так называемая дифференциальная формауравнения первого порядка.
Далее рассмотрим подробнее типы уравнений первого порядка и методы их решения.
23.Теорема Коши существования и единственности решения дифференциального уравнения первого порядка (без доказательства).
Теорема Коши. (теорема о существовании и единственности решения дифференциального уравнения 1- го порядка)
Если функция f(x, y) непрерывна в некоторой области D в плоскости XOY и имеет в этой области непрерывную частную производную , то какова бы не была точка (х0, у0) в области D, существует единственное решение уравнения , определенное в некотором интервале, содержащем точку х0, принимающее при х = х0 значение j(х0) = у0, т.
е. существует единственное решение дифференциального уравнения.
24.Дифференциальные уравнения первого порядка: с разделяющимися переменными, однородные, линейные.
Определение. Дифференциальным уравнением первого порядканазывается соотношение, связывающее функцию, ее первую производную и независимую переменную, т.е. соотношение вида:
Если такое соотношение преобразовать к виду то это дифференциальное уравнение первого порядка будет называться уравнением, разрешенным относительно производной.
Преобразуем такое выражение далее:
Функцию f(x,y) представим в виде: тогда при подстановке в полученное выше уравнение имеем:
— это так называемая дифференциальная формауравнения первого порядка.
Далее рассмотрим подробнее типы уравнений первого порядка и методы их решения.
Уравнения вида y’ = f(x).
Пусть функция f(x) – определена и непрерывна на некотором интервале
a < x < b.
В таком случае все решения данного дифференциального уравнения находятся как . Если заданы начальные условия х0 и у0, то можно определить постоянную С.
Учебные материалы по математике | Численное решение задачи коши для обыкновенных дифференциальных уравнений
Лекция. Численное решение задачи Коши для обыкновенных дифференциальных уравнений
Цель: Дать представление об основных идеях численного решения задачи Коши для обыкновенных дифференциальных уравнений и показать возможности MathCad для решения этой задачи.
Введение. Подавляющее большинство физических процессов описывается дифференциальными уравнениями. Простейшим примером может служить уравнение движения материальной точки:
(1) |
При определенных начальных условиях:
(2) |
Для химика дифференциальные уравнения — это, прежде всего, дифференциальные уравнения химической кинетики.
Для простейшей реакции разложения вещества скорость реакции пропорциональна первой степени концентрации (реакция первого порядка) и потому можно записать
(3) |
где k называется константой скорости реакции, а — начальная концентрация.
Это уравнение в силу своей простоты легко решается (без привлечения численных методов):
(4) |
Небольшое уточнение этой задачи приводит к гораздо более сложному уравнения.
Пусть порядок реакции будет равен n. Кроме того, рассмотрим реакцию с выделением тепла (тепловой эффект равен H). Если реактор помещен в термостат с температурой , то количество тепла, передаваемое от него к термостату, можно считать пропорциональным разности температуры T в реакторе и температуры . Если принять, что скорость выделения тепла пропорциональна скорости реакции, то для температуры получим дифференциальное уравнение
(5) |
Зависимость константы скорости реакции от температуры обычно описывается уравнением Аррениуса, и следовательно для концентрации можно записать дифференциальное уравнение:
(6) |
Для полученной системы уравнений (в которой концентрация C и температура T взаимосвязаны между собой) уже чрезвычайно трудно получить аналитическое решение, и приходится обращаться к численным методам.
Без учета температуры, типичная схема реакции может иметь, например, такой вид
(7) |
Обозначая концентрации веществ A, M, B, C, D и E через С1, С2, C3, C4, C5 и С6, можно записать систему дифференциальных кинетических уравнений для этой схемы реакций в виде:
(8) |
Обратите внимание, что суммарный баланс вещества должен быть равен нулю (в чем можно убедиться, сложив правые части уравнений). Эта систему уравнений должна решаться при определенных начальных условиях — начальных концентрациях.
Наличие нелинейностей в последней системе дифференциальных уравнений делает ее безнадежной с точки зрения получения аналитического решения.
Посмотрите, однако, что требуется набрать в MathCad, чтобы получить решение этой системы дифференциальных уравнений (рис1)..
На следующем рисунке приведены результаты расчет концентраций (их зависимости от времени) для всех веществ.
Обратите внимание на то, что результирующая концентрация продуктов (веществ B, D, E) равна в сумме концентрации исходного вещества A (0.4+0.4+0.2=1), что является дополнительной проверкой выполнения общего баланса вещества.
Как видите, запись системы дифференциальных уравнений в MathCad мало отличается от лычной математической записи на бумаге. Надо только эти уравнения и начальные условия заключить внутрь блока Given …..Odesolve.
Однако если щелкнуть правой кнопкой мыши по слову OdeSolve, то появится меню (рис.3), в котором вы можете выбрать метод решения дифференциальных уравнений. Для того, чтобы осознанно выполнять этот выбор для конкретной задачи, необходимо иметь общее представление об этих методах.
Целью данной лекции как раз и является изложение общих идей численных методов решения задачи Коши для обыкновенных дифференциальных уравнений.
Рисунок. 3. Выпадающее меню для выбора метода решения дифференциальных уравнений.
Постановка задачи
Требуется численно решить задачу Коши (с начальными условиями) для системы обыкновенных дифференциальных уравнений:
(9) |
Все последующее изложение будем вести для одного уравнения:
(10) |
Все сказанное без труда (и практически без каких-либо изменений) переносится на случай нескольких уравнений.
Метод Эйлера
Итак, требуется найти решение задачи(10).
Решение дифференциального уравнения представляет собой семейство интегральных кривых, среди которых выбирается одна, проходящая через начальную точку (). На рисунке 4 условно изображена эта искомая кривая, соответствующая решению задачи (10).
Кривая изображена пунктирной линией, поскольку она нам заранее неизвестна.
Основная идея численных методов решения задачи Коши содержится в методе Эйлера.
В окрестности точки (). Неизвестная функция может быть приближенно представлена формулой Тейлора:
,
что соответствует построению линейной функции, касательной к искомой функции y(x) в точке ().
Поэтому, если взять достаточно близко к и обозначить , то
Но величина также известна — ее можно вычислить из самого дифференциального уравнения . В итоге получим
(11) |
Теперь решение (хотя и приближенно) известно в точке (). Поэтому можно повторить все предыдущие рассуждения и найти решение в следующей точке
И вообще
(12) |
Можно повторять эти вычисления, получив последовательность значений , которая будет приближенно представлять решение данной задачи Коши.
Это и есть метод Эйлера.
Очевидно, чем меньше h (который называется шагом интегрирования), тем точнее будет решение.
Более того, можно заметить, что в формуле Тейлора ошибка e на каждом шаге имеет порядок . Если на всем отрезке интегрирования длиной L выполнить n шагов, то суммарная ошибка E будет суммой ошибок на всех отдельных шагах, то есть
То есть метод Эйлера имеет точность порядка O(h). Точную оценку получить затруднительно (она зависит от вида функции в правой части дифференциального уравнения), однако, полученная качественная информация оказывается очень полезной.
Уточнения метода Эйлера (методы второго порядка точности)
Чем обусловлена ошибка метода Эйлера?
Если бы производная от искомой функции не изменялась бы на отрезке , то касательная в точке () точно бы совпадала с интегральной кривой, и метод Эйлера дал бы точное решение. Значит, ошибка связана с тем, что указанная производная на отрезке не постоянна. Поэтому естественно попытаться как-то учесть это изменение. Самым простым способом учесть такое изменение является попытка вычислить некоторое среднее значение этой производной на отрезке .
Это можно сделать несколькими способами.
а) вычислим среднее арифметическое значение производной в точках () и ():
(13) |
Эти рассуждения проиллюстрированы на рисунке 5.
Рисунок 5
б) Можно также в качестве среднего значения производной на отрезке вычислить ее значение в промежуточной (например, средней) точке отрезка, то есть
(14) |
Эти рассуждения проиллюстрированы на рисунке 6.
Рисунок 6.
Можно показать, что оба последних метода имеют точность порядка , то есть если уменьшить величину шага h в 10 раз, то погрешность решения уменьшится в 100 раз.
Метод Рунге-Кутта четвертого порядка
По аналогии с предыдущим можно получить и последующие уточнения метода Эйлера. Но поскольку геометрическая интерпретация в этих случаях затруднительна, а вывод занимает довольно много места, то просто приведем окончательную формулу метода четвертого порядка точности.
Для того, чтобы ее можно было сравнивать с предыдущими методами 2-го порядка, перепишем последние, используя следующие обозначения:
(м-д Эйлера 1-го порядка)
(1-й м-д Эйлера 2-го порядка)
(2-й м-д Эйлера 2-го порядка)
Теперь можно легко поверить (опуская все выкладки), что метод 4-го порядка имеет вид
(15) |
Все перечисленные методы образуют группу так называемых методов Рунге-Кутта (различного порядка точности). Можно построить методы Рунге-Кутта и более высокого порядка точности, но они используются редко.
Многоточечные методы (методы Адамса)
Все предыдущие методы определяют значение в последующей точке по значению в одной предыдущей точке . По этой причине их называют одношаговыми методами. При этом, если решение уже получено в нескольких предыдущих точка, то полученная в этих точках информация о решении не учитывается. Более того, основные затраты методов связаны с вычислением функции ( — правой части дифференциального уравнения) в новых промежуточных точках, в то время как в предыдущих точках такие вычисления были уже выполнены, и использование этих значений может уменьшить время вычислений.
Этот недостаток исправляется в так называемых многошаговых методах Адамса.
Чтобы получить представление об этих методах, запишем метод Адамса с двумя предыдущими точками (рисунок 7).
Построим его по аналогии с уточнением (б) метода Эйлера, но теперь возьмем в качестве исходной точку (), а среднее значение производной будем вычислять в точке ().
В итоге получим
(16) |
Рисунок 7. Простейший многошаговый метод Адамса.
Уточнения одношаговых методов Рунге-Кутта связаны с добавлением внутренних точек на отрезке . Точно также уточнения многошаговых методов связаны с добавлением нескольких предыдущих точек. Из-за громоздкости вычислений здесь эти формулы не приводятся (их можно н6айти, например, в книге Хемминга [].
Неявные методы
Все предыдущие методы (и методы Рунге-Кутта и методы Адамса) явно вычисляют значение в точке по информации в предыдущих точках (одной или нескольких).
По этой причине их называют явными методами.
Можно, однако, построить методы, в которых искомое значение в точке входит неявным образом. Простейшим примером таких методов может служить неявный метод Эйлера.
Запишем метод Эйлера по аналогии с формулой (12), но теперь производную от искомого решения будем вычислять не в предыдущей (известной) точке, а в искомой точке (). В результате получим
(17) |
Эта формула по внешнему виду мало отличается от явного метода (12), но теперь для нахождения искомой величины необходимо решить неявное уравнение, поскольку она входит и в правую, и в левую части уравнения.
Можно точно также построить (по аналогии с приведенными ранее рассуждениями) неявные методы Рунге-Кутта более высокого порядка точности. Можно также построить неявные многошаговые методы.
На первый взгляд, необходимость решения неявного уравнения существенно усложняет метод.
Действительно теперь на каждом шаге придется выполнять дополнительные вычисления, связанные с решением неявного алгебраического уравнения типа (17). Однако, неявные методы обладают рядом существенных достоинств по сравнению с неявными методами. В частности, они гораздо более устойчивы и позволяют вести интегрирование дифференциального уравнения с гораздо большим шагом для получения той точности, чем это допускается в неявных методах. В результате в некоторых задачах (в частности, в так называемых «жестких» задачах, рассмотренных ниже) решение может быть получено только с использованием неявных методов.
Метод «прогноза–коррекции»
В реально используемых методах часто объединяют преимущества многошагового и неявного метода, получая так называемый метод прогноза–коррекции.
а) прогноз
По какому-либо явному многошаговому методу (например, по формуле (16), или используя более точный многошаговый метод Адамса) получают начальное приближение для . Обозначим это приближение через :
б) коррекция
Затем можно использовать неявный метод Эйлера (17) (или более точный неявный метод), решая неявное уравнение относительно методом простых итераций (см.
лекцию о нахождении корней алгебраических нелинейных уравнений). Выполняя последовательно итерации, будем получать последовательные приближения для искомой величины :
На практике, достаточно выполнять три-четыре итерации, чтобы получить нужную точность.
Понятие о неустойчивости численных методов
В большинстве случае явные методы (методы Рунге-Кутта или методы Адамса) вполне достаточны для получения решения с нужной точностью. И, как правило, решение может быть получено достаточно быстро (в чем вы убедитесь на лабораторных работах, используя для этих целей MathCad).
Однако имеются случаи, когда следует проявлять определенную осторожность и тщательно выбирать метод решения. Имеется несколько вопросов, которые необходимо понимать при численном решении дифференциальных уравнений.
Первый из них связан с возможной собственной неустойчивостью самого решения и с неустойчивостью численного метода.
Из курса математики известно, что само решение дифференциального уравнения может быть неустойчивым относительно начальных условий, то есть небольшие отклонения в начальных условиях могут приводить к большим отклонениям в решении.
Для иллюстрации рассмотрим задачу
Эта задача имеет точно решение .
Однако решение этой задачи при произвольных начальных условиях имеет вид (проверьте, решая уравнение разделением переменных):
Поэтому для начального условия (для любого малого ) получим решение, которое стремится к нулю при , а для начального условия получим неограниченно растущее решение (рисунок 8).
Таким образом, решение является неустойчивым относительно малых возмущений в начальных условиях. Поэтому решение практически невозможно получить численным способом, так как малейшие ошибки (неизбежно присутствующие в численных расчетах, например, за счет округления) уведут решение от истинного (y=2) на какое-то другое.
Такая неустойчивость самого решения дифференциального уравнения является, как правило, следствие физической постановки задачи. Например, движение материального шарика, помещенного на криволинейную поверхность, под действием сил тяжести описывается уравнением
где вектор сил реакции поверхности на шарик.
Рисунок
Ясно, что положение равновесия шарика на вершине поверхности (хотя и будет решением соответствующего дифференциального уравнения) будет неустойчивым. Малейшие отклонения в начальных условиях (отклонения от положения на вершине) заставят шарик скатываться по наклонной поверхности.
Разобранный пример иллюстрирует неустойчивость собственно самого решения дифференциального уравнения.
Однако, неустойчивость может быть свойством и численного метода (в то время как само решение уравнения является устойчивым в указанном выше смысле).
Для иллюстрации рассмотрим задачу
,
точное решение которой имеет вид . В указанном выше смысле это решение устойчиво относительно начальных условий.
Применим теперь для решения этой задачи численный метод ():
Для данной задачи . Поэтому метод в данном случае дает
Эта формула порождает некоторую последовательность , поведение которой может быть полностью проанализировано []:
.
Видно, что при (при любом h)_первое слагаемое стремится к нулю, а второе, осциллируя, стремится к бесконечности.
Таким образом, применяя выбранный метод, получить решение данной задачи невозможно.
В этом случае неустойчивым оказался сам численный метод (при устойчивом решении дифференциального уравнения).
Понятие о «жестких» дифференциальных уравнениях
Тот факт, что в строго устойчивых методах можно выбрать шаг достаточно малым и обеспечить его устойчивость, мало помогает в некоторых задач. В таких задачах шаг приходится выбирать настолько малым, что приводит к недопустимо большим затратам машинного времени. Подобные задачи называются жесткими.
Понятие жесткости можно проиллюстрировать на примере решения уравнения
Точным решением которого является
Применим (для простоты рассуждений) метод Эйлера, получим последовательность
,
где слагаемое аппроксимирует в точном решении.
Величина быстро убывает с ростом x, и решение, начиная с некоторого x, мало отличается от единицы.
При этом интуитивно кажется, что для интегрирования можно взять достаточно большой шаг (поскольку решение почти не меняется). Однако из последнего соотношения видно, что при величина будет расти, свидетельствуя о неустойчивости.
Таким образом, хотя слагаемое при больших x практически не вносит никакого вклада в решение, при численном решении его приходится аппроксимировать очень точно и выбирать h очень малым.
Реально описанная ситуация встречается при решении задач химической кинетики, описывающих систему реакций, характерные времена которых сильно отличаются (такое различие может достигать нескольких порядков) [].
В целом «жесткие» системы требуют применения специальных методов (это, как правило, неявные методы).
В Mathcad для решения «жестких» систем предлагаются методы BDF, Radau, Stiffb, Stiffr.
Метод AdamsBDF сам определяет, является ли система жесткой, и в этом случае вызывается метод BDF, если же система не жесткая, то вызывается обычный метод Adams.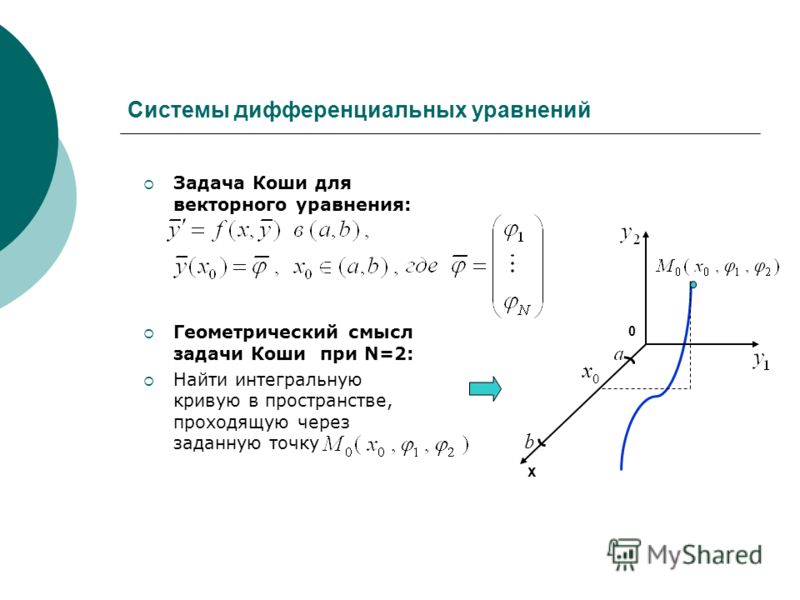
Все эти методы являются «неявными» методами, о которых речь шла выше.
Эти методы в качестве дополнительного аргумента могут использовать Якобиан от правых частей дифференциальных уравнений, что может значительно улучшить сходимость метода.
Совет: Загляните в Справку MathCad (разделу Calculus and Differntial Equations в шпаргалках (QuickShets)). Там вы можете найти достаточно много тем для семестровых работ. Еще лучше, если у вас к MathCad приложены электронные книги (E-books), среди которых имеется книга DIFFERENTIAL EQUATIONS SOLVE BLOCK, в которой вы можете найти массу интересных инженерных приложений (в том числе и пример с «жесткими» дифференциальными уравнениями — проблему Хайриса)
Краевые задачи для обыкновенных дифференциальных уравнений
В краевых задачах (в отличие от задачи Коши, в которой все дополнительные условия задаются в начальной точке) дополнительные условия задаются на концевых точках отрезка интегрирования (краях отрезка — отсюда и название «краевые задачи»).
Иногда такие задачи называют задачами с граничными условиями или просто «граничными задачами».
И хотя в краевой задаче само дифференциальное уравнение может быть точно таким же, как и в задаче с начальными условиями, краевая задача требует обычно для решения значительно больших усилий. Это проявляется и в численных методах.
Чтобы понять различие между краевой задачей и задачей с начальными условиями, рассмотрим движение материального тела.
Дифференциальное движение материальной точки описывается уравнениями Ньютона
Здесь V{u, v) –вектор скорости, — вектор сил.
Однако, для этого уравнения (второго порядка) можно рассматривать две различные задачи:
1) в начальной точке A известна и величина скорости и направление вектора скорости (угол a). В этом случае все условия заданы в одной начальной точке, и мы получаем задачу Коши.
2) в начальной точке известна только величина скорости (не известен угол a), но задана точка B, в которую должно попасть материальное тело.
В первом случае, зная все условия в начальной точке, можно решать задачу «пошагово» (например, методом Эйлера), получив после выполнения всех шагов искомую траекторию
Во втором случае такая «пошаговая» процедура невозможна. Чтобы попасть в заданную точку B, надо определить неизвестный угол a, но для этого надо решить задачу для всей траектории. В реальной жизни эта задача решается метод «пристрелки», когда многократно подбирается этот угол (корректируя «недолет–перелет»).
Таким образом, можно сказать, что для решения краевой задачи требуется многократно решить задачу с начальными условиями. Кстати, среди численных методов решения краевой задачи действительно существует метод, который так и называется «метод пристрелки».
Пример краевой задачи
Рассмотрим прямоточный химический реактор (в виде трубы постоянного сечения).
На вход в реактор со скоростью v подается реагент с начальной концентрацией .
Пусть в реакторе происходит простейшая реакция , скорость которой равна .
Составляя уравнение баланса вещества в бесконечно малом объеме, можно записать:
,
где второе слагаемой связано с конвективным переносом вещества; второе слагаемое — с диффузионным переносом (N), и третье слагаемое изменением общего потока вещества за счет реакции.
Приняв для диффузионного потока закон Фика (диффузионный поток пропорционален градиенту концентрации,
,
(коэффициент пропорциональности D называется коэффициентом диффузии), и считая скорость v постоянной, получим
.
В качестве граничных условий примем на левом конце (x=0):
,
А при будем считать, что реакция полностью закончилась, то есть
.
Можно также (что более естественно) задать условие преобладания конвективно переноса на выходе над диффузионным (см. далее).В итоге получили дифференциальное уравнения второго порядка с двумя граничными условиями.
В этом простейшем примере (если все коэффициенты постоянны) несложно получить и аналитическое решение уравнения, и тогда использование краевых условий сведется к нахождению произвольных постоянных интегрирования.
Но, если коэффициенты уравнения зависят от координаты x или от концентрации C, то, как правило, никакое аналитическое решение получить не удастся, и задачу можно решать только численно.
Прежде, чем переходить к обсуждению численного решения краевых задач, следует сделать одно существенное замечание. В приведенной постановке задачи следует перейти к так называемым безразмерным переменным.
Положив
, ,
И подставляя это в дифференциальное уравнение, получим
,
Или
(18) |
.
Здесь введены обозначения
и .
Обратите внимание, что величины P и R являются безразмерными (как и все дифференциальное уравнение).
Граничные условия в безразмерном виде запишутся как
(19) |
и | (20) |
.
Такая безразмерная форма не только более удобна для численного решения (по крайней мере, число безразмерных параметров — их в задаче всего два — меньше, чем число исходных физических параметров, x, D, v, C0, D, k), но и более физична.
Общие соображения о численном решении краевых задач
Часто для численного решения краевой задачи используют так называемые разностные методы. Основная идея довольно проста: разобьем отрезок интегрирования на достаточно большое количество малых подотрезков и на каждом из них заменим производные их конечно разностными аналогами:
,
Здесь i — номер узла разностной схемы.
В итоге получаем систему алгебраических n уравнений для n внутренних узлов, которую в принципе несложно решить. Для линейных задач эта схема работает достаточно хорошо. Основная трудность заключается в том, что получающаяся система может содержать достаточно много уравнений (в зависимости от задачи это число может достигать несколько тысяч или даже миллионов).
Это само по себе может приводить к катастрофическому накоплению ошибок округления. Но в целом для линейных задач эта схема работает достаточно надежно.
Мы не можем здесь углубляться во все тонкости разностных методов. Хотелось бы только предостеречь от бездумного использования разностных методов в серьезных нелинейных задачах (что, к сожалению, иногда даже встречается в учебниках по техническим дисциплинам).
Во-первых, можно обратить внимание, что первую производную, казалось бы можно заменить равносильными приближениями
или или
В простейших случаях эти схемы действительно равноценны. Но в более сложных случаях они могут работать совершенно по разному (например, схема с разностями «вперед» может оказаться неустойчивой, а схема с разностями «назад» — устойчивой, или наоборот). Кроме того, в нелинейных задачах, когда коэффициент при производных зависит от искомой величины, возникает вопрос, в какой точке его вычислять (когда коэффициенты постоянны, этого вопроса просто не возникает).
В этом отношении, прежде всего, надо иметь в виду, что разностная схема должна быть консервативной, то есть в ней должны сохраняться глобальные законы сохранения (массы, энергии и т. п.). Все это достаточно хорошо разработанные в вычислительные математике вопросы, но они требуют определенной квалификации. Поэтому мы советуем не очень увлекаться разработкой собственных программ, а при решении инженерных задач больше доверять методам, заложенным в стандартные пакеты. MathCad решает краевую задачу, сводя ее к задаче Коши, сначала «перегоняя» второе граничное условие в начальную точку (для этого используются функция sbval), и затем используя один из решателей задачи Коши в функции Odesolve.
В таких случаях мы советуем использовать пакеты типа COMSOL Multiphysics, в которых решение задачи выглядит более естественно, требуя от пользователя только понимания постановки задачи.
Ниже показано, как решить задачу (18-20) в COMSOL Multiphysics.
1. Сначала естественно выбирается физическое приложение, к которому относится наша задача.
Это стационарная (steady-state) одномерная (1D) задача из области Конвекции и диффузии (Convection and Diffusion).
2. Затем для удобства можно задать величину (опция меню Options->Constants) параметров P и R уравнения
3.Затем в меню Draw создается область решения. В данном случае это всего лишь отрезок прямой линии [0;1].
4. В окне установки физических параметров уравнения (Subdomain Settings) требуется ввести значения параметров нашей конкретной задачи
Обратите внимание на подсказку в верхней части окна, где в общем виде записано уравнение вашей физической задачи. Сопоставьте его со своим уравнением (18) и введите коэффициенты, как показано на рисунке.
4. Теперь надо задать граничные условия. На левом конце зададим начальную концентрацию (в безразмерном виде начальная концентрация равна 1), а на левом конце зададим условие свободно выхода продукта (convection flux)
4. После этого достаточно нажать кнопку (Solve) и вы увидите решение своей задачи
Замечание: В качестве семестровой работы можно выбрать следующее:
а) найти задачу химической кинетики для реальной системы реакций и решить ее в MathCad.
б) Выбрать (по согласованию с преподавателем) функции MathCad решения дифференциальных уравнений, не рассмотренных в этой лекции (можно обратиться к электронным книгам, поставляемым с пакетом, например к книге ODE Solve Blocks)
б) выбрать любой из примеров модуля Chemical Engineering пакета COMSOL Multiphysics и внести в него изменения по согласованию с преподавателем.
Перечень контрольных вопросов
1. Различие между краевой задачей и задачей Коши для обыкновенных дифференциальных уравнений.
2. Умение составлять систему кинетических уравнений для произвольной системы реакций.
3. Основная идея численного решения задачи Коши (метод Эйлера).
4. Уточнения метода Эйлера второго порядка (геометрическая иллюстрация).
5. Понятие многошаговых методов.
6. Понятие неявных методов.
7. Общие принципы выбора метода для различных задач. Выбор метода решения в MathCad.
8. Краевая задача для обыкновенного дифференциального уравнения (на примере прямоточного реактора).
Переход к безразмерной форме задачи.
9. Общее понятие о разностных методах краевой задачи.
10. (Не обязательно) Решение одномерной краевой задачи массопереноса с диффузий в пакете COMSOL.
Новейшие вопросы «задача Коши» — MathOverflow
Задавать вопрос
Тег cauchy-problem не имеет руководства по использованию.
- Учить больше…
- Лучшие пользователи
- Синонимы
23 вопросы
Новейший
Активный
Баунти
Без ответа
Сортировать поНет ответов
Ответ не принят
Имеет награду
Отсортировано поНовейший
Последние действия
Наивысший балл
Самый частый
Щедрость скоро закончится
ОтмеченМои просматриваемые теги
Следующие теги:
1 голос
1
отвечать
9m$ — $m$-мерный тор)
быть решением задачи Коши
$$\frac{d}{dt} f(t) = A f(t)$$
$$f(0).
..
- ap.analysis-of-pde
- linear-pde
- регулярность
- задача-коши
0 голосов
0 ответы
75 просмотров
Представление Фейнмана Каца для нелинейного уравнения теплопроводности 92/2}, \end{случаи} \end{выравнивание} …
- дифференциальные уравнения
- задача Коши
1 голос
1 отвечать
222 просмотров
Формула нападающих Фейнмана – Каца
Это может быть простой вопрос, но у меня возникли проблемы с ним.
Рассмотрим задачу Коши с окончательным условием.
\begin{уравнение}
\begin{случаи}
\frac{\partial u}{\partial t}(t,x) + \mathcal{L}u(t,x) .
{(n)})=0$ — система …
- ап.анализ-фпд
- задача-коши
1 голосование
2 ответы
228 просмотров
Возможна ли вариационная постановка абстрактной задачи Коши?
Недавно я столкнулся с методом, известным как «вариационный метод», в котором мы пытаемся установить слабые решения различных краевых задач, включающих обыкновенные производные, частные …
- ап.анализ-фдес
- ca.классический-анализ-и-оды
- пространства соболева
- задача-коши
4 голосов
3 ответы
299 просмотров
$u_t=Au+F(u)$, где $A$ — бесконечно малая образующая $C_0$-полугруппы
Я задал этот вопрос на Mathematics Stackexchange, но не получил ответа.
{n+… 9k} \…
- задача Коши
1 голосование
0 ответы
86 просмотров
Эквивалентность задач типа Коши и интегральных уравнений Вольтерра
Следующая теорема взята из книги Килбаса, Шриваставы и Трухильо «Теория и приложения дробных дифференциальных уравнений». Это Теорема 3.10 со страницы 163. Теорема. Пусть $ \alpha \in \…
- дробное исчисление
- задача Коши
2 голосов
1 ответ
234 просмотров
Сравнение решений задачи УЧП с разными начальными условиями
Мой вопрос(ы) о том, что произойдет с решением задачи, если мы изменим начальные условия.
Допустим, у нас есть проблема PDE:
$$
(1) \hspace{0,5 см} u_t+f(u)_x=0
$$
$$
(2) \hspace{0,5 см} .
..
- запрос-справка
- ap.analysis-of-pdes
- задача-коши
- законы сохранения
2 голосов
0 ответы
71 просмотров
Гладкая задача Коши на цилиндрическом многообразии (или как определить экспоненту дифференциального оператора)
Пусть $M$ — многообразие, $E \rightarrow M$ — вещественное или комплексное гладкое векторное расслоение, а $D: \Gamma_c(M,E) \rightarrow \Gamma_c(M,E)$ — (первое порядок при необходимости) дифференциальный оператор на гладкой…
- dg.дифференциальная-геометрия
- ап.анализ-pdes
- векторные расслоения
- гиперболическая-pde
- задача Коши
3 голосов
0 ответы
63 просмотров
Как решить эту линейную задачу Коши
в моей диссертации я борюсь со следующим PDE:
$u_t+a(x,y)u_{xx}+b(x,y)u_{xy}+c(x,y)u_{yy}+d(x,y)u_{x}+e(x ,y)u_{y}+f(x,y)u=0$
$и(Т,х,у)=1,$
где $a,b,c,d,e,f$ — многочлены, а .
..
- параболическая-частная
- линейная-частная
- задача Коши
на страницу
М. Л. Зайцев, В. Б. Аккерман, “Гипотеза об унификации решения задачи Коши для переопределенных систем дифференциальных уравнений”, Вестн. Южно-Урал. Гос. Ун-та. сер. Матем. мех. физ., 11:4 (2019), 12–25
| Вестн. Южно-Урал. Гос. Ун-та. сер. Матем. мех. физ., 2019, Том 11, Выпуск 4, Страницы 12–25 (ми вюрм424) |
Математика
Гипотеза об унификации решения задачи Коши для переопределенных систем дифференциальных уравнений
Зайцев М.Л. а Аккерман В.Б.
b Университет Западной Вирджинии, Моргантаун, США
Загрузить полный текст в формате PDF (750 КБ)
Ссылки:
HTML
DOI: https://doi.
org/10.14529/mmph2
Реферат: В данной работе исследуется возможность существования универсального решения задачи Коши для систем дифференциальных уравнений в частных производных (УЧП) в случае, если эта система является переопределенной так, что новая переопределенная система УЧП содержит все решения исходной система УЧП и, кроме того, сводится к системам обыкновенных дифференциальных уравнений (ОДУ), решение которых затем находится. Для этого в статье рассматривается модификация метода нахождения частных решений для любых переопределенных систем дифференциальных уравнений путем сведения к переопределенным системам неявных уравнений. В предыдущих работах авторов был предложен метод нахождения частных решений для переопределенных систем в частных производных. В этом методе для нахождения решений необходимо решать системы обыкновенных неявных уравнений. В этом случае можно показать, что нужные нам решения не могут зависеть от непрерывного параметра, т. е. они не более чем счетны.
Заранее требуется такая переопределение систем дифференциальных уравнений, чтобы их общие решения были не более чем счетными. Такого начального переопределения добиться довольно трудно. Однако предлагаемый метод также позволяет сводить переопределенные системы дифференциальных уравнений не только к системам неявных уравнений, но и к системам УЧП меньшей размерности, чем исходные системы УЧП. В частности, при определенных условиях возможно приведение к системам ОДУ. Предлагается выбирать решения для переопределенных систем УЧП с помощью параметризованной задачи Коши, которая ставится для параметризованных систем ОДУ при определенных условиях. Решением этой задачи Коши является некоторая функция начальных данных и их производных. Чтобы найти решение любой соответствующей задачи Коши для исходной системы УЧП, достаточно один раз вычислить универсальный решатель для редуцированной системы ОДУ. В этом случае решение будет не только существовать и быть единственным, но и непрерывно зависеть от исходных данных, поскольку это справедливо для систем ОДУ.
Целью данной работы является исследование задачи Коши с возможностью ее универсализации и параметризованной задачи Коши в целом для произвольных систем в частных производных.
Ключевые слова: переопределенные системы дифференциальных уравнений, уравнение в частных производных, обыкновенные дифференциальные уравнения, размерность дифференциальных уравнений, задача Коши, параметрические решения систем дифференциальных уравнений.
Получено: 08.02.2019
Тип документа: Артикул
УДК: 519.635
Язык: Русский
Ссылка: М. Л. Зайцев, В. Б. Аккерман, “Гипотеза об унификации решения задачи Коши для переопределенных систем дифференциальных уравнений”, Вестн. Южно-Урал. Гос. Ун-та. сер. Матем. мех. физ., 11:4 (2019), 12–25
Цитирование в формате AMSBIB
\RBibitem{ZayAkk19}
\by М. ~Л.~Зайцев, В.~Б.~Аккерман
\paper Гипотеза об унификации решения задачи Коши для переопределенных систем дифференциальных уравнений
\jour Вестн. Южно-Урал. Гос. Ун-та. сер. Матем. мех. Физ.
\год 2019
\том 11
\выпуск 4
\страниц 12--25
\mathnet{http://mi.mathnet.ru/vyurm424}
\crossref{https://doi.org/10.14529/mmph2 }
Варианты подключения:
Ссылки на статьи в Google Scholar: русские цитаты,
английские цитаты
Статьи по теме в Google Scholar: русские статьи,
Английские статьи
Летопись математических исследований | Издательство Принстонского университета
Одним из главных достижений математики девятнадцатого века было доказательство того, что геометрия линий в пространстве однозначно определяет декартовы координаты, вплоть до линейной неоднозначности. Что определяет алгебраическое разнообразие? развивается…
Основанная на p -адической программе Ленглендса, эта книга строит стеки, которые алгебраизируют кольца формальных деформаций Мазура локальных представлений Галуа. Точнее, он строит нётеровы формальные алгебраические стеки над Spf Z p, которые…
В Арифметика полиномиальных динамических пар Шарль Фавр и Томас Готье представляют новое математическое исследование в области арифметической динамики. В частности, авторы изучают одномерные алгебраические семейства пар, заданных…
В этой книге представлено окончательное доказательство глобальной нелинейной устойчивости пространства-времени Минковского как решения уравнений общей теории относительности Эйнштейна-Клейна-Гордона. Попутно разрабатывается новая надежная аналитическая структура…
Эта книга развивает новую теорию p -адических модулярных форм на модулярных кривых, распространяя классическую теорию Каца на суперсингулярное геометрическое место. Главное нововведение — перейти на бесконечный уровень и распространить коэффициенты на пучки периодов, идущие от…
Эта монография о приложениях кубических комплексов представляет собой прорыв в области геометрической теории групп и топологии трехмерных многообразий. Многие принципиально новые идеи и методологии представлены здесь впервые…
Теория хирургии, раздел геометрической топологии, изучает классификации многообразий. Курс теории хирургии предлагает современный взгляд на эту важную математическую дисциплину и некоторые ее приложения. В этой книге…
Один из основных нерешенных вопросов о черных дырах заключается в том, остаются ли они стабильными, когда подвергаются небольшим возмущениям. Утвердительный ответ на этот вопрос обеспечил бы сильную теоретическую поддержку физической реальности…
Диффузия Арнольда, касающаяся возникновения хаоса в классической механике, является одной из важнейших проблем в области динамических систем и математической физики. Поскольку он был обнаружен Владимиром Арнольдом в 1963 году, он…
Уильям Терстон (1946–2012) был одним из величайших математиков двадцатого века. Он был провидцем, чьи экстраординарные идеи произвели революцию в широком диапазоне областей математики, от слоений, контактных структур и…
Теория вычислимости — раздел математической логики и компьютерных наук, который в последние годы становится все более актуальным. В этой области развились растущие связи в различных областях математики с приложениями в …
Беркли Лекции по p-адической геометрии представляет собой важный прорыв в арифметической геометрии. В 2014 году ведущий математик Питер Шольце прочитал серию лекций в Калифорнийском университете в Беркли, посвященных новым идеям в…
Ту Эта книга дает четкое введение в эквивариантные когомологии, центральную тему алгебраической топологии. Эквивариантные когомологии занимаются алгебраической топологией пространств с групповым действием, или, другими словами, с…
В этой книге изучается взаимодействие между геометрией и топологией локально симметричных пространств, а также арифметические аспекты специальных значений L-функций.
Авторы изучают когомологии локально симметричных пространств для GL(N), где. ..
Арифметика и геометрия представляет основные моменты последних работ в области арифметической алгебраической геометрии некоторых ведущих математиков мира. Вместе эти лекции 2016 года, которые были прочитаны в честь десятой годовщины…
В этой книге описываются последние достижения в теории игр среднего поля, представляющих собой задачи оптимального управления континуумом игроков, каждый из которых взаимодействует со всем статистическим распределением популяции. Пока это…
В этой книге представлено полное доказательство гипотезы Блоха-Като и нескольких родственных гипотез Бейлинсона и Лихтенбаума в алгебраической геометрии. Собранные здесь впервые, эти предположения описывают строение…
Внешний бильярд представляет собой игрушечную модель движения планет и демонстрирует замысловатое и загадочное поведение даже для, казалось бы, простых примеров. Это динамическая система, в которой частица в плоскости движется вокруг внешней поверхности выпуклой…
Центральной задачей теории чисел является изучение принципов преобразования от локального к глобальному, которые описывают поведение глобального поля K в терминах поведения различных дополнений K . В этой книге рассматривается конкретный пример…
Эта книга предлагает обзор последних достижений в области анализа отражения-дифракции ударных волн, подробное представление оригинальных математических доказательств гипотез фон Неймана для потенциального потока, а также сборник связанных. ..
Асимптотическая дифференциальная алгебра стремится понять решения дифференциальных уравнений и их асимптотику с алгебраической точки зрения. Дифференциальное поле транссерий играет центральную роль в предмете. Помимо способностей…
Вдохновленный теорией турбулентности в жидкостях, физик и химик Ларс Онзагер в 1949 году предположил, что слабые решения уравнений Эйлера для несжимаемых жидкостей могут не сохранять энергию, если их пространственная регулярность ниже. ..
Это первая книга, в которой представлена полная характеристика оценок ограничения Фурье типа Стейна-Томаса для больших классов гладких гиперповерхностей в трех измерениях, включая все вещественно-аналитические гиперповерхности. Ассортимент…
В этой одной из первых книг по теории чисел на английском языке выдающийся математик Герман Вейль исследует фундаментальные понятия арифметики. Книга начинается с определений и свойств алгебраических полей…
Новый интерес к модулярным формам одной комплексной переменной был вызван главным образом работами Сельберга и Эйхлера. Но вводной работы, освещающей предысторию этих событий, не проводилось. Книжные обзоры Х. К. Ганнинга…
Центральной темой этого исследования является группа кос Артина и множество способов, которыми понятие косы оказалось важным в топологии малой размерности.
Один из величайших математиков ХХ века, Джон Милнор сделал фундаментальные открытия в самых разных областях математики, от топологии и динамических систем до алгебраических К -теор. Он известен как мастер…
Эта работа посвящена расширению классической теории Литтлвуда-Пэли в контексте симметричных диффузионных полугрупп. В этой общей постановке есть приложения к множеству проблем, например, возникающих при изучении…
Описание этой книги «Вклад в анализ Фурье». (AM-25), будет в ближайшее время.
Описание для этой книги, Группы узлов. Анналы математических исследований. (AM-56), Том 56, будет готов.
Эта книга содержит отчеты о выступлениях на симпозиуме в честь
Джона К. Мура в октябре 1983 г. в Принстонском университете. Работа
включает статьи по классической теории гомотопий, гомологической алгебре,
Описание к этой книге «Кривизна и числа Бетти». (AM-32), Том 32, будет готов.
Описание к этой книге Мероморфные функции и аналитические кривые. (AM-12), будет в ближайшее время.
Описание этой книги «Трансцендентные числа». (AM-16), будет в ближайшее время.
(АМ-95), Том 95 Рональд Г. Дуглас Последние разработки в различных областях математики предполагают изучение определенного класса расширений C*-алгебр. Здесь Рональд Дуглас использует методы гомологической алгебры для изучения этого набора расширений. Сначала он показывает…
Целью этой книги является изучение гармонических отображений, минимальных и параллельных погружений средней кривизны при наличии симметрии. В ряде случаев последнее позволяет свести исходную эллиптическую вариационную задачу к…
Пятнадцать статей, составляющих этот сборник, посвящены последним достижениям в комплексном анализе. Написанные известными исследователями комплексного анализа и смежных областей, они охватывают широкий спектр исследований с использованием методов парциального. ..
Описание для этой книги «Вклады в теорию нелинейных колебаний» (AM-20), том I будет готово.
Существует сходство идей в областях теории узлов, теории бесконечных дискретных групп и топологии трехмерных многообразий. Эта книга содержит пятнадцать статей, в которых доказываются новые результаты во всех трех областях. Эти бумаги…
Особенности решений дифференциальных уравнений составляют общую тему этих статей, взятых с семинара, проведенного в Институте перспективных исследований в Принстоне в 1919 г.77-1978. При этом часть лекций была посвящена анализу…
В этом томе исследуется взаимодействие между классической теорией автоморфных форм и современной теорией представлений групп аделей. Интерпретируя важные недавние работы Жаке и Ленглендса, автор представляет…
Пять статей выдающихся американских и европейских математиков описывают некоторые современные тенденции в математике с точки зрения недавнего прошлого и с точки зрения ожиданий на будущее. Среди обсуждаемых предметов алгебраические…
(АМ-81), Том 81 Джордж Люстиг В этой книге профессор Люстиг решает интересную задачу совершенно новыми методами, а именно, использованием когомологий зданий и связанных с ними комплексов.
В книге дается явное построение одного выдающегося члена, D(V), из…
Локально симметричные пространства являются обобщениями пространств постоянной кривизны. В этой книге автор представляет доказательство замечательного явления, которое он называет «сильной жесткостью»: это более сильная форма деформационной жесткости. ..
Эта работа представляет собой свежее изложение теории голоморфных кривых Альфорса-Вейля, учитывающее некоторые недавние разработки в теории Неванлинны и несколько комплексных переменных. Обработка дифференциально-геометрическая по всей…
Описание для этой книги «Линейные неравенства и родственные системы». (AM-38), Том 38, будет готов.
Эти лекции, прочитанные профессором Мамфордом в Гарварде в 1963-1964 гг., посвящены изучению свойств семейств алгебраических кривых на неособой проективной алгебраической кривой, заданной над алгебраически замкнутым полем…
Описание этой книги «Вклады в теорию игр» (AM-40), том IV будет опубликовано позже.
В качестве новоявленного доктора философии Пол Халмос пришел в Институт перспективных исследований в 1938 году, хотя у него и не было стипендии, чтобы учиться у многих гигантов математики, которые недавно присоединились к факультету. В итоге он стал…
По сути, это сборник материалов встречи 1967 года в Батон-Руж, в котором представлены важные статьи по топологии бесконечномерных линейных пространств, теории неподвижных точек в бесконечномерных пространствах, бесконечномерных. ..
Эта книга представляет собой расширенную версию лекций Германа Вейля, прочитанных в Институте перспективных исследований 19 января.86. Он обрисовывает в общих чертах то, что сейчас известно о неприводимых унитарных представлениях вещественных редуктивных групп, обеспечивая…
Измеренные геодезические слоистости являются естественным обобщением простых замкнутых кривых на поверхностях и играют решающую роль в различных разработках двух- и трехмерной топологии, геометрии и динамических систем. Эта книга…
Эта книга предлагает самостоятельный отчет об инвариантах 3-многообразия, возникающих из исходного многочлена Джонса. Это инварианты Виттена-Решетихина-Тураева и инварианты Тураева-Виро. Начиная с модели кронштейна Кауфмана для…
Джеймс Милгрэм Начиная с общего обсуждения бордизма, профессора Мэдсен и Милграм представляют гомотопическую теорию пространств, классифицирующих хирургию, и классифицирующие пространства для различных требуемых теорий расслоений. Следующая часть охватывает более…
Описание к этой книге «Изопериметрические неравенства в математической физике». (AM-27), Том 27, будет готов.
(АМ-101), Том 101 Майкл Б. Маркус и Жиль Пизье В этой книге авторы дают первые необходимые и достаточные условия равномерной сходимости п.н. случайных рядов Фурье на локально компактных абелевых группах и на компактных неабелевых группах. Они также получают много родственных…
В данной монографии p -адические домены периодов связаны с произвольными редуктивными группами. Используя концепцию жестко-аналитических отображений периодов, исследуется связь областей p -адических периодов с пространством модулей p -делимых групп. В…
Исследование 79 содержит сборник статей, представленных на конференции по разрывным группам и рикмановским поверхностям в Университете Мэриленда, 21–25 мая 1973 г. Статьи ведущих авторитетов в основном касаются фуксовых и клейнианских…
Описание этой книги «Вклады в теорию игр» (AM-24), том I будет опубликовано позже.
Алгебраическая К-теория описывает раздел алгебры, который сосредоточен вокруг двух функторов. K0 и K1, которые сопоставляют каждому ассоциативному кольцу ∧ абелеву группу K0∧ или K1∧ соответственно. Профессор Милнор излагает в настоящей работе…
В этом томе автор охватывает проконечные группы и их когомологии, когомологии Галуа и локальную теорию полей классов и завершает рассмотрением двойственности. Его цель состоит в том, чтобы эффективно представить этот материал на…
Эта книга представляет собой краткое введение в исчисления лямбда-преобразования, впервые открытые Алонзо Черчем и разработанные им в сотрудничестве со своими учениками С. К. Клини и Дж. Б. Россером. Первые четыре главы представляют…
Описание этой книги «Достижения в теории игр». (AM-52), Том 52, будет готов.
Основанная на семи циклах лекций, прочитанных ведущими экспертами на летней школе Пекинского университета в Пекине в 1984 г., эта книга содержит обзор последних достижений в областях гармонического анализа, наиболее тесно связанных с теорией сингулярных…
Тьюки Описание для этой книги «Сходимость и единообразие в топологии». (AM-2), Том 2, будет готов.
Описание для этой книги «Введение в линейные преобразования в гильбертовом пространстве». (AM-4), Том 4, будет готов.
Соломон Лефшец был пионером в области топологии — изучения свойств многогранных фигур и их способности деформироваться, скручиваться и растягиваться без изменения своей формы. По словам Лефшеца, «если просто крутить рукоятку…
Предметом этой работы является область лоренцевской геометрии, которая до сих пор мало исследовалась: существуют ли лоренцевы многообразия, все светоподобные геодезические которых являются периодическими? Удивительным фактом является то, что такие…
Равенел Нильпотентность и периодичность в стабильной гомотопической теории описывает некоторые крупные достижения в алгебраической топологии за последние годы, основанные на теоремах о нильпотентности и периодичности, которые были выдвинуты автором в 1977 году и доказаны…
В этой книге, адресованной исследователям и аспирантам, работающим в сфере активного анализа, геометрии и динамики, представлено исследование перенормировки квадратных полиномов и краткое введение в методы сложных…
(АМ-34), Том 34 Под редакцией CE Shannon и J. McCarthy. Описание для этой книги, Исследования автоматов. (AM-34), Том 34, будет готов.
Эта книга знакомит с новыми методами теории дифференциальных уравнений в частных производных, выводимых из лагранжиана. Эти методы частично представляют собой распространение на уравнения в частных производных методов симплектической геометрии и…
(АМ-87), Том 87 Питер Д. Лакс и Ральф С. Филлипс Применение Фадеевым и Павловым теории рассеяния Лакса-Филлипса к автоморфному волновому уравнению побудило профессоров Лакса и Филлипса пересмотреть это развитие в рамках своей теории. В этом томе изложены…
Написано и отредактировано Д. Б. А. Эпштейном.
(АМ-71), Том 71 Генри Б. Лауфер Тщательный и своевременный обзор особенностей двумерных нормальных комплексных аналитических многообразий, в этом томе суммированы результаты, полученные после диссертации Хирцебруха (1953) и представляет новые материалы. Во-первых, сингулярность…
Теория характеристических классов обеспечивает основу для различных дисциплин дифференциальной топологии, дифференциальной и алгебраической геометрии, когомологий и теории расслоений. Таким образом, это фундаментальный и необходимый…
Эта работа предлагает вклад в геометрическую форму теории нескольких комплексных переменных. Поскольку комплексные грассмановы многообразия служат классификационными пространствами комплексных векторных расслоений, структура когомологий комплексного грассманова…
Описание к этой книге «Теория перекрестных пространств». (AM-26), Том 26, будет готов.
Описание для этой книги, Семинар по теореме Атьи-Зингера об индексе. (AM-57), Том 57, будет готов.
Изучение экспоненциальных сумм над конечными полями, начатое Гауссом почти два века назад, в последние годы полностью изменилось благодаря достижениям в алгебраической геометрии, кульминацией которых стала работа Делиня о гипотезах Вейля. Сейчас…
Описание для этой книги, Степень приближения полиномами в комплексной области. (АМ-9), Том 9, будет готов.
Описание к этой книге «Метрические методы финслеровых пространств и в основаниях геометрии». (AM-8), будет в ближайшее время.
(АМ-5), Том 5 Эмиль Л. Пост Описание для этой книги «Двузначные итерационные системы математической логики». (AM-5), Том 5, будет готов.
Эта книга посвящена двум на первый взгляд непересекающимся областям математики, а также некоторым их аналогиям и взаимодействиям. Эти направления представляют собой теорию линейных дифференциальных уравнений с одной комплексной переменной с…
(АМ-132), Том 132 Пьер Делинь и Г. Даниэль Мостоу Первая часть этой монографии посвящена характеристике гипергеометрикоподобных функций, т. е. поворотов гипергеометрических функций от n -переменных. Они рассматриваются как ( n +1) размерное векторное пространство многозначных…
В этом сборнике собраны влиятельные статьи математиков, изучающих границы исследований топологии, одного из наиболее важных достижений современной математики. Работы охватывают широкий круг топологических специальностей…
Описание для этой книги «Вклады в теорию нелинейных колебаний» (AM-45), том V будет готово.
Эти два новых сборника под номерами 28 и 29 соответственно в Annals of Mathematics Studies продолжают высокий стандарт, установленный более ранними Annals Studies 20 и 24, объединяя важные вклады в теории игр. ..
В этой книге обсуждаются некоторые аспекты теории уравнений в частных производных с точки зрения теории вероятностей. Он предназначен не только для специалистов по уравнениям в частных производных или теории вероятностей, но и для…
Описание к этой книге «Множественные интегралы в вариационном исчислении и нелинейных эллиптических системах». (AM-105), том 105, будет готов.
Особенно своевременная работа, книга представляет собой введение в теорию p-адических L-функций, созданную Куботой и Леопольдтом в 1964 как p-адические аналоги классических L-функций Дирихле.
В этой книге представлена классификация всех (комплексных)
неприводимых представлений редуктивной группы с
связным центром над конечным полем. Для этого
Теория теплицевых операторов в последние годы становится все более похожей на классическую теорию псевдодифференциальных операторов. Например, операторы Теплица обладают символическим исчислением, аналогичным обычному символьному…
Этот сборник статей представляет собой обширный обзор последних достижений в области дифференциальной геометрии и ее взаимодействия с другими областями, особенно с уравнениями в частных производных и математической физикой. Этот район…
Перевод Морриса Тененбаума и Гарри Полларда
Описание к этой книге «Лекции по интегралам Фурье». (AM-42), Том 42, будет готов.
Летом 1965 г. в Университете Висконсина под руководством профессора Бинга прошел неофициальный семинар по геометрической топологии. Двадцать пять из этих лекций включены в данное исследование, в том числе лекция профессора Бинга…
Описание для этой книги «Вклады в теорию нелинейных колебаний» (AM-36), том III будет готово.
Описание для этой книги Преобразования Фурье. (AM-19), Том 19, будет готов.
Описание к этой книге «Общие проблемы стабильности движения». (AM-17), Том 17, будет готов.
Описание к этой книге «Исчисление многообразий Гейзенберга». (АМ-119), Том 119, будет готов.
В этой книге описывается инвариант l ориентированных рациональных гомологических 3-сфер, который является обобщением работы Эндрю Кассона в случае целочисленной гомологической сферы. Обозначим через R(X) пространство классов сопряженности представлений…
Описание для этой книги «Теоретические методы ветвления в алгебраической геометрии» (AM-43), том 43, будет опубликовано позже.
Настоящая монография выросла из пятого цикла лекций Германа Вейля, прочитанных профессором Гриффитсом в Институте перспективных исследований в Принстоне осенью 1974.
Описание этой книги «Семинар по группам трансформации». (AM-46), Том 46, будет готов.
(АМ-100), Том 100 Джон Эрик Форнесс Описание к этой книге «Недавние разработки в области нескольких сложных переменных». (AM-100), Том 100, будет готов.
Используя только очень элементарную структуру конечных вероятностных пространств, эта книга рассматривает ряд вопросов современной теории случайных процессов. Это стало возможным благодаря использованию небольшого количества нестандартных… 9 Абрахама Робинсона.0003
(АМ-106), Том 106 Под редакцией Филиппа А. Гриффитса Описание этой книги «Темы трансцендентальной алгебраической геометрии». (AM-106), том 106, будет готов.
В этой монографии авторы систематически пересматривают теорию, используя два разных подхода. Общий механизм деформации конструкций на многообразиях был разработан Дональдом Спенсером десять лет назад. Новая версия этого. ..
Одна из наиболее цитируемых книг по математике, изложение теории Морса Джона Милнора, была самой важной книгой по этому предмету на протяжении более сорока лет. Теория Морса была разработана в 1920-х годах математиком Марстоном Морзе….
В этой книге содержится ценное обсуждение перенормировки путем добавления контрчленов к лагранжиану, дающее первое полное доказательство отмены всех расходимостей в произвольном взаимодействии. Автор также…
Описание к этой книге «Лекции по дифференциальным уравнениям». (AM-14), Том 14, будет готов.
Описание к этой книге «Потоки на однородных пространствах». (AM-53), Том 53, будет готов.
Теория внешних дифференциальных систем обеспечивает основу для систематического рассмотрения типично нелинейных и часто переопределенных дифференциальных уравнений в частных производных, возникающих в дифференциальной геометрии. Адаптация…
Логику иногда называют основой математики: логик изучает виды рассуждений, используемых на отдельных этапах доказательства. Алонзо Черч был пионером в области математической логики, чей вклад в число…
Описание этой книги «Введение в нелинейную механику». (AM-11), Том 11, будет готов.
Описание к этой книге «Топологические методы в теории функций комплексного переменного». (AM-15), Том 15, будет готов.
Эта книга представляет собой первое связное описание области анализа, включающей группу Гейзенберга, квантование, исчисление Вейля, метаплектическое представление, волновые пакеты и связанные с ними концепции. Этот круг идей приходит…
В работе дается полное описание метода анализа допустимых комплексных представлений общей линейной группы G = Gl(N,F) неархимедова локального поля F в терминах структуры этих представления, когда они. ..
В первых двух главах этой книги читатель найдет полное и систематическое изложение теории гиперфункций на вполне вещественных подмногообразиях многомерного комплексного пространства, в частности теории гиперфункций в…
Описание к этой книге «Методы композиции в гомотопических группах сфер». (АМ-49), Том 49, будет готов.
Описание этой книги «К-теория форм». (АМ-98), том 98, будет готов.
Основанный на семинаре, спонсируемом Институтом перспективных исследований в 1977-1978 гг. , этот набор статей кратко и ясно знакомит математиков с аналитическим образованием с микролокальным анализом. Статьи посвящены теории…
Намерение авторов состоит в том, чтобы исследовать связь между кусочно-линейной структурой и дифференциальной структурой: связь, как они утверждают, может быть понята как гомотопическая теория препятствий и, следовательно, может быть изучена…
Описание для этой книги «Вклады в теорию нелинейных колебаний» (AM-41), том IV будет готово.
Описание для этой книги Семинар по минимальным подмногообразиям. (AM-103), том 103, будет готов.
Геометрия ортогональных пространств.
Эти два новых сборника под номерами 28 и 29 соответственно в Annals of Mathematics Studies продолжают высокий стандарт, установленный более ранними Annals Studies 20 и 24, объединяя важные вклады в теории игр. ..
Это исследование теории моделей со значениями истинности в компактном хаусдорфовом топологическом пространстве.
Новая группа вкладов в развитие этой теории ведущих специалистов в этой области. В число участников входят Л. Д. Берковиц, Л. Э. Дубинс, Х. Эверетт, У. Х. Флеминг, Д. Гейл, Д. Джиллетт, С. Карлин, Дж. Г. Кемени, Р….
Описание к этой книге «Теоремы существования в уравнениях с частными производными». (AM-23), Том 23, будет готов.
Описание этой книги «Карты, сохраняющие порядок, и процессы интеграции». (AM-31), Том 31, будет готов.
Описание этой книги «Эссе о единой теории специальных функций». (AM-18), Том 18, будет готов.
Цель этой книги — разработать формулу стабильного следа для унитарных групп с тремя переменными. Затем формула стабильного следа применяется для получения классификации автоморфных представлений. Эта работа представляет собой первую…
Торические многообразия — это алгебраические многообразия, возникающие из элементарных геометрических и комбинаторных объектов, таких как выпуклые многогранники в евклидовом пространстве с вершинами в точках решетки. Поскольку многие понятия алгебраической геометрии, такие как…
Риман ввел понятие «локальной системы» на P1-{конечном множестве точек} почти 140 лет назад. Его идея заключалась в том, чтобы изучить n линейных дифференциальных уравнений порядка путем изучения локальных систем ранга n (локальных голоморфных решений)…
Описание к этой книге «Элементарная дифференциальная топология». (AM-54), Том 54, будет готов.
Частично объясняя важную недавнюю работу и частично вводя некоторые методы современных дифференциальных уравнений в частных производных, эта монография представляет собой самостоятельное изложение проблемы Неймана для комплекса Коши-Римана и. ..
Описание к этой книге «Стационарные процессы и теория прогнозирования». (AM-44), Том 44, будет готов.
Курт Гёдель, математик и логик, был одним из самых влиятельных мыслителей двадцатого века. Гёдель бежал из нацистской Германии, опасаясь за свою жену-еврейку и сыт по горло вмешательством нацистов в дела математики. ..
Эта работа представляет собой всестороннее рассмотрение последних достижений в изучении эллиптических кривых и их пространств модулей. Арифметическое изучение пространств модулей началось с «Fundamenta Nova» Якоби в 1829 году., а современная теория была…
Миллер III Частично излагая и частично излагая новые результаты, эта монография посвящена той области математики, которая объединяет как комбинаторную теорию групп, так и математическую логику. Его основными темами являются словесная задача для групп,…
Описание этой книги «Степени неразрешимости». (AM-55), Том 55, будет готов.
Нойманн Эта книга дает новую основу для теории связей в трехмерном пространстве по образцу современных разработок Жако, Шалена, Йоханссона, Терстона и др. теории 3-многообразий. Базовая конструкция — это метод получения любой ссылки путем…
Эта книга служит как полностью самодостаточным введением, так и изложением новых результатов в области теории рекурсивных функций и ее приложений к формальным системам.
(АМ-111), Том 111 Под редакцией С. М. Герстена и Джона Р. Столлингса. Теория групп и топология тесно связаны. Область их взаимодействия, сочетающая логическую ясность алгебры с глубинами геометрической интуиции, составляет предмет Комбинаторная теория групп и топология . Работа…
Описание для этой книги «Вклад в теорию уравнений с частными производными». (AM-33), Том 33, будет готов.
Меры и интегралы
Описание для этой книги, Площадь поверхности. (AM-35), Том 35, будет готов.
(АМ-120), Том 120 Джеймс Артур и Лоран Клозель Общий принцип, открытый Робертом Ленглендсом и названный им «принципом функториальности», предсказывает отношения между автоморфными формами на арифметических подгруппах различных редуктивных групп. Функториальность Ленгленда связывает…
Арифметическая теорема Римана-Роха была недавно показана Висмутом-Жилле-Соулом. В доказательстве смешаны алгебра, арифметика и анализ. Цель этой книги — дать краткое введение в необходимые методы и представить. ..
Эта книга, написанная для студентов старших курсов бакалавриата и аспирантов первого года обучения, направлена на то, чтобы познакомить студентов с серьезным уровнем 9.0389 p -адический анализ с важными последствиями для теории чисел. Основной объект — изучение G-серии…
Фридлендер В этой книге представлен последовательный отчет о современном состоянии этальной гомотопической теории — топологической теории, введенной в абстрактную алгебраическую геометрию М. Артином и Б. Мазуром. Эрик М. Фридлендер представляет множество собственных приложений…
Со времен Пуанкаре топологов больше всего интересовали три вида многообразий. Самые примитивные из них — ТОР-многообразия — оставались довольно загадочными до 1968 года, когда Кирби обнаружил разворачивающийся теперь уже знаменитый тор. ..
Описание для этой книги «Римановы поверхности, связанные темы» (AM-97), том 97: Материалы конференции в Стоуни-Брук, 1978 г. (AM-97), будет в ближайшее время.
Об узлах — это путешествие по теории узлов, начиная с простейших комбинаторных идей — идей, возникающих при представлении узоров плетения. С этого начала непосредственно строятся топологические инварианты: сначала…
p -адическое соответствие Симпсона, недавно начатое Гердом Фалтингсом, направлено на описание всех p -адических представлений фундаментальной группы собственного гладкого многообразия над p -адическое поле в терминах линейной алгебры, а именно Хиггса…
В области действительных чисел аналитическая геометрия долгое время находилась в глубоком взаимодействии с алгебраической геометрией, принося последней многие из ее топологических открытий. В последние десятилетия к этой работе присоединилась теория моделей через…
В более ранней монографии Pseudo-reductive Groups Брайан Конрад, Офер Габбер и Гопал Прасад исследовали общую структуру псевдоредуктивных групп. В этой новой книге Классификация псевдоредуктивных групп Конрад и Прасад идут…
Петерссон,
и Ричард М. Вайс Спуск в Здания начинается с решения основного открытого вопроса о местной структуре зданий Брюа-Титс. Затем авторы помещают свое алгебраическое решение в геометрический контекст, разрабатывая общую фиксированную точку…
Эта книга развивает новую теорию многопараметрических сингулярных интегралов, связанных с шарами Карно-Каратеодори. Брайан Стрит впервые подробно описывает классическую теорию сингулярных интегралов Кальдерона-Зигмунда и приложения к линейным частным. ..
Одним из самых интересных новых предметов в алгебраической теории чисел и арифметической алгебраической геометрии является теория систем Эйлера. Эйлеровы системы — это специальные наборы классов когомологий, связанные с р-адическими представлениями Галуа…
В 1920 г. Пьер Фату высказал гипотезу о том, что — за исключением особых случаев — все критические точки рационального отображения сферы Римана стремятся к периодическим орбитам при итерации. Эта гипотеза остается главной открытой проблемой в…
Хирургической теории, лежащей в основе теории классификации многообразий, уже около сорока лет. К шестидесятилетию (14 декабря 1996 г.) C.T.C. Уолл, ведущий представитель поколения основателей темы, руководил редакторами. ..
В этой книге представлен новый результат в трехмерной топологии. Хорошо известно, что любое замкнутое ориентированное трехмерное многообразие может быть получено операцией на оснащенном зацеплении в S
3. В Глобальная формула хирургии для инварианта Кассона-Уокера, функция F…
Хирургической теории, лежащей в основе теории классификации многообразий, уже около сорока лет. За это время было сделано несколько экстраординарных достижений, которые привели к чрезвычайно разнообразному взаимодействию с алгеброй…
Первые две главы этой книги предлагают современное, самостоятельное изложение элементарной теории триангулированных категорий и их частных. Простое и элегантное изложение этих известных результатов делает эти главы…
Макмаллен За последнее десятилетие появилось много параллелей между сложной динамикой и гиперболической геометрией. Эта книга, основанная на работах Салливана и Терстона, дает единую трактовку построения неподвижных точек для перенормировки и…
Эта книга, основанная на лекциях, прочитанных в Чжэцзянском университете в Ханчжоу, Китай, и Университете Джона Хопкинса, знакомит с собственными функциями на римановых многообразиях. Кристофер Согге приводит доказательство точной формулы Вейля для распределения…
В этой книге Клэр Вуазен представляет введение в алгебраические циклы на комплексных алгебраических многообразиях, в основные гипотезы, связывающие их с когомологиями, и даже точнее в структуры Ходжа на когомологиях. Объем…
С момента введения Фридхельмом Вальдхаузеном в 1970-х годах алгебраическая К-теория пространств была признана основным инструментом для изучения параметризованных явлений в теории многообразий. Однако полное доказательство эквивалентности…
Эпштейн и Рэйф Маццео В этой книге представлены математические основы для анализа класса вырожденных эллиптических операторов, определенных на многообразиях с углами, которые возникают в различных приложениях, таких как популяционная генетика, математические финансы…
Это исчерпывающее описание формулы Гросса-Цагира для кривых Шимуры над вполне вещественными полями связывает высоты точек Хегнера на абелевых многообразиях с производными L-рядов. Формула будет иметь новые приложения для…
В этой книге рассматривается основной вопрос дифференциальной геометрии, который впервые был рассмотрен физиками Стэнли Дезером и Адамом Швиммером в 1993 году при изучении конформных аномалий. Вопрос касается конформно-инвариантных…
Группы Мамфорда-Тейта являются фундаментальными группами симметрии теории Ходжа, предмета, лежащего в основе современной комплексной алгебраической геометрии. Эта книга представляет собой первое всестороннее исследование групп Мамфорда-Тейта и…
В этой книге рассматриваются так называемые маловероятные пересечения, тема, которая охватывает хорошо известные проблемы, такие как проблемы Ланга и Манина-Мамфорда, касающиеся точек кручения в подмногообразиях торов или абелевых многообразий. В общем, книга…
Эта книга вносит существенный вклад в неожиданно сложный вопрос о существовании производных Фреше липшицевых отображений банаховых пространств в многомерные пространства. Потому что вопрос оказывается тесно связанным…
Свертка и равнораспределение исследует важный аспект теории чисел — теорию экспоненциальных сумм над конечными полями и их преобразований Меллина — с новой, категоричной точки зрения. В книге представлены фундаментальные…
Робин Грэм Эта книга развивает и применяет теорию объемлющей метрики в конформной геометрии. Это метрика Лоренца в n + 2 измерений, который кодирует конформный класс метрик в n измерений. Метрика окружения имеет альтернативное воплощение…
Первоначальная цель, которая в конечном итоге привела к написанию этого тома, заключалась в построении «мотивной теории когомологий», существование которой было выдвинуто гипотезой А. Бейлинсоном и С. Лихтенбаумом. Это достигается в четвертой статье книги с использованием результатов…
В этой книге гипоэллиптический лапласиан используется для вычисления полупростых орбитальных интегралов в формализме, объединяющем теорию индексов и формулу следов. Гипоэллиптический лапласиан — это семейство операторов, которые должны интерполировать…
Группа Вейля, кратная ряду Дирихле, является обобщением дзета-функции Римана. Подобно дзета-функции Римана, они представляют собой ряды Дирихле с аналитическим продолжением и функциональными уравнениями, имеющими приложения к аналитическим числам…
Модульные формы чрезвычайно важны в различных областях математики, от теории чисел и алгебраической геометрии до комбинаторики и решеток. Их коэффициенты Фурье, типичным примером которых является тау-функция Рамануджана, имеют глубокие…
(АМ-160): (АМ-160) — Третье издание Джон Милнор В этом томе изучается динамика итерированных голоморфных отображений римановой поверхности в себя с упором на классический случай рациональных отображений римановой сферы. Эта тема большая и быстрорастущая. Эти лекции…
Теория Рамсея — это быстро развивающаяся область комбинаторики, тесно связанная с другими областями математики, такими как топологическая динамика, эргодическая теория, математическая логика и алгебра. Область теории Рамсея, связанная с типами Рамсея. ..
В этой книге изучаются когомологии пересечения многообразий Шимуры, ассоциированных с унитарными группами любого ранга над Q. В общем случае эти многообразия не компактны. Когомологии пересечения многообразия Шимуры, связанные с…
Внешний бильярд — это базовая динамическая система, определенная относительно выпуклой формы на плоскости. Б. Х. Нейман ввел эту систему в 19 в.50-х годов, а Дж. Мозер популяризировал его как игрушечную модель для небесной механики. Все это время так называемый…
Результаты, установленные в этой книге, представляют собой новое направление в эргодической теории и значительное расширение ее области применения. Традиционные эргодические теоремы фокусировались на аменабельных группах и полагались на существование асимптотически…
Теория высших категорий обычно считается технической и неприступной, но часть ее значительно более податлива: теория бесконечных категорий, высших категорий, в которых все высшие морфизмы предполагаются обратимыми. В…
Эта книга представляет собой эффектное введение в современную математическую дисциплину, известную как теория игр. Гарольд Кун впервые представил эти лекции в Принстонском университете в 1952 году. Они лаконично передают суть теории, в…
Эта книга представляет собой первое объединенное исследование взаимосвязи между преобразованиями Радона на симметричных пространствах компактного типа и инфинитезимальными версиями двух фундаментальных проблем жесткости в римановой геометрии. Его первичный…
Этот сборник новых и оригинальных статей по математическим аспектам нелинейных дисперсионных уравнений включает как пояснительные, так и технические статьи, отражающие ряд последних достижений в этой области. В пояснительных статьях описывается…
Кац В течение сотен лет изучение эллиптических кривых играло центральную роль в математике. В частности, в прошлом столетии в этом исследовании был достигнут огромный прогресс, начиная с теоремы Морделла в 1922 к работе Уайлса и Тейлор-Уайлс в…
Разрешение особенностей — мощный и часто используемый инструмент в алгебраической геометрии. В этой книге Янош Коллар всесторонне рассматривает характерный нулевой случай. Он описывает более дюжины доказательств кривых…
(АМ-169) Казуя Като и Сампей Усуи В 1970, Филлип Гриффитс предположил, что бесконечно удаленные точки могут быть добавлены к классифицирующему пространству D поляризованных структур Ходжа. В этой книге Кадзуя Като и Сампей Усуи реализуют эту мечту, создав логарифмическую теорию Ходжа…
В The Structure of Affine Buildings Ричард Вайс дает подробное представление полного подтверждения классификации зданий Брюа-Титса, впервые выполненной Жаком Титсом в 1986 году. Книга включает многочисленные результаты о…
В этой книге представлены аналитические основы теории гипоэллиптического лапласиана. Предполагается, что гипоэллиптический лапласиан, оператор второго порядка, действующий на кокасательное расслоение компактного многообразия, интерполирует между…
В этой книге доказывается аналог знаменитой теоремы Уильяма Терстона о гиперболической хирургии Дена в контексте сложных гиперболических дискретных групп, а затем из нее выводятся два основных геометрических следствия. Во-первых, это строительство…
В этой книге описываются теория и приложения дискретных ортогональных многочленов — многочленов, ортогональных на конечном множестве. В отличие от других книг, Discrete Orthogonal Polynomials рассматривает полностью общие весовые функции и…
(АМ-162) Владимир Григорьевич Беркович Среди многих различий между классическими и р-адическими объектами особое место занимают те, которые относятся к дифференциальным уравнениям. Например, замкнутая p-адическая аналитическая форма, определенная в односвязной области, не обязательно…
Модульные формы и специальные циклы на кривых Симуры представляет собой тщательное исследование производящих функций, построенных из специальных циклов, как делителей, так и нулевых циклов, на арифметической поверхности «М», прикрепленной к кривой Симуры «М» над. ..
Прошло уже около тридцати лет с тех пор, как Делинь впервые доказал свою общую теорему о равнораспределении, тем самым установив фундаментальный результат, определяющий статистические свойства достаточно «чистых» алгебро-геометрических семейств сумм характеров…
Гриффитс В последние годы достигнут значительный прогресс в изучении алгебраических циклов с помощью инфинитезимальных методов. Эти методы обычно применялись к теоретико-ходжевым конструкциям, таким как класс циклов и отображение Абеля-Якоби…
В этой книге представлен обзор последних достижений в области локализации квазипериодических решеточных операторов Шредингера и теории квазипериодичности в гамильтоновых эволюционных уравнениях. Физическая мотивация этих…
Т.Р. Маклафлин,
и Питер Д. Миллер Эта книга представляет собой первый асимптотический анализ с помощью полностью интегрируемых методов начальной задачи для фокусирующего нелинейного уравнения Шредингера в квазиклассическом асимптотическом режиме. Эта проблема является ключевой моделью…
Самым большим вкладом Киёси Ито в теорию вероятностей может быть введение им стохастических дифференциальных уравнений для объяснения теории Колмогорова-Феллера марковских процессов. Начиная с геометрических идей, которыми он руководствовался, этот. ..
В этой книге методы теории моделей применяются к изучению некоторых конечных групп перестановок, групп автоморфизмов структур фиксированного конечного языка с ограниченным числом орбит на четверках. Примитивные группы перестановок…
Целью этой книги является, во-первых, доказать локальную гипотезу Ленглендса для GLn над p-адическим полем и, во-вторых, выявить действие группы разложения в простом плохом редукции на l-адических когомологиях «простого» Шимуры. ..
Теория бесконечных пространств петель была в последнее время в центре внимания алгебраической топологии. Фрэнк Адамс делает обзор этой обширной работы для исследователей и студентов. Среди основных рассматриваемых тем — обобщенные когомологии…
Этот том, предназначенный для исследователей римановых поверхностей, обобщает значительную часть работы, проделанной в этой области в течение 19 лет. 66 по 1971 год.
Описание для этой книги «Вклад в теорию римановых поверхностей». (AM-30), Том 30, будет готов.
Восстановление пространственно-временного коэффициента диффузии при субдиффузии: устойчивость, аппроксимация и анализ погрешностей | Журнал численного анализа IMA
Фильтр поиска панели навигации IMA Journal of Numerical AnalysisIMA JournalsЧисленный анализКнигиЖурналыOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации IMA Journal of Numerical AnalysisIMA JournalsЧисленный анализКнигиЖурналыOxford Academic Термин поиска на микросайте
Расширенный поиск
Журнальная статья
Получить доступ
Банти Джин,
Банти Джин
Ищите другие работы этого автора на:
Оксфордский академический
Google ученый
Чжи Чжоу
Чжи Чжоу
Ищите другие работы этого автора на:
Оксфордский академический
Google ученый
Журнал численного анализа IMA , drac051, https://doi. org/10.1093/imanum/drac051
Опубликовано:
26 сентября 2022 г.
История статьи
Получено:
10 октября 2021 г.
Получена редакция:
02 апреля 2022 г.
Опубликовано:
26 сентября 2022 г.
- Содержание статьи
- Рисунки и таблицы
- видео
- Аудио
- Дополнительные данные
Цитировать
Процитировать
Банти Джин, Чжи Чжоу, Восстановление зависящего от пространства-времени коэффициента диффузии при субдиффузии: стабильность, приближение и анализ ошибок, IMA Journal of Numerical Analysis , 2022;, drac051, https://doi.
org/10.1093/imanum/drac051Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)
Закрыть
Разрешения
- Электронная почта
- Твиттер
- Фейсбук
- Подробнее
2
Фильтр поиска панели навигации IMA Journal of Numerical AnalysisIMA JournalsЧисленный анализКнигиЖурналыOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации IMA Journal of Numerical AnalysisIMA JournalsЧисленный анализКнигиЖурналыOxford Academic Термин поиска на микросайте
Advanced Search
Abstract
В данной работе исследуется обратная задача восстановления зависящего от пространства-времени коэффициента диффузии в модели субдиффузии по распределенному наблюдению, где математическая модель включает дробную производную Джрбашяна–Капуто порядка | $\альфа\в (0,1)$| во время. 2(\varOmega ))$| оценка ошибки согласуется с условной устойчивостью. Далее проиллюстрируем анализ некоторыми числовыми примерами.
© Автор(ы), 2022 г. Опубликовано Oxford University Press от имени Института математики и ее приложений. Все права защищены.
© Автор(ы), 2022 г. Опубликовано Oxford University Press от имени Института математики и ее приложений. Все права защищены.
Раздел выпуска:
Статьи
В настоящее время у вас нет доступа к этой статье.
Скачать все слайды
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.
- Щелкните Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
- Находясь на сайте учреждения, используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Войти через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Вход через личный кабинет
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.
Просмотр учетных записей, вошедших в систему
Щелкните значок учетной записи в правом верхнем углу, чтобы:
- Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
- Просмотр институциональных учетных записей, предоставляющих доступ.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
Ведение счетов учреждения
Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.
Покупка
Стоимость подписки и заказ этого журнала
Варианты покупки книг и журналов в Oxford Academic
Краткосрочный доступ
Чтобы приобрести краткосрочный доступ, войдите в свою учетную запись Oxford Academic выше.
У вас еще нет учетной записи Oxford Academic? регистр
Восстановление пространственно-временного коэффициента диффузии при субдиффузии: стабильность, аппроксимация и анализ ошибок — 24-часовой доступ
ЕВРО €30,00
22 фунта стерлингов
39 долларов США.