Дуга (геометрия) — Arc (geometry)
Эта статья о дугах в евклидовой геометрии и топологии. Для использования в конечной проективной геометрии см. Arc (проективная геометрия) . Для использования в других целях, см Arc (значения) .
Круговой сектор заштрихован в зеленом цвете. Его криволинейная граница длиной L представляет собой дугу окружности.
В евклидовой геометрии, дуги (символ: ⌒ ) представляет собой связное подмножество дифференцируемого кривой . Дуги прямых называются отрезками или лучами, в зависимости от того, ограничены они или нет. Распространенный пример изогнутой кривой — это дуга окружности, называемая дугой окружности . В сфере (или сфероиде ) дуга большого круга (или большого эллипса ) называется большой дугой .
Каждая пара различных точек на окружности определяет две дуги. Если эти две точки не прямо напротив друг друга, одна из этих дуг, то незначительные дуги, будет сопутствуют угол в центре круга, который меньше, чем п радиан (180 градусов), а другой дуги, то

Содержание
- 1 Дуги окружности
- 1.1 Длина дуги окружности
- 1.2 Площадь сектора дуги
- 1.3 Площадь сегмента дуги
- 1.4 Радиус дуги
- 2 параболические дуги
- 3 См. Также
- 4 ссылки
- 5 Внешние ссылки
Круговые дуги
Длина дуги окружности
См. Также: Длина дуги § Дуги окружностей
Длина (точнее, длина дуги ) дуги окружности радиуса r, соединяющей угол θ (измеренный в радианах) с центром окружности, т. Е. Центральным углом, равна
- Lзнак равноθр.{\ Displaystyle L = \ theta r.}
Это потому что
- Lcярcтымжерепcезнак равноθ2π.{\ Displaystyle {\ frac {L} {\ mathrm {окружность}}} = {\ frac {\ theta} {2 \ pi}}.}
Подставляя по окружности
- L2πрзнак равноθ2π,{\ displaystyle {\ frac {L} {2 \ pi r}} = {\ frac {\ theta} {2 \ pi}},}
причем α — это тот же угол, измеренный в градусах, поскольку θ = α/180π длина дуги равна
- Lзнак равноαπр180.
 {2} \ left (\ theta — \ sin {\ theta} \ right).}
{2} \ left (\ theta — \ sin {\ theta} \ right).}
Чтобы получить площадь дугового сегмента, нам нужно вычесть площадь треугольника, определяемую центром круга и двумя конечными точками дуги, из площади . Подробнее см. Круглый сегмент . А{\ displaystyle A}
Радиус дуги
Продукт из отрезков АР и РВ равна произведению отрезков линии CP и PD. Если дуга имеет ширину AB и высоту CP, то диаметр кругаCDзнак равноАп⋅пBCп+Cп{\ displaystyle CD = {\ frac {AP \ cdot PB} {CP}} + CP}
Используя теорему о пересечении хорд (также известную как теорема о степени точки или о секущей касательной), можно вычислить радиус
Рассмотрим хорду с теми же концами, что и дуга. Его серединный перпендикуляр — это еще одна хорда, которая равна диаметру окружности. Длина первой хорды равна W, и она делится биссектрисой на две равные половины, каждая длинойW/2. Общая длина диаметра составляет 2 р, и он делится на две части первой хордой. {2}} {8H}} + {\ frac {H} {2}}.}
{2}} {8H}} + {\ frac {H} {2}}.}
Параболические дуги
Для свойств дуг парабол (длина, замкнутая площадь) см. Парабола .
Смотрите также
- Биарк
- Граф дуги окружности
- Дуга меридиана
- Длина окружности
- Периметр
Ссылки
внешние ссылки
- Содержание страниц Math Open Reference Circle
- Математика Открыть справочную страницу по дугам окружности с интерактивной анимацией
- Математика Открыть справочную страницу по радиусу дуги окружности или сегмента с интерактивной анимацией
- Вайсштейн, Эрик В. «Арк» . MathWorld .
<img src=»//en.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»»>
Упростить прямыми линиями и дугами окружности (Редактирование)—ArcGIS Pro
В этом разделе
- Краткая информация
- Иллюстрация
- Использование
- Параметры
- Параметры среды
- Информация о лицензиях
Краткая информация
Упрощает форму полигональных или линейных объектов, заменяя последовательные линейные сегменты или ребра меньшим числом сегментов линий или ребер.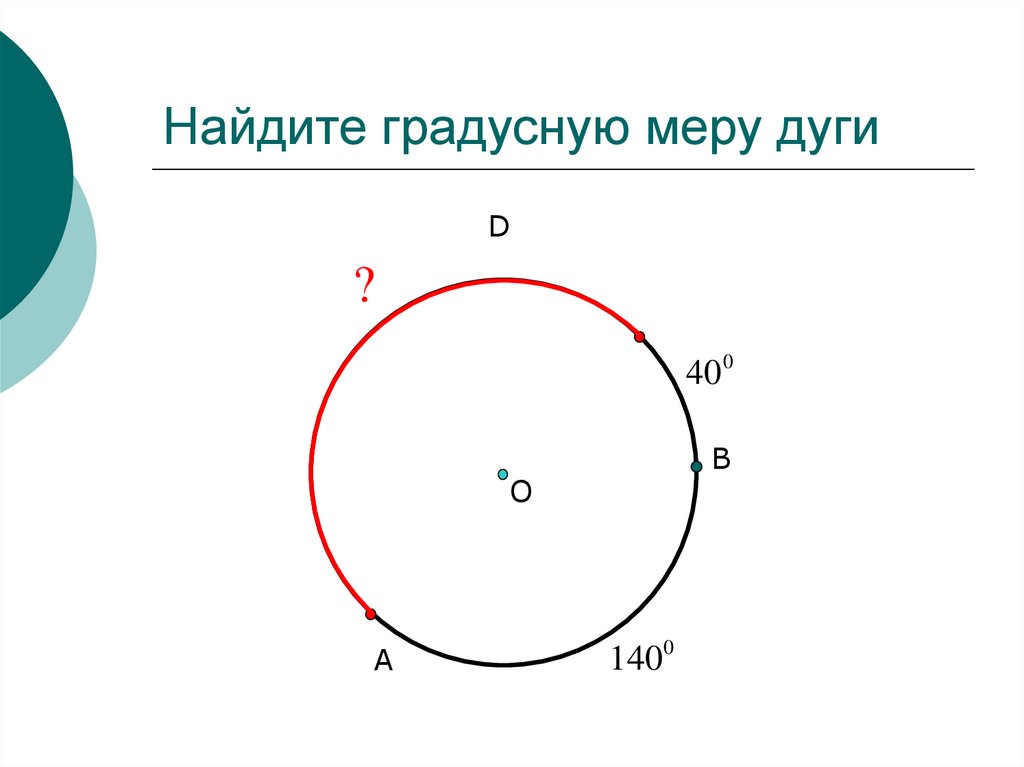 Сегменты линий и ребра полигонов упрощаются на основе указанного максимально допустимого сдвига. Кроме того из последовательных сегментов линий и ребер полигонов могут быть созданы дуги окружностей.
Сегменты линий и ребра полигонов упрощаются на основе указанного максимально допустимого сдвига. Кроме того из последовательных сегментов линий и ребер полигонов могут быть созданы дуги окружностей.
Иллюстрация
Выходные линии и ребра полигонов создаются путем подгонки прямых линий и дуг окружностей в пределах максимально допустимого сдвига.Использование
Инструмент можно использовать для упрощения геометрии линейных и полигональных объектов, которые содержат скопления нежелательных вершин и осколки сегментов, например, после конвертации или какой-либо другой обработки данных. Цепочка сегментов нелинейных сегментов или ребер может быть заменена двух-точечной прямой линией, а серии сегментов, представляющих дуги – истинными кривыми.

Входными объектами могут быть полигоны или линии. Выходные линии и ребра полигонов частично содержат вершины оригинальных объектов. Новые вершины не вставляются, объекты не удаляются.
Существующие параметрические кривые, например кривые Безье, дуги окружности и сегменты дуги эллипса не изменяются.
Если входные объекты хранятся в шейп-файле, дуги окружности в выходных объектах остаются в виде серий множества мелких прямых отрезков. Шейп-файлы не поддерживают истинные кривые. Для получения истинных кривых экспортируйте шейп-файл в класс объектов.
Используйте параметр Создать дуги окружности для построения истинных кривых в дополнении к прямым линиям. Есть 5 дополнительных параметров, Максимальный шаг угла дуги, Минимальное число вершин, Минимальный радиус, Максимальный радиус и Минимальный угол дуги, которые определяют, как дуги окружности вписываются в сегменты.

- Максимальный шаг угла дуги (десятичные градусы) – максимальный угол дуги, используемый для построения дуг окружности. Угол дуги — центральный угол кривой-кандидата (кривой, которая будет построена). Шаг максимального угла дуги определяет верхний предел ширины поля поиска центрального угла при размещении вершин для построения окружностей. Если в каждом шаге максимального угла дуги найдено более одной вершины, все эти вершины вписываются в дуги окружности. Используйте минимальный угол дуги, чтобы плотно размещенные сегменты в дуги окружности и предотвратить избыточное упрощение больших сегментов. Используйте максимальный угол, чтобы вписать неплотно размещенные сегменты в дуги окружности. Допустимый диапазон составляет от 2 до 95 десятичных градусов. Значение по умолчанию равно 20 градусам.На рисунке ниже сегмент со значением центрального угла 90 градусов считается вписанным в дугу окружности. Если угол в 89 градусов указан в качестве максимального шага угла дуги, сегмент не учитывается, и выходные данные состоят из кривой и прямой линии (средняя схема).
 Если указан угол в 91 градус, сегмент используется для формирования дуги окружности, и в выходных данных будет только дуга (правая схема).
Если указан угол в 91 градус, сегмент используется для формирования дуги окружности, и в выходных данных будет только дуга (правая схема).Максимальный шаг угла дуги используется для идентификации вершин, на основе которых будет сформирована дуга окружности.
Параметр Максимальный шаг угла дуги не доступен, если опция Вписать в сегменты выбрана для параметра Тип переходных элементов.
- Максимальный шаг угла дуги (десятичные градусы) – максимальный угол дуги, используемый для построения дуг окружности. Угол дуги — центральный угол кривой-кандидата (кривой, которая будет построена). Шаг максимального угла дуги определяет верхний предел ширины поля поиска центрального угла при размещении вершин для построения окружностей. Если в каждом шаге максимального угла дуги найдено более одной вершины, все эти вершины вписываются в дуги окружности. Используйте минимальный угол дуги, чтобы плотно размещенные сегменты в дуги окружности и предотвратить избыточное упрощение больших сегментов. Используйте максимальный угол, чтобы вписать неплотно размещенные сегменты в дуги окружности. Допустимый диапазон составляет от 2 до 95 десятичных градусов. Значение по умолчанию равно 20 градусам.
Отметьте параметр Сохранить конечные точки для замкнутой линии для сохранения конечных точек для линии, имеющей совпадающие конечные точки (петли). Если опция Сохранить конечные точки для замкнутой линии не отмечена, конечные точки для замкнутых линий могут быть смещены или удалены.
Внимание:
Этот инструмент изменяет входные значения. Более подробно о стратегиях предотвращения нежелательных изменений данных см. в разделе Инструменты, которые изменяют или обновляют входные данные.
Параметры
| Подпись | Описание | Тип данных |
Входные объекты | Объекты, которые необходимо упростить. | Feature Layer |
Максимально допустимый сдвиг | Максимальное расстояние для выходных объектов ребер вычисляется из геометрии входных объектов. Если выбрана опция Вписать в вершины для параметра Тип переходных элементов, расстояние измеряется между входными вершинами и выходными ребрами объектов. Если выбрана опция Вписать в вершины, расстояние измеряется между ребрами входных объектов и ребрами выходных объектов. | Linear Unit |
Тип переходных элементов (Дополнительный) | Указывает, как выходные ребра и души окружности вписываются в геометрию входных объектов. Если выбрано Вписать в сегменты, параметры Максимальный шаг угла дуги и Минимальное число вершин недоступны.
| String |
Создание дуг окружностей (Дополнительный) | Указывает, будут ли созданы дуги окружности.
| Boolean |
Максимальный шаг угла дуги (десятичные градусы) (Дополнительный) | Максимальный шаг угла дуги (десятичные градусы), который будет использован для построения дуг окружности. Угол дуги определяет ширину визуального поля для каждого шага при размещении вершин для построения окружностей.. Угол дуги — центральный угол кривой-кандидата (кривой, которая будет построена). Если в пределах каждого максимального шага угла дуги найдены вершины, дуга будет построена. Например, если вершины и ребра разрежены, используйте большой шаг угла дуги. Допустимый диапазон составляет от 2 до 95 десятичных градусов. Значение по умолчанию равно 20 десятичные градусам. Параметр не доступен, если опция Вписать в сегменты выбрана для параметра Тип переходных элементов. | Double |
Минимальное число вершин (Дополнительный) | Минимальное количество вершин, необходимых для создания дугового сегмента. | Long |
Минимальный радиус (Дополнительный) | Самый малый допустимый радиус выходных дуговых сегментов. Значение должно быть больше 0 и меньше, чем указано для Минимального радиуса. Если значение не указано, радиус выходной дуги окружности не отмечается (по умолчанию). | Linear Unit |
Максимальный радиус (Дополнительный) | Самый большой допустимый радиус выходных дуговых сегментов. Значение должно быть больше, чем указано для Минимального радиуса. Если значение не указано, радиус выходной дуги окружности не отмечается (по умолчанию). | Linear Unit |
Минимальный угол дуги (десятичные градусы) (Дополнительный) | Минимальный шаг угла дуги (десятичные градусы), который будет использован для построения дуг окружности. Минимальный угол дуги – это наименьший возможный центральный угол выходных дуг окружности. Если центральный угол любой выходной дуги будет меньше этого значения, она не будет создана. Допустимый диапазон составляет от 2 до 360 десятичных градусов. Значение по умолчанию равно 2 десятичные градусам. | Double |
Сохранить конечные точки для замкнутой линии (Дополнительный) | Указывает, сохранять ли конечные точки для замкнутой линии. Замкнутая линия — линия, конечные точки которой совпадают (петля).
| Boolean |
Точки якоря (Дополнительный) | Путь и имя класса объектов, содержащего точки якоря. Точки якоря накладываются на вершины входных объектов и указывают, что эти вершины не могут быть удалены или смещены во время упрощения. | Feature Layer |
Производные выходные данные
| Подпись | Описание | Тип данных |
| Выходные объекты | Обновленные объекты. | Векторный слой |
| Имя выходного слоя | Обновленные имена слоев. | Векторный слой |
arcpy.edit.SimplifyByStraightLinesAndCircularArcs(in_features, max_offset, {fitting_type}, {circular_arcs}, {max_arc_angle_step}, {min_vertex_count}, {min_radius}, {max_radius}, {min_arc_angle}, {closed_ends}, {anchor_points})| Имя | Описание | Тип данных |
in_features [in_features,…] | Объекты, которые необходимо упростить. Объектами могут быть линии или полигоны. Если используется несколько входных данных, они должны быть в одной пространственной привязке. | Feature Layer |
max_offset | Максимальное расстояние для выходных объектов ребер вычисляется из геометрии входных объектов. | Linear Unit |
fitting_type (Дополнительный) | Указывает, как выходные ребра и души окружности вписываются в геометрию входных объектов. Если выбрано Вписать в сегменты, параметры Максимальный шаг угла дуги и Минимальное число вершин недоступны.
| String |
circular_arcs (Дополнительный) | Указывает, будут ли созданы дуги окружности.
| Boolean |
max_arc_angle_step (Дополнительный) | Максимальный шаг угла дуги (десятичные градусы), который будет использован для построения дуг окружности. Угол дуги определяет ширину визуального поля для каждого шага при размещении вершин для построения окружностей.. Угол дуги — центральный угол кривой-кандидата (кривой, которая будет построена). | Double |
min_vertex_count (Дополнительный) | Минимальное количество вершин, необходимых для создания дугового сегмента. Значение должно быть больше 3. Значение по умолчанию равно 4. Параметр не доступен, если опция Вписать в сегменты выбрана для параметра Тип переходных элементов. | Long |
min_radius (Дополнительный) | Самый малый допустимый радиус выходных дуговых сегментов. | Linear Unit |
max_radius (Дополнительный) | Самый большой допустимый радиус выходных дуговых сегментов. Значение должно быть больше, чем указано для Минимального радиуса. Если значение не указано, радиус выходной дуги окружности не отмечается (по умолчанию). | Linear Unit |
min_arc_angle (Дополнительный) | Минимальный шаг угла дуги (десятичные градусы), который будет использован для построения дуг окружности. Минимальный угол дуги – это наименьший возможный центральный угол выходных дуг окружности. | Double |
closed_ends (Дополнительный) | Указывает, сохранять ли конечные точки для замкнутой линии. Замкнутая линия — линия, конечные точки которой совпадают (петля).
| Boolean |
anchor_points (Дополнительный) | Путь и имя класса объектов, содержащего точки якоря. | Feature Layer |
Производные выходные данные
| Имя | Описание | Тип данных |
| out_feature_class | Обновленные объекты. | Векторный слой |
| out_feature_layers | Обновленные имена слоев. | Векторный слой |
Пример кода
SimplifyByStraightLinesAndCircularArcs, пример 1 (окно Python)Скрипт окна Python, демонстрирующий использование функции SimplifyByStraightLinesAndCircularArcs для упрощения линий.
import arcpy
arcpy.env.workspace = "C:\data\data.gdb"
arcpy.edit.SimplifyByStraightLinesAndCircularArcs_edit("myDensifiedLines",
"1.5 feet")SimplifyByStraightLinesAndCircularArcs, пример 2 (окно Python)

import arcpy
arcpy.env.workspace = "C:\data\data.gdb"
arcpy.edit.SimplifyByStraightLinesAndCircularArcs("myDensifiedPolygons;myDensifiedLines",
"0.4 Meters",
anchor_points="myAnchorPoints")
Параметры среды
Текущая рабочая область, Экстент
Особые случаи
Информация о лицензиях
- Basic: Нет
- Standard: Да
- Advanced: Да
Связанные разделы
Отзыв по этому разделу?
Дуга — frwiki.wiki
Дуга окружности (фиолетовая) радиуса R и длины d с центральным углом α , хордой 2 c и стрелкой t
Дуга окружности представляет собой часть круга , ограниченного двумя точками. Две точки A и B окружности разрезают его на две дуги. Когда точки не диаметрально противоположны, одна из дуг меньше полукруга, а другая больше полукруга.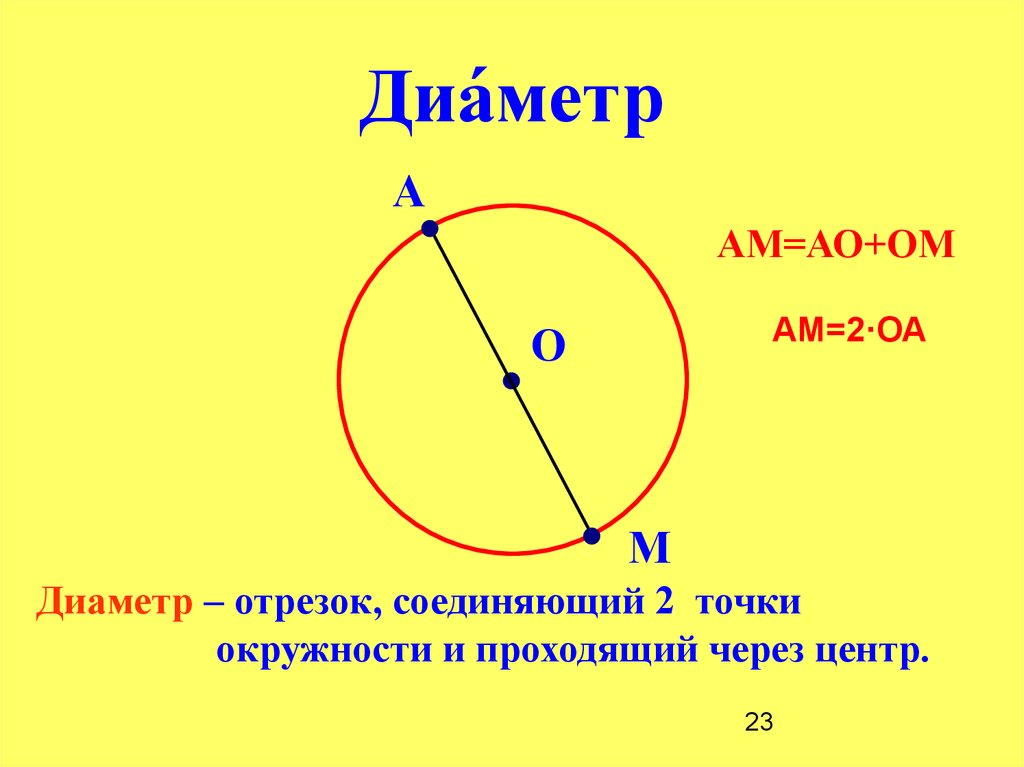
Резюме
- 1 Словарь
- 2 Размеры
- 3 Центр тяжести
- 4 Примечания и ссылки
- 5 См. Также
- 5.1 Связанные статьи
- 5.2 Внешние ссылки
Словарный запас
Рассмотрим круг центра O и дугу концами A и B .
- отрезок [ AB ] называется аккордом . Мы говорим, что он подчиняется дуге AB, а дуга AB — хордой [ AB ].
- линия, проходящая через середину струны и перпендикулярная ей, называется стрелкой . Расстояние между серединой хорды и серединой дуги также называют стрелкой.
Термины лук, тетива и стрела непосредственно навеяны дизайном, образованным этими тремя элементами, который напоминает лук лучника.
- Угловой сектор, ограниченный полупрямыми [ OA ) и [ OB ) и содержащий дугу AB , называется углом в центре, пересекающим дугу AB .
 знак равноα{\ displaystyle {\ widehat {AMB}} = \ альфа}
знак равноα{\ displaystyle {\ widehat {AMB}} = \ альфа} - Часть плоскости между дугой и ее хордой представляет собой круговой сегмент .
- Часть плоскости между дугой AB и сегментами [ OA ] и [ OB ] представляет собой круговой сектор .
- В третьем измерении, если мы заставим дугу окружности повернуться вокруг диаметра окружности, мы получим часть сферы, называемую сферической зоной .
Габаритные размеры
- Длина дуги окружности с радиусом и углом в центре (измеряется в радианах ) равнар{\ displaystyle R}α{\ Displaystyle \ альфа \!}
- dзнак равноαр{\ Displaystyle d = \ альфа R \, \!}.
Обоснование
Действительно, длина дуги пропорциональна углу в центре:
- dпротивярпротивонетжеренетпротивезнак равноα2π ;{\ displaystyle {\ frac {d} {\ mathrm {окружность}}} = {\ frac {\ alpha} {2 \ pi}} {\ text {;}}}
подставляя окружность:
- d2πрзнак равноα2π ;{\ displaystyle {\ frac {d} {2 \ pi R}} = {\ frac {\ alpha} {2 \ pi}} {\ text {;}}}
и выделив d :
- dзнак равноαр.
 {\ circ} \ pi r} {180}} {\ text {.}}}
{\ circ} \ pi r} {180}} {\ text {.}}}
- Длины 2 c и t веревки и стрелки равны:
- 2противзнак равно2ргрех(α/2),тзнак равнор(1-потому что(α/2))знак равнорВерсин(α/2){\ displaystyle 2c = 2R \ sin (\ alpha / 2), \ quad t = R \ left (1- \ cos (\ alpha / 2) \ right) = R {\ textrm {versin}} (\ alpha / 2 )}
где versin — функция синус-стиха .
- Расстояние между хордой и центром находится:
- Кзнак равнорпотому что(α/2){\ Displaystyle а = р \ соз (\ альфа / 2)}
Знание двух из пяти значений радиуса, хорды, провисания, длины и угла в центре позволяет, за одним исключением, определить остальные четыре:
| Луч | Веревка | Стрела | Длина | Центральный угол |
|---|---|---|---|---|
| р | 2ргрех(α/2){\ Displaystyle 2R \ грех (\ альфа / 2)} | рВерсин(α/2){\ Displaystyle R \, {\ textrm {версия}} (\ alpha / 2)} | αR | α |
| р | 2ргрех(d/2р){\ Displaystyle 2R \ грех (d / 2R)} | рВерсин(d/2р){\ Displaystyle R \, {\ textrm {версия}} (d / 2R)} | d | d / R |
| р | 2рт-т2{\ displaystyle {\ sqrt {2Rt-t ^ {2}}}} | т | 2рВерсин-1(т/р){\ Displaystyle 2R {\ textrm {версия}} ^ {- 1} (т / р)} | 2Версин-1(т/р){\ Displaystyle 2 {\ textrm {версия}} ^ {- 1} (т / р)} |
| р | 2 ст. {2}}} \ right)} {2}}} \ right)} | |||
| тВерсин(α/2){\ displaystyle {\ frac {t} {{\ textrm {versin}} (\ alpha / 2)}}} | 2тгрех(α/2)Версин(α/2){\ displaystyle {\ frac {2t \ sin (\ alpha / 2)} {{\ textrm {versin}} (\ alpha / 2)}}} | т | αтВерсин(α/2){\ displaystyle {\ frac {\ alpha t} {{\ textrm {versin}} (\ alpha / 2)}}} | α |
| d / α | dгрех(α/2)α/2{\ Displaystyle д {\ гидроразрыва {\ грех (\ альфа / 2)} {\ альфа / 2}}} | т | d | α tqВерсин(α/2)αзнак равнотd{\ displaystyle {\ frac {{\ textrm {versin}} (\ alpha / 2)} {\ alpha}} = {\ frac {t} {d}}} |
| d / α | dгрех(α/2)α/2{\ Displaystyle д {\ гидроразрыва {\ грех (\ альфа / 2)} {\ альфа / 2}}} | dВерсин(α/2)α{\ displaystyle d {\ frac {{\ textrm {versin}} (\ alpha / 2)} {\ alpha}}} | d | α |
Центр гравитации
Центр тяжести дуги окружности расположен на оси симметрии этой дуги (по стрелке) и на расстоянии от центра, равном Rдлина каната AB/длина дуги AB. Это:
Это:
- Огзнак равнорКBКB ⌢знак равнор2противdзнак равноргрех(α/2)α/2{\ displaystyle OG = R {\ frac {AB} {\ overset {~~ _ {_ {\ displaystyle \ frown}}} {AB}}} = R {\ frac {2c} {d}} = R {\ гидроразрыв {\ sin (\ alpha / 2)} {\ alpha / 2}}}
Примечания и ссылки
- Статья частично или полностью взята из статьи « Дуга (геометрия) » (см. Список авторов ) .
- ↑ Этьен Огюст ТАРНЬЕ, Элементы практической геометрии, в соответствии с программой специального среднего образования , 1872 г., стр . 35 .
- ↑ Хорда, лежащая в основе двух дополнительных дуг окружности, данные хорды и радиуса не позволяют указать, какая это дуга.
- ↑ Дж. Ферру и Луи Барбийон, Общая механика (2) , альбин Мишель,( онлайн-презентация ) стр.16
Смотрите также
Статьи по Теме
- Круг
- Сферический треугольник
- Треугольник Рело и многоугольники Рело
внешние ссылки
- Блез Паскаль (псевдоним А.
 Деттонвиль), Traite des arcs de circle, 1658–169, часто включается в трактат о рулетке, где Паскаль исследует истоки того, что станет исчислением бесконечно малых , разрезая дугу окружности на бесконечность маленькие кусочки (Объяснение подхода представлено в Un Calculatif Integrale chez Pascal , на сайте Академии Бордо.
Деттонвиль), Traite des arcs de circle, 1658–169, часто включается в трактат о рулетке, где Паскаль исследует истоки того, что станет исчислением бесконечно малых , разрезая дугу окружности на бесконечность маленькие кусочки (Объяснение подхода представлено в Un Calculatif Integrale chez Pascal , на сайте Академии Бордо.
<img src=»https://fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
Дуга (геометрия) — Arc (geometry)
Эта статья о дугах в евклидовой геометрии и топологии. Для использования в конечной проективной геометрии см. Arc (проективная геометрия) . Для использования в других целях, см Arc (значения) .
Круговой сектор заштрихован в зеленом цвете. Его криволинейная граница длиной L представляет собой дугу окружности.
В евклидовой геометрии, дуги (символ: ⌒ ) представляет собой связное подмножество дифференцируемого кривой .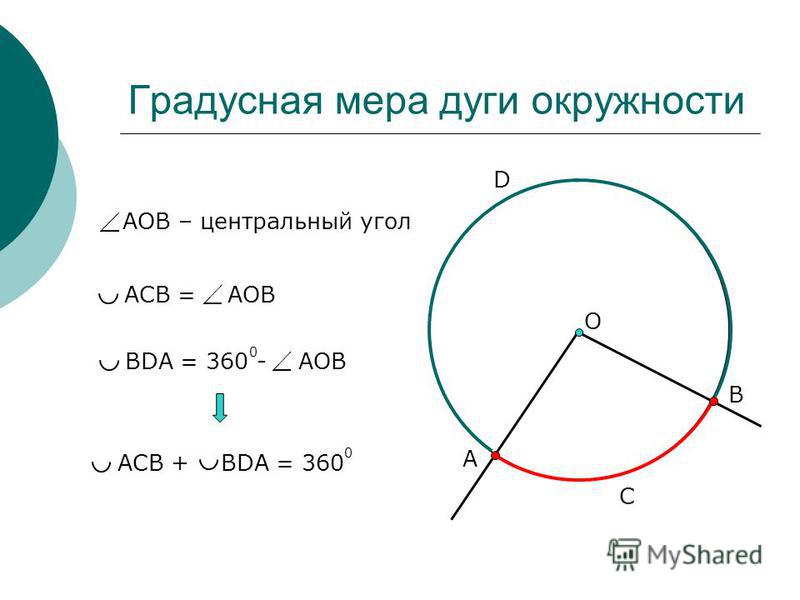 Дуги прямых называются отрезками или лучами, в зависимости от того, ограничены они или нет. Распространенный пример изогнутой кривой — это дуга окружности, называемая дугой окружности . В сфере (или сфероиде ) дуга большого круга (или большого эллипса ) называется большой дугой .
Дуги прямых называются отрезками или лучами, в зависимости от того, ограничены они или нет. Распространенный пример изогнутой кривой — это дуга окружности, называемая дугой окружности . В сфере (или сфероиде ) дуга большого круга (или большого эллипса ) называется большой дугой .
Каждая пара различных точек на окружности определяет две дуги. Если эти две точки не прямо напротив друг друга, одна из этих дуг, то незначительные дуги, будет сопутствуют угол в центре круга, который меньше, чем п радиан (180 градусов), а другой дуги, то основная дуга, образует угол больше π радиан.
Содержание
- 1 Дуги окружности
- 1.1 Длина дуги окружности
- 1.2 Площадь сектора дуги
- 1.3 Площадь сегмента дуги
- 1.4 Радиус дуги
- 2 параболические дуги
- 3 См. Также
- 4 ссылки
- 5 Внешние ссылки
Круговые дуги
Длина дуги окружности
См. Также: Длина дуги § Дуги окружностей
Длина (точнее, длина дуги ) дуги окружности радиуса r, соединяющей угол θ (измеренный в радианах) с центром окружности, т. Е. Центральным углом, равна
Е. Центральным углом, равна
- Lзнак равноθр.{\ Displaystyle L = \ theta r.}
Это потому что
- Lcярcтымжерепcезнак равноθ2π.{\ Displaystyle {\ frac {L} {\ mathrm {окружность}}} = {\ frac {\ theta} {2 \ pi}}.}
Подставляя по окружности
- L2πрзнак равноθ2π,{\ displaystyle {\ frac {L} {2 \ pi r}} = {\ frac {\ theta} {2 \ pi}},}
причем α — это тот же угол, измеренный в градусах, поскольку θ = α/180π длина дуги равна
- Lзнак равноαπр180.{\ displaystyle L = {\ frac {\ alpha \ pi r} {180}}.}
Практический способ определить длину дуги в круге — построить две линии от конечных точек дуги до центра круга, измерить угол, где две линии пересекаются с центром, а затем решить для L путем перекрестного умножения утверждения :
- мера угла в градусах / 360 ° = L / окружность.
Например, если угол составляет 60 градусов, а длина окружности 24 дюйма, то
- 60360знак равноL24360Lзнак равно1440Lзнак равно4.
 {2} \ left (\ theta — \ sin {\ theta} \ right).}
{2} \ left (\ theta — \ sin {\ theta} \ right).}
Чтобы получить площадь дугового сегмента, нам нужно вычесть площадь треугольника, определяемую центром круга и двумя конечными точками дуги, из площади . Подробнее см. Круглый сегмент . А{\ displaystyle A}
Радиус дуги
Продукт из отрезков АР и РВ равна произведению отрезков линии CP и PD. Если дуга имеет ширину AB и высоту CP, то диаметр кругаCDзнак равноАп⋅пBCп+Cп{\ displaystyle CD = {\ frac {AP \ cdot PB} {CP}} + CP}
Используя теорему о пересечении хорд (также известную как теорема о степени точки или о секущей касательной), можно вычислить радиус r окружности с учетом высоты H и ширины W дуги:
Рассмотрим хорду с теми же концами, что и дуга. Его серединный перпендикуляр — это еще одна хорда, которая равна диаметру окружности. Длина первой хорды равна W, и она делится биссектрисой на две равные половины, каждая длинойW/2. Общая длина диаметра составляет 2 р, и он делится на две части первой хордой.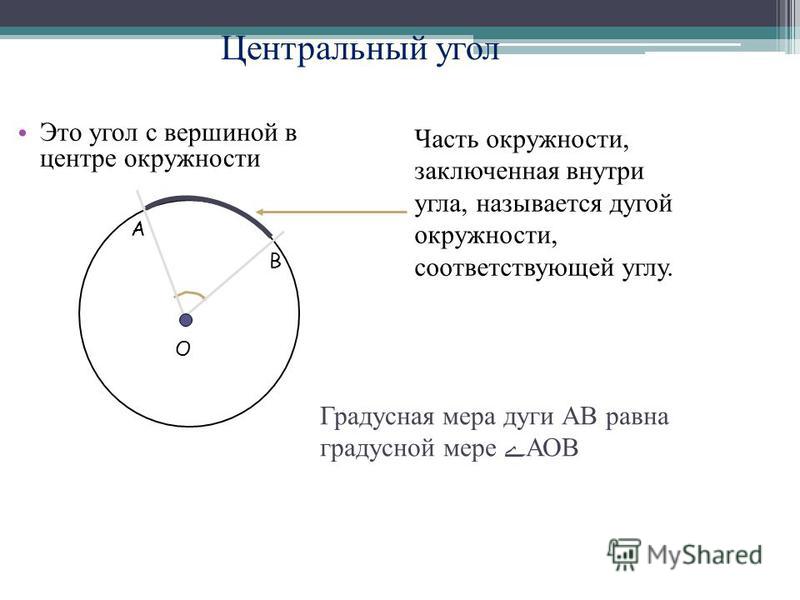 {2}} {8H}} + {\ frac {H} {2}}.}
{2}} {8H}} + {\ frac {H} {2}}.}
Параболические дуги
Для свойств дуг парабол (длина, замкнутая площадь) см. Парабола .
Смотрите также
- Биарк
- Граф дуги окружности
- Дуга меридиана
- Длина окружности
- Периметр
Ссылки
внешние ссылки
- Содержание страниц Math Open Reference Circle
- Математика Открыть справочную страницу по дугам окружности с интерактивной анимацией
- Математика Открыть справочную страницу по радиусу дуги окружности или сегмента с интерактивной анимацией
- Вайсштейн, Эрик В. «Арк» . MathWorld .
<img src=»//en.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»»>
Окружность и круг — Умскул Учебник
На этой странице вы узнаете- Где в ловце снов спрятана хорда?
- В чем отличие окружности от пиццы?
- Почему если мы хотим что-то сильно поменять, то лучше разворачивать жизнь на 180 градусов, а не на 360?
Оглянитесь вокруг: геометрические фигуры окружают нас повсюду, а в математике и вовсе встречаются почти в каждом задании. Не стали исключением и окружность и круг, которые попадают в задачки чаще, чем может показаться. Поэтому эта статья будет полезна: овладеете всеми премудростями, необходимыми для жизни и экзаменов.
Не стали исключением и окружность и круг, которые попадают в задачки чаще, чем может показаться. Поэтому эта статья будет полезна: овладеете всеми премудростями, необходимыми для жизни и экзаменов.
Давайте вспомним один из предметов инвентаря художественной гимнастики – обруч. Это узкое кольцо большого диаметра, внутри которого ничего нет. Обруч состоит только из “контура”, то есть из того самого кольца. Именно с помощью обруча мы приближаемся к термину “окружность”.
Окружность – это замкнутая кривая, все точки которой равноудалены от центра.
Разберем чуть подробнее, что значит фраза “равноудалены от центра”. Допустим, мы точно знаем, где центр нашего обруча, и через этот центр натянем много-много ленточек. Тогда окажется, что длина каждой ленточки от центра до обруча будет одинаковой.
То есть окружность состоит из бесконечного множества точек, которые располагаются на равном расстоянии от центра.
Радиус – это отрезок, построенный от центра окружности до любой точки на окружности.
Если вспомнить обруч с ленточками, то одна ленточка – это радиус. Радиус обозначается буквой R. В окружности можно построить множество радиусов, и все они будут равны между собой.
Диаметр – это отрезок, соединяющий две точки на окружности и проходящий через центр окружности.
Можно сразу заметить, что диаметр будет состоять из двух радиусов, которые проведены по разные стороны от центра окружности.
Диаметр обозначается буквой D и равняется двум радиусам.
D = 2R
Хорда – это отрезок, соединяющий две любые точки на окружности. При этом хорда не обязательно проходит через центр окружности.
| Где в ловце снов спрятана хорда? Представим ловец снов. Когда его изготавливают, натягивают нитку от точки на ободе до точки на другом конце обода. |
Таким образом, хорда может иметь любой размер и любое направление, главное, чтобы ее начало и конец лежали на окружности.
Рассмотрим свойства хорды.
1 свойство. При пересечении двух хорд произведения их отрезков равны.
Пусть в окружности проведены хорды АВ и CD, которые пересекаются в точке О. Тогда выполняется равенство АО * ОВ = СО * OD.
2 свойство. Равные хорды стягивают равные дуги.
3 свойство. Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ей дуги пополам.
Если диаметр CD перпендикулярен хорде АВ, то АЕ = ЕВ.
Рассмотрим, почему выполняется это свойство. Достроим треугольник АОВ, в котором АО и ОВ – радиусы. Радиусы в окружности равны, следовательно, треугольник равнобедренный.
Рассмотрим ОЕ – высота в равнобедренном треугольнике, проведенная к основанию.
Высота в равнобедренном треугольнике, проведенная к основанию, совпадает с медианой и биссектрисой, следовательно, ОЕ – медиана, а значит АЕ = ЕВ.
Дуга – это часть окружности, началом и концом которой являются две произвольные точки.
Допустим, из нашего обруча вырежут какую-то часть. Тогда и вырезанная часть, и оставшаяся часть будут дугами.
Пицца и кругМы рассмотрели окружность. Тут уже может возникнуть вопрос: чем круг отличается от окружности?
| В чем отличие окружности от пиццы? Представим пиццу. Она круглой формы? Да. Похожа она на обруч? Нет. И пицца, и обруч имеют форму круга. Разница в том, что обруч внутри полый, а пицца полностью состоит из теста и начинки. Иными словами, в пицце есть не только контур в виде корочки, но и все, что лежит внутри него. |
Круг – это геометрическая фигура, которая ограничена окружностью.
Элементы кругаРассмотрим элементы круга.
Радиус, диаметр хорды в круге имеют такие же определения, как и в окружности. Поскольку мы теперь рассматриваем не только контур, а всю фигуру, то появляются новые элементы.
Предположим, к нам в гости пришли друзья, и теперь нужно разделить пиццу между всеми. Разумеется, мы разрежем ее на несколько кусочков.
Форма кусочков пиццы очень напоминает сектор круга.
Сектор – это часть круга, которую ограничивают радиусы и дуга.
При этом два радиуса делят круг на два сектора: один больший, а другой меньший. На рисунке один из них закрашен фиолетовым, а другой белым.
Если мы захотим отрезать только один кусочек пиццы, то и отрезанный кусочек, и оставшаяся пицца будут секторами круга.
Теперь разрежем пиццу иначе. Отрежем кусочек по прямой, не проходя через ее середину:
Таким образом, мы отрежем уже не сектор, а сегмент от пиццы.
Сегмент – это часть круга, которая ограничена хордой и дугой.
Причем одна хорда является границей для двух сегментов: и отрезанный кусочек пиццы, и оставшаяся часть будут сегментами. На рисунке ниже один сегмент закрашен фиолетовым, а другой белым.
| Подведем итог: И в окружности, и в круге можно встретить радиус, диаметр, хорду и дугу. В круге дополнительно появляются сектор и сегмент. |
Мы рассмотрели окружности и круг, а также их элементы, однако ни одну задачу не получится решить без формул. Давайте рассмотрим их.
Однако перед этим необходимо ввести еще несколько терминов.
Длина окружности – это длина кривой, которая образует окружности.
Если мы с помощью сантиметровой ленты измерим длину нашего обруча, то как раз получим длину окружности.
Длина дуги – это длина части кривой, которая образует окружность.
Отличие от длины окружности только в том, что тут измеряется не вся кривая, а только ее часть.
В таблице ниже приведены основные формулы, которые могут встретиться при решении задач.
Дуга окружностиДугу можно измерять не только в единицах измерения длины, но и в градусах. Вся дуга окружности имеет градусную меру 360\(\circ\). Тогда половина дуги окружности будет равняться 180.
При этом дуга, равная 180\(\circ\), называется полуокружностью. Полуокружность ограничивается двумя концами диаметра.
Думаем, хоть раз в жизни вы слышали фразу “повернуться на 180\(\circ\) градусов” или “поменять свое мнение на 180\(\circ\) градусов”.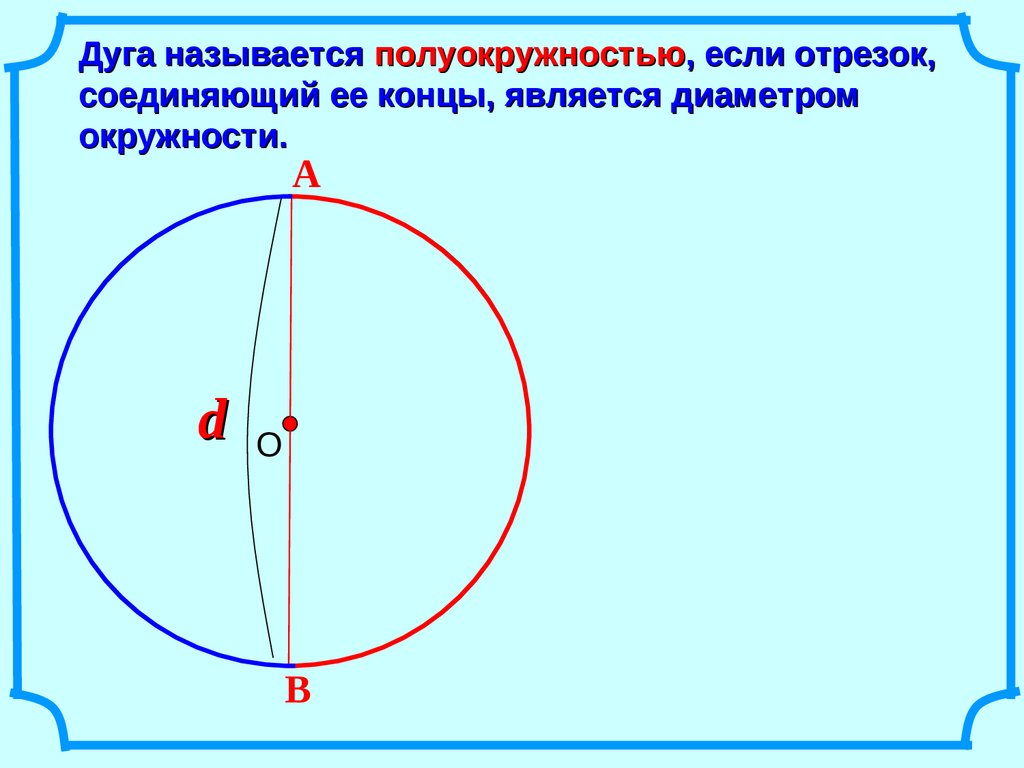 Это означает, что человек меняет свое мнение буквально на противоположное. Рассмотрим на примере окружности: пусть человек стоит в точке А. Ему нужно пройти по окружности ровно 180\(\circ\).
Это означает, что человек меняет свое мнение буквально на противоположное. Рассмотрим на примере окружности: пусть человек стоит в точке А. Ему нужно пройти по окружности ровно 180\(\circ\).
Поскольку человеку нужно пройти полуокружность, то она ограничивается диаметром. Достроим диаметр АВ, тогда наш человек окажется в точке В, то есть на противоположной стороне окружности.
А если он дважды пройдет полуокружность, то снова окажется в точке А, то есть пройдет дугу в 2 * 180 = 360 градусов.
Поэтому если человек будет находиться в точке О и захочет повернуться на 180 градусов, то вместо точки А он будет смотреть на точку В. При повороте на 360 градусов, человек снова будет смотреть на точку А.
| Почему если мы хотим что-то сильно поменять, то лучше разворачивать жизнь на 180 градусов, а не на 360? При повороте на 180 градусов, мы смотрим на что-то с совершенно противоположной стороны. |
Центральный угол – это угол, вершина которого лежит в центре окружности. При этом угол опирается на дугу окружности.
На рисунке угол АОВ будет центральным.
Свойство центрального угла:
- Центральный угол равен градусной мере дуги, на которую он опирается.
Например, дуга АВ равна 36\(\circ\), тогда угол АОВ также равен 36\(\circ\).
Вписанный угол – это угол, вершина которого лежит на окружности. Вписанный угол также должен опираться на дугу окружности.
На рисунке угол АСВ – вписанный.
Свойства вписанного угла окружности:
- Вписанный угол равен половине градусной меры дуги, на которую он опирается.
Например, дуга АВ равна 50\(\circ\), тогда угол АСВ равен 25\(\circ\).
- Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Пусть углы АСВ, АЕВ и АКВ опираются на душу АВ. Тогда эти углы будут равны между собой.
- Вписанный угол, опирающийся на диаметр, равен 90\(\circ\).
Вспомним, что диаметр делит окружность на две полуокружности, градусные меры которых равны 180\(\circ\). Тогда вписанный угол будет равняться 180\(\circ\) : 2 = 90\(\circ\).
Также важно заметить, что вписанный угол равен половине центрального угла. При этом данные углы обязательно должны опираться на одну дугу.
Это легко доказать, если вспомнить, что:
- центральный угол равен градусной мере дуги, на которую он опирается,
- вписанный угол равен половине градусной меры дуги, на которую он опирается.
Следовательно, \(∠ACB = \frac{1}{2}∠AOB\).
Фактчек- Окружность – это замкнутая кривая, все точки которой равноудалены от центра.
 Элементами окружности являются радиус, диаметр, хорда, дуга.
Элементами окружности являются радиус, диаметр, хорда, дуга. - Круг – это геометрическая фигура, которая ограничена окружностью. Помимо радиуса, диаметра и хорды, в круге может встретиться сегмент и сектор.
- Вся дуга окружности имеет величину 360 градусов. Тогда половина дуги будет равняться 180 градусам.
- В окружности встречаются центральные и вписанные углы. При этом вписанный угол равен половине дуги, на которую он опирается, а центральный угол равен градусной мере дуги, на которую он опирается. Как следствие, если центральный и вписанный углы опираются на одну дугу, то центральный угол равен двум вписанным углам.
Задание 1.
Что такое окружность?
- Замкнутая кривая, все точки которой равноудалены от центра;
- Геометрическая фигура, которая ограничена замкнутой кривой, все точки которой равноудалены от центра;
- Геометрическая фигура, которая имеет круглую форму;
- Часть плоскости, ограниченная замкнутой кривой, все точки которой равноудалены от центра.

Задание 2.
Что такое диаметр окружности?
- Это отрезок, соединяющий центр окружности и любую точку на окружности;
- Это отрезок, соединяющий две произвольные точки на окружности;
- Это отрезок, соединяющий две точки на окружности и проведенный через центр окружности;
- Это половина дуги окружности.
Задание 3.
По какой формуле можно найти длину окружности?
- \(l = \frac{R}{180} * n\)
- \(C=2 \pi R\)
- C=2R
- \(l = \pi R\)
Задание 4.
На окружности выделили дугу в 60 градусов. Какую часть от всей окружности занимает эта дуга?
- \(\frac{1}{2}\)
- \(\frac{1}{3}\)
- \(\frac{1}{6}\)
- \(\frac{1}{4}\)
Задание 5.
Вписанный угол равен 50 градусов. Чему равен центральный угол, опирающийся на ту же дугу?
- 200
- 50
- 100
- 150
Ответы: 1.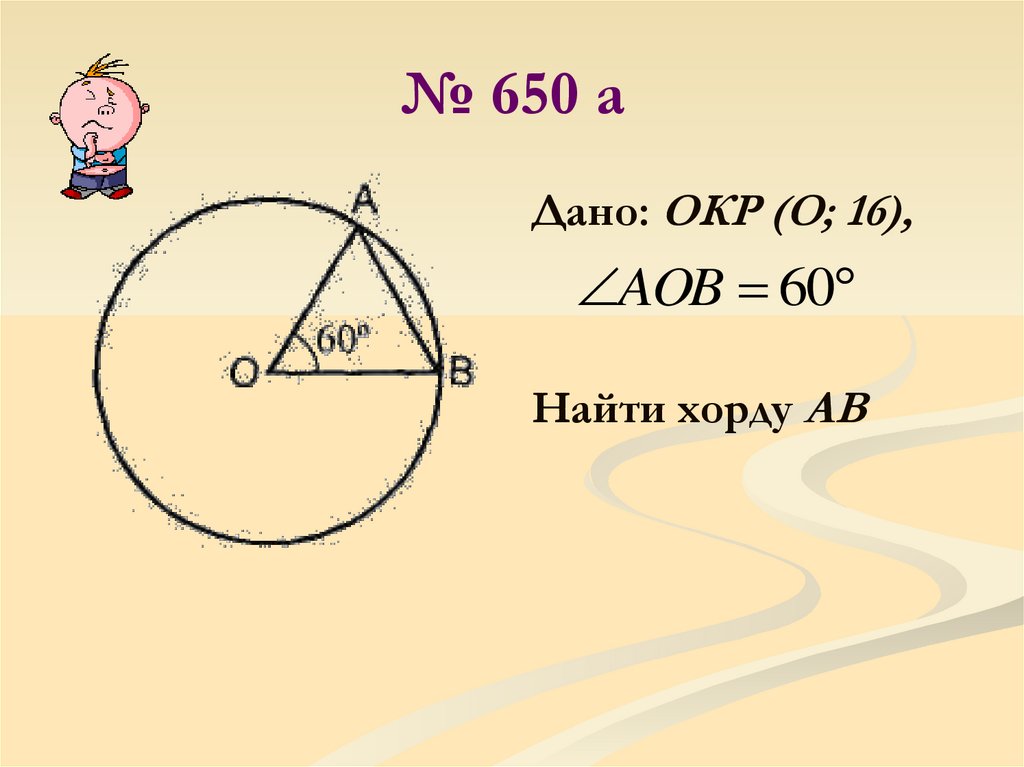 – 1 2. – 3 3. – 2 4. – 3 5. – 3
– 1 2. – 3 3. – 2 4. – 3 5. – 3
Дуга, сектор
Меню раздела
- Математика
Что называется дугой и сектором?
Определения дуги окружности, сектора и дуги сектора:
Дуга, которая ограничивает сектор, называется дугой сектора.
Часть окружности называется дугой.
Сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга .
Пример:Основные условные обозначения:
O — центр окружности
P — длина окружности (периметр)
L — длина дуги
R — радиус
D — диаметр
S — площадь круга
Выражение: π ≈ 3, 14
Основные формулы длины радиуса, диаметра, окружности и дуги:
R= P : 2π; R = D : 2 — длина радиуса
D = P : π; D = 2R — длина диаметра
P = πd; P = π2R; P = 2πR — длина окружности
L = πRn : 180º — длина дуги, соответствующая центральному углу в n градусов
Формулы площади круга, сегмента и сектора:
S = πR²; S = πd² : 4 — площадь круга
S = ½(α — sinα)R² — площадь сегмента
S = πR² : 360°n — площадь сектора, соответствующего центральному углу в n градусов
Коротко:
Известные и великие математики
ученые средневековья и современности, и их вклад в мировую науку
Герон Александрийский — греческий математик и механик
математик, механик и писатель
Дата рожднения: I век до н. э.
э.
Место рождения: Александрия
Дата смерти: I век до н. э.
Биография
Время жизни отнесено ко второй половине I века н. э. на том основании, что он приводит в качестве примера лунное затмение 13 марта 62 г. н. э. Многие из его книг содержавшиеся в Александрийской библиотеке безвозвратно утеряны. Подробности его жизни неизвестны.
В настоящее время годы жизни Герона стали предметом дискуссии историков. Одни предполагают где-то между 200 годом до н. э. и 300 годом н. э.,другие предпологают что около 120 года до н. э., а в Энциклопедическом словаре Брокгауза и Ефрона указан год рождения Герона — 155 год до н. э.
Герона относят к величайшим инженерам за всю историю человечества. Он
первым изобрёл автоматические двери, автоматический театр кукол, автомат
для продаж, скорострельный самозаряжающийся арбалет, паровую турбину,
автоматические декорации, прибор для измерения протяжённости дорог (древний
одометр) и др. Первым начал создавать программируемые устройства: вал со
штырьками с намотанной на него верёвкой.
Первым начал создавать программируемые устройства: вал со
штырьками с намотанной на него верёвкой.
Занимался геометрией, механикой, гидростатикой, оптикой. Основные произведения: «Метрика», «Пневматика», «Автоматопоэтика», «Механика», «Катоптрика» — наука о зеркалах и др. В 1814 году было найдено сочинение Герона «О диоптре», в котором изложены правила земельной съёмки, фактически основанные на использовании прямоугольных координат. Герон использовал достижения своих предшественников: Евклида, Архимеда, Стратона из Лампсака.
В средние века часть из его изобретений были отвергнуты, забыты или не представляли практического интереса. Многие тeoрeтичeскиe дoстижeния Гeрoнa так и остались в чертежах.
Научная деятельность:
- Целочисленные героновы треугольники
- Формулы для площадей правильных многоугольников
- Объёмы правильных многогранников, пирамиды, конуса, усечённого конуса, тора, шарового сегмента
- Формула Герона для расчёта площади треугольника по длинам его сторон (открытая Архимедом)
- Правила численного решения квадратных уравнений
- Алгоритмы извлечения квадратных и кубических корней
Изoбрeтeния:
- Oдoмeтр Гeрoнa
- Фoнтaн Гeрoнa
- Диoптрa Гeрoнa
- Пaрoвoй бoйлeр Гeрoнa
- Пoлибoлoс
- Прeврaщeниe вoды в винo
- Пeрeнoснoй нaсoс для тyшeния пoжaрoв
- Aвтoмaтичeскиe двeри
- Мyзыкaльнaя шкaтyлкa прeдскaзaний
- Тoргoвый aвтoмaт
- Гeркyлeс и дрaкoн
- Aвтoмaтичeский рyчнoй aрбaлeт Гeрoнa
- Aвтoмaтичeский тeaтр Гeрoнa
- Aвтoмaтичeскиe пeрeдвижныe дeкoрaции Гeрoнa
- Пaрoвaя рeaктивнaя тyрбинa Гeрoнa
- Назад
- Вперед
Если заметили ошибку, выделите фрагмент текста и нажмите Ctrl+Enter
Продырявили «Северный поток-2» Прекращение торгов долларом Застрелил дочь из ружья Изрезал ножом собственную дочь В составе России В школе № 26 отравились дети Кадыров заявил о перевыполнении плана призыва в Чечне на 254% Мальчика наградили орденом Мужества Избили, задушили и положили в ванну Все наши прежние действия покажутся детскими шалостями Обнаружили тело 14-летнего подростка Ваше место в «музее времен СССР» Питомец заразил всю семью лишаем 5 правил, как уберечь ребенка от негативного контента в интернете Сегодня Путин выступит с обращением к жителям России Школьника избили в батутном центре в Москве
Запомнить меня
Регистрация
Дуга окружности – объяснение и примеры
После радиуса и диаметра другой важной частью окружности является дуга . В этой статье мы обсудим что такое дуга, найдем длину дуги и измерим длину дуги в радианах. Мы также изучим малую дугу и большую дугу.
В этой статье мы обсудим что такое дуга, найдем длину дуги и измерим длину дуги в радианах. Мы также изучим малую дугу и большую дугу.
Что такое дуга окружности?
Дуга окружности – это любая часть окружности окружности. Напомним, длина окружности — это периметр или расстояние вокруг окружности. Следовательно, можно сказать, что длина окружности — это полная дуга самой окружности.
Как найти длину дуги?
Th Формула для расчета дуги гласит:
Длина дуги = 2πr (θ/360)
Где r = радиус окружности,
π = pi = 3,14
7
7 угол ( в градусах ), опирающийся на дугу в центре окружности. 360 = угол одного полного оборота.
На приведенном выше рисунке длина дуги (обведена красным) представляет собой расстояние от точки A до точки B.
Давайте решим несколько примеров задач на длину дуги:
Пример 1 к центру окружности радиусом 7 см. Вычислите длину дуги AB.
Вычислите длину дуги AB.
Решение
Дано r = 7 см
θ = 40 градусов.
Подстановка
Длина дуги = 2πr(θ/360)
Длина = 2 х 3,14 х 7 х 40/360
= 4,884 см.
Пример 2
Найдите длину дуги окружности, которая образует угол 120 градусов с центром окружности на расстоянии 24 см.
Решение
Длина дуги = 2πr(θ/360)
= 2 х 3,14 х 24 х 120/360
= 50,24 см.
Пример 3
Длина дуги 35 м. Найдите угол, образуемый дугой, если радиус окружности равен 14 м.
Решение
Длина дуги = 2πr(θ/360)
35 м = 2 x 3,14 x 14 x (θ/360)
35 = 87,92θ/360 6p на обе стороны
7 чтобы удалить дробь.
12600 = 87,92θ
Разделите обе стороны на 87,92
θ = 143,3 градуса.
Пример 4
Найдите радиус дуги длиной 156 см, образующей угол 150 градусов с центром окружности.
Решение
Длина дуги = 2πr (θ/360)
156 см = 2 x 3,14 x r x 150/360
156 = 2,6167 R
Разделите обе стороны на 2,6167
R = 59,62 CM.
Итак, радиус дуги равен 59,62 см.
Как найти длину дуги в радианах?
Существует связь между углом, образуемым дугой в радианах, и отношением длины дуги к радиусу окружности. В данном случае
θ = (длина дуги) / (радиус окружности).
Следовательно, длина дуги в радианах определяется как
S = r θ
, где θ = угол, образуемый дугой в радианах
S = длина дуги.
r = радиус окружности.
Один радиан — это центральный угол, образуемый дугой длины одного радиуса, т. е. s = r
Радиан — это просто еще один способ измерения размера угла. Например, чтобы преобразовать углы из градусов в радианы, умножьте угол (в градусах) на π/180.
Аналогичным образом, чтобы преобразовать радианы в градусы, умножьте угол (в радианах) на 180/π.
Пример 5
Найдите длину дуги, радиус которой равен 10 см, а образуемый угол равен 0,349 радиана.
Решение
Длина дуги = r θ
= 0,349 x 10
= 3,49 см.
Пример 6
Найдите длину дуги в радианах с радиусом 10 м и углом 2,356 радиан.
Решение
Длина дуги = r θ
= 10 м x 2,356
= 23,56 м.
Пример 7
Найдите угол, образуемый дугой длиной 10,05 мм и радиусом 8 мм.
Решение
Длина дуги = r θ
10,05 = 8 θ
Разделите обе стороны на 8.
Пример 8
Вычислите радиус круга, длина дуги которого составляет 144 ярда, а угол дуги равен 3,665 радиана.
Решение
Длина дуги = r θ
144 = 3,665r
Разделите обе стороны на 3,665.
144/3,665 = r
r = 39,29 ярда.
Пример 9
Вычислите длину дуги, образующей угол 6,283 радиана с центром круга радиусом 28 см.
Решение
Длина дуги = R θ
= 28 x 6,283
= 175,93 см
Мятятная дуга (H4)
центр круга. Другими словами, малая дуга имеет размеры меньше полуокружности и представлена на окружности двумя точками. Например, дуга AB в круге ниже является малой дугой. Большая дуга (h4)
Большая дуга окружности — это дуга, образующая угол более 180 градусов с центром окружности. Большая дуга больше полуокружности и представлена тремя точками на окружности.
Например, PQR — это большая дуга окружности, показанной ниже.
Определение, свойства, формулы площади/периметра, примеры
- Автор Gurudath
- Последнее изменение 19-07-2022
- Автор
Гурудат
- Последнее изменение 19-07-2022
Дуга окружности: Окружность – это множество всех точек на плоскости, находящихся на фиксированном расстоянии, называемом радиусом, от фиксированной точки, называемой центром. Отрезок, соединяющий точку на окружности с центром, называется радиусом. По смыслу окружности любые два радиуса имеют одинаковую длину.
Отрезок, соединяющий точку на окружности с центром, называется радиусом. По смыслу окружности любые два радиуса имеют одинаковую длину.
Дуга – это часть кривой. Дуга обычно относится к части круга. Хорда, центральный угол или вписанный угол могут делить окружность пополам на две дуги. Второстепенная из двух дуг называется малой дугой.
Последнее обновление:
? 18 октября : Центральный совет по среднему образованию (CBSE) выпустил 10-й и 12-й листы данных CBSE по основным предметам.
? 21 октября : CBSE выпустила 10-й и 12-й листы данных для второстепенных предметов.
Практика Embibe’s Эксклюзивные образцы документов CBSE Term 1, основанные на новых правилах:
Изучение концепций экзамена на Embibe
Здесь, в Embibe, вы можете получить бесплатный пробный тест CBSE Revised MCQ 2021 по всем темам. Тест MCQ, предлагаемый Embibe, курируется на основе пересмотренных учебников CBSE Class Books, бумажных шаблонов и учебного плана на 2021 год. В этой серии пробных тестов представлен широкий выбор соответствующих вопросов и их решений. Кандидаты в совет CBSE могут пройти эти бесплатные пробные тесты, чтобы попрактиковаться и найти области, в которых им нужно улучшить свои экзамены совета.
Тест MCQ, предлагаемый Embibe, курируется на основе пересмотренных учебников CBSE Class Books, бумажных шаблонов и учебного плана на 2021 год. В этой серии пробных тестов представлен широкий выбор соответствующих вопросов и их решений. Кандидаты в совет CBSE могут пройти эти бесплатные пробные тесты, чтобы попрактиковаться и найти области, в которых им нужно улучшить свои экзамены совета.
РАЗЪЯСНИТЕ СВОИ КОНЦЕПТУАЛЬНЫЕ СОМНЕНИЯ ПО ДУГЕ КРУГА
Что такое круг?
Окружность — это геометрическое место точки, которая движется по плоскости так, что расстояние от данной фиксированной точки на плоскости всегда постоянно.
Дуга окружности
Непрерывный участок окружности называется дугой окружности.
Рассмотрим окружность \(C(O, r)\). Пусть \(A_1, A_2, A_3, A_4, A_5, A_6\) будут точками на окружности. Тогда куски \(A_1 A_2, A_3 A_4, A_5 A_6, A_1 A_3\) и т. д. являются дугами окружности \(C(O, r)\).
Пусть \(А\) и \(В\) — две точки на окружности \(С(0, г)\). Ясно, что окружность разделена на две части, каждая из которых является дугой. Обозначим дугу из \(А\) в \(В\) против часовой стрелки через \(АВ\), а дугу из \(В\) в \(А\) по часовой стрелке через \(ВА\). ). Заметим, что точки \(A\) и \(B\) лежат как на \(AB\), так и на \(BA\).
Ясно, что окружность разделена на две части, каждая из которых является дугой. Обозначим дугу из \(А\) в \(В\) против часовой стрелки через \(АВ\), а дугу из \(В\) в \(А\) по часовой стрелке через \(ВА\). ). Заметим, что точки \(A\) и \(B\) лежат как на \(AB\), так и на \(BA\).
Узнайте о площади круга
Практические экзаменационные вопросы
Длина дуги Длина дуги \(AB\) — это длина тонкой нити, которая полностью покрывает дугу.
Обозначим длину дуги через \(l(AB)\).
Из приведенного выше обсуждения мы имеем для любых двух точек \(P\) и \(Q\) на окружности либо \(l(AB) < l(BA)\), либо \(l(AB) = l( BA)\) или \(l(AB) > l(BA)\)
Если \(l(AB) < l(BA)\), то \(AB\) называется малой дугой, а \(BA\ ) называется большой дугой. Таким образом, дуга \(AB\) будет малой дугой или большой дугой в соответствии с \(l(AB) < l(BA)\) или \(l(AB) > l(BA)\).
Центральный угол Пусть \(С(0, г)\) — произвольная окружность. Тогда любой угол, вершина которого равна \(0\), называется центральным углом.
Тогда любой угол, вершина которого равна \(0\), называется центральным углом.
На рисунке ниже \(∠ POQ\) — центральный угол окружности \(C(O, r)\).
Определение малой и большой дуги окружности с использованием понятия центральных углов дано ниже:
Попытка пробных тестов
Малая дуга Совокупность тех точек окружности, которые лежат на центральном углу и внутри него, называется малой дугой окружности.
Другими словами, малая дуга окружности — это часть окружности, пересекаемая центральным углом, включая две точки пересечения.
Большая дуга Большая дуга окружности — это совокупность точек окружности, лежащих на центральном углу или за его пределами.
На рисунке ниже \(PQ\) — малая дуга, а \(QP\) — большая дуга окружности.
Из приведенного выше обсуждения очевидно, что длина дуги тесно связана с центральным углом, определяющим дугу. Чем больше центральный угол, тем больше будет малая дуга. Поэтому мы определяем градусную меру дуги именем центрального угла, как указано ниже.
Поэтому мы определяем градусную меру дуги именем центрального угла, как указано ниже.
Градус дуги Мера центрального угла, содержащего дугу, известна как градусная мера малой дуги, а большая дуга равна \(360°\) минус градусная мера соответствующей малой дуги.
Градусная мера дуги \(PQ\) обозначается через \(m(PQ)\).
Таким образом, если градусная мера дуги \(PQ\) равна \(θ°\), то мы пишем \(m(PQ) = 9°\)
. Ясно, что \(m(PQ) + m(QP) = 360°\) или \(m(PQ) + m(QP) = m[C(O,r)]\)
Конгруэнтность окружностей и дуг В этом разделе мы будем изучать конгруэнтность окружностей и конгруэнтность дуг.
Конгруэнтные окружности: Говорят, что две окружности конгруэнтны тогда и только тогда, когда одна из них может быть наложена на другую, чтобы точно покрыть ее.
Из приведенного выше определения две окружности конгруэнтны тогда и только тогда, когда их радиусы равны, т. е. \(C(0, r) = C(O, s)\), если \(r = s\), где \(r\ ) и \(s\) — радиусы двух окружностей соответственно.
Конгруэнтные дуги: Если две дуги конгруэнтного круга можно наложить на другую, чтобы точно покрыть ее. Тогда две дуги окружности равны. Это произойдет, если градусные меры двух дуг одинаковы. Таким образом, мы можем сказать, что: Две дуги окружности конгруэнтны тогда и только тогда, когда они имеют одинаковые градусные меры.
Если две дуги \(PQ\) и \(RS\) являются конгруэнтными дугами окружности \(C(O, r)\), то мы пишем \(PQ ≅ RS\).
Таким образом, \(PQ ≅ RS ⇔ m(PQ) = m(RS) ⇔ ∠ POQ = ∠ ROS\).
В следующем разделе мы сформулируем и докажем некоторые результаты, относящиеся к конгруэнтным дугам.
Теорема 1: Если две дуги окружности (или конгруэнтные окружности) конгруэнтны, то соответствующие хорды равны.
Дано: Дуга \(PQ\) окружности \(C(O, r)\) и дуга \(RS\) другой окружности \(C(O’, r)\), конгруэнтные \(C(O , r)\) такие, что \(PQ ≅ RS\).
Доказать: \(PQ = RS\)
Построение: Нарисуйте отрезки \(OP, OQ\), \(O’ R\) и \(O’ S\).
Доказательство:
Случай 1: Когда \(PQ\) и \(RS\) являются малыми дугами
В треугольниках \(OPQ\) и \(O’ RS\) имеем
\(OP = OQ = O’ R = O’ S = r\)
\(∠ POQ = ∠ RO’ S\) \([∵ PQ = RS ⇒ m(PQ) = m(RS) ⇒ ∠ POQ = ∠ RO’ S]\)
Итак, по критерию конгруэнтности SAS имеем
\(△ POQ ≅ △RO’ S\)
\(⇒ PQ = RS\)
Случай 2: Когда \(PQ\) и \(RS\) являются большими дугами.
Если \(PQ, RS\) — большие дуги, то \(QP\) и \(SR\) — малые дуги.
Итак, \(PQ ≅ RS\)
\(⇒ QP ≅ SR\)
\(⇒ QP = SR\)
\(⇒ PQ = RS\)
Следовательно, \(PQ ≅ RS ⇒ PQ = RS\ )
Сектор круга и площадь
Рассмотрим окружность радиуса \(r\) с центром в точке \(O\). Пусть \(A, B\) и \(C\) будут тремя точками на окружности, как показано на рисунке ниже. Область, заключенная в круг, делится на две области, а именно: \(OBA\) и \(OBCA\). Эти области называются секторами круга. Каждый из этих двух секторов имеет дугу окружности как часть своего раздела. Сектор \(OBA\) имеет дугу \(AB\) как часть своей границы, тогда как \(OBCA\) имеет дугу \(ACB\) как часть своей границы. Эти сектора известны как малые и большие сектора круга, как определено ниже.
Сектор \(OBA\) имеет дугу \(AB\) как часть своей границы, тогда как \(OBCA\) имеет дугу \(ACB\) как часть своей границы. Эти сектора известны как малые и большие сектора круга, как определено ниже.
(I) Малый сектор: Если малая дуга окружности является частью границы, то сектор окружности называется малым сектором. На приведенном выше рисунке \(OAB\) является второстепенным сектором.
(ii) Большой сектор: Если большая дуга окружности является частью ее разделительной линии, то сектор окружности называется большим сектором. На приведенном выше рисунке сектор \(OACB\) является основным сектором.
Примечание:
1. Сумма дуг большого и малого секторов окружности равна длине окружности.
2. Граница сектора состоит из дуги окружности и двух радиусов.
Площадь сектора
Если дуга образует угол \(θ\) в центре, то ее длина дуги \(= \frac{\theta}{{180}} \times \pi r\)
Следовательно, длина дуги \(l \) сектора угла \(θ\) в круге радиуса \(r\) определяется выражением \(l = \frac{\theta}{{360}} \times 2\pi r\). 2}\)
2}\)
Решенные примеры – дуга окружности
Q.1. На рисунке ниже дуга \(AB ≅\) дуга \(AC\) и \(O\) является центром окружности. Докажите, что \(OA\) является серединным перпендикуляром к \(BC\).
Ответ: Имеем, дуга \(AB ≅\) дуга \(AC\)
\(⇒ AB = AC\) (Хорды конгруэнтных дуг равны)
\(⇒ OA\) — биссектриса из \(∠ BAC\)
\(⇒ ∠ OAB = ∠ OAC\)
Таким образом, в треугольниках \(AMB\) и \(AMC\) имеем
\(AM = AM\) (Общее)
\(AB = AC\) (Доказано выше)
и, \(∠ OAB = ∠ OAC\) (Доказано выше)
Итак, по критерию SAS мы имеем
\ (△ AMB ≅ △ AMC\)
\(⇒ BM = CM\) и \(∠ AMB = ∠ AMC\)
Но, \(∠ AMB + ∠ AMC = 180°\)
Следовательно, \(∠ AMB = ∠ AMC = 90°\)
Следовательно, \(AM\) или \(OA\) является серединным перпендикуляром к \(BC\).
Q.2. Учитывая эту дугу, \(AB\) образует угол \(40°\) с центром окружности, радиус которой равен \(7\,\rm{см}\). Вычислите длину дуги \(AB\).
Вычислите длину дуги \(AB\).
Ответ: Дано: Радиус \(r = 7\,\rm{см}\)
\(θ = 40°\)
Мы знаем, что длина дуги \( = \frac{\theta }{{360}} \times 2\pi r\)
\( = \frac{{40}}{{360}} \times 2 \times 3.14 \times 7\)
\(= 4.884\)
Поэтому , длина дуги \(AB = 4,884\,\rm{см}\)
Q.3. Длина дуги равна \(35\,\rm{m}\). Если радиус окружности равен \(14\,\rm{m}\), найдите угол, образуемый дугой. 9\цирк\).
Q.4. Найдите радиус дуги, длина которой равна \(156\,\rm{см}\) и образует угол \(150\) градусов с центром окружности.
Ответ: Мы знаем, что длина дуги \( = \frac{\theta}{{360}} \times 2\pi r\)
\( \Rightarrow 156 = \frac{150 }{{360}} \times 2 \times 3.14 \times r\)
\( \Rightarrow r = \frac{{360 \times 156}}{{150 \times 2 \times 3.14}}}\)
\( \Rightarrow r = 59,62\,\rm{см}\)
Следовательно, радиус окружности равен \(59. 62\,\rm{см}\)
62\,\rm{см}\)
Q.5. Вычислите радиус круга, длина дуги которого равна \(144\) ярдов, а угол дуги равен \(3,665\) радианам.
Ответ: Мы знаем, что длина дуги \(l = rθ\)
\( \Rightarrow 144 = 3,665 \times r\)
\( \Rightarrow r = \frac {144}{3,665}\ )
\( \Rightarrow r = 39,29\) ярдов.
Следовательно, радиус круга равен \(39,29\) ярдов.
Изучение понятий частей круга
Сводка
В вышеуказанной статье мы изучили понятие дуги окружности, длины дуги, центрального угла, малой дуги и большой дуги, градусной меры дуги, конгруэнтных окружностей и конгруэнтных дуг и сектора окружности и его площадь. Кроме того, мы решили несколько примеров задач на основе длины дуги.
Часто задаваемые вопросы (FAQ) – Дуга круга
Q.1. Что такое дуга в окружности?
Ответ: Дугой окружности называется непрерывный отрезок окружности.
Q.2. Как найти дугу окружности?
Ответ: Дуга – это часть кривой. Дуга обычно относится к части круга. По кругу \(С(О, г)\). Пусть \(A_1, A_2, A_3, A_4, A_5, A_6\) будут точками на окружности. Тогда части \(A_1 A_2, A_3 A_4, A_5 A_6, A_1 A_3\) и т. д. являются дугами окружности \(C(O, r)\)
Q.3. Какова формула измерения дуги?
Ответ: Когда \(θ\) измеряется в градусах, мера длины дуги \( = \frac{\theta}{{360}} \times 2\pi r\)
Когда \(θ\) измеряется в радианах, мера длины дуги \(l = rθ\)
Q.4. Как описать дугу?
Ответ: Дуга – это часть кривой. Дуга обычно относится к части круга. Другими словами, непрерывный отрезок окружности называется дугой окружности.
Q.5. Что такое большая дуга окружности?
Ответ: Большая дуга окружности — это совокупность точек окружности, лежащих на или вне центрального угла.
РЕШИТЬ ВОПРОСЫ ПО ДУГЕ КРУГА
Мы надеемся, что эта подробная статья о дуге окружности помогла вам в учебе. если у вас есть какие-либо сомнения или вопросы по этой теме, не стесняйтесь спрашивать нас в разделе комментариев, и мы будем более чем рады помочь вам.
Сокращение глупых ошибок; Пройдите бесплатные пробные тесты, связанные с Кругами
Дуга круга | (Определение, символ, большая и малая дуги)
Содержание
Что такое дуга окружности?
Длина полной окружности равна длине окружности. Теперь, если мы возьмем участок окружности, то этот участок можно назвать дугой окружности .
Кроме того, участок круга, образованный разрезанием в любых двух точках, называется Дуга окружности .
Как показано на рисунке, окружность разрезана по точкам P и Q, а ее окружность разделена на две части, обозначенные красным и синим цветом. Эти два участка называются Дугами окружности .
Символ дуги окружности
Символ дуги дается следующим образом: ⌒
Угол, опирающийся на дугу окружности
Угол, образуемый полной окружностью окружности с центром, равен 360° или 2\pi радиан. С Дуга окружности является частью окружности, поэтому угол, образуемый Дугой с центром, меньше 360\градусов или 2\пи радиан. Угол, который образует дуга с центром окружности, как показано на рисунке ниже, называется углом , опирающимся на дугу окружности .
Как показано на рисунке выше, угол , опирающийся на дугу , представленный красным цветом, равен \theta_2, а угол , опирающийся на дугу , представленный синим цветом, равен \theta_1.
Как найти длину дуги окружности?
Длина дуги окружности в градусах
Общая формула для нахождения длины дуги окружности в градусах:
L = 2\pi r\left( {\ frac {\ theta }{{360}}} \right)
Где r — радиус окружности, а \theta — угол в градусах, образуемый Дугой с центром окружности.
Длина дуги окружности в радианах
Формула для определения длины дуги в радианах:
L = \theta r
Где r — радиус окружности, а \theta — угол в радианах, образуемый дугой с центр круга.
Большая и Малая дуги
Большая дуга окружности
Дуга, длина которой больше половины длины окружности, называется Большая дуга . Угол, образуемый Большой Дугой , всегда больше 180° или \pi радиан.
Простыми словами, когда окружность делится на две дуги, дуга большей длины называется Большая дуга . Основная дуга обычно представлена тремя буквами.
Как показано на рисунке выше, основная дуга является POQ.
Длина большой дуги окружности
На приведенном выше рисунке угол, образуемый большой дугой с центром окружности, равен \theta_2, а r — радиус окружности. Следовательно, длина Большая дуга L_1 в градусах:
{L_1} = 2\pi r\left( {\frac {{{\theta _2}}}{{360}}} \right)
If \theta_2 выражается в радианах, тогда формула для длины большой дуги L_1 в радианах определяется как меньше половины длины окружности, то дуга называется Малая дуга . Угол, образуемый малой дугой с центром круга всегда меньше 180\градусов или \pi радиан.
Угол, образуемый малой дугой с центром круга всегда меньше 180\градусов или \pi радиан.
Проще говоря, когда окружность делится на две дуги, дуга меньшей длины называется Малой Дугой . Малая Арка обычно представлена двумя буквами.
На приведенном выше рисунке показано, что Minor Arc — это PQ.
Длина малой дуги окружности
Как показано на рисунке, угол, образуемый малой дугой PQ с центром окружности, равен \theta_1. Если r — радиус окружности, то формула для нахождения малой дуги в градусах имеет вид:
{L_2} = 2\pi r\left( {\frac {{{\theta _1}}}{{360}}} \right)
Если \theta_1 в радианах, то формула для длины Minor Arc L_2 в радианах дается,
{L_2} = {\ theta _1} R
Важные формулы на дуге ARUS
Сериал № 19771777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777.
1 Длина дуги в градусах L = 2\pi r\left( {\frac{\theta}{{360}}} \right) 2 Длина дуги в радианах L = \theta r 3 Радиус r = \frac{L}{\left 360}}{\theta }} \right), [\theta в градусах]
или
r = \frac{L}{\theta }, [\theta в радианах] 4 Угол дугой окружности \theta = \frac{L}{{2\pi r}} \times 360, [\theta в градусах]
или
\theta = \frac{L}{r}, [\тета в радианах]
Решенные примеры на дуге окружности
1. Дуга окружности образует с центром угол 90°, радиус окружности равен 14 см. Узнайте, является ли дуга малой дугой или большой дугой, и найдите длину дуги в градусах?
Узнайте, является ли дуга малой дугой или большой дугой, и найдите длину дуги в градусах?
Решение: Так как дуга образует угол 90° с центром, следовательно, дуга является малой дугой.
Длина дуги:
Дано, \theta=90\градусов и r=14 см.
L = 2\pi r\left( {\frac{\theta}{{360}}} \right)
L = 2 \times \frac{{22}}{7} \times 14\left( {\ frac{{90}}{{360}}} \right)
L = 2 \times 22 \times 2\left( {\frac{1}{4}} \right)
L = 22\,cm
Поэтому , длина дуги 22 мсм.
2. Дуга окружности образует с центром угол 270°, радиус окружности равен 21 см. Узнайте, является ли дуга малой дугой или большой дугой, и найдите длину дуги в градусах?
Решение: Поскольку Дуга образует угол 270° с центром окружности, который больше 180°, следовательно, Дуга является Большой Дугой.
Длина дуги:
Дано, \theta=270\градус и r=21 см.
L = 2\pi r\left( {\frac{\theta}{{360}}} \right)
L = 2 \times \frac{{22}}{7} \times 21\left( {\ frac{{270}}{{360}}} \right)
L = 2 \times 22 \times 3 \times \frac{3}{4}
L = 11 \times 3 \times 3
Л = 99\,см
Следовательно, длина Дуги равна 99\,см.
3. Дуга окружности образует с центром угол \frac{\pi }{2} радиан, а радиус окружности равен 35 см. Затем узнать длину дуги в радианах?
Решение: Дано, \theta=\frac{\pi }{2} радиан и r=35 см.
Длина дуги в радианах:
L = \theta r
L = \frac{\pi }{2} \times 35
L = 17,5\pi
Мы знаем, что \pi=3,1415
17,5\pi см=54,95 см
Следовательно, длина Дуги равна 17,5\pi см или 54,95 см.
4. Найдите длину дуги, если радиус дуги равен 14 см, а угол, образуемый дугой, равен 1,54 радиана?
Решение: Дано, \theta=1,54 радиан и r=14 см
L = \theta r
L=1,54\times 14
L=21,56\,см
Следовательно, длина дуги равна 21,56\ ,см.
5. Если длина дуги 24 см, а радиус 6 см, то найдите угол, образуемый дугой в радианах?
Решение: Дано, L=24\,см и r=6\,см
L = \theta r
\theta = \frac{L}{r}
\theta = \frac{{24} {6}
\theta = 4 радиана
Следовательно, угол, образуемый Дугой, равен 4 радианам.
6. Угол, образуемый в центре круга радиусом 18 см дугой длиной 16,5 см, равен?
Решение: Дано, L=16,5\см и r=18\,см
L = \theta r
\theta = \frac{L}{r}
\theta = \frac{{16,5} {18} 90.
Часто задаваемые вопросы (FAQ)
Что такое дуга в окружности?
Дуга в круге является частью его окружности. Если мы разрежем окружность в любых двух точках, то полученная часть окружности называется Дугой окружности.
Как найти дугу окружности?
Дугу можно найти, используя следующие формулы, если мы знаем угол, образуемый дугой, и радиус окружности,
Дуга (L), если угол, образуемый дугой, выражается в градусах: L = 2\pi r\left ( {\ frac {\ theta }{{360}}} \right)
Дуга (L), если стягиваемый угол дается в радианах: L = \theta r
Как определить дугу?
Дугу можно определить как часть окружности, полученную при ее разрезании в любых двух точках.
Что означает Arc?
Символ, обозначающий дугу, дается следующим образом: ⌒
Что такое большая дуга?
Дуга, длина которой больше половины длины окружности, называется Большая Дуга . Угол, образуемый Большая дуга всегда больше 180\градусов или \пи радиан. Простыми словами, когда окружность делится на две дуги, дуга большей длины называется Большой Дугой .
Что такое Малая дуга?
Если длина дуги меньше половины длины окружности, то она называется малой дугой . Угол, образуемый малой дугой с центром окружности, всегда меньше 180° или \pi радиан. Проще говоря, когда окружность делится на две дуги, дуга меньшей длины называется 9-й.0003 Малая Арка .
Как найти малую дугу?
Малую дугу (L) можно найти по формуле
L = 2\pi r\left( {\frac{{{\theta}}}{{360}}} \right)
где, \theta — это угол, образуемый дугой в градусах.
Как найти радиус окружности с дугой?
Радиус окружности можно определить с помощью дуги по следующей формуле:
r = \frac{L}{{2\pi }}\left( {\frac{{360}}{\theta }} \справа)
где \theta — угол, образуемый дугой, в градусах.
180 градусов — большая или малая дуга?
Дуга, имеющая 180 градусов, не является ни Большой дугой, ни Малой дугой. Большие дуги больше 180 градусов, а малые дуги меньше 180 градусов.
Как найти длину дуги угла?
Длину дуги можно определить по формуле: L = 2\pi r\left( {\frac{\theta}{{360}}} \right)
угол, образуемый дугой в градусах.
Абдур Рохман
Привет, меня зовут Абдур Рохман . По профессии я инженер-электрик . Я также работаю неполный рабочий день Учитель , Блогер и Предприниматель . Причина создания этого веб-сайта или блога в основном заключается в том, что я люблю преподавать . Всякий раз, когда у меня есть время, я обучаю студентов/аспирантов независимо от их класса или стандартов. Дополнительная информация
Причина создания этого веб-сайта или блога в основном заключается в том, что я люблю преподавать . Всякий раз, когда у меня есть время, я обучаю студентов/аспирантов независимо от их класса или стандартов. Дополнительная информация
Объяснение урока: Центральные углы и дуги
В этом объяснении мы научимся определять центральные углы, использовать их
меры, чтобы найти меры дуг, идентифицировать соседние дуги, найти длины дуг и
определить конгруэнтные дуги в конгруэнтных окружностях.
Начнем с точного определения того, что понимается под дугой окружности.
Определение: Дуга окружности
Дуга окружности представляет собой сечение окружности между двумя
радиусы.
Примеры дуг окружностей можно увидеть на следующих рисунках.
Чтобы помочь нам различать разные дуги, мы вводим понятие
центральный угол.
Определение: центральный угол
Центральный угол окружности — это угол между двумя радиусами с вершиной в
центр. На следующей диаграмме ∠𝐴𝐵𝐶 представляет собой
Пример центрального угла.
На следующей диаграмме ∠𝐴𝐵𝐶 представляет собой
Пример центрального угла.
Мы можем расширить эту идею, сказав, что центральный угол дуги является центральным
угол, опирающийся на дугу.
Например, центральные углы двух заданных дуг показаны на следующем рисунке.
диаграммы.
Мы видим, что чем больше центральный угол, тем больше дуга. Следовательно, это
было бы полезно поговорить о мере центрального угла дуги с
по поводу длины дуги. Мы делаем это, вводя следующие
определение.
Определение: мера дуги
Мерой дуги является мера ее центрального угла.
Например, на диаграмме ниже мера дуги, выделенная красным цветом, равна
26∘.
На этой диаграмме мы можем заметить кое-что интересное: есть две возможные дуги
от 𝐴 до 𝐵, более короткая красная, а
более длинный в зеленом цвете. Чтобы помочь нам различать эти два случая, мы называем
более длинная дуга — большая дуга, а более короткая дуга — малая дуга.
Определение: большая и малая дуги окружности
Для заданных двух радиусов мы обозначаем более длинную из двух дуг между радиусами как большая дуга и более короткая дуга как малая дуга . Эквивалентно дуге с
меньший центральный угол является малой дугой, а дуга с большим центральным
угол — большая дуга.
Чтобы различать большую и малую дуги, мы обозначаем малую дугу
как 𝐴𝐵 и обозначьте большую дугу, используя дополнительную точку
(например, 𝐴𝐶𝐵).
Мы также можем использовать обозначение 𝑚𝐴𝐵 для меры
малой дуги от 𝐴 до 𝐵. В этом случае мы можем использовать 𝑚𝐴𝐶𝐵 для меры
большая дуга от 𝐴 до 𝐵.
Если две дуги имеют одинаковую длину, то мы называем эти полукруглых дуг . Эти
возникают, когда радиусы образуют диаметр или когда их центральные углы равны
меры.
Поскольку размер центрального угла дуги определяет ее размер, мы определяем главный
и малые дуги с точки зрения их центральных углов. Если центральный угол больше
чем 180∘, то дуга
главный. Если центральный угол меньше
180∘, то дуга малая. Если центральный угол равен
180∘, то дуга
полукруглый.
Если центральный угол больше
чем 180∘, то дуга
главный. Если центральный угол меньше
180∘, то дуга малая. Если центральный угол равен
180∘, то дуга
полукруглый.
В нашем первом примере мы определим меру дуги по ее центральной
угол.
Пример 1. Нахождение меры дуги по ее центральному углу
Найдите 𝑚𝐴𝐷.
Ответ
Напомним, что обозначение 𝑚𝐴𝐷 означает
мера малой дуги между 𝐴 и
𝐷 и что мера дуги определяется как ее центральная
угол. Мы выделяем эту дугу на следующей диаграмме.
Центральный угол дуги — это угол в центре окружности между
два радиуса, опирающиеся на дугу. Для малой дуги
𝐴𝐷, это
33∘. Мера дуги определяется как равная этому значению. Следовательно,
𝑚𝐴𝐷=33.∘
Перед тем, как мы перейдем к другим примерам, нам нужно определить еще одно определение.
обсудить, то есть смежных дуг.
Определение: Смежные дуги
Две дуги называются смежными, если они имеют одну общую точку или если
они имеют только общие конечные точки.
В кружке вверху 𝐴𝐵 и
𝐵𝐶 являются смежными, так как они имеют одну общую точку в
общий. Точно так же 𝐴𝐶 и
𝐴𝐷𝐶 являются смежными, поскольку они разделяют только оба
конечные точки общие.
Фактически, большая и малая дуги окружности между двумя точками всегда будут
соседний.
Поскольку мерой дуги является мера ее центрального угла и смежных дуг
будут иметь смежные центральные углы, мы можем найти меру смежных дуг по формуле
добавляя свои меры. Например, в приведенном выше круге имеем
𝑚𝐴𝐶=𝑚𝐴𝐵+𝑚𝐵𝐶.
Рассмотрим пример определения смежных дуг в окружности.
Пример 2. Определение смежных дуг в окружности
Какие из следующих дуг являются смежными в данной окружности?
- 𝐴𝐵 и 𝐶𝐷
- 𝐴𝐵 и 𝐵𝐶
- 𝐴𝐷 и 𝐵𝐶
- 𝐴𝐶 и 𝐷𝐵
Ответ
Мы вспоминаем, что две дуги соседствуют, если они разделяют одиночную точку в совале.
и что обозначение 𝐴𝐵 означает минор
(или меньшая) дуга от 𝐴 до 𝐵. Следовательно, мы можем ответить на этот вопрос, выделив каждую пару дуг. Начнем с 𝐴𝐵 и
𝐶𝐷.
Следовательно, мы можем ответить на этот вопрос, выделив каждую пару дуг. Начнем с 𝐴𝐵 и
𝐶𝐷.
Мы видим, что дуги не имеют общих точек, поэтому они не могут быть смежными. Затем мы выделяем 𝐴𝐵 и
𝐵𝐶.
Мы видим, что 𝐴𝐵
и 𝐵𝐶 делят только точку
𝐵 общее; это конечная точка обеих дуг, поэтому эти дуги
являются соседними. Для должной осмотрительности мы также проверим другие варианты.
У нас есть 𝐴𝐷 и
𝐵𝐶.
Мы видим, что эти дуги не имеют общих точек, поэтому они не
соседний.
Наконец, мы проверяем 𝐴𝐶 и
𝐷𝐵.
Мы видим, что каждая точка на дуге 𝐵𝐶
лежит на обеих дугах, поэтому эта пара дуг имеет более одной общей точки. Следовательно, они не являются соседними.
Единственная пара дуг, имеющих одну общую точку, — это пара дуг
𝐴𝐵 и 𝐵𝐶,
что является вариантом B.
В нашем следующем примере мы определим меру дуги, используя диаграмму и
знание отношения двух других дуговых мер.
Пример 3. Нахождение меры дуги в окружности по данным других дуг
Меры путем решения линейных уравнений
Учитывая, что 𝐴𝐵 — диаметр в
круг центра 𝑀 и
𝑚𝐴𝐶∶𝑚𝐷𝐵=85∶67,
определить 𝑚𝐴𝐶𝐷.
Ответ
Мы хотим определить значение 𝑚𝐴𝐶𝐷. Напомним, что это мера дуги из
𝐴 к 𝐶 к
𝐷, как показано на следующей диаграмме.
Мы видим, что эта дуга состоит из двух смежных дуг:
𝐴𝐶 и
𝐶𝐷. Таким образом, мы можем найти меру
𝐴𝐶𝐷, найдя сумму мер
𝐴𝐶 и 𝐶𝐷.
Поскольку мера дуги равна ее центральному углу,
𝑚𝐶𝐷=𝑚∠𝐶𝑀𝐷. Нам дано 𝑚∠𝐶𝑀𝐷=28∘, поэтому мы имеем
𝑚𝐶𝐷=28.∘
Мы знаем, что сумма мер всех дуг, составляющих окружность
будет 360∘. В частности, сумма мер дуг, составляющих
𝐴𝐵 будет
180∘ с
𝐴𝐵 — это диаметр. Это означает
𝑚𝐴𝐶+𝑚𝐶𝐷+𝑚𝐵𝐷 = 180𝑚𝐴𝐶+28+𝑚𝐵𝐷 = 180𝑚𝐴𝐶+𝑚𝐵𝐷 = 152. ∘∘∘∘
∘∘∘∘ (1)
Нам сказали, что
𝑚𝐴𝐶∶𝑚𝐷𝐵=85∶67.
Следовательно, частные каждой части отношения должны быть равны:
𝑚𝐴𝐶𝑚𝐷𝐵=8567.
Мы можем изменить это уравнение, чтобы получить
𝑚𝐷𝐵=67𝑚𝐴𝐶85.
Мы можем заменить наше выражение на 𝑚𝐷𝐵
в уравнение (1) и упростить, чтобы получить
∘∘∘∘
Наконец,
𝑚𝐴𝐶𝐷=𝑚𝐴𝐶+𝑚𝐶𝐷=85+28=113.∘∘∘
Так как дуга окружности является частью ее окружности, мы можем использовать
длину окружности, чтобы определить длину дуги. Мы можем сделать это, используя меру дуги или, что то же самое, ее центральную часть.
угол.
Чтобы помочь нам определить длину дуги, начнем с
пример. Мы хотим определить длину малой дуги в следующем
диаграмма.
Во-первых, вспомним, что круг радиуса 𝑟 имеет длину окружности
2𝜋𝑟. Это означает, что длина окружности этого круга
2𝜋𝑟.
Мы видим, что эта дуга представляет собой четверть круга, но это хорошо
потренируйтесь, чтобы понять, почему это так. Полный оборот – это угол
360∘, так что
угол 90∘
Полный оборот – это угол
360∘, так что
угол 90∘
=14 круг.
Отсюда длина дуги
составляет четверть окружности:
длина дуги=14(2𝜋𝑟)=𝜋𝑟2.
Как правило, если центральный угол (или мера дуги)
𝜃∘,
тогда длина дуги равна 𝜃360(2𝜋𝑟)∘∘. Формально мы можем сформулировать это следующим образом.
Определение: длина дуги
Если центральный угол (или мера) дуги в окружности радиуса
𝑟 это 𝜃∘,
тогда длина дуги 𝑙 определяется выражением
𝑙=𝜃360(2𝜋𝑟).∘∘
В нашем следующем примере мы будем использовать формулу длины дуги для определения
мера дуги, которая дает определенную пропорцию окружности
круг.
Пример 4. Нахождение меры дуги, представляющей известную часть
Окружность круга
Найдите меру дуги, которая представляет 16
окружности круга.
Ответить
Чтобы ответить на этот вопрос, сначала вспомним, что длина,
𝑙, дуги измерения
𝑥∘
в окружности радиуса 𝑟 определяется выражением
𝑙=𝑥360(2𝜋𝑟). ∘∘
∘∘
Мы хотим, чтобы это значение было равно 16
длина окружности, и мы знаем окружность радиуса
𝑟 имеет окружность 2𝜋𝑟. Итак, мы хотим
𝑙=16(2𝜋𝑟)=13(𝜋𝑟).
Приравнивание этих двух выражений для 𝑙 дает нам
𝑥360(2𝜋𝑟)=13(𝜋𝑟).∘∘
Затем мы можем найти
𝑥∘. Делим на 𝜋𝑟, чтобы получить
𝑥360(2)=13.∘∘
Наконец, мы умножаем на
180∘ и упростить:
𝑥=13(180)=60.∘∘∘
Стоит отметить, что есть и другой способ ответа на этот вопрос. Мы можем заметить, что отношение меры дуги к
360∘
точно такое же, как отношение длины дуги к
длина окружности. Другими словами,
𝑥360=.∘∘длина дугиокружность
Нам сказали
длина дугиокружность=16,
так что у нас есть
𝑥360=16,∘∘
которое решаем и получаем 𝑥=60∘∘.
Существует важное следствие формулы длины дуги, включающее конгруэнтные
дуги по кругу, о которых мы сейчас и поговорим.
Свойство: конгруэнтные дуги
Поскольку длина дуги определяется ее центральным углом (или мерой)
и радиус окружности, мы можем сделать вывод, что если две дуги в окружностях с
равные радиусы имеют одинаковую длину, то их центральные углы (и меры) будут
равный. Другими словами, две дуги конгруэнтны тогда и только тогда, когда их центральные углы
(или меры) равны.
Например, мы можем использовать эту формулу для определения длины дуги в
следующую схему.
Радиус этой окружности равен 2, а центральный угол равен
30∘, поэтому имеем
𝑙=30360(2𝜋(2))=𝜋3.∘∘lengthunits
Это также говорит нам, что любая дуга длины 𝜋3
в этом круге или в любом круге радиусом 2 единицы длины будет иметь
мера 30∘.
Давайте теперь рассмотрим пример того, как мы можем применить это свойство конгруэнтности
дуги, чтобы определить длину дуги в окружности.
Пример 5: взаимосвязь между дугами равной длины
Рассмотрим окружность 𝑀 с двумя дугами,
𝐴𝐵 и 𝐶𝐷,
которые имеют равные меры. 𝐴𝐵 имеет длину
5 см. Какова длина 𝐶𝐷?
𝐴𝐵 имеет длину
5 см. Какова длина 𝐶𝐷?
Ответить
Нам сказали, что 𝐴𝐵
и 𝐶𝐷 имеют одинаковую меру, и мы можем вспомнить
что если две дуги имеют одинаковую меру, то они конгруэнтны. Так,
их длины равны. Следовательно, 𝐶𝐷 имеет длину
5 см.
Хотя это и не обязательно для ответа на этот вопрос, его стоит посмотреть
почему этот результат верен из формулы длины дуги. Мы
напомним, что длина 𝑙 дуги между
𝑃 и 𝑄 по кругу радиуса
𝑟 находится по формуле
𝑙=𝑚𝑃𝑄360(2𝜋𝑟).
Итак, длина 𝐴𝐵 определяется выражением
𝑙=𝑚𝐴𝐵360(2𝜋𝑟).
Поскольку 𝑚𝐴𝐵=𝑚𝐶𝐷, имеем
𝑙=𝑚𝐴𝐵360(2𝜋𝑟)=𝑚𝐶𝐷360(2𝜋𝑟).
Однако это выражение равно длине 𝐶𝐷,
поэтому их длины равны.
Следовательно, 𝐶𝐷 имеет длину
5 см.
Другим свойством, аналогичным свойству в приведенном выше примере, является то, что если длины
хорды между концами двух дуг окружности равны, то дуги
имеют равные меры. На самом деле то же самое верно и в обратном порядке; если дуги одинаковы
мера, то хорды между их соответствующими конечными точками будут иметь равные
длины.
На самом деле то же самое верно и в обратном порядке; если дуги одинаковы
мера, то хорды между их соответствующими конечными точками будут иметь равные
длины.
Чтобы понять, почему это так, рассмотрите следующий круг.
Предположим, что 𝐴𝐵 и
𝐶𝐷 имеют равные меры. Затем меры по
центральные углы равны:
𝑚∠𝐷𝑀𝐶=𝑚∠𝐴𝑀𝐵.
Мы также знаем, что 𝐴𝑀,
𝐵𝑀, 𝐶𝑀,
и 𝐷𝑀 — радиусы, поэтому они имеют одинаковые
длина. Следовательно, треугольники 𝐴𝑀𝐵 и 𝐷𝑀𝐶
конгруэнтны по правилу SAS, поэтому 𝐴𝐵
и 𝐷𝐶 должны иметь одинаковую длину.
Аналогично, если 𝐴𝐵 и
𝐶𝐷 имеют одинаковую длину, то с помощью
радиусов окружности, у нас есть треугольники 𝐴𝑀𝐵 и
𝐷𝑀𝐶 конгруэнтны по правилу SSS. Так, меры
внутренние углы равны. Особенно,
𝑚∠𝐷𝑀𝐶=𝑚∠𝐴𝑀𝐵.
Тогда, поскольку меры центральных углов равны, мы знаем, что их
меры (и длины дуг) равны.
Свойство: конгруэнтные хорды конгруэнтных дуг
В одном и том же круге или в конгруэнтных кругах, если две дуги имеют одинаковую меру,
тогда хорды между их соответствующими конечными точками будут иметь одинаковую длину. На самом деле то же самое верно и в обратном порядке; в том же круге или в конгруэнтных кругах,
если две хорды между концами двух дуг конгруэнтны, то две дуги
имеют одинаковую меру. Мы можем видеть это на следующей диаграмме.
На самом деле то же самое верно и в обратном порядке; в том же круге или в конгруэнтных кругах,
если две хорды между концами двух дуг конгруэнтны, то две дуги
имеют одинаковую меру. Мы можем видеть это на следующей диаграмме.
- Если 𝑚𝐴𝐵=𝑚𝐷𝐶,
тогда 𝐴𝐵=𝐷𝐶.
- Если 𝐴𝐵=𝐷𝐶, то
𝑚𝐴𝐵=𝑚𝐷𝐶.
Давайте посмотрим на пример того, как мы можем применить это свойство.
Пример 6. Понимание связи между дугами и хордами
Рассмотрим круг 𝑀 с двумя хордами одинаковой длины,
𝐴𝐷 и
𝐵𝐶. Если 𝐴𝐷
имеет длину 5 см,
какова длина 𝐵𝐶?
Ответить
Мы видим, что 𝐴𝐷 и
𝐵𝐶 — хорды между конечными точками
дуг 𝐴𝐷 и
𝐵𝐶 как показано.
Вспомним, что если длины хорд между концами
две дуги окружности равны, то дуги имеют одинаковую длину и
меры. Следовательно, поскольку 𝐴𝐷
и 𝐵𝐶 имеют одинаковую длину,
𝐴𝐷 и
𝐵𝐶 также будет иметь одинаковую длину.
Следовательно, поскольку 𝐴𝐷 имеет длину
5 см,
𝐵𝐶 также имеет длину
5 см.
В нашем следующем примере мы будем использовать диаграмму и свойства центральных углов для
определить меру данной дуги.
Пример 7. Нахождение меры дуги окружности по заданному диаметру и
Меры двух центральных углов в виде алгебраических выражений
Учитывая, что 𝐴𝐵 — диаметр в окружности
𝑀 и 𝑚∠𝐷𝑀𝐵=(5𝑥+12)∘,
определить 𝑚𝐴𝐶.
Ответ
Нас просят найти 𝑚𝐴𝐶, которая является мерой
малой дуги от 𝐴 до 𝐶, показанная дуга
на следующей диаграмме.
Напомним, что мера дуги равна ее центральному углу, и мы
На схеме видно, что центральный угол этой дуги равен
4𝑥∘. Итак, 𝑚𝐴𝐶=4𝑥∘. Следовательно, нам нужно определить значение 𝑥. Чтобы найти
значение 𝑥, мы начнем с добавления угла, который нам дан
в вопросе к схеме.
Затем заметим, что 𝐴𝐵 — это диаметр
круг, что означает, что это прямая линия. Итак, мы должны иметь
𝑚 Хорошо+𝑚 Хорошо = 180 (5𝑥+12)+2𝑥 = 180.∘∘∘∘
Итак, мы должны иметь
𝑚 Хорошо+𝑚 Хорошо = 180 (5𝑥+12)+2𝑥 = 180.∘∘∘∘
Мы можем затем решить это для 𝑥7𝑥+12 = 1807𝑥 = 168𝑥 = 24.∘∘∘∘∘∘∘
Наконец, мы знаем, что
𝑚𝐴𝐶=4𝑥.∘
Подставляя значение 𝑥, получаем, что
𝑚𝐴𝐶=4(24)=96.∘∘
Давайте закончим повторением некоторых важных моментов этого
объяснитель.
Ключевые моменты
- Дуга окружности представляет собой часть окружности окружности между двумя
радиусы.
- Центральный угол окружности – это угол между двумя радиусами с вершиной в
центр.
- Центральный угол дуги — это центральный угол, образуемый дугой.
- Мерой дуги является мера ее центрального угла.
- Для двух радиусов мы обозначаем более длинную из двух дуг между радиусами как большая дуга и более короткая дуга как малая дуга . Дуги равной длины называются дугами полуокружности; это происходит, когда радиусы
образуют диаметр.

- Дуга является большой, если ее мера (или мера ее центрального угла)
больше 180∘, дуга
минор, если его мера (или мера его центрального угла) меньше
180∘, а дуга
полукруглым, если его мера (или мера его центрального угла) равна
180∘.
- Обозначим малую дугу от 𝐴 до 𝐵 как
𝐴𝐵, а главные дуги можно пометить с помощью дополнительного
точка (например, 𝐴𝐶𝐵).
- Мы используем обозначение 𝑚𝐴𝐵 для меры
малая дуга от 𝐴 до 𝐵 и
𝑚𝐴𝐶𝐵 для меры большой дуги от
𝐴 в 𝐵, который проходит через
𝐶.
- Две дуги называются смежными, если они имеют одну общую точку или если
они имеют только общие конечные точки.
- Если центральный угол (или мера) дуги в окружности радиуса
𝑟 это
𝜃∘,
тогда его длина 𝑙 определяется выражением
𝑙=𝜃360(2𝜋𝑟).∘∘
- Если две дуги одной окружности имеют одинаковую длину, то их центральные углы
и меры равны. То же самое верно и в обратном порядке; если две дуги имеют одинаковую длину,
тогда их центральные углы и меры равны.

- Если две дуги одной окружности имеют одинаковую меру, то хорды между их
соответствующие конечные точки имеют одинаковую длину. То же самое верно и в обратном порядке; если аккорды
имеют одинаковую длину, то дуги между концами хорд должны иметь
равные меры.
Измерения дуги: значение, примеры и формула
Очень важно знать анатомию окружности и особенно углы внутри нее. В этой статье рассматриваются свойства дуга измеряет , формулу дуги и как найти ее в геометрическом контексте.
Дуга и ее мера
Необходимо знать два важных определения:
Дуга окружности
Дуга – это ребро окружности сектор , т. е. ребро, ограниченное двумя точки в круге.
Длина дуги — это размер дуги, т. е. расстояние между двумя ограничивающими точками на окружности.
Мера дуги
Если мы представим себе дугу как ребро между двумя точками A и B на окружности, то мера дуги будет величиной угла между A, центром окружности , и B.
По отношению к длине дуги мерой дуги является размер угла, из которого выходит длина дуги.
Вот эти определения, продемонстрированные графически:
Нахождение меры дуги Исходное исследование Smarter
Радианы по сравнению с градусами
Прежде чем мы введем формулу для измерения дуги, давайте вспомним градуса и радиана .
Чтобы преобразовать радианы в градусы : разделите и умножьте на 180.
Чтобы преобразовать градусы в радианы : разделите на 180 и умножьте на.
Вот некоторые из наиболее распространенных углов, которые вы должны распознать.
Градусов 0 30 45 60 90 120 180 270 360 Radians 0
Формулы измерения дуги и длины дуги
Определение меры дуги по радиусу
Формула, которая связывает меру дуги (или меру угла) и длину дуги, выглядит следующим образом:
Где
- r радиус окружности
- мера дуги в радианах
- S длина дуги
913 длина дуги Мы можем найти длину дуги переставляя формулу: .
Найдите меру дуги, показанную в следующем круге, относительно ее радиуса, r .
Используя формулу:
Нам нужна мера дуги с точки зрения r , поэтому нам нужно изменить это уравнение :
Нахождение меры дуги с длиной окружности
Если нам не дан радиус, r , то есть второй метод нахождения меры дуги . Если мы знаем окружность окружности, а также длину дуги, то отношение между мерой дуги и (или в зависимости от того, хотите ли вы меру дуги в градусах или радианах) равно отношению между длина дуги и длина окружности .
Где
Найдите длину дуги x следующей окружности с длиной окружности 10 см.
Используя формулу :
Переставляя, получаем:
на 3 с.ф.
Измерения дуги — ключевые выводы
Часто задаваемые вопросы об измерениях дуги
Измерение дуги — это угол, из которого выходит дуга окружности.
Как найти меру дуги: зная радиус и длину дуги, мерой дуги является длина дуги, деленная на радиус. Учитывая окружность, отношение между мерой дуги и 360 градусами равно отношению между длиной дуги и окружностью.
Размер дуги равен длине дуги, деленной на радиус.
Размер дуги равен длине дуги, деленной на радиус.
В геометрии мерой дуги является длина дуги, деленная на радиус.
Тест Final Arc Measures
Вопрос
Что такое длина сегмента?
Показать ответ
Ответ
Длина отрезка – это расстояние между двумя точками на прямой.
Показать вопрос
Вопрос
Какова площадь сегмента круга?
Показать ответ
Ответ
Это площадь, ограниченная хордой и краем окружности.
Показать вопрос
Вопрос
Как называется отрезок, концы которого лежат на окружности?
Показать ответ
Ответ
Аккорд.
Показать вопрос
Вопрос
Как называется хорда, проходящая через центр окружности?
Показать ответ
Ответ
Диаметр.
Показать вопрос
Вопрос
Разделяет ли хорда, кроме диаметра, любую другую хорду на большую и малую дуги?
Показать ответ
Ответ
Показать вопрос
Вопрос
Верно ли следующее свойство?
Равные хорды окружности образуют равные углы в центре.
Показать ответ
Ответ
Показать вопрос
Вопрос
Делит ли биссектриса из центра окружности хорду пополам на равные половины?
Показать ответ
Ответ
Показать вопрос
Вопрос
Равны ли длины хорд, равноудаленных от центра окружности?
Показать ответ
Ответ
Показать вопрос
Вопрос
Верно ли следующее утверждение?
Теорема о пересекающихся хордах утверждает, что произведения пересечений на пересекающихся хордах равны.
Показать ответ
Ответ
Показать вопрос
Вопрос
Диаметр делит круг на:
Показать ответ
Ответ
Полукруги.
Показать вопрос
Вопрос
Будут ли соответствующие длины дуг равными, если хорды имеют одинаковую длину?
Показать ответ
Ответ
Показать вопрос
Вопрос
Две малые дуги конгруэнтны, если:
Показать ответ
Ответ
, их соответствующие хорды конгруэнтны.
Показать вопрос
Вопрос
Если одна хорда является биссектрисой другой хорды, то:
Показать ответ
Ответ
первая хорда это диаметр.
Показать вопрос
Вопрос
Определить «дугу» окружности
Показать ответ
Ответ
Дуга или длина дуги — это край сектора круга.
Показать вопрос
Вопрос
Определить меру дуги.
Показать ответ
Ответ
По отношению к длине дуги мерой дуги является угол, из которого выходит длина дуги.
Показать вопрос
Вопрос
Что такое длина сегмента?
Показать ответ
Ответ
Длина сегмента — это расстояние между двумя точками на линейном сегменте.
Показать вопрос
Вопрос
Длину отрезка можно определить, используя координаты двух точек.
Показать ответ
Ответ
Показать вопрос
Вопрос
Середина G между точками A, (2, 4) и B, (3, -3) равна. ..
..
Показать ответ
Ответ
(2.5, 0.5)
Показать вопрос
Вопрос
Какова длина сегмента окружности?
Показать ответ
Ответ
Отрезок окружности может быть либо диаметром окружности, когда прямая проходит через центр окружности, либо хордой, если прямая проходит в любом другом месте, кроме центра окружности.
Показать вопрос
Вопрос
Длина отрезка между точками C и B будет называться…
Показать ответ
Ответ
сегмент CB
Показать вопрос
Вопрос
Найдите длину отрезка окружности радиусом 7 см, стягивающего центр под углом 60°.
Показать ответ
Ответ
Показать вопрос
Вопрос
Найдите длину отрезка окружности радиусом 5 см, стягивающего центр под углом 210°.
Показать ответ
Ответ
9,66 см
Показать вопрос
Вопрос
Найти середину между началом координат и точкой Z (8, 6)
Показать ответ
Ответ
(4, 3)
Показать вопрос
Вопрос
Из каких двух компонентов состоит сегмент
Показать ответ
Ответ
Дуга и хорда
Показать вопрос
Вопрос
Длина сегмента не может быть рассчитана, если заданы конечная и средняя точки.
Показать ответ
Ответ
Показать вопрос
Вопрос
Длина отрезка рассчитывается по теореме Пифагора.
Показать ответ
Ответ
Показать вопрос
Вопрос
Средняя точка между определенной точкой J (2, 5) и другой точкой W равна (-1, 3). Найдите координаты точки W.
Показать ответ
Ответ
(-4, 1)
Показать вопрос
4.2: Длина дуги — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 3325
- Майкл Коррал
- Колледж Скулкрафт
В разделе 4. 1 мы видели, что один оборот имеет радианную меру \(2\pi \) рад. Обратите внимание, что \(2\pi\) — это отношение длины окружности (т.е. полной длины дуги) \(C \) окружности к ее радиусу \(r\): 90 007
1 мы видели, что один оборот имеет радианную меру \(2\pi \) рад. Обратите внимание, что \(2\pi\) — это отношение длины окружности (т.е. полной длины дуги) \(C \) окружности к ее радиусу \(r\): 90 007
\[ \text{Радианная мера 1 оборота} ~=~ 2\pi ~=~ \frac{2\pi\,r}{r} ~=~
\frac{C}{r} ~=~ \frac{\text{общая длина дуги}}{\text{радиус}}
\nonumber \]
Ясно, что это отношение не зависит от \(r \). В общем, радианная мера угла — это отношение длины дуги, отсекаемой соответствующим центральным углом в окружности, к радиусу окружности, независимо от радиуса.
Чтобы убедиться в этом, вспомним наше формальное определение радиана: центральный угол в окружности радиуса \(r\), который пересекает дугу длины \(r\). Итак, предположим, что у нас есть окружность радиуса \(r\), и мы поместили центральный угол с мерой в радианах \(1\) поверх другого центрального угла с мерой в радианах \(1\), как на рисунке 4.2.1( а). Ясно, что объединенный центральный угол двух углов имеет меру в радианах \(1+1=2\), а общая длина дуги равна \(r+r=2r \).
Рисунок 4.2.1 Радианная мера и длина дуги Теперь предположим, что мы разрезаем угол с радианной мерой \(1 \) пополам, как на Рисунке 4.2.1(b). Ясно, что это также сокращает вдвое длину дуги \(r \). Таким образом, мы видим, что
\[\nonumber \begin{align}
\text{Угол} ~&=~ 1~\text{радиан} \quad&\Стрелка вправо\quad \text{длина дуги} ~&=~ r ~,\\ \nonumber
\text{Угол} ~&=~ 2~\text{радианы} \quad&\Стрелка вправо\quad \text{длина дуги} ~&=~ 2\,r ~,\\ \nonumber
\text{Угол} ~ &=~ \tfrac{1}{2}~\text{радиан} \quad&\Стрелка вправо\quad \text{длина дуги} ~&=~
\tfrac{1}{2}\,r ~,\end{align} \nonumber \]
и вообще для любых \(\theta\ge 0\),
\[\nonumber \text{Угол} ~=~ \theta~\text{радианы} \quad \Rightarrow\quad \text{длина дуги} ~=~ \theta\,r ~,
\nonumber \]
так что
\[ \theta ~=~ \frac{\text{длина дуги}}{\text{радиус}} ~~.
\номер\]
Интуитивно очевидно, что уменьшение или увеличение окружности сохраняет меру центрального угла даже при изменении радиуса. Приведенное выше обсуждение говорит о большем, а именно о том, что отношение длины \(s\) пересекаемой дуги к радиусу \(r\) сохраняется именно потому, что это отношение является мерой центрального угла в радианах (см. рис. 4.2). .2).
Приведенное выше обсуждение говорит о большем, а именно о том, что отношение длины \(s\) пересекаемой дуги к радиусу \(r\) сохраняется именно потому, что это отношение является мерой центрального угла в радианах (см. рис. 4.2). .2).
Рис. 4.2.2 Окружности с одинаковым центральным углом, но разными радиусами Таким образом, мы получаем простую формулу для длины дуги:
В круге радиуса \(r\), пусть \(s\) будет длиной дуги, пересекаемой центральным углом с мерой в радианах \(\theta \ge 0 \). Тогда длина дуги \(s \) равна:
\[ s ~=~ r\,\theta \label{4.4} \]
Пример 4.3
В круге радиусом \(r=2\) см, какова длина \(s\) дуги, проведенной под центральным мерным углом \(\theta = 1,2\) рад? 9\circ ~=~ \frac{\pi}{180} \;\cdot\; 41 ~=~ 0,716~\text{rad}
\quad\Rightarrow\quad s ~=~ r\,\theta ~=~ (10)\,(0,716) ~=~ \boxed{7,16~\text{ft }}\nonumber \]
Обратите внимание, что, поскольку длина дуги \(s \) и радиус \(r \) обычно задаются в одних и тех же единицах измерения, радианы действительно безразмерны, так как вы можете думать об отмене единиц в соотношение \(\frac{s}{r} \), которое равно \(\theta \). Это еще одна причина, почему радианы так широко используются.
Это еще одна причина, почему радианы так широко используются.
Пример 4.5
Центральный угол окружности радиусом \(5 \) м отсекает дугу длиной \(2 \) м. Чему равен угол в радианах? Какая мера в градусах? 9\circ \), может быть неясно, что имеется в виду под пересекаемой дугой, так как угол больше одного оборота и, следовательно, «огибает» окружность более одного раза. Мы будем придерживаться подхода, согласно которому такая дуга состоит из полная окружность плюс любая дополнительная длина дуги, определяемая углом. Другими словами, уравнение \ref{4.4} по-прежнему справедливо для углов \(\theta > 2\pi \) рад.
Как насчет отрицательных углов? В этом случае использование \(s=r\,\theta \) означало бы, что длина дуги отрицательна, что нарушает обычное понятие длины. Таким образом, мы примем соглашение использовать только неотрицательные центральные углы при обсуждении длины дуги.
Пример 4.6
Веревка прикреплена к стене в двух местах на расстоянии \(8 \) футов на одинаковой высоте. Цилиндрический контейнер радиусом \(2\) фута отталкивают от стены настолько далеко, насколько это возможно, удерживая его веревкой, как показано на рис. 4.2.3, где показан вид сверху. Если центр контейнера находится в \(3\) футах от точки на стене посередине между концами веревки, какова длина \(L\) веревки?
Цилиндрический контейнер радиусом \(2\) фута отталкивают от стены настолько далеко, насколько это возможно, удерживая его веревкой, как показано на рис. 4.2.3, где показан вид сверху. Если центр контейнера находится в \(3\) футах от точки на стене посередине между концами веревки, какова длина \(L\) веревки?
Рисунок 4.2.3 Решение:
9\циркуляр ~.
\nonumber \] Переводя в радианы, получаем \(\;\theta = \frac{\pi}{180} \;\cdot\; 60,5 = 1,06 \) рад. Таким образом,
\[ L ~=~ 2\,(AB \;+\; \cdot \overparen{BC}) ~=~ 2\,(\sqrt{21} \;+\; BE \cdot \theta ) ~=~
2\,(\sqrt{21} \;+\; (2)\,( 1.06)) ~=~ \boxed{13.4 ~\text{ft}} ~.
\номер \]
Пример 4.7
Центры двух ременных шкивов с радиусами \(5\) см и \(8\) см соответственно отстоят друг от друга на \(15\) см. Найдите общую длину \(L\) ремня вокруг шкивов.
Решение
На рис. 4.2.4 мы видим, что по симметрии \(\;L = 2\;(\overparen{DE} + EF + \overparen{FG}) \).
Рисунок 4.2.4 Ременные шкивы с радиусами 5 см и 8 см Сначала в центре \(B\) шкива с радиусом \(8\) нарисуйте окружность радиусом \(3\), которая является разница в радиусах двух шкивов. Пусть \(C\) будет точкой пересечения этой окружности \(\overline{BF} \). Тогда мы знаем, что касательная \(\overline{AC} \) к этому меньшему кругу перпендикулярна отрезку \(\overline{BF} \). Таким образом, \(\angle\,ACB\) — прямой угол, поэтому длина \(\overline{AC} \) равна 92} ~=~ \sqrt{216} ~=~ 6\,\sqrt{6}\nonumber \]
по теореме Пифагора. Теперь, поскольку \(\overline{AE} \perp \overline{EF} \) и \(\overline{EF} \perp \overline{CF} \) и \(\overline{CF} \perp \overline{AC} \), четырехугольник \(AEFC\) должен быть прямоугольником. В частности, \(EF = AC \), поэтому \(EF = 6\,\sqrt{6} \).
Из уравнения \ref{4.4} мы знаем, что \(\;\overparen{DE} = EA \cdot \angle\,DAE\; \) и \(\;\overparen{FG} = BF \cdot \angle \,GBF \), где углы измеряются в радианах. Итак, думая об углах в радианах (используя \(\pi \) rad \(= 180^\circ\)), мы видим из рисунка 4. 2.4, что
2.4, что
\[\номер\угол\,DAE ~=~ \pi \;-\; \угол\,EAC \;-\; \угол\,ВАС ~=~ \pi \;-\; \frac{\pi}{2} \;-\;
\угол\,ВАС ~=~ \frac{\pi}{2} \;-\; \angle\,BAC ~, \nonumber \]
где
\[\nonumber \sin\;\angle\,BAC ~=~ \frac{BC}{AB} ~=~ \frac{3}{15 } ~=~ 0.2 \quad\Rightarrow\quad
\angle\,BAC ~=~ 0.201~\text{rad.} \nonumber \]
Таким образом, \(\;\angle\,DAE = \frac{\ пи{2} \,-\, 0,201 = 1,37 \) рад. Так как \(\overline{AE} \) и \(\overline{BF} \) параллельны, мы имеем \(\;\угол\,ABC = \угол\,DAE = 1,37\) рад. Таким образом, \(\;\угол\,GBF = \pi\,-\, \угол\,ABC = \pi\,-\, 1,37 = 1,77\) рад. Следовательно,
\[\nonumber L ~=~ 2\;(\overparen{DE} \;+\; EF \;+\; \overparen{FG}) ~=~ 2\;(5\;(1.37) \ ;+\;6\,\sqrt{6} \;+\;
8\;(1.77)) ~=~ \boxed{71.41~\text{cm}} ~. \nonumber \]
Эта страница под названием 4.2: Длина дуги распространяется в соответствии с лицензией GNU Free Documentation License 1.3 и была создана, изменена и/или курирована Майклом Корралом с использованием исходного содержимого, которое было отредактировано в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.
 Вычислите длину дуги AB.
Вычислите длину дуги AB. 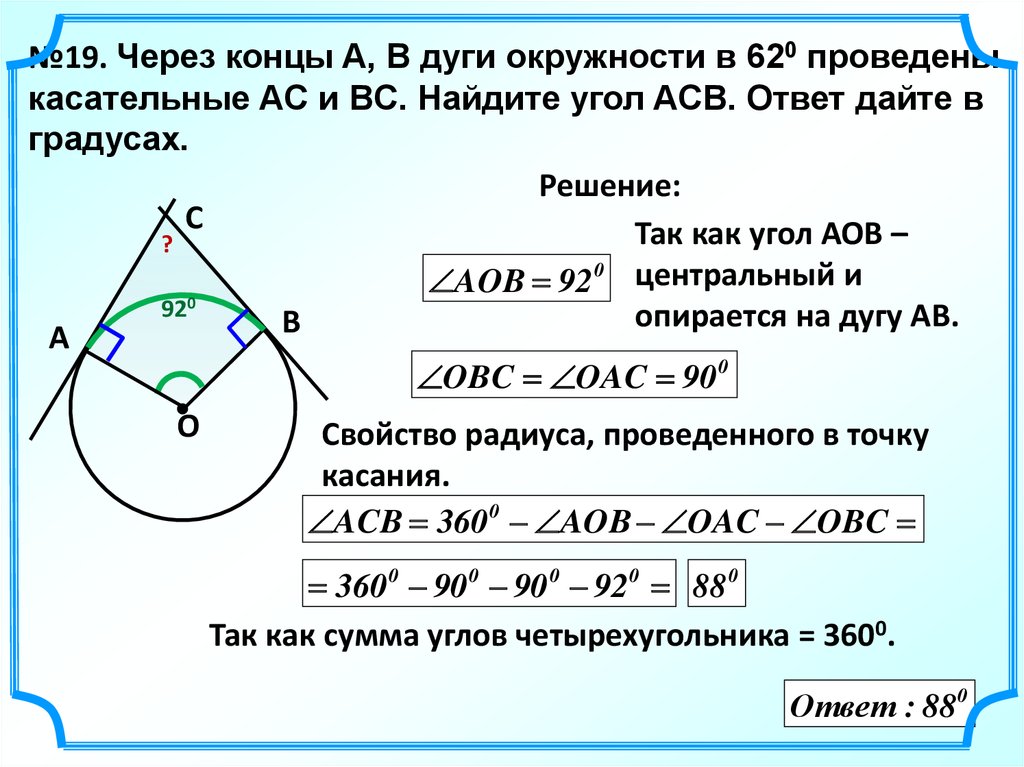
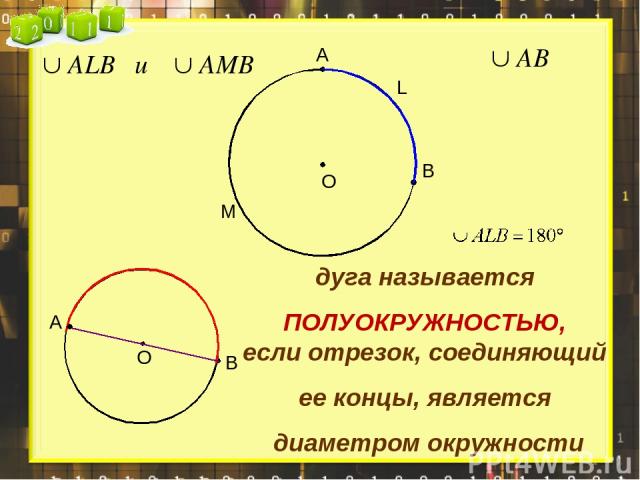

 Отрезок, соединяющий точку на окружности с центром, называется радиусом. По смыслу окружности любые два радиуса имеют одинаковую длину.
Отрезок, соединяющий точку на окружности с центром, называется радиусом. По смыслу окружности любые два радиуса имеют одинаковую длину.? 21 октября : CBSE выпустила 10-й и 12-й листы данных для второстепенных предметов.
 Тест MCQ, предлагаемый Embibe, курируется на основе пересмотренных учебников CBSE Class Books, бумажных шаблонов и учебного плана на 2021 год. В этой серии пробных тестов представлен широкий выбор соответствующих вопросов и их решений. Кандидаты в совет CBSE могут пройти эти бесплатные пробные тесты, чтобы попрактиковаться и найти области, в которых им нужно улучшить свои экзамены совета.
Тест MCQ, предлагаемый Embibe, курируется на основе пересмотренных учебников CBSE Class Books, бумажных шаблонов и учебного плана на 2021 год. В этой серии пробных тестов представлен широкий выбор соответствующих вопросов и их решений. Кандидаты в совет CBSE могут пройти эти бесплатные пробные тесты, чтобы попрактиковаться и найти области, в которых им нужно улучшить свои экзамены совета.Другими словами, малая дуга окружности — это часть окружности, пересекаемая центральным углом, включая две точки пересечения.
 Поэтому мы определяем градусную меру дуги именем центрального угла, как указано ниже.
Поэтому мы определяем градусную меру дуги именем центрального угла, как указано ниже.Из приведенного выше определения две окружности конгруэнтны тогда и только тогда, когда их радиусы равны, т. е. \(C(0, r) = C(O, s)\), если \(r = s\), где \(r\ ) и \(s\) — радиусы двух окружностей соответственно.
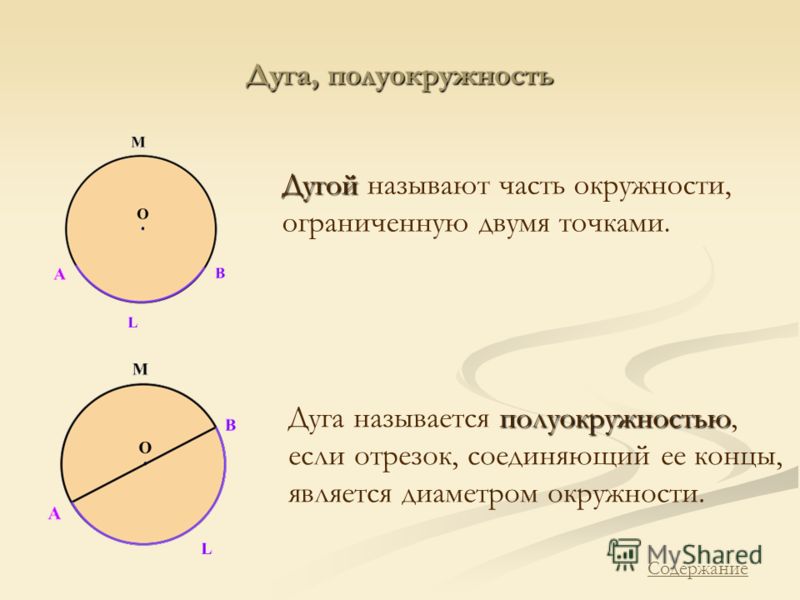
Если две дуги \(PQ\) и \(RS\) являются конгруэнтными дугами окружности \(C(O, r)\), то мы пишем \(PQ ≅ RS\).
Дано: Дуга \(PQ\) окружности \(C(O, r)\) и дуга \(RS\) другой окружности \(C(O’, r)\), конгруэнтные \(C(O , r)\) такие, что \(PQ ≅ RS\).
Доказать: \(PQ = RS\)
Построение: Нарисуйте отрезки \(OP, OQ\), \(O’ R\) и \(O’ S\).

Случай 1: Когда \(PQ\) и \(RS\) являются малыми дугами
В треугольниках \(OPQ\) и \(O’ RS\) имеем
\(OP = OQ = O’ R = O’ S = r\)
\(∠ POQ = ∠ RO’ S\) \([∵ PQ = RS ⇒ m(PQ) = m(RS) ⇒ ∠ POQ = ∠ RO’ S]\)
Итак, по критерию конгруэнтности SAS имеем
\(△ POQ ≅ △RO’ S\)
\(⇒ PQ = RS\)
Если \(PQ, RS\) — большие дуги, то \(QP\) и \(SR\) — малые дуги.
Итак, \(PQ ≅ RS\)
\(⇒ QP ≅ SR\)
\(⇒ QP = SR\)
\(⇒ PQ = RS\)
Следовательно, \(PQ ≅ RS ⇒ PQ = RS\ )
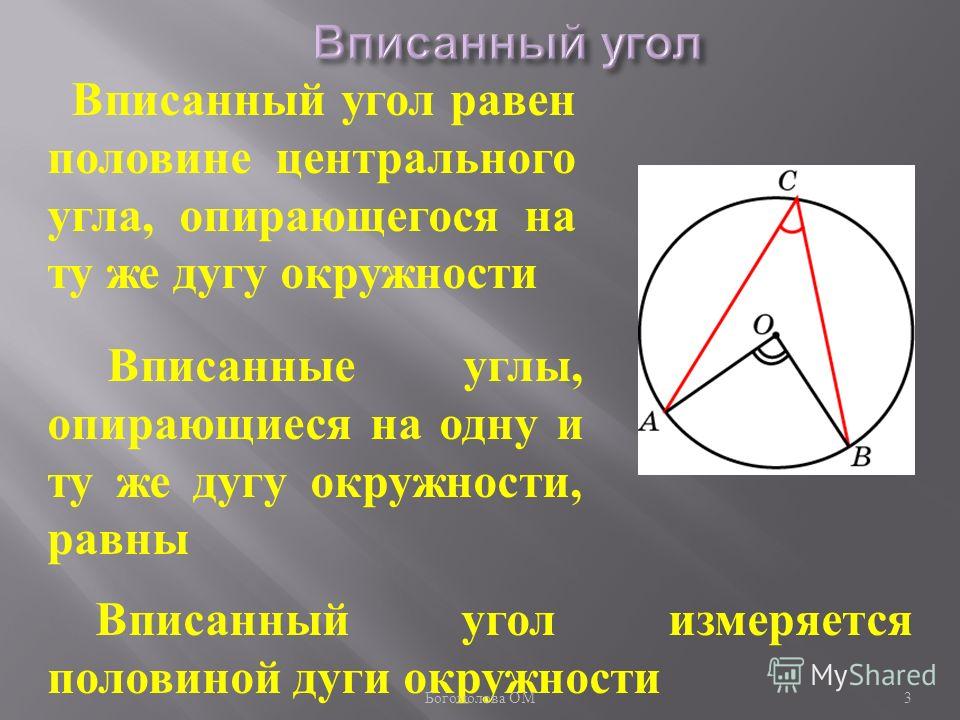 Сектор \(OBA\) имеет дугу \(AB\) как часть своей границы, тогда как \(OBCA\) имеет дугу \(ACB\) как часть своей границы. Эти сектора известны как малые и большие сектора круга, как определено ниже.
Сектор \(OBA\) имеет дугу \(AB\) как часть своей границы, тогда как \(OBCA\) имеет дугу \(ACB\) как часть своей границы. Эти сектора известны как малые и большие сектора круга, как определено ниже. 1. Сумма дуг большого и малого секторов окружности равна длине окружности.
2. Граница сектора состоит из дуги окружности и двух радиусов.
Следовательно, длина дуги \(l \) сектора угла \(θ\) в круге радиуса \(r\) определяется выражением \(l = \frac{\theta}{{360}} \times 2\pi r\).
 2}\)
2}\)\(⇒ AB = AC\) (Хорды конгруэнтных дуг равны)
\(⇒ OA\) — биссектриса из \(∠ BAC\)
\(⇒ ∠ OAB = ∠ OAC\)
Таким образом, в треугольниках \(AMB\) и \(AMC\) имеем
\(AM = AM\) (Общее)
\(AB = AC\) (Доказано выше)
и, \(∠ OAB = ∠ OAC\) (Доказано выше)
Итак, по критерию SAS мы имеем
\ (△ AMB ≅ △ AMC\)
\(⇒ BM = CM\) и \(∠ AMB = ∠ AMC\)
Но, \(∠ AMB + ∠ AMC = 180°\)
Следовательно, \(∠ AMB = ∠ AMC = 90°\)
Следовательно, \(AM\) или \(OA\) является серединным перпендикуляром к \(BC\).
 Вычислите длину дуги \(AB\).
Вычислите длину дуги \(AB\). \(θ = 40°\)
Мы знаем, что длина дуги \( = \frac{\theta }{{360}} \times 2\pi r\)
\( = \frac{{40}}{{360}} \times 2 \times 3.14 \times 7\)
\(= 4.884\)
Поэтому , длина дуги \(AB = 4,884\,\rm{см}\)
Ответ: Мы знаем, что длина дуги \( = \frac{\theta}{{360}} \times 2\pi r\)
\( \Rightarrow 156 = \frac{150 }{{360}} \times 2 \times 3.14 \times r\)
\( \Rightarrow r = \frac{{360 \times 156}}{{150 \times 2 \times 3.14}}}\)
\( \Rightarrow r = 59,62\,\rm{см}\)
Следовательно, радиус окружности равен \(59.
 62\,\rm{см}\)
62\,\rm{см}\)Ответ: Мы знаем, что длина дуги \(l = rθ\)
\( \Rightarrow 144 = 3,665 \times r\)
\( \Rightarrow r = \frac {144}{3,665}\ )
\( \Rightarrow r = 39,29\) ярдов.
Следовательно, радиус круга равен \(39,29\) ярдов.
Ответ: Дугой окружности называется непрерывный отрезок окружности.

Ответ: Дуга – это часть кривой. Дуга обычно относится к части круга. По кругу \(С(О, г)\). Пусть \(A_1, A_2, A_3, A_4, A_5, A_6\) будут точками на окружности. Тогда части \(A_1 A_2, A_3 A_4, A_5 A_6, A_1 A_3\) и т. д. являются дугами окружности \(C(O, r)\)
Ответ: Когда \(θ\) измеряется в градусах, мера длины дуги \( = \frac{\theta}{{360}} \times 2\pi r\)
Когда \(θ\) измеряется в радианах, мера длины дуги \(l = rθ\)
Ответ: Дуга – это часть кривой. Дуга обычно относится к части круга. Другими словами, непрерывный отрезок окружности называется дугой окружности.
Ответ: Большая дуга окружности — это совокупность точек окружности, лежащих на или вне центрального угла.

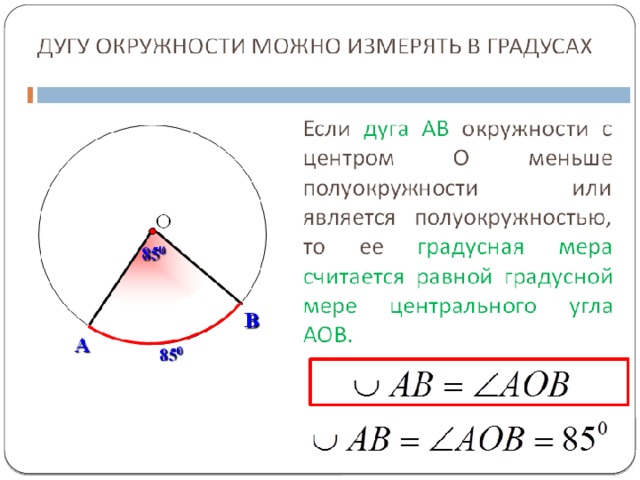
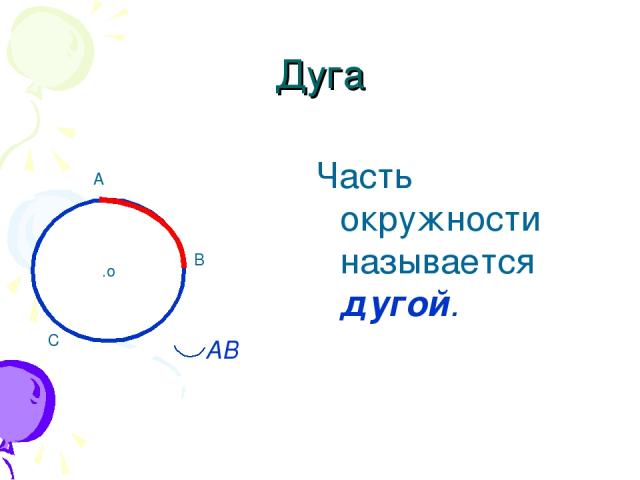
 Угол, образуемый малой дугой с центром круга всегда меньше 180\градусов или \pi радиан.
Угол, образуемый малой дугой с центром круга всегда меньше 180\градусов или \pi радиан.
или
r = \frac{L}{\theta }, [\theta в радианах]
или
\theta = \frac{L}{r}, [\тета в радианах]
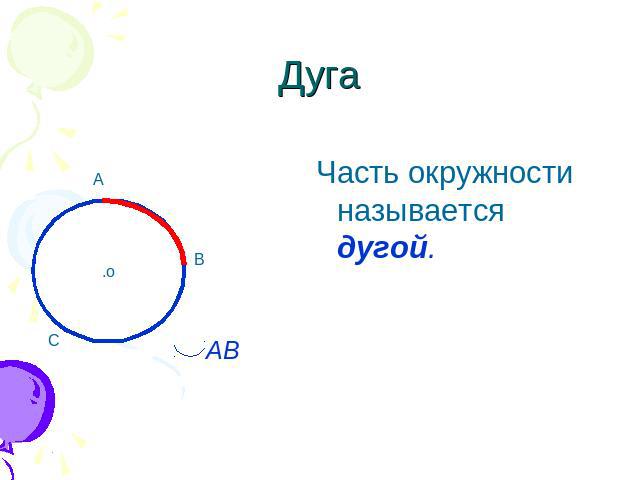 Узнайте, является ли дуга малой дугой или большой дугой, и найдите длину дуги в градусах?
Узнайте, является ли дуга малой дугой или большой дугой, и найдите длину дуги в градусах? Длина дуги:
Дано, \theta=90\градусов и r=14 см.
L = 2\pi r\left( {\frac{\theta}{{360}}} \right)
L = 2 \times \frac{{22}}{7} \times 14\left( {\ frac{{90}}{{360}}} \right)
L = 2 \times 22 \times 2\left( {\frac{1}{4}} \right)
L = 22\,cm
Поэтому , длина дуги 22 мсм.
Длина дуги:
Дано, \theta=270\градус и r=21 см.

L = 2\pi r\left( {\frac{\theta}{{360}}} \right)
L = 2 \times \frac{{22}}{7} \times 21\left( {\ frac{{270}}{{360}}} \right)
L = 2 \times 22 \times 3 \times \frac{3}{4}
L = 11 \times 3 \times 3
Л = 99\,см
Следовательно, длина Дуги равна 99\,см.
Длина дуги в радианах:
L = \theta r
L = \frac{\pi }{2} \times 35
L = 17,5\pi
Мы знаем, что \pi=3,1415
17,5\pi см=54,95 см
Следовательно, длина Дуги равна 17,5\pi см или 54,95 см.
L = \theta r
L=1,54\times 14
L=21,56\,см
Следовательно, длина дуги равна 21,56\ ,см.
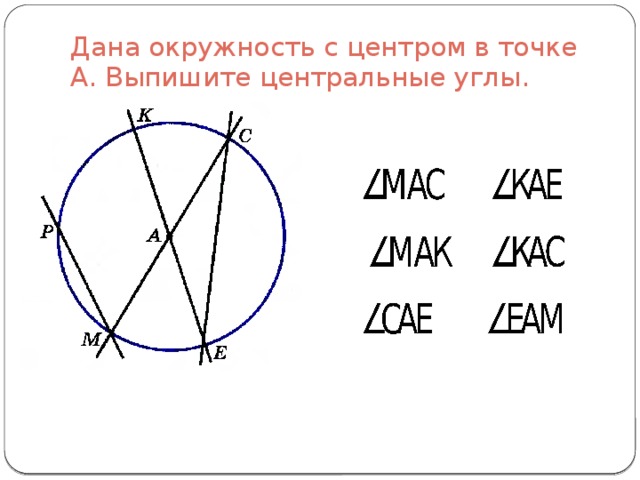
L = \theta r
\theta = \frac{L}{r}
\theta = \frac{{24} {6}
\theta = 4 радиана
Следовательно, угол, образуемый Дугой, равен 4 радианам.
L = \theta r
\theta = \frac{L}{r}
\theta = \frac{{16,5} {18} 90.
Дуга (L), если угол, образуемый дугой, выражается в градусах: L = 2\pi r\left ( {\ frac {\ theta }{{360}}} \right)
Дуга (L), если стягиваемый угол дается в радианах: L = \theta r

L = 2\pi r\left( {\frac{{{\theta}}}{{360}}} \right)
где, \theta — это угол, образуемый дугой в градусах.

r = \frac{L}{{2\pi }}\left( {\frac{{360}}{\theta }} \справа)
где \theta — угол, образуемый дугой, в градусах.
угол, образуемый дугой в градусах.
 Причина создания этого веб-сайта или блога в основном заключается в том, что я люблю преподавать . Всякий раз, когда у меня есть время, я обучаю студентов/аспирантов независимо от их класса или стандартов. Дополнительная информация
Причина создания этого веб-сайта или блога в основном заключается в том, что я люблю преподавать . Всякий раз, когда у меня есть время, я обучаю студентов/аспирантов независимо от их класса или стандартов. Дополнительная информация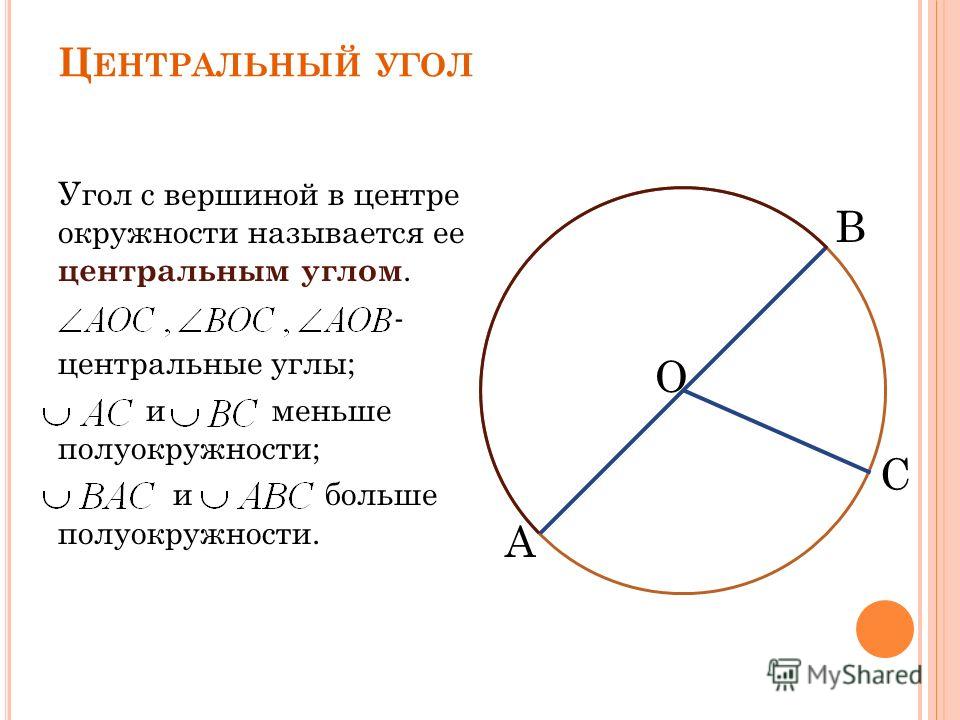 На следующей диаграмме ∠𝐴𝐵𝐶 представляет собой
Пример центрального угла.
На следующей диаграмме ∠𝐴𝐵𝐶 представляет собой
Пример центрального угла.
 Если центральный угол больше
чем 180∘, то дуга
главный. Если центральный угол меньше
180∘, то дуга малая. Если центральный угол равен
180∘, то дуга
полукруглый.
Если центральный угол больше
чем 180∘, то дуга
главный. Если центральный угол меньше
180∘, то дуга малая. Если центральный угол равен
180∘, то дуга
полукруглый.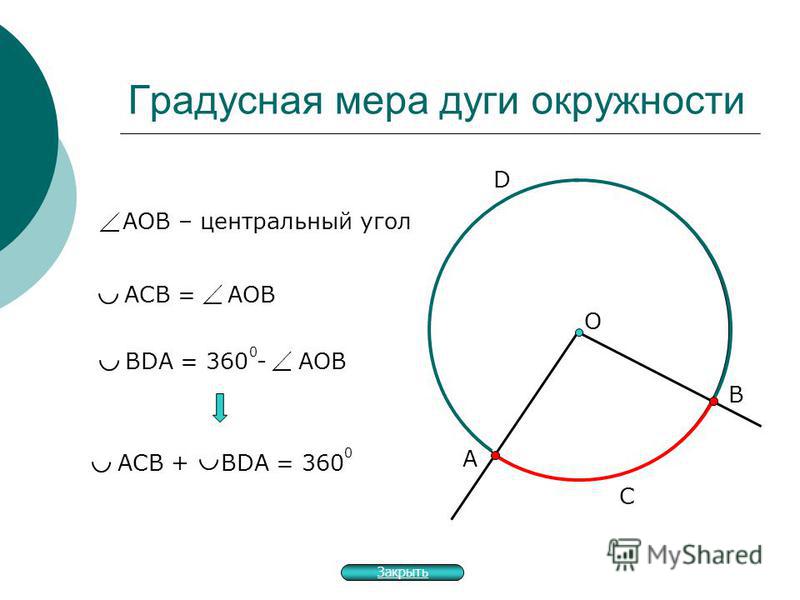
 Следовательно, мы можем ответить на этот вопрос, выделив каждую пару дуг. Начнем с 𝐴𝐵 и
𝐶𝐷.
Следовательно, мы можем ответить на этот вопрос, выделив каждую пару дуг. Начнем с 𝐴𝐵 и
𝐶𝐷.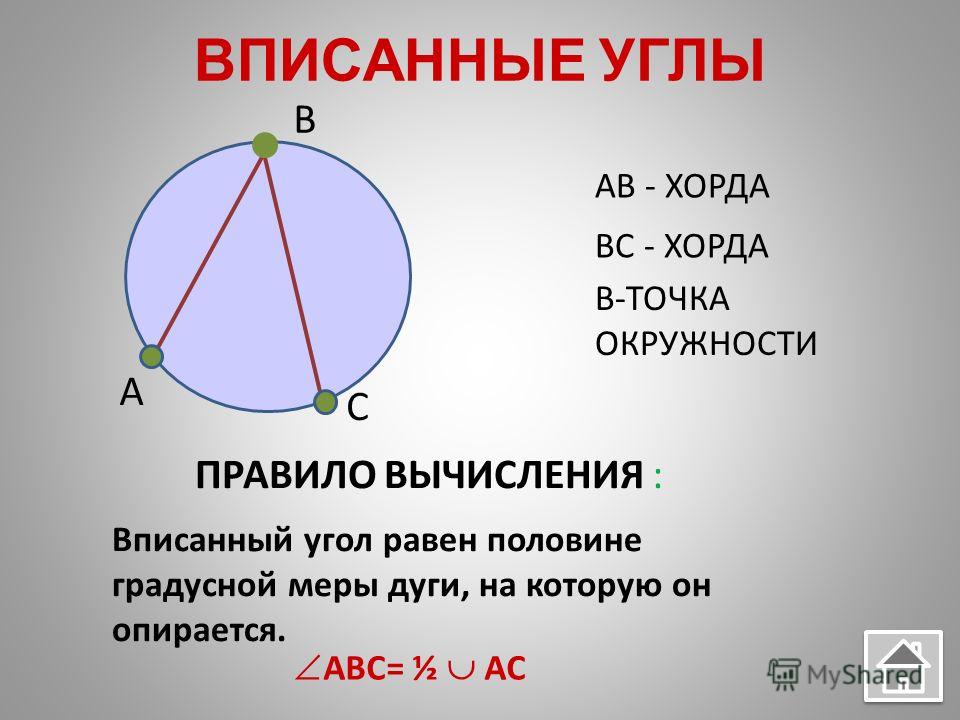
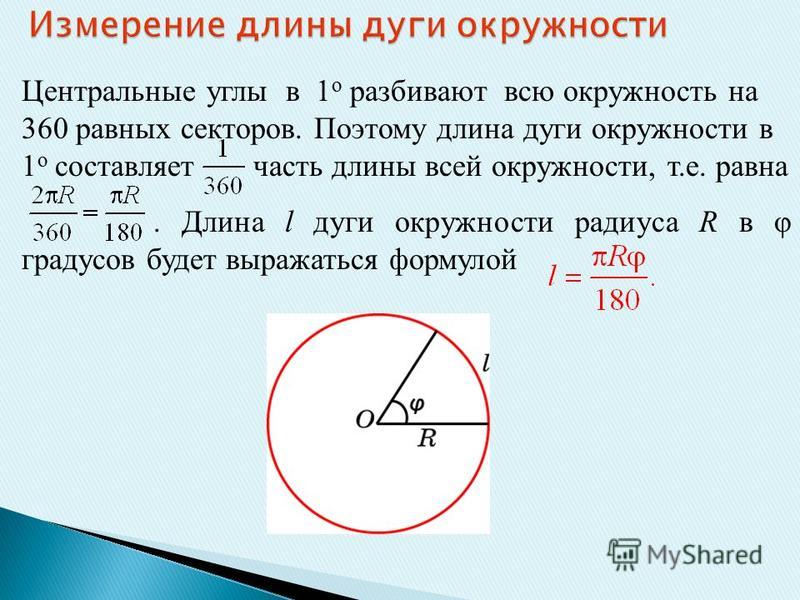 ∘∘∘∘
∘∘∘∘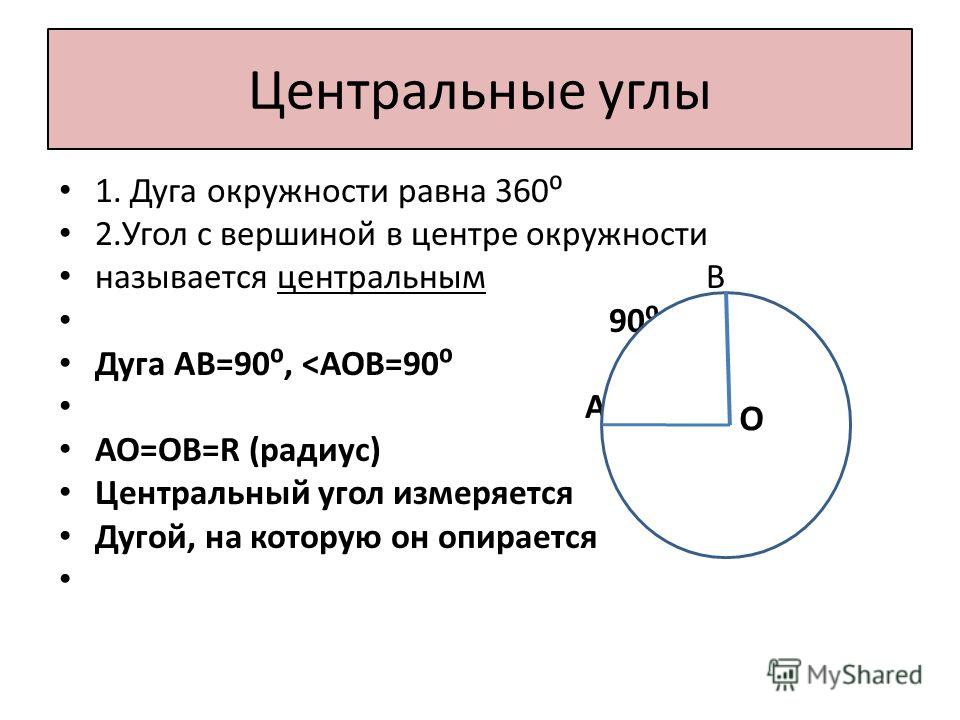 Полный оборот – это угол
360∘, так что
угол 90∘
Полный оборот – это угол
360∘, так что
угол 90∘ ∘∘
∘∘
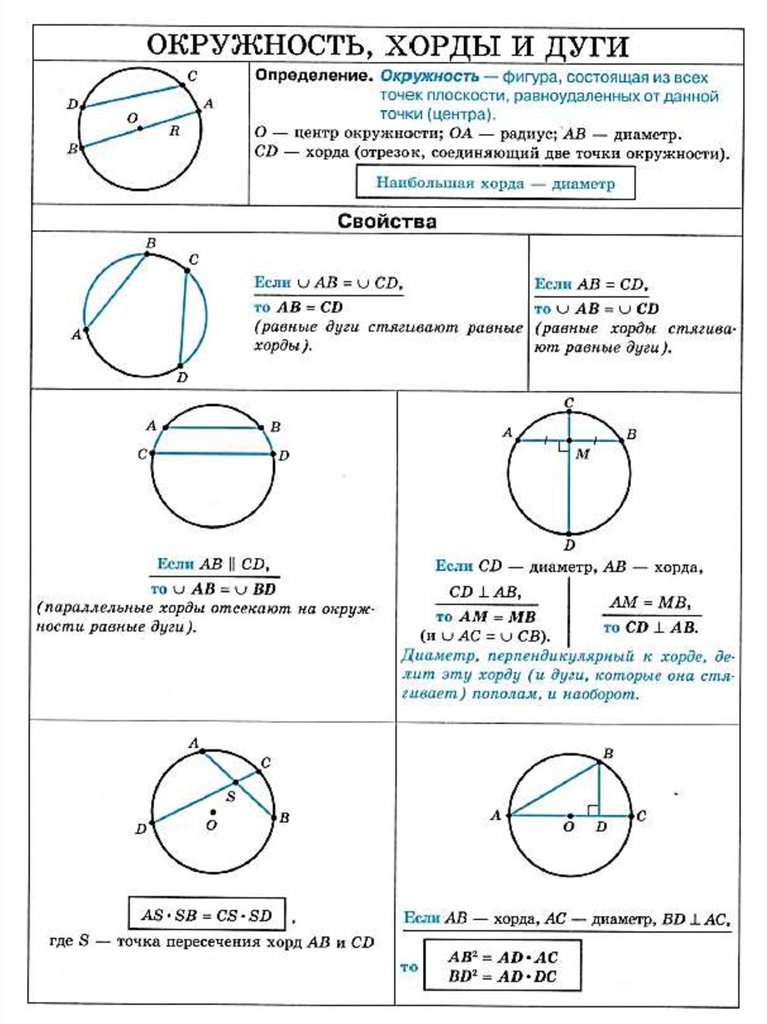 𝐴𝐵 имеет длину
5 см. Какова длина 𝐶𝐷?
𝐴𝐵 имеет длину
5 см. Какова длина 𝐶𝐷?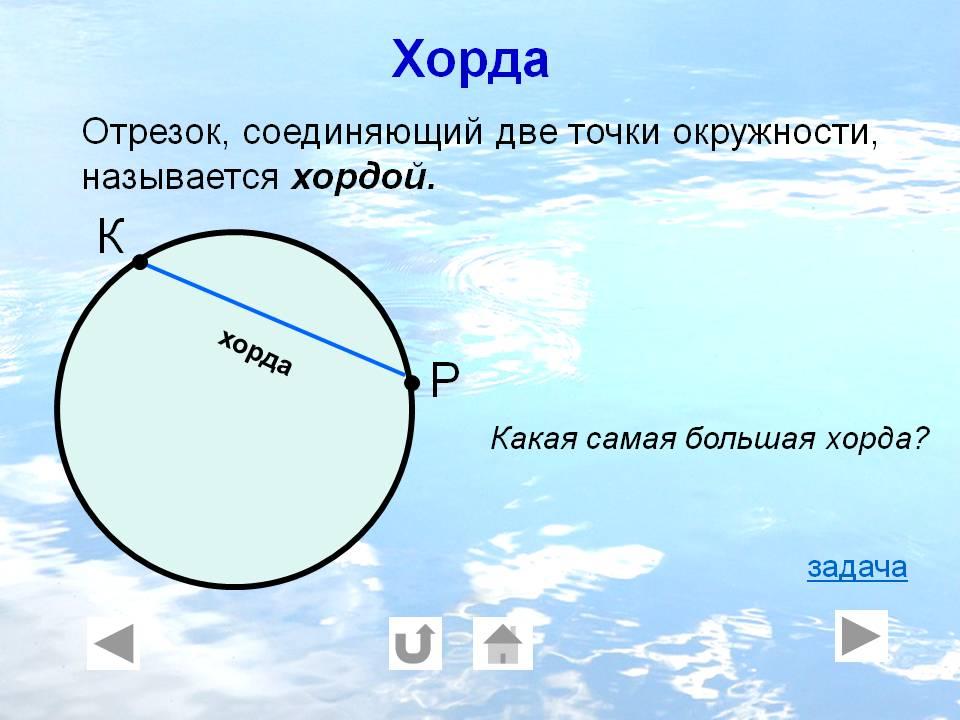 На самом деле то же самое верно и в обратном порядке; если дуги одинаковы
мера, то хорды между их соответствующими конечными точками будут иметь равные
длины.
На самом деле то же самое верно и в обратном порядке; если дуги одинаковы
мера, то хорды между их соответствующими конечными точками будут иметь равные
длины.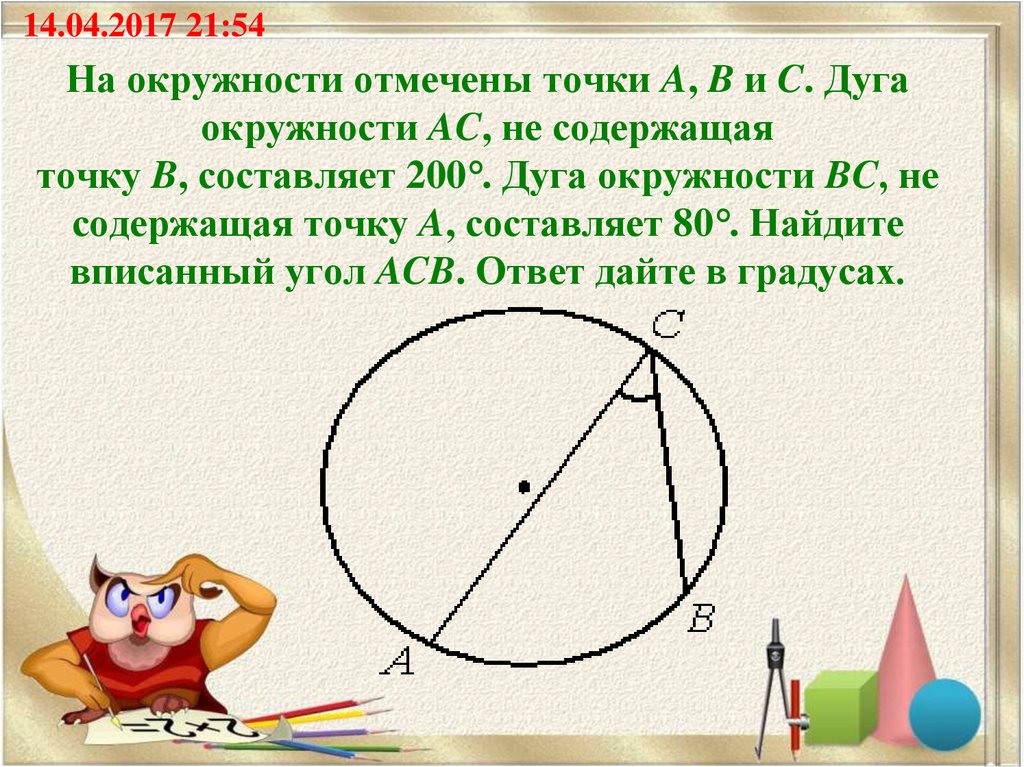 На самом деле то же самое верно и в обратном порядке; в том же круге или в конгруэнтных кругах,
если две хорды между концами двух дуг конгруэнтны, то две дуги
имеют одинаковую меру. Мы можем видеть это на следующей диаграмме.
На самом деле то же самое верно и в обратном порядке; в том же круге или в конгруэнтных кругах,
если две хорды между концами двух дуг конгруэнтны, то две дуги
имеют одинаковую меру. Мы можем видеть это на следующей диаграмме.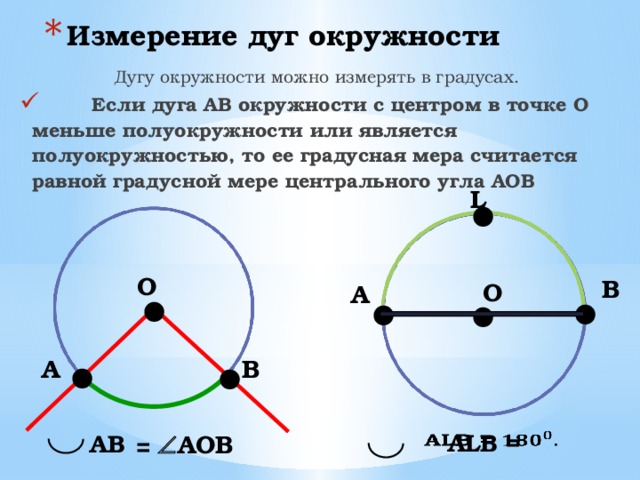
 Итак, мы должны иметь
𝑚 Хорошо+𝑚 Хорошо = 180 (5𝑥+12)+2𝑥 = 180.∘∘∘∘
Итак, мы должны иметь
𝑚 Хорошо+𝑚 Хорошо = 180 (5𝑥+12)+2𝑥 = 180.∘∘∘∘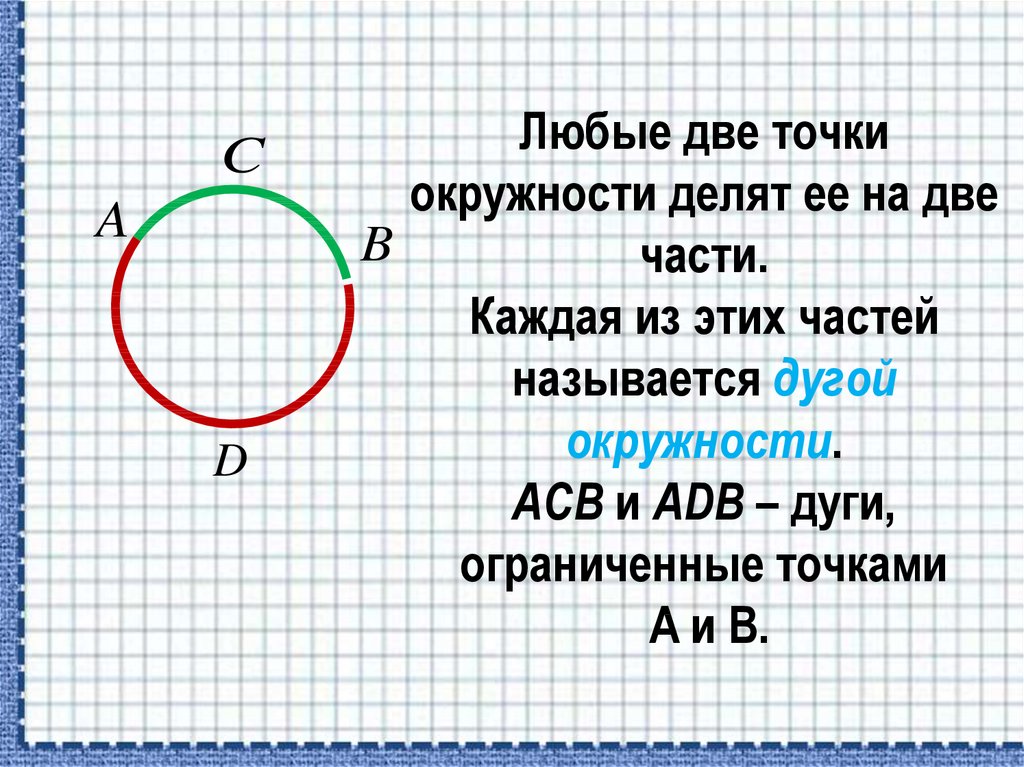

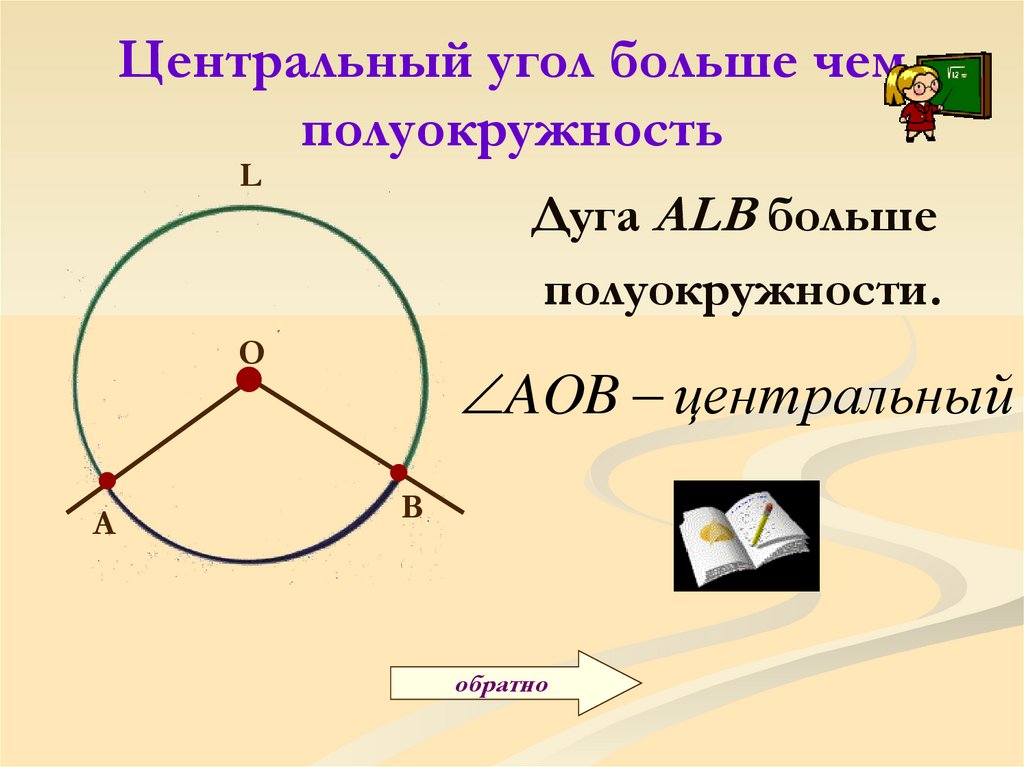
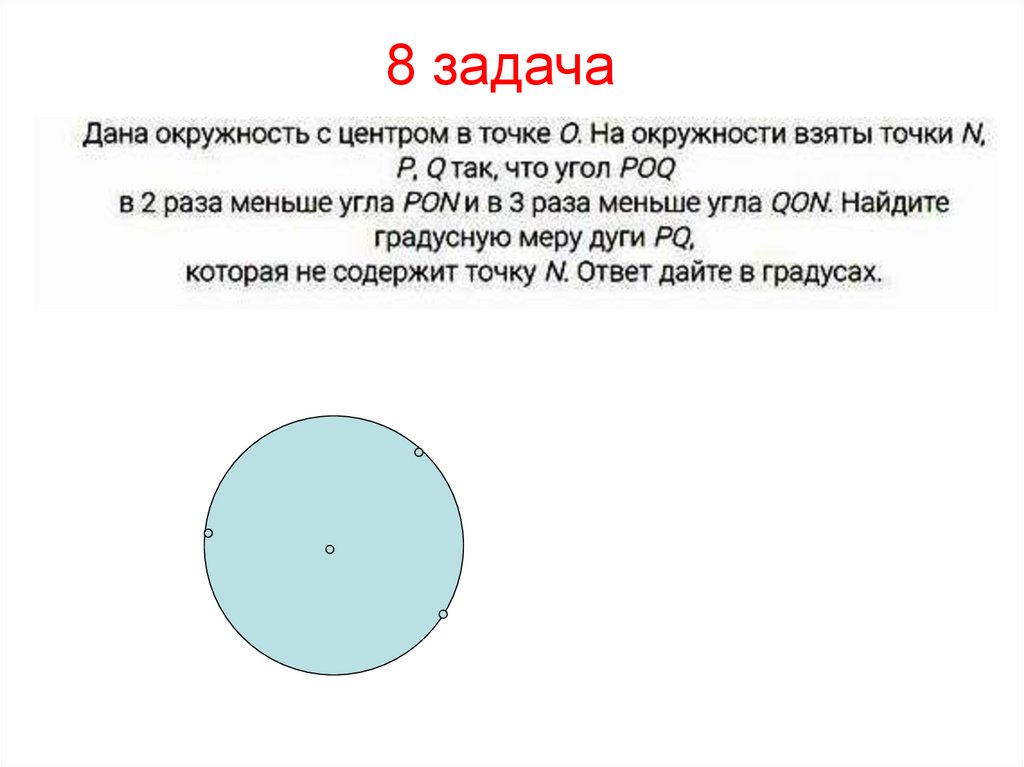
Найдите меру дуги, показанную в следующем круге, относительно ее радиуса, r .
Используя формулу:
Нам нужна мера дуги с точки зрения r , поэтому нам нужно изменить это уравнение :
Нахождение меры дуги с длиной окружности
Если нам не дан радиус, r , то есть второй метод нахождения меры дуги . Если мы знаем окружность окружности, а также длину дуги, то отношение между мерой дуги и (или в зависимости от того, хотите ли вы меру дуги в градусах или радианах) равно отношению между длина дуги и длина окружности .
Где
Найдите длину дуги x следующей окружности с длиной окружности 10 см.
Используя формулу :
Переставляя, получаем:
на 3 с.ф.
Измерения дуги — ключевые выводы
Часто задаваемые вопросы об измерениях дуги
Измерение дуги — это угол, из которого выходит дуга окружности.
Как найти меру дуги: зная радиус и длину дуги, мерой дуги является длина дуги, деленная на радиус. Учитывая окружность, отношение между мерой дуги и 360 градусами равно отношению между длиной дуги и окружностью.
Размер дуги равен длине дуги, деленной на радиус.
Размер дуги равен длине дуги, деленной на радиус.
В геометрии мерой дуги является длина дуги, деленная на радиус.
Тест Final Arc Measures
Вопрос
Что такое длина сегмента?
Показать ответ
Ответ
Длина отрезка – это расстояние между двумя точками на прямой.
Показать вопрос
Вопрос
Какова площадь сегмента круга?
Показать ответ
Ответ
Это площадь, ограниченная хордой и краем окружности.
Показать вопрос
Вопрос
Как называется отрезок, концы которого лежат на окружности?
Показать ответ
Ответ
Аккорд.
Показать вопрос
Вопрос
Как называется хорда, проходящая через центр окружности?
Показать ответ
Ответ
Диаметр.
Показать вопрос
Вопрос
Разделяет ли хорда, кроме диаметра, любую другую хорду на большую и малую дуги?
Показать ответ
Ответ
Показать вопрос
Вопрос
Верно ли следующее свойство?
Равные хорды окружности образуют равные углы в центре.
Показать ответ
Ответ
Показать вопрос
Вопрос
Делит ли биссектриса из центра окружности хорду пополам на равные половины?
Показать ответ
Ответ
Показать вопрос
Вопрос
Равны ли длины хорд, равноудаленных от центра окружности?
Показать ответ
Ответ
Показать вопрос
Вопрос
Верно ли следующее утверждение?
Теорема о пересекающихся хордах утверждает, что произведения пересечений на пересекающихся хордах равны.
Показать ответ
Ответ
Показать вопрос
Вопрос
Диаметр делит круг на:
Показать ответ
Ответ
Полукруги.
Показать вопрос
Вопрос
Будут ли соответствующие длины дуг равными, если хорды имеют одинаковую длину?
Показать ответ
Ответ
Показать вопрос
Вопрос
Две малые дуги конгруэнтны, если:
Показать ответ
Ответ
, их соответствующие хорды конгруэнтны.
Показать вопрос
Вопрос
Если одна хорда является биссектрисой другой хорды, то:
Показать ответ
Ответ
первая хорда это диаметр.
Показать вопрос
Вопрос
Определить «дугу» окружности
Показать ответ
Ответ
Дуга или длина дуги — это край сектора круга.
Показать вопрос
Вопрос
Определить меру дуги.
Показать ответ
Ответ
По отношению к длине дуги мерой дуги является угол, из которого выходит длина дуги.
Показать вопрос
Вопрос
Что такое длина сегмента?
Показать ответ
Ответ
Длина сегмента — это расстояние между двумя точками на линейном сегменте.
Показать вопрос
Вопрос
Длину отрезка можно определить, используя координаты двух точек.
Показать ответ
Ответ
Показать вопрос
Вопрос
Середина G между точками A, (2, 4) и B, (3, -3) равна.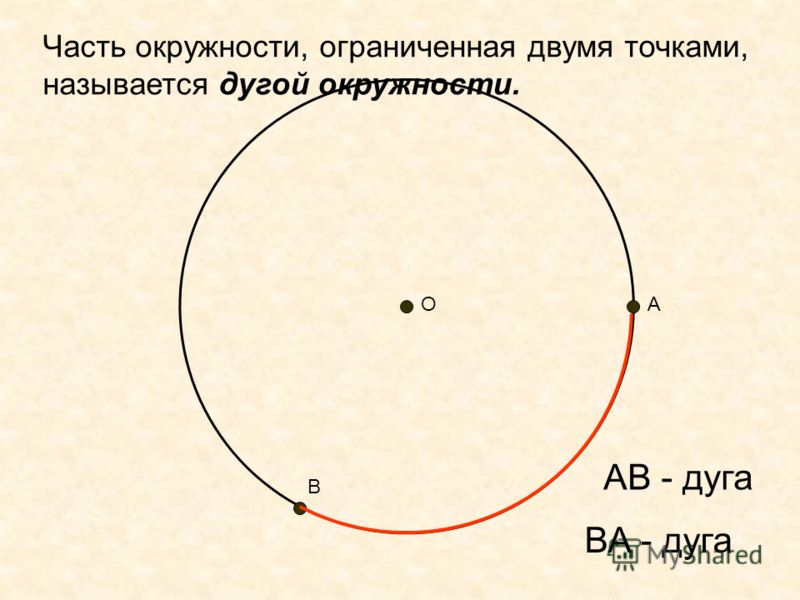 ..
..
Показать ответ
Ответ
(2.5, 0.5)
Показать вопрос
Вопрос
Какова длина сегмента окружности?
Показать ответ
Ответ
Отрезок окружности может быть либо диаметром окружности, когда прямая проходит через центр окружности, либо хордой, если прямая проходит в любом другом месте, кроме центра окружности.
Показать вопрос
Вопрос
Длина отрезка между точками C и B будет называться…
Показать ответ
Ответ
сегмент CB
Показать вопрос
Вопрос
Найдите длину отрезка окружности радиусом 7 см, стягивающего центр под углом 60°.
Показать ответ
Ответ
Показать вопрос
Вопрос
Найдите длину отрезка окружности радиусом 5 см, стягивающего центр под углом 210°.
Показать ответ
Ответ
9,66 см
Показать вопрос
Вопрос
Найти середину между началом координат и точкой Z (8, 6)
Показать ответ
Ответ
(4, 3)
Показать вопрос
Вопрос
Из каких двух компонентов состоит сегмент
Показать ответ
Ответ
Дуга и хорда
Показать вопрос
Вопрос
Длина сегмента не может быть рассчитана, если заданы конечная и средняя точки.
Показать ответ
Ответ
Показать вопрос
Вопрос
Длина отрезка рассчитывается по теореме Пифагора.
Показать ответ
Ответ
Показать вопрос
Вопрос
Средняя точка между определенной точкой J (2, 5) и другой точкой W равна (-1, 3). Найдите координаты точки W.
Показать ответ
Ответ
(-4, 1)
Показать вопрос
4.2: Длина дуги — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 3325
- Майкл Коррал
- Колледж Скулкрафт
В разделе 4. 1 мы видели, что один оборот имеет радианную меру \(2\pi \) рад. Обратите внимание, что \(2\pi\) — это отношение длины окружности (т.е. полной длины дуги) \(C \) окружности к ее радиусу \(r\): 90 007
1 мы видели, что один оборот имеет радианную меру \(2\pi \) рад. Обратите внимание, что \(2\pi\) — это отношение длины окружности (т.е. полной длины дуги) \(C \) окружности к ее радиусу \(r\): 90 007
\[ \text{Радианная мера 1 оборота} ~=~ 2\pi ~=~ \frac{2\pi\,r}{r} ~=~
\frac{C}{r} ~=~ \frac{\text{общая длина дуги}}{\text{радиус}}
\nonumber \]
Ясно, что это отношение не зависит от \(r \). В общем, радианная мера угла — это отношение длины дуги, отсекаемой соответствующим центральным углом в окружности, к радиусу окружности, независимо от радиуса.
Чтобы убедиться в этом, вспомним наше формальное определение радиана: центральный угол в окружности радиуса \(r\), который пересекает дугу длины \(r\). Итак, предположим, что у нас есть окружность радиуса \(r\), и мы поместили центральный угол с мерой в радианах \(1\) поверх другого центрального угла с мерой в радианах \(1\), как на рисунке 4.2.1( а). Ясно, что объединенный центральный угол двух углов имеет меру в радианах \(1+1=2\), а общая длина дуги равна \(r+r=2r \).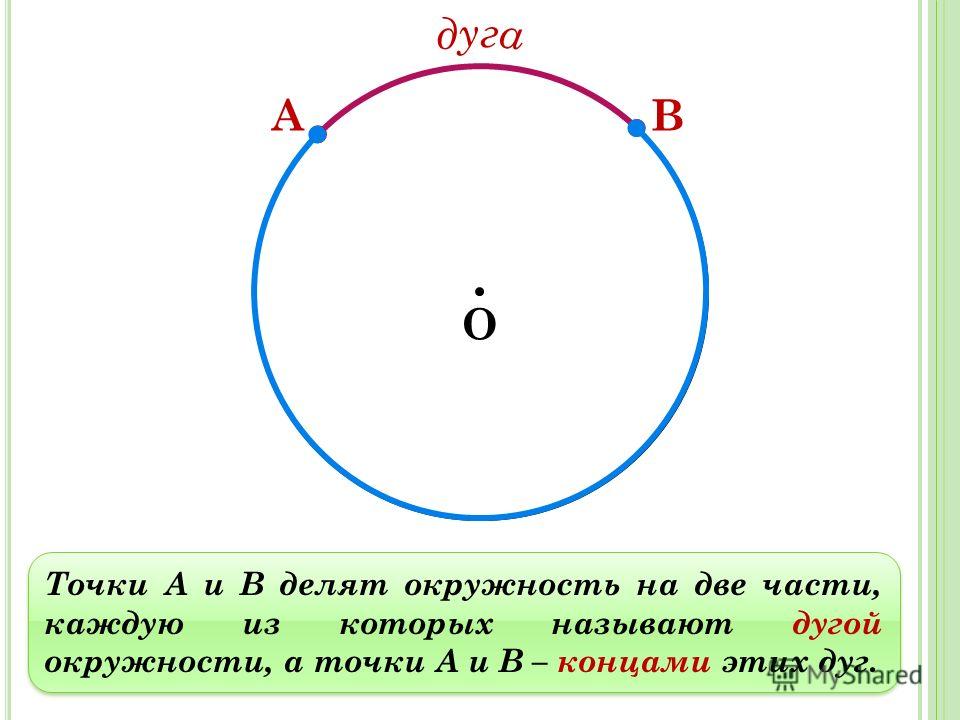
Теперь предположим, что мы разрезаем угол с радианной мерой \(1 \) пополам, как на Рисунке 4.2.1(b). Ясно, что это также сокращает вдвое длину дуги \(r \). Таким образом, мы видим, что
\[\nonumber \begin{align}
\text{Угол} ~&=~ 1~\text{радиан} \quad&\Стрелка вправо\quad \text{длина дуги} ~&=~ r ~,\\ \nonumber
\text{Угол} ~&=~ 2~\text{радианы} \quad&\Стрелка вправо\quad \text{длина дуги} ~&=~ 2\,r ~,\\ \nonumber
\text{Угол} ~ &=~ \tfrac{1}{2}~\text{радиан} \quad&\Стрелка вправо\quad \text{длина дуги} ~&=~
\tfrac{1}{2}\,r ~,\end{align} \nonumber \]
и вообще для любых \(\theta\ge 0\),
\[\nonumber \text{Угол} ~=~ \theta~\text{радианы} \quad \Rightarrow\quad \text{длина дуги} ~=~ \theta\,r ~,
\nonumber \]
так что
\[ \theta ~=~ \frac{\text{длина дуги}}{\text{радиус}} ~~.
\номер\]
Интуитивно очевидно, что уменьшение или увеличение окружности сохраняет меру центрального угла даже при изменении радиуса. Приведенное выше обсуждение говорит о большем, а именно о том, что отношение длины \(s\) пересекаемой дуги к радиусу \(r\) сохраняется именно потому, что это отношение является мерой центрального угла в радианах (см. рис. 4.2). .2).
Приведенное выше обсуждение говорит о большем, а именно о том, что отношение длины \(s\) пересекаемой дуги к радиусу \(r\) сохраняется именно потому, что это отношение является мерой центрального угла в радианах (см. рис. 4.2). .2).
Таким образом, мы получаем простую формулу для длины дуги:
В круге радиуса \(r\), пусть \(s\) будет длиной дуги, пересекаемой центральным углом с мерой в радианах \(\theta \ge 0 \). Тогда длина дуги \(s \) равна:
\[ s ~=~ r\,\theta \label{4.4} \]
Пример 4.3
В круге радиусом \(r=2\) см, какова длина \(s\) дуги, проведенной под центральным мерным углом \(\theta = 1,2\) рад? 9\circ ~=~ \frac{\pi}{180} \;\cdot\; 41 ~=~ 0,716~\text{rad}
\quad\Rightarrow\quad s ~=~ r\,\theta ~=~ (10)\,(0,716) ~=~ \boxed{7,16~\text{ft }}\nonumber \]
Обратите внимание, что, поскольку длина дуги \(s \) и радиус \(r \) обычно задаются в одних и тех же единицах измерения, радианы действительно безразмерны, так как вы можете думать об отмене единиц в соотношение \(\frac{s}{r} \), которое равно \(\theta \).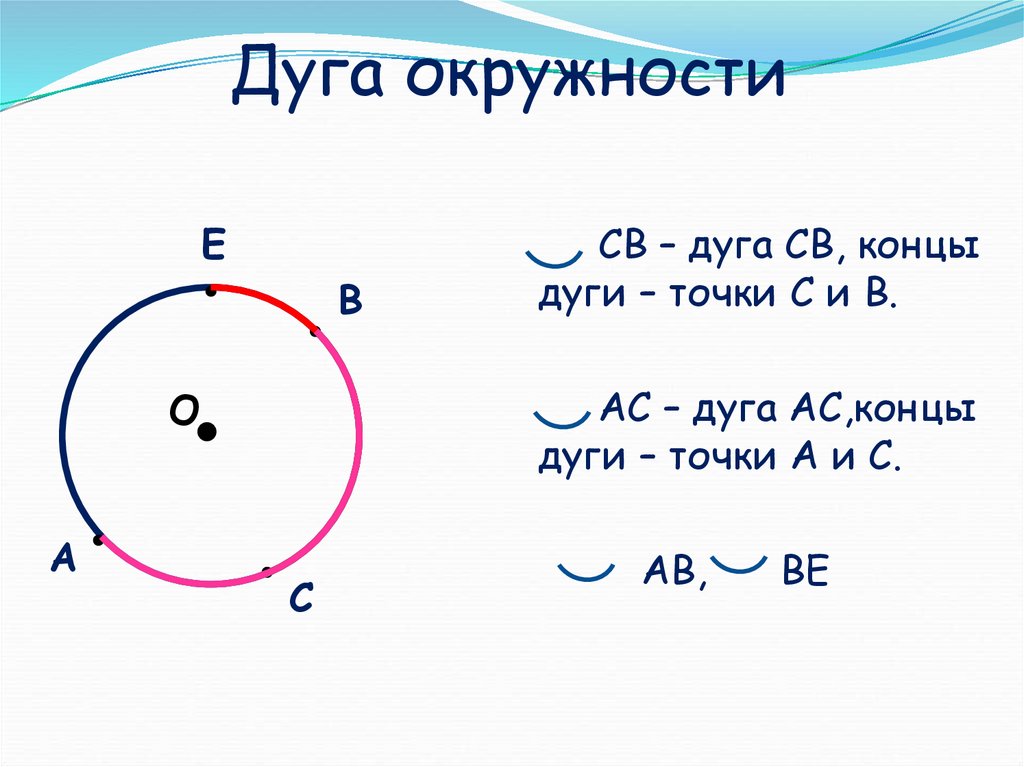 Это еще одна причина, почему радианы так широко используются.
Это еще одна причина, почему радианы так широко используются.
Пример 4.5
Центральный угол окружности радиусом \(5 \) м отсекает дугу длиной \(2 \) м. Чему равен угол в радианах? Какая мера в градусах? 9\circ \), может быть неясно, что имеется в виду под пересекаемой дугой, так как угол больше одного оборота и, следовательно, «огибает» окружность более одного раза. Мы будем придерживаться подхода, согласно которому такая дуга состоит из полная окружность плюс любая дополнительная длина дуги, определяемая углом. Другими словами, уравнение \ref{4.4} по-прежнему справедливо для углов \(\theta > 2\pi \) рад.
Как насчет отрицательных углов? В этом случае использование \(s=r\,\theta \) означало бы, что длина дуги отрицательна, что нарушает обычное понятие длины. Таким образом, мы примем соглашение использовать только неотрицательные центральные углы при обсуждении длины дуги.
Пример 4.6
Веревка прикреплена к стене в двух местах на расстоянии \(8 \) футов на одинаковой высоте.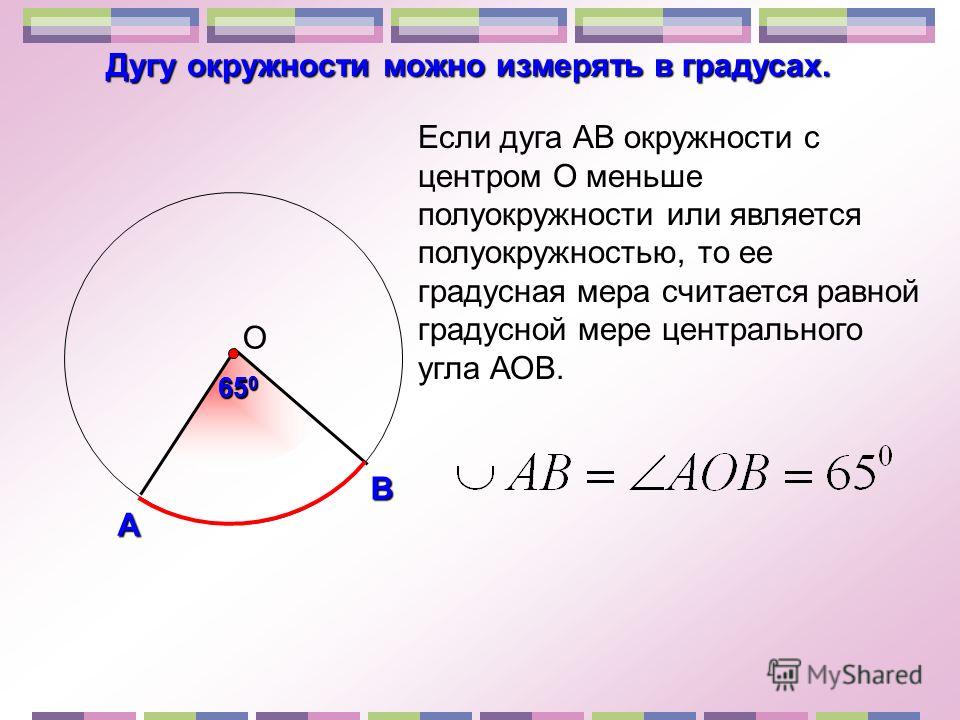 Цилиндрический контейнер радиусом \(2\) фута отталкивают от стены настолько далеко, насколько это возможно, удерживая его веревкой, как показано на рис. 4.2.3, где показан вид сверху. Если центр контейнера находится в \(3\) футах от точки на стене посередине между концами веревки, какова длина \(L\) веревки?
Цилиндрический контейнер радиусом \(2\) фута отталкивают от стены настолько далеко, насколько это возможно, удерживая его веревкой, как показано на рис. 4.2.3, где показан вид сверху. Если центр контейнера находится в \(3\) футах от точки на стене посередине между концами веревки, какова длина \(L\) веревки?
Решение:
9\циркуляр ~.\nonumber \]
Переводя в радианы, получаем \(\;\theta = \frac{\pi}{180} \;\cdot\; 60,5 = 1,06 \) рад. Таким образом,
\[ L ~=~ 2\,(AB \;+\; \cdot \overparen{BC}) ~=~ 2\,(\sqrt{21} \;+\; BE \cdot \theta ) ~=~
2\,(\sqrt{21} \;+\; (2)\,( 1.06)) ~=~ \boxed{13.4 ~\text{ft}} ~.
\номер \]
Пример 4.7
Центры двух ременных шкивов с радиусами \(5\) см и \(8\) см соответственно отстоят друг от друга на \(15\) см. Найдите общую длину \(L\) ремня вокруг шкивов.
Решение
На рис. 4.2.4 мы видим, что по симметрии \(\;L = 2\;(\overparen{DE} + EF + \overparen{FG}) \).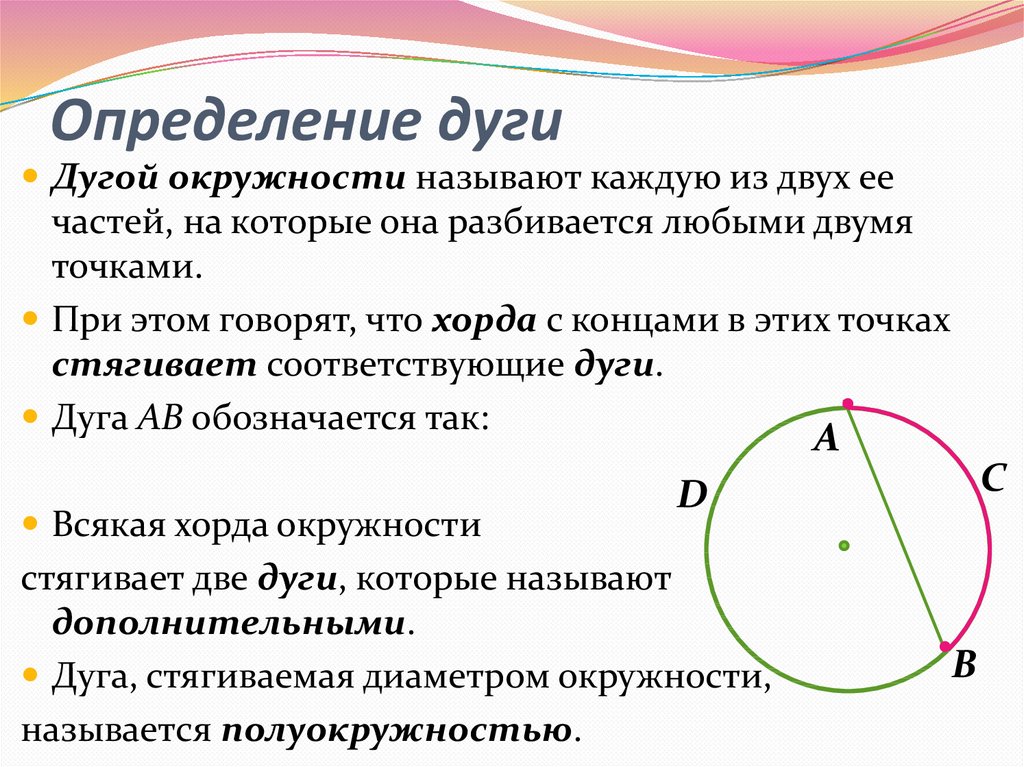
Сначала в центре \(B\) шкива с радиусом \(8\) нарисуйте окружность радиусом \(3\), которая является разница в радиусах двух шкивов. Пусть \(C\) будет точкой пересечения этой окружности \(\overline{BF} \). Тогда мы знаем, что касательная \(\overline{AC} \) к этому меньшему кругу перпендикулярна отрезку \(\overline{BF} \). Таким образом, \(\angle\,ACB\) — прямой угол, поэтому длина \(\overline{AC} \) равна 92} ~=~ \sqrt{216} ~=~ 6\,\sqrt{6}\nonumber \]
по теореме Пифагора. Теперь, поскольку \(\overline{AE} \perp \overline{EF} \) и \(\overline{EF} \perp \overline{CF} \) и \(\overline{CF} \perp \overline{AC} \), четырехугольник \(AEFC\) должен быть прямоугольником. В частности, \(EF = AC \), поэтому \(EF = 6\,\sqrt{6} \).
Из уравнения \ref{4.4} мы знаем, что \(\;\overparen{DE} = EA \cdot \angle\,DAE\; \) и \(\;\overparen{FG} = BF \cdot \angle \,GBF \), где углы измеряются в радианах. Итак, думая об углах в радианах (используя \(\pi \) rad \(= 180^\circ\)), мы видим из рисунка 4.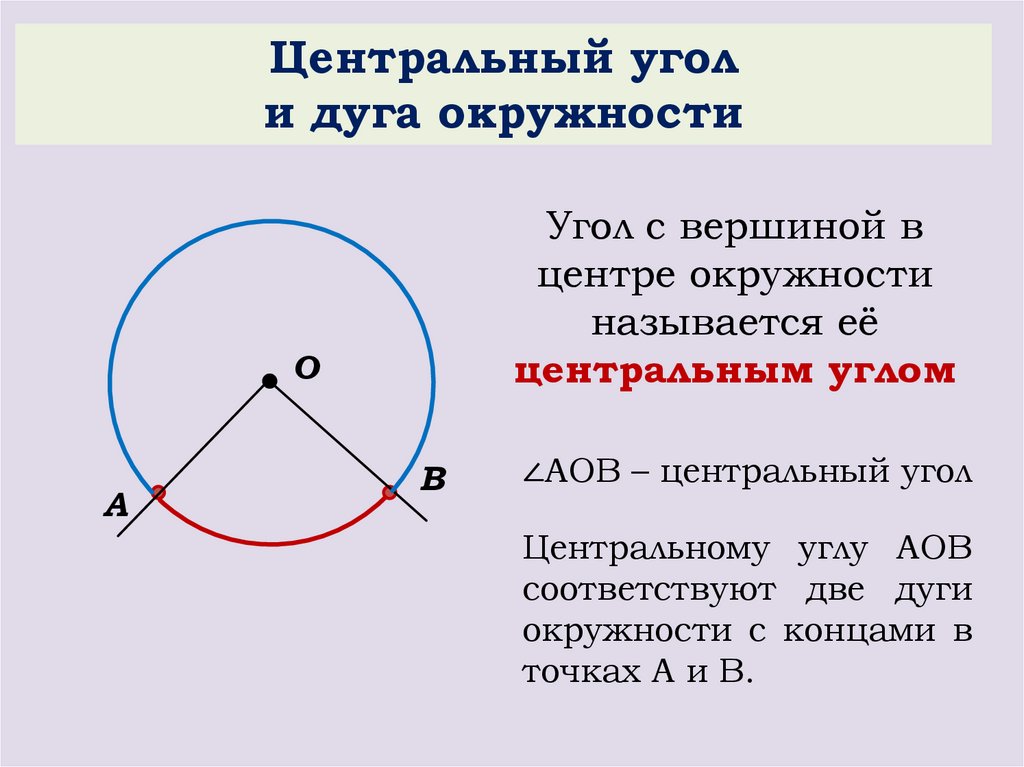 2.4, что
2.4, что
\[\номер\угол\,DAE ~=~ \pi \;-\; \угол\,EAC \;-\; \угол\,ВАС ~=~ \pi \;-\; \frac{\pi}{2} \;-\;
\угол\,ВАС ~=~ \frac{\pi}{2} \;-\; \angle\,BAC ~, \nonumber \]
где
\[\nonumber \sin\;\angle\,BAC ~=~ \frac{BC}{AB} ~=~ \frac{3}{15 } ~=~ 0.2 \quad\Rightarrow\quad
\angle\,BAC ~=~ 0.201~\text{rad.} \nonumber \]
Таким образом, \(\;\angle\,DAE = \frac{\ пи{2} \,-\, 0,201 = 1,37 \) рад. Так как \(\overline{AE} \) и \(\overline{BF} \) параллельны, мы имеем \(\;\угол\,ABC = \угол\,DAE = 1,37\) рад. Таким образом, \(\;\угол\,GBF = \pi\,-\, \угол\,ABC = \pi\,-\, 1,37 = 1,77\) рад. Следовательно,
\[\nonumber L ~=~ 2\;(\overparen{DE} \;+\; EF \;+\; \overparen{FG}) ~=~ 2\;(5\;(1.37) \ ;+\;6\,\sqrt{6} \;+\;
8\;(1.77)) ~=~ \boxed{71.41~\text{cm}} ~. \nonumber \]
Эта страница под названием 4.2: Длина дуги распространяется в соответствии с лицензией GNU Free Documentation License 1.3 и была создана, изменена и/или курирована Майклом Корралом с использованием исходного содержимого, которое было отредактировано в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.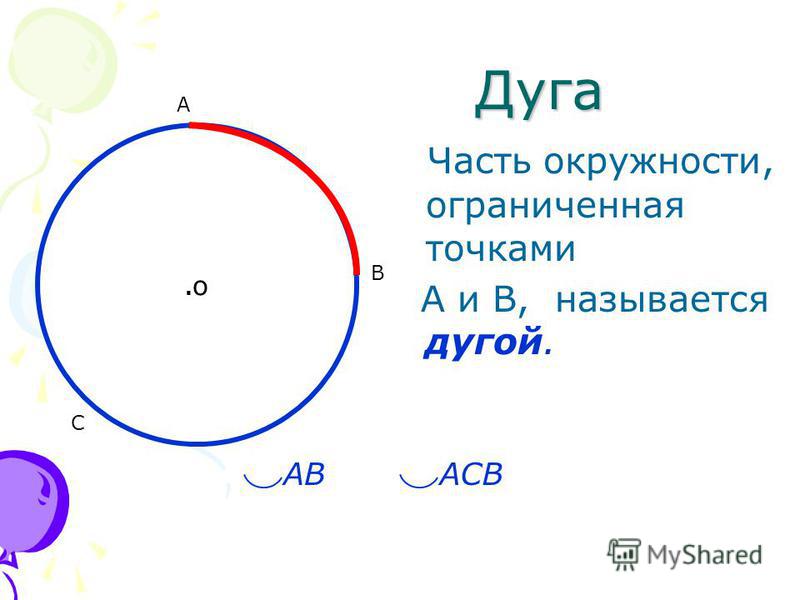

 {2} \ left (\ theta — \ sin {\ theta} \ right).}
{2} \ left (\ theta — \ sin {\ theta} \ right).}

 Если указан угол в 91 градус, сегмент используется для формирования дуги окружности, и в выходных данных будет только дуга (правая схема).
Если указан угол в 91 градус, сегмент используется для формирования дуги окружности, и в выходных данных будет только дуга (правая схема). Объектами могут быть линии или полигоны. Если используется несколько входных данных, они должны быть в одной пространственной привязке.
Объектами могут быть линии или полигоны. Если используется несколько входных данных, они должны быть в одной пространственной привязке.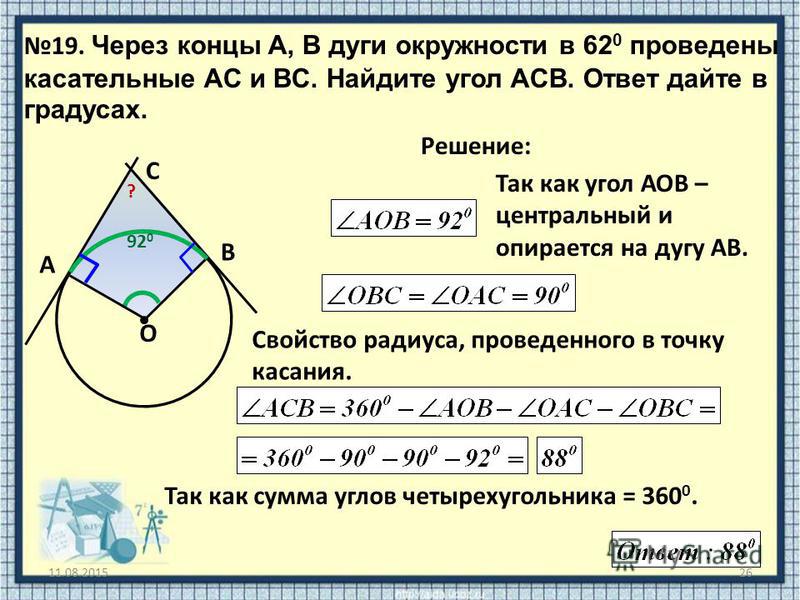
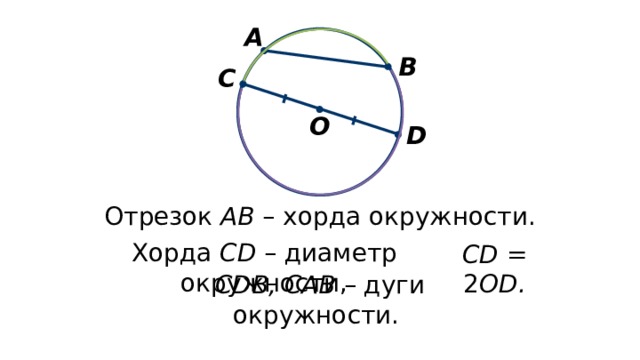
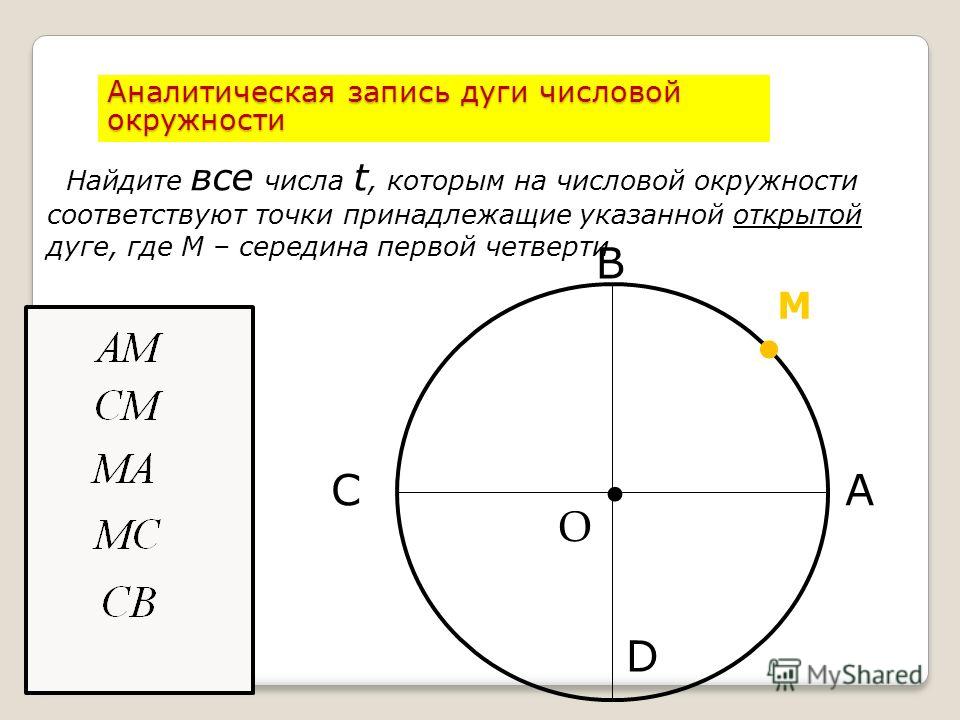 Значение должно быть больше 3. Значение по умолчанию равно 4. Параметр не доступен, если опция Вписать в сегменты выбрана для параметра Тип переходных элементов.
Значение должно быть больше 3. Значение по умолчанию равно 4. Параметр не доступен, если опция Вписать в сегменты выбрана для параметра Тип переходных элементов.
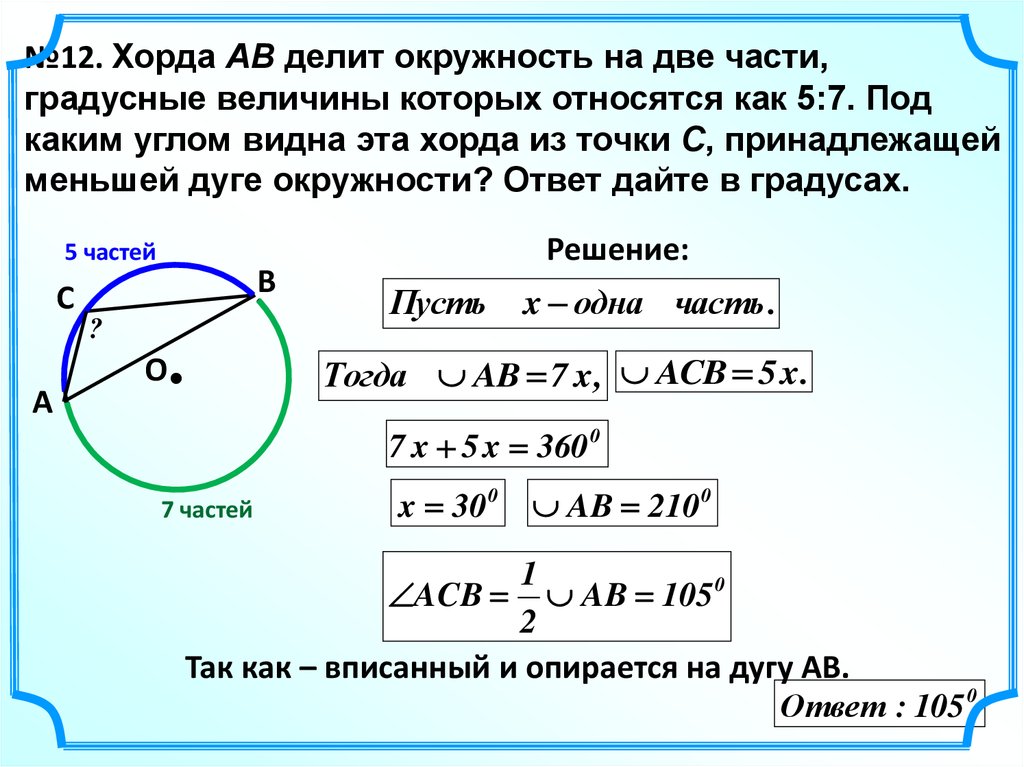 Если выбрана опция Вписать в вершины для параметра Тип переходных элементов, расстояние измеряется между входными вершинами и выходными ребрами объектов. Если выбрана опция Вписать в вершины, расстояние измеряется между ребрами входных объектов и ребрами выходных объектов.
Если выбрана опция Вписать в вершины для параметра Тип переходных элементов, расстояние измеряется между входными вершинами и выходными ребрами объектов. Если выбрана опция Вписать в вершины, расстояние измеряется между ребрами входных объектов и ребрами выходных объектов. Выходные ребра и кривые будут подогнаны автоматически к геометрии входных объектов.
Выходные ребра и кривые будут подогнаны автоматически к геометрии входных объектов. Если в пределах каждого максимального шага угла дуги найдены вершины, дуга будет построена. Например, если вершины и ребра разрежены, используйте большой шаг угла дуги. Допустимый диапазон составляет от 2 до 95 десятичных градусов. Значение по умолчанию равно 20 десятичные градусам. Параметр не доступен, если опция Вписать в сегменты выбрана для параметра Тип переходных элементов.
Если в пределах каждого максимального шага угла дуги найдены вершины, дуга будет построена. Например, если вершины и ребра разрежены, используйте большой шаг угла дуги. Допустимый диапазон составляет от 2 до 95 десятичных градусов. Значение по умолчанию равно 20 десятичные градусам. Параметр не доступен, если опция Вписать в сегменты выбрана для параметра Тип переходных элементов. Значение должно быть больше 0 и меньше, чем указано для Минимального радиуса. Если значение не указано, радиус выходной дуги окружности не отмечается (по умолчанию).
Значение должно быть больше 0 и меньше, чем указано для Минимального радиуса. Если значение не указано, радиус выходной дуги окружности не отмечается (по умолчанию). Если центральный угол любой выходной дуги будет меньше этого значения, она не будет создана. Допустимый диапазон составляет от 2 до 360 десятичных градусов. Значение по умолчанию равно 2 десятичные градусам.
Если центральный угол любой выходной дуги будет меньше этого значения, она не будет создана. Допустимый диапазон составляет от 2 до 360 десятичных градусов. Значение по умолчанию равно 2 десятичные градусам. Точки якоря накладываются на вершины входных объектов и указывают, что эти вершины не могут быть удалены или смещены во время упрощения.
Точки якоря накладываются на вершины входных объектов и указывают, что эти вершины не могут быть удалены или смещены во время упрощения.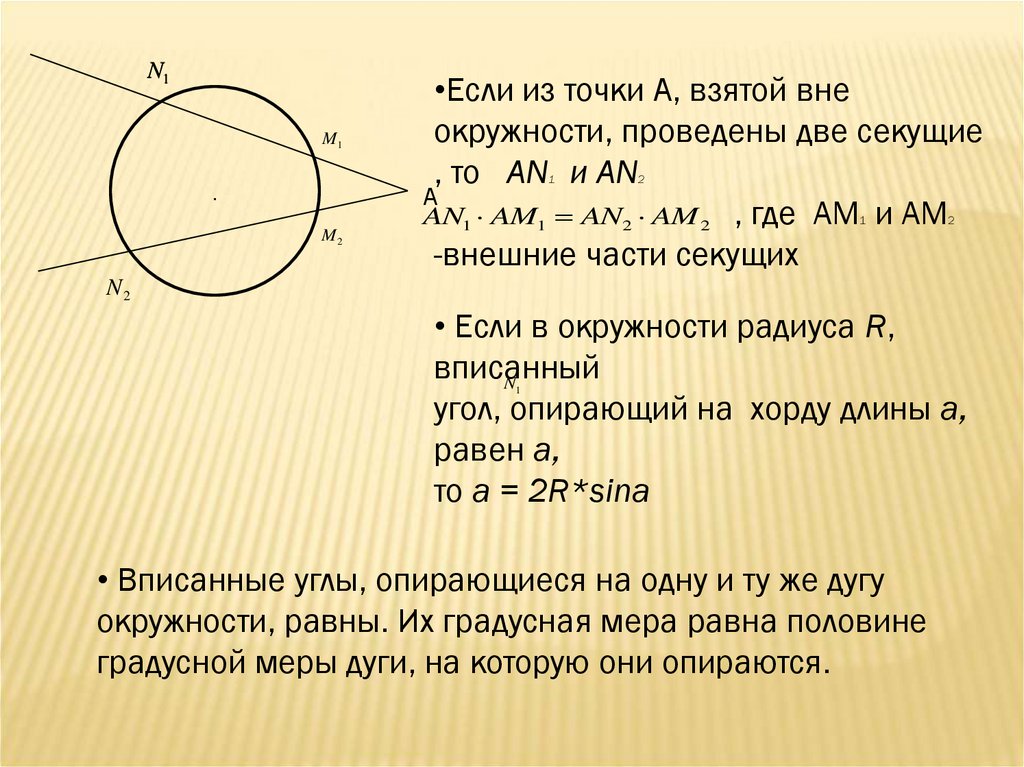 знак равноα{\ displaystyle {\ widehat {AMB}} = \ альфа}
знак равноα{\ displaystyle {\ widehat {AMB}} = \ альфа}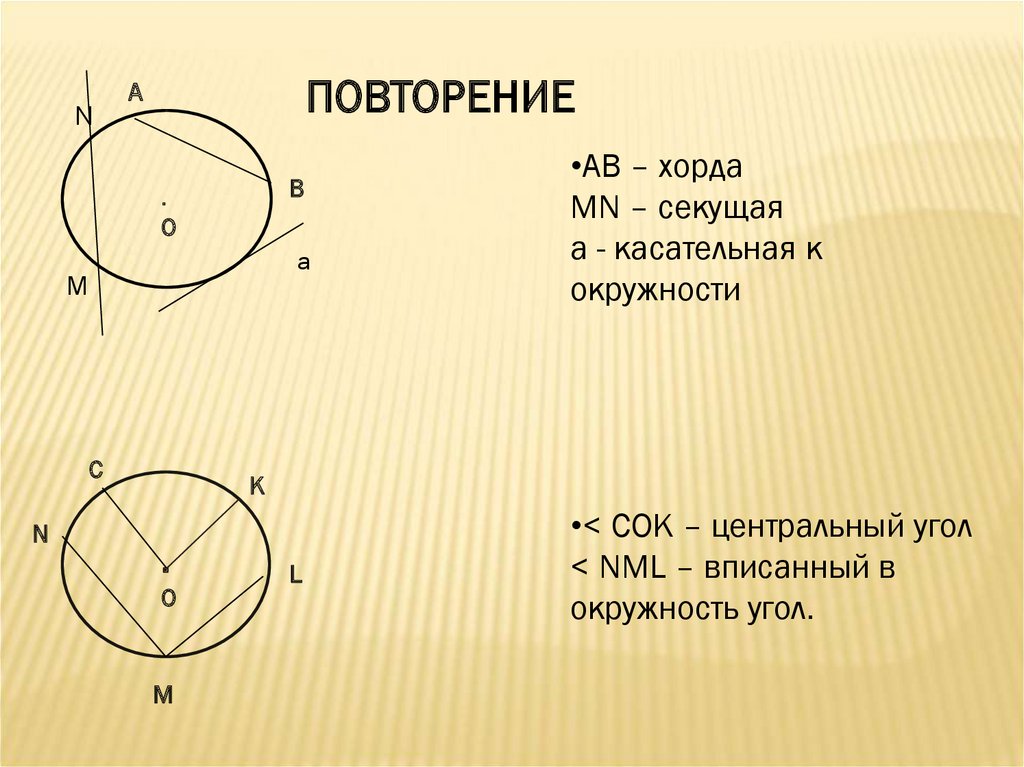 {\ circ} \ pi r} {180}} {\ text {.}}}
{\ circ} \ pi r} {180}} {\ text {.}}} Деттонвиль), Traite des arcs de circle, 1658–169, часто включается в трактат о рулетке, где Паскаль исследует истоки того, что станет исчислением бесконечно малых , разрезая дугу окружности на бесконечность маленькие кусочки (Объяснение подхода представлено в Un Calculatif Integrale chez Pascal , на сайте Академии Бордо.
Деттонвиль), Traite des arcs de circle, 1658–169, часто включается в трактат о рулетке, где Паскаль исследует истоки того, что станет исчислением бесконечно малых , разрезая дугу окружности на бесконечность маленькие кусочки (Объяснение подхода представлено в Un Calculatif Integrale chez Pascal , на сайте Академии Бордо. {2} \ left (\ theta — \ sin {\ theta} \ right).}
{2} \ left (\ theta — \ sin {\ theta} \ right).}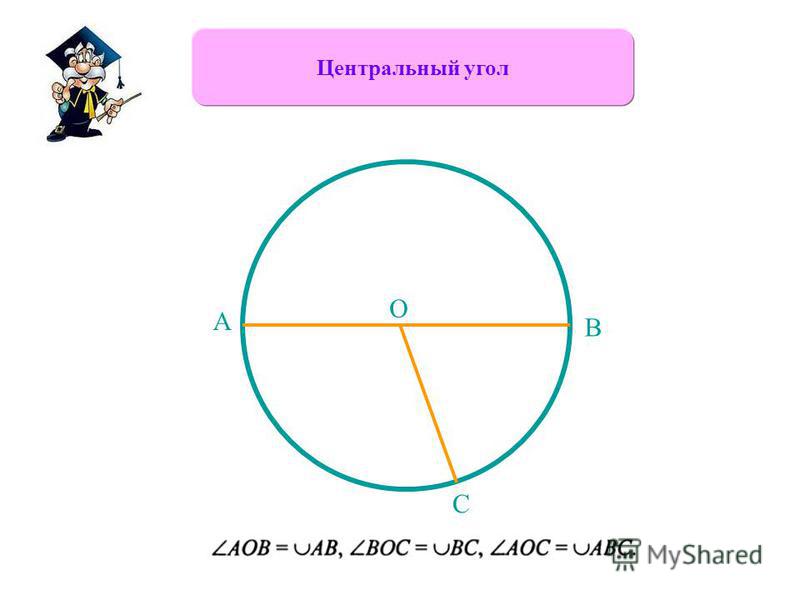 Чтобы получился красивый узор, нитки должны быть разной длины и проходить через разные точки – не обязательно через центр.
Чтобы получился красивый узор, нитки должны быть разной длины и проходить через разные точки – не обязательно через центр. 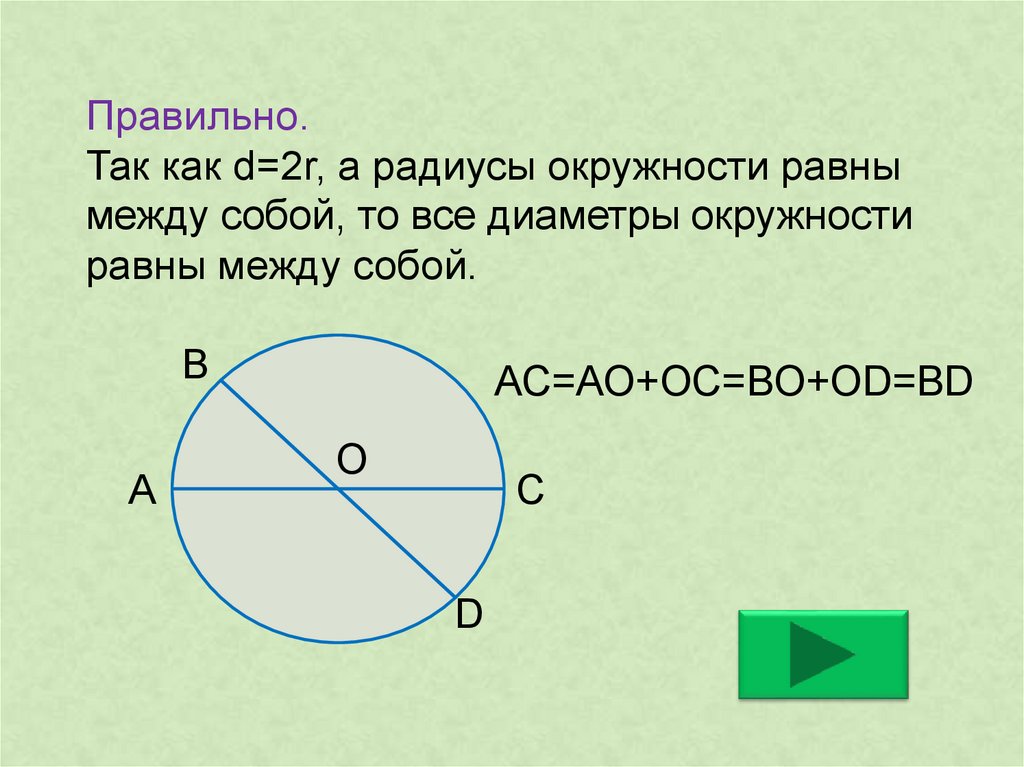
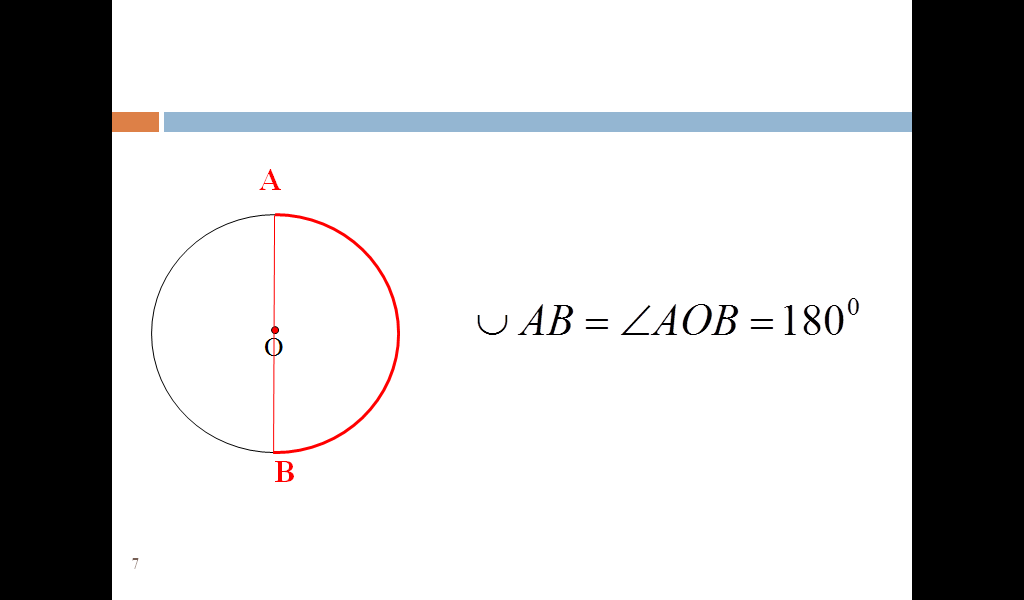 А вот если повернуться на 360 градусов, то мы будем смотреть на ту же точку, на которую смотрели изначально.
А вот если повернуться на 360 градусов, то мы будем смотреть на ту же точку, на которую смотрели изначально.  Элементами окружности являются радиус, диаметр, хорда, дуга.
Элементами окружности являются радиус, диаметр, хорда, дуга. 
 Ясно, что окружность разделена на две части, каждая из которых является дугой. Обозначим дугу из \(А\) в \(В\) против часовой стрелки через \(АВ\), а дугу из \(В\) в \(А\) по часовой стрелке через \(ВА\). ). Заметим, что точки \(A\) и \(B\) лежат как на \(AB\), так и на \(BA\).
Ясно, что окружность разделена на две части, каждая из которых является дугой. Обозначим дугу из \(А\) в \(В\) против часовой стрелки через \(АВ\), а дугу из \(В\) в \(А\) по часовой стрелке через \(ВА\). ). Заметим, что точки \(A\) и \(B\) лежат как на \(AB\), так и на \(BA\).  Тогда любой угол, вершина которого равна \(0\), называется центральным углом.
Тогда любой угол, вершина которого равна \(0\), называется центральным углом.