Пример №2:
Нужно вычислить приблизительное значение заданной функции arctg 1.02. При этом производя замену приращения функции ее дифференциалом.
Рассмотрим подробно функцию y= arctg x.
Для данной функции нужно вычислить значение в точке равной 1,02.
Для этого выразим функцию в следующем выражении: \[x=x_{0}+\Delta x\].
Значения двух точек \[\mathrm{x}_{0}\]и \[\Delta x\] подбираются таким образом, чтобы при вычислении значений функции и ее производных было легко проводить расчеты. При этом желательно числа выбирать так, чтобы значение \[\Delta x\]. было достаточно минимальным по значению.
Учитывая все требования можно сделать следующий вывод:
\[x=1.02=1+0.02\] , а именно \[ x_{0}=1 \text { и } \Delta x=0,02 .\]
Определим значения для заданной функции y= arctg x в первой точке равной \[\mathrm{x}_{0} = 1\]
\[y\left(x_{0}\right)=y(1)=\operatorname{arctg} 1=\frac{\pi}{4}\].
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.
Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие
простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции.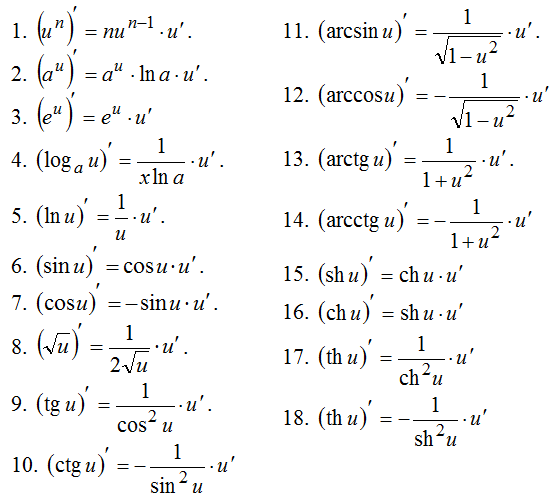 Далее производные элементарных функций находим в таблице
производных, а формулы производных произведения, суммы и частного — в правилах
дифференцирования. Таблица производных и
правила дифференцирования даны после первых двух примеров.
Далее производные элементарных функций находим в таблице
производных, а формулы производных произведения, суммы и частного — в правилах
дифференцирования. Таблица производных и
правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2. Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило,
проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования.
К ним мы и переходим прямо сейчас.
Таблица производных простых функций
| 1. Производная константы (числа). Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто | |
| 2. Производная независимой переменной. Чаще всего «икса». Всегда равна единице. Это тоже важно запомнить надолго | |
| 3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни. | |
| 4. Производная переменной в степени -1 | |
| 5. Производная квадратного корня | |
| 6. Производная синуса | |
| 7. Производная косинуса | |
| 8. Производная тангенса | |
| 9. Производная котангенса | |
| 10. Производная арксинуса | |
| 11. Производная арккосинуса | |
12. Производная арктангенса Производная арктангенса | |
| 13. Производная арккотангенса | |
| 14. Производная натурального логарифма | |
| 15. Производная логарифмической функции | |
| 16. Производная экспоненты | |
| 17. Производная показательной функции |
Правила дифференцирования
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной :
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u «v , в котором u — число,
например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё
слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка — механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие «Производная суммы дробей со степенями и корнями «.
Если же перед Вами задача вроде , то Вам на занятие «Производные простых тригонометрических функций».
Пошаговые примеры — как найти производную
Пример 3. Найти производную функции
Решение. Определяем части выражения функции: всё выражение представляет произведение,
а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель.
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль. Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как производную «икса». Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
А проверить решение задачи на производную можно на .
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного:
производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Применяем формулу дифференцирования частного:
производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями» .
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень
из независимой переменной, с производной которого мы ознакомились в таблице производных. По
правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
В данной функции видим произведение, один из сомножителей которых — квадратный корень
из независимой переменной, с производной которого мы ознакомились в таблице производных. По
правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Проверить решение задачи на производную можно на калькуляторе производных онлайн .
Пример 6. Найти производную функции
Решение. В данной функции видим частное, делимое которого — квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .
Дата: 20.11.2014
Таблица производных.
Производная — одно из главных понятий высшей математики. В этом уроке мы познакомимся с этим понятием. Именно познакомимся, без строгих математических формулировок и доказательств.
Это знакомство позволит:
Понимать суть несложных заданий с производной;
Успешно решать эти самые несложные задания;
Подготовиться к более серьёзным урокам по производной.
Сначала — приятный сюрприз.)
Строгое определение производной основано на теории пределов и штука достаточно сложная. Это огорчает. Но практическое применение производной, как правило, не требует таких обширных и глубоких знаний!
Для успешного выполнения большинства заданий в школе и ВУЗе достаточно знать всего несколько терминов — чтобы понять задание, и всего несколько правил — чтобы его решить. И всё. Это радует.
Приступим к знакомству?)
Термины и обозначения.
В элементарной математике много всяких математических операций. Сложение, вычитание умножение, возведение в степень, логарифмирование и т.д. Если к этим операциям добавить ещё одну, элементарная математика становится высшей. Эта новая операция называется дифференцирование. Определение и смысл этой операции будут рассмотрены в отдельных уроках.
Определение и смысл этой операции будут рассмотрены в отдельных уроках.
Здесь же важно понять, что дифференцирование — это просто математическая операция над функцией. Берём любую функцию и, по определённым правилам, преобразовываем её. В результате получится новая функция. Вот эта новая функция и называется: производная.
Дифференцирование — действие над функцией.
Производная — результат этого действия.
Так же, как, например, сумма — результат сложения. Или частное — результат деления.
Зная термины, можно, как минимум, понимать задания.) Формулировки бывают такие: найти производную функции; взять производную; продифференцировать функцию; вычислить производную и т.п. Это всё одно и то же. Разумеется, бывают и более сложные задания, где нахождение производной (дифференцирование) будет всего лишь одним из шагов решения задания.
Обозначается производная с помощью штришка вверху справа над функцией. Вот так: y» или f»(x) или S»(t) и так далее.
Вот так: y» или f»(x) или S»(t) и так далее.
Читается игрек штрих, эф штрих от икс, эс штрих от тэ, ну вы поняли…)
Штрих также может обозначать производную конкретной функции, например: (2х+3)» , (x 3 )» , (sinx)» и т.д. Часто производная обозначается с помощью дифференциалов, но такое обозначение в этом уроке мы рассматривать не будем.
Предположим, что понимать задания мы научились. Осталось всего ничего — научиться их решать.) Напомню ещё раз: нахождение производной — это преобразование функции по определённым правилам. Этих правил, на удивление, совсем немного.
Чтобы найти производную функции, надо знать всего три вещи. Три кита, на которых стоит всё дифференцирование. Вот они эти три кита:
1. Таблица производных (формулы дифференцирования).
3. Производная сложной функции.
Начнём по порядку. В этом уроке рассмотрим таблицу производных.
Таблица производных.

В мире — бесконечное множество функций. Среди этого множества есть функции, которые наиболее важны для практического применения. Эти функции сидят во всех законах природы. Из этих функций, как из кирпичиков, можно сконструировать все остальные. Этот класс функций называется элементарные функции. Именно эти функции и изучаются в школе — линейная, квадратичная, гипербола и т.п.
Дифференцирование функций «с нуля», т.е. исходя из определения производной и теории пределов — штука достаточно трудоёмкая. А математики — тоже люди, да-да!) Вот и упростили себе (и нам) жизнь. Они вычислили производные элементарных функций до нас. Получилась таблица производных, где всё уже готово.)
Вот она, эта табличка для самых популярных функций. Слева — элементарная функция, справа — её производная.
| Функция y | Производная функции y y» | |
| 1 | C (постоянная величина) | C» = 0 |
| 2 | x | x» = 1 |
| 3 | x n (n — любое число) | (x n)» = nx n-1 |
| x 2 (n = 2) | (x 2)» = 2x | |
| 4 | sin x | (sin x)» = cosx |
| cos x | (cos x)» = — sin x | |
| tg x | ||
| ctg x | ||
| 5 | arcsin x | |
| arccos x | ||
| arctg x | ||
| arcctg x | ||
| 4 | a x | |
| e x | ||
| 5 | log a x | |
| ln x (a = e ) |
Рекомендую обратить внимание на третью группу функций в этой таблице производных. Производная степенной функции — одна из самых употребительных формул, если только не самая употребительная! Намёк понятен?) Да, таблицу производных желательно знать наизусть. Кстати, это не так трудно, как может показаться. Попробуйте решать побольше примеров, таблица сама и запомнится!)
Производная степенной функции — одна из самых употребительных формул, если только не самая употребительная! Намёк понятен?) Да, таблицу производных желательно знать наизусть. Кстати, это не так трудно, как может показаться. Попробуйте решать побольше примеров, таблица сама и запомнится!)
Найти табличное значение производной, как вы понимаете, задание не самое трудное. Поэтому очень часто в подобных заданиях встречаются дополнительные фишки. Либо в формулировке задания, либо в исходной функции, которой в таблице — вроде и нету…
Рассмотрим несколько примеров:
1. Найти производную функции y = x 3
Такой функции в таблице нет. Но есть производная степенной функции в общем виде (третья группа). В нашем случае n=3. Вот и подставляем тройку вместо n и аккуратно записываем результат:
(x 3) » = 3·x 3-1 = 3x 2
Вот и все дела.
Ответ: y» = 3x 2
2. Найти значение производной функции y = sinx в точке х = 0.
Это задание означает, что надо сначала найти производную от синуса, а затем подставить значение х = 0 в эту самую производную. Именно в таком порядке! А то, бывает, сразу подставляют ноль в исходную функцию… Нас же просят найти не значение исходной функции, а значение её производной. Производная, напомню — это уже новая функция.
По табличке находим синус и соответствующую производную:
y» = (sin x)» = cosx
Подставляем ноль в производную:
y»(0) = cos 0 = 1
Это и будет ответ.
3. Продифференцировать функцию:
Что, внушает?) Такой функции в таблице производных и близко нет.
Напомню, что продифференцировать функцию — это просто найти производную этой функции. Если забыть элементарную тригонометрию, искать производную нашей функции достаточно хлопотно. Таблица не помогает…
Но если увидеть, что наша функция — это косинус двойного угла , то всё сразу налаживается!
Да-да! Запомните, что преобразование исходной функции до дифференцирования вполне допускается! И, случается, здорово облегчает жизнь. По формуле косинуса двойного угла:
По формуле косинуса двойного угла:
Т.е. наша хитрая функция есть не что иное, как y = cosx . А это — табличная функция. Сразу получаем:
Ответ: y» = — sin x .
Пример для продвинутых выпускников и студентов:
4. Найти производную функции:
Такой функции в таблице производных нет, разумеется. Но если вспомнить элементарную математику, действия со степенями… То вполне можно упростить эту функцию. Вот так:
А икс в степени одна десятая — это уже табличная функция! Третья группа, n=1/10. Прямо по формуле и записываем:
Вот и всё. Это будет ответ.
Надеюсь, что с первым китом дифференцирования — таблицей производных — всё ясно. Осталось разобраться с двумя оставшимися китами. В следующем уроке освоим правила дифференцирования.
Навигация по странице.
Производная постоянной.
При выводе самой первой формулы таблицы будем исходить из определения производной функции в точке. Возьмем , где x
– любое действительное число, то есть, x
– любое число из области определения функции . Запишем предел отношения приращения функции к приращению аргумента при :
Возьмем , где x
– любое действительное число, то есть, x
– любое число из области определения функции . Запишем предел отношения приращения функции к приращению аргумента при :
Следует заметить, что под знаком предела получается выражение , которое не является , так как в числителе находится не бесконечно малая величина, а именно ноль. Другими словами, приращение постоянной функции всегда равно нулю.
Таким образом, производная постоянной функции равна нулю на всей области определения .
Пример.
Найти производные следующих постоянных функций
Решение.
В первом случае мы имеем производную натурального числа 3 , во втором случае нам приходится брать производную от параметра а , который может быть любым действительным числом, в третьем — производную иррационального числа , в четвертом случае имеем производную нуля (ноль является целым числом), в пятом – производную рациональной дроби .
Ответ:
Производные всех этих функций равны нулю для любого действительного x (на всей области определения)
Производная степенной функции.

Формула производной степенной функции имеет вид , где показатель степени p – любое действительное число.
Докажем сначала формулу для натурального показателя степени, то есть, для p = 1, 2, 3, …
Будем пользоваться определением производной. Запишем предел отношения приращения степенной функции к приращению аргумента:
Для упрощения выражения в числителе обратимся к формуле :
Следовательно,
Этим доказана формула производной степенной функции для натурального показателя.
Следует рассмотреть два случая: при положительных x и отрицательных x .
Сначала будем полагать . В этом случае . Выполним логарифмирование равенства по основанию e
и применим свойство логарифма:
Пришли к неявно заданной функции. Находим ее производную:
Осталось провести доказательство для отрицательных x .
Когда показатель p
представляет собой четное число, то степенная функция определена и при , причем является четной (смотрите раздел ). То есть, . В этом случае и также можно использовать доказательство через логарифмическую производную.
То есть, . В этом случае и также можно использовать доказательство через логарифмическую производную.
Когда показатель p
представляет собой нечетное число, то степенная функция определена и при , причем является нечетной. То есть, . В этом случае и логарифмическую производную использовать нельзя. Для доказательства формулы в этом случае можно воспользоваться правилами дифференцирования и правилом нахождения производной сложной функции:
Последний переход возможен в силу того, что если p — нечетное число, то p-1 либо четное число, либо нуль (при p=1 ), поэтому, для отрицательных x справедливо равенство .
Таким образом, формула производной степенной функции доказана для любого действительного p .
Пример.
Найти производные функций .
Решение.
Первую и третью функцию приведем к табличному виду , используя свойства степени, и применим формулу производной степенной функции:
Производная показательной функции.
Вывод формулы производной приведем на основе определения:
Пришли к неопределенности. Для ее раскрытия введем новую переменную , причем при . Тогда . В последнем переходе мы использовали формулу перехода к новому основанию логарифма.
Для ее раскрытия введем новую переменную , причем при . Тогда . В последнем переходе мы использовали формулу перехода к новому основанию логарифма.
Выполним подстановку в исходный предел:
По определению производной для функции синуса имеем .
Воспользуемся формулой разности синусов:
Осталось обратиться к первому замечательному пределу:
Таким образом, производная функции sin x есть cos x .
Абсолютно аналогично доказывается формула производной косинуса.
При решении задач дифференцирования мы будем постоянно обращаться к таблице производных основных функций, иначе зачем мы ее составляли и доказывали каждую формулу. Рекомендуем запомнить все эти формулы, в дальнейшем это сэкономит Вам массу времени.
Copyright by cleverstudents
Все права защищены.
Охраняется законом об авторском праве. Ни одну часть сайта , включая внутренние материалы и внешнее оформление, нельзя воспроизводить в какой-либо форме или использовать без предварительного письменного разрешения правообладателя.
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Геометрический и физический смысл производной
Пусть есть функция f(x) , заданная в некотором интервале (a, b) . Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте .
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
Как найти производные за 3 шага
В этой статье
Что такое производная?
3 шага, чтобы найти деривативы
4 практических упражнения
Что такое производная?
Производные измеряют мгновенную скорость изменения функции. Когда мы говорим о скорости изменения, мы говорим о склонах.
Мгновенная скорость изменения функции в точке равна наклону функции в этой точке. Когда мы находим наклон кривой в одной точке, мы находим наклон касательной. Касательная к функции в точке — это линия, едва касающаяся функции в этой точке.
Когда мы находим наклон кривой в одной точке, мы находим наклон касательной. Касательная к функции в точке — это линия, едва касающаяся функции в этой точке.
Таким образом, производная функции в одной точке равна наклону касательной в этой точке.
Чтобы визуализировать касательную, давайте рассмотрим пример, в котором уравнение для касательной уже рассчитано. Рассмотрим функцию f(x)=ln(x)f(x) = \ln{(x)}f(x)=ln(x), обозначенную синей линией.
Предположим, мы хотим найти производную от f(x)f(x)f(x) в точке (1,0)(1,0)(1,0). Касательная линия к кривой f(x)f(x)f(x) в точке (1,0)(1, 0)(1,0) представлена красной линией, f(x)=x−1f( х) = х — 1f(x)=x−1. Обратите внимание, как эта линия касается f(x)=ln(x)f(x) = \ln{(x)}f(x)=ln(x) только в одной точке, (1,0)(1, 0 )(1,0).
Касательная линия f(x)=x−1f(x) = x — 1f(x)=x−1 задается в форме пересечения наклона f(x)=mx+bf(x) = mx +bf(x )=mx+b, где mmm — наклон. Итак, мы можем легко увидеть, что наклон функции f(x)=x−1f(x) = x — 1f(x)=x−1 равен 1,
. Это означает, что мгновенная скорость изменения или производная функции f(x)=ln(x)f(x) = \ln{(x)}f(x)=ln(x) в точке ( 0,1)(0, 1)(0,1) равно 1.
Это означает, что мгновенная скорость изменения или производная функции f(x)=ln(x)f(x) = \ln{(x)}f(x)=ln(x) в точке ( 0,1)(0, 1)(0,1) равно 1.
Мгновенная скорость изменения fff при aaa или производная от fffat aaa представлена обозначением f’(a)f’(a)f’(a). Мы читаем вслух символ f’(a)f’(a)f’(a) либо как «производная от fff, оцененная в aaa», либо как «fff простое число в aaa».
Общая производная функция y=f(x)y = f(x)y=f(x) обычно представлена либо f'(x)f'(x)f'(x), либо dydx\frac{dy} {дх}дхди. (При необходимости вы можете прочитать больше о значении dy/dx.) Эта функция сообщает нам мгновенную скорость изменения fff по отношению к xxx в любой точке кривой.
Ниже вы можете посмотреть, как доктор Ханна Фрай объясняет, что такое производная.
3 шага для поиска производных
Далее мы узнаем, как именно найти производную функции. До сих пор мы узнали, что наклон в точке кривой называется наклоном касательной или мгновенной скоростью изменения.
До сих пор мы узнали, что наклон в точке кривой называется наклоном касательной или мгновенной скоростью изменения.
Напротив, наклон между двумя отдельными точками на кривой называется наклоном секущей. Это значение наклона также называется средней скоростью изменения. Средняя скорость изменения поможет нам вычислить производную функции.
Чтобы найти среднюю скорость изменения, мы делим изменение выходных значений (значения y) на изменение входных значений (значения x). Дельта-символ Δx\Delta{x}Δx представляет «изменение xxx», то есть значение, на которое изменяется xxx. Средняя скорость изменения функции fff на интервале [a,b][a, b][a,b] равна:
Средняя скорость изменения = ΔyΔx = y2−y1x2−x1 = f(b)−f(a)b−a\text{Средняя скорость изменения} = \frac{\Delta{y}}{ \Delta{x}} = \frac{y_2 — y_1}{x_2 — x_1} = \frac{f(b)-f(a)}{b-a}Средняя скорость изменения=ΔxΔy=x2−x1y2 −y1=b−af(b)−f(a) |
Приблизив Δx\Delta{x}Δx к 0, мы можем найти мгновенную скорость изменения. Взгляните на предельное определение производной ниже.
Взгляните на предельное определение производной ниже.
Производная fff в точке xxx равна пределу средней скорости изменения fff на интервале [x,x+∆x][x, x+\Delta{x}][x,x+∆x] при ∆x\ Delta{x}Δx приближается к 0. Этот предел определяется формулой:
f'(x)=limΔx→0ΔyΔx=limΔx→0f(x+Δx)−f(x)Δx=Lf'(x) = \mathop {\lim }\limits_{\Delta{x } \to 0}\frac{\Delta{y}}{\Delta{x}}=\mathop{\lim }\limits_{\Delta{x} \to 0} \frac{{f\left( {x + \Delta{x} } \right) — f\left( x\right)}}{\Delta{x} }=Lf'(x)=Δx→0limΔxΔy=Δx→0limΔxf(x+ Δx)−f(x)=L
Если этот предел существует, то f(x)f(x)f(x) дифференцируема, а производная функции fff в точке xxx равна LLL. Краткий обзор лимитов см. в статье Что такое лимиты? и Как найти пределы.
92f(x)=2×2 в предельное определение производной. Поначалу правильная замена первого члена числителя определения предела может быть сложной задачей. Суть в том, чтобы просто заменить xxx на (x+Δx)(x + \Delta{x})(x+Δx) везде, где xxx встречается в функции. 2}{\Delta{x}}=Δx→0limΔx2(x+Δx)2−2×2 92}{\Delta{x}}=Δx→0limΔx4xΔx+2Δx2
2}{\Delta{x}}=Δx→0limΔx2(x+Δx)2−2×2 92}{\Delta{x}}=Δx→0limΔx4xΔx+2Δx2=limΔx→04x+2Δx= \mathop {\lim }\limits_{\Delta{x} \to 0}4x + 2 \Delta{x}=Δx→0lim4x+2Δx
Шаг 3
Наконец, мы можем оценить предел, когда Δx\Delta{x}Δx приближается к 0. Поскольку у нас осталась полиномиальная функция, а полиномы всегда непрерывной, мы можем просто подставить Δx=0\Delta{x} = 0Δx=0 в функцию, с которой мы остались.
f'(x)=limΔx→04x+2Δxf'(x)= \mathop {\lim }\limits_{\Delta{x} \to 0}4x + 2\Delta{x}f'(x )=Δx→0lim4x+2Δx 92f(x)=2×2 равно 4x4x4x. Если вы хотите найти производную в одной точке, вы можете просто подставить x=ax = ax=a в f’(x)=4xf’(x) = 4xf’(x)=4x. Например:
f’(1)=4(1)=4f’(1) = 4(1) = 4f’(1)=4(1)=4. Это значение представляет собой наклон касательной при x=1x = 1x=1.
f’(2)=4(2)=8f’(2) = 4(2) = 8f’(2)=4(2)=8. Это значение представляет собой наклон касательной при x=2x = 2x=2.
f’(100)=4(100)=400f’(100) = 4(100) = 400f’(100)=4(100)=400.
 Это значение представляет собой наклон касательной при x=100x = 100x=100.
Это значение представляет собой наклон касательной при x=100x = 100x=100.
Стандартные правила для производных
Теперь, когда вы знакомы с предельным определением производной, вы можете начать запоминать приведенные ниже стандартные правила для производной. Эти производные правила выводятся из предельного определения производной. Они позволяют нам оценивать производные намного быстрее.
Вот некоторые из наиболее распространенных производных правил, которые необходимо знать:
Постоянное правило
ddxc=0\frac{d}{dx}c = 0dxdc=0
9{n-1}dxd(xn)=nxn−1Частный случай степенного правила (где n=1): ddx(x)=1\frac d{dx}(x)=1dxd(x) =1
Постоянное множественное правило
ddx(c⋅f(x))=c⋅f′(x)\frac d{dx}(c\cdot f(x))=c\cdot f'(x) dxd(c⋅f(x))=c⋅f′(x)
Цепное правило
ddxf(g(x))=f'(g(x))g'(x)\frac{d} {dx}f(g(x)) = f'(g(x))g'(x)dxdf(g(x))=f'(g(x))g'(x)
Продукт Правило
ddx[f(x)⋅g(x)]=f'(x)⋅g(x)+f(x)⋅g'(x)\frac{d}{dx}[f(x) \cdot g(x)] = f'(x) \cdot g(x) + f(x)\cdot g'(x)dxd[f(x)⋅g(x)]=f'(x) ⋅г(х)+f(х)⋅г'(х) 9xdxd(ex)=ex
Д-р Тим Шартье объясняет больше о производных правилах произведения и частного.
4 практических упражнения
Упражнение 1
Пусть f(x)=7x−1f(x) = 7x — 1f(x)=7x−1. Используя предельное определение производной, найдите f’(x)f’(x)f’(x).
Решение
Подстановка вашей функции в определение предела может оказаться самым трудным шагом для функций с несколькими терминами. Не забудьте перепроверить свой ответ, использовать круглые скобки там, где это необходимо, и правильно распределять отрицательные знаки.
f'(x)=limΔx→0f(x+Δx)−f(x)Δxf'(x)= \mathop {\lim}\limits_{\Delta{x} \to 0} \frac{ {f\left( {x + \Delta{x}} \right) — f\left( x \right)}}{\Delta{x}}f'(x)=Δx→0limΔxf(x+Δx )−f(x)
=limΔx→07(x+Δx)−1−(7x−1)Δx= \mathop {\lim }\limits_{\Delta{x} \to 0} \frac {7(x + \Delta{x}) — 1 — (7x — 1)}{\Delta{x}}=Δx→0limΔx7(x+Δx)−1−(7x−1)
= limΔx→07x+7Δx−1−7x+1Δx= \mathop {\lim }\limits_{\Delta{x} \to 0} \frac{7x + 7\Delta{x} — 1 — 7x + 1} {\Delta{x}}=Δx→0limΔx7x+7Δx−1−7x+1
=limΔx→07ΔxΔx= \mathop {\lim }\limits_{\Delta{x} \to 0} \frac{7\Delta{x}}{\Delta{x}}=Δx→0limΔx7Δx
=limΔx→07= \mathop {\lim }\limits_{\Delta{x} \to 0} 7=Δx→0lim7
=7=7=7
Итак, f'(x )=7f'(х) = 7f'(х)=7.
Упражнение 2
Пусть f(x)=1xf(x) = \frac{1}{x}f(x)=x1. Используя предельное определение производной, найдите f’(x)f’(x)f’(x).
Раствор
После подстановки нашей функции в определение предела нам нужно объединить две дроби в числителе, найдя общий знаменатель, а затем умножив его соответствующим образом.
f'(x)=limΔx→0f(x+Δx)−f(x)Δxf'(x)= \mathop {\lim}\limits_{\Delta{x} \to 0} \frac{ {f\left( {x + \Delta{x}} \right) — f\left( x \right)}}{\Delta{x}}f'(x)=Δx→0limΔxf(x+Δx )−f(x)
=limΔx→01x+Δx−1xΔx= \mathop {\lim }\limits_{\Delta{x} \to 0} \frac{\frac{1}{x + \ Delta{x}} — \frac{1}{x}}{\Delta{x}}=Δx→0limΔxx+Δx1−x1
=limΔx→0xx(x+Δx)−( x + Δx) x (x + Δx) Δx = \ mathop {\ lim } \ limits _ {\ Delta {x} \ to 0} \ frac {\ frac {x} {x (x + \ Delta {x})} — \frac{(x+ \Delta{x})}{x(x+ \Delta{x})}}{\Delta{x}}=Δx→0limΔxx(x+Δx)x−x(x+ Δx)(x+Δx)
= limΔx→0x−x−Δxx(x+Δx)Δx= \mathop {\lim }\limits_{\Delta{x} \to 0} \frac{\frac{x-x-\Delta{x} }{x(x+\Delta{x})}}{\Delta{x}}=Δx→0limΔxx(x+Δx)x−x−Δx
=limΔx→0−Δxx(x +Δx)⋅1Δx= \mathop {\lim }\limits_{\Delta{x} \to 0} \frac{-\Delta{x}}{x(x+ \Delta{x})} \cdot \frac{ 1}{\Delta{x}}=Δx→0limx(x+Δx)−Δx⋅Δx1
=limΔx→0−1x(x+Δx)= \mathop {\lim }\limits_ {\Delta{x} \to 0} \frac{-1}{x(x+\Delta{x})}=Δx→0limx(x+Δx)−1
=−1x(x+0 )= \frac{-1}{x(x+0)}=x(x+0)−1
9{cos{(x)}}f(x)=3×2+ecos(x). Используя правила производных, найдите f’(x)f’(x)f’(x).
Используя правила производных, найдите f’(x)f’(x)f’(x).Раствор
Для этой задачи нам нужно использовать правило суммы. Правило суммы гласит, что производная суммы функций равна сумме их производных. Чтобы найти производную каждой отдельной функции, мы можем использовать правило степени и правило постоянного множителя для первого члена, а также цепное правило, правила тригонометрии и экспоненциальное правило для второго члена. 9{\cos{(x)}}f'(x)=6x−sin(x)ecos(x).
Упражнение 4
Пусть f(x)=2xsin(5x)f(x) = 2x\sin{(5x)}f(x)=2xsin(5x). Используя правила производных, найдите f’(x)f’(x)f’(x).
Раствор
Для этой задачи нам нужно использовать правило продукта. Правило произведения гласит, что производная произведения функций равна сумме первой функции, умноженной на производную от второй, и второй функции, умноженной на производную от первой.
Первая функция в нашем продукте — 2x2x2x. Чтобы найти производную от этого, мы используем частный случай правила произведения с n = 1n = 1n = 1, а также правило постоянного множителя с c = 2c = 2c = 2. Применяя эти правила, мы находим, что производная 2x2x2x равна
Применяя эти правила, мы находим, что производная 2x2x2x равна
ddx(2x)=2⋅1=2\frac d{dx}\left(2x\right)=2\cdot1=2dxd(2x)=2⋅1=2
Для второй функции в нашем произведении , у нас есть композиция функций с sin(5x)\sin{(5x)}sin(5x). Цепное правило гласит, что производная композиции функций находится, если сначала взять производную «внешней» функции и оставить «внутреннюю» неизменной, а затем умножить на производную «внутренней» функции.
Таким образом, чтобы найти производную sin(5x)\sin{(5x)}sin(5x), мы можем просто использовать правила тригонометрии для sin, а затем умножить на 555, что является производной внутренней функции 5x5x5x. Производная внутренней функции находится с использованием специального случая степенного правила для n=1n=1n=1 и постоянного кратного правила.
Подставив найденные производные в Правило продукта, мы получим:
f'(x)=2x⋅cos(5x)⋅5+sin(5x)⋅2f'(x) = 2x \cdot \cos{(5x)} \cdot 5 + \sin{(5x) } \cdot 2f'(x)=2x⋅cos(5x)⋅5+sin(5x)⋅2
f'(x)=10xcos(5x)+2sin(5x)f'(x) = 10x\cos{(5x)} + 2\sin{(5x)}f'(x)=10xcos( 5x)+2sin(5x)
Итак, f'(x)=10xcos(5x)+2sin(5x)f'(x) = 10x\cos{(5x)} + 2\sin{(5x) }f'(x)=10xcos(5x)+2sin(5x).
Outlier (от соучредителя MasterClass) собрал лучших в мире преподавателей, дизайнеров игр и кинематографистов для создания будущего онлайн-колледжа.
Ознакомьтесь с этими связанными курсами:
Исчисление I
Исследуйте курс
Исчисление I
Математика изменений.
Изучить курс
Предварительное исчисление
Изучить курс
Предварительное исчисление
Освоить строительные блоки исчисления.
Исследуйте курс
калькулятор производных — Google
AlleBilderVideosBücherMapsNewsShopping
suchoptionen
Калькулятор производных • С шагами!
www.derivative-calculator.net
Решайте производные с помощью этого бесплатного онлайн-калькулятора. Пошаговое решение и графики прилагаются!
Переменная дифференцирования: ax_____abcdfghjklmnopqrstuvwxyz
Сколько раз дифференцировать?: 1 2 3 4 5
Калькулятор производных — Symbolab со всеми шагами. Введите любую производную функции, чтобы получить решение, шаги и график.
Введите любую производную функции, чтобы получить решение, шаги и график.
Первая производная · Калькулятор первообразной производной · Калькулятор производной в точке
Калькулятор производной — Wolfram|Alpha
www.wolframalpha.com производные порядка и более высокого порядка, предоставляя информацию, необходимую для понимания производных …
Калькулятор производных — Mathway
www.mathway.com › Калькулятор › производный-калькулятор
Калькулятор производных поддерживает вычисление первой, второй…., четвертой производной, а также неявное дифференцирование и нахождение нулей/корней.
Пошаговый калькулятор производных | Калькулятор дифференциации
calculate-derivative.com
Калькулятор производных поможет вам оценить производные онлайн. Калькулятор дифференцирования с шагами показывает промежуточные шаги, графики, корни, домен и т. д.
Калькулятор производных — MathPapa
www. mathpapa.com › калькулятор производных
mathpapa.com › калькулятор производных
Калькулятор производных дает пошаговую помощь в поиске производных. Этот калькулятор находится в стадии бета-тестирования. Мы ценим ваши отзывы, чтобы помочь нам улучшить его.
Ähnliche Fragen
Как рассчитать производные?
Какой лучший калькулятор для деривативов?
Какая производная от 3х2?
Калькулятор деривативов — Börse Frankfurt
www.boerse-frankfurt.de › деривативы › деривативы-…
Калькулятор производных. С помощью калькулятора деривативов вы можете проанализировать, как будет вести себя цена вашего дериватива в будущем, если цена базового актива …
Пошаговый калькулятор производных — Open Omnia
openomnia.com › калькулятор производных
Рассчитать производная функции. Получите пошаговые решения. Попробуйте Open Omnia сегодня.
Калькулятор и решатель производных — SnapXam
www.snapxam.com › калькуляторы › вычисление производных.


 Это значение представляет собой наклон касательной при x=100x = 100x=100.
Это значение представляет собой наклон касательной при x=100x = 100x=100.