Возрастание и убывание функции — как найти?
Мы видим, что функция убывает при любом значении х ≠ 0. Это можно записать так: функция убывает при х∈ (– ∞ ;0) ∪ (0; + ∞). Подытожим эту информацию небольшой схемой.
Возрастание и убывание функции на интервале
Мы еще не закончили с возрастающими и убывающими функциями — эх, если бы все было так просто! Дело в том, что нас, математиков, интересуют вот какие вопросы:
Как найти промежутки возрастания и убывания функции по графику?
Что делать, если просят определить характер на числовом промежутке?
Как определить поведение функции без построения?
Давайте разбираться! Сначала узнаем, как определить характер функции на промежутке:
Подставим значение х из промежутка в функцию.
Проанализируем полученные значения у.
Если при увеличении х увеличивается и у — это промежуток возрастания функции.
Если у уменьшается при увеличении х — это промежуток убывания функции.

Достаточно просто, правда? 🙂
Пример
Возьмем функцию y = 4x – 6 и определим ее характер на промежутке [0;2]. Подставим числа из промежутка вместо х в функцию:
Мы видим, что при возрастании х возрастает и значение у, т. е. на этом промежутке функция возрастает.
Точки экстремума, экстремумы функции
Не пугайтесь этих страшных слов! Сейчас разберем их подробнее — это проще, чем кажется.
Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве.
На графике выше y min — минимальное значение функции, точка минимума.
Точка минимума — это значение переменной х, при которой функция минимальна.
На том же графике y мах — максимальное значение функции, точка максимума.
Точка максимума — это значение переменной х, при которой функция максимальна.
Иначе точки минимума и максимума в математике принято называть точками экстремума, а значения функции, которые соответствуют точкам экстремума — экстремумами функции.
В точках экстремума функция меняет свой характер. Обратите внимание на рисунок ниже: функция стремительно возрастала до точки максимума, но после нее начала также стремительно уменьшаться. И наоборот, после прохождения точки минимума функция снова начинает возрастать.
Здесь вам может стать интересно: наибольшее/наименьшее значение функции на промежутке — это то же самое или нет. Отвечаем: к сожалению, нет. Эти значения иногда могут совпадать, но часто определяются разными точками.
У нас есть две новости: хорошая и не очень. Начнем с первой: если использовать достаточные условия возрастания/убывания, можно определить промежутки монотонности функции. И для этого даже не придется строить график! Но здесь нам пригодится производная.
Производная функции
Иначе говоря, производная функции показывает, как быстро увеличивается функция при бесконечно малом увеличении х.
К сожалению, в рамках этой статьи мы не будем долго останавливаться на производных. Как это сделать с помощью таблицы и правил дифференцирования, мы уже разбирали в статье «Таблица производных функций». Советуем почитать!
Достаточные признаки возрастания и убывания функции на интервале:
если производная функции y = f(x) положительна для любого x из интервала, то функция возрастает на этом интервале;
если производная функции y = f(x) отрицательна для любого x из интервала, то функция убывает на этом интервале.
Составим алгоритм действий, который поможет найти интервалы возрастания и убывания функции:
Найдем область определения функции.
Найдем производную функции.
Решим неравенства ƒ`(x) > 0 и ƒ`(x) < 0 на области определения.
К полученным промежуткам добавим граничные точки, в которых функция определена и непрерывна.

Проверим достаточные признаки возрастания и убывания функции, подставив значения из промежутков.
Задача 3
Укажите промежутки возрастания и убывания функции у = х2 + 5х + 6
Решение
Область определения функции: х ∈ R
Найдем производную функции: y’ = 2х + 5
Решим неравенство: 2х + 5 > 0
2х+5 >0 2x>-5 x> –2,5 Исследуем знаки производной с помощью числовой прямой.
Ответ: Функция убывает при х∈ (– ∞; –2,5], возрастает при х∈ [–2,5; +∞)
Задача 4
Определите интервалы возрастания и убывания функции у = х3 – 18х.
Решение
Область определения функции: х ∈ R.
Найдем производную функции: y’ = 3x2 + (–18).
Решим неравенство:
3x2 + (–18) > 0 3 (x2–9) > 0 3(x – 3)(x + 3) > 0 Исследуем знаки производной с помощью числовой прямой.
 Чтобы определить знак на каждом промежутке, подставим произвольное значение из этого промежутка в выражение для производной.
Чтобы определить знак на каждом промежутке, подставим произвольное значение из этого промежутка в выражение для производной.
Ответ: Функция убывает при х∈ [–3;3], возрастает при х∈ (–∞;—3] ∪ [3; +∞).
Первое достаточное условие экстремума
Пусть для функции у = f(x) определены следующие условия:
Функция непрерывна в окрестности точки x0 (нет разрыва).
ƒ′(x0) = 0 или ƒ′(x0) не существует;
Производная ƒ′(x) при переходе через точку x0 меняет свой знак.
Тогда в точке x = x0 функция y = f(x) имеет экстремум, причем это минимум, если при переходе через точку x0 производная меняет свой знак с минуса на плюс; максимум, если при переходе через точку x0 производная меняет свой знак с плюса на минус.
Если производная в точке x0 не меняет свой знак, то в этой точке нет экстремума.
Итак, точки 1 и 4 — точки максимума, точка 3 — точка минимума. В точке 2 экстремума нет.
В точке 2 экстремума нет.
Алгоритм для нахождения точек экстремума
Теперь разберемся, как найти точки экстремума функции. Для этого пройдем по этим шагам:
Найдем область определения функции.
Найдем производную функции на этой области.
Определим нули и точки, где функция не существует.
Определим знак производной на интервалах.
Выберем точки, где функция меняет знак.
Найдем точки минимума/максимума и экстремумы функции.
Задача 5
Найдите экстремумы функции у = –x2 + 8x – 7.
Решение
Область определения функции: х ∈ R.
Производная функции: y’ = –2x + 8
Решим неравенство:
–2x + 8 > 0 –2x > –8 x < 4 Определим знак производной на числовой прямой. Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.

В точке х = 4 функция меняет свой знак с «+» на «–», значит, точка х = 4 — это точка максимума.
Ответ: у(4) = 9 — экстремум функции.
Задача 6
Найдите экстремумы функции у = ⅓ x3 + 2x2 – 12x + 6.
Решение
Область определения функции: х ∈ R.
Производная функции: y’ = x2 + 4x – 12.
Решим неравенство:
x2 + 4x – 12 > 0 (x – 2)(x + 6) > 0 Определим знак производной на числовой прямой. Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.
Так на интервале (–∞; –6) и (2; +∞) производная положительна — на них функция возрастает. На интервале (–6;2) производная отрицательна — функция убывает.
Ответ: x = 2 — точка минимума, у(2) = –7 ⅓ — экстремум функции; х = –6 — точка максимума, у(–6) = 78 — экстремум функции.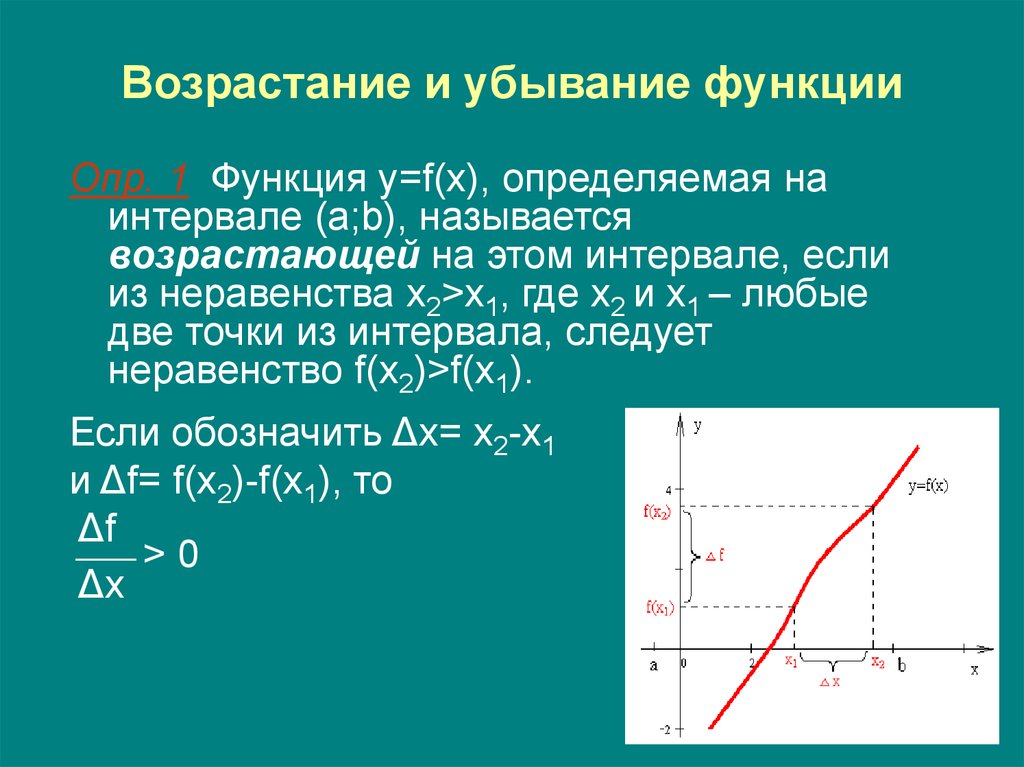
Как можно запомнить переход знаков для точек максимум или минимум:
Когда функция возрастает, а потом убывает, мы будто поднимались на вершину горы — значит, посетили точку максимума.
Когда функция убывает, а потом возрастает, мы будто спускались в овраг и выбрались из него — а значит, были в точке минимума.
Второе достаточное условие экстремума
x0 — это точка экстремума функции f(x), если вторая производная функции в этой точке не равна нулю (f »(x) ≠ 0). Причем, если вторая производная больше нуля (f »(x) > 0), то точкой минимума, а если вторая производная меньше нуля (f »(x) < 0), то точкой максимума.
Рассмотрим это условие экстремума на примере из задачи 6 — функции у = ⅓ x3 + 2x2 – 12x + 6:
Ее первая производная равна y’= x2 + 4x – 12.
Определим нули производной — значение х, при котором производная обращается в ноль: x2 + 4x – 12 = 0 при х = 2 и х = –6.

Возьмем вторую производную функции y’’= 2х + 4.
Подставим значения х = 2 и х = –6 во вторую производную и определим, являются ли эти точки максимумом или минимумом:
y’’(2) = 8, y’’ > 0, значит, х = 2 является точкой минимума, y’’(–6) = –8, y’’ < 0, значит, х = –6 является точкой максимум.
В этом условии есть два важных замечания:
Если в точке x0 и первая, и вторая производные обращаются в ноль, то в этом случае нужно воспользоваться первым достаточным признаком экстремума функции, по второму признаку нельзя судить о наличии или отсутствии экстремумов.
Второй достаточный признак нельзя применять, когда в стационарной точке (нуле производной) первая производная не существует. Ведь тогда не существует и вторая производная.
Третье достаточное условие экстремума
Это условие не используется в школьной программе, так как требует большого количества вычислений и логических размышлений. Мы все равно познакомим вас с ним — возможно, вам захочется изучить это усaловие самостоятельно и блеснуть знаниями перед учителем. Что ж, мы только за!
Мы все равно познакомим вас с ним — возможно, вам захочется изучить это усaловие самостоятельно и блеснуть знаниями перед учителем. Что ж, мы только за!
Пусть функция y=f(x) имеет производные до n-ого порядка в ε-окрестности точки x0 и производные до n+1-го порядка в самой точке x0. Пусть ƒ′(x0) = ƒn(x0) = ƒm(x0) = … = ƒ(n)(x0) = 0 и ƒ(n+1)(x0) ≠ 0.
Тогда,
если n – четное, то x0 — точка перегиба;
если n – нечетное, то x0 — точка экстремума, причем
если ƒ(n+1)(x0) > 0, то x0 — точка минимума;
если ƒ(n+1)(x0) < 0, то x0 — точка максимума.
Думаем, вы убедились, что тема «Возрастание и убывание функции» достаточно интересна. В то же время, она требует умения исследовать графики, находить первую и вторую производную функции, определять знаки по числовым прямым. Получить практический опыт решения таких заданий можно на курсах по профильной математике в школе Skysmart! Там мы сможем закрепить полученные знания, подготовиться к контрольным работам и даже к ОГЭ! Заинтригованы? Тогда мы ждем вас на занятиях!
Получить практический опыт решения таких заданий можно на курсах по профильной математике в школе Skysmart! Там мы сможем закрепить полученные знания, подготовиться к контрольным работам и даже к ОГЭ! Заинтригованы? Тогда мы ждем вас на занятиях!
Возрастание и убывание функции на интервале, экстремумы
Чтобы определить характер функции и говорить о ее поведении, необходимо находить промежутки возрастания и убывания. Этот процесс получил название исследования функции и построения графика. Точка экстремума используется при нахождении наибольшего и наименьшего значения функции, так как в них происходит возрастание или убывание функции из интервала.
Данная статья раскрывает определения, формулируем достаточный признак возрастания и убывания на интервале и условие существования экстремума. Это применимо к решению примеров и задач. Следует повторить раздел дифференцирования функций, потому как при решении необходимо будет использовать нахождение производной.
Возрастание и убывание функции на интервале
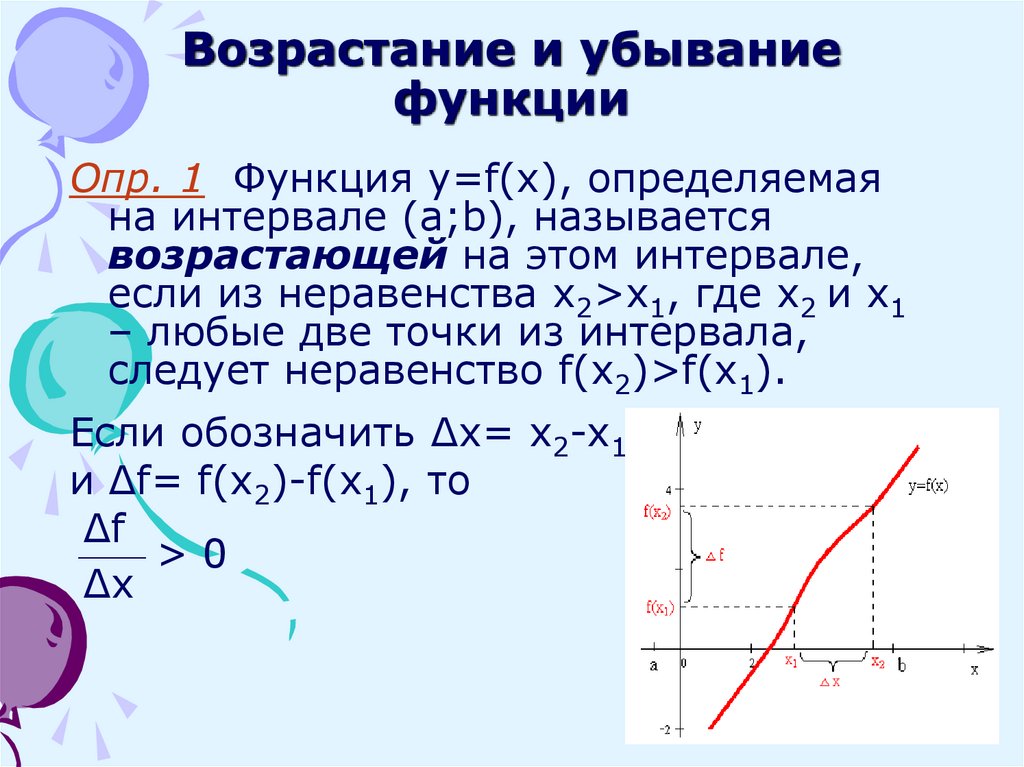
Определение 1Функция y=f(x) будет возрастать на интервале x, когда при любых x1∈X и x2∈X , x2>x1неравенство f(x2)>f(x1) будет выполнимо. Иначе говоря, большему значению аргумента соответствует большее значение функции.
Иначе говоря, большему значению аргумента соответствует большее значение функции.
Функция y=f(x) считается убывающей на интервале x, когда при любых x1∈X, x2∈X, x2>x1 равенство f(x2)>f(x1) считается выполнимым. Иначе говоря, большему значению функции соответствует меньшее значение аргумента. Рассмотрим рисунок, приведенный ниже.
Замечание: Когда функция определенная и непрерывная в концах интервала возрастания и убывания, то есть (a;b), где х=а, х=b, точки включены в промежуток возрастания и убывания. Определению это не противоречит, значит, имеет место быть на промежутке x.
Основные свойства элементарных функций типа y=sinx – определенность и непрерывность при действительных значениях аргументах. Отсюда получаем, что возрастание синуса происходит на интервале -π2; π2, тогда возрастание на отрезке имеет вид -π2; π2.
Точки экстремума, экстремумы функции
Определение 3Точка х0 называется точкой максимума для функции y=f(x), когда для всех значений x неравенство f(x0)≥f(x) является справедливым. Максимум функции – это значение функции в точке, причем обозначается ymax.
Максимум функции – это значение функции в точке, причем обозначается ymax.
Точка х0 называется точкой минимума для функции y=f(x), когда для всех значений x неравенство f(x0)≤f(x) является справедливым. Минимум функции – это значение функции в точке, причем имеет обозначение вида ymin.
Окрестностями точки х0 считаются точки экстремума, а значение функции, которое соответствует точкам экстремума. Рассмотрим рисунок, приведенный ниже.
Экстремумы функции с набольшим и с наименьшим значением функции. Рассмотрим рисунок, приведенный ниже.
Первый рисунок говорит о том, что необходимо найти наибольшее значение функции из отрезка [a;b]. Оно находится при помощи точек максимума и равняется максимальному значению функции, а второй рисунок больше походит на поиск точки максимума при х=b.
Достаточные условия возрастания и убывания функции
Чтобы найти максимумы и минимумы функции, необходимо применять признаки экстремума в том случае, когда функция удовлетворяет этим условиям. Самым часто используемым считается первый признак.
Самым часто используемым считается первый признак.
Первое достаточное условие экстремума
Определение 4Пусть задана функция y=f(x), которая дифференцируема в ε окрестности точки x0, причем имеет непрерывность в заданной точке x0. Отсюда получаем, что
- когда f'(x)>0 с x∈(x0-ε; x0) и f'(x)<0 при x∈(x0; x0+ε), тогда x0 является точкой максимума;
- когда f'(x)<0 с x∈(x0-ε; x0) и f'(x)>0 при x∈(x0; x0+ε), тогда x0 является точкой минимума.
Иначе говоря, получим их условия постановки знака:
- когда функция непрерывна в точке x0, тогда имеет производную с меняющимся знаком, то есть с + на -, значит, точка называется максимумом;
- когда функция непрерывна в точке x0, тогда имеет производную с меняющимся знаком с — на +, значит, точка называется минимумом.
Алгоритм для нахождения точек экстремума
Чтобы верно определить точки максимума и минимума функции, необходимо следовать алгоритму их нахождения:
- найти область определения;
- найти производную функции на этой области;
- определить нули и точки, где функция не существует;
- определение знака производной на интервалах;
- выбрать точки, где функция меняет знак.

Рассмотрим алгоритм на примере решения нескольких примеров на нахождение экстремумов функции.
Пример 1Найти точки максимума и минимума заданной функции y=2(x+1)2x-2.
Решение
Область определения данной функции – это все действительные числа кроме х=2. Для начала найдем производную функции и получим:
y’=2x+12x-2’=2·x+12’·(x-2)-(x+1)2·(x-2)'(x-2)2==2·2·(x+1)·(x+1)’·(x-2)-(x+1)2·1(x-2)2=2·2·(x+1)·(x-2)-(x+2)2(x-2)2==2·(x+1)·(x-5)(x-2)2
Отсюда видим, что нули функции – это х=-1, х=5, х=2, то есть каждую скобку необходимо приравнять к нулю. Отметим на числовой оси и получим:
Теперь определим знаки производной из каждого интервала. Необходимо выбрать точку, входящую в интервал, подставить в выражение. Например, точки х=-2, х=0, х=3, х=6.
Получаем, что
y'(-2)=2·(x+1)·(x-5)(x-2)2x=-2=2·(-2+1)·(-2-5)(-2-2)2=2·716=78>0, значит, интервал -∞; -1 имеет положительную производную. Аналогичным образом получаем, что
y'(0)=2·(0+1)·0-50-22=2·-54=-52<0y'(3)=2·(3+1)·(3-5)(3-2)2=2·-81=-16<0y'(6)=2·(6+1)·(6-5)(6-2)2=2·716=78>0
Так как второй интервал получился меньше нуля, значит, производная на отрезке будет отрицательной. Третий с минусом, четвертый с плюсом. Для определения непрерывности необходимо обратить внимание на знак производной, если он меняется, тогда это точка экстремума.
Третий с минусом, четвертый с плюсом. Для определения непрерывности необходимо обратить внимание на знак производной, если он меняется, тогда это точка экстремума.
Получим, что в точке х=-1 функция будет непрерывна, значит, производная изменит знак с + на -. По первому признаку имеем, что х=-1 является точкой максимума, значит получаем
ymax=y(-1)=2·(x+1)2x-2x=-1=2·(-1+1)2-1-2=0
Точка х=5 указывает на то, что функция является непрерывной, а производная поменяет знак с – на +. Значит, х=-1 является точкой минимума, причем ее нахождение имеет вид
ymin=y(5)=2·(x+1)2x-2x=5=2·(5+1)25-2=24
Графическое изображение
Ответ: ymax=y(-1)=0, ymin=y(5)=24.
Стоит обратить внимание на то, что использование первого достаточного признака экстремума не требует дифференцируемости функции с точке x0, этим и упрощает вычисление.
Пример 2Найти точки максимума и минимума функции y=16×3=2×2+223x-8.
Решение.
Область определения функции – это все действительные числа. Это можно записать в виде системы уравнений вида:
Это можно записать в виде системы уравнений вида:
-16×3-2×2-223x-8, x<016×3-2×2+223x-8, x≥0
После чего необходимо найти производную:
y’=16×3-2×2-223x-8′, x<016×3-2×2+223x-8′, x>0y’=-12×2-4x-223, x<012×2-4x+223, x>0
Точка х=0 не имеет производной, потому как значения односторонних пределов разные. Получим, что:
lim y’x→0-0=lim yx→0-0-12×2-4x-223=-12·(0-0)2-4·(0-0)-223=-223lim y’x→0+0=lim yx→0-012×2-4x+223=12·(0+0)2-4·(0+0)+223=+223
Отсюда следует, что функция непрерывна в точке х=0, тогда вычисляем
lim yx→0-0=limx→0-0-16×3-2×2-223x-8==-16·(0-0)3-2·(0-0)2-223·(0-0)-8=-8lim yx→0+0=limx→0-016×3-2×2+223x-8==16·(0+0)3-2·(0+0)2+223·(0+0)-8=-8y(0)=16×3-2×2+223x-8x=0=16·03-2·02+223·0-8=-8
Необходимо произвести вычисления для нахождения значения аргумента, когда производная становится равной нулю:
-12×2-4x-223, x<0D=(-4)2-4·-12·-223=43×1=4+432·-12=-4-233<0x2=4-432·-12=-4+233<0
12×2-4x+223, x>0D=(-4)2-4·12·223=43×3=4+432·12=4+233>0x4=4-432·12=4-233>0
Все полученные точки нужно отметить на прямой для определения знака каждого интервала. Поэтому необходимо вычислить производную в произвольных точках у каждого интервала. Например, у нас можно взять точки со значениями x=-6, x=-4, x=-1, x=1, x=4, x=6. Получим, что
Поэтому необходимо вычислить производную в произвольных точках у каждого интервала. Например, у нас можно взять точки со значениями x=-6, x=-4, x=-1, x=1, x=4, x=6. Получим, что
y'(-6)=-12×2-4x-223x=-6=-12·-62-4·(-6)-223=-43<0y'(-4)=-12×2-4x-223x=-4=-12·(-4)2-4·(-4)-223=23>0y'(-1)=-12×2-4x-223x=-1=-12·(-1)2-4·(-1)-223=236<0y'(1)=12×2-4x+223x=1=12·12-4·1+223=236>0y'(4)=12×2-4x+223x=4=12·42-4·4+223=-23<0y'(6)=12×2-4x+223x=6=12·62-4·6+223=43>0
Изображение на прямой имеет вид
Значит, приходим к тому, что необходимо прибегнуть к первому признаку экстремума. Вычислим и получим, что
x=-4-233, x=0, x=4+233, тогда отсюда точки максимума имеют значениx=-4+233, x=4-233
Перейдем к вычислению минимумов:
ymin=y-4-233=16×3-22+223x-8x=-4-233=-8273ymin=y(0)=16×3-22+223x-8x=0=-8ymin=y4+233=16×3-22+223x-8x=4+233=-8273
Произведем вычисления максимумов функции. Получим, что
ymax=y-4+233=16×3-22+223x-8x=-4+233=8273ymax=y4-233=16×3-22+223x-8x=4-233=8273
Графическое изображение
Ответ:
ymin=y-4-233=-8273ymin=y(0)=-8ymin=y4+233=-8273ymax=y-4+233=8273ymax=y4-233=8273
Второй признак экстремума функции
Если задана функция f'(x0)=0, тогда при ее f»(x0)>0 получаем, что x0 является точкой минимума, если f»(x0)<0, то точкой максимума. Признак связан с нахождением производной в точке x0.
Признак связан с нахождением производной в точке x0.
Найти максимумы и минимумы функции y=8xx+1.
Решение
Для начала находим область определения. Получаем, что
D(y): x≥0x≠-1⇔x≥0
Необходимо продифференцировать функцию, после чего получим
y’=8xx+1’=8·x’·(x+1)-x·(x+1)'(x+1)2==8·12x·(x+1)-x·1(x+1)2=4·x+1-2x(x+1)2·x=4·-x+1(x+1)2·x
При х=1 производная становится равной нулю, значит, точка является возможным экстремумом. Для уточнения необходимо найти вторую производную и вычислить значение при х=1. Получаем:
y»=4·-x+1(x+1)2·x’==4·(-x+1)’·(x+1)2·x-(-x+1)·x+12·x'(x+1)4·x==4·(-1)·(x+1)2·x-(-x+1)·x+12’·x+(x+1)2·x'(x+1)4·x==4·-(x+1)2x-(-x+1)·2x+1(x+1)’x+(x+1)22x(x+1)4·x==-(x+1)2x-(-x+1)·x+1·2x+x+12x(x+1)4·x==2·3×2-6x-1x+13·x3⇒y»(1)=2·3·12-6·1-1(1+1)3·(1)3=2·-48=-1<0
Значит, использовав 2 достаточное условие экстремума, получаем, что х=1 является точкой максимума. Иначе запись имеет вид ymax=y(1)=811+1=4.
Графическое изображение
Ответ: ymax=y(1)=4. .
.
Третье достаточное условие экстремума
Определение 5Функция y=f(x) имеет ее производную до n-го порядка в ε окрестности заданной точки x0 и производную до n+1-го порядка в точке x0. Тогда f'(x0)=f»(x0)=f»'(x0)=…=fn(x0)=0.
Отсюда следует, что когда n является четным числом, то x0 считается точкой перегиба, когда n является нечетным числом, то x0 точка экстремума, причем f(n+1)(x0)>0, тогда x0 является точкой минимума, f(n+1)(x0)<0, тогда x0 является точкой максимума.
Пример 4Найти точки максимума и минимума функции yy=116(x+1)3(x-3)4.
Решение
Исходная функция – целая рациональная, отсюда следует, что область определения – все действительные числа. Необходимо продифференцировать функцию. Получим, что
y’=116x+13′(x-3)4+(x+1)3x-34’==116(3(x+1)2(x-3)4+(x+1)34(x-3)3)==116(x+1)2(x-3)3(3x-9+4x+4)=116(x+1)2(x-3)3(7x-5)
Данная производная обратится в ноль при x1=-1, x2=57, x3=3. То есть точки могут быть точками возможного экстремума. Необходимо применить третье достаточное условие экстремума. Нахождение второй производной позволяет в точности определить наличие максимума и минимума функции. Вычисление второй производной производится в точках ее возможного экстремума. Получаем, что
Необходимо применить третье достаточное условие экстремума. Нахождение второй производной позволяет в точности определить наличие максимума и минимума функции. Вычисление второй производной производится в точках ее возможного экстремума. Получаем, что
y»=116x+12(x-3)3(7x-5)’=18(x+1)(x-3)2(21×2-30x-3)y»(-1)=0y»57=-368642401<0y»(3)=0
Значит, что x2=57 является точкой максимума. Применив 3 достаточный признак, получаем, что при n=1 и f(n+1)57<0.
Необходимо определить характер точек x1=-1, x3=3. Для этого необходимо найти третью производную, вычислить значения в этих точках. Получаем, что
y»’=18(x+1)(x-3)2(21×2-30x-3)’==18(x-3)(105×3-225×2-45x+93)y»'(-1)=96≠0y»'(3)=0
Значит, x1=-1 является точкой перегиба функции, так как при n=2 и f(n+1)(-1)≠0. Необходимо исследовать точку x3=3. Для этого находим 4 производную и производим вычисления в этой точке:
y(4)=18(x-3)(105×3-225×2-45x+93)’==12(105×3-405×2+315x+57)y(4)(3)=96>0
Из выше решенного делаем вывод, что x3=3 является точкой минимума функции.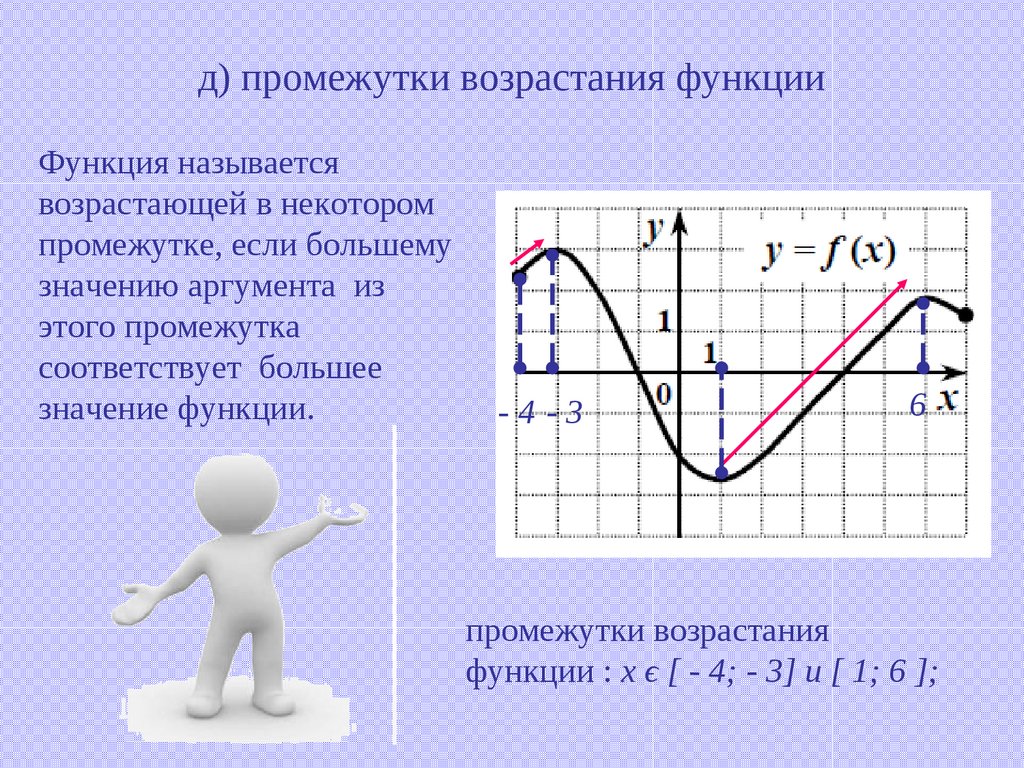
Графическое изображение
Ответ: x2=57 является точкой максимума, x3=3 — точкой минимума заданной функции.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.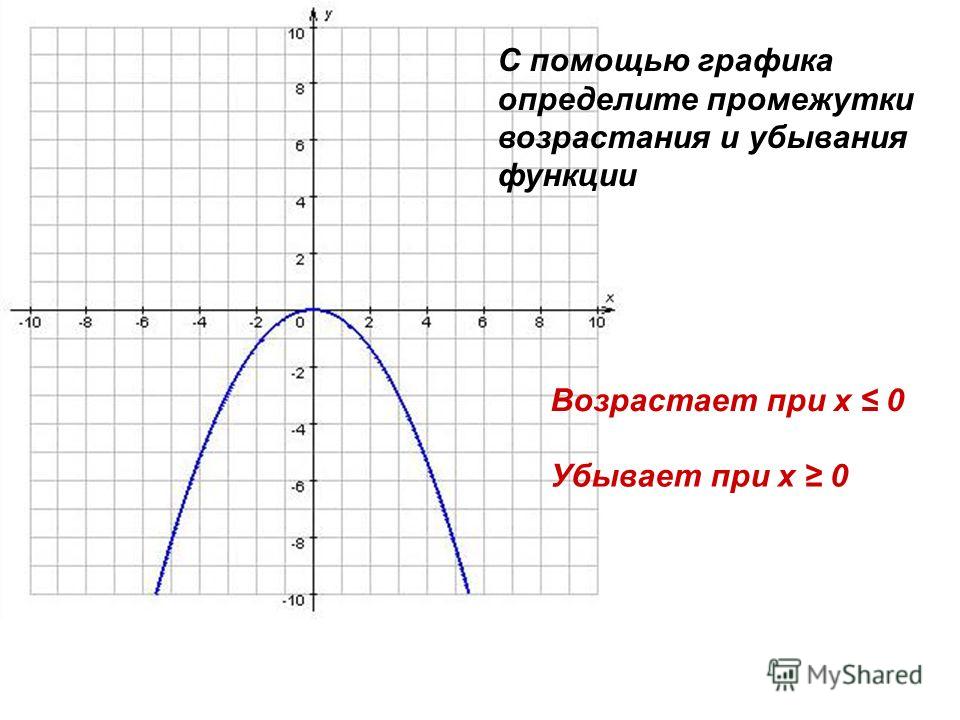
Возрастание, убывание и монотонность функции
- Понятие возрастания, убывания и монотонности функции
- Признаки постоянства, возрастания и убывания функции
Исследование функции на возрастание и убывание может быть как самостоятельной задачей, так и одним из этапов полного исследования функции и построения её графика.
Функции, у которых имеет место убывание или возрастание на некотором числовом промежутке, называются монотонными функциями.
Возрастание функции. Функция называется возрастающей на интервале ]a, b[, принадлежащем области определения функции, если бОльшим значениям независимой переменной из этого интервала соответствуют бОльшие значения функции, т.е. если
x2 > x1 → f(x2) > f(x1)
для всех x1 и x2, принадлежащих интервалу. Кстати, будет полезным
открыть в новом окне материал Свойства и графики элементарных функций.
Кстати, будет полезным
открыть в новом окне материал Свойства и графики элементарных функций.
Убывание функции. Функция называется убывающей на интервале ]a, b[, если бОльшим значениям независимой переменной из этого интервала соответствуют меньшие значения функции, т.е. если
x2 > x1 → f(x2) < f(x1) для всех x1 и x2, принадлежащих интервалу.
Теорема 1. Если во всех точках некоторого промежутка производная функции равна нулю (f ‘(x) = 0), то функция f(x) сохраняет в этом промежутке постоянное значение.
Этот промежуток может быть замкнутым или открытым, конечным или бесконечным.
Теорема 2 (достаточный признак возрастания). Если
во всех точках некоторого промежутка производная функции больше нуля (f ‘(x) > 0),
то функция f(x)
возрастает в этом промежутке.
Теорема 3 (достаточный признак убывания). Если во всех точках некоторого промежутка производная функции меньше нуля (f ‘(x) < 0), то функция f(x) убывает на этом промежутке.
Замечание. Условия теорем 2 и 3 не являются в полной мере необходимыми. Их можно несколько ослабить, а именно заменить нестрогими неравенствами и считать, что производная функции больше или равна нулю (f ‘(x) ≥ 0) или меньше или равна нулю (f ‘(x) ≤ 0), так как заключения теорем остаются справедливыми и тогда, когда производная обращается в нуль в конечном множестве точек.
Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.
Пример 1. Найти промежутки возрастания и убывания функции
Решение. Находим производную функции:
(Для разложения квадратного двухчлена на множители решали квадратное уравнение).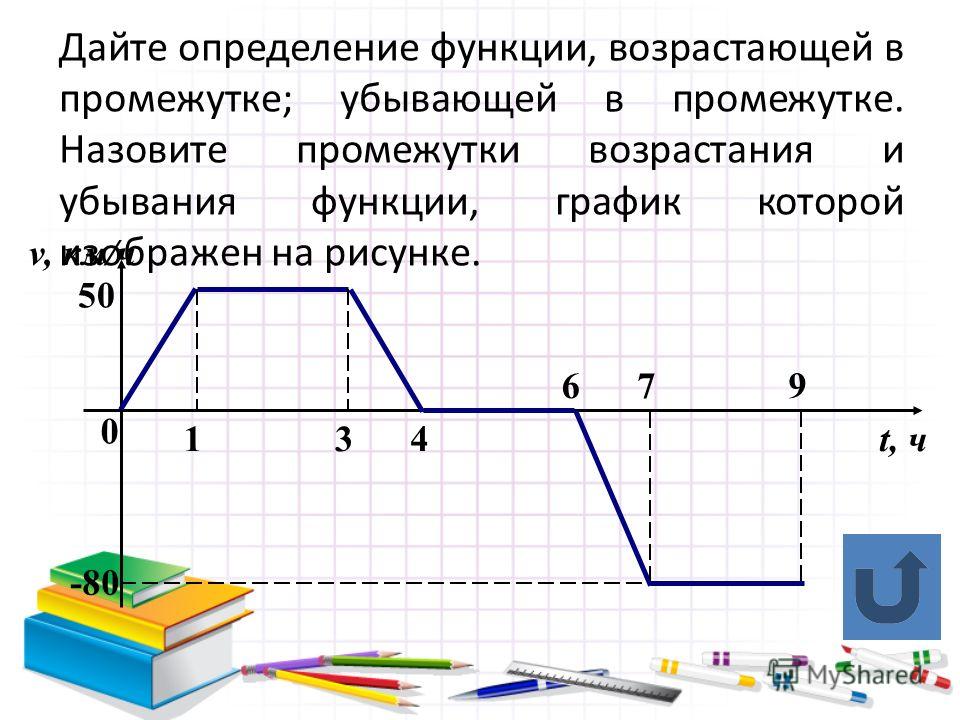
Для отыкания промежутков возрастания и убывания функции найдём точки, в которых . Такими точками являются и .
Исследуем знаки производной в промежутках, ограниченных этими точками. От до точки знак положителен, от точки до точки знак отрицателен, от точки до знак положителен. Ответ на вопрос задания: промежутки возрастания данной функции — и , а промежуток убывания функции — .
Нет времени вникать в решение? Можно заказать работу!
Пример 2. Найти промежутки возрастания и убывания функции .
Решение. Находим производную функции:
Решая уравнение , получаем точки, в которых производная функции равна нулю:
.
Исследуем знаки производной. От до точки знак положителен, от точки до точки знак отрицателен, от точки до знак положителен. Наше исследование показало, что промежутки возрастания данной функции и , а промежуток убывания —
Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.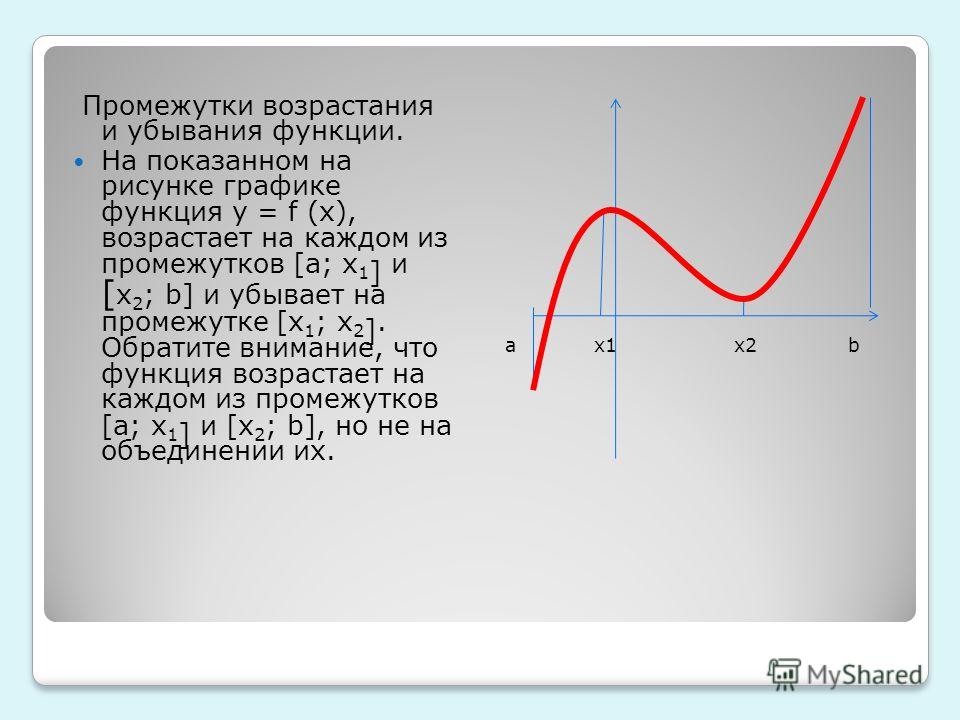
Пример 3. Найти промежутки возрастания и убывания функции .
Решение. Область определения функции — промежуток , так как логарифмическая функция определена при .
Далее находим производную функции:
.
Решая уравнение , получаем точку, в которой производная равна нулю:
Исследуем знаки производной. От 0 до точки знак отрицателен, от точки до знак положителен. Ответ: промежуток убывания функции — , а промежуток возрастания — .
| Назад | Листать | Вперёд>>> |
К началу страницы
Пройти тест по теме Производная, дифференциал и их применение
Весь блок «Производная»
- Что такое производная
- Найти производную: алгоритм и примеры решений
- Производные произведения и частного функций
- Производная суммы дробей со степенями и корнями
- Производные простых тригонометрических функций
- Производная сложной функции
- Производная логарифмической функции
- Дифференциал функции
- Дифференциал сложной функции, инвариантность формы дифференциала
- Уравнение касательной и уравнение нормали к графику функции
- Правило Лопиталя
- Частные производные
- Применение производной к исследованию функций
- Экстремумы функции
- Наименьшее и наибольшее значения функции
- Асимптоты
- Возрастание, убывание и монотонность функции
- Выпуклость и вогнутость графика функции, точки перегиба
- Полное исследование функций и построение графиков
- Функции двух и трёх переменных
- Экстремумы функции двух переменных
- Условные экстремумы и функция Лагранжа
| 1 | Trovare la Derivata — d/dx | натуральный логарифм x | |
| 2 | Вычислим интеграл | интеграл натурального логарифма x по x | |
| 3 | Trovare la Derivata — d/dx | e^x | |
| 4 | Вычислим интеграл | интеграл e^(2x) по x | |
| 5 | Trovare la Derivata — d/dx | 1/x | |
| 6 | Trovare la Derivata — d/dx | x^2 | |
| 7 | Trovare la Derivata — d/dx | 1/(x^2) | |
| 8 | Trovare la Derivata — d/dx | sin(x)^2 | |
| 9 | Trovare la Derivata — d/dx | sec(x) | |
| 10 | Вычислим интеграл | интеграл e^x по x | |
| 11 | Вычислим интеграл | интеграл x^2 по x | |
| 12 | Вычислим интеграл | интеграл квадратного корня из x по x | |
| 13 | Trovare la Derivata — d/dx | cos(x)^2 | |
| 14 | Вычислим интеграл | интеграл 1/x по x | |
| 15 | Вычислим интеграл | интеграл sin(x)^2 по x | |
| 16 | Trovare la Derivata — d/dx | x^3 | |
| 17 | Trovare la Derivata — d/dx | sec(x)^2 | |
| 18 | Вычислим интеграл | интеграл cos(x)^2 по x | |
| 19 | Вычислим интеграл | интеграл sec(x)^2 по x | |
| 20 | Trovare la Derivata — d/dx | e^(x^2) | |
| 21 | Вычислим интеграл | интеграл в пределах от 0 до 1 кубический корень из 1+7x по x | |
| 22 | Trovare la Derivata — d/dx | sin(2x) | |
| 23 | Trovare la Derivata — d/dx | tan(x)^2 | |
| 24 | Вычислим интеграл | интеграл 1/(x^2) по x | |
| 25 | Trovare la Derivata — d/dx | 2^x | |
| 26 | График | натуральный логарифм a | |
| 27 | Trovare la Derivata — d/dx | cos(2x) | |
| 28 | Trovare la Derivata — d/dx | xe^x | |
| 29 | Вычислим интеграл | интеграл 2x по x | |
| 30 | Trovare la Derivata — d/dx | ( натуральный логарифм от x)^2 | |
| 31 | Trovare la Derivata — d/dx | натуральный логарифм (x)^2 | |
| 32 | Trovare la Derivata — d/dx | 3x^2 | |
| 33 | Вычислим интеграл | интеграл xe^(2x) по x | |
| 34 | Trovare la Derivata — d/dx | 2e^x | |
| 35 | Trovare la Derivata — d/dx | натуральный логарифм 2x | |
| 36 | Trovare la Derivata — d/dx | -sin(x) | |
| 37 | Trovare la Derivata — d/dx | 4x^2-x+5 | |
| 38 | Trovare la Derivata — d/dx | y=16 корень четвертой степени из 4x^4+4 | |
| 39 | Trovare la Derivata — d/dx | 2x^2 | |
| 40 | Вычислим интеграл | интеграл e^(3x) по x | |
| 41 | Вычислим интеграл | интеграл cos(2x) по x | |
| 42 | Trovare la Derivata — d/dx | 1/( квадратный корень из x) | |
| 43 | Вычислим интеграл | интеграл e^(x^2) по x | |
| 44 | Вычислить | e^infinity | |
| 45 | Trovare la Derivata — d/dx | x/2 | |
| 46 | Trovare la Derivata — d/dx | -cos(x) | |
| 47 | Trovare la Derivata — d/dx | sin(3x) | |
| 48 | Trovare la Derivata — d/dx | 1/(x^3) | |
| 49 | Вычислим интеграл | интеграл tan(x)^2 по x | |
| 50 | Вычислим интеграл | интеграл 1 по x | |
| 51 | Trovare la Derivata — d/dx | x^x | |
| 52 | Trovare la Derivata — d/dx | x натуральный логарифм от x | |
| 53 | Trovare la Derivata — d/dx | x^4 | |
| 54 | Оценить предел | предел (3x-5)/(x-3), если x стремится к 3 | |
| 55 | Вычислим интеграл | интеграл x^2 натуральный логарифм x по x | |
| 56 | Trovare la Derivata — d/dx | f(x) = square root of x | |
| 57 | Trovare la Derivata — d/dx | x^2sin(x) | |
| 58 | Вычислим интеграл | интеграл sin(2x) по x | |
| 59 | Trovare la Derivata — d/dx | 3e^x | |
| 60 | Вычислим интеграл | интеграл xe^x по x | |
| 61 | Trovare la Derivata — d/dx | y=x^2 | |
| 62 | Trovare la Derivata — d/dx | квадратный корень из x^2+1 | |
| 63 | Trovare la Derivata — d/dx | sin(x^2) | |
| 64 | Вычислим интеграл | интеграл e^(-2x) по x | |
| 65 | Вычислим интеграл | интеграл натурального логарифма квадратного корня из x по x | |
| 66 | Trovare la Derivata — d/dx | e^2 | |
| 67 | Trovare la Derivata — d/dx | x^2+1 | |
| 68 | Вычислим интеграл | интеграл sin(x) по x | |
| 69 | Trovare la Derivata — d/dx | arcsin(x) | |
| 70 | Оценить предел | предел (sin(x))/x, если x стремится к 0 | |
| 71 | Вычислим интеграл | интеграл e^(-x) по x | |
| 72 | Trovare la Derivata — d/dx | x^5 | |
| 73 | Trovare la Derivata — d/dx | 2/x | |
| 74 | Trovare la Derivata — d/dx | натуральный логарифм 3x | |
| 75 | Trovare la Derivata — d/dx | x^(1/2) | |
| 76 | Trovare la Derivata — d/d@VAR | f(x) = square root of x | |
| 77 | Trovare la Derivata — d/dx | cos(x^2) | |
| 78 | Trovare la Derivata — d/dx | 1/(x^5) | |
| 79 | Trovare la Derivata — d/dx | кубический корень из x^2 | |
| 80 | Вычислим интеграл | интеграл cos(x) по x | |
| 81 | Вычислим интеграл | интеграл e^(-x^2) по x | |
| 82 | Trovare la Derivata — d/d@VAR | f(x)=x^3 | |
| 83 | Вычислим интеграл | интеграл 4x^2+7 в пределах от 0 до 10 по x | |
| 84 | Вычислим интеграл | интеграл ( натуральный логарифм x)^2 по x | |
| 85 | Trovare la Derivata — d/dx | логарифм x | |
| 86 | Trovare la Derivata — d/dx | arctan(x) | |
| 87 | Trovare la Derivata — d/dx | натуральный логарифм 5x | |
| 88 | Trovare la Derivata — d/dx | 5e^x | |
| 89 | Trovare la Derivata — d/dx | cos(3x) | |
| 90 | Вычислим интеграл | интеграл x^3 по x | |
| 91 | Вычислим интеграл | интеграл x^2e^x по x | |
| 92 | Trovare la Derivata — d/dx | 16 корень четвертой степени из 4x^4+4 | |
| 93 | Trovare la Derivata — d/dx | x/(e^x) | |
| 94 | Оценить предел | предел arctan(e^x), если x стремится к 3 | |
| 95 | Вычислим интеграл | интеграл (e^x-e^(-x))/(e^x+e^(-x)) по x | |
| 96 | Trovare la Derivata — d/dx | 3^x | |
| 97 | Вычислим интеграл | интеграл xe^(x^2) по x | |
| 98 | Trovare la Derivata — d/dx | 2sin(x) | |
| 99 | Вычислить | sec(0)^2 | |
| 100 | Trovare la Derivata — d/dx | натуральный логарифм x^2 |
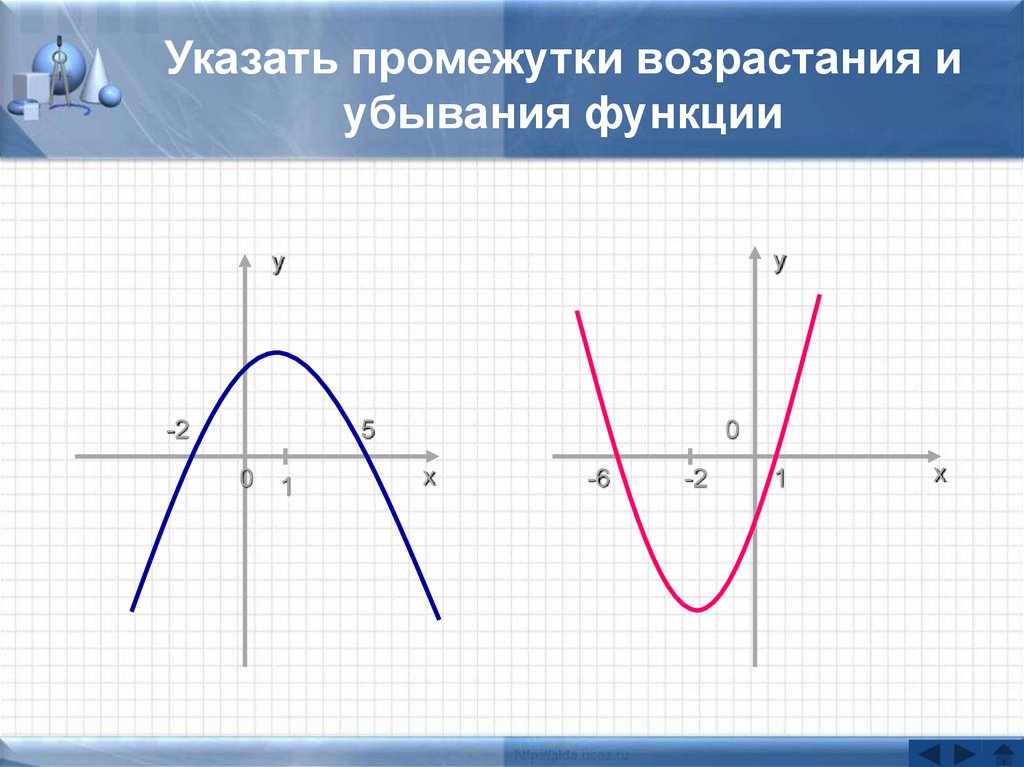
Промежутки возрастания и убывания функции » задачи
Нужно найти интервалы возрастания и убывания.
 {3} } =0 \\ \left \{ {{32-10x=0} \atop {x eq 0}} \right. $$
{3} } =0 \\ \left \{ {{32-10x=0} \atop {x eq 0}} \right. $$x=3,2 x≠0
Получили две критические точки,
которые разбивают область определения на три интервала.
Находим знак производной на каждом из интервалов:
x | -∞;0 | 0;3,2 | 3,2;+∞
y’ | — | + | —
y | убыв | возр | убыв
Дана функция у = 0,5х в 4 степени — 4х в квадрате. Найдите: а) промежутки возрастания и убывания функции; б) точки экстремума; в) наибольшее и наименьшее значения функции на отрезке [-1;3]
Решение:
у = 0,5х⁴ — 4х²
у’ = 2х³ — 8х
Найдём точки, где у’ = 0
2х³ — 8х = 0
2х·(х² — 4) = 0
х₁ = 0 или х₂,₃ = ±2
1) Найдём интервалы монотонности, для этого разобьём ось х на интервалы и определим знаки производной в этих интервалах
———— -2 —————0————— 2 ———-
у’(-3) = 2·(-27) — 8·(-3) = -30 у’
у’(-1) = 2·(-1) — 8·(-1) = 6 у’ > 0, у возрастает
у’(1) = 2·1 — 8·1 = -6 у’
у’(3) = 2·27 — 8·3 = 30 у’ > 0, у возрастает
Итак, промежутки возрастания и убываня функции:
Функция возрастает при х∈[-2, 0] и [2, +∞)
Функция убывает при х∈(-∞, -2] и [0, 2]
2) Найдём точки локальных экстремумов и экстремальные значения функции.
В точке х = -2 производная меняет знак с — на +, поэтому это точка минимума
В точке х = 0 производная меняет знак с + на -, поэтому это точка максимума
В точке х = 2 производная меняет знак с — на +, поэтому это точка минимума
y min 1 = y(-2) = 0,5·16 — 4·4 = -8
y min 2 = y(2) = 0,5·16 — 4·4 = -8
y max = y(0) = 0,5·0 — 4·0 = 0
3) Найдём наибольшее и наименьшее значения функции на отрезке [-1;3]
На концах интервала функция принимает значения:
у(-1) = 0,5·1 — 4·1 = -3,5
у(3) = 0,5·81 — 4·9 = 4,5
В указанном интервале [-1;3] мы имеем один локальный максимум
y max = y(0) = 0
и один локальный минимум
y min = y(2) = -8
Сравнивая все четыре значения функции, видим, что
у наиб = у(3) = 4,5
у наим = y(2) = -8
Укажите промежутки возрастания функции:y=-x в четвертой степени +4х во второй степени -3
Решение: Y = X^4 + 4X^2 — 3
A = X^2
Y = A^2 +4A — 3
D = 16 — 4*1*(-3) = 16 + 12 = 28 V D = 5.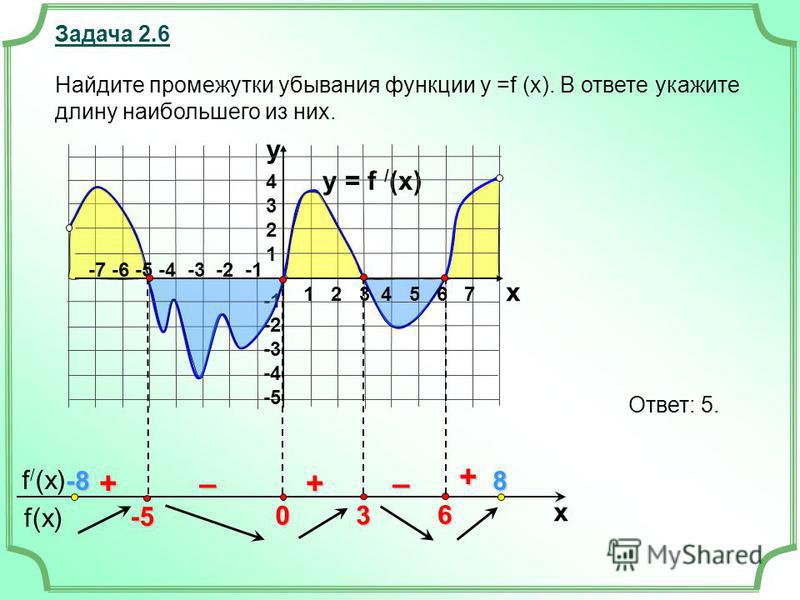 2(2a)=sin(2a)
2(2a)=sin(2a)
Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа
| Справочник по математике | Элементы математического анализа | Производная функции |
| Интервалы возрастания и убывания функции |
| Достаточные условия для возрастания и убывания функции |
| Экстремумы (максимумы и минимумы) функции |
| «Подозрительные» на наличие экстремума точки функции. Теорема Ферма |
| Достаточные условия для существования экстремума функции |
| Пример исследования поведения функции |
Интервалы возрастания и убывания функции
Для того, чтобы найти интервалы, на которых функция возрастает или убывает, часто используется метод, основанный на анализе знаков производной рассматриваемой функции.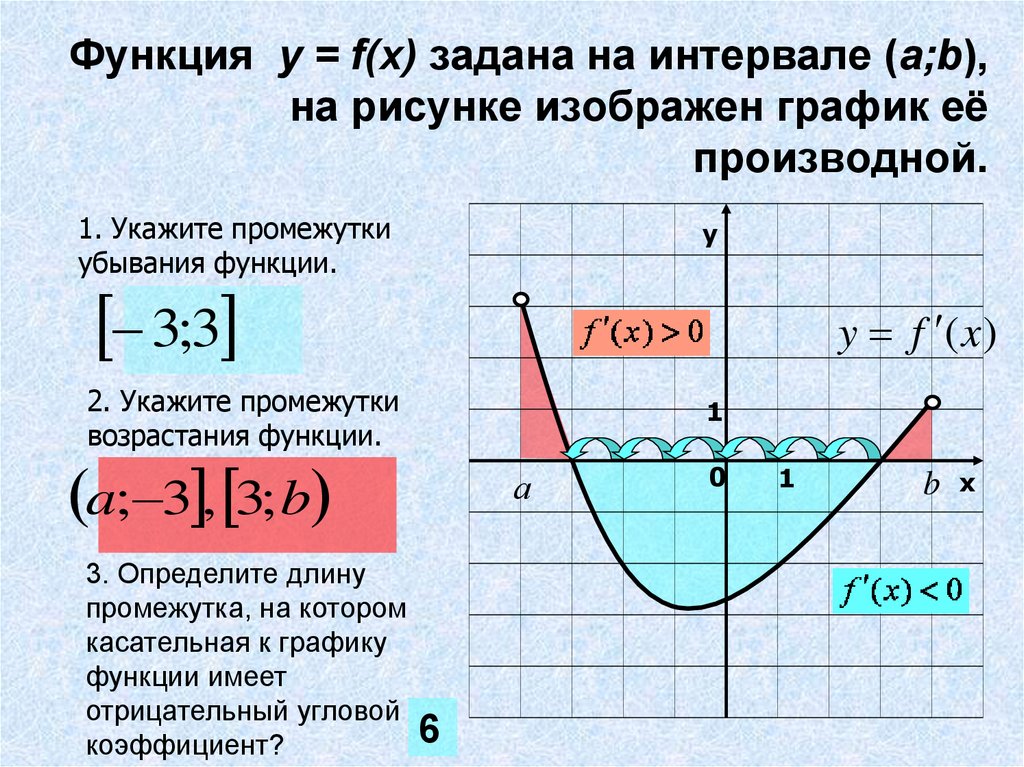 Суть этого метода состоит в следующем.
Суть этого метода состоит в следующем.
Если на интервале (a, b) функция y = f (x) строго возрастает и в каждой точке x0 интервала имеет производную, то, как показано на рисунке 1, а также на рисунке 2,
Рис.1
Рис.2
угол α наклона касательной к графику функции будет острым, откуда вытекает неравенство:
f ‘ (x0) = tg α > 0
Если же на интервале (a, b) функция y = f (x) строго убывает и в каждой точке x0 интервала имеет производную, то, как показано на рисунках 3 и 4,
Рис.3
Рис.4
угол α наклона касательной к графику функции будет тупым, откуда вытекает неравенство:
f ‘ (x0) = tg α < 0
Достаточные условия для возрастания и убывания функции
В следующем утверждении, доказательство которого выходит за рамки школьного курса математики, сформулированы достаточные условия для возрастания и убывания функции.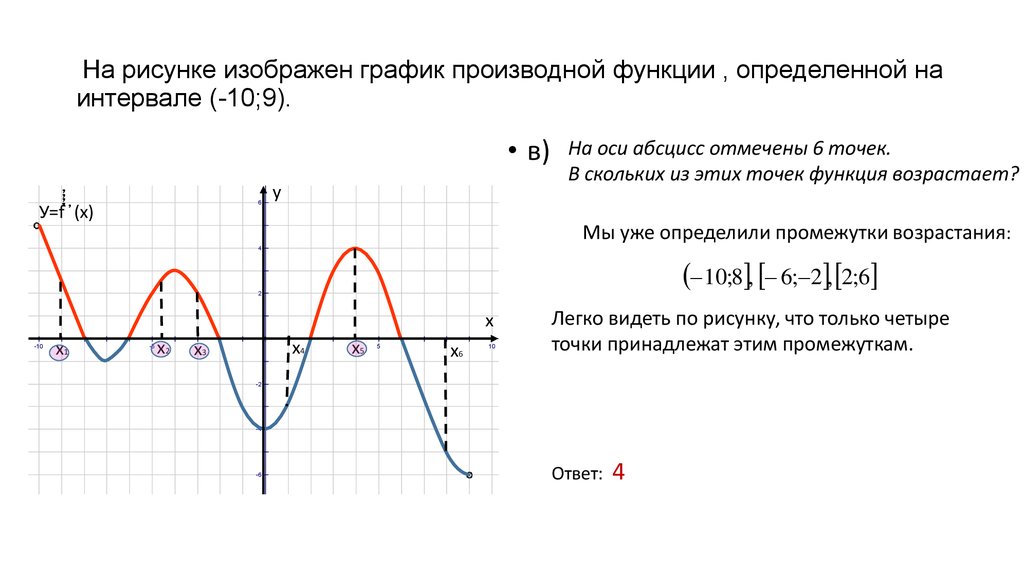
Утверждение 1.
а). Если в каждой точке x интервала (a, b) производная f ‘ (x) существует и удовлетворяет неравенству
f ‘ (x) > 0 ,
то функция f (x) строго возрастает на интервале (a, b) .
б). Если в каждой точке x интервала (a, b) производная f ‘ (x) существует и удовлетворяет неравенству
то функция f (x) возрастает (не убывает) на интервале (a, b) .
в). Если в каждой точке x интервала (a, b) производная f ‘ (x) существует и удовлетворяет неравенству
f ‘ (x) < 0 ,
то функция f (x) строго убывает на интервале (a, b) .
г). Если в каждой точке x интервала (a, b) производная f ‘ (x) существует и удовлетворяет неравенству
Если в каждой точке x интервала (a, b) производная f ‘ (x) существует и удовлетворяет неравенству
то функция f (x) убывает (не возрастает) на интервале (a, b) .
Экстремумы (максимумы и минимумы) функции
Определение 1. Точку x0 называют точкой максимума функции f (x) , если существует интервал (a, b) , такой, что a 0b , для точек x которого выполнено неравенство
.
Таким образом, если x0 – точка максимума функции f (x) , то в интервале (a, b) значение функции f (x0) больше всех остальных значений функции.
Определение 2. Точку x0 называют точкой минимума функции f (x) , если существует интервал (a, b) , такой, что a < x0 < b , для точек x которого выполнено неравенство
Точку x0 называют точкой минимума функции f (x) , если существует интервал (a, b) , такой, что a < x0 < b , для точек x которого выполнено неравенство
.
Другими словами, если x0 – точка минимума функции f (x) , то в интервале (a, b) значение функции f (x0) меньше всех остальных значений функции.
Определение 3. Точки максимума и минимума функции называют точками экстремума функции, а значения функции в точках экстремума называют экстремумами функции.
«Подозрительные» на наличие экстремума точки функции.
Теорема Ферма
Определение 4.Стационарной точкой функции называют такую точку, в которой производная функции равна нулю.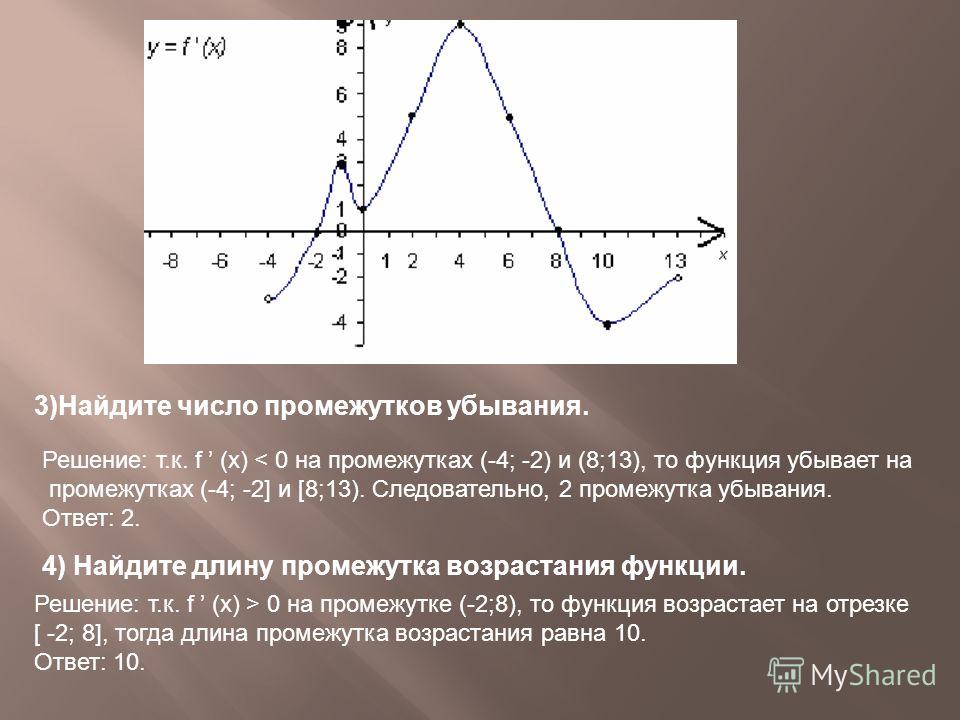
Определение 5.Критической точкой функции называют такую точку, в которой производная функции равна нулю или не существует.
Таким образом, если точка x0 является критической точкой функции, то точка x0 либо является стационарной точкой функции, либо производная функции в точке x0 не существует.
Теорема Ферма. Если точка x0 является точкой экстремума функции f (x) , то точка x0 является критической точкой функции f (x) .
Доказательство. Если в точке x0 у функции y = f (x) не существует производная, то точка x0 является критической точкой по определению. Докажем, что если в точке x0 у функции y = f (x) существует производная, то точка x0 является стационарной, то есть f ‘ (x0) = 0 .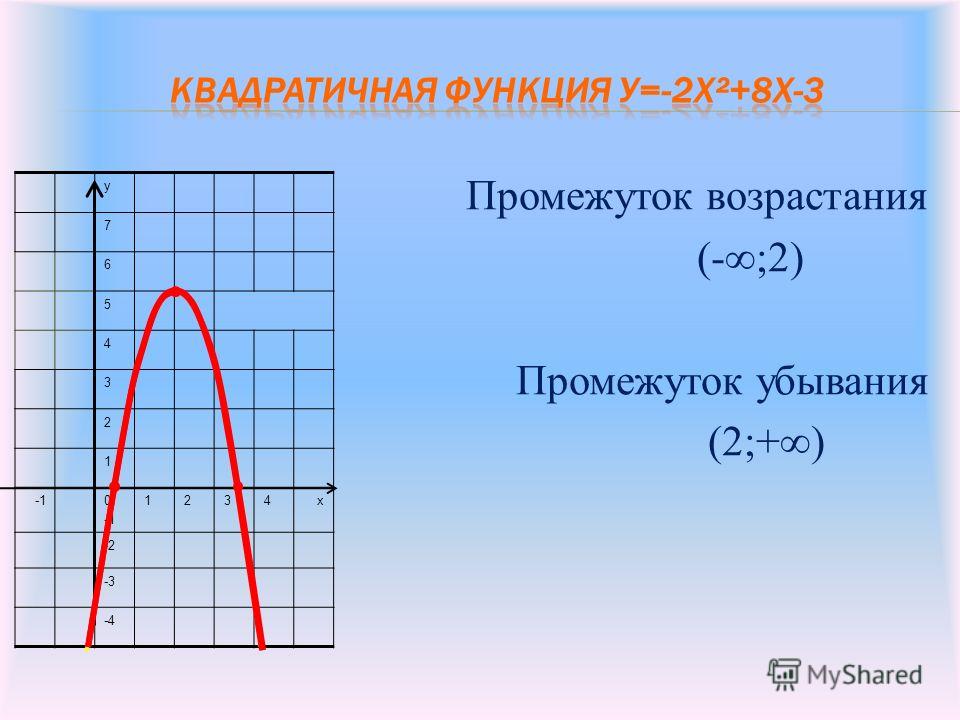
Предположим сначала, что точка x0 является точкой максимума функции y = f (x) (рис. 5).
Рис.5
Поскольку x0 – точка максимума, то для любой точки x1 такой, что x1x0 , выполнено неравенство f (x1) < f (x0) , поэтому
.
Точно так же, для любой точки x2 такой, что x2 > x0 , выполнено неравенство f (x2) < f (x0) , поэтому
.
Таким образом, в случае, когда точка x0 является точкой максимума функции y = f (x), выполнено равенство f ‘ (x0) = 0 .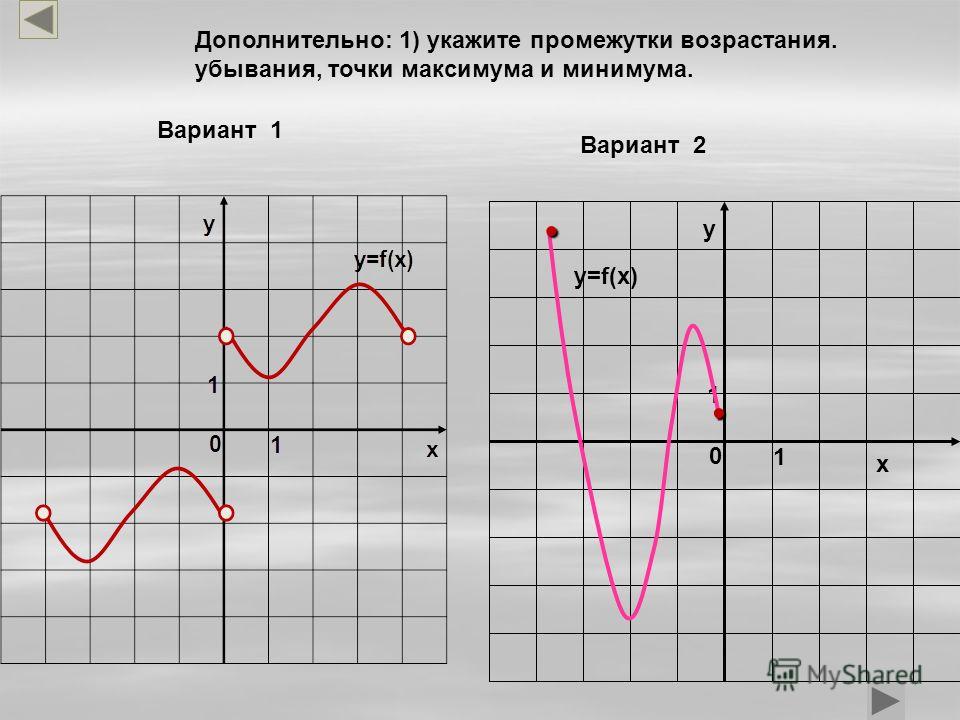 Касательная к графику функции y = f (x) в точке A= (x0; f (x0)) параллельна оси Ox.
Касательная к графику функции y = f (x) в точке A= (x0; f (x0)) параллельна оси Ox.
Совершенно аналогично доказывается, что и в случае, когда точка x0 является точкой минимума функции y = f (x), выполнено равенство f ‘ (x0) = 0 .
Замечание 1. Из утверждения 2 следует, что точки экстремумов функции (точки максимумов и точки минимумов) нужно искать лишь среди критических точек функции, так как в других (некритических) точках экстремумов быть не может. По этой причине критические точки функции часто называют точками, подозрительными на экстремум.
Достаточные условия для существования экстремума функции
В следующем утверждении, доказательство которого выходит за рамки школьного курса математики и в нашем справочнике не приводится, сформулированы достаточные условия для экстремума функции.
Утверждение 3. Рассмотрим функцию f (x) , непрерывную в интервале (a, b), содержащем точку x0 , производная которой существует в каждой точке этого интервала, кроме, быть может, самой точки x0 .
а). Если для точек выполнено условие:
f ‘ (x) > 0 при x 0 и f ‘ (x) < 0 при x > x0 ,
то точка x0 является точкой максимума функции f (x) (рис. 6).
Рис.6
б). Если для точек выполнено условие:
f ‘ (x) < 0 при x < x0 и f ‘ (x) > 0 при x > x0 ,
то точка x0 является точкой минимума функции f (x) (рис. 7).
7).
Рис.7
Замечание 2. Условия а) и б) утверждения 3 часто формулируют так: «Если при переходе через точку x0 производная функции меняет знак с «+» на «–» , то точка x0 является точкой максимума функции. Если при переходе через точку x0 производная функции меняет знак с «–» на «+» , то точка x0 является точкой минимума функции».
Пример исследования поведения функции
Пример. Найти интервалы возрастания, убывания и экстремумы функции
| y = | x3 + 3x2 | | (1) |
Решение. Исследуем сначала на возрастание, убывание и экстремумы функцию
| y1 = x3 + 3x2 | (2) |
и построим ее график.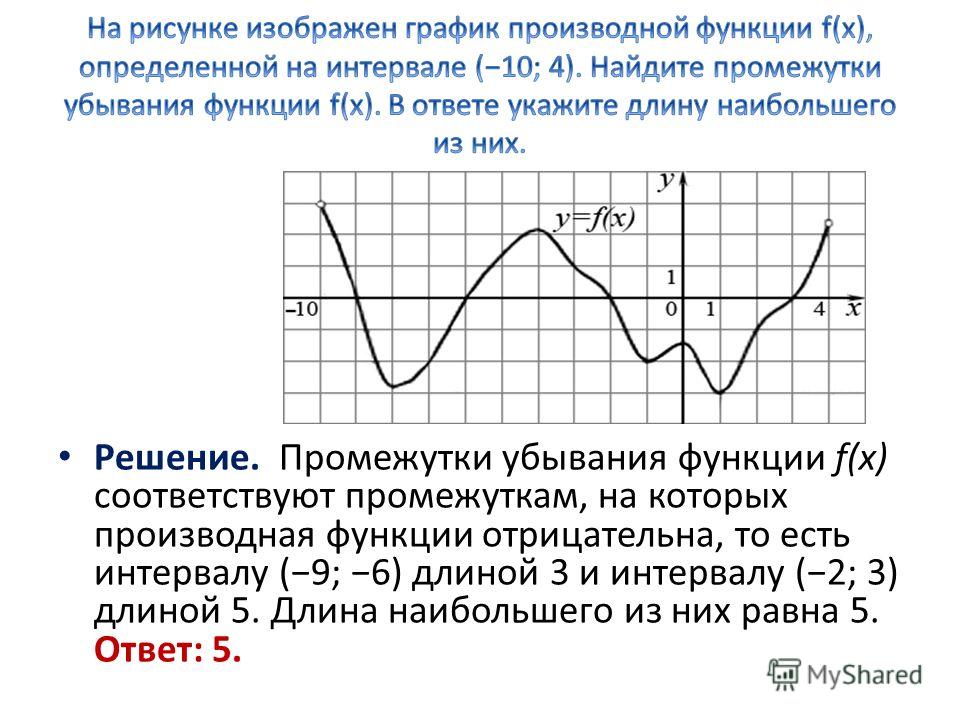 Для этого представим формулу (2) в виде
Для этого представим формулу (2) в виде
y1 = x2 (x + 3)
и заметим, что
а) y1 = 0 при x = 0 и x = – 3 ,
б) y1 > 0 при x > – 3 ; y1 < 0 при x < – 3 .
Теперь вычислим производную функции (2):
| (3) |
и разложим на множители правую часть формулы (3):
| (4) |
На рисунке 8 при помощи метода интервалов изобразим на числовой оси знаки производной (4)
Рис.8
Поскольку решением неравенства
3x (x + 2) > 0
является множество
| , | (5) |
то в соответствии с утверждением 1 функция y1 возрастает на каждом из интервалов и .
С другой стороны, поскольку решением неравенства
3x (x + 2)
является интервал
| (– 2, 0), | (6) |
то в соответствии с утверждением 1 функция y1 убывает на интервале (– 2, 0) .
Так как решениями уравнения
3x (x + 2) = 0
являются точки
| x = – 2; x = 0; | (7) |
то эти точки являются стационарными точками функции y1 .
Поскольку при переходе через точку x = – 2 производная функции y1 меняет знак с «+» на «–» (рис. 8), то в соответствии с утверждением 3 точка x = – 2 является точкой максимума функции y1 , при этом
y1 (– 2) = 4 .
При переходе через точку x = 0 производная функции y1 меняет знак с «–» на «+» (рис. 8), поэтому в соответствии с утверждением 3 точка x = 0 является точкой минимума функции y1, при этом
y1 (0) = 0 .
Заметим, что при анализе поведения функции по знакам ее производной, удобно использовать следующую диаграмму, на которой стрелками указаны интервалы возрастания и убывания функции (рис. 9).
Рис.9
Теперь мы можем построить график функции y1 (рис. 10).
Рис.10
Перейдем к построению графика функции y = | x3 + 3x2 | .
В силу определения модуля, справедливо равенство
Из этого равенства вытекает, что, если мы симметрично отразим относительно оси Ox часть графика функции y1 = x3 + 3x2 (рис. 10), лежащую в нижней полуплоскости, оставив без изменения часть этого графика, лежащую в верхней полуплоскости, то мы получим график функции y = | x3 + 3x2 | (рис.11) .
10), лежащую в нижней полуплоскости, оставив без изменения часть этого графика, лежащую в верхней полуплоскости, то мы получим график функции y = | x3 + 3x2 | (рис.11) .
Рис.11
В точке x = – 3 производная функции y = | x3 + 3x2 | не существует. Во всех остальных точках числовой оси производная функции y = | x3 + 3x2 | существует.
Точки x = – 3 и x = 0 являются точками минимума, причем y ( – 3) = y (0) = 0 .
Точка x = – 2 является точкой максимума, причем y ( – 2) = 4 .
Функция y = | x3 + 3x2 | возрастает на каждом из интервалов (– 3, – 2) и .
Функция y = | x3 + 3x2 | убывает на каждом из интервалов и (– 2, 0).
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
Как найти возрастающие интервалы с помощью графических функций
Все ресурсы исчисления 1
10 Диагностические тесты 438 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
Исчисление 1 Помощь » Функции » Графические функции » Интервалы » Увеличение интервалов » Как найти возрастающие интервалы по графикам функций
На каких интервалах увеличивается f(x) = (1/3)x 3 + 2,5x 2 – 14x + 25?
Возможные ответы:
(–∞, –7)
(–∞, –7) и (2, ∞)
(2, ∞)
–– (2, ∞) (–7, 2) и (2, ∞)
(–7, 2) и (2, ∞)
Правильный ответ:
(–∞, –7) и (2, ∞)
Объяснение:
Мы будем использовать наклон касательной, чтобы определить увеличение/уменьшение f(x). Для этого начнем с первой производной от f(x):
Для этого начнем с первой производной от f(x):
f'(x) = x 2 + 5x – 14
Найдите потенциальные относительные максимумы и минимумы, установив f'(x) равным 0 и решив:
x 2 + 5x – 14 = 0 ; (x – 2)(x + 7) = 0
Возможные относительные максимумы/минимумы: x = 2, x = –7
Мы должны проверить следующие интервалы: (–∞, –7), (–7, 2 ), (2, ∞)
f'(–10) = 100 – 50 – 14 = 36
f'(0) = –14
f'(10) = 100 + 50 – 14 = 136
Следовательно, уравнение возрастает на (–∞, –7) и (2, ∞)
Сообщить об ошибке
Найдите интервал(ы), в котором следующая функция возрастает. График, чтобы перепроверить свой ответ.
Возможные ответы:
Всегда
Никогда
Правильный ответ:
4
55
5
Объяснение: Чтобы определить, когда функция возрастает, вы должны сначала взять производную, затем приравнять ее к 0, а затем найти, между какими нулевыми значениями функция положительна.
Сначала возьмем производную:
Приравняем к 0 и решим:
Теперь проверьте значения со всех сторон, чтобы найти, когда функция положительна и, следовательно, возрастает. Я проверю значения -6, 0 и 2.
Поскольку значения являются положительными, когда x = -6 и 2, интервал увеличивается на интервалах, которые включают эти значения. . Поэтому наш ответ:
Сообщить об ошибке
Найдите интервал(ы), когда следующая функция возрастает. График, чтобы перепроверить свой ответ.
Возможные ответы:
Всегда
Никогда
Правильный ответ:
4
55
5
Объяснение: Чтобы определить, когда функция возрастает, вы должны сначала взять производную, затем приравнять ее к 0, а затем найти, между какими нулевыми значениями функция положительна.
Сначала возьмем производную:
Приравняем к 0 и решим:
Теперь проверьте значения со всех сторон, чтобы найти, когда функция положительна и, следовательно, возрастает. Я проверю значения 0, 2 и 10.
Поскольку значение является положительным, когда x = 0 и 10, интервал увеличивается в обоих этих интервалах. Поэтому наш ответ:
Сообщить об ошибке
Увеличивается или уменьшается на интервале?
Возможные ответы:
Возрастание. на интервале.
Увеличение. на интервале.
Невозможно определить на основании предоставленной информации
Уменьшается. на интервале.
Уменьшение. на интервале.
Правильный ответ:
Возрастание. на интервале.
Объяснение:
Чтобы найти возрастающие и убывающие интервалы, нам нужно найти, где наша первая производная больше или меньше нуля. Если наша первая производная положительна, наша исходная функция возрастает, а если g'(x) отрицательна, g(x) убывает.
Если наша первая производная положительна, наша исходная функция возрастает, а если g'(x) отрицательна, g(x) убывает.
Начните с:
Если мы подставим любое число от 3 до 6, мы получим положительное число для g'(x). Таким образом, эта функция должна возрастать на интервале {3,6 }, так как g'(x) положительна.
Сообщить об ошибке
Увеличивается или уменьшается на интервале?
Возможные ответы:
Увеличивается, потому что отрицательно.
Уменьшение, поскольку положительно.
Возрастание, поскольку положительно.
Уменьшение, поскольку отрицательно.
не увеличивается и не уменьшается на заданном интервале.
Правильный ответ:
Возрастает, потому что положительно.
Объяснение:
Чтобы узнать, возрастает функция или убывает, нам нужно определить, положительна или отрицательна первая производная на заданном интервале.
Итак, начиная с:
Мы получаем:
используя степенное правило .
Найдите функцию на каждом конце интервала.
Итак, первая производная положительна на всем интервале, поэтому g(t) возрастает на интервале.
Сообщить об ошибке
Является ли следующая функция возрастающей или убывающей на интервале?
Возможные ответы:
Убывающий, т.к. положителен на данном интервале.
Функция не возрастает и не убывает на интервале.
Возрастание, так как на данном интервале положительно.
По убыванию, так как на данном интервале отрицательно.
Возрастание, поскольку отрицательно на заданном интервале.
Правильный ответ:
Возрастание, т.к. положительно на данном интервале.
Объяснение:
Функция возрастает на интервале, если для каждой точки этого интервала первая производная положительна.
Итак, нам нужно найти первую производную, а затем подставить конечные точки нашего интервала.
Найдите первую производную с помощью степенного правила
Подставьте конечные точки и оцените функцию.
Оба положительны, поэтому наша функция возрастает на данном интервале.
Сообщить об ошибке
С какими интервалами увеличивается следующая функция?
Возможные ответы:
Правильный ответ:
Пояснение:
Первый шаг — найти первую производную.
Помните, что производная от
Далее найдите критические точки, которые являются точками, где или не определены. Чтобы найти точки, установите числитель на , чтобы найти неопределенные точки, установите знаменатель на . Критические точки и
Последним шагом является проверка точек во всех регионах, чтобы увидеть, какой диапазон дает положительное значение для .
Если мы подставим число из первого диапазона, т.е. получим отрицательное число.
Из второго диапазона мы получаем положительное число.
Из третьего диапазона мы получаем отрицательное число.
Из последнего диапазона мы получаем положительное число.
Таким образом, второй и последний диапазоны — это те, где увеличивается.
Сообщить об ошибке
Ниже приведен полный график . На каком интервале(ах) происходит увеличение?
Возможные ответы:
Правильный ответ:
Объяснение:
увеличивается, когда является положительным (над осью). Это происходит на интервалах .
Сообщить об ошибке
Функция A
Функция B
9 10004
Function C
Function D
Function E
5 graphs of different functions are shown выше. На каком графике показана возрастающая/неубывающая функция ?
На каком графике показана возрастающая/неубывающая функция ?
Возможные ответы:
Функция D
Функция E
Функция B
Функция A
Функция C
Правильный ответ:
Функция E
Объяснение:
Функция возрастает, если для любого , (т. е. наклон всегда больше или равен нулю)
Функция – единственная функция, обладающая этим свойством. Обратите внимание, что функция E возрастает, но не строго возрастает
Сообщить об ошибке
Найдите возрастающие интервалы следующей функции на интервале :
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти возрастающие интервалы заданной функции, нужно определить интервалы, на которых функция имеет положительную первую производную. Чтобы найти эти интервалы, сначала найдите критические значения или точки, в которых первая производная функции равна нулю.
Чтобы найти эти интервалы, сначала найдите критические значения или точки, в которых первая производная функции равна нулю.
Для данной функции .
Эта производная была найдена с помощью правила степени
.
При нулевом значении . Поскольку мы рассматриваем только открытый интервал (0,5) для этой функции, мы можем игнорировать . Далее мы смотрим интервалы вокруг критического значения , которые равны и . На первом интервале первая производная функции отрицательна (подстановка значений дает нам отрицательное число), что означает, что функция на этом интервале убывает. Однако для второго интервала первая производная положительна, что указывает на возрастание функции на этом интервале.
Сообщить об ошибке
← Назад 1 2 3 Далее →
Уведомление об авторских правах
Все ресурсы исчисления 1
10 Диагностические тесты
438 практических тестов
Вопрос дня
Карточки
Learn by Concept
Увеличение и уменьшение интервалов — определение, формулы
Задумывались ли вы, почему расстояние сокращается, как только вы приближаетесь к дому вашего друга? И почему это происходит наоборот, когда вы едете в противоположном направлении? Это из-за функций. В исчислении возрастающие и убывающие функции — это функции, для которых значение f (x) увеличивается и уменьшается соответственно с увеличением значения x.
В исчислении возрастающие и убывающие функции — это функции, для которых значение f (x) увеличивается и уменьшается соответственно с увеличением значения x.
Чтобы проверить изменение функций, нужно найти производные таких функций. Если значение функции увеличивается со значением x, то функция положительна. Если значение функции уменьшается с увеличением значения x, то говорят, что функция отрицательна.
Интервалы возрастания и убывания действительных чисел — это действительнозначные функции, которые имеют тенденцию возрастать и уменьшаться при изменении значения зависимой переменной функции. Чтобы найти интервалы возрастания и убывания, нужно определить первую производную функции. Это делается для того, чтобы найти знак функции, будь то отрицательный или положительный. Интервал функции называется положительным, если значение функции f(x) увеличивается с увеличением значения x. Напротив, интервал функции называется отрицательным, если значение функции f (x) уменьшается с увеличением значения x.
Альтернативно, интервал функции положителен, если положительный знак первой производной. Интервал функции отрицательный, если знак первой производной отрицательный. Следовательно, положительный интервал увеличивается, тогда как отрицательный интервал называется убывающим интервалом.
Как записать интервалы возрастания и убывания? Вы можете представлять интервалы возрастания и убывания, понимая простые математические понятия, приведенные ниже:
- Говорят, что значение интервала увеличивается для каждого x < y, где f (x) ≤ f (y) для действительнозначной функции f (x).
- Если значение интервала f (x) ≥ f (y) для каждого x < y, то интервал называется убывающим.
Вы также можете использовать первую производную, чтобы найти интервалы возрастания и убывания и соответственно записать их.
- Если первая производная функции равна f’ (x) ≥ 0, интервал увеличивается.
- С другой стороны, если значение производной f’ (x) ≤ 0, то интервал называется убывающим.

Определение интервалов возрастания и убывания Поскольку вы умеете записывать интервалы возрастания и убывания, пора научиться находить интервалы возрастания и убывания. Давайте научимся находить интервалы возрастания и убывания на примере.
Рассмотрим функцию f(x) = x 3 + 3x 2 – 45x + 9. Чтобы найти интервалы возрастания и убывания, нужно продифференцировать их относительно x. После дифференцирования вы получите первую производную как f’(x).
Следовательно, f’(x) = 3x 2 + 6x – 45
Вынимая из всего члена 3 общих, получаем 3 (x 2 + 2x -15). Теперь, находя множители этого уравнения, мы получаем, 3 (x + 5) (x – 3). Если вы замените эти значения эквивалентными нулю, вы получите значения x.
Следовательно, значение x = -5, 3.
Чтобы найти значение функции, подставьте эти значения в исходную функцию, и вы получите значения, как показано в таблице ниже.
Interval Value of x f'(x) Increasing/Decreasing (-∞, -5) x = -6 f ‘(-6) = 27 > 0 Возрастание (-5, 3) x = 0 f'(0) = -45 < 0 Уменьшение ) x = 4 f'(4) = 27 > 0 Возрастание
Следовательно, для данной функции f (x) = x 3 + 3x 2 – 45x + 9 возрастающие интервалы равны (-∞, -5) и (3, ∞), а убывающие интервалы равны (-5, 3).
Частный случай: функция «один к одному»
Строго возрастающие или убывающие функции обладают особым свойством, называемым инъективными или взаимно однозначными функциями. Это означает, что вы никогда не получите одно и то же значение функции дважды.
Например, вы можете получить значение функции дважды на первом графике. Однако на втором графике у вас никогда не будет одинакового значения функции. Следовательно, график справа известен как взаимно однозначная функция.
Это полезно, потому что инъективные функции могут быть обращены. Вы можете вернуться от значения «y» функции к значению «x». Обычно это невозможно, так как существует более одного возможного значения x.
Пример 1: Какими будут интервалы возрастания и убывания функции f (x) = -x 3 + 3x 2 + 9?
Решение: Чтобы найти интервалы возрастания и убывания, нужно продифференцировать функцию относительно x. Следовательно, f’(x) = -3x 2 + 6x.
Следовательно, f’(x) = -3x 2 + 6x.
Теперь, убрав из уравнения 3 обычных, мы получим -3x (x – 2). Чтобы найти значения x, приравняем это уравнение к нулю, получим f'(x) = 0
⇒ -3x (x – 2) = 0
⇒ x = 0 или x = 2.
Следовательно , интервалы для функции f (x) равны (-∞, 0), (0, 2) и (2, ∞). Чтобы найти значения функции, ознакомьтесь с таблицей ниже.
Interval Value of x f'(x) Increasing/Decreasing (-∞, 0) x = -1 f ‘(-1) = -9 < 0 Убывающая (0, 2) x = 1 f'(1) = 3 > 0 Возрастающая 9 x = 4 f'(4) = -24 < 0 Уменьшение
Следовательно, (-∞, 0) и (2, ∞) — убывающие интервалы, а (0, 2) — возрастающие интервалы.
Пример 2: Считаете ли вы, что интервал (-∞, ∞) является строго возрастающим интервалом для f(x) = 3x + 5? Если да, то докажите это.
Решение: Чтобы доказать утверждение, рассмотрим два действительных числа x и y в интервале (-∞, ∞), такие что x < y.
Тогда 3x < 3y.
⇒ 3x + 5 < 3y + 5
⇒ f (x) < f (y)
Так как x и y являются произвольными значениями, следовательно, f (x) < f (y) всякий раз, когда x < y. Следовательно, интервал (-∞, ∞) является строго возрастающим интервалом для f(x) = 3x + 5. Следовательно, утверждение доказано.
Пример 3: Найдите, является ли функция f (x) x 3 −4x для x в интервале [−1, 2] возрастающей или убывающей.
Решение: вам нужно начать с -1, чтобы построить функцию на графике. -1 выбрано потому, что интервал [−1, 2] начинается с этого значения. При x = -1 функция убывает. Как только он достигнет значения 1,2, функция увеличится. После того, как функция достигла значения больше 2, значение будет продолжать увеличиваться. При точном анализе нельзя найти, увеличивается интервал или уменьшается. Итак, скажем, в интервале [−1, 2],
Итак, скажем, в интервале [−1, 2],
- Кривая спадает в интервале [−1, прибл. 1,2]
- Кривая возрастает в интервале [прибл. 1,2, 2]
Определение интервалов возрастания и убывания с помощью графика В приведенных выше разделах вы научились писать интервалы возрастания и убывания. В этом разделе вы узнаете, как находить интервалы возрастания и убывания с помощью графиков. Было бы полезно, если бы вы изучили приведенную ниже таблицу, чтобы четко понять концепцию.
Возрастающий интервал Уменьшающийся интервал На приведенном ниже графике показана возрастающая функция. Это можно определить, взглянув на приведенный график. Поскольку график идет вверх по мере движения слева направо по оси X, говорят, что график увеличивается. На приведенном ниже графике показана убывающая функция. Это можно определить, взглянув на приведенный график. Поскольку график идет вниз при движении слева направо по оси X, говорят, что график уменьшается.
Поскольку график идет вниз при движении слева направо по оси X, говорят, что график уменьшается.
Наводит на размышления - Функция выдаст постоянное значение и будет называться постоянной, если f’(x) = 0 в течение этого интервала.
- Для вещественнозначной функции f (x) интервал I называется строго возрастающим интервалом, если для каждого x < y выполняется f (x) < f (y).
- Для вещественнозначной функции f (x) интервал I называется строго убывающим интервалом, если для каждого x < y выполняется f (x) > f (y).
- Для функции f (x), когда x1 < x2, тогда f (x1) ≤ f (x2), интервал называется возрастающим.
- Для функции f (x), когда x1 < x2, а затем f (x1) < f (x2), интервал называется строго возрастающим. Нужно быть внимательным, глядя на знаки возрастающих и строго возрастающих функций.
- Для функции f (x), когда x1 < x2, тогда f (x1) ≥ f (x2), интервал называется убывающим.
- Для функции f (x), когда x1 < x2, то f (x1) > f (x2), интервал называется строго убывающим.

- Если значение функции не меняется при изменении значения x, то говорят, что функция является постоянной функцией.
Интервалы возрастания и убывания — определение, формулы, примеры
LearnPracticeDownload
Интервалы возрастания и убывания — это интервалы действительных чисел, в которых вещественные функции возрастают и убывают соответственно. Чтобы определить возрастающие и убывающие интервалы, мы используем критерий производной первого порядка для проверки знака производной в каждом интервале. Интервал увеличивается, если значение функции f(x) увеличивается с увеличением значения x, и убывает, если f(x) уменьшается с уменьшением x.
В этой статье мы научимся определять возрастающие и убывающие интервалы с помощью теста производной первого порядка и графика функции с помощью примеров для лучшего понимания концепции.
1. Что такое возрастающие и убывающие интервалы? 2.
Увеличение и уменьшение интервалов Определение 3. Нахождение возрастающих и убывающих интервалов 4. Увеличение и уменьшение интервалов с помощью графика 5. Часто задаваемые вопросы об увеличении и уменьшении интервалов
Что такое возрастающие и убывающие интервалы?
Интервалы возрастания или убывания функций называются возрастающими и убывающими интервалами. Эти интервалы можно оценить, проверив знак первой производной функции на каждом интервале. Если первая производная функции на интервале положительна, то этот интервал называется возрастающим, а если первая производная функции на интервале отрицательна, то этот интервал называется убывающим. Давайте пройдемся по их формальным определениям, чтобы понять их смысл:
Увеличение и уменьшение интервалов Определение
Определения увеличения и уменьшения интервалов приведены ниже.
- Для вещественнозначной функции f(x) интервал I называется возрастающим интервалом, если для каждого x < y выполняется f(x) ≤ f(y).
- Для действительнозначной функции f(x) интервал I называется убывающим интервалом, если для каждого x < y выполняется f(x) ≥ f(y).
Мы также можем определить возрастающий и убывающий интервалы, используя первую производную функции f(x) как:
- Если f'(x) ≥ 0 на I, то I называется возрастающим интервалом.
- Если f'(x) ≤ 0 на I, то I называется убывающим интервалом.
Нахождение возрастающих и убывающих интервалов
Теперь, когда мы поняли значение возрастающих и убывающих интервалов, давайте теперь научимся вычислять возрастающие и убывающие интервалы функций. Мы решим пример, чтобы лучше понять концепцию. Рассмотрим f(x) = x 3 + 3x 2 — 45x + 9. Дифференцируем f(x) по x, чтобы найти f'(x).
f'(x) = 3x 2 + 6x — 45
= 3(x 2 + 2x — 15)
= 3 (x + 5) (x — 3)
90’004 Заменить f х) = 0 ⇒ х = -5, х = 3
Теперь пересечения по оси х для f'(x) равны х = -5 и х = 3. Имеющиеся у нас интервалы равны (-∞, -5), (-5, 3) и (3, ∞). Мы проверим знак f'(x) в каждом из этих интервалов, чтобы определить возрастающие и убывающие интервалы.
Имеющиеся у нас интервалы равны (-∞, -5), (-5, 3) и (3, ∞). Мы проверим знак f'(x) в каждом из этих интервалов, чтобы определить возрастающие и убывающие интервалы.
Интервал Значение x ф'(х) Увеличение/уменьшение (-∞, -5) х = -6 f'(-6) = 27 > 0 Увеличение (-5, 3) х = 0 f'(0) = -45 < 0 Уменьшение (3, ∞) х = 4 f'(4) = 27 > 0 Увеличение
Следовательно, возрастающие интервалы для f(x) = x 3 + 3x 2 — 45x + 9 равны (-∞, -5) и (3, ∞), а убывающий интервал f( х) равно (-5, 3).
Увеличение и уменьшение интервалов с помощью графика
Мы научились определять возрастающие и убывающие интервалы с помощью первой производной функции. Теперь мы определим интервалы, просто увидев график. Ниже приведены образцы двух графиков различных функций. На первом графике показана возрастающая функция по мере того, как график идет вверх по мере движения слева направо по оси x. На втором графике показана убывающая функция по мере того, как график движется вниз по мере движения слева направо по оси x.
Ниже приведены образцы двух графиков различных функций. На первом графике показана возрастающая функция по мере того, как график идет вверх по мере движения слева направо по оси x. На втором графике показана убывающая функция по мере того, как график движется вниз по мере движения слева направо по оси x.
Важные замечания по увеличению и уменьшению интервалов
- Для действительнозначной функции f(x) интервал I называется строго возрастающим интервалом, если для каждого x < y выполняется f(x ) < f(y).
- Для вещественнозначной функции f(x) интервал I называется строго убывающим интервалом, если для каждого x < y выполняется f(x) > f(y).
- Функция постоянна на интервале, если f'(x) = 0 на протяжении этого интервала.
Связанные темы
- Применение производных
- Дифференциальные уравнения
- Исчисление
Примеры увеличения и уменьшения интервалов
Пример 1: Определить интервалы возрастания и убывания функции f(x) = -x 3 + 3x 2 + 9.
Решение: Дифференцировать f(x) = -x 3 + 3x 2 + 9 вес. x
f'(x) = -3x 2 + 6x
= -3x(x — 2)
⇒ f'(x) = 0
⇒ -3x(x — 2) = 0
⇒ x = 0 или x = 2
Имеющиеся у нас интервалы равны (-∞, 0), (0, 2) и (2, ∞). Нам нужно определить возрастающие и убывающие интервалы от них.
Интервал Значение x ф'(х) Увеличение/уменьшение (-∞, 0) х = -1 f'(-1) = -9 < 0 Уменьшение (0, 2) х = 1 f'(1) = 3 > 0 Увеличение (2, ∞) х = 4 f'(4) = -24 < 0 Уменьшение
Ответ: Следовательно, (-∞, 0) и (2, ∞) — убывающие интервалы, а (0, 2) — возрастающие интервалы.
Пример 2: Покажите, что (-∞, ∞) является строго возрастающим интервалом для f(x) = 3x + 5.
Решение: Рассмотрим два действительных числа x и y в (-∞, ∞), что х < у. Тогда имеем
x < y
⇒ 3x < 3y
⇒ 3x + 5 < 3y + 5
⇒ f(x) < f(y)
Поскольку x и y произвольны, поэтому f(x ) < f(y), если x < y.
Ответ: Следовательно, (-∞, ∞) — строго возрастающий интервал для f(x) = 3x + 5,
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Увеличение и уменьшение интервалов Вопросы
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об увеличении и уменьшении интервалов
Что такое возрастающие и убывающие интервалы в алгебре?
Возрастающие и убывающие интервалы — это интервалы действительных чисел, в которых вещественнозначные функции возрастают и убывают соответственно.
Почему при описании возрастающих и убывающих интервалов используются только значения X?
Значения X используются для описания возрастающих и убывающих интервалов, поскольку значения функции f(x) увеличиваются или уменьшаются с увеличением значений x, т. е. изменение f(x) зависит от значения Икс.
Как найти интервалы возрастания и убывания функции?
Мы можем найти возрастающие и убывающие интервалы функции, используя ее первую производную. Мы можем найти критические точки и, следовательно, интервалы. Затем мы можем проверить знак производной в каждом интервале, чтобы определить возрастающие и убывающие интервалы.
Как найти возрастающие и убывающие интервалы с помощью графика?
Мы можем найти возрастающие и убывающие интервалы с помощью графика, наблюдая, движется ли график вверх или вниз при движении слева направо вдоль оси x. Для графиков, движущихся вверх, интервал увеличивается, а для графиков, движущихся вниз, интервал уменьшается.
Как узнать, что функция увеличивается?
Говорят, что функция f(x) возрастает на интервале I, если для любых двух чисел x и y из I, таких что x < y, выполняется f(x) ≤ f(y).
Какая функция не имеет возрастающих и убывающих интервалов?
Постоянная функция не возрастает и не убывает, поскольку график постоянной функции представляет собой прямую линию, параллельную оси x, а ее производная всегда равна 0.0005
Мэтуэй | Популярные проблемы
1 Найдите производную — d/dx натуральное бревно х 2 Оценить интеграл интеграл натурального логарифма x относительно x 3 Найдите производную — d/dx 92) 21 Оценить интеграл интеграл от 0 до 1 кубического корня из 1+7x относительно x 22 Найдите производную — d/dx грех(2x) 23 Найдите производную — d/dx 9(3x) по отношению к x 41 Оценить интеграл интеграл от cos(2x) по x 42 Найдите производную — d/dx 1/(корень квадратный из х) 43 Оцените интеграл 9бесконечность 45 Найдите производную — d/dx х/2 46 Найдите производную — d/dx -cos(x) 47 Найдите производную — d/dx грех(3x) 92+1 68 Оценить интеграл интеграл от sin(x) по x 69 Найдите производную — d/dx угловой синус(х) 70 Оценить предел предел, когда x приближается к 0 из (sin(x))/x 92 по отношению к х 85 Найдите производную — d/dx лог х 86 Найдите производную — d/dx арктан(х) 87 Найдите производную — d/dx бревно натуральное 5х92
Увеличение и уменьшение интервалов — GeeksforGeeks
Производные — это способ измерения скорости изменения переменной. Когда дело доходит до функций и исчисления, производные дают нам много информации о форме функции и ее графике. Они дают информацию об областях, где функция увеличивается или уменьшается. Они также полезны для определения максимального и минимального значений, достигаемых функцией. График функции, построенный на основе информации, собранной из производных, может помочь нам узнать предел и другую информацию о поведении функции.
Когда дело доходит до функций и исчисления, производные дают нам много информации о форме функции и ее графике. Они дают информацию об областях, где функция увеличивается или уменьшается. Они также полезны для определения максимального и минимального значений, достигаемых функцией. График функции, построенный на основе информации, собранной из производных, может помочь нам узнать предел и другую информацию о поведении функции.
Производные
Производная — это точка на функции, которая дает нам меру скорости изменения функции в этой конкретной точке. Говоря геометрически, они дают нам информацию о наклоне касательной в этой точке. Эту информацию можно использовать для определения интервалов или областей, в которых функция возрастает или убывает. Зная такие интервалы, несложно определить впадины и холмы на графике функции. На рисунке ниже показана функция f(x) и ее интервалы возрастания и убывания.
Для функции f(x). Для интервала, который я определил в своей области.
- Говорят, что функция f(x) возрастает на интервале I, если для любого a < b выполняется f(a) ≤ f(b).
- Говорят, что функция f(x) убывает на интервале I, если для любого a < b выполняется f(a) ≥ f(b).
Функция называется строго возрастающей, если для любого a < b выполняется f(a) < f(b). Аналогичное определение справедливо для строго убывающего случая.
Увеличение и уменьшение интервалов
Цель состоит в том, чтобы определить эти области, не глядя на график функции. Для этого посмотрим на производные функции в этих областях. То, что эти производные есть не что иное, как наклон касательных к этой кривой, уже установлено. На рисунке ниже показаны наклоны касательных в разных точках этой кривой.
Обратите внимание, что в областях, где функция уменьшается, наклон кривой фактически отрицательный и положительный для областей, где функция возрастает. Уклон на вершинах и долинах равен нулю. Так сказать формально.
Пусть f(x) — функция, непрерывная на [a, b] и дифференцируемая на интервале (a, b).
- Если f'(c) > 0 для всех c в (a, b), то говорят, что f(x) возрастает в интервале.
- Если f'(c) < 0 для всех c в (a, b), то говорят, что f(x) убывает на интервале.
- Если f'(c) = 0 для всех c в (a, b), то говорят, что f(x) постоянна на интервале.
Критические точки
На предыдущей диаграмме обратите внимание на то, как функция переходит от убывания к возрастанию или от возрастания к убыванию. Есть долина или вершина. Эти впадины и пики являются крайними точками функции, поэтому их называют экстремумами. Из рисунка хорошо видно, что в этих точках производная функции обращается в нуль. В этих точках функция достигает минимума и максимума.
Примечание. Функция может иметь любое количество критических точек. При этом все критические точки не обязательно дают максимальное и минимальное значение функции. Но каждая критическая точка — это долина, то есть точка минимума в локальной области.
Но каждая критическая точка — это долина, то есть точка минимума в локальной области.
На рисунке выше три экстремума, два из них минимумы, но есть только один глобальный максимум и глобальные минимумы. Таким образом, формально
Для функции f(x) точка x = c является экстремумом, если
f'(c) = 0
Определение возрастающих и убывающих интервалов
Из приведенных выше рисунков становится ясно, что каждый экстремум функции является точкой смены знака ее производной. То есть функция либо идет от возрастания к убыванию, либо наоборот. При поиске областей, в которых функция увеличивается или уменьшается, становится важным искать крайние значения. Для любой функции f(x) и заданного интервала необходимо выполнить следующие шаги, чтобы найти эти интервалы:
- Проверить, является ли функция дифференцируемой и непрерывной на заданном интервале.
- Решите уравнение f'(x) = 0, решения этого уравнения дают нам крайности.

- Для экстремальной точки x = c просмотрите область вблизи этой точки и проверьте знаки производных, чтобы найти интервалы возрастания или убывания функции.
Давайте рассмотрим несколько примеров задач, связанных с этими понятиями.
Примеры задач
Вопрос 1. Для данной функции укажите, возрастает она или убывает в области [-1,1]
f(x) = e x
Решение:
Для анализа 9 любой функции, первым шагом является поиск критических точек. f(x) = e x
f'(x) = e x …. (1)
Решение уравнения f'(x) = 0
e x = 0
Для этой функции в данной области нет критической точки. Это означает, что в данной области эта функция должна быть либо монотонно возрастающей, либо монотонно убывающей. Для этого проверьте производную функции в этой области.
f'(x) > 0 в интервале [0,1].
Таким образом, функция возрастает.
Вопрос 2. Для данной функции укажите, возрастает она или убывает в области [2,4]
f(x) = x 2 – x – 4
2 Решение:
Для анализа любой функции первым шагом является поиск критических точек.
f(x) = x 2 – x – 4
f'(x) = 2x – 1 …. (1)
Решение уравнения f'(x) = 0
2x – 1 = 0
⇒ x = 0,5
Критическая точка находится вне интересующей области. Это означает, что в данной области эта функция должна быть либо монотонно возрастающей, либо монотонно убывающей. Для этого проверьте производную функции в этой области.
f'(x) > 0 в интервале [2,4].
Таким образом, функция возрастает.
Вопрос 3: Найдите области возрастания или убывания данной функции.
f(x) = 3x + 4
Решение:
Чтобы проанализировать любую функцию, первым шагом является поиск критических точек.
f(x) = 3x + 4
f'(x) = 3
Это уравнение не равно нулю ни при каком x. Это означает, что производная этой функции постоянна во всей области определения.
Поскольку f'(x) > 0 для всех значений x.
Функция монотонно возрастает в своей области определения.
Вопрос 4: Найдите области возрастания или убывания данной функции.
f(x) = x 2 + 4x + 4
Решение.
f(x) = x 2 + 4x + 4
f'(x) = 2x + 4 …. (1)
Решение уравнения f'(x) = 0
2x + 4 = 0
⇒ x = -2
Таким образом, при x = -2 производная этой функции меняет знак. Проверьте знак производной в его окрестности.
при x = -1
f'(x) = 2(-1) + 4 = 2 > 0
Это означает, что при x > -2 функция возрастает.
при x = -3
f'(x) = 2(-3) + 4 = -2 < 0
При x < -2 функция убывает.
Вопрос 5: Найдите области возрастания или убывания данной функции.
f(x) = x 2 + 3x
Решение:
Чтобы проанализировать любую функцию, первым шагом является поиск критических точек.
f(x) = x 2 + 3x
f'(x) = 2x + 3 …. (1)
Решение уравнения f'(x) = 0
2x + 3 = 0
⇒ x = -1,5
Таким образом, при x = -1,5 производная этой функции меняет знак. Проверьте знак производной в его окрестности.
при x = -1
f'(x) = 2(-1) + 3 = 1 > 0
Это означает, что при x > -1,5 функция возрастает.
при x = -3
f'(x) = 2(-3) + 3 = -3 < 0
При x < -1,5 функция убывает.
Вопрос 6: Найдите области возрастания или убывания данной функции.
f(x) = e x + e -x
Решение:
f(x) = e x + e -x
f'(x) = e x – e -x …. (1)
(1)
Решение уравнения f ‘(x) = 0
E x -E -x = 0
⇒ E x = E -x
⇒ E 2x = 1
⇒ E 2x = 1
⇒ E 2x = 1
⇒ E 2x = 1 9005
e 2x = e 0
Сравнивая обе части уравнения,
⇒ 2x = 0
⇒ x = 0
Таким образом, при x = 0 производная этой функции меняет знак. Проверьте знак производной в его окрестности.
при x = 1
f'(x) = e 1 – e -1 > 0
Это означает, что при x > 0 функция возрастает.
при x = –1
f'(x) = e -1 – e 1 < 0
При x < 0 функция убывает.
Интервалы возрастания и убывания
Интервалы возрастания и убывания
Чтобы понять, как изменяется функция, нам нужно знать интервалы, в течение которых функция изменяется определенным образом. Функция увеличивается в течение интервала, когда значения выхода функции увеличиваются по мере того, как мы увеличиваем входные значения функции.
Функция увеличивается в течение интервала, когда значения выхода функции увеличиваются по мере того, как мы увеличиваем входные значения функции.
Таким же образом функция уменьшается в интервале, когда значения выхода функции уменьшаются по мере того, как мы уменьшаем входные значения функции. Мы знаем, что наклон отображает среднюю скорость изменения функции в данной точке. Если наклон положительный , то мы говорим, что функция возрастает. Отрицательный наклон изображает убывающую функцию, а нулевой наклон показывает, что функция остается постоянной за указанный интервал.
Лучшие репетиторы по математике
Поехали
Локальный максимум и локальный минимум
Все функции не увеличиваются и не уменьшаются по всему домену. Иногда функция меняется с возрастающей на убывающую для значения входа, т. е. по мере увеличения значения входа значение функции уменьшается. Это значение входа, при котором значение функции претерпевает переход от увеличения к уменьшению, известно как локальный максимум . Когда у нас есть более одного такого входного значения, мы называем их локальными максимумами .
Это значение входа, при котором значение функции претерпевает переход от увеличения к уменьшению, известно как локальный максимум . Когда у нас есть более одного такого входного значения, мы называем их локальными максимумами .
Есть еще один случай, когда значение функции меняется с убывающего на возрастающее по мере увеличения входного значения. Входное значение в этом случае известно как локальный минимум . Если таких входных значений больше, то мы называем их локальными минимумами . И локальные максимумы, и минимумы известны как локальный экстремум или локальный экстремум . В экстремумах функция не возрастает и не убывает, а остается постоянной.
Поскольку производная функции изображает мгновенную скорость изменения функции в данной точке, поэтому мы можем использовать ее для определения интервалов возрастания и убывания функции. В следующем разделе мы объясним это подробно.
В следующем разделе мы объясним это подробно.
Возрастающий интервал
Если f дифференцируема в точке a, то f строго возрастает в точке a, если .
Убывающий интервал
Если f дифференцируема в точке a, то f строго убывает в точке a if
Чтобы определить, возрастает или убывает функция в точке, важно, чтобы она была дифференцируемой. В следующем разделе мы решим несколько примеров для определения возрастающих и убывающих интервалов с использованием производных функции.
Пример 1
Изучить интервалы возрастания и убывания функции.
Раствор
Мы выполним следующие шаги, чтобы определить интервалы возрастания и убывания вышеуказанной функции:
Шаг 1 — Найдите производную функции
На этом шаге мы продифференцируем функцию .
Шаг 2 — Получение корней первой производной функции f ‘(x)
На этом шаге мы получим корни первой производной функции следующим образом:
9Шаг 3. Проверка точек из всех интервалов Эти корни показывают, что у нас есть три интервала, которые равны , и .
Проверка точек из всех интервалов Эти корни показывают, что у нас есть три интервала, которые равны , и .
Мы возьмем значение из каждого интервала и посмотрим, увеличивается оно или уменьшается.
Возьмем -2 из интервала и подставим в производную функции:
Так как f ‘(x) больше 0, то функция на этом интервале возрастает.
Теперь возьмем точку из интервала (-1, 1).
Так как f'(x)<0, то на этом интервале функция убывает.
Теперь возьмем точку из интервала и подставим ее в производную функции:
Поскольку f ‘(x) >0, значит, функция на этом интервале возрастает.
Шаг 4. Запишите возрастающие и убывающие интервалы
На шаге 3 мы проверили точки из каждого интервала и подставили их в производную функции. У нас есть два интервала, где функция возрастала, и один интервал, где функция убывала. Следовательно, мы можем записать возрастающие и убывающие интервалы как:
Возрастающие:
Убывающие:
Пример 2
Изучите интервалы возрастания и убывания функции .
Решение
Мы выполним следующие шаги, чтобы определить интервалы возрастания и убывания вышеуказанной функции:
Шаг 1 — Найдите производную функции
На этом шаге мы продифференцируем функцию .
Шаг 2 — Получить корни первой производной функции f ‘(x)
На этом шаге мы получим корни первой производной функции следующим образом:
У этой производной есть только один корень.
Шаг 3 — Проверка точек из всех интервалов
У нас есть один корень производной функции. У нас будет два интервала с учетом единственного корня функции. Эти интервалы равны и .
Мы возьмем значение из каждого интервала и посмотрим, увеличивается оно или уменьшается.
Возьмем -4 из интервала и подставим в производную функции:
Поскольку f ‘(x) < 0, значит, функция на этом интервале убывает.
Теперь возьмем точку из интервала
Так как f ‘(x) > 0, значит функция на этом интервале возрастает.
Шаг 4. Запишите возрастающие и убывающие интервалы
На шаге 3 мы проверили точки из каждого интервала и подставили их в производную функции. У функции только один корень, поэтому у нас два интервала. Мы можем записать возрастающие и убывающие интервалы как:
Возрастание:
Убывание:
Пример 3
Изучите интервалы возрастания и убывания функции .
Решение
Мы выполним следующие шаги, чтобы определить интервалы возрастания и убывания вышеуказанной функции:
Шаг 1 — Найдите производную функции
На этом шаге мы продифференцируем функцию .
Шаг 2 — Получить корни первой производной функции f ‘(x)
На этом шаге мы получим корни первой производной функции следующим образом:
Существует только один корень производной этой функции.
Чтобы определить, когда функция возрастает, вы должны сначала взять производную, затем приравнять ее к 0, а затем найти, между какими нулевыми значениями функция положительна.
Сначала возьмем производную:
Приравняем к 0 и решим:
Теперь проверьте значения со всех сторон, чтобы найти, когда функция положительна и, следовательно, возрастает. Я проверю значения -6, 0 и 2.
Поскольку значения являются положительными, когда x = -6 и 2, интервал увеличивается на интервалах, которые включают эти значения. . Поэтому наш ответ:
Сообщить об ошибке
Найдите интервал(ы), когда следующая функция возрастает. График, чтобы перепроверить свой ответ.
Возможные ответы:
Всегда
Никогда
Правильный ответ:
4
55
5
Объяснение: Чтобы определить, когда функция возрастает, вы должны сначала взять производную, затем приравнять ее к 0, а затем найти, между какими нулевыми значениями функция положительна.
Сначала возьмем производную:
Приравняем к 0 и решим:
Теперь проверьте значения со всех сторон, чтобы найти, когда функция положительна и, следовательно, возрастает. Я проверю значения 0, 2 и 10.
Поскольку значение является положительным, когда x = 0 и 10, интервал увеличивается в обоих этих интервалах. Поэтому наш ответ:
Сообщить об ошибке
Увеличивается или уменьшается на интервале?
Возможные ответы:
Возрастание. на интервале.
Увеличение. на интервале.
Невозможно определить на основании предоставленной информации
Уменьшается. на интервале.
Уменьшение. на интервале.
Правильный ответ:
Возрастание. на интервале.
Объяснение:
Чтобы найти возрастающие и убывающие интервалы, нам нужно найти, где наша первая производная больше или меньше нуля. Если наша первая производная положительна, наша исходная функция возрастает, а если g'(x) отрицательна, g(x) убывает.
Если наша первая производная положительна, наша исходная функция возрастает, а если g'(x) отрицательна, g(x) убывает.
Начните с:
Если мы подставим любое число от 3 до 6, мы получим положительное число для g'(x). Таким образом, эта функция должна возрастать на интервале {3,6 }, так как g'(x) положительна.
Сообщить об ошибке
Увеличивается или уменьшается на интервале?
Возможные ответы:
Увеличивается, потому что отрицательно.
Уменьшение, поскольку положительно.
Возрастание, поскольку положительно.
Уменьшение, поскольку отрицательно.
не увеличивается и не уменьшается на заданном интервале.
Правильный ответ:
Возрастает, потому что положительно.
Объяснение:
Чтобы узнать, возрастает функция или убывает, нам нужно определить, положительна или отрицательна первая производная на заданном интервале.
Итак, начиная с:
Мы получаем:
используя степенное правило .
Найдите функцию на каждом конце интервала.
Итак, первая производная положительна на всем интервале, поэтому g(t) возрастает на интервале.
Сообщить об ошибке
Является ли следующая функция возрастающей или убывающей на интервале?
Возможные ответы:
Убывающий, т.к. положителен на данном интервале.
Функция не возрастает и не убывает на интервале.
Возрастание, так как на данном интервале положительно.
По убыванию, так как на данном интервале отрицательно.
Возрастание, поскольку отрицательно на заданном интервале.
Правильный ответ:
Возрастание, т.к. положительно на данном интервале.
Объяснение:
Функция возрастает на интервале, если для каждой точки этого интервала первая производная положительна.
Итак, нам нужно найти первую производную, а затем подставить конечные точки нашего интервала.
Найдите первую производную с помощью степенного правила
Подставьте конечные точки и оцените функцию.
Оба положительны, поэтому наша функция возрастает на данном интервале.
Сообщить об ошибке
С какими интервалами увеличивается следующая функция?
Возможные ответы:
Правильный ответ:
Пояснение:
Первый шаг — найти первую производную.
Помните, что производная от
Далее найдите критические точки, которые являются точками, где или не определены. Чтобы найти точки, установите числитель на , чтобы найти неопределенные точки, установите знаменатель на . Критические точки и
Последним шагом является проверка точек во всех регионах, чтобы увидеть, какой диапазон дает положительное значение для .
Если мы подставим число из первого диапазона, т.е. получим отрицательное число.
Из второго диапазона мы получаем положительное число.
Из третьего диапазона мы получаем отрицательное число.
Из последнего диапазона мы получаем положительное число.
Таким образом, второй и последний диапазоны — это те, где увеличивается.
Сообщить об ошибке
Ниже приведен полный график . На каком интервале(ах) происходит увеличение?
Возможные ответы:
Правильный ответ:
Объяснение:
увеличивается, когда является положительным (над осью). Это происходит на интервалах .
Сообщить об ошибке
Функция A
Функция B
9 10004
Function C
Function D
Function E
5 graphs of different functions are shown выше. На каком графике показана возрастающая/неубывающая функция ?
На каком графике показана возрастающая/неубывающая функция ?
Возможные ответы:
Функция D
Функция E
Функция B
Функция A
Функция C
Правильный ответ:
Функция E
Объяснение:
Функция возрастает, если для любого , (т. е. наклон всегда больше или равен нулю)
Функция – единственная функция, обладающая этим свойством. Обратите внимание, что функция E возрастает, но не строго возрастает
Сообщить об ошибке
Найдите возрастающие интервалы следующей функции на интервале :
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти возрастающие интервалы заданной функции, нужно определить интервалы, на которых функция имеет положительную первую производную. Чтобы найти эти интервалы, сначала найдите критические значения или точки, в которых первая производная функции равна нулю.
Чтобы найти эти интервалы, сначала найдите критические значения или точки, в которых первая производная функции равна нулю.
Для данной функции .
Эта производная была найдена с помощью правила степени
.
При нулевом значении . Поскольку мы рассматриваем только открытый интервал (0,5) для этой функции, мы можем игнорировать . Далее мы смотрим интервалы вокруг критического значения , которые равны и . На первом интервале первая производная функции отрицательна (подстановка значений дает нам отрицательное число), что означает, что функция на этом интервале убывает. Однако для второго интервала первая производная положительна, что указывает на возрастание функции на этом интервале.
Сообщить об ошибке
← Назад 1 2 3 Далее →
Уведомление об авторских правах
Все ресурсы исчисления 1
10 Диагностические тесты
438 практических тестов
Вопрос дня
Карточки
Learn by Concept
Увеличение и уменьшение интервалов — определение, формулы
Задумывались ли вы, почему расстояние сокращается, как только вы приближаетесь к дому вашего друга? И почему это происходит наоборот, когда вы едете в противоположном направлении? Это из-за функций. В исчислении возрастающие и убывающие функции — это функции, для которых значение f (x) увеличивается и уменьшается соответственно с увеличением значения x.
В исчислении возрастающие и убывающие функции — это функции, для которых значение f (x) увеличивается и уменьшается соответственно с увеличением значения x.
Чтобы проверить изменение функций, нужно найти производные таких функций. Если значение функции увеличивается со значением x, то функция положительна. Если значение функции уменьшается с увеличением значения x, то говорят, что функция отрицательна.
Интервалы возрастания и убывания действительных чисел — это действительнозначные функции, которые имеют тенденцию возрастать и уменьшаться при изменении значения зависимой переменной функции. Чтобы найти интервалы возрастания и убывания, нужно определить первую производную функции. Это делается для того, чтобы найти знак функции, будь то отрицательный или положительный. Интервал функции называется положительным, если значение функции f(x) увеличивается с увеличением значения x. Напротив, интервал функции называется отрицательным, если значение функции f (x) уменьшается с увеличением значения x.
Альтернативно, интервал функции положителен, если положительный знак первой производной. Интервал функции отрицательный, если знак первой производной отрицательный. Следовательно, положительный интервал увеличивается, тогда как отрицательный интервал называется убывающим интервалом.
Как записать интервалы возрастания и убывания? Вы можете представлять интервалы возрастания и убывания, понимая простые математические понятия, приведенные ниже:
- Говорят, что значение интервала увеличивается для каждого x < y, где f (x) ≤ f (y) для действительнозначной функции f (x).
- Если значение интервала f (x) ≥ f (y) для каждого x < y, то интервал называется убывающим.
Вы также можете использовать первую производную, чтобы найти интервалы возрастания и убывания и соответственно записать их.
- Если первая производная функции равна f’ (x) ≥ 0, интервал увеличивается.
- С другой стороны, если значение производной f’ (x) ≤ 0, то интервал называется убывающим.

Определение интервалов возрастания и убывания Поскольку вы умеете записывать интервалы возрастания и убывания, пора научиться находить интервалы возрастания и убывания. Давайте научимся находить интервалы возрастания и убывания на примере.
Рассмотрим функцию f(x) = x 3 + 3x 2 – 45x + 9. Чтобы найти интервалы возрастания и убывания, нужно продифференцировать их относительно x. После дифференцирования вы получите первую производную как f’(x).
Следовательно, f’(x) = 3x 2 + 6x – 45
Вынимая из всего члена 3 общих, получаем 3 (x 2 + 2x -15). Теперь, находя множители этого уравнения, мы получаем, 3 (x + 5) (x – 3). Если вы замените эти значения эквивалентными нулю, вы получите значения x.
Следовательно, значение x = -5, 3.
Чтобы найти значение функции, подставьте эти значения в исходную функцию, и вы получите значения, как показано в таблице ниже.
Interval Value of x f'(x) Increasing/Decreasing (-∞, -5) x = -6 f ‘(-6) = 27 > 0 Возрастание (-5, 3) x = 0 f'(0) = -45 < 0 Уменьшение ) x = 4 f'(4) = 27 > 0 Возрастание
Следовательно, для данной функции f (x) = x 3 + 3x 2 – 45x + 9 возрастающие интервалы равны (-∞, -5) и (3, ∞), а убывающие интервалы равны (-5, 3).
Частный случай: функция «один к одному»
Строго возрастающие или убывающие функции обладают особым свойством, называемым инъективными или взаимно однозначными функциями. Это означает, что вы никогда не получите одно и то же значение функции дважды.
Например, вы можете получить значение функции дважды на первом графике. Однако на втором графике у вас никогда не будет одинакового значения функции. Следовательно, график справа известен как взаимно однозначная функция.
Это полезно, потому что инъективные функции могут быть обращены. Вы можете вернуться от значения «y» функции к значению «x». Обычно это невозможно, так как существует более одного возможного значения x.
Пример 1: Какими будут интервалы возрастания и убывания функции f (x) = -x 3 + 3x 2 + 9?
Решение: Чтобы найти интервалы возрастания и убывания, нужно продифференцировать функцию относительно x. Следовательно, f’(x) = -3x 2 + 6x.
Следовательно, f’(x) = -3x 2 + 6x.
Теперь, убрав из уравнения 3 обычных, мы получим -3x (x – 2). Чтобы найти значения x, приравняем это уравнение к нулю, получим f'(x) = 0
⇒ -3x (x – 2) = 0
⇒ x = 0 или x = 2.
Следовательно , интервалы для функции f (x) равны (-∞, 0), (0, 2) и (2, ∞). Чтобы найти значения функции, ознакомьтесь с таблицей ниже.
Interval Value of x f'(x) Increasing/Decreasing (-∞, 0) x = -1 f ‘(-1) = -9 < 0 Убывающая (0, 2) x = 1 f'(1) = 3 > 0 Возрастающая 9 x = 4 f'(4) = -24 < 0 Уменьшение
Следовательно, (-∞, 0) и (2, ∞) — убывающие интервалы, а (0, 2) — возрастающие интервалы.
Пример 2: Считаете ли вы, что интервал (-∞, ∞) является строго возрастающим интервалом для f(x) = 3x + 5? Если да, то докажите это.
Решение: Чтобы доказать утверждение, рассмотрим два действительных числа x и y в интервале (-∞, ∞), такие что x < y.
Тогда 3x < 3y.
⇒ 3x + 5 < 3y + 5
⇒ f (x) < f (y)
Так как x и y являются произвольными значениями, следовательно, f (x) < f (y) всякий раз, когда x < y. Следовательно, интервал (-∞, ∞) является строго возрастающим интервалом для f(x) = 3x + 5. Следовательно, утверждение доказано.
Пример 3: Найдите, является ли функция f (x) x 3 −4x для x в интервале [−1, 2] возрастающей или убывающей.
Решение: вам нужно начать с -1, чтобы построить функцию на графике. -1 выбрано потому, что интервал [−1, 2] начинается с этого значения. При x = -1 функция убывает. Как только он достигнет значения 1,2, функция увеличится. После того, как функция достигла значения больше 2, значение будет продолжать увеличиваться. При точном анализе нельзя найти, увеличивается интервал или уменьшается. Итак, скажем, в интервале [−1, 2],
Итак, скажем, в интервале [−1, 2],
- Кривая спадает в интервале [−1, прибл. 1,2]
- Кривая возрастает в интервале [прибл. 1,2, 2]
Определение интервалов возрастания и убывания с помощью графика В приведенных выше разделах вы научились писать интервалы возрастания и убывания. В этом разделе вы узнаете, как находить интервалы возрастания и убывания с помощью графиков. Было бы полезно, если бы вы изучили приведенную ниже таблицу, чтобы четко понять концепцию.
Возрастающий интервал Уменьшающийся интервал На приведенном ниже графике показана возрастающая функция. Это можно определить, взглянув на приведенный график. Поскольку график идет вверх по мере движения слева направо по оси X, говорят, что график увеличивается. На приведенном ниже графике показана убывающая функция. Это можно определить, взглянув на приведенный график. Поскольку график идет вниз при движении слева направо по оси X, говорят, что график уменьшается.
Поскольку график идет вниз при движении слева направо по оси X, говорят, что график уменьшается.
Наводит на размышления - Функция выдаст постоянное значение и будет называться постоянной, если f’(x) = 0 в течение этого интервала.
- Для вещественнозначной функции f (x) интервал I называется строго возрастающим интервалом, если для каждого x < y выполняется f (x) < f (y).
- Для вещественнозначной функции f (x) интервал I называется строго убывающим интервалом, если для каждого x < y выполняется f (x) > f (y).
- Для функции f (x), когда x1 < x2, тогда f (x1) ≤ f (x2), интервал называется возрастающим.
- Для функции f (x), когда x1 < x2, а затем f (x1) < f (x2), интервал называется строго возрастающим. Нужно быть внимательным, глядя на знаки возрастающих и строго возрастающих функций.
- Для функции f (x), когда x1 < x2, тогда f (x1) ≥ f (x2), интервал называется убывающим.
- Для функции f (x), когда x1 < x2, то f (x1) > f (x2), интервал называется строго убывающим.

- Если значение функции не меняется при изменении значения x, то говорят, что функция является постоянной функцией.
Интервалы возрастания и убывания — определение, формулы, примеры
LearnPracticeDownload
Интервалы возрастания и убывания — это интервалы действительных чисел, в которых вещественные функции возрастают и убывают соответственно. Чтобы определить возрастающие и убывающие интервалы, мы используем критерий производной первого порядка для проверки знака производной в каждом интервале. Интервал увеличивается, если значение функции f(x) увеличивается с увеличением значения x, и убывает, если f(x) уменьшается с уменьшением x.
В этой статье мы научимся определять возрастающие и убывающие интервалы с помощью теста производной первого порядка и графика функции с помощью примеров для лучшего понимания концепции.
1. Что такое возрастающие и убывающие интервалы? 2.
Увеличение и уменьшение интервалов Определение 3. Нахождение возрастающих и убывающих интервалов 4. Увеличение и уменьшение интервалов с помощью графика 5. Часто задаваемые вопросы об увеличении и уменьшении интервалов
Что такое возрастающие и убывающие интервалы?
Интервалы возрастания или убывания функций называются возрастающими и убывающими интервалами. Эти интервалы можно оценить, проверив знак первой производной функции на каждом интервале. Если первая производная функции на интервале положительна, то этот интервал называется возрастающим, а если первая производная функции на интервале отрицательна, то этот интервал называется убывающим. Давайте пройдемся по их формальным определениям, чтобы понять их смысл:
Увеличение и уменьшение интервалов Определение
Определения увеличения и уменьшения интервалов приведены ниже.
- Для вещественнозначной функции f(x) интервал I называется возрастающим интервалом, если для каждого x < y выполняется f(x) ≤ f(y).
- Для действительнозначной функции f(x) интервал I называется убывающим интервалом, если для каждого x < y выполняется f(x) ≥ f(y).
Мы также можем определить возрастающий и убывающий интервалы, используя первую производную функции f(x) как:
- Если f'(x) ≥ 0 на I, то I называется возрастающим интервалом.
- Если f'(x) ≤ 0 на I, то I называется убывающим интервалом.
Нахождение возрастающих и убывающих интервалов
Теперь, когда мы поняли значение возрастающих и убывающих интервалов, давайте теперь научимся вычислять возрастающие и убывающие интервалы функций. Мы решим пример, чтобы лучше понять концепцию. Рассмотрим f(x) = x 3 + 3x 2 — 45x + 9. Дифференцируем f(x) по x, чтобы найти f'(x).
f'(x) = 3x 2 + 6x — 45
= 3(x 2 + 2x — 15)
= 3 (x + 5) (x — 3)
90’004 Заменить f х) = 0 ⇒ х = -5, х = 3
Теперь пересечения по оси х для f'(x) равны х = -5 и х = 3. Имеющиеся у нас интервалы равны (-∞, -5), (-5, 3) и (3, ∞). Мы проверим знак f'(x) в каждом из этих интервалов, чтобы определить возрастающие и убывающие интервалы.
Имеющиеся у нас интервалы равны (-∞, -5), (-5, 3) и (3, ∞). Мы проверим знак f'(x) в каждом из этих интервалов, чтобы определить возрастающие и убывающие интервалы.
Интервал Значение x ф'(х) Увеличение/уменьшение (-∞, -5) х = -6 f'(-6) = 27 > 0 Увеличение (-5, 3) х = 0 f'(0) = -45 < 0 Уменьшение (3, ∞) х = 4 f'(4) = 27 > 0 Увеличение
Следовательно, возрастающие интервалы для f(x) = x 3 + 3x 2 — 45x + 9 равны (-∞, -5) и (3, ∞), а убывающий интервал f( х) равно (-5, 3).
Увеличение и уменьшение интервалов с помощью графика
Мы научились определять возрастающие и убывающие интервалы с помощью первой производной функции. Теперь мы определим интервалы, просто увидев график. Ниже приведены образцы двух графиков различных функций. На первом графике показана возрастающая функция по мере того, как график идет вверх по мере движения слева направо по оси x. На втором графике показана убывающая функция по мере того, как график движется вниз по мере движения слева направо по оси x.
Ниже приведены образцы двух графиков различных функций. На первом графике показана возрастающая функция по мере того, как график идет вверх по мере движения слева направо по оси x. На втором графике показана убывающая функция по мере того, как график движется вниз по мере движения слева направо по оси x.
Важные замечания по увеличению и уменьшению интервалов
- Для действительнозначной функции f(x) интервал I называется строго возрастающим интервалом, если для каждого x < y выполняется f(x ) < f(y).
- Для вещественнозначной функции f(x) интервал I называется строго убывающим интервалом, если для каждого x < y выполняется f(x) > f(y).
- Функция постоянна на интервале, если f'(x) = 0 на протяжении этого интервала.
Связанные темы
- Применение производных
- Дифференциальные уравнения
- Исчисление
Примеры увеличения и уменьшения интервалов
Пример 1: Определить интервалы возрастания и убывания функции f(x) = -x 3 + 3x 2 + 9.
Решение: Дифференцировать f(x) = -x 3 + 3x 2 + 9 вес. x
f'(x) = -3x 2 + 6x
= -3x(x — 2)
⇒ f'(x) = 0
⇒ -3x(x — 2) = 0
⇒ x = 0 или x = 2
Имеющиеся у нас интервалы равны (-∞, 0), (0, 2) и (2, ∞). Нам нужно определить возрастающие и убывающие интервалы от них.
Интервал Значение x ф'(х) Увеличение/уменьшение (-∞, 0) х = -1 f'(-1) = -9 < 0 Уменьшение (0, 2) х = 1 f'(1) = 3 > 0 Увеличение (2, ∞) х = 4 f'(4) = -24 < 0 Уменьшение
Ответ: Следовательно, (-∞, 0) и (2, ∞) — убывающие интервалы, а (0, 2) — возрастающие интервалы.
Пример 2: Покажите, что (-∞, ∞) является строго возрастающим интервалом для f(x) = 3x + 5.
Решение: Рассмотрим два действительных числа x и y в (-∞, ∞), что х < у. Тогда имеем
x < y
⇒ 3x < 3y
⇒ 3x + 5 < 3y + 5
⇒ f(x) < f(y)
Поскольку x и y произвольны, поэтому f(x ) < f(y), если x < y.
Ответ: Следовательно, (-∞, ∞) — строго возрастающий интервал для f(x) = 3x + 5,
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Увеличение и уменьшение интервалов Вопросы
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об увеличении и уменьшении интервалов
Что такое возрастающие и убывающие интервалы в алгебре?
Возрастающие и убывающие интервалы — это интервалы действительных чисел, в которых вещественнозначные функции возрастают и убывают соответственно.
Почему при описании возрастающих и убывающих интервалов используются только значения X?
Значения X используются для описания возрастающих и убывающих интервалов, поскольку значения функции f(x) увеличиваются или уменьшаются с увеличением значений x, т. е. изменение f(x) зависит от значения Икс.
Как найти интервалы возрастания и убывания функции?
Мы можем найти возрастающие и убывающие интервалы функции, используя ее первую производную. Мы можем найти критические точки и, следовательно, интервалы. Затем мы можем проверить знак производной в каждом интервале, чтобы определить возрастающие и убывающие интервалы.
Как найти возрастающие и убывающие интервалы с помощью графика?
Мы можем найти возрастающие и убывающие интервалы с помощью графика, наблюдая, движется ли график вверх или вниз при движении слева направо вдоль оси x. Для графиков, движущихся вверх, интервал увеличивается, а для графиков, движущихся вниз, интервал уменьшается.
Как узнать, что функция увеличивается?
Говорят, что функция f(x) возрастает на интервале I, если для любых двух чисел x и y из I, таких что x < y, выполняется f(x) ≤ f(y).
Какая функция не имеет возрастающих и убывающих интервалов?
Постоянная функция не возрастает и не убывает, поскольку график постоянной функции представляет собой прямую линию, параллельную оси x, а ее производная всегда равна 0.0005
Мэтуэй | Популярные проблемы
1 Найдите производную — d/dx натуральное бревно х 2 Оценить интеграл интеграл натурального логарифма x относительно x 3 Найдите производную — d/dx 92) 21 Оценить интеграл интеграл от 0 до 1 кубического корня из 1+7x относительно x 22 Найдите производную — d/dx грех(2x) 23 Найдите производную — d/dx 9(3x) по отношению к x 41 Оценить интеграл интеграл от cos(2x) по x 42 Найдите производную — d/dx 1/(корень квадратный из х) 43 Оцените интеграл 9бесконечность 45 Найдите производную — d/dx х/2 46 Найдите производную — d/dx -cos(x) 47 Найдите производную — d/dx грех(3x) 92+1 68 Оценить интеграл интеграл от sin(x) по x 69 Найдите производную — d/dx угловой синус(х) 70 Оценить предел предел, когда x приближается к 0 из (sin(x))/x 92 по отношению к х 85 Найдите производную — d/dx лог х 86 Найдите производную — d/dx арктан(х) 87 Найдите производную — d/dx бревно натуральное 5х92
Увеличение и уменьшение интервалов — GeeksforGeeks
Производные — это способ измерения скорости изменения переменной. Когда дело доходит до функций и исчисления, производные дают нам много информации о форме функции и ее графике. Они дают информацию об областях, где функция увеличивается или уменьшается. Они также полезны для определения максимального и минимального значений, достигаемых функцией. График функции, построенный на основе информации, собранной из производных, может помочь нам узнать предел и другую информацию о поведении функции.
Когда дело доходит до функций и исчисления, производные дают нам много информации о форме функции и ее графике. Они дают информацию об областях, где функция увеличивается или уменьшается. Они также полезны для определения максимального и минимального значений, достигаемых функцией. График функции, построенный на основе информации, собранной из производных, может помочь нам узнать предел и другую информацию о поведении функции.
Производные
Производная — это точка на функции, которая дает нам меру скорости изменения функции в этой конкретной точке. Говоря геометрически, они дают нам информацию о наклоне касательной в этой точке. Эту информацию можно использовать для определения интервалов или областей, в которых функция возрастает или убывает. Зная такие интервалы, несложно определить впадины и холмы на графике функции. На рисунке ниже показана функция f(x) и ее интервалы возрастания и убывания.
Для функции f(x). Для интервала, который я определил в своей области.
- Говорят, что функция f(x) возрастает на интервале I, если для любого a < b выполняется f(a) ≤ f(b).
- Говорят, что функция f(x) убывает на интервале I, если для любого a < b выполняется f(a) ≥ f(b).
Функция называется строго возрастающей, если для любого a < b выполняется f(a) < f(b). Аналогичное определение справедливо для строго убывающего случая.
Увеличение и уменьшение интервалов
Цель состоит в том, чтобы определить эти области, не глядя на график функции. Для этого посмотрим на производные функции в этих областях. То, что эти производные есть не что иное, как наклон касательных к этой кривой, уже установлено. На рисунке ниже показаны наклоны касательных в разных точках этой кривой.
Обратите внимание, что в областях, где функция уменьшается, наклон кривой фактически отрицательный и положительный для областей, где функция возрастает. Уклон на вершинах и долинах равен нулю. Так сказать формально.
Пусть f(x) — функция, непрерывная на [a, b] и дифференцируемая на интервале (a, b).
- Если f'(c) > 0 для всех c в (a, b), то говорят, что f(x) возрастает в интервале.
- Если f'(c) < 0 для всех c в (a, b), то говорят, что f(x) убывает на интервале.
- Если f'(c) = 0 для всех c в (a, b), то говорят, что f(x) постоянна на интервале.
Критические точки
На предыдущей диаграмме обратите внимание на то, как функция переходит от убывания к возрастанию или от возрастания к убыванию. Есть долина или вершина. Эти впадины и пики являются крайними точками функции, поэтому их называют экстремумами. Из рисунка хорошо видно, что в этих точках производная функции обращается в нуль. В этих точках функция достигает минимума и максимума.
Примечание. Функция может иметь любое количество критических точек. При этом все критические точки не обязательно дают максимальное и минимальное значение функции. Но каждая критическая точка — это долина, то есть точка минимума в локальной области.
Но каждая критическая точка — это долина, то есть точка минимума в локальной области.
На рисунке выше три экстремума, два из них минимумы, но есть только один глобальный максимум и глобальные минимумы. Таким образом, формально
Для функции f(x) точка x = c является экстремумом, если
f'(c) = 0
Определение возрастающих и убывающих интервалов
Из приведенных выше рисунков становится ясно, что каждый экстремум функции является точкой смены знака ее производной. То есть функция либо идет от возрастания к убыванию, либо наоборот. При поиске областей, в которых функция увеличивается или уменьшается, становится важным искать крайние значения. Для любой функции f(x) и заданного интервала необходимо выполнить следующие шаги, чтобы найти эти интервалы:
- Проверить, является ли функция дифференцируемой и непрерывной на заданном интервале.
- Решите уравнение f'(x) = 0, решения этого уравнения дают нам крайности.

- Для экстремальной точки x = c просмотрите область вблизи этой точки и проверьте знаки производных, чтобы найти интервалы возрастания или убывания функции.
Давайте рассмотрим несколько примеров задач, связанных с этими понятиями.
Примеры задач
Вопрос 1. Для данной функции укажите, возрастает она или убывает в области [-1,1]
f(x) = e x
Решение:
Для анализа 9 любой функции, первым шагом является поиск критических точек. f(x) = e x
f'(x) = e x …. (1)
Решение уравнения f'(x) = 0
e x = 0
Для этой функции в данной области нет критической точки. Это означает, что в данной области эта функция должна быть либо монотонно возрастающей, либо монотонно убывающей. Для этого проверьте производную функции в этой области.
f'(x) > 0 в интервале [0,1].
Таким образом, функция возрастает.
Вопрос 2. Для данной функции укажите, возрастает она или убывает в области [2,4]
f(x) = x 2 – x – 4
2 Решение:
Для анализа любой функции первым шагом является поиск критических точек.
f(x) = x 2 – x – 4
f'(x) = 2x – 1 …. (1)
Решение уравнения f'(x) = 0
2x – 1 = 0
⇒ x = 0,5
Критическая точка находится вне интересующей области. Это означает, что в данной области эта функция должна быть либо монотонно возрастающей, либо монотонно убывающей. Для этого проверьте производную функции в этой области.
f'(x) > 0 в интервале [2,4].
Таким образом, функция возрастает.
Вопрос 3: Найдите области возрастания или убывания данной функции.
f(x) = 3x + 4
Решение:
Чтобы проанализировать любую функцию, первым шагом является поиск критических точек.
f(x) = 3x + 4
f'(x) = 3
Это уравнение не равно нулю ни при каком x. Это означает, что производная этой функции постоянна во всей области определения.
Поскольку f'(x) > 0 для всех значений x.
Функция монотонно возрастает в своей области определения.
Вопрос 4: Найдите области возрастания или убывания данной функции.
f(x) = x 2 + 4x + 4
Решение.
f(x) = x 2 + 4x + 4
f'(x) = 2x + 4 …. (1)
Решение уравнения f'(x) = 0
2x + 4 = 0
⇒ x = -2
Таким образом, при x = -2 производная этой функции меняет знак. Проверьте знак производной в его окрестности.
при x = -1
f'(x) = 2(-1) + 4 = 2 > 0
Это означает, что при x > -2 функция возрастает.
при x = -3
f'(x) = 2(-3) + 4 = -2 < 0
При x < -2 функция убывает.
Вопрос 5: Найдите области возрастания или убывания данной функции.
f(x) = x 2 + 3x
Решение:
Чтобы проанализировать любую функцию, первым шагом является поиск критических точек.
f(x) = x 2 + 3x
f'(x) = 2x + 3 …. (1)
Решение уравнения f'(x) = 0
2x + 3 = 0
⇒ x = -1,5
Таким образом, при x = -1,5 производная этой функции меняет знак. Проверьте знак производной в его окрестности.
при x = -1
f'(x) = 2(-1) + 3 = 1 > 0
Это означает, что при x > -1,5 функция возрастает.
при x = -3
f'(x) = 2(-3) + 3 = -3 < 0
При x < -1,5 функция убывает.
Вопрос 6: Найдите области возрастания или убывания данной функции.
f(x) = e x + e -x
Решение:
f(x) = e x + e -x
f'(x) = e x – e -x …. (1)
(1)
Решение уравнения f ‘(x) = 0
E x -E -x = 0
⇒ E x = E -x
⇒ E 2x = 1
⇒ E 2x = 1
⇒ E 2x = 1
⇒ E 2x = 1 9005
e 2x = e 0
Сравнивая обе части уравнения,
⇒ 2x = 0
⇒ x = 0
Таким образом, при x = 0 производная этой функции меняет знак. Проверьте знак производной в его окрестности.
при x = 1
f'(x) = e 1 – e -1 > 0
Это означает, что при x > 0 функция возрастает.
при x = –1
f'(x) = e -1 – e 1 < 0
При x < 0 функция убывает.
Интервалы возрастания и убывания
Интервалы возрастания и убывания
Чтобы понять, как изменяется функция, нам нужно знать интервалы, в течение которых функция изменяется определенным образом. Функция увеличивается в течение интервала, когда значения выхода функции увеличиваются по мере того, как мы увеличиваем входные значения функции.
Функция увеличивается в течение интервала, когда значения выхода функции увеличиваются по мере того, как мы увеличиваем входные значения функции.
Таким же образом функция уменьшается в интервале, когда значения выхода функции уменьшаются по мере того, как мы уменьшаем входные значения функции. Мы знаем, что наклон отображает среднюю скорость изменения функции в данной точке. Если наклон положительный , то мы говорим, что функция возрастает. Отрицательный наклон изображает убывающую функцию, а нулевой наклон показывает, что функция остается постоянной за указанный интервал.
Лучшие репетиторы по математике
Поехали
Локальный максимум и локальный минимум
Все функции не увеличиваются и не уменьшаются по всему домену. Иногда функция меняется с возрастающей на убывающую для значения входа, т. е. по мере увеличения значения входа значение функции уменьшается. Это значение входа, при котором значение функции претерпевает переход от увеличения к уменьшению, известно как локальный максимум . Когда у нас есть более одного такого входного значения, мы называем их локальными максимумами .
Это значение входа, при котором значение функции претерпевает переход от увеличения к уменьшению, известно как локальный максимум . Когда у нас есть более одного такого входного значения, мы называем их локальными максимумами .
Есть еще один случай, когда значение функции меняется с убывающего на возрастающее по мере увеличения входного значения. Входное значение в этом случае известно как локальный минимум . Если таких входных значений больше, то мы называем их локальными минимумами . И локальные максимумы, и минимумы известны как локальный экстремум или локальный экстремум . В экстремумах функция не возрастает и не убывает, а остается постоянной.
Поскольку производная функции изображает мгновенную скорость изменения функции в данной точке, поэтому мы можем использовать ее для определения интервалов возрастания и убывания функции. В следующем разделе мы объясним это подробно.
В следующем разделе мы объясним это подробно.
Возрастающий интервал
Если f дифференцируема в точке a, то f строго возрастает в точке a, если .
Убывающий интервал
Если f дифференцируема в точке a, то f строго убывает в точке a if
Чтобы определить, возрастает или убывает функция в точке, важно, чтобы она была дифференцируемой. В следующем разделе мы решим несколько примеров для определения возрастающих и убывающих интервалов с использованием производных функции.
Пример 1
Изучить интервалы возрастания и убывания функции.
Раствор
Мы выполним следующие шаги, чтобы определить интервалы возрастания и убывания вышеуказанной функции:
Шаг 1 — Найдите производную функции
На этом шаге мы продифференцируем функцию .
Шаг 2 — Получение корней первой производной функции f ‘(x)
На этом шаге мы получим корни первой производной функции следующим образом:
9Шаг 3. Проверка точек из всех интервалов Эти корни показывают, что у нас есть три интервала, которые равны , и .
Проверка точек из всех интервалов Эти корни показывают, что у нас есть три интервала, которые равны , и .
Мы возьмем значение из каждого интервала и посмотрим, увеличивается оно или уменьшается.
Возьмем -2 из интервала и подставим в производную функции:
Так как f ‘(x) больше 0, то функция на этом интервале возрастает.
Теперь возьмем точку из интервала (-1, 1).
Так как f'(x)<0, то на этом интервале функция убывает.
Теперь возьмем точку из интервала и подставим ее в производную функции:
Поскольку f ‘(x) >0, значит, функция на этом интервале возрастает.
Шаг 4. Запишите возрастающие и убывающие интервалы
На шаге 3 мы проверили точки из каждого интервала и подставили их в производную функции. У нас есть два интервала, где функция возрастала, и один интервал, где функция убывала. Следовательно, мы можем записать возрастающие и убывающие интервалы как:
Возрастающие:
Убывающие:
Пример 2
Изучите интервалы возрастания и убывания функции .
Решение
Мы выполним следующие шаги, чтобы определить интервалы возрастания и убывания вышеуказанной функции:
Шаг 1 — Найдите производную функции
На этом шаге мы продифференцируем функцию .
Шаг 2 — Получить корни первой производной функции f ‘(x)
На этом шаге мы получим корни первой производной функции следующим образом:
У этой производной есть только один корень.
Шаг 3 — Проверка точек из всех интервалов
У нас есть один корень производной функции. У нас будет два интервала с учетом единственного корня функции. Эти интервалы равны и .
Мы возьмем значение из каждого интервала и посмотрим, увеличивается оно или уменьшается.
Возьмем -4 из интервала и подставим в производную функции:
Поскольку f ‘(x) < 0, значит, функция на этом интервале убывает.
Теперь возьмем точку из интервала
Так как f ‘(x) > 0, значит функция на этом интервале возрастает.
Шаг 4. Запишите возрастающие и убывающие интервалы
На шаге 3 мы проверили точки из каждого интервала и подставили их в производную функции. У функции только один корень, поэтому у нас два интервала. Мы можем записать возрастающие и убывающие интервалы как:
Возрастание:
Убывание:
Пример 3
Изучите интервалы возрастания и убывания функции .
Решение
Мы выполним следующие шаги, чтобы определить интервалы возрастания и убывания вышеуказанной функции:
Шаг 1 — Найдите производную функции
На этом шаге мы продифференцируем функцию .
Шаг 2 — Получить корни первой производной функции f ‘(x)
На этом шаге мы получим корни первой производной функции следующим образом:
Существует только один корень производной этой функции.
Чтобы определить, когда функция возрастает, вы должны сначала взять производную, затем приравнять ее к 0, а затем найти, между какими нулевыми значениями функция положительна.
Сначала возьмем производную:
Приравняем к 0 и решим:
Теперь проверьте значения со всех сторон, чтобы найти, когда функция положительна и, следовательно, возрастает. Я проверю значения 0, 2 и 10.
Поскольку значение является положительным, когда x = 0 и 10, интервал увеличивается в обоих этих интервалах. Поэтому наш ответ:
Сообщить об ошибке
Увеличивается или уменьшается на интервале?
Возможные ответы:
Возрастание. на интервале.
Увеличение. на интервале.
Невозможно определить на основании предоставленной информации
Уменьшается. на интервале.
Уменьшение. на интервале.
Правильный ответ:
Возрастание. на интервале.
Объяснение:
Чтобы найти возрастающие и убывающие интервалы, нам нужно найти, где наша первая производная больше или меньше нуля.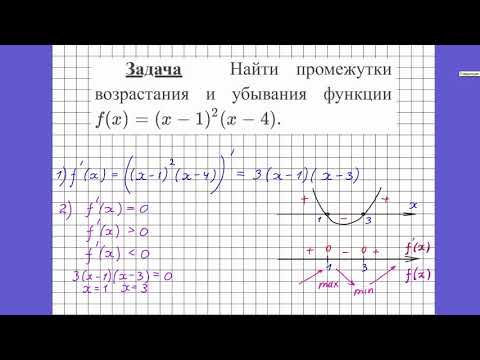 Если наша первая производная положительна, наша исходная функция возрастает, а если g'(x) отрицательна, g(x) убывает.
Если наша первая производная положительна, наша исходная функция возрастает, а если g'(x) отрицательна, g(x) убывает.
Начните с:
Если мы подставим любое число от 3 до 6, мы получим положительное число для g'(x). Таким образом, эта функция должна возрастать на интервале {3,6 }, так как g'(x) положительна.
Сообщить об ошибке
Увеличивается или уменьшается на интервале?
Возможные ответы:
Увеличивается, потому что отрицательно.
Уменьшение, поскольку положительно.
Возрастание, поскольку положительно.
Уменьшение, поскольку отрицательно.
не увеличивается и не уменьшается на заданном интервале.
Правильный ответ:
Возрастает, потому что положительно.
Объяснение:
Чтобы узнать, возрастает функция или убывает, нам нужно определить, положительна или отрицательна первая производная на заданном интервале.
Итак, начиная с:
Мы получаем:
используя степенное правило .
Найдите функцию на каждом конце интервала.
Итак, первая производная положительна на всем интервале, поэтому g(t) возрастает на интервале.
Сообщить об ошибке
Является ли следующая функция возрастающей или убывающей на интервале?
Возможные ответы:
Убывающий, т.к. положителен на данном интервале.
Функция не возрастает и не убывает на интервале.
Возрастание, так как на данном интервале положительно.
По убыванию, так как на данном интервале отрицательно.
Возрастание, поскольку отрицательно на заданном интервале.
Правильный ответ:
Возрастание, т.к. положительно на данном интервале.
Объяснение:
Функция возрастает на интервале, если для каждой точки этого интервала первая производная положительна.
Итак, нам нужно найти первую производную, а затем подставить конечные точки нашего интервала.
Найдите первую производную с помощью степенного правила
Подставьте конечные точки и оцените функцию.
Оба положительны, поэтому наша функция возрастает на данном интервале.
Сообщить об ошибке
С какими интервалами увеличивается следующая функция?
Возможные ответы:
Правильный ответ:
Пояснение:
Первый шаг — найти первую производную.
Помните, что производная от
Далее найдите критические точки, которые являются точками, где или не определены. Чтобы найти точки, установите числитель на , чтобы найти неопределенные точки, установите знаменатель на . Критические точки и
Последним шагом является проверка точек во всех регионах, чтобы увидеть, какой диапазон дает положительное значение для .
Если мы подставим число из первого диапазона, т.е. получим отрицательное число.
Из второго диапазона мы получаем положительное число.
Из третьего диапазона мы получаем отрицательное число.
Из последнего диапазона мы получаем положительное число.
Таким образом, второй и последний диапазоны — это те, где увеличивается.
Сообщить об ошибке
Ниже приведен полный график . На каком интервале(ах) происходит увеличение?
Возможные ответы:
Правильный ответ:
Объяснение:
увеличивается, когда является положительным (над осью). Это происходит на интервалах .
Сообщить об ошибке
Функция A
Функция B
9 10004
Function C
Function D
Function E
5 graphs of different functions are shown выше. На каком графике показана возрастающая/неубывающая функция ?
На каком графике показана возрастающая/неубывающая функция ?
Возможные ответы:
Функция D
Функция E
Функция B
Функция A
Функция C
Правильный ответ:
Функция E
Объяснение:
Функция возрастает, если для любого , (т. е. наклон всегда больше или равен нулю)
Функция – единственная функция, обладающая этим свойством. Обратите внимание, что функция E возрастает, но не строго возрастает
Сообщить об ошибке
Найдите возрастающие интервалы следующей функции на интервале :
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти возрастающие интервалы заданной функции, нужно определить интервалы, на которых функция имеет положительную первую производную. Чтобы найти эти интервалы, сначала найдите критические значения или точки, в которых первая производная функции равна нулю.
Чтобы найти эти интервалы, сначала найдите критические значения или точки, в которых первая производная функции равна нулю.
Для данной функции .
Эта производная была найдена с помощью правила степени
.
При нулевом значении . Поскольку мы рассматриваем только открытый интервал (0,5) для этой функции, мы можем игнорировать . Далее мы смотрим интервалы вокруг критического значения , которые равны и . На первом интервале первая производная функции отрицательна (подстановка значений дает нам отрицательное число), что означает, что функция на этом интервале убывает. Однако для второго интервала первая производная положительна, что указывает на возрастание функции на этом интервале.
Сообщить об ошибке
← Назад 1 2 3 Далее →
Уведомление об авторских правах
Все ресурсы исчисления 1
10 Диагностические тесты 438 практических тестов Вопрос дня Карточки Learn by Concept
Увеличение и уменьшение интервалов — определение, формулы
Задумывались ли вы, почему расстояние сокращается, как только вы приближаетесь к дому вашего друга? И почему это происходит наоборот, когда вы едете в противоположном направлении? Это из-за функций. В исчислении возрастающие и убывающие функции — это функции, для которых значение f (x) увеличивается и уменьшается соответственно с увеличением значения x.
В исчислении возрастающие и убывающие функции — это функции, для которых значение f (x) увеличивается и уменьшается соответственно с увеличением значения x.
Чтобы проверить изменение функций, нужно найти производные таких функций. Если значение функции увеличивается со значением x, то функция положительна. Если значение функции уменьшается с увеличением значения x, то говорят, что функция отрицательна.
Интервалы возрастания и убывания действительных чисел — это действительнозначные функции, которые имеют тенденцию возрастать и уменьшаться при изменении значения зависимой переменной функции. Чтобы найти интервалы возрастания и убывания, нужно определить первую производную функции. Это делается для того, чтобы найти знак функции, будь то отрицательный или положительный. Интервал функции называется положительным, если значение функции f(x) увеличивается с увеличением значения x. Напротив, интервал функции называется отрицательным, если значение функции f (x) уменьшается с увеличением значения x.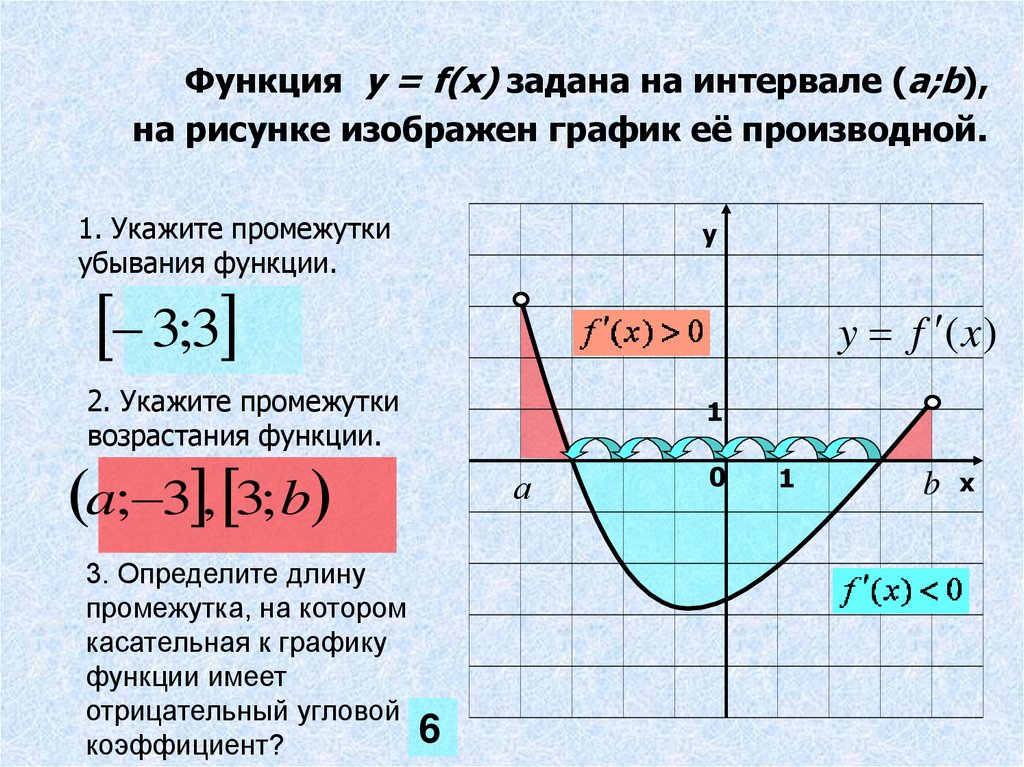
Альтернативно, интервал функции положителен, если положительный знак первой производной. Интервал функции отрицательный, если знак первой производной отрицательный. Следовательно, положительный интервал увеличивается, тогда как отрицательный интервал называется убывающим интервалом.
Как записать интервалы возрастания и убывания?Вы можете представлять интервалы возрастания и убывания, понимая простые математические понятия, приведенные ниже:
- Говорят, что значение интервала увеличивается для каждого x < y, где f (x) ≤ f (y) для действительнозначной функции f (x).
- Если значение интервала f (x) ≥ f (y) для каждого x < y, то интервал называется убывающим.
Вы также можете использовать первую производную, чтобы найти интервалы возрастания и убывания и соответственно записать их.
- Если первая производная функции равна f’ (x) ≥ 0, интервал увеличивается.
- С другой стороны, если значение производной f’ (x) ≤ 0, то интервал называется убывающим.

Поскольку вы умеете записывать интервалы возрастания и убывания, пора научиться находить интервалы возрастания и убывания. Давайте научимся находить интервалы возрастания и убывания на примере.
Рассмотрим функцию f(x) = x 3 + 3x 2 – 45x + 9. Чтобы найти интервалы возрастания и убывания, нужно продифференцировать их относительно x. После дифференцирования вы получите первую производную как f’(x).
Следовательно, f’(x) = 3x 2 + 6x – 45
Вынимая из всего члена 3 общих, получаем 3 (x 2 + 2x -15). Теперь, находя множители этого уравнения, мы получаем, 3 (x + 5) (x – 3). Если вы замените эти значения эквивалентными нулю, вы получите значения x.
Следовательно, значение x = -5, 3.
Чтобы найти значение функции, подставьте эти значения в исходную функцию, и вы получите значения, как показано в таблице ниже.
| Interval | Value of x | f'(x) | Increasing/Decreasing | |||||
| (-∞, -5) | x = -6 | f ‘(-6) = 27 > 0 | Возрастание | |||||
| (-5, 3) | x = 0 | f'(0) = -45 < 0 | Уменьшение | | ) | x = 4 | f'(4) = 27 > 0 | Возрастание | |
Следовательно, для данной функции f (x) = x 3 + 3x 2 – 45x + 9 возрастающие интервалы равны (-∞, -5) и (3, ∞), а убывающие интервалы равны (-5, 3).
Частный случай: функция «один к одному»
Строго возрастающие или убывающие функции обладают особым свойством, называемым инъективными или взаимно однозначными функциями. Это означает, что вы никогда не получите одно и то же значение функции дважды.
Например, вы можете получить значение функции дважды на первом графике. Однако на втором графике у вас никогда не будет одинакового значения функции. Следовательно, график справа известен как взаимно однозначная функция.
Это полезно, потому что инъективные функции могут быть обращены. Вы можете вернуться от значения «y» функции к значению «x». Обычно это невозможно, так как существует более одного возможного значения x.
Пример 1: Какими будут интервалы возрастания и убывания функции f (x) = -x 3 + 3x 2 + 9?
Решение: Чтобы найти интервалы возрастания и убывания, нужно продифференцировать функцию относительно x. Следовательно, f’(x) = -3x 2 + 6x.
Следовательно, f’(x) = -3x 2 + 6x.
Теперь, убрав из уравнения 3 обычных, мы получим -3x (x – 2). Чтобы найти значения x, приравняем это уравнение к нулю, получим f'(x) = 0
⇒ -3x (x – 2) = 0
⇒ x = 0 или x = 2.
Следовательно , интервалы для функции f (x) равны (-∞, 0), (0, 2) и (2, ∞). Чтобы найти значения функции, ознакомьтесь с таблицей ниже.
| Interval | Value of x | f'(x) | Increasing/Decreasing | |||
| (-∞, 0) | x = -1 | f ‘(-1) = -9 < 0 | Убывающая | |||
| (0, 2) | x = 1 | f'(1) = 3 > 0 | Возрастающая | 9x = 4 | f'(4) = -24 < 0 | Уменьшение |
Следовательно, (-∞, 0) и (2, ∞) — убывающие интервалы, а (0, 2) — возрастающие интервалы.
Пример 2: Считаете ли вы, что интервал (-∞, ∞) является строго возрастающим интервалом для f(x) = 3x + 5? Если да, то докажите это.
Решение: Чтобы доказать утверждение, рассмотрим два действительных числа x и y в интервале (-∞, ∞), такие что x < y.
Тогда 3x < 3y.
⇒ 3x + 5 < 3y + 5
⇒ f (x) < f (y)
Так как x и y являются произвольными значениями, следовательно, f (x) < f (y) всякий раз, когда x < y. Следовательно, интервал (-∞, ∞) является строго возрастающим интервалом для f(x) = 3x + 5. Следовательно, утверждение доказано.
Пример 3: Найдите, является ли функция f (x) x 3 −4x для x в интервале [−1, 2] возрастающей или убывающей.
Решение: вам нужно начать с -1, чтобы построить функцию на графике. -1 выбрано потому, что интервал [−1, 2] начинается с этого значения. При x = -1 функция убывает. Как только он достигнет значения 1,2, функция увеличится. После того, как функция достигла значения больше 2, значение будет продолжать увеличиваться. При точном анализе нельзя найти, увеличивается интервал или уменьшается. Итак, скажем, в интервале [−1, 2],
Итак, скажем, в интервале [−1, 2],
- Кривая спадает в интервале [−1, прибл. 1,2]
- Кривая возрастает в интервале [прибл. 1,2, 2]
В приведенных выше разделах вы научились писать интервалы возрастания и убывания. В этом разделе вы узнаете, как находить интервалы возрастания и убывания с помощью графиков. Было бы полезно, если бы вы изучили приведенную ниже таблицу, чтобы четко понять концепцию.
| Возрастающий интервал | Уменьшающийся интервал |
| На приведенном ниже графике показана возрастающая функция. Это можно определить, взглянув на приведенный график. Поскольку график идет вверх по мере движения слева направо по оси X, говорят, что график увеличивается. | На приведенном ниже графике показана убывающая функция. Это можно определить, взглянув на приведенный график. Поскольку график идет вниз при движении слева направо по оси X, говорят, что график уменьшается. Поскольку график идет вниз при движении слева направо по оси X, говорят, что график уменьшается. |
- Функция выдаст постоянное значение и будет называться постоянной, если f’(x) = 0 в течение этого интервала.
- Для вещественнозначной функции f (x) интервал I называется строго возрастающим интервалом, если для каждого x < y выполняется f (x) < f (y).
- Для вещественнозначной функции f (x) интервал I называется строго убывающим интервалом, если для каждого x < y выполняется f (x) > f (y).
- Для функции f (x), когда x1 < x2, тогда f (x1) ≤ f (x2), интервал называется возрастающим.
- Для функции f (x), когда x1 < x2, а затем f (x1) < f (x2), интервал называется строго возрастающим. Нужно быть внимательным, глядя на знаки возрастающих и строго возрастающих функций.
- Для функции f (x), когда x1 < x2, тогда f (x1) ≥ f (x2), интервал называется убывающим.
- Для функции f (x), когда x1 < x2, то f (x1) > f (x2), интервал называется строго убывающим.

- Если значение функции не меняется при изменении значения x, то говорят, что функция является постоянной функцией.
Интервалы возрастания и убывания — определение, формулы, примеры
LearnPracticeDownload
Интервалы возрастания и убывания — это интервалы действительных чисел, в которых вещественные функции возрастают и убывают соответственно. Чтобы определить возрастающие и убывающие интервалы, мы используем критерий производной первого порядка для проверки знака производной в каждом интервале. Интервал увеличивается, если значение функции f(x) увеличивается с увеличением значения x, и убывает, если f(x) уменьшается с уменьшением x.
В этой статье мы научимся определять возрастающие и убывающие интервалы с помощью теста производной первого порядка и графика функции с помощью примеров для лучшего понимания концепции.
| 1. | Что такое возрастающие и убывающие интервалы? |
2.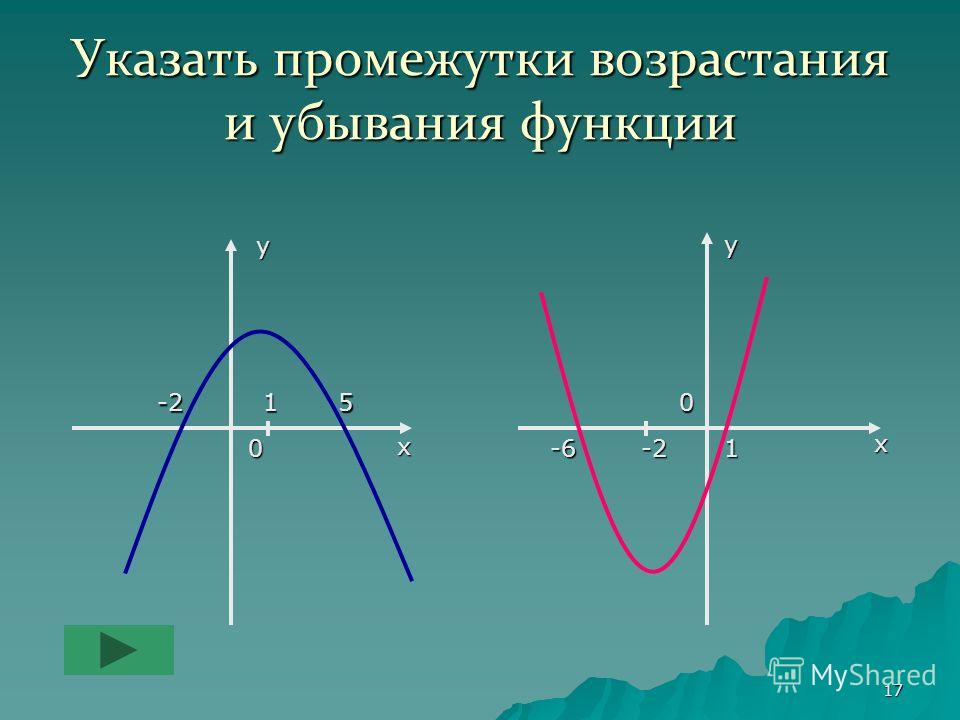 | Увеличение и уменьшение интервалов Определение |
| 3. | Нахождение возрастающих и убывающих интервалов |
| 4. | Увеличение и уменьшение интервалов с помощью графика |
| 5. | Часто задаваемые вопросы об увеличении и уменьшении интервалов |
Что такое возрастающие и убывающие интервалы?
Интервалы возрастания или убывания функций называются возрастающими и убывающими интервалами. Эти интервалы можно оценить, проверив знак первой производной функции на каждом интервале. Если первая производная функции на интервале положительна, то этот интервал называется возрастающим, а если первая производная функции на интервале отрицательна, то этот интервал называется убывающим. Давайте пройдемся по их формальным определениям, чтобы понять их смысл:
Увеличение и уменьшение интервалов Определение
Определения увеличения и уменьшения интервалов приведены ниже.
- Для вещественнозначной функции f(x) интервал I называется возрастающим интервалом, если для каждого x < y выполняется f(x) ≤ f(y).
- Для действительнозначной функции f(x) интервал I называется убывающим интервалом, если для каждого x < y выполняется f(x) ≥ f(y).
Мы также можем определить возрастающий и убывающий интервалы, используя первую производную функции f(x) как:
- Если f'(x) ≥ 0 на I, то I называется возрастающим интервалом.
- Если f'(x) ≤ 0 на I, то I называется убывающим интервалом.
Нахождение возрастающих и убывающих интервалов
Теперь, когда мы поняли значение возрастающих и убывающих интервалов, давайте теперь научимся вычислять возрастающие и убывающие интервалы функций. Мы решим пример, чтобы лучше понять концепцию. Рассмотрим f(x) = x 3 + 3x 2 — 45x + 9. Дифференцируем f(x) по x, чтобы найти f'(x).
f'(x) = 3x 2 + 6x — 45
= 3(x 2 + 2x — 15)
= 3 (x + 5) (x — 3)
90’004 Заменить f х) = 0⇒ х = -5, х = 3
Теперь пересечения по оси х для f'(x) равны х = -5 и х = 3.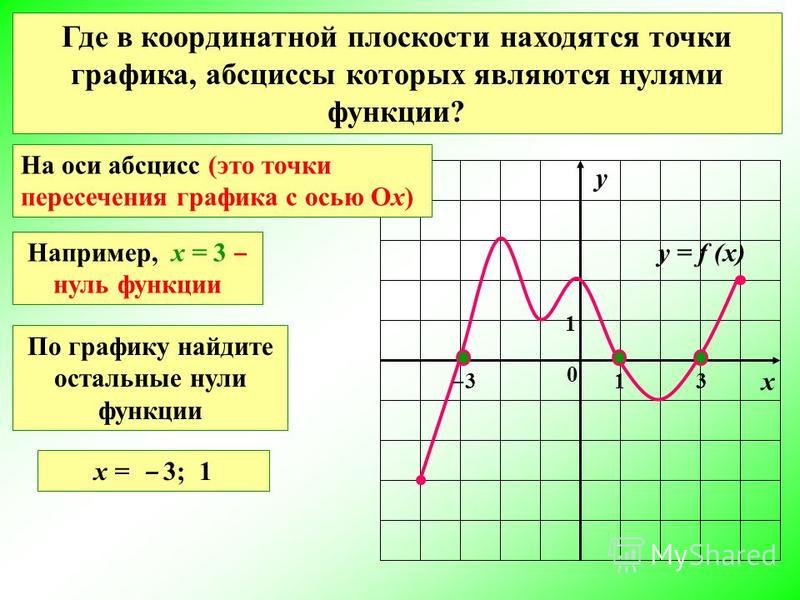 Имеющиеся у нас интервалы равны (-∞, -5), (-5, 3) и (3, ∞). Мы проверим знак f'(x) в каждом из этих интервалов, чтобы определить возрастающие и убывающие интервалы.
Имеющиеся у нас интервалы равны (-∞, -5), (-5, 3) и (3, ∞). Мы проверим знак f'(x) в каждом из этих интервалов, чтобы определить возрастающие и убывающие интервалы.
| Интервал | Значение x | ф'(х) | Увеличение/уменьшение |
|---|---|---|---|
| (-∞, -5) | х = -6 | f'(-6) = 27 > 0 | Увеличение |
| (-5, 3) | х = 0 | f'(0) = -45 < 0 | Уменьшение |
| (3, ∞) | х = 4 | f'(4) = 27 > 0 | Увеличение |
Следовательно, возрастающие интервалы для f(x) = x 3 + 3x 2 — 45x + 9 равны (-∞, -5) и (3, ∞), а убывающий интервал f( х) равно (-5, 3).
Увеличение и уменьшение интервалов с помощью графика
Мы научились определять возрастающие и убывающие интервалы с помощью первой производной функции. Теперь мы определим интервалы, просто увидев график. Ниже приведены образцы двух графиков различных функций. На первом графике показана возрастающая функция по мере того, как график идет вверх по мере движения слева направо по оси x. На втором графике показана убывающая функция по мере того, как график движется вниз по мере движения слева направо по оси x.
Ниже приведены образцы двух графиков различных функций. На первом графике показана возрастающая функция по мере того, как график идет вверх по мере движения слева направо по оси x. На втором графике показана убывающая функция по мере того, как график движется вниз по мере движения слева направо по оси x.
Важные замечания по увеличению и уменьшению интервалов
- Для действительнозначной функции f(x) интервал I называется строго возрастающим интервалом, если для каждого x < y выполняется f(x ) < f(y).
- Для вещественнозначной функции f(x) интервал I называется строго убывающим интервалом, если для каждого x < y выполняется f(x) > f(y).
- Функция постоянна на интервале, если f'(x) = 0 на протяжении этого интервала.
Связанные темы
- Применение производных
- Дифференциальные уравнения
- Исчисление
Примеры увеличения и уменьшения интервалов
Пример 1: Определить интервалы возрастания и убывания функции f(x) = -x 3 + 3x 2 + 9.

Решение: Дифференцировать f(x) = -x 3 + 3x 2 + 9 вес. x
f'(x) = -3x 2 + 6x
= -3x(x — 2)
⇒ f'(x) = 0
⇒ -3x(x — 2) = 0
⇒ x = 0 или x = 2
Имеющиеся у нас интервалы равны (-∞, 0), (0, 2) и (2, ∞). Нам нужно определить возрастающие и убывающие интервалы от них.
Интервал Значение x ф'(х) Увеличение/уменьшение (-∞, 0) х = -1 f'(-1) = -9 < 0 Уменьшение (0, 2) х = 1 f'(1) = 3 > 0 Увеличение (2, ∞) х = 4 f'(4) = -24 < 0 Уменьшение Ответ: Следовательно, (-∞, 0) и (2, ∞) — убывающие интервалы, а (0, 2) — возрастающие интервалы.
Пример 2: Покажите, что (-∞, ∞) является строго возрастающим интервалом для f(x) = 3x + 5.

Решение: Рассмотрим два действительных числа x и y в (-∞, ∞), что х < у. Тогда имеем
x < y
⇒ 3x < 3y
⇒ 3x + 5 < 3y + 5
⇒ f(x) < f(y)
Поскольку x и y произвольны, поэтому f(x ) < f(y), если x < y.
Ответ: Следовательно, (-∞, ∞) — строго возрастающий интервал для f(x) = 3x + 5,
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Увеличение и уменьшение интервалов Вопросы
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об увеличении и уменьшении интервалов
Что такое возрастающие и убывающие интервалы в алгебре?
Возрастающие и убывающие интервалы — это интервалы действительных чисел, в которых вещественнозначные функции возрастают и убывают соответственно.
Почему при описании возрастающих и убывающих интервалов используются только значения X?
Значения X используются для описания возрастающих и убывающих интервалов, поскольку значения функции f(x) увеличиваются или уменьшаются с увеличением значений x, т. е. изменение f(x) зависит от значения Икс.
Как найти интервалы возрастания и убывания функции?
Мы можем найти возрастающие и убывающие интервалы функции, используя ее первую производную. Мы можем найти критические точки и, следовательно, интервалы. Затем мы можем проверить знак производной в каждом интервале, чтобы определить возрастающие и убывающие интервалы.
Как найти возрастающие и убывающие интервалы с помощью графика?
Мы можем найти возрастающие и убывающие интервалы с помощью графика, наблюдая, движется ли график вверх или вниз при движении слева направо вдоль оси x. Для графиков, движущихся вверх, интервал увеличивается, а для графиков, движущихся вниз, интервал уменьшается.
Как узнать, что функция увеличивается?
Говорят, что функция f(x) возрастает на интервале I, если для любых двух чисел x и y из I, таких что x < y, выполняется f(x) ≤ f(y).
Какая функция не имеет возрастающих и убывающих интервалов?
Постоянная функция не возрастает и не убывает, поскольку график постоянной функции представляет собой прямую линию, параллельную оси x, а ее производная всегда равна 0.0005
| 1 | Найдите производную — d/dx | натуральное бревно х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найдите производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найдите производную — d/dx | грех(2x) | |
| 23 | Найдите производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) по x | |
| 42 | Найдите производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оцените интеграл 9бесконечность | ||
| 45 | Найдите производную — d/dx | х/2 | |
| 46 | Найдите производную — d/dx | -cos(x) | |
| 47 | Найдите производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найдите производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | предел, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найдите производную — d/dx | лог х | |
| 86 | Найдите производную — d/dx | арктан(х) | |
| 87 | Найдите производную — d/dx | бревно натуральное 5х92 |
Увеличение и уменьшение интервалов — GeeksforGeeks
Производные — это способ измерения скорости изменения переменной. Когда дело доходит до функций и исчисления, производные дают нам много информации о форме функции и ее графике. Они дают информацию об областях, где функция увеличивается или уменьшается. Они также полезны для определения максимального и минимального значений, достигаемых функцией. График функции, построенный на основе информации, собранной из производных, может помочь нам узнать предел и другую информацию о поведении функции.
Когда дело доходит до функций и исчисления, производные дают нам много информации о форме функции и ее графике. Они дают информацию об областях, где функция увеличивается или уменьшается. Они также полезны для определения максимального и минимального значений, достигаемых функцией. График функции, построенный на основе информации, собранной из производных, может помочь нам узнать предел и другую информацию о поведении функции.
Производные
Производная — это точка на функции, которая дает нам меру скорости изменения функции в этой конкретной точке. Говоря геометрически, они дают нам информацию о наклоне касательной в этой точке. Эту информацию можно использовать для определения интервалов или областей, в которых функция возрастает или убывает. Зная такие интервалы, несложно определить впадины и холмы на графике функции. На рисунке ниже показана функция f(x) и ее интервалы возрастания и убывания.
Для функции f(x). Для интервала, который я определил в своей области.
- Говорят, что функция f(x) возрастает на интервале I, если для любого a < b выполняется f(a) ≤ f(b).
- Говорят, что функция f(x) убывает на интервале I, если для любого a < b выполняется f(a) ≥ f(b).
Функция называется строго возрастающей, если для любого a < b выполняется f(a) < f(b). Аналогичное определение справедливо для строго убывающего случая.
Увеличение и уменьшение интервалов
Цель состоит в том, чтобы определить эти области, не глядя на график функции. Для этого посмотрим на производные функции в этих областях. То, что эти производные есть не что иное, как наклон касательных к этой кривой, уже установлено. На рисунке ниже показаны наклоны касательных в разных точках этой кривой.
Обратите внимание, что в областях, где функция уменьшается, наклон кривой фактически отрицательный и положительный для областей, где функция возрастает. Уклон на вершинах и долинах равен нулю. Так сказать формально.
Пусть f(x) — функция, непрерывная на [a, b] и дифференцируемая на интервале (a, b).
- Если f'(c) > 0 для всех c в (a, b), то говорят, что f(x) возрастает в интервале.
- Если f'(c) < 0 для всех c в (a, b), то говорят, что f(x) убывает на интервале.
- Если f'(c) = 0 для всех c в (a, b), то говорят, что f(x) постоянна на интервале.
Критические точки
На предыдущей диаграмме обратите внимание на то, как функция переходит от убывания к возрастанию или от возрастания к убыванию. Есть долина или вершина. Эти впадины и пики являются крайними точками функции, поэтому их называют экстремумами. Из рисунка хорошо видно, что в этих точках производная функции обращается в нуль. В этих точках функция достигает минимума и максимума.
Примечание. Функция может иметь любое количество критических точек. При этом все критические точки не обязательно дают максимальное и минимальное значение функции.
Но каждая критическая точка — это долина, то есть точка минимума в локальной области.
На рисунке выше три экстремума, два из них минимумы, но есть только один глобальный максимум и глобальные минимумы. Таким образом, формально
Для функции f(x) точка x = c является экстремумом, если
f'(c) = 0
Определение возрастающих и убывающих интервалов
Из приведенных выше рисунков становится ясно, что каждый экстремум функции является точкой смены знака ее производной. То есть функция либо идет от возрастания к убыванию, либо наоборот. При поиске областей, в которых функция увеличивается или уменьшается, становится важным искать крайние значения. Для любой функции f(x) и заданного интервала необходимо выполнить следующие шаги, чтобы найти эти интервалы:
- Проверить, является ли функция дифференцируемой и непрерывной на заданном интервале.
- Решите уравнение f'(x) = 0, решения этого уравнения дают нам крайности.

- Для экстремальной точки x = c просмотрите область вблизи этой точки и проверьте знаки производных, чтобы найти интервалы возрастания или убывания функции.
Давайте рассмотрим несколько примеров задач, связанных с этими понятиями.
Примеры задач
Вопрос 1. Для данной функции укажите, возрастает она или убывает в области [-1,1]
f(x) = e x
Решение:
Для анализа 9 любой функции, первым шагом является поиск критических точек.f(x) = e x
f'(x) = e x …. (1)
Решение уравнения f'(x) = 0
e x = 0
Для этой функции в данной области нет критической точки. Это означает, что в данной области эта функция должна быть либо монотонно возрастающей, либо монотонно убывающей. Для этого проверьте производную функции в этой области.
f'(x) > 0 в интервале [0,1].
Таким образом, функция возрастает.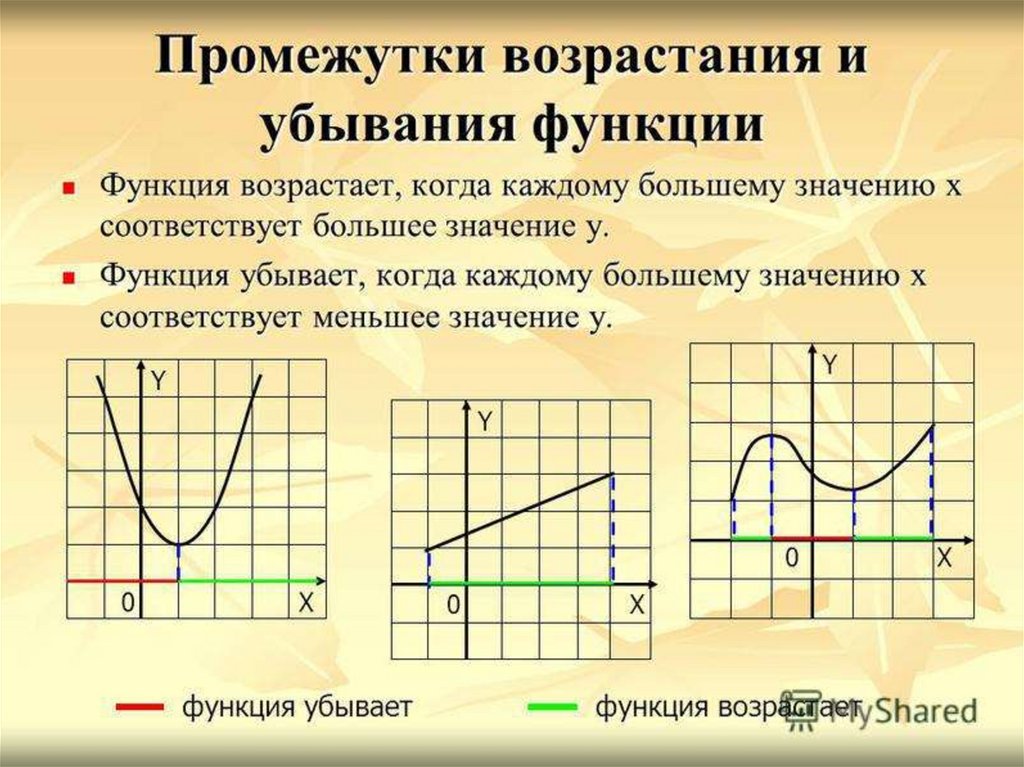
Вопрос 2. Для данной функции укажите, возрастает она или убывает в области [2,4]
f(x) = x 2 – x – 4
2 Решение:
Для анализа любой функции первым шагом является поиск критических точек.
f(x) = x 2 – x – 4
f'(x) = 2x – 1 …. (1)
Решение уравнения f'(x) = 0
2x – 1 = 0
⇒ x = 0,5
Критическая точка находится вне интересующей области. Это означает, что в данной области эта функция должна быть либо монотонно возрастающей, либо монотонно убывающей. Для этого проверьте производную функции в этой области.
f'(x) > 0 в интервале [2,4].
Таким образом, функция возрастает.
Вопрос 3: Найдите области возрастания или убывания данной функции.
f(x) = 3x + 4
Решение:
Чтобы проанализировать любую функцию, первым шагом является поиск критических точек.
f(x) = 3x + 4
f'(x) = 3
Это уравнение не равно нулю ни при каком x. Это означает, что производная этой функции постоянна во всей области определения.
Поскольку f'(x) > 0 для всех значений x.
Функция монотонно возрастает в своей области определения.
Вопрос 4: Найдите области возрастания или убывания данной функции.
f(x) = x 2 + 4x + 4
Решение.
f(x) = x 2 + 4x + 4
f'(x) = 2x + 4 …. (1)
Решение уравнения f'(x) = 0
2x + 4 = 0
⇒ x = -2
Таким образом, при x = -2 производная этой функции меняет знак. Проверьте знак производной в его окрестности.
при x = -1
f'(x) = 2(-1) + 4 = 2 > 0
Это означает, что при x > -2 функция возрастает.
при x = -3
f'(x) = 2(-3) + 4 = -2 < 0
При x < -2 функция убывает.
Вопрос 5: Найдите области возрастания или убывания данной функции.
f(x) = x 2 + 3x
Решение:
Чтобы проанализировать любую функцию, первым шагом является поиск критических точек.
f(x) = x 2 + 3x
f'(x) = 2x + 3 …. (1)
Решение уравнения f'(x) = 0
2x + 3 = 0
⇒ x = -1,5
Таким образом, при x = -1,5 производная этой функции меняет знак. Проверьте знак производной в его окрестности.
при x = -1
f'(x) = 2(-1) + 3 = 1 > 0
Это означает, что при x > -1,5 функция возрастает.
при x = -3
f'(x) = 2(-3) + 3 = -3 < 0
При x < -1,5 функция убывает.
Вопрос 6: Найдите области возрастания или убывания данной функции.
f(x) = e x + e -x
Решение:
f(x) = e x + e -x
f'(x) = e x – e -x …. (1)
(1)
Решение уравнения f ‘(x) = 0
E x -E -x = 0
⇒ E x = E -x
⇒ E 2x = 1
⇒ E 2x = 1
⇒ E 2x = 1
⇒ E 2x = 1 9005
e 2x = e 0
Сравнивая обе части уравнения,
⇒ 2x = 0
⇒ x = 0
Таким образом, при x = 0 производная этой функции меняет знак. Проверьте знак производной в его окрестности.
при x = 1
f'(x) = e 1 – e -1 > 0
Это означает, что при x > 0 функция возрастает.
при x = –1
f'(x) = e -1 – e 1 < 0
При x < 0 функция убывает.
Интервалы возрастания и убывания
Интервалы возрастания и убывания
Чтобы понять, как изменяется функция, нам нужно знать интервалы, в течение которых функция изменяется определенным образом.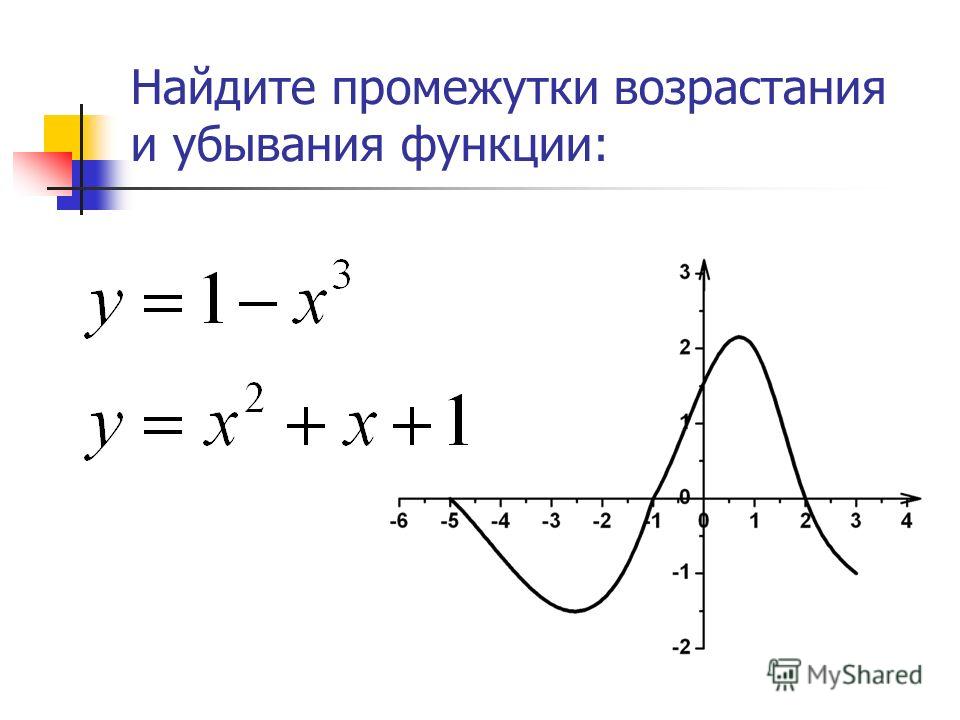 Функция увеличивается в течение интервала, когда значения выхода функции увеличиваются по мере того, как мы увеличиваем входные значения функции.
Функция увеличивается в течение интервала, когда значения выхода функции увеличиваются по мере того, как мы увеличиваем входные значения функции.
Таким же образом функция уменьшается в интервале, когда значения выхода функции уменьшаются по мере того, как мы уменьшаем входные значения функции. Мы знаем, что наклон отображает среднюю скорость изменения функции в данной точке. Если наклон положительный , то мы говорим, что функция возрастает. Отрицательный наклон изображает убывающую функцию, а нулевой наклон показывает, что функция остается постоянной за указанный интервал.
Лучшие репетиторы по математике
Поехали
Локальный максимум и локальный минимум
Все функции не увеличиваются и не уменьшаются по всему домену. Иногда функция меняется с возрастающей на убывающую для значения входа, т. е. по мере увеличения значения входа значение функции уменьшается.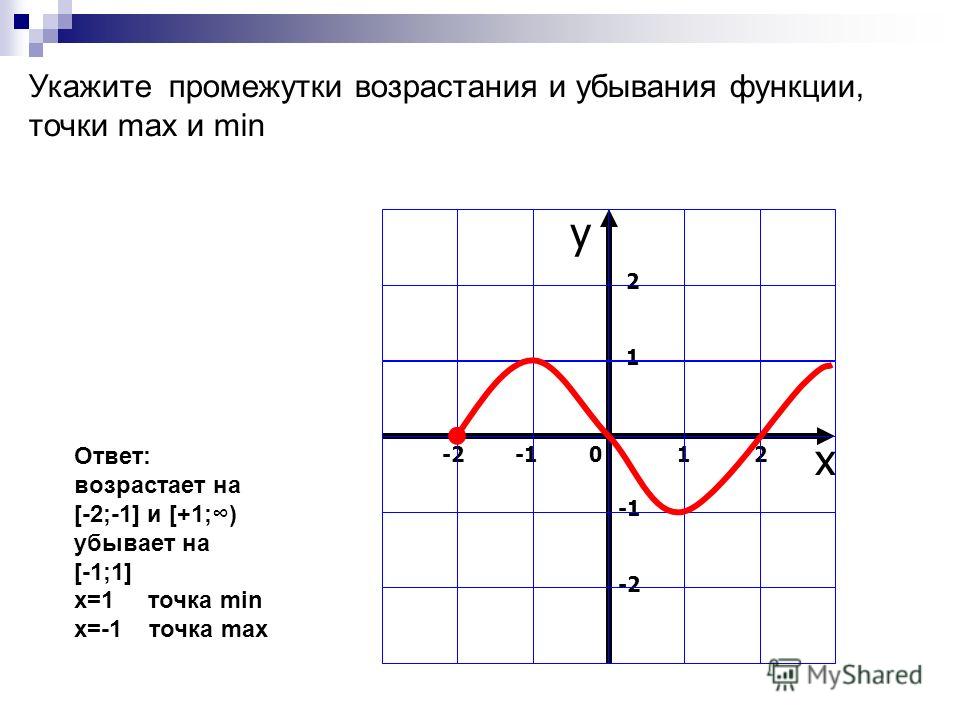 Это значение входа, при котором значение функции претерпевает переход от увеличения к уменьшению, известно как локальный максимум . Когда у нас есть более одного такого входного значения, мы называем их локальными максимумами .
Это значение входа, при котором значение функции претерпевает переход от увеличения к уменьшению, известно как локальный максимум . Когда у нас есть более одного такого входного значения, мы называем их локальными максимумами .
Есть еще один случай, когда значение функции меняется с убывающего на возрастающее по мере увеличения входного значения. Входное значение в этом случае известно как локальный минимум . Если таких входных значений больше, то мы называем их локальными минимумами . И локальные максимумы, и минимумы известны как локальный экстремум или локальный экстремум . В экстремумах функция не возрастает и не убывает, а остается постоянной.
Поскольку производная функции изображает мгновенную скорость изменения функции в данной точке, поэтому мы можем использовать ее для определения интервалов возрастания и убывания функции.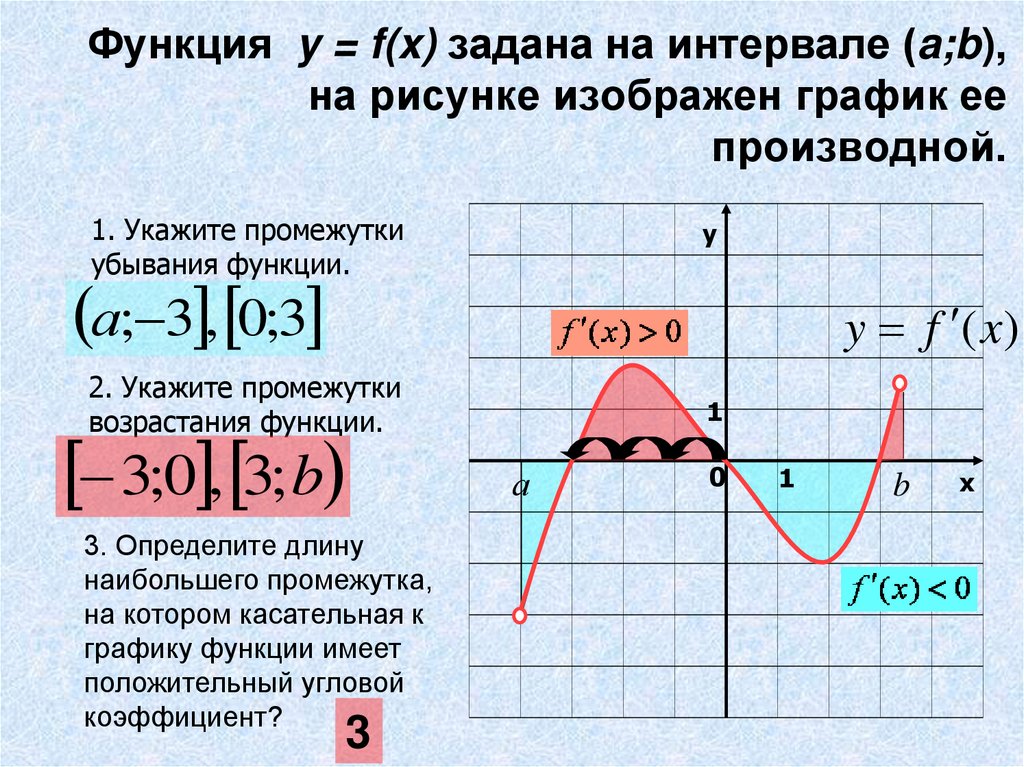 В следующем разделе мы объясним это подробно.
В следующем разделе мы объясним это подробно.
Возрастающий интервал
Если f дифференцируема в точке a, то f строго возрастает в точке a, если .
Убывающий интервал
Если f дифференцируема в точке a, то f строго убывает в точке a if
Чтобы определить, возрастает или убывает функция в точке, важно, чтобы она была дифференцируемой. В следующем разделе мы решим несколько примеров для определения возрастающих и убывающих интервалов с использованием производных функции.
Пример 1
Изучить интервалы возрастания и убывания функции.
Раствор
Мы выполним следующие шаги, чтобы определить интервалы возрастания и убывания вышеуказанной функции:
Шаг 1 — Найдите производную функции
На этом шаге мы продифференцируем функцию .
Шаг 2 — Получение корней первой производной функции f ‘(x)
На этом шаге мы получим корни первой производной функции следующим образом:
9Шаг 3.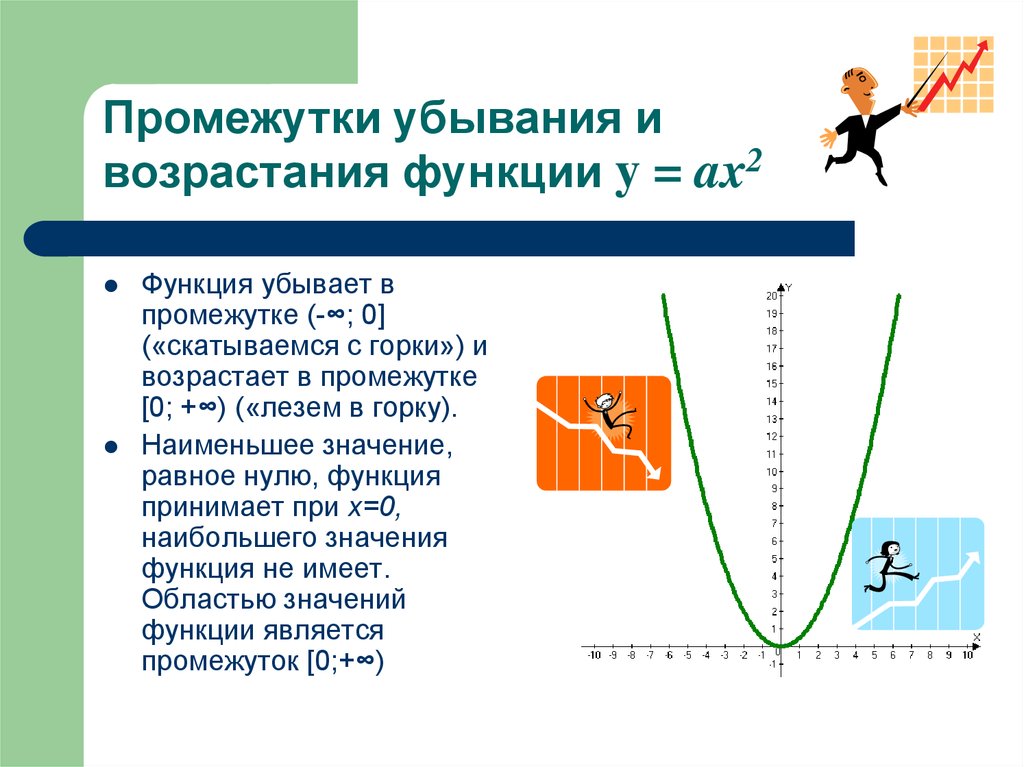 Проверка точек из всех интервалов Эти корни показывают, что у нас есть три интервала, которые равны , и .
Проверка точек из всех интервалов Эти корни показывают, что у нас есть три интервала, которые равны , и .
Мы возьмем значение из каждого интервала и посмотрим, увеличивается оно или уменьшается.
Возьмем -2 из интервала и подставим в производную функции:
Так как f ‘(x) больше 0, то функция на этом интервале возрастает.
Теперь возьмем точку из интервала (-1, 1).
Так как f'(x)<0, то на этом интервале функция убывает.
Теперь возьмем точку из интервала и подставим ее в производную функции:
Поскольку f ‘(x) >0, значит, функция на этом интервале возрастает.
Шаг 4. Запишите возрастающие и убывающие интервалы
На шаге 3 мы проверили точки из каждого интервала и подставили их в производную функции. У нас есть два интервала, где функция возрастала, и один интервал, где функция убывала. Следовательно, мы можем записать возрастающие и убывающие интервалы как:
Возрастающие:
Убывающие:
Пример 2
Изучите интервалы возрастания и убывания функции .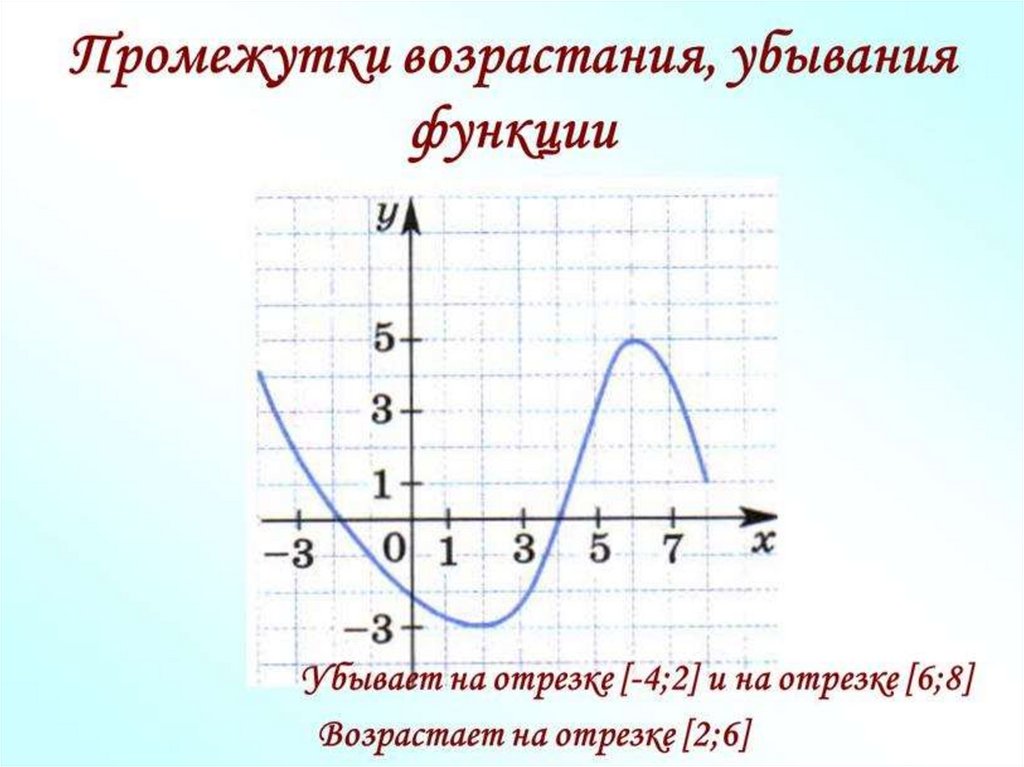
Решение
Мы выполним следующие шаги, чтобы определить интервалы возрастания и убывания вышеуказанной функции:
Шаг 1 — Найдите производную функции
На этом шаге мы продифференцируем функцию .
Шаг 2 — Получить корни первой производной функции f ‘(x)
На этом шаге мы получим корни первой производной функции следующим образом:
У этой производной есть только один корень.
Шаг 3 — Проверка точек из всех интервалов
У нас есть один корень производной функции. У нас будет два интервала с учетом единственного корня функции. Эти интервалы равны и .
Мы возьмем значение из каждого интервала и посмотрим, увеличивается оно или уменьшается.
Возьмем -4 из интервала и подставим в производную функции:
Поскольку f ‘(x) < 0, значит, функция на этом интервале убывает.
Теперь возьмем точку из интервала
Так как f ‘(x) > 0, значит функция на этом интервале возрастает.
Шаг 4. Запишите возрастающие и убывающие интервалы
На шаге 3 мы проверили точки из каждого интервала и подставили их в производную функции. У функции только один корень, поэтому у нас два интервала. Мы можем записать возрастающие и убывающие интервалы как:
Возрастание:
Убывание:
Пример 3
Изучите интервалы возрастания и убывания функции .
Решение
Мы выполним следующие шаги, чтобы определить интервалы возрастания и убывания вышеуказанной функции:
Шаг 1 — Найдите производную функции
На этом шаге мы продифференцируем функцию .
Шаг 2 — Получить корни первой производной функции f ‘(x)
На этом шаге мы получим корни первой производной функции следующим образом:
Существует только один корень производной этой функции.


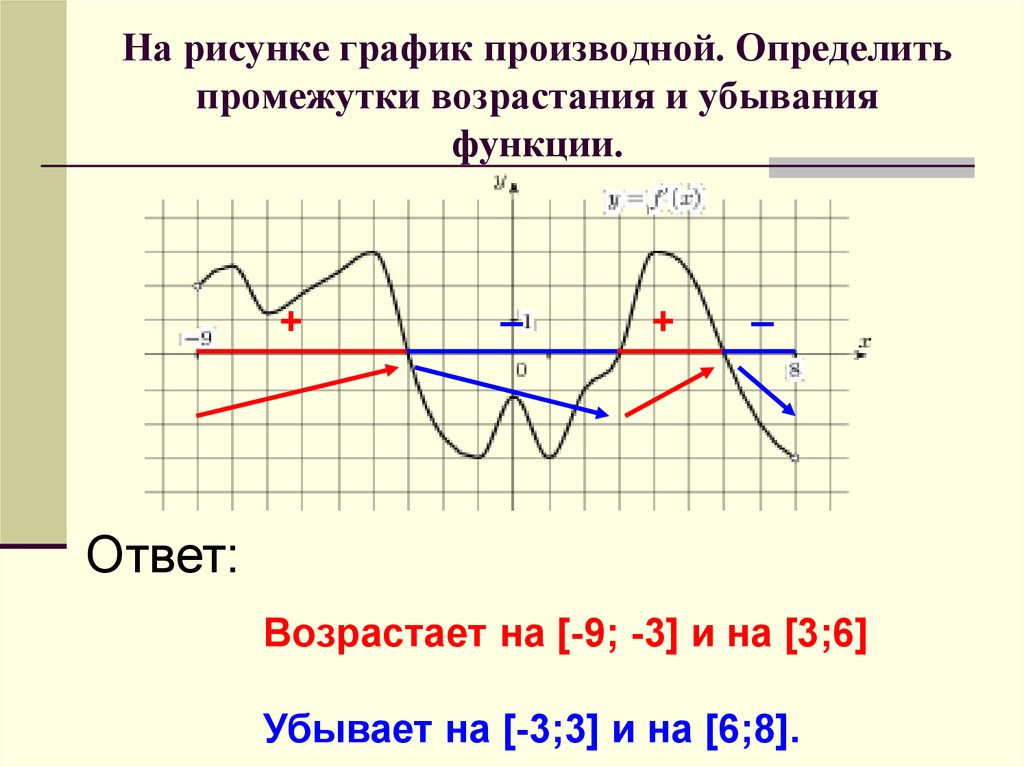
 Чтобы определить знак на каждом промежутке, подставим произвольное значение из этого промежутка в выражение для производной.
Чтобы определить знак на каждом промежутке, подставим произвольное значение из этого промежутка в выражение для производной.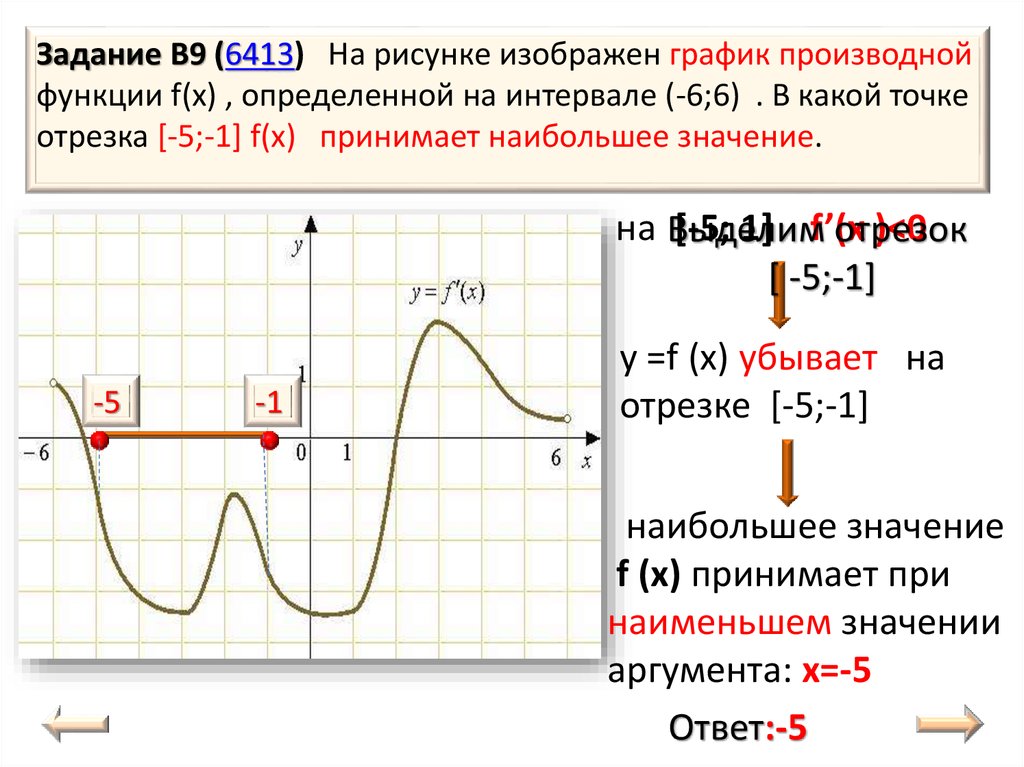


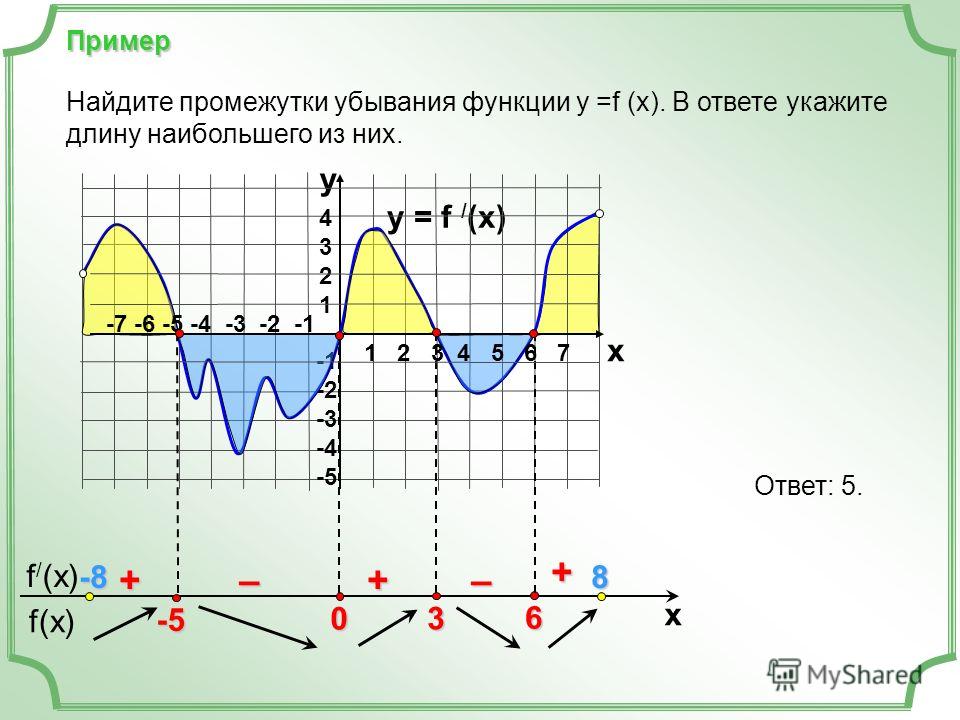
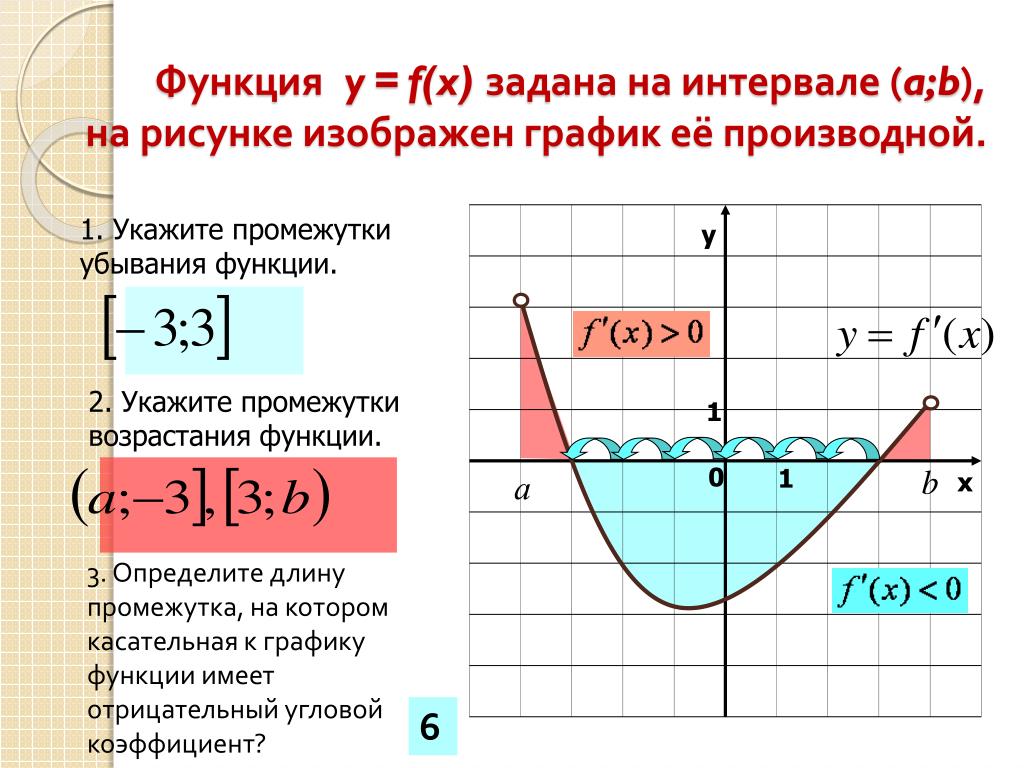



 Но каждая критическая точка — это долина, то есть точка минимума в локальной области.
Но каждая критическая точка — это долина, то есть точка минимума в локальной области.