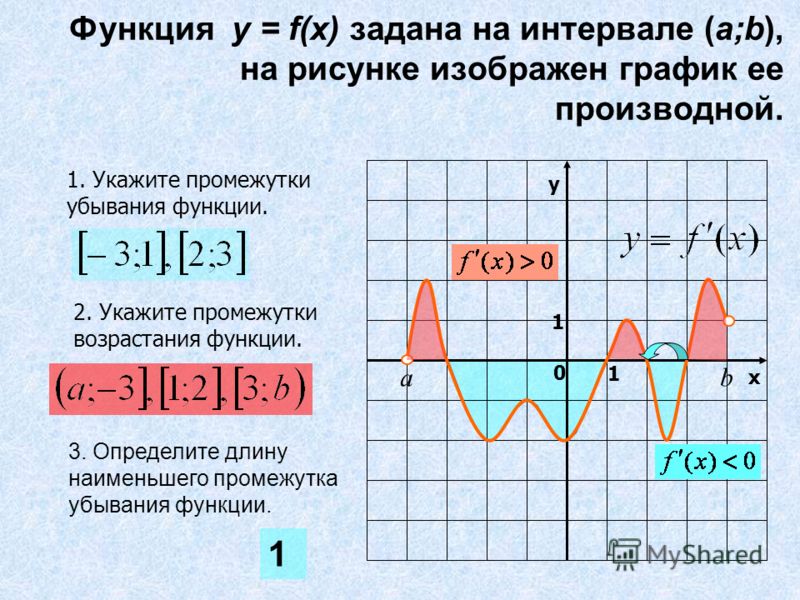
§ Возрастание и убывание функции
Что такое возрастание функции
В начале прочитаем определение возрастания функции.
Запомните!
Функция « y(x) » называется возрастающей на некотором промежутке, если
для любых
« x1 » и « x2 »
принадлежащих данному промежутку, таких, что « x2 > x1 »
выполняется неравенство
« y( x2 ) > y( x1 )».
Определение сложно понять без наглядного примера. Поэтому сразу перейдём к разбору задачи на возрастание функции.
По-другому можно сказать, что, если каждому бóльшему значению « x » соответствует бóльшее значение « y », значит, функция « y(x) » возрастает.
x2 > x1 | Обязательное условие возрастания функции |
Давайте разберем определение возрастания функции на конкретном примере.
Разбор примера
Возрастающей или убывающей является функция « y = 9x − 4 » ?
Для начала определим область определения функции « y = 9x − 4 ».
y = 9x − 4
D(y): x ∈ R ,
то есть « x » —
любое действительное число.
Построим график функции
« y = 9x − 4 ».
Так как функция
« y = 9x − 4 »
линейная, ее график — прямая.
Используем правила построения графика линейной функции. Нам достаточно найти две точки, чтобы построить ее график.
Область определения функции
« y = 9x − 4 » — все действительные числа,
поэтому можно подставить любое число вместо « x » и вычислить « y » по
формуле функции
« y = 9x − 4 ». Например, возьмем
« x = 0 ».
x = 0
y(x) = 9x − 4
y(0) = 9 · 0 − 4 = −4
Для второй точки возьмем « x = 1 ».
x = 1
y(x) = 9x − 4
y(1) = 9 · 1 − 4 = 5
Отметим две полученные
точки «(0; −4)» и «(1; 5)» на
координатной плоскости
и проведем через них прямую.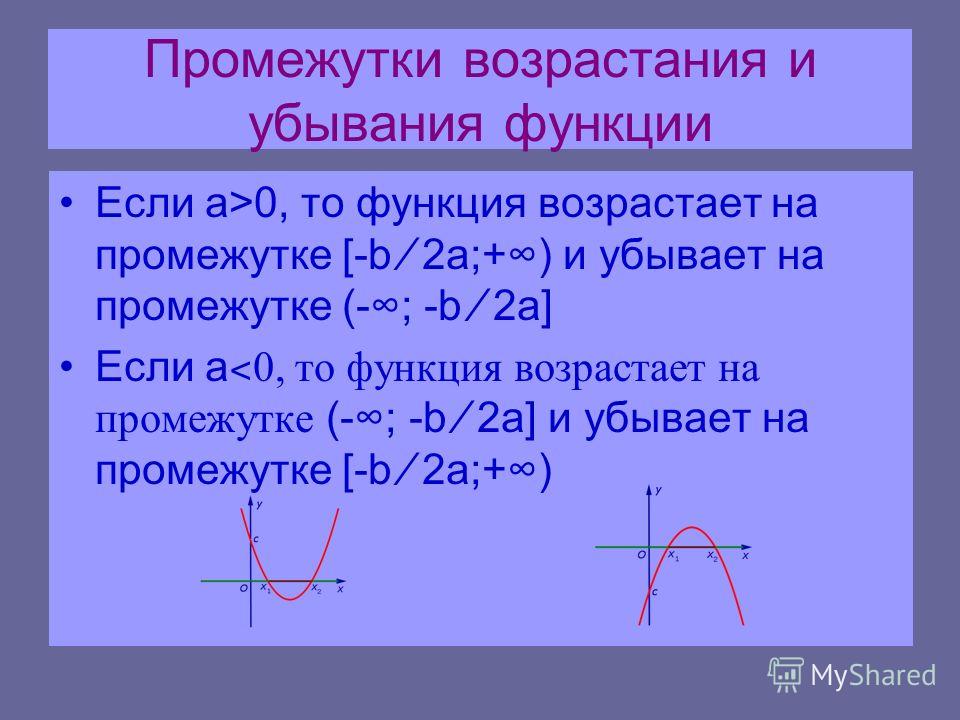
Докажем, что функция « y = 9x − 4 » возрастает на всей своей области определения двумя способами: по ее графику и аналитически (по ее формуле).
Как определить по графику, что
функция возрастаетПо определению возрастания функции мы знаем, что
если « x » увеличивается,
то « y » тоже должен увеличиваться.
На рисунке ниже видно, что график функции « y = 9x − 4 » «идет в гору». Другими словами, при увеличении « x » ↑ растет значение « y » ↑.
В этом можно убедиться, если взять две любые точки на графике. Например, точки, по
которым мы построили график функции. Назовем эти точки:
« (·)A » и « (·)B ».
У первой точки « (·)A »
координаты:
x1 = 0 ; y1 = − 4
У второй точки « (·)B » координаты:
x
На примере точек « (·)A » и « (·)B » видно, что
при увеличении
« x ↑ ( x2 > x1 )»
растет
« y ↑ ( y2 > y1 ) ».
Поэтому график зрительно «идет в гору».
Как по формуле доказать, что функция возрастает
Вернёмся к нашей функции
« y = 9x − 4 ».
По графику мы поняли, что
функция « y = 9x − 4 » возрастает,
так как ее график «идет в гору».
Но как доказать по формуле, что функция
возрастает на всей своей области определения?
Запомните!
Функция возрастает на всей области определения, когда при
« x2 > x1 »
выполняется условие
« y( x2 ) > y( x1 ) ».
Формулировка выше не самая простая для понимания. Давайте разберем ее на практике.
По определению возрастания функции нам нужно доказать, что при
« x 2 > x1 » увеличивается значение функции
« y( x2 ) > y( x1 ) ».
Но как нам найти значения функции
« y( x1 )» и
«y( x2 ) »?
Для нахождения « y( x1 )» и
«y( x2 ) »
достаточно подставить « x1 » и
« x2 » в исходную формулу « y = 9x − 4 ».
y( x1 ) = 9x1 − 4
y( x2 ) = 9x2 − 4
Теперь запишем обязательное условие возрастания функции.
x2 > x1 | Обязательное условие возрастания функции |
Подставим в неравенство
« y( x
« y( x1 ) = 9x1 − 4» и
« y( x2 ) = 9x2 − 4 » .
y( x2 ) > y( x1 )
9x2 − 4 > 9x1 − 4
Упростим полученное неравенство.
9x2 − 9x1 > − 4 + 4
9x2 − 9x1 > 0
Вынесем общий множитель в левой части неравенства.
9(x2 − x1) > 0
Разделим левую и правую часть на «9».
9(x2 − x1) > 0 | : 9
| 9(x2 − x1) |
| 9 |
При делении нуля на любое число получается ноль.
x2 − x1 > 0
x2 > x1
Мы доказали, что выполняется исходное условие возрастания функции «x 2 > x1».
Отсюда следует, что функция
« y = 9x − 4 » возрастает на всей области определения.
В завершении вместо ответа следует написать фразу:
«Что и требовалось доказать».
Посмотрим другой пример, где требуется доказать, что функция возрастает.
Разбор примера
Доказать, что функция возрастает на всей области определения: y = 13x − 1
По аналогии с предыдущим примером составим неравенства, которые доказывают, что функция возрастает.
x2 > x1 | Обязательное условие возрастания функции |
Вместо « y( x1 )» и
«y( x2 ) » запишем
формулу функции « y = 13x − 1 » и упростим полученное неравенство.
y( x2 ) > y( x1 )
13x2 − 1 > 13x1 − 1
13x2 − 13x1 > 1 − 1
13(x2 − x1) > 0 |: 13
| 13(x2 − x1) |
| 13 |
>
x2 − x1 > 0
x2 > x1
Что и требовалось доказать.
Что такое убывание функции
Запомните!
Функция « y(x) » называется убывающей на некотором промежутке, если для любых
« x1 » и « x2 »
принадлежащих данному промежутку, таких,
что « x2 > x1 »
выполняется неравенство « y( x2 ) 1 )».
x2 > x 1 | Обязательное условие убывания функции |
Как по графику понять, что функция убывает
Разбор примера
Доказать, что функция убывает на всей области определения: y = 1 − 3x
По определению убывания функции мы знаем, что,
если « x »
↑ растет, то
« y » ↓ должен уменьшаться.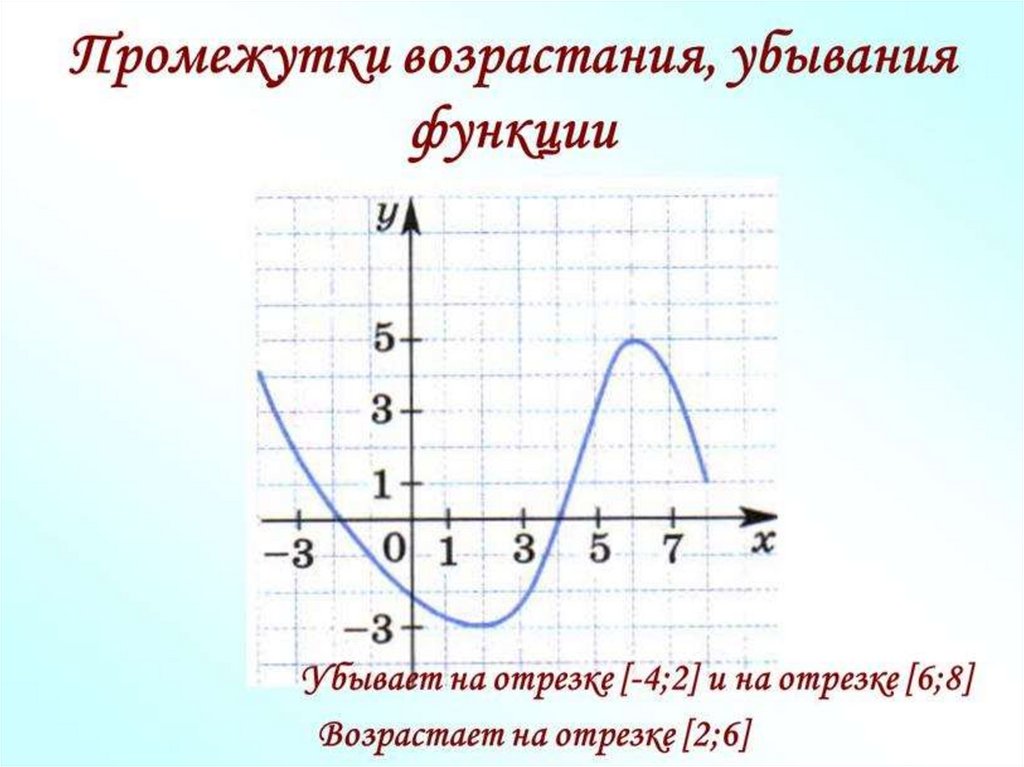
Построим график функции
« y = 1 − 3x ». Ее график — прямая, поэтому нам будет достаточно двух точек.
Область определения функции
« y = 1 − 3x » — все действительные числа,
поэтому можно поставить любое число вместо « x » и вычислить « у » по
формуле функции
« y = 1 − 3x ». Например, возьмем
« x = 0 »
и « x = 1 ».
x = 0
y(x) = 1 − 3x
(·) А (0; 1)
x = 1
y(1) = 1 − 3x
y(1) = 1 − 3 · 1 = 1 − 3 = −2
(·) B (1; −2)
Построим график функции
« y = 1 − 3x » по полученным точкам
« (·)A » и « (·)B ».
На графике функции видно, что зрительно график «спускается с горы», то есть функция убывает. Другими словами, при увеличении
« x »
↑ уменьшается
значение
« y » ↓.
Как по формуле доказать, что функция убывает
Вернёмся к нашей функции
« y = 1 − 3x ».
По ее графику мы поняли, что функция убывает, так как график «спускается с горы».
Но как доказать по формуле,
что функция « y = 1 − 3x » убывает на всей области определения?
Запомните!
Чтобы доказать, что функция убывает требуется доказать, что при любых
« x2 > x1 » выполняется
« y( x2 ) 1 ) ».
« y = 1 − 3x ». Докажем, что она убывает на всей своей области определения.
x2 > x1 | Обязательное условие убывания функции |
Подставим « y( x1 )» и «y( x2 ) » в формулу функции « y = 1 − 3x » и упростим полученное неравенство.
y( x2 ) 1 )
1 − 3x21
3x1 − 3x2 3(x1 − x2)
| 3(x1 − x2) |
| 3 |
x1 − x2 −x21
Умножим на « −1 » левую и правую часть неравенства.
−x21 | · (−1)
x2 > x1
Что и требовалось доказать.
Как по графику функции определить
возрастание и убывание
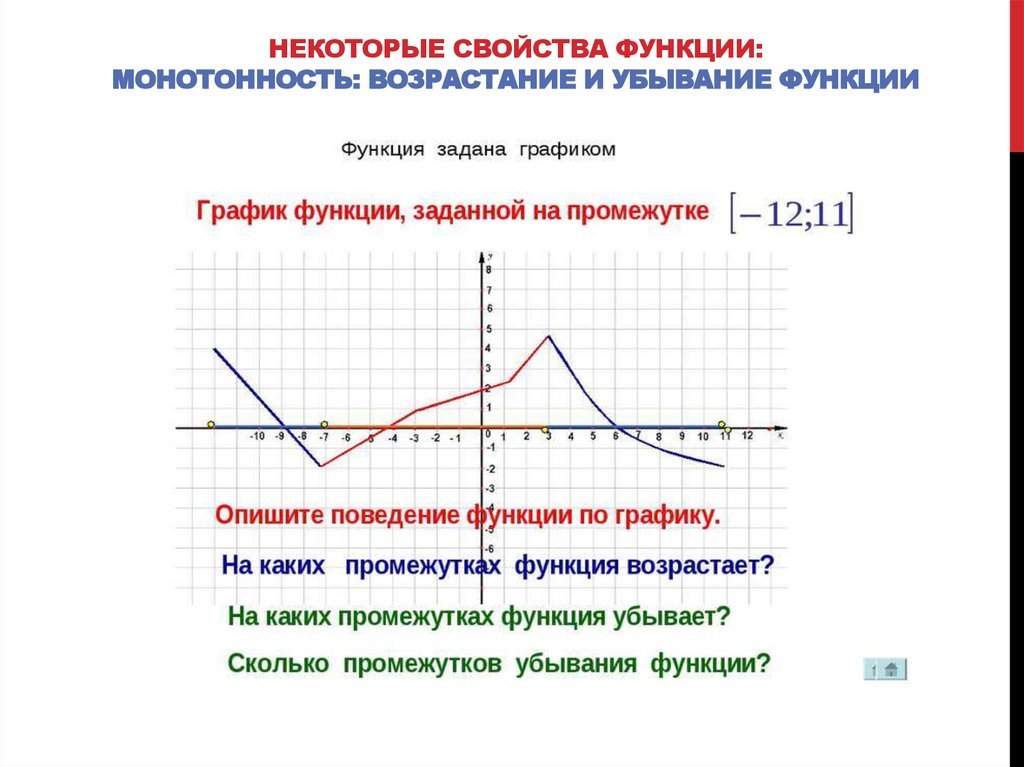
Потренируемся только по графику функции определять промежутки возрастания и убывания функции.
Разбор примера
На рисунке ниже изображён график функции, определенной на множестве действительных чисел. Используя график, найдите промежутки возрастания и промежутки убывания функции.
Отметим с помощью штриховых линий промежутки, где график функции убывает («спускается с горы») и где он возрастает («идет в гору»).
Запишем через знаки неравенств, какие значения принимает « x » на полученных промежутках. Обратите внимание, что во всех случаях при указании промежутков, мы указываем, что их концы входят в промежуток, то есть используем знаки нестрогого неравенства.
Остаётся записать полученные промежутки возрастания и убывания функции в ответ.
Ответ:
- функция убывает при
x ≤ −2; 0 ≤ x ≤ 3,5 - функция возрастает при
−2 ≤ x ≤ 0 ; x ≥ 3,5
Более грамотно будет записать ответ с помощью специальных математических символов.
Ответ:
- функция убывает на промежутках x ∈ (−∞ ; −2] ∪ [0; 3,5]
- функция возрастает на промежутках x ∈ [−2 ; 0] ∪ [3,5 ; +∞]
При каких значениях
« m » функция является убывающей или возрастающей
Ещё один тип заданий, в которых требуется определить,
при каких
« m » ( « а, b » или других буквах) функция убывает или возрастает.
Разбор примера
При каких значениях « m » функция
« y = mx − m − 3 + 2x » является убывающей?
Обратимся снова к определению убывания функции. Вспомним, как записать условия убывания функции с точки зрения формул.
x2 > x1 | Обязательное условие убывания функции |
Запишем эти условия, используя формулу функции « y = mx − m − 3 + 2x », заданную в
задаче.
Вместо
« x »
подставим « x1 » и « x2 ».
y( x2 ) 1 )
mx2 − m − 3 + 2x21 − m − 3 + 2x1
Упростим полученное неравенство. Перенесем из правой части все члены неравенства в левую часть с противоположными знаками.
mx2 − m − 3 + 2x2 − mx1 + m + 3 − 2x1
Упростим полученное выражение. Некоторые члены неравенства взаимоуничтожатся.
mx2 − mx1 − m + m − 3 + 3 + 2x2 − 2x1 mx2 − mx1 + 2x2 − 2x1
Вынесем общие множители за скобки.
m( x2 − x1) + 2(x2 − x1)
Теперь
вынесем общий множитель
« ( x2 − x1 ) ».
( x2 − x1) (m + 2)
Вспомним обязательное условие убывания функции.
x2 > x1 | Обязательное условие убывания функции |
Преобразуем исходное условие убывания функции « x2 > x1 ». Перенесем все в левую часть.
x2 > x1
x2 − x1 > 0
По условию убывания функции
« x2 − x1 > 0 »,
значит, чтобы
произведение
«( x2 − x1) (m + 2)
» было меньше нуля, требуется, чтобы множитель «(m + 2)» был меньше нуля. Так как по
правилу знаков:
плюс на минус даёт минус.
| + | · | − | |
| (x2 − x1) | · | (m + 2) |
Решим полученное неравенство.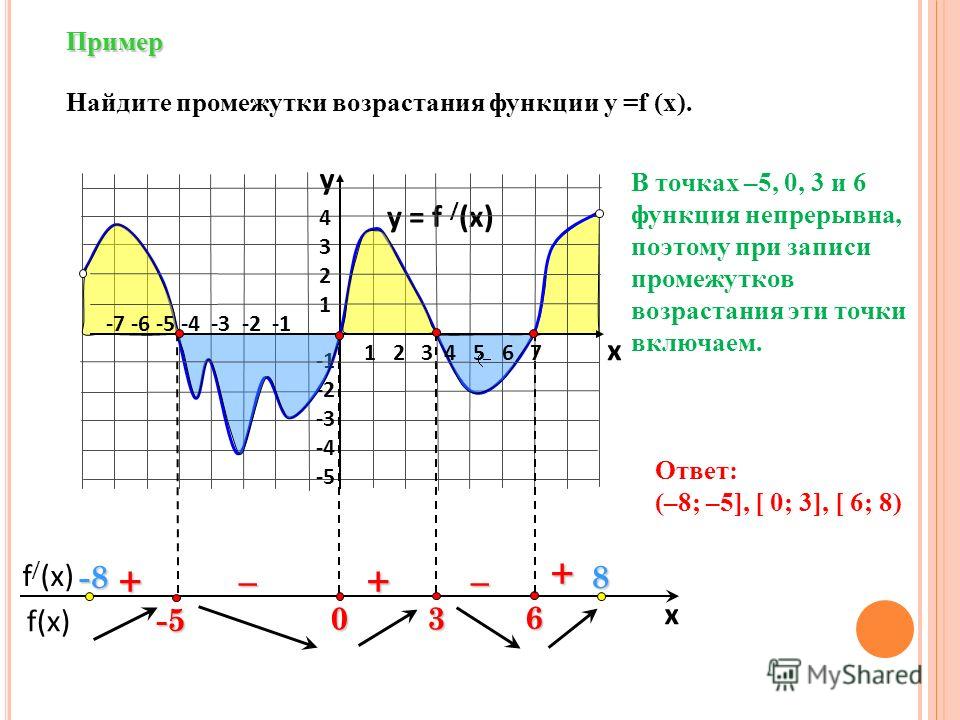
{-x}$ возрастает. 9{-х}$ ;
Если мы положим x = 0, то мы получим 2 (что положительно), что означает, что при 0 функция достигает минимальных значений….
, пожалуйста, помогите мне найти интервал, в котором она увеличивается… Когда функция достигает минимума значение равно 0, я думаю, что начиная с 0 оно начинает увеличиваться… но не может найти интервал….
- исчисление
- функции
- производные
$\endgroup$
1 9{-x}$ всегда положителен, поэтому вам нужно смотреть только на $x(2-x)$. Выясните, на каком интервале он положительный. Он положителен, если два фактора оба положительны или оба отрицательны. Но первый множитель отрицателен, только если $x<0$, а на этом интервале $2-x$ положителен. Далее заметьте, что $2-x$ положительна именно тогда, когда $x<2$. Вы должны быть в состоянии взять его оттуда.
$\endgroup$
2
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Критические точки, монотонное возрастание и убывание
Функция называется возрастающей , если она возрастает при входе $x$ движется слева направо и называется , уменьшая если это уменьшается при движении $x$ слева направо. Конечно, функция может увеличиваться в одних местах и уменьшаться в других: вот осложнение.
Мы можем заметить, что функция возрастает, если наклон ее тангенс положителен и уменьшается, если наклон его тангенса отрицательный. Продолжая идею о том, что наклон касательной есть производная: функция возрастает там, где ее производная положительна и убывает там, где ее производная отрицательна .
Это отличный принцип, потому что нам не нужно строить график функции
или иным образом перечислите множество значений, чтобы выяснить, где оно увеличивается
и уменьшается. Во всяком случае, это должно быть большим подспорьем в построении графика для
знать заранее, где график идет вверх и где он идет вниз.
И точки, где касательная горизонтальна, т. е. где производная равна нулю, составляют критических точек . Точки, где график имеет пик или впадину обязательно будет лежать среди критические точки, хотя есть и другие возможности для также критические точки.
Кроме того, для функций, с которыми мы здесь будем иметь дело, имеется довольно систематический способ получить всю эту информацию: найти интервалы возрастания и убывания функции $f$:
- Вычислить производную $f’$ от $f$ и решить уравнение $f'(x)=0$ для $x$, чтобы найти все критические точки, которые мы перечисляем в заказать как $x_1
- (При наличии точек разрыва или недифференцируемость, эти точки следует добавить в список! Но точки разрыва или недифференцируемости — это , а не . называется критическими точками .)
- Нам нужна вспомогательная точка : Слева от крайней левой
критическую точку $x_1$ выберите любую удобную точку $t_o$ между каждой парой
последовательные критические точки $x_i,x_{i+1}$ выбирают любую удобную точку
$t_i$, а справа от крайней правой критической точки $x_n$ выбираем
удобная точка $t_n$.
- Оценить производную $f’$ на всех вспомогательных точек $t_i$.
- Вывод: если $f'(t_{i+1})>0$, то $f$ равно , увеличивая на $(x_i,x_{i+1})$, а если $f'(t_{i+1}) уменьшается на тот интервал.
- Вывод: на «внешнем» интервале $(-\infty,x_o)$ функция $f$ увеличивается на на , если $f'(t_o)>0$, и на уменьшается на , если $f'(t_o) увеличивается, если $f'(t_n)>0$, и на уменьшается на , если $f'(t_n)
Это правда, что есть много возможных путей к этому процедура, особенно для полиномов низкой степени или других довольно специальные функции. Однако, если вы можете быстро вычислить значения из (производных!) функций на вашем калькуляторе, вы также можете использовать эта процедура, как и любая другая.
Какие именно вспомогательные точки мы выберем не имеет значения, т.к.
пока они попадают в правильные интервалы, так как нам просто нужно
один образец на каждом интервале, чтобы узнать, является ли $f’$ положительным или
негатив там.