Варианты самостоятельных и контрольных работ для программы элективного курса «Исследование функции без применения метода математического анализа»
Варианты самостоятельных и контрольных работ для программы элективного курса «Исследование функции без применения метода математического анализа»- Степченкова Анна Евгеньевна, учитель математики
Разделы: Математика
Цель программы: обратить внимание школьников при изучении данной темы в средней и старшей школе, чтобы не допустить формального усвоения темы.
Задачи: разобрать примеры исследования элементарных непрерывных функций, без применения точного определения предела и использования производной, предложить варианты самостоятельных и контрольных работ.
Данная работа является продолжением авторской программы элективного курса «Исследование функции без применения метода математического анализа», базируется на изучении теоретических и практических исследований непрерывных функций одной переменной простейшими методами авторов Шахмейстер А.Х., Шестаков С.А. и других.
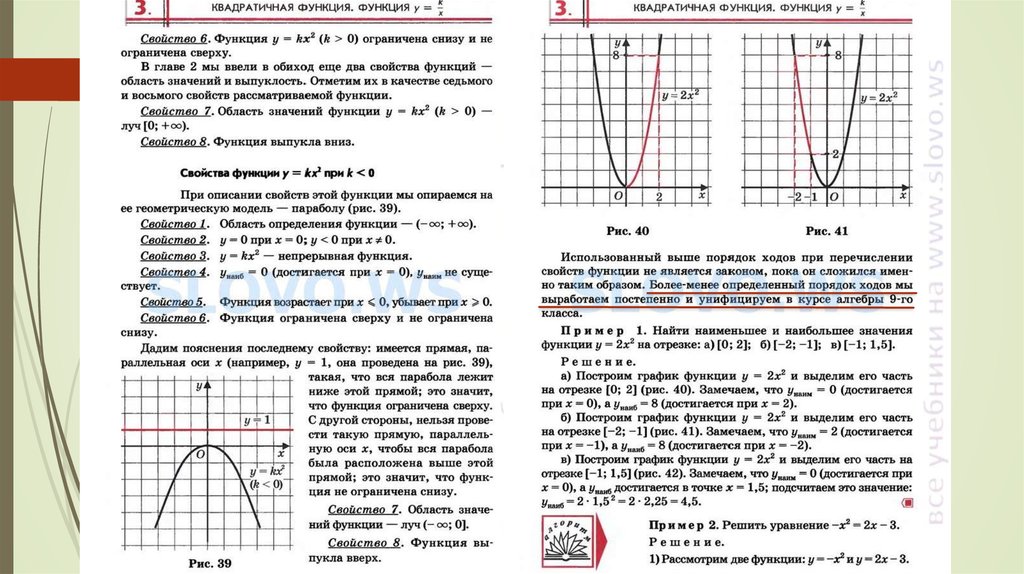
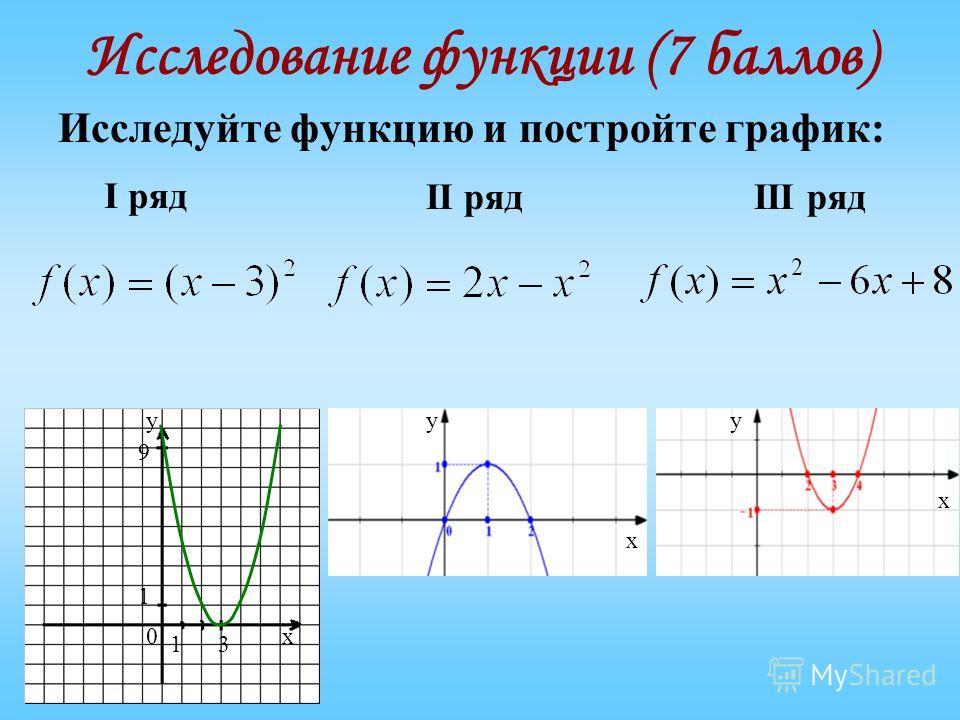
Примеры исследования функции
Примеры исследования функции
Библиографический список
- Райхмист Р.Б. Графики функций: задачи и упражнения. – М.: Школа-Пресс, 1997. – 384 с.
- Шахмейстер. А.Х. Построение графиков функций элементарными методами. – 3-е изд., исправленное и дополненное – СПб.: «Петроглиф» : «Викторина плюс» : М.: Издательство МЦНМО, 2011.-184 с.
- Шестаков С.А. ЕГЭ 2015. Математика. Задача 14. Производная и первообразная. Исследование функций.
Рабочая тетрадь / Под ред. И.В. Ященко – М.: МЦНМО, 2015.–112 с. - Корянов А.Г., Надежкина Н.В. Задания В14. Исследование функций.
- Ажгалиев У. «Возможно ли исследование и построение графика дробно-рациональной функции без использования производной.» («Математика в школе», №7, 2010, ООО «Школьная Пресса»).
- Александрова Л.А. Алгебра и начала анализа. 10 кл. Самостоятельные работы: Учеб. пособие для общеобразоват. учреждений / Под ред. А.Г. Мордковича. – 2-е изд., испр. – М.: Мнемозина, 2006. – 132 с.
- Александрова Л.А. Алгебра и начала анализа. 11 кл. (базовый уровень). Самостоятельные работы для учащихся общеобразовательных учреждений / Л.А. Александрова; под ред. А.Г. Мордковича. – 5-е изд., стер. – М.: Мнемозина, 2012. – 100 с.
- Мордкович А.Г., Тульчинская Е.Е.
- Глизбург В.И. Алгебра и начала математического анализа. 11 класс. Контрольные работы для учащихся общеобразовательных учреждений (базовый уровень) / В.И. Глизбург ; под ред. А.Г. Мордковича.– М.: Мнемозина, 2009. – 32 с.
- Глизбург В.И. Алгебра и начала математического анализа. Контрольные работы для 11 класса общеобразовательных учреждений (профильный уровень) / В.И. Глизбург ; под ред. А.Г. Мордковича.– М.: Мнемозина, 2008. – 55 с.
Рабочая тетрадь / Под ред. И.В. Ященко – М.: МЦНМО, 2015.–112 с.
учреждений – 2-е изд. – М.: Мнемозина, 2003. – 62 с.
Применение производной для исследования функций на монотонность
Вопросы занятия:
· рассмотреть исследование функции на монотонность с помощью производных.
Материал урока.
Прежде
чем приступить к изучению нового материала, выполните упражнение.
Упражнение.
Давайте изобразим график произвольной возрастающей дифференцируемой функции y = f(x). Возьмём на графике произвольно две точки и проведём касательные к графику функции в точках x1 и x2. Теперь рассмотрим эти касательные подробнее. Касательная, проведённая в точке x1 с положительным направлением оси Ox образует острый угол, то есть тангенс этого угла больше нуля. Это значит, что угловой коэффициент этой касательной – положительный. А мы помним, что угловой коэффициент касательной – это ни что иное, как значение производной функции
Теперь рассмотрим касательную к графику
функции в точке x2.
Эта касательная также образует острый угол с положительным направлением оси Ox,
то есть проведя аналогичные рассуждения можно записать, что f‘(x2)
> 0.
В точке x
= 0
касательная совпала с осью Ox, в этой точке выполняется равенство f‘(x2)
= 0.
Если мы с вами будем продолжать брать точки на графике функции и проводить в них касательные, то угловые коэффициенты всех касательных будут больше либо равны нуля. То есть для возрастающей функции в любой точке выполняется неравенство f‘(x) ≥ 0.
Давайте теперь рассмотрим график убывающей
дифференцируемой функции. Возьмём две произвольные точки на этом графике и
проведём касательные к графику функций в этих точках. И рассмотрим угловые
коэффициенты этих касательных. Касательные с положительным направлением оси Ox
образуют тупые углы, то есть тангенсы этих углов меньше нуля, значит, f‘(x)
< 0. Это неравенство выполняется для всех точек данного
графика за исключением тех, касательные в которых параллельны оси Ox
(в этих случаях f‘(x)
= 0).
Обобщая можно сказать, что в любой точке графика убывающей функции выполняется
неравенство f‘(x)
≤ 0.
Из рассмотренных случаев можно вывести
закономерность:
Верны и обратные утверждения. Мы сформулируем их в виде теорем. Обратите внимание, что мы рассматриваем только открытые промежутки, то есть интервалы или открытые лучи. Это делается потому, что некорректно ставить вопрос о производной в концах промежутков.
Итак, сформулируем теоремы. Доказывать мы их не будем.
Теорема 1.
Если во всех точках открытого промежутка X
выполняется неравенство f‘(x)
≥ 0 (причём, f‘(x)
= 0 либо
не выполняется, либо выполняется лишь в конечном множестве точек), то функция y
= f(x) возрастает на промежутке X.
Теорема 2.
Если во всех точках открытого промежутка X выполняется неравенство f‘(x) ≤ 0 (причём, f‘(x) = 0 либо не выполняется, либо выполняется лишь в конечном множестве точек), то функция y = f(x) убывает на промежутке X.
Давайте рассмотрим физическое истолкование теорем.
Пусть колобок убегает от пенька, на
котором сидит зайчик. Пенёк возьмём за начало отсчёта, и пусть расстояние от
пенька до колобка задано функцией S = S (t). Если скорость колобка
положительна, то очевидно, что он будет двигаться от пенька, то есть расстояние
между пеньком и колобком будет увеличиваться. Математически можно сказать, что
функция S (t)
будет возрастать. Если в какой-то момент скорость колобка станет равна нулю, а
потом опять станет положительной, то он в указанный момент как бы
притормаживает, а потом продолжает удаляться от пенька.
А что такое скорость материальной точки? Это производная пути по времени. То есть от знака производной (в нашем случае скорости) зависит характер монотонности функции – в данном случае функции S = S (t). В этом и заключается суть теорем.
Давайте рассмотрим несколько примеров.
Пример.
Пример.
Рассмотрим ещё один пример.
Пример.
Мы с вами рассмотрели случай, когда на
промежутке X производная больше либо меньше нуля. А что делать, если на
всем промежутке X производная
равна нулю? Тогда речь идёт о функции y = C, где C
– постоянная.
Таким образом можно сформулировать ещё одну теорему, которую мы
тоже не будем доказывать.
Теорема 3.
Если во всех точках открытого промежутка X выполняется равенство f‘(x) = 0, то функция y = f(x) постоянна на промежутке X.
Давайте ещё раз повторим основные теоремы, показывающие зависимость промежутков монотонности функции от знака производной.
Теорема 1.
Если во всех точках открытого промежутка X выполняется неравенство f‘(x) ≥ 0 (причём, f‘(x) = 0 либо не выполняется, либо выполняется лишь в конечном множестве точек), то функция y = f(x) возрастает на промежутке X.
Теорема 2.
Если во всех точках открытого промежутка X
выполняется неравенство f‘(x)
≤ 0 (причём, f‘(x)
= 0 либо
не выполняется, либо выполняется лишь в конечном множестве точек), то функция y
= f(x) убывает на промежутке X.
Теорема 3.
Если во всех точках открытого промежутка X выполняется равенство f‘(x) = 0, то функция y = f(x) постоянна на промежутке X.
10-й класс-квадратик-тест-с-ответами – Googlesuche
AlleBilderVideosBücherMapsNewsShopping
.15.1.5.quadraticsreview.pdf
Самопроверка повторения квадратичных чисел в 10 классе… Сделайте набросок каждого квадратичного уравнения и заполните пустые поля ниже… Используйте это место, чтобы подготовить ответы к №5.
[PDF] 10 класс Академическая математика — Квадратика 1 Тест А Ответы на …
www.mathwiz.ca › видео › q1_pta
Академическая математика 10 класса. Квадраты 1 Тест А. Ответы в конце теста. 1. Определите первые 3 шага и график.
Математический блок 10 класса 5 — Решение квадратичных уравнений (Ontario MPM2D)
www.
jensenmath.ca › math20-unit-5
Бесплатные уроки, рабочие листы и видеоуроки для учащихся и учителей. Темы этого раздела включают: решение квадратных уравнений с помощью факторинга, …
Квадратное уравнение 10 класс – Тест
quizizz.com › admin › викторина › квадратное уравнение-10 класс
Квадратное уравнение 10 класс … СЕССИЯ ПОД УПРАВЛЕНИЕМ ПРЕПОДАВАТЕЛЕМ Начните живую викторину … выбор ответа. х.х.х. х.х.х.х. х.х.х.х.х. х10. 2. Множественный выбор.
MPM2D-EXERCISES-GRADE10
www.fridaymath.com › staticExercises › Exercise10
Упражнения на свойства квадратичных отношений. ЗАДАНИЕ на квадратичные отношения; ВИКТОРИНА по квадратичным соотношениям; Образец ТЕСТА по квадратичным соотношениям …
Десятый класс (10 класс) Квадратные уравнения и выражения …
www.helpteaching.com › вопросы › Grade_10
Десятый класс (10 класс) Квадратные уравнения и выражения вопросы для ваших пользовательских печатных тестов и рабочих листов.
В спешке, спешу?
Квадратичный тест для 10 класса — YouTube
www.youtube.com › смотреть
30.06.2021 · Хорошо! Проверьте себя, насколько хорошо вы знаете квадратные уравнения. Часть вопросов следует…
Дата: 45:25
Прислан: 30.06.2021
Es fehlt: ответы | Muss Folgendes enthalten:ответы
10 класс — Квадратные уравнения | Практика по математике, вопросы, тесты…
us.edugain.com › математика › Квадратные уравнения
Каждый раз, когда вы нажимаете кнопку «Новый рабочий лист», вы получаете новый печатный рабочий лист в формате PDF по квадратным уравнениям. Вы можете включить ответы и …
Модуль 4: Квадратичные функции (Математика 10 класса г-жи Макферсон)
Teachers.wrdsb.ca › kathrynmcpherson › unit-4-qua…
Переключить навигацию. Математика 10 класса г-жи Макферсон… Блок 4: Квадратичные функции… БЛОК-ТЕСТ ПО КВАДРАТИЧНЫМ ФУНКЦИЯМ – ВТОРНИК, 20 НОЯБРЯ. ТЕСТ-РЕШЕНИЯ.
Bilder
Alle anzeigen
Alle anzeigen
Ähnlichesuchanfragen
Викторина по квадратным уравнениям с ответами PDF0003
Квадратичный тестовый ответ Ключ
Уровень 10 Квадратичные уравнения Рабочие листы PDF
Квадратичные класс 10
Квадратичные уравнения класс 10 PDF
MPM2D Квадратичные отношения. учащиеся 6–12 классов.
Почему это помогает
Начиная с 6 класса, учащиеся SpringBoard English Language Arts развивают и совершенствуют навыки критического мышления, внимательного чтения, письма в различных жанрах и проведения исследований.
В ходе программы они читают и анализируют широкий спектр текстов различных жанров, включая поэзию, романы, пьесы, биографии, научно-популярные рассказы, выступления и фильмы. Они также учатся писать в таких формах, как эссе, личные рассказы, аргументированные тексты, такие как редакционные статьи и исследовательские работы.
Как это работает
На каждом уровне обучения используются сложные тексты, соответствующие их классам, которые позволяют учащимся изучить идею с разных точек зрения, работая с различными жанрами.
Студенты переходят от чтения под руководством через совместные проекты к уверенной, самостоятельной работе.
6 класс
В модулях, посвященных теме «Изменения», учащиеся:
- Прочтите работы Лэнгстона Хьюза, Джона Стейнбека и Сандры Сиснерос.
- Пишите повествовательные, пояснительные и аргументированные тексты.
- Изучите стратегии планирования, составления, пересмотра и редактирования собственного письма.
- Изучите основы исследований, включая цитирование и способы оценки достоверности источников.
- Углубить свое понимание тем с помощью фильмов и мультимедиа.
Класс 7
В модулях, построенных вокруг темы «Выбор», учащиеся:
- Прочтите работы Нельсона Манделы, Роберта Фроста, Соджорнер Трут и Шекспира.
- Изучите стратегии внимательного чтения, чтобы обнаружить явное и скрытое содержание текстов.
- Пишите в аргументированном, объяснительном и повествовательном режимах.
- Узнайте, как идеи передаются в фильмах и мультимедиа.
Класс 8
В модулях, построенных вокруг темы «Задачи», учащиеся будут:
- Прочтите работы Рэя Брэдбери и Уолта Уитмена, эссе о героях Гражданской войны, рассказы о Холокосте и речь Эли Визеля на вручении Нобелевской премии.
- Узнайте об архетипе героя и рассказах о путешествии героя.
- Написание повествовательных, объяснительных, аргументационных и других текстов.
- Исследуйте проблему в текущих событиях, а затем создайте мультимедийную презентацию.
- Прочитать сцены из пьесы Шекспира Сон в летнюю ночь , затем посмотрите сцены на пленке и проанализируйте, чем адаптация отличается от первоисточника.
Класс 9
В модулях, изучающих использование языка, учащиеся будут:
- Прочтите произведения таких авторов, как Маргарет Этвуд, Луиза Эрдрич, Уильям Шекспир, Джошуа Беннетт, Тони Моррисон, а также избранную документальную литературу.
- Научитесь собирать доказательства из текстов и включать их в письменные и устные ответы.
- Пишите в аргументированном, информационном, повествовательном и других режимах.
- Исследуйте и представьте выводы по текущей проблеме.
10 класс
В модулях, изучающих способность языка убеждать, студенты будут:
- Прочтите такие работы, как « вещи разваливаются » Чинуа Ачебе, « Антигона » Софокла, «О праве женщин голосовать» Сьюзен Б. Энтони и речь Кофи Аннана на вручении Нобелевской премии.
- Узнайте, как культура влияет на мировоззрение.
- Включите текстовые доказательства в письменный аргумент.
- Пишите в аргументированном, повествовательном, информационном и других режимах.
- Исследуйте культуру и представьте результаты в совместной презентации с использованием цифровых медиа.
11 класс
В модулях, посвященных теме «Американская мечта», учащиеся:
- Прочитайте основополагающие документы, такие как Декларация независимости и Вторая инаугурационная речь Линкольна, эссе Генри Дэвида Торо и Ральфа Уолдо Эмерсона, а также роман Зоры Нил Херстон Их глаза смотрели на Бога .
- Напишите описательное эссе, определяющее, что значит быть американцем.
- Напишите обобщающее эссе о том, предоставляет ли Америка по-прежнему доступ к американской мечте.
- Пишите в различных режимах и жанрах.
- Сравните печатную и киноверсию пьесы Артура Миллера Горнило .
- Создайте выпуск новостей на основе реальных новостных организаций.
12 класс
В модулях, построенных вокруг темы «Перспектива», учащиеся:
- Прочтите такие произведения, как «Незнакомец в деревне» Джеймса Болдуина, «Стрельба в слона» Джорджа Оруэлла, «Отелло» Шекспира и « Пигмалион » Джорджа Бернарда Шоу.
- Применение нескольких точек зрения к сложным текстам.
- Применять различные виды литературной критики: архетипическую, марксистскую, феминистскую, историческую, культурологическую и читательскую.
- Выполняйте тщательное чтение и письмо, синтезирующее обучение.
- Проанализируйте, как исторический контекст повлиял на выступления Отелло , и сравните несколько киноверсий драмы.
Должны ли ученики начинать программу в 6 классе?
Нет. Хотя программа ориентирована по вертикали, так что учащиеся приобретают академические навыки, учащиеся могут приступить к курсовой работе в любое время и при этом получить пользу.
Читать больше
Что произойдет, если у меня есть изучающие английский язык или испытывающие трудности с чтением?
Версия для учителей каждого курса предлагает стратегии дифференцированного обучения, поэтому вы можете адаптировать каждый раздел. Для учащихся, которым было бы полезно более интенсивное обучение языку, SpringBoard также предлагает языковые семинары на уровне своего класса, скоординированные с подразделениями ELA.
Читать больше
Цинковое зажигание
Видеообзор нового модуля Reading Ignition от Zinc, который создает для учащихся индивидуальную траекторию обучения на основе данных оценки с помощью интерактивных видеороликов, обучающих навыкам понимания сложных текстов.