Как найти угол зная радиус и длину дуги?
Как найти угол зная радиус и длину дуги?
Через центральный угол в градусах и радиус Длина (L) дуги сектора равняется числу π, умноженному на радиус круга (r), умноженному на центральный угол в градусах (α°), деленному на 180°.
Как найти радиус окружности если известна длина дуги?
Основные формулы окружности:
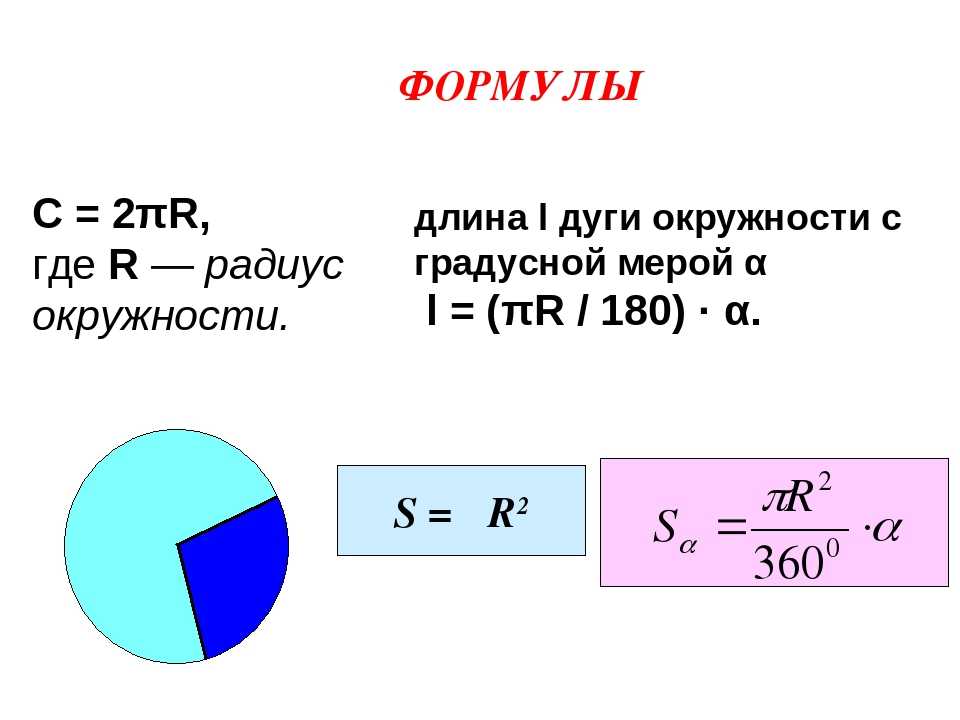
- C = 2πR, где C — длина окружности
- R = С/(2π) = D/2, где С/(2π) — длина дуги окружности
- D = C/π = 2R, где D — диаметр
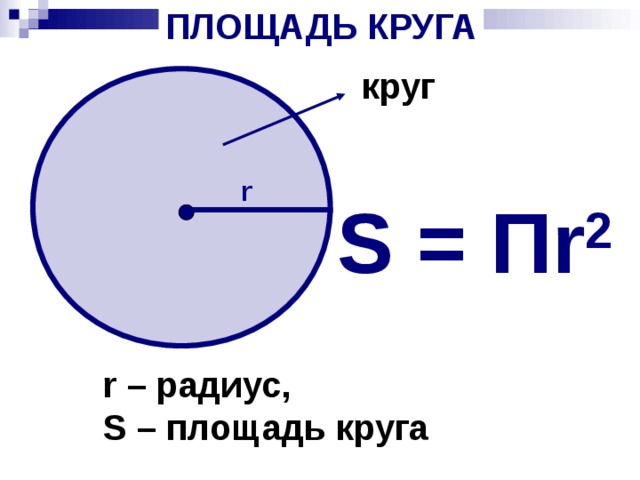
- S = πR2, где S — площадь круга
- S = ((πR2)/360)α, где S — площадь кругового сектора
Как найти радиус окружности зная центральный угол?
Умножьте площадь сектора на 360 градусов. Разделите результат на произведение пи и центрального угла….
- R — искомый радиус окружности.
- S — площадь сектора круга.
- α — центральный угол.
- π (пи) — константа, равная 3,14.
Как найти радиус дуги?
Ну а дальше все просто: измеряем расстояние от пересечения дуг до начала (или конца) рассматриваемой дуги, а затем расстояние от пересечения дуг до точки, соответствующей высоте сегмента.
Как найти радиус окружности по точкам?
Зная координаты точки центра и любой точки окружности можно вычислить длину радиуса, что позволит при необходимости рассчитать длину окружности и площадь круга — плоскости, расположенной внутри окружности. l = 2π • r; S = 2π • r2, где l — длина окружности; r — радиус окружности; S — площадь круга; Пи — 3,14.
Как найти радиус окружности по ее длине?
Онлайн калькулятор радиуса круга. Как узнать радиус круга, окружности.
- Если нам известна длина: Формула для расчета радиуса круга через его длину: R=P/(2π)
- Если нам известна площадь: Формула для расчета радиус круга через площадь: R=√S/π
- Если нам известен диаметр: Формула для расчета радиус круга через диаметр: R=D/2.
Как найти центр окружности если известен диаметр?
Самое простое- это вписать в круг квадрат или прямоугольник. Затем провести диагонали соединяющие противоположные углы. Место пересечения этих линий и будет центром окружности, а каждая из этих линий будет являться ее диаметром. Место пересечения диаметров окружности всегда будет является ее центром.
Как найти координаты окружности?
Уравнение окружности ω (A; R) имеет вид (x – a)2 + (y – b)2 = R2, где a и b – координаты центра A окружности ω (A; R) .
Как определить находится ли точка в круге?
Найдите расстояние между центром круга и заданными точками. Если расстояние между ними меньше радиуса, то точка находится внутри окружности. если расстояние между ними равно радиусу окружности, то точка находится на окружности окружности. если расстояние больше радиуса, то точка находится вне круга.
Как определить положение точки относительно окружности?
Если расстояние от точки до центра окружности больше радиуса, то точка лежит вне нашего круга (0).
Если расстояние до центра меньше радиуса, то точка лежит внутри нашего круга (2). Если расстояние до центра равно радиусу, то точка лежит на окружности (1).
Как составить уравнение окружности по рисунку?
Уравнение окружности: (x-a)² + (y — b)² = R², здесь а — х координата центра окружности, b — у координата центра окружности, R — радиус окружности.
Как составить уравнение касательной к окружности?
х 2 + у 2 = R 2 . Пусть Р ( х1 , у 1 ) – точка окружности ( рис. 1 ), тогда уравнение касательной к окружности в данной точке имеет вид: ( х1 – х0 ) ( х – х0 ) + ( у1 – у 0 ) ( у – у 0 ) = R 2 .
Как выглядит уравнение прямой?
Уравнение прямой в отрезках имеет вид xa+yb=1 x a + y b = 1 , где a и b – это некоторые действительные числа, которые не равны нулю. Абсолютные величины чисел a и b равны длине отрезков, которые отсекаются прямой линией на осях координат.
Как привести уравнение плоскости к нормальному виду?
Если плоскость задана другим уравнением, а необходимо произвести вычисление от заданной точки до плоскости, необходимо привести уравнение к виду нормального уравнения плоскости, используя формулу p=opencos α⋅x0+cos β⋅y0+cos γ⋅z0−p| p = cos α · x 0 + cos β · y 0 + cos γ · z 0 — p .
Что такое D в уравнении плоскости?
При D = 0 уравнение определяет плоскость, проходящую через начало координат, так как координаты точки 0(0; 0; 0) удовлетворяют этому уравнению. 2. При A = 0 уравнение определяет плоскость, параллельную оси Ox, поскольку вектор нормали этой плоскости перпендикулярен оси Ox (его проекция на ось Ox равна нулю).
Как составить уравнение нормали к плоскости?
В пределах заданной системы координат плоскость и общее уравнение, ее определяющее, неразрывно связаны: каждой плоскости отвечает общее уравнение плоскости вида Ax+By+Cz+D=0 A x + B y + C z + D = 0 ( при конкретных значениях чисел A, B, C, D A , B , C , D ).
Что такое нормаль к плоскости?
Нормаль к поверхности в заданной её точке — прямая, перпендикулярная к касательной плоскости в указанной точке поверхности.
Как определить вектор нормали к плоскости?
Для определения нормального вектора →n=(A, B, C) n → = ( A , B , C ) в плоскости необходимо наличие общего уравнения плоскости, имеющее вид Ax+By+Cz+D=0 A x + B y + C z + D = 0 .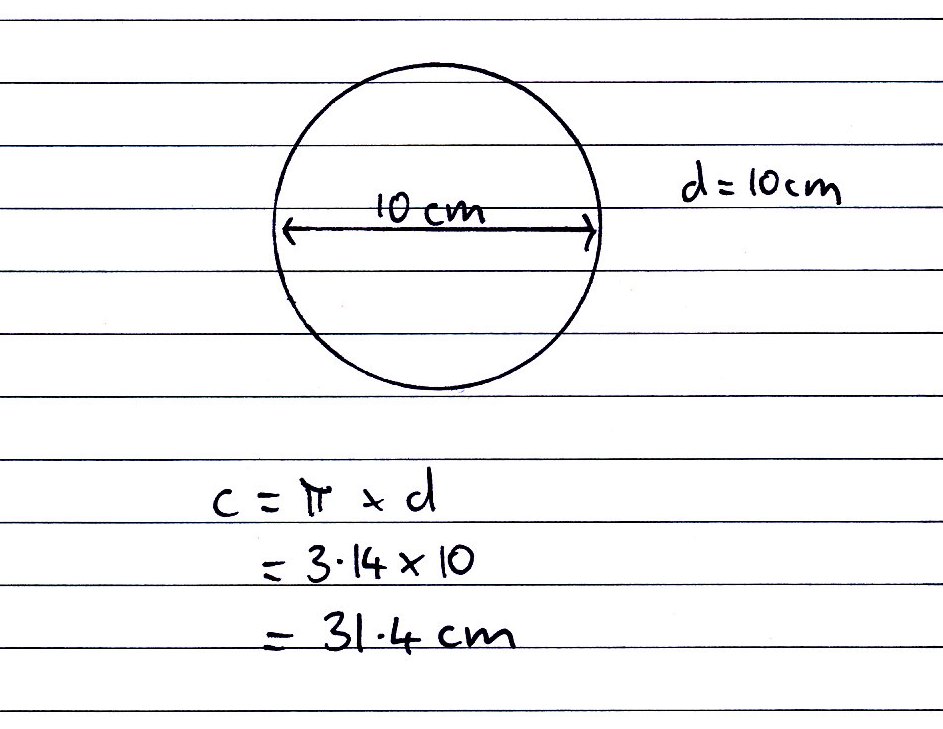
То есть достаточно иметь уравнение плоскости, тогда появится возможность для нахождения координат нормального вектора.
Какой вид имеет уравнение плоскости по точке и вектору нормали?
Теорема. Если в пространстве задана точка М0(х0, у0, z0), то уравнение плоскости, проходящей через точку М0 перпендикулярно вектору нормали (A, B, C) имеет вид: A(x – x0) + B(y – y0) + C(z – z0) = 0.
Как найти координаты направляющего вектора?
Чтобы вычислить координаты направляющего вектора, нам нужно взять числа из знаменателя канонического уравнения прямой. Приведем пример задачи. В прямоугольной системе координат задана прямая, которую можно описать уравнением x−14=y+12−3 x — 1 4 = y + 1 2 — 3 .
Как называется вектор перпендикулярный плоскости?
1 Нормальный вектор плоскости – определение, примеры, иллюстрации. 2 Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости по уравнению плоскости.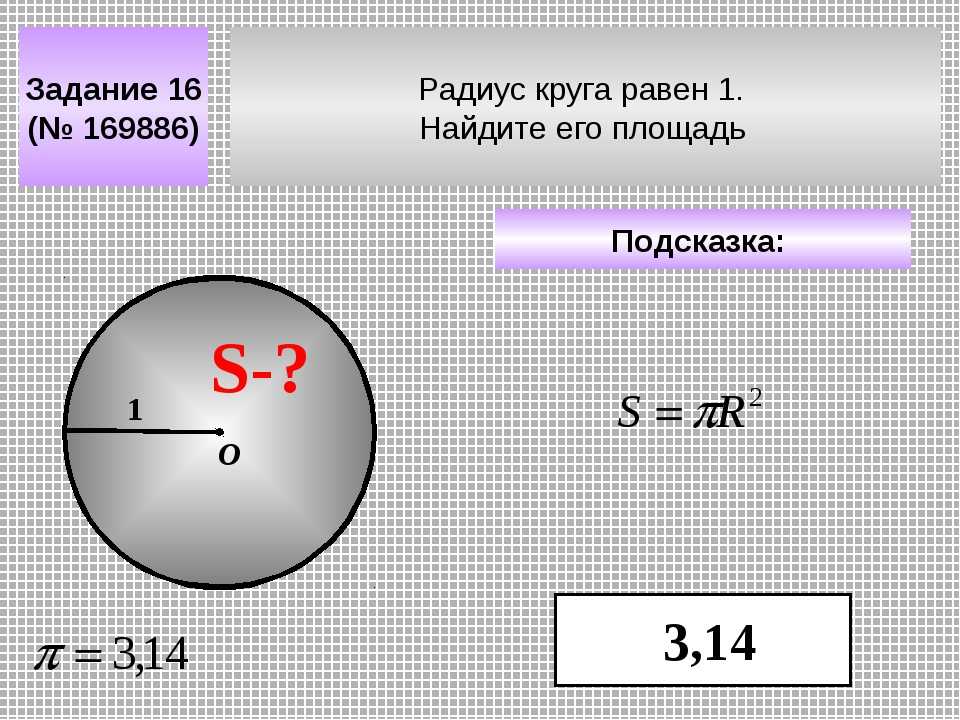
Как найти радиус круга — «Добрый-Совет.Ru»
В жизни достаточно часто приходится пользоваться школьными знаниями геометрии. Эти знания могут пригодиться в строительстве и дизайне, в частности, ландшафтном. В определенных ситуациях необходимо знать радиус круга. Как его найти? Есть несколько способов.
Круг и окружность
В геометрии есть 2 фигуры, которые, вроде бы очень похожи, но при этом отличаются. И отличия заключаются не только во внешнем виде, но и в формулах вычисления отдельных элементов данных фигур.
Окружность
По своей сути окружность — это всего лишь линия, а точнее, кривая линия, начало и конец которой совпадают (замкнутая линия).
Все точки этой кривой удалены на равное расстояние от центра. Этот центр находится в той же плоскости, что и кривая. Внутри окружности ничего нет. То есть имеется центр и имеется линия, проведенная вокруг этого центра на определенном расстоянии.
Круг
Круг — это практически та же самая окружность, проведенная на определенном расстоянии от центра, но область между линией и центром заполнена множеством точек, которые находятся на расстоянии от центра, не большем, чем радиус этого круга.
Вычисление радиуса
Радиус можно посчитать разными способами.
Если известен диаметр
Этот способ самый простой. Диаметр равен двум радиусам. Поэтому радиус будет высчитываться по формуле r=d/2.
Если известна длина окружности круга
Также несложно будет узнать радиус, если известна длина окружности круга. Формула для расчета длины окружности C=2πr, в которой C является длиной окружности, π=3,14, а r — это как раз искомый радиус.
Преобразовав данную формулу, получим: r=C/2π. Вообще, число «Пи» в формуле — это постоянное значение, округленное до 3,14. На самом деле «Пи» выглядит так:
Означает данное значение отношение длины окружности к диаметру той же окружности.
Если известна площадь круга
Формула площади круга выглядит так: A= π(r²). Эту формулу можно преобразовать в формулу радиуса:
В ней A — это площадь круга, число «Пи» мы уже знаем, оно равно округленно 3,14, а r — это и есть искомое значение радиуса.
Как найти радиус круга, все школьники учат на геометрии.
Взрослые, конечно, со временем забывают эти формулы. Но, прочитав данную статью, радиус круга может найти каждый: и взрослый, и ребенок.
Радиус круга онлайн
Если всё же возникли сложности и высчитать радиус круга по формулам не получается, то можно воспользоваться онлайн-калькуляторами и узнать нужное значение с помощью них.
Для вычисления радиуса нужно только ввести известное значение длины окружности или площади круга в пустую ячейку и нажать кнопку «вычислить».
Вот так легко и просто можно решить поставленную задачку.
Видео по теме
https://www.youtube.com/watch?v=N72pPXzIhgIVideo can’t be loaded because JavaScript is disabled: Круг — радиус, диаметр, длина окружности (https://www.youtube.com/watch?v=N72pPXzIhgI)
Подпишитесь на наши интересные статьи в соцетях!
Или подпишитесь на рассылку
Сохрани статью себе в соцсеть!
Счет, математика и статистика — набор академических навыков
Геометрия окружности
Главное меню ContentsToggle 1 Определение 2 Окружность 2.
1 Определение 2.2 Примеры работы 3 Область 3.1 Определение 3.2 Примеры работы 4 Рабочая тетрадь 5 См. также 6 Внешние ресурсы 7 Проверьте себя
Определение
Расстояние вокруг границы круга называется окружностью .
Расстояние по окружности через центр называется диаметр .
Расстояние от центра круга до любой точки на границе называется радиусом . Радиус равен половине диаметра; $2r=d$.
Отрезок, соединяющий две точки окружности, представляет собой хорду . Каждый диаметр является хордой, но не каждая хорда является диаметром.
Область, которую отсекает хорда, называется сегментом .
Область внутри круга, ограниченная двумя радиусами, представляет собой сектор .
Длина между двумя точками по окружности равна дуге .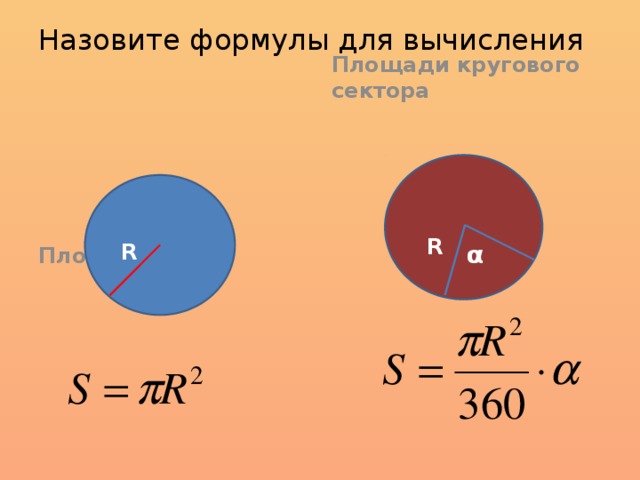
Окружность
Определение
Формула для вычисления длины окружности: \[C = \pi d \qquad\text{или } \qquad C = 2\pi r\], где $d$ — диаметр, а $r$ это радиус.
Примеры работы
Пример 1
Радиус данной окружности равен $r=4$см. Вычислите окружность.
Решение
\begin{align} C &= 2\pi r\\ &= 2 \times \pi \times 4\\ &= 8 \pi \\ &\ приблизительно 25,1 \text{см (до 1 десятичного знака) place)} \end{align}
Пример 2
Найдите диаметр круга с длиной окружности $18$см.
Решение
\begin{align} C&=\pi d\\ 18 &= \pi d \end{align} Разделите обе стороны на $\pi$: \begin{align} \frac{18}{\pi } &= d \\ d &= \frac{18}{\pi}\\ d &\примерно 5,7 \text{см (до 1 знака после запятой)} \end{align} 92 &= \frac{50}{\pi}\\ r &= \sqrt{\frac{50}{\pi} }\\ r &\приблизительно 4,0 \text{см (до 1 знака после запятой)} \end {align}
Рабочая тетрадь
- Круг
См. также
- Длина дуги и площадь сектора
Внешние ресурсы
- Рабочая тетрадь по геометрии круга на математика центр.
Проверь себя
Проверь себя: Площадь геометрических фигур
Как найти радиус круга по площади тремя простыми способами
Как найти радиус круга по площади тремя простыми способами
Яна Russick
02 мая 2021 г.
Онлайн-репетиторство
,
Математика
Если вы хотите знать, как найти радиус круга с площадью, вы должны знать формулу площади круга. Также необходимо ознакомиться с такими понятиями, как длина окружности, сектор и диаметр круга. Для начала давайте определим, что такое радиус.
Что такое радиус окружности?
Нижняя буква r в центре круга ниже представляет его радиус.
Как видите, радиус круга отмечен отрезком, идущим от края круга к центру круга.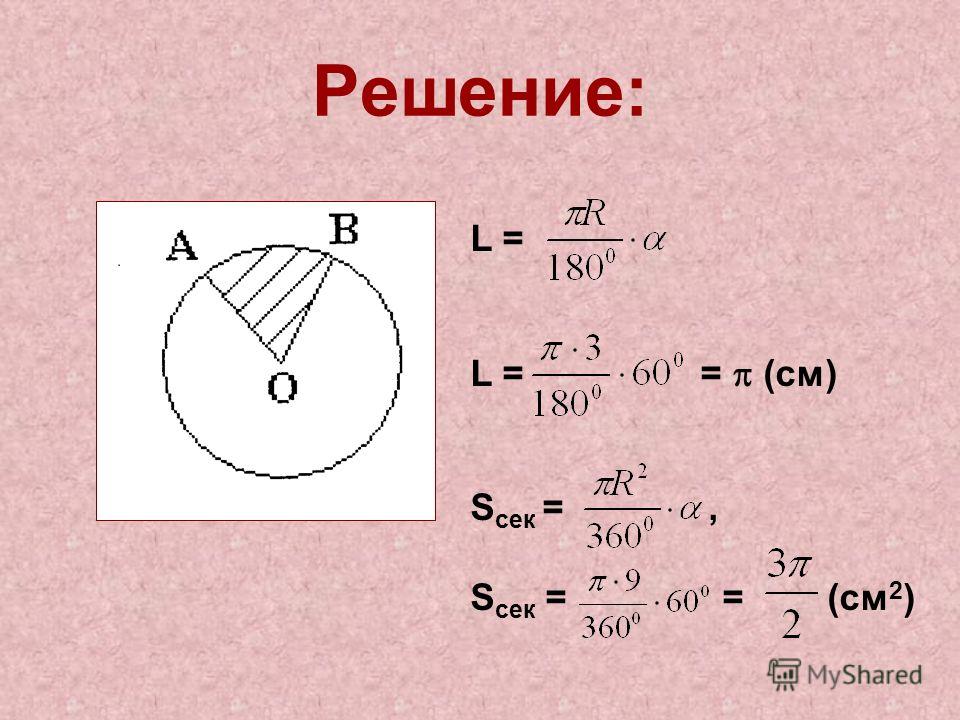
Если бы вы провели линию от верха круга к низу, пересекающую радиус, вы бы образовали полукруг:
Диаметр и длина окружности
Круг вверху показывает окружность и диаметр. Окружность круга — это расстояние вокруг края всего круга. Диаметр круга — это длина от одного конца круга до другого, проходящая через центр круга. Поскольку отрезок диаметра пересекает центр окружности, диаметры всегда в два раза больше длины радиуса.
Сектор круга
Заштрихованная область круга ниже показывает сектор, который представляет собой срезанный участок круга:
Внутренние отрезки сектора равны радиусу окружности. Угол, который составляют эти два измерения, называется центральным углом.
Как найти радиус круга с помощью формул площади и длины окружности
Если радиус неизвестен, можно использовать формулу длины окружности, площади круга или площади сектора:
Давайте воспользуемся этими формулами для определения радиуса трех различных кругов, начиная с формулы площади круга.