Как найти радиус окружности зная хорду и расстояние от центра окружности: Как найти хорду окружности зная радиус

Длина хорды окружности

В элементарной геометрии хордой называют отрезок прямой линии, который соединяет две точки, лежащие на некоторой кривой (окружности, эллипсе, параболе). Хорда, которая проходит через центр окружности, называется ее диаметром.

Определение длины хорды окружности

 

Длина хорды окружности может быть определена по формуле:

 

L = 2r × sin ( α / 2 )

 

L – хорда

r – радиус окружности

O – центр окружности

α – центральный угол

 

Следует заметить, что такую величину, как длина хорды, инженерам, конструкторам различных машин и механизмов, а также архитекторам приходится вычислять не так уж и редко. Чаще всего этот параметр необходим для того, чтобы правильно сконструировать и разметить весьма распространенные в технике фланцевые соединения.

Основные их элементы, фланцы, представляют собой плоские кольца, на которых на одинаковом друг от друга расстоянии располагаются отверстия, куда устанавливаются резьбовые шпильки или болты. Фланцы используются для соединения между собой участков различных трубопроводов и валов, причем применяются они в большинстве случаев попарно. Для того чтобы определить, в каких именно местах при изготовлении этих деталей следует просверлить отверстия, необходимо знать, какова длина хорды окружности, проходящей через их центры. При этом имеется в виду та хорда, которая располагается между центрами соседних отверстий. Зная этот параметр, можно не только составить правильный чертеж, по которому в дальнейшем будут производиться фланцы, но и впоследствии проконтролировать точность их изготовления. С большой точностью определить такой параметр, как длина хорды, требуется и тогда, когда разрабатываются детали машин и механизмов, имеющих форму криволинейных скоб: именно он определяет расстояние между конечными точками этих изделий.

Важную роль длина хорды играет и в баллистике – науке, изучающей движение тел, брошенных в пространстве. Дело в том, что перемещаются они по эллиптической траектории, и для того чтобы определить такой параметр, как, скажем, расстояние по прямой, которое при тех или иных условиях преодолеет пуля или баллистическая ракета, требуется вычислить именно длину хорды. При этом специалистами используются достаточно сложные математические методы и формулы, учитывающие большое количество различных параметров, и для того, чтобы определить такую, казалось бы, простую величину, как длина хорды, в баллистике широко применяется современная высокопроизводительная вычислительная техника.

Что касается хорд в архитектуре, то их чаше всего можно встретить там, где используются различные сводчатые и арочные конструкции. Например, для того, чтобы точно рассчитать ширину дверного проема, верхняя часть которого выполнена в виде арки, требуется вычислить именно такой параметр, как длина хорды. При проектировании строений, которые увенчаны куполами (например, христианские храмы), архитекторам также в обязательном порядке нужно пользоваться формулами расчета хорд для того, чтобы правильно определить параметры снования этих конструкций (например, требуемые их диаметры).

Окружность и круг. 5-й класс

Образовательные цели. Обеспечить усвоение учащимися понятий окружности, круга и их элементов (радиуса, диаметра, хорды). Рассмотреть соотношение между диаметром и радиусом окружности.

Развивающие цели. Создать условия для развития у учащихся способностей анализировать и сравнивать предложенные геометрические объекты. Развивать практические умения пользоваться чертежными инструментами.

Воспитательные цели. Способствовать формированию умений работать в группах и индивидуально, осуществлять рефлексию своей деятельности. Создать условия для формирования навыков аккуратного построения фигур.

Метод: исследование с помощью предметных моделей и компьютера.

Тип урока: изучение и первичное закрепление нового материала.

Форма: коллективная и индивидуальная работа.

Время: 45 мин.

Оборудование:

• циркуль, линейка, ножницы, стакан, маркер и альбомный лист (на каждого ученика).
• мультимедийный проектор.
• Технологическая карта урока

1. Цели урока.

(Слайд 1) Посмотрите на представленные фотографии и картинки и ответьте на вопрос: что же объединяет все эти предметы?

Математической моделью всех представленных предметов является окружность или круг.

Как вы и догадались тема нашего урока “Окружность и круг”. Откройте тетради и запишите число и тему урока. (Слайд 2). Окружность – удивительно гармоничная фигура, древние греки считали ее самой совершенной. Зная свойства окружности и свойства других линий можно создавать зрительные иллюзии, как, например, на следующих слайдах.

(Слайды 4-9).

Сегодня мы научимся различать окружность и круг, дадим определение окружности и всех ее элементов, рассмотрим практические задачи и узнаем много интересных фактов по построению окружности.

2. Мотив деятельности.

На каждой парте перед вами есть круглый предмет, в нашем случае стакан. Берем стакан, ставим на лист бумаги и обводим его маркером.

Ребята, посмотрите какой след оставил маркер?

А теперь возьмите в руки ножницы и аккуратно вырежьте окружность.

Что у вас получилось?

Обратите внимание, что в начале у нас была окружность, но если мы вырежем ее, то получается фигура, которая называется, — круг. (Слайд 10).

Как вы думаете: сама окружность принадлежит кругу или нет?

Возможно ли построить окружность без циркуля?

Вот несколько примеров, которые я вам продемонстрирую.

С помощью веревки. Берем отрезок веревки, один конец придерживаем пальцем, а другим концом, натягивая веревку и придерживая мел/ручку, чертим окружность.

С помощью расчески. Берем обыкновенную расческу с отверстием на одном конце. Закрепим один край расчески кнопкой (или булавкой) и, вставив между соответствующими зубьями остро заточенный карандаш, поворачиваем расческу и чертим окружность.

Что общего в этих способах построения? (Слайд 11). Запишите определения круга и окружности в тетрадь.

3. Организация учебно-познавательной деятельности учащихся (поисково-исследовательская).

Сегодня на уроке мы с вами научимся чертить окружность с помощью циркуля.

(Слайд 12) Построение окружности радиусом 3 см с помощью циркуля.

Алгоритм построения окружности запишите в тетрадь.

1. Отметьте в тетради точку и обозначьте ее буквой О. Эта точка называется центром окружности.
   Слово “центр” произошло от латинского слова “центриум” – палка с заостренным концом, которой погоняли быков; позднее оно стало означать заостренную ножку циркуля, а потом и точку, которую оставляет ножка циркуля на листе бумаги.
2. Возьмите циркуль и линейку, отмерьте нужное расстояние (например, 3 см) между “ножками” циркуля.
3. Поставьте иголку циркуля в точку О, а другой “ножкой” циркуля проведите замкнутую линию.
4. Если нужно построить круг, то закрасьте часть плоскости внутри окружности.

А теперь, когда окружность построена в тетрадях, давайте познакомимся с ее основными элементами.

(Слайд 13) И первый элемент, с которым мы познакомимся будет радиус окружности. Для этого:

1. Точка О – называется центром окружности.
2. Отметим на окружности две точки А и М.
3. Соединим точки О и М, О и А.
4. Отрезки ОА и ОМ – называются радиусами окружности.

И записываем следующее определение. Отрезок, соединяющий центр окружности с точкой, лежащей на окружности, называется радиусом.

(Слайд 14) Опрос:

• Как вы думаете, сколько радиусов можно провести в окружности?
• Радиус ОМ и МО – это один и тот же радиус или разные радиусы окружности?
• А что вы можете сказать о длинах радиусов?

Запишите в тетради равенство, выделенное красным цветом ОА = ОМ = r.

Ребята, а теперь посмотрите, (учитель берет вырезанный круг в руки) если я сверну круг пополам, то сгиб образует линию, которая разделит круг на две равные части. Эта линия будет диаметром круга. Диаметр делит круг пополам. (Слайд 15) И следующее наше знакомство с понятием диаметр окружности. Для этого проделаем следующие построения.

1. Продолжим отрезок АО до пересечения с окружностью.
2. Обозначим точку пересечения буквой К.
3. Отрезок АК называется диаметром окружности.

И записываем следующее определение. Диаметр – это отрезок, соединяющий две точки на окружности и проходящий через ее центр.

Опрос:

• А как вы думаете, сколько диаметров я могу провести в окружности?
• Диаметры АК и КА один и тот же диаметр или разные диаметры окружности?
• Равны ли длины диаметров в окружности?

Ребята, обратите внимание. (Учитель наглядно показывает на модели вырезанного круга). Если согнуть круг несколько раз пополам, то линии сгиба пересекутся в одной точке, эта точка — центр круга, а линии сгибов – диаметры, они пересекаются и точкой пересечения делятся пополам. Линия, соединяющая центр с краем круга – это радиус.

(Слайд 16) Сравните радиус окружности и ее диаметр.

• Как относится диаметр к радиусу окружности?
• Какой вывод мы можем сделать?

Полученное выражение запишите в тетради d = 2r.

(Слайд 17) И в заключение нашего знакомства с основными элементами окружности давайте познакомимся с понятием хорда.

1. Соединим точки А и М, М и К.
2. Отрезки АМ и МК – называются хордами окружности.

И записываем определение. Хорда – это отрезок, соединяющий две точки окружности.

Опрос:

• Хорда АМ и МА – это одна и та же хорда, или разные? (Одна и та же).
• Как вы думаете, если хорда и диаметр – это отрезки, соединяющие две точки окружности, то тогда чем они отличаются?

Действительно, диаметр – отрезок, обязательно проходящий через центр, а хорда – любой отрезок, не обязательно проходящий через центр.

• Тогда можно ли дать другое определение диаметра?

Верно, диаметр – это хорда, проходящая через центр окружности.

(Слайд 18) Давайте закрепим наши полученные знания. Перечислите все радиусы, диаметры и хорды окружности.

(радиусы – OA, OB, OC, OF, OK,

диаметры – BF, CK,

хорды – BL, DF, LE, BF, CK).

4. Совместная деятельность учащихся в структуре урока.

Ребята, теперь Вам нужно в течение 2-ух минут разделиться на 6 групп (по 4-5 человек) и выбрать для решения одно из предложенных заданий.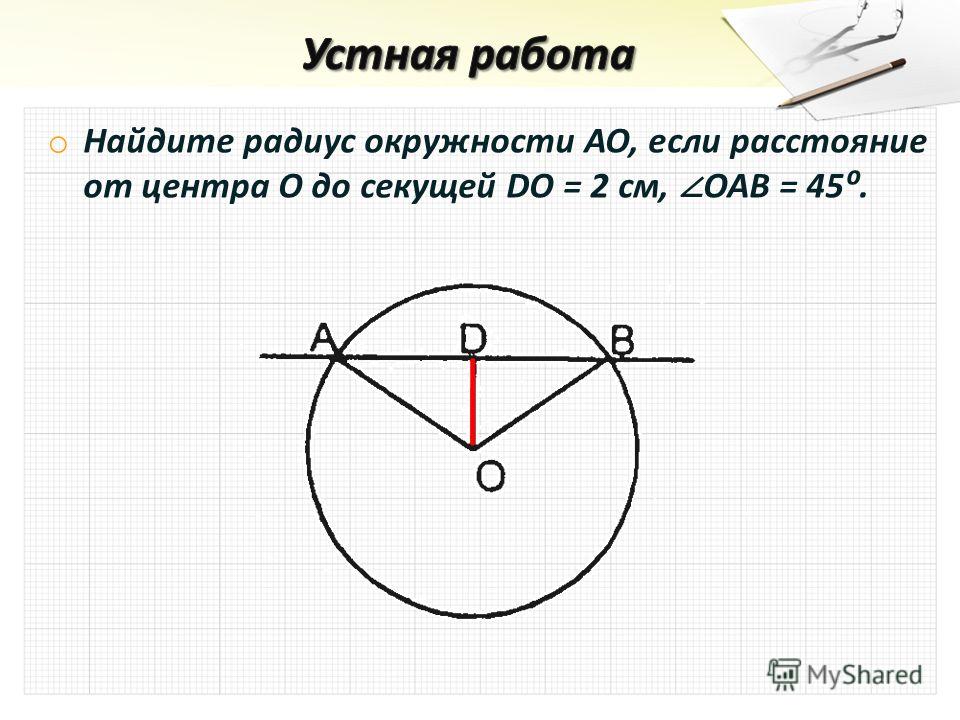 Задания разные по сложности и по построению. Обязанности — кто, что решает — вы определите между собой сами. Анализ решения заданий будем проводить, обсуждая коллективно. Время на выполнение задания 7 мин. (Учитель ставит песочные часы или будильник, чтобы дети могли контролировать время).

(Слайд 19) Задание 1

Начертите окружность с центром в точке О радиуса 3 см 2 мм.

а) Отметьте точки Р и В, расстояния от которых до точки О равны 3 см 2 мм. Принадлежат ли точки Р и В окружности? Кругу?

б) Отметьте точки А и С, расстояния от которых до точки О равны 2 см 3мм. Принадлежат ли точки А и С окружности? Кругу?

(Слайд 20) Задание 2

Начертите окружность с центром в точке О радиуса 2см 4мм. Проведите две хорды и диаметр. Сравните длины хорд с длиной диаметра.

(Слайд 21) Задание 3

Начертите две окружности с общим центром, такие, что радиус первой окружности равен 4 см и это составляет 2 радиуса второй окружности.

(Слайд 22) Задание 4.

На рисунке диаметр меньшей окружности равен 6 см.

а) Чему равен диаметр большей окружности?

б) Чему равен ее радиус?

5. Индивидуальная работа учащихся в структуре урока.

Ребята, все вы молодцы и хорошо поработали в группах. А теперь давай рассмотрим следующее задание, которое каждый постарается решить сам (Слайд 23). Время на выполнение индивидуального задания 5 минут.

(Учитель ставит песочные часы или будильник, чтобы учащиеся контролировали время).

Обращаю ваше внимание, что любую окружность мы строим по радиусу. Поэтому подумайте, как зная диаметр найти радиус окружности, которую нужно построить.

6. Регулятивные действия учащихся.

Ребята, заканчивая урок, давайте посмотрим со стороны, что мы узнали и чему научились на сегодняшнем уроке. Для этого давайте ответим на следующие вопросы по вариантам (Слайд 24).

7. Домашнее задание.

Для закрепления знаний и умений, полученных на сегодняшнем уроке, дома разберите записанные нами определения и выполните следующие задания в учебнике №406 б, №407 б. (Слайд 25).

Ребята, спасибо за урок (Слайд 26).

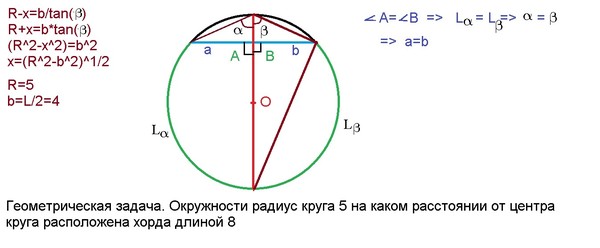
геометрия — Как найти радиус окружности по хорде и сечению радиуса?

$\begingroup$

Нарисовать круг с центром O .

Линия AD представляет собой хорду длиной 8 см. Дуга вверху меньше, чем внизу.

B является центром AD .

Леска CB — леска длиной 2 см. Соответствует AD при 90°.

Схема:

92$, так что $R = 5. $

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Аккорды окружности – объяснение и примеры

Из этой статьи вы узнаете:

• Что такое хорда окружности.
• Свойства хорды и; и
• Как найти длину хорды по разным формулам.

 

Что такое хорда окружности?

По определению, хорда — это прямая линия, соединяющая 2 точки на окружности. Диаметр окружности считается самой длинной хордой, потому что она соединяется с точками на окружности окружности.

В круге ниже AB, CD и EF являются хордами круга. Хорда CD — это диаметр окружности.

Свойства хорды

• Радиус окружности — это биссектриса хорды.

• Длина хорды увеличивается по мере уменьшения перпендикулярного расстояния от центра окружности до хорды и наоборот.
• Диаметр — это самая длинная хорда окружности, при этом расстояние по перпендикуляру от центра окружности до хорды равно нулю.
• Два радиуса, соединяющие концы хорды с центром окружности, образуют равнобедренный треугольник.

• Две хорды равны по длине, если они равноудалены от центра окружности. Например, хорда AB равна хорде CD , если PQ = QR.

Как найти хорду окружности?

Есть две формулы для определения длины хорды. Каждая формула используется в зависимости от предоставленной информации.

• Длина хорды, заданная радиусом и расстоянием до центра окружности.

Если известна длина радиуса и расстояние между центром и хордой, то формула для определения длины хорды имеет вид:

Длина хорды = 2√ (r ² – d ² )

Где r = радиус окружности, а d = расстояние по перпендикуляру от центра окружности до хорды.

На приведенном выше рисунке длина хорды PQ = 2√ (r ² – d ² )

• Длина хорды, учитывая радиус и центральный угол

Если известны радиус и центральный угол хорды, то длина хорды определяется как

Длина хорды = 2 × r × синус (C/2)

= 2r синус (C/2)

Где r = радиус окружности

C = угол, образуемый в центре хордой

d = расстояние по перпендикуляру от центра окружности до хорды.

Давайте разработаем несколько примеров с хордой окружности.

Пример 1

Радиус окружности равен 14 см, а расстояние по перпендикуляру от хорды до центра равно 8 см. Найдите длину хорды.

Решение

При заданном радиусе r = 14 см и перпендикулярном расстоянии d = 8 см

По формуле Длина хорды = 2√(r ² −d ² )

Длина хорды = 2√ (14 ² −8 ² )

= 2√ (196 − 64)

= 2√ (132)

= 2 х 11,5

= 23 см хорда 3

3 90

Пример 2

Расстояние по перпендикуляру от центра окружности до хорды равно 8 м. Вычислите длину хорды, если диаметр окружности равен 34 м.

Решение

При заданном расстоянии d = 8 м.

Диаметр, D = 34 м. Итак, радиус r = D/2 = 34/2 = 17 м

Длина хорда = 2√ (R ² -D ² )

по замене,

Длина хорда = 2√ (17 ² — 8 ² )

= 2 — 8 ² ) – 64)

= 2√ (225)

= 2 х 15

= 30

Итак, длина хорды 30 м.

Пример 3

Длина хорды окружности 40 дюймов. Предположим, что перпендикулярное расстояние от центра до хорды составляет 15 дюймов. Каков радиус хорды?

Решение

Дано, длина хорды = 40 дюймов.

Расстояние, d = 15 дюймов

Радиус, r =?

по формуле, длина хорды = 2√ (r ² -D ² )

40 = 2√ (r ² — 15 ² )

40 = 2чина (R ² − 225)

Квадрат с обеих сторон

1600 = 4 (r ² – 225)

1600 = 4r ² – 900

Доп.

2500 = 4R ²

делят обе стороны на 4, мы получаем,

R ² = 625

√r ² = √625

R = -25 или 25

. отрицательное число, поэтому мы выбираем только положительные 25.

Следовательно, радиус окружности равен 25 дюймам.

Пример 4

Учитывая, что радиус показанного ниже круга равен 10 ярдам, а длина PQ равна 16 ярдам. Рассчитать расстояние ОМ .

Решение

PQ = длина хорды = 16 ярдов.

Радиус, r = 10 ярдов.

ОМ = расстояние, d =?

Длина хорда = 2√ (R ² -D ² )

16 = 2√ (10 ² — D ² )

16 = 2? (100 — D ² )

Квадрат с обеих сторон.

256 = 4(100 − d ² )

256 = 400 − 4d ²

Вычесть 400 с обеих сторон.

-144 = − 4d ²

Разделите обе части на -4.

36 = d ²

d = -6 или 6.

Таким образом, перпендикулярное расстояние равно 6 ярдам.

Пример 5:

Рассчитайте длину хорды PQ в круге, показанном ниже.

Решение

Учитывая центральный угол, C = 80 ⁰

Радиус окружности, r = 28 см

Длина хорды PQ =?

По формуле длина хорды = 2r синуса (С/2)

Подставить.

No related posts.