Минус деленный на минус дает: Что будет минус на минус?

Что будет минус на минус?

Что будет минус на минус?

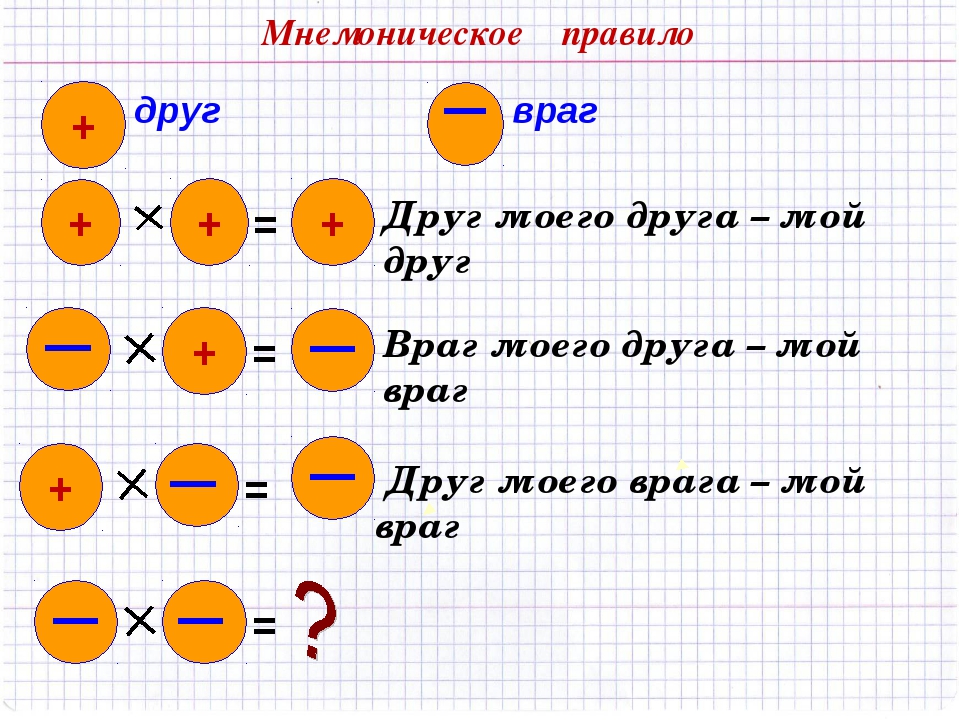
Минус умноженный на минус дает плюс, минус деленный на минус будет плюс. Произведение двух отрицательного чисел — положительное число, частное двух отрицательного чисел — число положительное. При делении или умножении двух отрицательных чисел получается положительное число.

Почему минус на минус дает плюс?

Иначе говоря, чтобы умножение было осмысленным, «минус на плюс» должен давать «минус«. Этих принципов достаточно, чтобы вывести правило для «минус на минус«. Разумно устроить умножение на отрицательные числа так, что произведение любого числа и нуля дает ноль. … Это и значит, что «минус на минус» дает «плюс«.

Сколько будет плюс умножить на минус?

Правила знаков для умножения Запомнить правило знаков для умножения очень просто. Данное правило совпадает с правилом раскрытия скобок. Минус на минус даёт плюс, Плюс на минус даёт минус.

Когда два минуса дают плюс?

При вычитания двух чисел, в которых оба отрицательные, следует знать правило: минус на минус дает плюс. То есть, если стоят рядом два минуса, в сумме получается плюс.

Что будет если отрицательное число умножить на положительное?

То есть произведение двух чисел, одно из которых положительное, а другое — отрицательное, является отрицательным числом. … При умножении двух отрицательных чисел получается положительное число. Поэтому если количество чисел со знаком «-» чётное, результат является числом положительным, если нечётное — отрицательным.

Что нужно сделать чтобы перемножить два отрицательных числа?

Правило умножения отрицательных чисел заключается в том, что для того, чтобы умножить два отрицательных числа, необходимо перемножить их модули. Данное правило записывается так: для любых отрицательных чисел –a, −b данное равенство считается верным. (−а)⋅(−b)=a⋅b.

Что нужно сделать чтобы вычесть числа с разными знаками?

Правило вычитания чисел с разными знаками Его формулировка такова: вычесть из числа a число b – это все равно, что к числу a прибавить число −b, где b и −b – противоположные числа. В буквенном виде это правило вычитания имеет вид a−b=a+(−b), где a и b – любые действительные числа.

Как выполнить сложение и вычитание дробей с разными знаменателями?

Чтобы сложить две дроби с разными знаменателями, надо привести их к общему положительному знаменателю и сложить полученные дроби. Чтобы вычесть две дроби с одинаковым положительными знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.

Как складывать и вычитать дроби с целыми числами?

Сложение дроби и целого числа:

1. Приводим дроби к общему знаменателю.
2. Складываем дроби
3. Если есть возможность, то сокращаем полученную дробь.
4. Если же получилась неправильная дробь, то вычисляем из нее целую часть.

Как вычислить из целого числа дробь?

Чтобы из целого числа вычесть правильную дробь нужно представить это натуральное число в виде смешанного числа. Для этого занимаем единицу в натуральном числе и представляем её в виде неправильной дроби, знаменатель которой равен знаменателю вычитаемой дроби.

Как из смешанной дроби вычесть целое число?

Запишем правило вычитания натурального числа из смешанного числа: чтобы вычесть из смешанного числа натуральное число, надо вычесть данное натуральное число из целой части смешанного числа, а дробную часть оставить без изменения.

Как вычесть из смешанной дроби?

Вычитание смешанных дробей производится по тому же принципу: целая часть вычитается из целой части, дробная вычитается из дробной. Результаты этих разностей складываются. В приведённом выражении вычитаем целые и дробные части. Разность целых чисел равна 3, разность дробных чисел равна тём седьмым.

Деление отрицательных чисел: правило и примеры

В данной статье дадим определение деления отрицательного числа на отрицательное, сформулируем и обоснуем правило, приведем примеры деления отрицательных чисел и разберем ход их решения.

Деление отрицательных чисел. Правило

Напомним, в чем суть операции деления. Данное действие представляет собой нахождение неизвестного множителя по известному произведению и известному другому множителю. Число с называется частным от деления чисел a и b, если верно произведение c·b=a. При этом, a÷b=c.

Правило деления отрицательных чисел

Частное ои деления одного отрицательного числа на другое отрицательное число равно частному от деления модулей этих чисел.

Пусть a и b — отрицательные числа. Тогда

a÷b=a÷b.

Данное правило сводит деление двух отрицательных чисел к делению положительных чисел. Оно справедливо не только для целых чисел, но также для рациональных и действительных чисел. Результат деления отрицательного числа на отрицательное есть всегда положительное число.

Приведем еще одну формулировку данного правила, подходящую для рациональных и действительных чисел. Она дается с помощью взаимно-обратных чисел и гласит: для деления отрицательного числа a на число undefined умножить на число b-1, обратное числу b.

a÷b=a·b-1.

Это же правило, сводящее деление к умножению, можно применять также и для деления чисел с разными знаками. 

Равенство a ÷ b = a · b — 1 можно доказать, используя свойство умножения действительных чисел и определение взаимно обратных чисел. Запишем равенства: 

a·b-1·b=a·b-1·b=a·1=a.

В силу определения операции деления, данное равенство доказывает, что  есть частное от деления числа  на число b.
Перейдем к рассмотрению примеров.

 

Деление отрицательных чисел. Примеры

Начнем с простых случаяв, переходя к более сложным.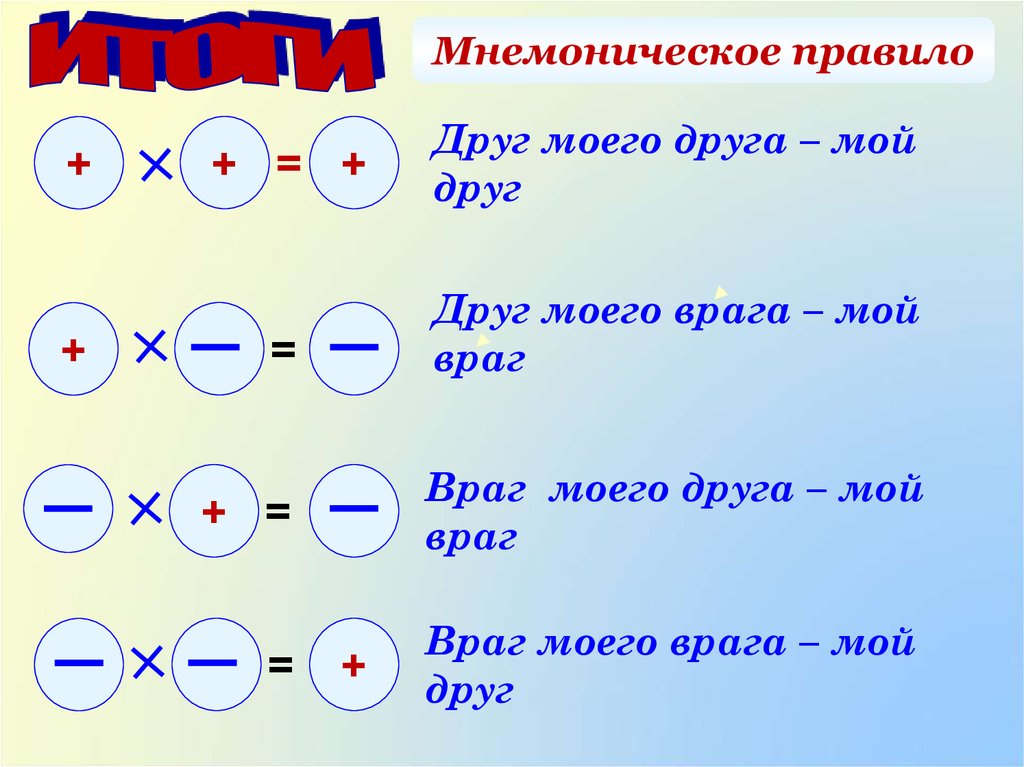

Пример 1. Как делить отрицательные числа

Разделим -18  на -3.
Модули делителя и делимого соответственно равны 3 и 18. Запишем:

-18÷-3=-18÷-3=18÷3=6.

Пример 2. Как делить отрицательные числа

Разделим -5 на -2.
Аналогично, записываем по правилу:

-5÷-2=-5÷-2=5÷2=52=212.

Такой же результат получится, если использовать вторую формурировку правила с обратным числом.

-5÷-2=-5·-12=5·12=52=212.

Деля дробные рациональные числа удобнее всего представлять их в виде обыкновенных дробей. Однако, можно делить и конечные десятичные дроби.

Пример 3. Как делить отрицательные числа

Разделим -0,004 на -0,25.

Сначала записываем модули этих чисел: 0,004 и 0,25.

Теперь можно выбрать один из двух способов:

1. Разделить десятичные дроби столбиком.
2. Перейти к обыкновенным дробям и выполнить деление.

Разберем оба способа.

1. Выполняя деление десятичных дробей столбиком, перенесем запятую на две цифры вправо.

Ответ: -0,004÷0,25=0,016

2. Теперь приведем решение с переводом десятичных дробей в обыкновенные.

0,004=41000; 0,25=251000,004÷0,25=41000÷25100=41000·10025=4250=0,016

Полученные результаты совпадают.

В заключение отметим, что если делимое и делитель являются иррациональными числами и задаются в виже корней, степеней, логарифмов и т.д., результат деления записывается в виде числового выражения, приблизительное значение которого вычисляется в случае необходимости.

Пример 4. Как делить отрицательные числа

Вычислим частное от деления чисел -0,5 и -5.

-0,5÷-5=-0,5÷-5=0,5÷5=12·15=125=510.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р.

Реферат от 1 дня / от 700 р.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Деление положительных и отрицательных чисел

Деление
положительных и отрицательных чисел происходит по тем же правилам, что и умножение
положительных и отрицательных чисел. Мы разместим их здесь для вас, используя примеры деления вместо
умножения:

Правило 1: Положительное число, деленное на положительное число, дает положительное число
.

Пример 1: Это то деление, которым вы занимались годами, плюс
числа, разделенные на положительные числа. Это будет выглядеть так: 12/3 = 4. 12 положительно,

3 положительно, таким образом, 4 положительно. Мы знаем, что 12 и 3 оба положительны, потому что перед
нет отрицательных знаков.

Правило 2: Положительное число, деленное на отрицательное, дает отрицательное число
.

Пример 2: Это новинка — например, у вас может быть 12/-3. 12 положительное,
, но 3 отрицательное, поэтому наш ответ должен быть отрицательным. Таким образом, делим числа
, как обычно, а затем поставить знак минус перед нашим ответом. Итак, 12/-3
= -4. Обратите внимание, что это также работает, когда отрицательное число идет первым, а
положительное число идет вторым. Например, вы можете увидеть написанное -12/3 = -4, но
не запутайтесь. Комбинация одного положительного и одного отрицательного числа, независимо от того, в каком порядке они идут, означает, что ваш ответ будет отрицательным.

Правило 3: Отрицательное число, деленное на отрицательное число, дает положительное число 9.0003 номер.

Пример 3: Это тоже новшество, и кажется, что оно не имеет особого смысла, но это правило
, которому мы должны следовать при делении отрицательных чисел. Так, например, у нас может быть
с проблемой -12/-4. И 12, и 4 отрицательные, поэтому мы знаем, что наш ответ
будет положительным. Следовательно, -12/-4 = 3,

Тест на деление положительных и отрицательных чисел

Вот несколько задач, которые помогут вам попрактиковаться в работе с положительными и отрицательными числами.
Выполните их самостоятельно, а затем сверьтесь с нашими ответами.

1. 15/3	2. -24/6	3. 98/-2	4. -75/-25	5. -3/-1
6. 88/-11	7. 49/7	8. 100/-50	9. -34/17	10. -9/-3

Решения

1. 5	2. -4	3. -49	4. 3	5. 3
6. -8	7. 7	8. -2	9. -2	10. 3

Правила для положительных и отрицательных чисел математика, а также повседневные операции, такие как управление деньгами или измерение веса.

• Положительное число имеет значение больше нуля. Его знак положительный, но обычно он пишется без знака плюс перед ним (например, 4, 51, а не +4, +51).
• Отрицательное число имеет значение меньше нуля. Его знак считается отрицательным и записывается со знаком минус перед ним (например, -2, -23).
• Сумма положительного числа и равного ему отрицательного числа равна нулю.
• Ноль не является ни положительным, ни отрицательным числом.

Существуют правила сложения, вычитания, умножения и деления положительных и отрицательных чисел. Как правило, операции с отрицательными числами проще выполнять, если они заключены в квадратные скобки, чтобы разделить их. Числовые линии также могут облегчить понимание положительных чисел и чисел.

Сложение и вычитание положительных и отрицательных чисел

При сложении или вычитании положительных и отрицательных чисел знак ответа зависит от того, одинаковы ли знаки или какое число имеет большее значение.

Складывать положительные и отрицательные числа просто, если оба числа имеют одинаковый знак. Просто найдите сумму чисел и сохраните знак. Например:

• 3 + 2 = 5
• (-4) + (-2) = -6

Найдите сумму положительного и отрицательного числа, вычитая число с меньшим значением из числа с меньшим значением. большее значение. Знак соответствует большему числу.

• (-7) + 2 = -5
• 4 + (-8) = 4 – 8 = -4
• (-3) + 8 = 5
• 10 + (-2) = 10 – 2 = 8
• (-5) + 4 = -1

Правила вычитания аналогичны правилам сложения. Для двух положительных чисел, если первое число больше второго, результатом будет еще одно положительное число.

• 12 – 10 = 2
• 4 -3 = 1

Если из меньшего положительного числа вычесть большое положительное число, получится отрицательное число.

• 5 – 6 = -1
• 2 – 4 = -2

Простой способ сделать это – вычесть меньшее число из большего числа и изменить знак ответа на минус.

Когда вы вычитаете положительное число из отрицательного числа, это то же самое, что и сложение отрицательного числа. Другими словами, это делает отрицательное число еще более отрицательным.

• (-4) – 3 = (-4) + (-3) = -7
• (-10) – 12 = (-10) + (-12) = -24

Вычитание отрицательного числа от положительного числа отменяет отрицательные знаки и становится простым сложением. Это делает положительное число более положительным.

• 4 – (-3) = 4 + 3 = 7
• 5 – (-2) = 5 + 2 = 7

Когда вы вычитаете отрицательное число из другого отрицательного числа, отрицательные знаки снова отменяют каждое другой, чтобы стать знаком плюс. Ответ имеет знак большего числа.

• (-2) – (-7) = (-2) + 7 = 5
• (-5) – (-3) = (-5) + 3 = -2

Умножение и деление положительных и отрицательные числа

Если вы умножите или разделите одинаковые знаки, вы получите положительное число. Умножение или деление положительных и отрицательных чисел дает отрицательное число.

Правила умножения и деления просты:

• Если оба числа положительные, результат положительный.
• Если оба числа отрицательные, результат положительный. (В принципе, два отрицательных значения компенсируют друг друга).
• Если одно число положительное, а другое отрицательное, результат отрицательный.
• При умножении или делении нескольких чисел суммируйте количество отрицательных знаков. Если есть четное число, ответ четный. Если число отрицательных знаков нечетное, ответ отрицательный.
• Умножение любого числа (положительного или отрицательного) на ноль дает ответ 0.
• Ноль, деленный на любые числа, равен 0.

  No related posts.