Ранг матрицы и способы его вычисления
Рангом матрицы называется наивысший порядок отличных от нуля миноров. Его обозначают через или .
СВОЙСТВА РАНГА МАТРИЦЫ
1. Ранг матрицы равен нулю только для нулевой матрицы. В других случаях ранг матрицы равен некоторому положительном числу.
2. Ранг прямоугольной матрицы не превышает меньшего из двух чисел и т.е. .
3. Для квадратной матрицы -го порядка только тогда, когда матрица невырожденная.
4. В случае квадратной матрицы если то определитель матрицы равен нулю.
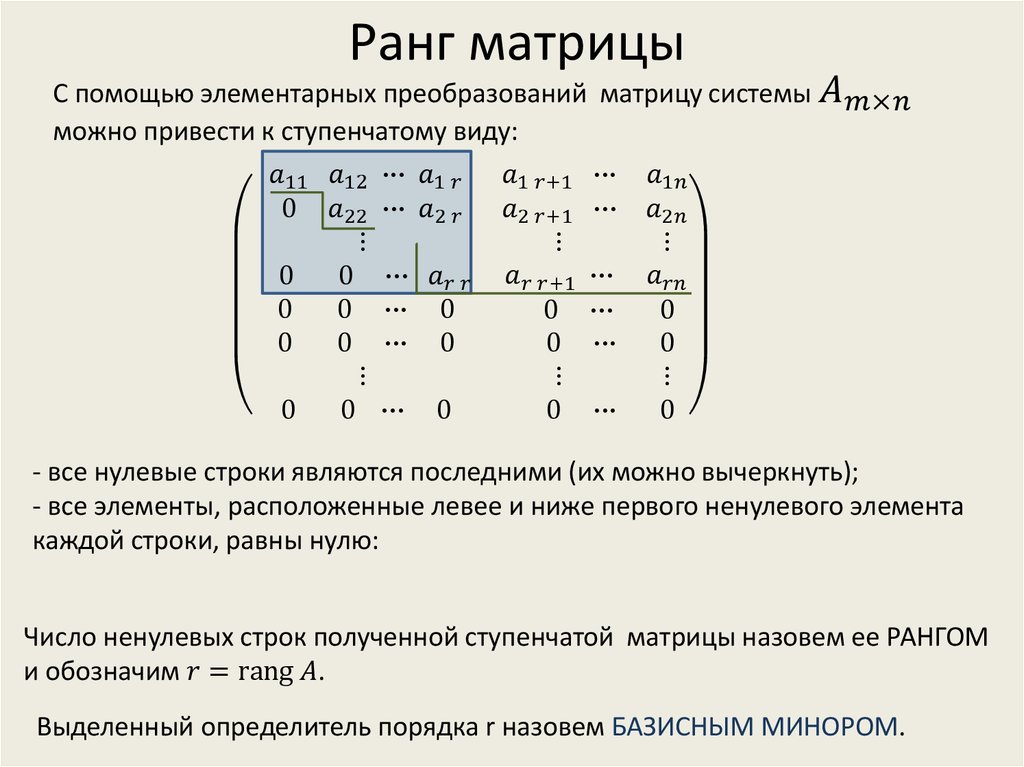
При нахождении ранга матрицы, как правило, нужно вычислять большое количество определителей. Чтобы облегчить задачу студентам давным-давно найдены элементарные преобразования с помощью которых можно слегка поменяв вид матрицы без вычисления определителей посчитать ранг.
ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ МАТРИЦЫ
1. Транспонирование, т.е. замена каждой строки столбцом с тем же номером и наоборот.
2. Перестановка двух строк или двух столбцов.
Перестановка двух строк или двух столбцов.
3. Умножение всех элементов строки или столбца на любое число не равное нулю.
4. Добавление всех элементов строки или столбца соответствующих элементов параллельного ряда, умноженного на одно и то же число.
Матрицы, полученные одна из второй элементарными преобразованиями называются эквивалентными. Эквивалентные матрицы не равны друг другу, но при элементарных преобразованиях матрицы ее ранг не меняется. Если матрицы и эквивалентны то это записывается так:
Рассмотрим два основных метода нахождения ранга матрицы.
Первый метод –- метод окантовки — заключается в следующем:
Если все миноры 1-го порядка, т.е. элементы матрицы равны нулю, то .
Если хоть один из миноров 1-го порядка не равен нулю, а все миноры 2-го порядка равны нулю то .
Если минор 2-го порядка отличен от нуля то исследуем миноры 3-го порядка. Таким образом находят минор -го порядка и проверяют, не равны ли нулю миноры -го порядка.
Если все миноры -го порядка равны нулю, то ранг матрицы равен числу . Такие миноры -го порядка, как правило, находят путем «окантовки» минора -го порядка.
Такие миноры -го порядка, как правило, находят путем «окантовки» минора -го порядка.
Второй метод определения ранга матрицы заключается в применении элементарных преобразований матрицы при возведении ее к диагональному виду. Ранг такой матрицы равно числу отличных от нуля диагональных элементов.
Рассмотрим примеры применения каждого метода.
—————————————————
Пример 1.
Задание. Найти ранг матрицы методом окантовки.
Решение. Матрица содержит ненулевые элементы миноры 1-го порядка, следовательно ее ранг может быть равен единице. Согласно правила ранг матрицы не превышает трем . Минор 2-го порядка
равен нулю, но следующий минор
отличен от нуля. Окантовывая минор второго порядка проверим третий: для этого разложим его по третьей колонке
Рассмотрим минор четвертого порядка, окантовывает настоящее
Он равен нулю, поскольку последняя строка нулевой. Остается вычислить еще один минор
Искомый ранг матрицы равен четырем (). На примере можно видеть, что выбор окантовки не всегда можно удачно выбрать и нужно числить большое количество миноров.
На примере можно видеть, что выбор окантовки не всегда можно удачно выбрать и нужно числить большое количество миноров.
—————————————————
Пример 2.
Задание. Найти ранг матрицы .
Решение.
1.Переставим четвертый столбец на первое место, а все остальные сместим вправо.
2. Превратим в ноль все элементы в первой строке после . Для этого к столбцам добавим первый умноженный на соответственно.
3. Третий столбец поделим на . К четвертого и пятого столбцов добавим третий, умноженный на .
4. До пятого столбца добавим четвертый, умноженный на .
5. Переставим третий и четвертый столбцы на второе и третье места, а второй столбец на место четвертого.
В исходной матрицы вычеркнут последний столбец с нулевыми элементами
Ранг эквивалентной матрицы равен четырем, а следовательно и . Можно заметить, что матрицы в первом и втором примерах эквивалентные между собой (имеют одинаковые ранги).
—————————————————————
Как найти ранг матрицы? расширенной, разными методами
Главная » Математика
Математика
Автор Violetta На чтение 4 мин. Просмотров 1.4k. Опубликовано
Ранг матрицы — это наибольшее число строк, которые линейно независимы и могут быть рассмотрены в качестве векторов. Более простым языком можно сказать, что рангом матрицы называется количество строк, в которых не все элементы равны нулю, после преобразования матрицы к ступенчатому виду. Ненулевыми строками называют те, в которых хотя бы один элемент имеет значение, отличное от нуля. В этой статье рассматриваются способы, с помощью которых можно найти ранг матрицы.
В этой статье рассматриваются способы, с помощью которых можно найти ранг матрицы.
Содержание
- Необходимые понятия
- Способы для поиска ранга
- Метод единиц и нулей
- Сведение матрицы к ступенчатому виду
- Метод окаймляющих миноров
- Онлайн-калькуляторы для поиска ранга матрицы
Необходимые понятия
Элементарные преобразования – это преобразования, после которых полученная матрица является эквивалентной для исходной.
Элементарные преобразования означают следующие действия:
- Умножить строку или столбец на число не равное 0;
- Поменять местами любые 2 строки или 2 столбца;
- Прибавить к строке другую строку (или к столбцу другой столбец) соответственно, помноженных на некоторое ненулевое число.
Матрица является ступенчатой, если она содержит хотя бы одну нулевую строку. Кроме этого если 1-й элемент некоторой строки не равный нулю расположен в i-м столбце, то этот элемент следующей строки должен находится в столбце с номером большим за i.
Кроме этого если 1-й элемент некоторой строки не равный нулю расположен в i-м столбце, то этот элемент следующей строки должен находится в столбце с номером большим за i.
Минор k-го порядка – это определитель матрицы размера k на k, состоящей из k строк и такого же числа столбцов исходной матрицы. Порядок в этих строках и столбцах при этом остаётся прежним.
Способы для поиска ранга
Метод единиц и нулей
После применения элементарных преобразований, каждая матрица может быть приведена к такому виду, при котором все её столбцы будут состоять строго из нулей или иметь в своём составе максимум одну единицу. Посчитав количество единиц, мы сможем определить ранг.
Алгоритм, реализующий данный метод:
- Выполняем элементарные преобразования до тех пор, пока матрица не будет состоять только из нулей и единиц
- Считаем количество единиц
- Количество единиц равно искомому рангу
Пример поиска ранга, используя метод нулей и единиц:
- Первоначально дана матрица такого вида:
- 3-й столбец разделим на 2.
 1-ую строку умножим на -2 и сложим с 4-й.
1-ую строку умножим на -2 и сложим с 4-й. - Умножим 2-й столбец на -2 и сложим его с 4-м столбцом. После этого умножим 2-й столбец на -4 и сложим его с 1-м. Далее прибавим 2-й столбец к 5-му.
- 3-ю строку умножим на -2. Прибавим её ко 2-ой.
- Сложим 5-й столбец с 1-м.
- 3-й столбец умножим на 3 и сложим с 1-м.
- Умножим 3-й столбец на -1 и прибавим к нему 2-й и 4-й.
- Умножим 4-й столбец на -3 и сложим с 5-м. Наконец умножим 4-й столбец на -1. Итоговая матрица принимает следующий вид:
Количество единиц составляет 3, следовательно ранг имеет такое же значение.
Сведение матрицы к ступенчатому виду
Для данного способа также, как и для предыдущего, сперва нужно привести матрицу к определённому виду. Сведение её к ступенчатой позволяет найти ранг матрицы методом элементарных преобразований.
Алгоритм для данного метода:
- Выполняем элементарные преобразования, пока матрица не станет ступенчатой
- Считаем количество строк
- Количество строк равно искомому рангу.

Метод окаймляющих миноров
Чтобы найти ранг матрицы методом окаймляющих миноров нужно рассмотреть большое количество миноров.
Алгоритм, реализующий данный метод:
- Находим наименьшее число из величины матрицы по горизонтали и вертикали. Оно будет максимальным возможным значением ранга.
- Далее начинаем поиск миноров от самых меньших.
- Если минор имеет значение 0, то рассматриваем другие миноры этого порядка. Если все они имеют значение 0, то ранг равняется предыдущему порядку.
- Если существует хотя бы один минор не равный 0, то увеличиваем порядок на 1 и рассматриваем окаймляющие миноры. Возвращаемся на 3-й пункт.
Онлайн-калькуляторы для поиска ранга матрицы
Иногда у пользователя нет времени, чтобы самостоятельно изучить методы для поиска ранга. Из-за этого возникает вопрос: «Как найти ранг матрицы для чайников?».
В сети «Интернет» достаточно калькуляторов, которые помогают найти ранг матрицы онлайн с подробным решением. Однако почти все они производят поиск ранга, применяя при этом элементарные преобразования. Найти ранг матрицы методом окаймляющих миноров онлайн чаще всего не предоставляется возможным, так как этот способ не очень удобен и требует большого количества вычисления определителей.
Однако почти все они производят поиск ранга, применяя при этом элементарные преобразования. Найти ранг матрицы методом окаймляющих миноров онлайн чаще всего не предоставляется возможным, так как этот способ не очень удобен и требует большого количества вычисления определителей.
Видео с вопросами: нахождение ранга матрицы 3 × 3 с использованием определителей
Найдите ранг следующей матрицы: [1, 2, 4 и 7, −1, −2 и 2, 4, 8].Стенограмма видео
Найдите ранг следующего матрица.
Напомним, что ранг матрицы 𝐴
это количество строк или столбцов в наибольшей квадратной подматрице 𝐴 с
отличный от нуля определитель. Напомним также, что ранг 𝐴 равен
больше или равно нулю и меньше или равно минимуму 𝑝 и 𝑞,
где 𝑝 — количество строк в 𝐴, а 𝑞 — количество столбцов в 𝐴. Поскольку 𝐴 в данном случае является
матрица три на три, ранг 𝐴 находится между нулем и тремя. Напомним также, что ранг 𝐴 равен
равна нулю тогда и только тогда, когда 𝐴 — нулевая матрица. Эта матрица явно не нулевая
матрица. Поэтому его ранг не может быть
нуль.
Поскольку 𝐴 в данном случае является
матрица три на три, ранг 𝐴 находится между нулем и тремя. Напомним также, что ранг 𝐴 равен
равна нулю тогда и только тогда, когда 𝐴 — нулевая матрица. Эта матрица явно не нулевая
матрица. Поэтому его ранг не может быть
нуль.
Максимально возможная площадь подматрица этой матрицы сама по себе, матрица три на три. Взяв определитель матрицу разложив по верхней строке, получим нулевой результат. Это единственное возможное подматрица три на три в 𝐴, и ее определитель равен нулю. Следовательно, ранг 𝐴 не может быть три. Теперь мы ищем подматрицу два на два 𝐴 с ненулевым определителем. Это проблема, потому что есть девять возможных подматриц размера два на два матрицы 𝐴, и нам может понадобиться проверить каждую один из них.
Рассмотрим, например, если
исходная матрица выглядела так. Единственная подматрица два на два, которую мы
может выбрать то, что может иметь ненулевой определитель. В этом гипотетическом примере
выбор очевиден, но он может быть не для нашего вопроса. Если мы посмотрим на исходную матрицу,
мы можем видеть, что нижняя строка является точным скалярным числом, кратным верхней строке. Любая выбранная подматрица два на два
определитель из этих двух строк будет равен нулю. И мы могли бы предположить из этого, что
это означает, что нет подматриц два на два с ненулевым определителем.
Единственная подматрица два на два, которую мы
может выбрать то, что может иметь ненулевой определитель. В этом гипотетическом примере
выбор очевиден, но он может быть не для нашего вопроса. Если мы посмотрим на исходную матрицу,
мы можем видеть, что нижняя строка является точным скалярным числом, кратным верхней строке. Любая выбранная подматрица два на два
определитель из этих двух строк будет равен нулю. И мы могли бы предположить из этого, что
это означает, что нет подматриц два на два с ненулевым определителем.
Отсюда можно предположить, что
в 𝐴 нет подматриц размера два на два с ненулевым определителем. Однако, если мы выберем два на два
подматрица, состоящая не только из этих двух строк, скалярно кратных
друг друга, например, удалив нижнюю строку и крайний правый столбец, мы
получить ненулевой определитель. Таким образом, мы нашли
подматрица два на два матрицы 𝐴 с ненулевым определителем.
Nagwa использует файлы cookie, чтобы обеспечить вам максимальное удобство на нашем веб-сайте. Узнайте больше о нашей Политике конфиденциальности.
Ранг матрицы | Superprof
Введение в ранг матрицы
ранг матрицы может быть определен двумя следующими способами: матрица»
ИЛИ
«Ранг матрицы относится к наибольшему числу из линейно независимых строк в матрице»
Ваш результат будет эквивалентен, используете ли вы векторы-столбцы или векторы-строки матрица для расчета ранга. Следовательно, мы можем сказать, что количество линейно независимых строк или столбцов представляет собой ранг матрицы.
Линейно независимая строка означает, что она не является результатом линейной комбинации других строк. Однако, если строка является линейной комбинацией других строк матрицы, то она не называется линейно независимой строкой, и мы можем отбросить ее при вычислении ранга матрицы. То же самое и со столбцами.
То же самое и со столбцами.
Лучшие репетиторы по математике
Поехали
Метод исключения Гаусса
Используя это определение, мы можем вычислить ранг, применяя метод исключения Гаусса. Метод исключения Гаусса уменьшает матрицу, чтобы нам было легче найти ранг. При этих трех условиях мы исключаем строку или столбец при вычислении рангов матриц, используя метод исключения Гаусса:- Все элементы в строке или столбце равны нулю
- Строка или столбец пропорциональны другой строке или столбцу.
- Строка или столбец являются результатом линейной комбинации других строк и столбцов. и каждая строка имеет n элементов. В качестве альтернативы вы можете сказать, что эта матрица имеет набор из n векторов-столбцов, и каждый столбец имеет m элементов.
Рассмотрим матрицу m x n ,
- Если n равно больше , чем m, то наивысший ранг матрицы равен m.
- Если n на меньше , чем m, то наивысший ранг матрицы равен n.

Нулевая матрица — это матрица без элементов. Вам может быть интересно, каков будет ранг нулевой матрицы. Ранг нулевой матрицы равен ноль . Точно так же, если матрица имеет только один элемент, то ее минимальный ранг будет равен единице.
Вычисление ранга матрицы для определителей
Матрица, имеющая одинаковое количество строк и столбцов, называется квадратной матрицей . Следовательно, если у нас есть матрица с двумя строками и двумя столбцами, то мы говорим, что это квадратная матрица порядка 2. Точно так же, если у нас есть матрица с тремя строками и тремя столбцами, то мы говорим, что это матрица порядок 3.
В этом разделе мы увидим, как найти ранг матриц с помощью определителей. Прежде чем находить ранги матриц с помощью этого метода, вы должны знать, как найти определитель матрицы.
- Предположим, у вас есть следующая матрица 2 x 2:
Ее определитель будет вычисляться следующим образом:
3 Предположим, у вас есть следующая матрица 3 .


 1-ую строку умножим на -2 и сложим с 4-й.
1-ую строку умножим на -2 и сложим с 4-й.