| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| Найти точное значение | sin((4pi)/3) | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Тригонометрия и окружность . Магия математики [Как найти x и зачем это нужно]
Пока что наши знания о тригонометрических функциях ограничиваются прямоугольными треугольниками. Для решения повседневных задач этого, в принципе, более чем достаточно.
Но разве вам не интересно узнать, как они ведут себя в других углах, а не только в тех, значения которых колеблются исключительно в диапазоне от 0° до 90° (ведь в прямоугольном треугольнике один из углов всегда прямой, а два оставшихся – острые)? Конечно, интересно, и именно этим мы и займемся в этом разделе – посмотрим на тригонометрические функции через призму единичного круга и разберемся в особенностях поведения синусов, косинусов и тангенсов углов других типов.
Надеюсь, вы не забыли, что единичным называется такой круг, радиус которого равен 1, а центр расположен в точке начала координат (0, 0). Для него отлично работает уравнение
Давайте попробуем найти некую точку (x, y), расположенную на окружности выше и левее точки (1, 0) и образующую с центром круга и осью x острый угол A:
Для того чтобы найти x и y, нам нужно начертить прямоугольный треугольник и применить к нему наши формулы косинусов и синусов:
Другими словами, значения координат (x, y) составят (cos A, sin A).
Если обобщать, то при радиусе, равном r, (x, y) = (r cos A, r sin A).
Для любого угла A нам нужно определить (cos A, sin A), то есть место расположения на окружности его вершины. При этом cos A будет соответствовать значению координаты по оси x, а sin A – по оси у, вот так:
А вот еще одно общее представление. Только теперь мы разделим единичный круг на много углов с шагом 30° (и сделаем один шаг в 45° для большей наглядности) – так мы получим углы из уже очень хорошо знакомых нам треугольников. Помните, я советовал вам выучить значения косинусов и синусов для углов 0°, 30°, 45°, 60° и 90°?
К углам этим можно прийти с помощью простого отражения значений, содержащихся в первой четверти окружности.
Прибавление или вычитание 360° на величину угла никак не повлияет (мы просто обойдем вокруг него с одной или другой стороны), а значит, для любого ?A
sin (A ± 360°) = sin A cos (A ± 360°) = cos A
Имея дело с отрицательными значениями углов, мы двигаемся по окружности слева направо: так, угол, равный –30°, ничем, по сути, не отличается от угла, равного 330°.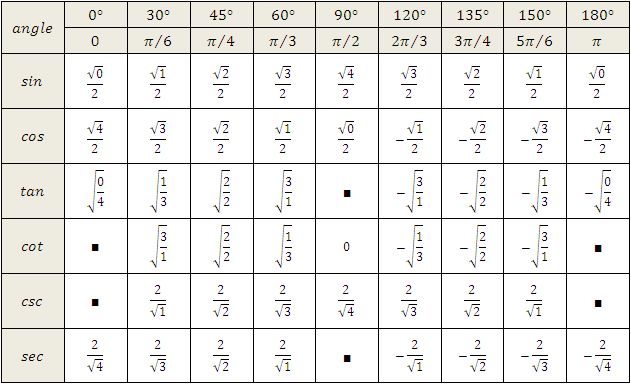
Обратите внимание, что сдвиг на A градусов по часовой стрелке приводит нас к той же x-координате, что и сдвиг на те же A градусов против часовой стрелки. Y-координата же при этом сменит знак на противоположный. Другими словами, для любого значения угла A
cos (–A) = cos A sin (–A) = –sin A
Например,
cos (–30°) = cos 30° = ?3/2 sin (–30°) = –sin 30° = –1/2
Обратное происходит, когда мы «отзеркаливаем» ?A через ось y. Значение y-координаты получившегося таким образом дополнительного угла 180 – A остается неизменным, а значение x-координаты меняет знак на противоположный. То есть
cos (180 – A) = –cos A sin (180 – A) = sin A
Скажем, при A = 30°
cos 150° = –cos 30° = –?3/2 sin 150° = sin 30° = 1/2
Остальные тригонометрические функции определяются по старой схеме (например, tan A = sin A/cos A).
Оси x и y «разрезают» поверхность окружности на четыре сектора-квадранта. Пронумеруем их римскими цифрами по часовой стрелке – I, II, III и IV, – начиная с правой верхней, то есть с диапазона углов от 0° до 90°. Квадрант II, таким образом, охватит диапазон от 90° до 180°, квадрант III – от 180° до 270°, а квадрант IV – от 270° до 360°. Обратите внимание, что в разных квадрантах разные тригонометрические функции будут вести себя по-разному: положительные значения синуса мы получим в квадрантах I и II, косинуса – в квадрантах I и IV, тангенса – в квадрантах I и III. Чтобы это запомнить, некоторые из моих учеников любят повторять «Все студенты таскают калькуляторы» (посмотрите на первые буквы в каждом слове этой «запоминалки»: «в» – «все функции» в квадранте I, «с» – «синусы» в квадранте II, «т» – «тангенсы» в квадранте III, «к» – «косинусы» в квадранте IV).
Ну и еще немного терминологии. Для определения неизвестных значений углов нужны обратные тригонометрические (циклометрические, круговые) функции.
Например, обратным синусом 1/2 будет sin–1(1/2)[32]. Такого рода функция говорит нам, что мы имеем дело с неким ?A, синус которого равен 1/2. А так как мы знаем, что sin 30° = 1/2, получаем
sin–1(1/2) = 30°
Функция sin–1 (которая также называется арксинусом) всегда даст нам угол в диапазоне от –90° до 90°, но мы-то с вами знаем, что есть и другие углы с тем же значением синуса – синус 150°, например, будет также равен 1/2. То же происходит и с любым кратным 360° значением, прибавляемым к 30° или 150° – синусы будут равны.
Для треугольника с длинами сторон 3, 4 и 5 (см. рисунок) калькулятор может рассчитать ?A тремя различными способами, каждый из которых будет основан на своей обратной функции:
?A = sin–1(3/5) = cos–1(4/5) = tan–1(3/4) ? 36,87° ? 37°
Самое время применять все эти знания на деле.
В «геометрической» главе мы доказали теорему Пифагора, с помощью которой можно вычислить длину гипотенузы прямоугольного треугольника, зная длины его катетов. Здесь же, в главе «тригонометрической», мы можем сделать практически то же самое для любого треугольника. В этом нам поможет закон косинусов.
Теорема (закон косинусов): Длина стороны c любого треугольника ABC, в котором стороны a и b образуют ?C, соответствует
c? = a? + b? – 2ab cos C.
Для примера взгляните на изображенный ниже треугольник ABC. Между двумя его сторонами с длинами 21 и 26 лежит угол 15°. Согласно закону косинусов, длина третьей стороны с составит
c? = 21? + 26? – 2(21)(26) cos 15°
А так как cos 15° ? 0,9659, уравнение упрощается сначала до c? = 62,21, а потом и до c ? 7,89.
Отступление
Доказательство: Чтобы доказать эту теорему, рассмотрим три частных случая – в зависимости от того, будет ли ?C прямым, острым или тупым. Если ?C – прямой, его косинус будет равен cos 90° = 0, что упрощает закон косинусов до c? = a? + b?, то есть до уже доказанной нами теоремы Пифагора.
Если ?C – острый (как на рисунке), опустим перпендикуляр из ?B к стороне AC до лежащей на ней точки D. Получим два треугольника. Применим теорему Пифагора к CBD – a? = h? + x? и придем к
h? = a? – x?
Треугольник же ABD можно просчитать как c? = h? + (b – x)? = h? + b? – 2bx + x?, то есть
h? = c? – b? + 2bx – x?
Составим из двух равных h? частей уравнение:
c? – b? + 2bx – x? = a? – x?
Следовательно,
c? = a? + b? – 2bx
В треугольнике CBD cos C = x/a, поэтому x = a cos C.
Следовательно, если ?C является острым, то
c? = a? + b? – 2ab cos C
Если же ?C – тупой, дополним треугольник ABC прямоугольным треугольником CBD, как на рисунке:
Для него, как и для получившегося большого, верна теорема Пифагора: a? = h? + x? и c? = h? + (b + x)?. Как и в случае с острым ?C, соединим уравнения:
c? = a? + b? + 2bx
В треугольнике CBD cos (180° – C) = x/a, то есть x = a cos (180° – C) = –a cos C. И мы вновь приходим к искомому:
c? = a? + b? – 2ab cos C?
Кроме того с помощью функций можно рассчитать площадь треугольника.
Сопутствующая теорема: В любом треугольнике ABC со сторонами a и b и лежащим между ними ?C
Отступление
Доказательство: Площадь треугольника с длиной основания b и высотой h равна Все три треугольника, рассмотренные при доказательстве закона косинусов, имеют основание b. Определим высоту h. В остроугольном треугольнике обратим внимание на то, что sin C = h/a, то есть h = a sin C. В тупоугольном треугольнике sin (180° – C) = h/a, поэтому опять имеем h = a sin (180° – C) = a sin C. В прямоугольном же треугольнике h = a, что равно a sin C, потому что C = 90°, а sin 90° = 1. Следовательно, так как во всех трех случаях h = a sin C, площадь треугольников составит что и требовалось доказать.
Следствия этой теоремы очевидны:
Другими словами, в треугольнике ABC (sin C)/c равен его удвоенной площади, разделенной на произведение длин трех его сторон. Какой угол выбрать, по большому счету не так уж и важно – (sin B)/b или (sin A)/a дадут нам тот же результат. И это доказывает одну очень полезную теорему.
Теорема (закон синусов): В любом треугольнике ABC, длины сторон которого соответственно равны a, b и c,
Закон синусов – это еще один способ вычислить высоту нашей горы. На этот раз мы сосредоточимся на a – диагонали, пролегающей между нами и вершиной:
Способ № 5 (закон синусов): В треугольнике ABD ?BAD = 32°, а ?BDA = 180° – 40° = 140°. Следовательно, ?ABD = 8°. Согласно закону синусов получаем
Умножим обе части на sin 32°, что даст нам a = 300 sin 32°/ sin 8° ? 1143 метров.
А так как sin 40 ? 0,6428 = h/a, то
h = a sin 40 ? (1143)(0,6428) = 735
что полностью совпадает с ответом, к которому мы пришли в прошлом разделе.
Отступление
Не менее замечательна в этом отношении формула Герона, с помощью которой можно найти площадь треугольника по длинам его сторон a, b и c. Сначала мы находим полупериметр p:
А потом и площадь S:
S = ?p(p – a)(p – b)(p – c)
Например, если взять треугольник со сторонами 3, 14 и 15 (узнаете первые пять цифр числа ??), полупериметр будет равен (3 + 14 + 15)/2 = 16, а площадь, таким образом, – ?(16(16 – 3)(16 – 14)(16 – 15)) = ?416 ? 20,4.
Несложно, правда? Уверен, внимательный читатель не сможет не заметить здесь закон косинусов, слегка приправленный алгеброй.
Как найти значение sin 150 без калькулятора?
Тригонометрия — это раздел математики, изучающий специфические функции углов и их применение. В тригонометрии используются шесть функций угла: синус (sin), косинус (cos), тангенс (tan), котангенс (cot), секанс (sec) и косеканс (csc). Все эти функции основаны на измерении треугольника.
Грех противоположен/гипотенуза,
Cos смежн/гипотенуза,
Тан находится напротив/смежно.
Секанс является инверсией Cos, Косеканс является инверсией Sin, а Cot является инверсией Tan.
Тригонометрическая функция/ угол | 0 o 900 30 | 30 о | 45 о | 60 или | 90 о |
| Sin | 0 | 1/2 | 1/√2 | √3/2 | 9001 7 1|
| Cos | 1 | √3/2 | 1 /√2 | 1/2 | 0 |
| Тан | 0 | 1/√3 | 1 90 026 | √3 | Н. Д. |
| Косеканс | Н.Д. | 2 | √2 | 2/√3 | 1 |
| Сеанс | 1 | 2/√3 | √2 | 2 | 0 |
| Детская кроватка | Н.Д | √3 | 1 | 1/ 3 | 0 |
Дополнительный угол sin равен cos, tan равен cot, cosec равен sec, и наоборот.
Все эти углы измеряются в градусах и на основании этого декартова плоскость делится на 4 квадранта.
Квадранты
1 ст Квадрант; 0-90 0
2 й квадрант; 90-180 o
3 rd квадрант; 180-270 o
4 -й квадрант; 270-360 o
Все углы положительны в первом квадранте.
Положительны только углы sin и cosec, а остальные углы во втором квадранте отрицательны.
Положительны только углы tan и cot, а остальные углы отрицательны в третьем квадранте.
Только углы cos и sec положительны, а остальные углы отрицательны в четвертом квадранте.
Когда угол записывается в виде 90+θ, он превращается в дополнительные углы, а когда он записывается в виде 180+θ, он остается прежним. Положительный он или отрицательный проверяется на основе квадрантов.
Пример: чему равен sin(150)?
Решение:
Можно записать в виде sin(90 + 60)
Так как он находится во 2-м квадранте, а члены sin положительны во втором квадранте.
поэтому sin(150) = sin(90+60) = cos(60)
=1/2
Пример. Чему равно cos(150)?
Решение:
Это можно записать в виде cos(90 + 60)
Так как оно находится во 2-м квадранте, а члены cos во втором квадранте отрицательны.
поэтому cos(150) = cos(90 + 60) = -sin(60)
= -√3/2
Примеры задач
Задача 1. Каково значение tan (210)?
Решение:
Можно записать в виде тангенса (180 + 30)
Так как он находится в 3-м квадранте, а члены тангенса в третьем квадранте положительны
так тан(210) ) = tan = (180+30) = tan(30)
= 1/√3
Задача 2. Каково значение кроватки (240)?
Решение:
Можно записать в виде cot(180 + 60)
Так как он находится в 3-м квадранте, а члены cot в третьем квадранте отрицательны
so cot(210) = кроватка (180+30) = -кроватка(60)
= -1/√3
Задача 3. Каково значение кроватки (330)?
Решение:
Можно записать в виде tan(360 – 30)
Так как он находится в 4-м квадранте, а члены cot положительны в четвертом квадранте
так кроватка(330) = кроватка(360-30) = кроватка(30)
= √3
Задача 4.
Каково значение cosec(150)?
Решение:
Это может быть записано в виде cosec(180 – 30)
Поскольку оно находится во 2-м квадранте, а члены cosec положительны во втором квадранте
поэтому cosec(150) = cosec(180-30) = cosec(30)
= 2
Задача 5. Каково значение cosec(210)?
Решение:
Это может быть записано в форме COSEC (180 + 30)
, как это находится в 3 -м квадранте, а термины COSEC отрицательны во втором квадранте
, так что CoSec (210) = cosec(180+30) = -cosec(30)
= -2
Задача 6. Каково значение cot(150)?
Решение:
Это можно записать в виде cos(180 – 30)
Так как оно находится во 2-м квадранте, а члены cot положительны во втором квадранте
так кроватка(150) = кроватка(180-30) = -кроватка(30)
= -2
Задача 7.
Каково значение cos(300)?
Решение:
Это может быть записано в виде cos(270 + 30)
Поскольку оно находится в 4-м квадранте, а члены cos положительны в четвертом квадранте
поэтому cos(30 0) = sin (270+30) = sin(30)
= 1/2
Кто-нибудь может объяснить, почему sin(30°) = sin(150°)
Тригонометрия
Ясень С.
спросил 26.01.19Кто-нибудь может объяснить, почему sin(30°) = sin(150°) (или ). Обратитесь как к единичному кругу, так и к графику синусоиды. Дайте как можно больше подробностей.
Подписаться І 1
Подробнее
Отчет
1 ответ эксперта
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Раймонд Б.
ответил 21.06.19
Репетитор
5 (2)
Математика, микроэкономика или уголовное правосудие
См. таких репетиторов
Смотрите таких репетиторов
От нуля до 180 градусов синусоида идет от нуля до максимума 1 при 90 градусах, а затем возвращается к нулю при 180 градусах. Это симметричный холм, высота которого увеличивается от минимума 0 до максимума 1, затем 1 возвращается к 0. Вершина холма равна 1 на 9.0 градусов. 30 градусов на 60 меньше 90. 150 на 60 больше 90. 30 и 150 — противоположные стороны холма, на одинаковом расстоянии вниз от вершины. Cos 30 = 1/2 Cos 150 равно 1/2. Двигаясь от начала координат к вершине, вы на полпути вверх по левой стороне, затем вы наполовину вниз по правой стороне.
На единичном круге 30 градусов — это несколько знакомый прямоугольный треугольник 2:1:квадратный корень из 3, с гипотенузой 1/2 из 2, прилежащая сторона равна 1/2 квадратного корня из 3, а противолежащая сторона равна 1 /2 от 1 = 1/2
синус 30 равен стороне, противоположной гипотенузе, или 1/2 относительно 1 = 1/2 над гипотенузой = 1/2 над 1 = 1/2.
150 градусов это 180-30 градусов.
Прямоугольный треугольник в 3-м квадранте равен 30 градусам, если опустить вертикаль вниз от конца
гипотенузы на единичной окружности.
Другой способ представить это — взять синусоиды и сдвинуть ее влево на 90 градусов. Это дает
кривую косинуса, которая является четной функцией. В четных функциях. график симметричен относительно оси
y. f(x) = f(-x) cosx = cos(-x) То, что было 30 градусов, теперь равно -60 градусам, с
сдвигом влево на 90 градусов 30-90=-60 Cos(-60)=Cos( 60), потому что это четная функция. Cos(60)
, сдвинутый назад вправо на 90 градусов, равен sin(60+90) или sin 150. Сдвиг вправо на 90 градусов и
функция косинуса становится функцией синуса. Cos(-60) сдвинут вправо 90 градусов равно
Sin(-60+90)=Sin30 Sin30=Sin150 точно так же, как Cos(-60)=Cos(60)
Голосовать за 0 Понизить
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
