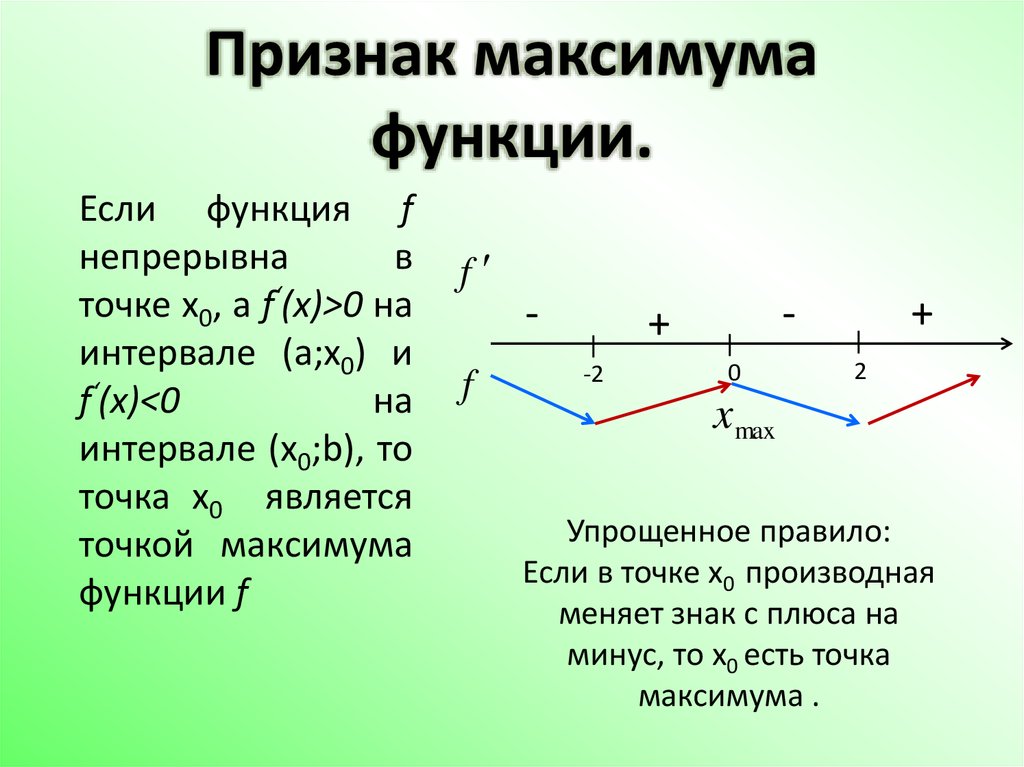
Как найти минимальное и максимальное значения функции?
Максимумы и минимумы
(1) Говорят, что функция f(x) достигает максимума в точке x = a, если существует окрестность (a – δ, a + δ), такая что f(x) < f (а) для всех x ∈ (a – δ, a + δ), x ≠ a
⇒ f(x) – f(a) < 0 для всех x ∈ (a – δ, a + δ), x ≠ a
В таком случае говорят, что f (a) является максимальным значением f(x) при x = a.
(2) Говорят, что функция f(x) достигает минимума при x = a, если существует nbd(a – δ, a + δ) такое, что f(x) > f(a) для всех x ∈ (а – δ, а + δ), х ≠
⇒ f(x) – f(a) > 0 для всех x ∈ (a – δ, a + δ), x ≠ a
В таком случае f(a) называется минимальным значением f (х) при х = а. Точки, в которых функция достигает максимальных или минимальных значений, называются экстремальными точками или поворотными точками, а максимальные и минимальные значения f(x) называются экстремальными или экстремальными значениями.
Точки, в которых функция достигает максимальных или минимальных значений, называются экстремальными точками или поворотными точками, а максимальные и минимальные значения f(x) называются экстремальными или экстремальными значениями.
Таким образом, функция достигает экстремального значения при x = a, если f(a) является либо максимальным, либо минимальным значением. Следовательно, в крайней точке a функция f(x) – f(a) сохраняет один и тот же знак для всех значений x в удаленном nbd элемента a.
Необходимое условие для экстремальных значений
Необходимое условие для того, чтобы f(a) было экстремальным значением функции f(x), состоит в том, что f’(a) = 0, если оно существует.
Примечание:
- Этот результат утверждает, что если производная существует, она должна быть равна нулю в крайних точках. Однако функция может достигать экстремального значения в какой-либо точке, но не быть там выводной.
Например, функция f(x) = |x| достигает минимального значения в начале координат, хотя и не дифференцируема в x = 0, - Это условие является лишь необходимым условием для того, чтобы точка x = a была крайней точкой.
 Недостаточно , т. е. f’(a) = 0 не обязательно означает, что x = a является крайней точкой. Существуют функции, производные которых обращаются в нуль в точке, но не имеют экстремального значения в точке , например, . f(x) = x 3 при x = 0 не достигает экстремального значения при x = 0 и f'(0) = 0.
Недостаточно , т. е. f’(a) = 0 не обязательно означает, что x = a является крайней точкой. Существуют функции, производные которых обращаются в нуль в точке, но не имеют экстремального значения в точке , например, . f(x) = x 3 при x = 0 не достигает экстремального значения при x = 0 и f'(0) = 0. - Геометрически это условие означает, что касательная к кривой y = f(x) в точке, где ордината максимальна или минимальна, параллельна x — ось.
- Значения x , для которых f’(x) = 0, называются стационарными значениями или критическими значениями x , а соответствующие значения f(x) называются стационарными или поворотными значениями f(x).
- Точки, в которых функция достигает максимума (или минимума), также называются точками локального максимума (или локального минимума), а соответствующие значения f(x) называются значениями локального максимума (или локального минимума).
Достаточные критерии экстремальных значений (1
st тест производной) Пусть f(x) — функция, дифференцируемая при x = a.
Тогда (a) x = a является точкой локального максимума f(x), если
- f'(a) = 0 и
- f'(a) меняет знак с положительного на отрицательный при прохождении x a, т. е. f'(x) > 0 в каждой точке левой окрестности (a – δ, a) a и f'(x) < 0 в каждой точке правой окрестности (a, a + δ) от до .
(б) x = a является точкой локального минимума f(x), если
- f'(a) = 0 и
- f'(a) меняет знак с отрицательного на положительный, когда x проходит через a, т. е. ., f'(x) < 0 в каждой точке левая окрестность (a – δ, a) a и f'(x) > 0 в каждой точке правой окрестности (a, a + δ) a .
(c) Если f'(a) = 0, но f'(a) не меняет знака, т. е. имеет тот же знак во всей окрестности a , то a не является ни точкой локальный максимум, ни точка локального минимума.
Рабочее правило для определения экстремальных значений функции f(x)
Если dy/dx меняет знак с положительного на отрицательный при переходе x через c 1 , то функция достигает локального максимума в точке x = с 1 . Если dy/dx меняет знак с отрицательного на положительный при прохождении x через c 1 , то функция достигает локального минимума при x = c 1 . Если нет смены знака, то x = c 1 не является ни точкой локального максимума, ни точкой локального минимума.
Если dy/dx меняет знак с отрицательного на положительный при прохождении x через c 1 , то функция достигает локального минимума при x = c 1 . Если нет смены знака, то x = c 1 не является ни точкой локального максимума, ни точкой локального минимума.
Проверка производной высшего порядка
- Найдите f’(x) и приравняйте ее к нулю. Решите f’(x) = 0, пусть его корни равны x = a 1 , a 2 …..
- Найдите f’’(x) и при x = a 1 ;
- Если f’’(a 1 ) положительна, то f(x) минимальна при x = a 1 .
- Если f’’(a 1 ) отрицательно, то f(x) максимальна при x = a 1 .
- Если f’’(a 1 ) = 0, перейти к шагу 3.
- Если при x = a 1 , f’’(a 1 ) = 0, затем найти f’’’(x). Если f’’’(a 1 ) ≠ 0, то f(x) не является ни максимальным, ни минимальным при x = a 1 .

Если f’’’(a 1 ) = 0, то найти f iv (x).
Если f iv (x) равно + ve (минимальное значение)
f iv (x) равно – ve (максимальное значение) - Если при x = a 1 8 90910 (a 1 ) = 0, затем найдите f v (x) и действуйте аналогично.
Свойства максимумов и минимумов
- Максимумы и минимумы возникают попеременно, то есть между двумя максимумами находится один минимум и наоборот.
- Если f(x) → ∞ при x → a или b и f'(x) = 0 только для одного значения x (скажем, c) между a и b, то f(c) обязательно является минимальным и наименьшим ценить.
Если f(x) → -∞ при x → a или b, то f(c) обязательно является максимальным и наибольшим значением.
Наибольшее и наименьшее значения функции, заданной на интервале [a, b]
Максимальным (или минимальным) или локальным максимальным (или локальным минимумом) значением функции f(x) в точке c ∈ [a, b] называется наибольшее (или наименьшее) значение в непосредственной окрестности точки x = с. Это не означает наибольший или абсолютный максимум (или наименьший или абсолютный минимум) f(x) в интервале [a, b].
Это не означает наибольший или абсолютный максимум (или наименьший или абсолютный минимум) f(x) в интервале [a, b].
Функция может иметь несколько локальных максимумов или локальных минимумов в заданном интервале, и даже локальный минимум может быть больше относительного максимума.
Таким образом, локальное максимальное значение не может быть наибольшим (абсолютным максимумом), а локальное минимальное значение не может быть наименьшим (абсолютным минимумом) значением функции в любом заданном интервале.
Однако, если функция f(x) непрерывна на отрезке [a, b], то она достигает абсолютного максимума (абсолютного минимума) в критических точках или в концах отрезка [a, b] . Таким образом, для нахождения абсолютного максимального (абсолютного минимума) значения функции выбирается наибольшее и наименьшее среди чисел f(a), f(c 1 ), f(c 2 ),….f( c n ), f(b) где x = c 1 , c 2 , ….., c n — критические точки.
Maxima и Minima Проблемы с решениями
1.
Решение:
2.
Решение:
3.
.
Решение:
5.
Решение:
6.
Решение:
7.
7.
0024 Решение:
8.
Решение:
9.
Решение:
10.
. Решение:
10.
. :
Как найти максимум и минимум функции?
Максимум и минимум — это максимальное или минимальное значение функции в заданном диапазоне. В этом пошаговом руководстве вы узнаете, как найти максимумы и минимумы функции.
В этом пошаговом руководстве вы узнаете, как найти максимумы и минимумы функции.
Максимумы и минимумы известны как экстремумы функции. Максимум будет самой высокой точкой кривой в заданном диапазоне, а минимум будет самой низкой точкой кривой.
Пошаговое руководство по поиску максимума и минимума функции
Максимум и минимум — это пики и впадины на кривой функции. Для функции может быть любое количество максимумов и минимумов. В исчислении мы можем найти максимальное и минимальное значения каждой функции, даже не глядя на функциональную диаграмму. Максимум будет самой высокой точкой кривой в заданном диапазоне, а минимум будет самой низкой точкой кривой.
Комбинация максимума и минимума является экстремумом. На картинке ниже мы видим разные пики и впадины на диаграмме. При \(x=a\) и при \(x=0\) мы получаем максимальные значения функции, а при \(x=b\) и \(x=c\) получаем минимальные значения функции функция. Все пики являются максимумами, а впадины — минимумами.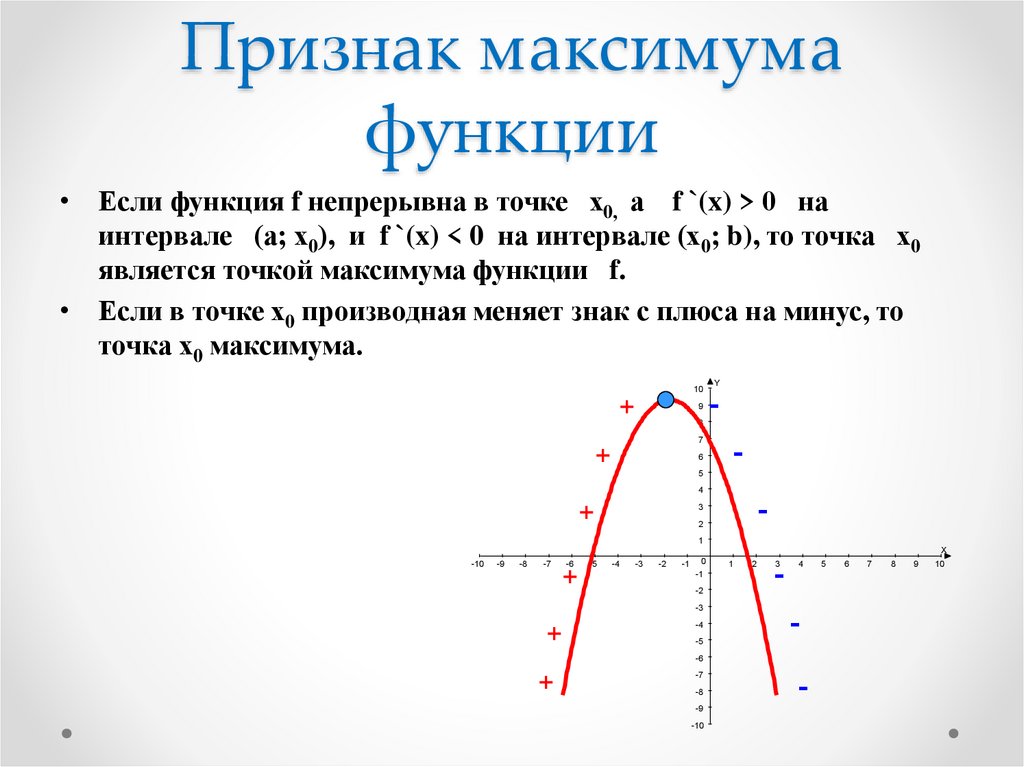
В функции существует два типа максимума и минимума:
- Локальные максимумы и минимумы
- Абсолютные или глобальные максимумы и минимумы
Локальные максимумы и минимумы — это максимум и минимум функции, генерируемой в определенном интервале. Локальный максимум — это значение функции в точке заданного интервала, где значения функции, близкие к этой точке, всегда меньше значения функции в этой точке. В то время как локальный минимум — это значение функции в точке, где значения функции, близкие к этой точке, больше, чем значение функции в этой точке.
- Локальные максимумы: Точка \(x=b\) является точкой локального максимума для \(f(x)\), если она находится в окрестности \(b\), т.е. в \((b−𝛿 , b+𝛿)\), где \(𝛿\) можно сделать сколь угодно малым, \(f(x)< f(b)\) для всех \(x ∈ \frac{(b−𝛿, b+𝛿) {{b}}\). Это просто означает, что если мы рассмотрим небольшую область (интервал) вокруг \(x=b, f(b)\), она должна быть максимальной в этом интервале.

- Локальные минимумы: Точка \(x=a\) является точкой локального минимума для \(f(x)\), если она находится в окрестности \(a\), т. е. в \((a −𝛿,a+𝛿)\), (где \(𝛿\) может принимать сколь угодно малые значения), \(f(x)>f(a)\) для всех \(x ∈ \frac{(a−𝛿 ,a+𝛿)}{{a}}\). Это означает, что если мы рассмотрим небольшой интервал вокруг \(x=a\), \(f(a)\) должно быть минимумом в этом интервале.
Абсолютные максимумы и минимумы
Высшая точка функции во всей области называется абсолютным максимумом функции, а самая нижняя точка функции во всей области функции известна как абсолютный минимум функция. Может быть только один абсолютный максимум функции и один абсолютный минимум функции во всей области. Абсолютные максимумы и минимумы функции также можно назвать глобальными максимумами и глобальными минимумами функции.
- Абсолютные максимумы: Точка \(x=a\) является точкой глобального максимума для \(f(x)\), если \(f(x)≤ f(a)\) для всех \( x∈ D\) (область определения \(f(x)\)).

- Абсолютные минимумы: Точка \(x=a\) является точкой глобального минимума для \(f(x)\), если \(f(x) ≥ f(a)\) для всех \(x ∈ D\) (область определения \(f(x)\)).
Нахождение максимума и минимума функции
Максимум и минимум функции можно вычислить с помощью теста производной первого порядка и теста производной второго порядка.
Проверка производной первого порядка для максимумов и минимумов
Первая производная функции показывает наклон функции. Вблизи точки максимума наклон кривой увеличивается по мере приближения к точке максимума, затем уменьшается до нуля в точке максимума, а затем уменьшается по мере удаления от точки максимума. Точно так же вблизи точки минимума наклон функции уменьшается по мере продвижения к точке минимума, затем становится равным 0 в точке минимума, а затем увеличивается по мере удаления от точки минимума.
Предположим, что у нас есть функция \(f\), непрерывная в критической точке и определенная в открытом интервале \(I\) и \(f'(c)=0\) (наклон равен \(0\ ) в \(с\)). Затем мы исследуем значение \(f'(x)\) в левой точке кривой и справа от кривой и исследуем природу \(f'(x)\), тогда мы можем сказать, что данная точка будет:
Затем мы исследуем значение \(f'(x)\) в левой точке кривой и справа от кривой и исследуем природу \(f'(x)\), тогда мы можем сказать, что данная точка будет:
- Локальные максимумы: Если \(f'(x)\) меняет знак с положительного на отрицательный при возрастании \(x\) через точку \(c\), то \(f(c) \) дает максимальное значение функции в этом диапазоне.
- Локальные минимумы: Если \(f'(x)\) меняет знак с отрицательного на положительный при возрастании \(x\) через точку \(c\), то \(f(c)\) дает минимальное значение функции в этом диапазоне.
- Точка перегиба: Если знак \(f'(x)\) не меняется при увеличении \(x\) через \(c\), а точка \(c\) не является максимумов и минимумов функции, то точка \(с\) называется точкой перегиба.
Тест производной второго порядка для максимумов и минимумов
В тесте производной второго порядка для максимумов и минимумов мы находим первую производную функции, и если она дает значение наклона, равное \(0\) в критической точке \(x=c ( f'(c)=0)\), то находим вторую производную функции.

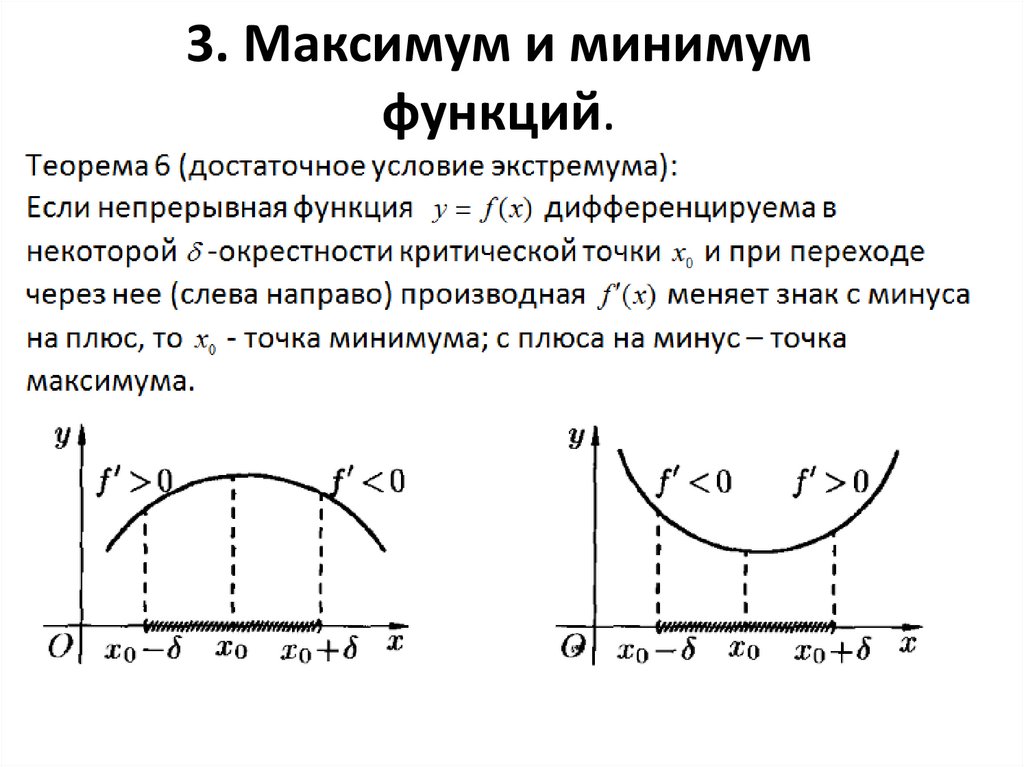 Недостаточно , т. е. f’(a) = 0 не обязательно означает, что x = a является крайней точкой. Существуют функции, производные которых обращаются в нуль в точке, но не имеют экстремального значения в точке , например, . f(x) = x 3 при x = 0 не достигает экстремального значения при x = 0 и f'(0) = 0.
Недостаточно , т. е. f’(a) = 0 не обязательно означает, что x = a является крайней точкой. Существуют функции, производные которых обращаются в нуль в точке, но не имеют экстремального значения в точке , например, . f(x) = x 3 при x = 0 не достигает экстремального значения при x = 0 и f'(0) = 0.