Как найти среднюю линию равнобедренной трапеции: Все формулы средней линии равнобедренной трапеции

формулы через стороны, основания и тд

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение высоты равнобедренной (равнобокой) трапеции

В данной публикации мы рассмотрим различные формулы, с помощью которых можно вычислить высоту равнобедренной (равнобокой) трапеции.

Напомним, высотой трапеции называется перпендикуляр, соединяющий оба ее основания. Также, в равнобедренной трапеции боковые стороны равны.

• Нахождение высоты равнобедренной трапеции
  • Через длины сторон
  • Через боковую сторону и прилежащий угол
  • Через основания и прилежащий угол
  • Через площадь и основания
  • Через диагонали и угол между ними

Через длины сторон

Зная длины всех сторон равнобедренной трапеции, вычислить ее высоту можно, используя формулу ниже:

Через боковую сторону и прилежащий угол

Если известна длина боковой стороны равнобедренной трапеции и угол между ней и основанием фигуры, найти высоту можно следующим образом:

Через основания и прилежащий угол

Вычислить высоту трапеции можно, если известны длины ее оснований и угол при любом из оснований (например, при большем).

Через площадь и основания

Также высоту равнобедренной трапеции удастся найти через ее площадь и длины оснований:

Данная формула может быть представлена в другом виде, если вместо оснований дана средняя линия (m).

m – средняя линия, равняется полусумме оснований, т.е. m = ^(a+b)/₂.

Через диагонали и угол между ними

И еще один способ вычислить высоту равнобедренной трапеции, если известны ее диагонали (которые имеют одинаковую длину), угол между ними и основания.

Та же самая формула, но со средней линией (m) вместо суммы оснований:

Примечание: если диагонали равнобедренной трапеции взаимно перпендикулярны, то ее высота равняется половине суммы оснований или, другими словами, средней линии.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Площадь, средняя линия и высота трапеции — калькулятор онлайн | Математика

Создан: 14. 03.2020 | Категория: Математика

Формулы трапеции

Что ищем?

Площадь трапецииСреднюю линию трапецииВысоту трапеции

Что известно?

Основания и высотаСредняя линия и высота

Введите a

Введите b

Введите h

Введите m

Введите h

Введите a

Введите b

Что известно?

Площадь и основанияПлощадь и средняя линия

Введите S

Введите a

Введите b

Введите S

Введите m

Результат округлять до 012345 знаков после запятой

подробнее

НайтиОчистить поля

❓Инструкция

 Калькулятор для нахождения площади, средней линии и высоты трапеции.

 Как пользоваться:

 Необходимо выбрать неизвестную величину трапеции
 Указать известные величины
 Получить ответ

 Ответ возможно получить с этапами решения, если выставить галочку «Подробнее».
 Также, есть возможность указать точность ответа. То есть количество знаков после запятой.

 

Ограничения:

Числа на входе должны быть:
 Вещественными
 Больше 0, но не больше 100 000.
 С точностью не более 10 знаков после запятой.

📖 Теория

трапеция

 Трапеция представляет собой 4-стороннюю плоскую форму с прямыми сторонами, у которой пара противоположных сторон параллельна (отмечены стрелками ниже):

 Трапеция:

 имеет пару параллельных сторон
 является равнобедренной, если боковые стороны равны и углы при основаниях попарно равны.

 Площадь трапеции

Площадь трапеции равняется полусумме оснований, умноженную на высоту.

$$S = \frac{a + b}{2} * h$$, где $$S$$ — площадь, $$a,b$$ — основания трапеции, $$h$$ — высота.

 Периметр трапеции

Периметр является суммой длин  всех сторон :

$$P = a + b + c + d$$, где $$P$$ — периметр, $$a,b,c,d$$ — стороны трапеции.

 Медиана трапеции

Медиана (называемая также средней линией) представляет собой отрезок линии на полпути между двумя основаниями.

Средняя линия трапеции равняется полусумме оснований.

$$m = \frac{a + b}{2}$$, где $$m$$ — средняя линия трапеции, $$a,b$$ — основания трапеции.

Посмотрев на формулу площади трапеции, а затем на формулу средней линии, мы легко можем заметить, что площадь трапеции также можно найти как среднюю линию, умноженную на высоту.

$$S = m * h$$

 Высота трапеции

Высоту трапеции можно найти при известных площади и средней линии трапеции как:

$$h = \frac{S}{m}$$, где $$h$$ — высота, $$S$$ — площадь, $$m$$ — средняя линия трапеции.

А также при известных площади и двух оснований трапеции следующим образом:

$$h = \frac{2S}{a + b}$$, где $$h$$ — высота, $$S$$ — площадь, $$a,b$$ — основания трапеции.

Последняя формула опять же вытекает из формулы средней линии трапеции.

➕ Примеры

 Пример 1: Две стороны трапеции имеют длину 6 м и 4 м и высоту 3 м. Какова его площадь?

$$S = \frac{6 м + 4 м}{2} * 3 м = 5 м * 3 м = 15 м^2$$. 2}{14 см} = 4 см$$.

Свойства равнобедренной трапеции – Math Blow the Blowfish

Добро пожаловать в четвертую часть второго урока «Свойства равнобедренной трапеции!» После прочтения этого урока вы должны использовать свойства равнобедренной трапеции для решения задачи по геометрии и применить определение равнобедренной трапеции и теоремы о свойствах равнобедренной трапеции. Прежде чем мы перейдем к свойствам равнобедренной трапеции, давайте сначала обсудим теорему о среднем отрезке трапеции.

ПРЕДПРОВЕРКА

Что за ловушка!

Выполните описанную ниже процедуру и ответьте на следующие вопросы.
Материалы: высокосортная бумага, карандаш, линейка и транспортир
Процедура:
1. Нарисуйте трапецию TRAP, где TRP ⊥ PA, TP = 5 см, TR = 4 см и PA = 8 см.
2. Обозначьте середины TP и RA как G и O соответственно.
3. Соедините G и O, чтобы сформировать сегмент.
Вопросы:
• Смотрит ли ГО параллельно основаниям трапеции?
• Измерить GO. Как долго это?
• Какова сумма оснований TRAP?
• Сравните сумму оснований и длину GO. Что ты нашел?

Теорема 6

• Медиана трапеции параллельна каждому основанию трапеции и ее длина равна половине суммы длин оснований трапеции.

Пример:

Трапеция МИНС имеет медиану TR. Является ли  TR||IN и TR||MS? Да, потому что по теореме 6 медиана трапеции параллельна каждому основанию трапеции. IN и MS — основания данной трапеции выше.

TR = 1/2(MS + IN)? Да, потому что согласно теореме 6 медиана трапеции равна половине суммы длин оснований трапеции.

* Медиана – отрезок, соединяющий середины катетов трапеции.

Теперь приступим к самому уроку.

Теоремы о равнобедренной трапеции

Теорема 7

• Углы при основании равнобедренной трапеции равны.

Пример:

Равнобедренная трапеция AMOR. ∠A ≅ ∠R? Да, потому что по теореме 7 углы при основании равнобедренной трапеции равны.

Является ли ∠M ≅ ∠O? Да, потому что по теореме 7 углы при основании равнобедренной трапеции равны.

Теорема 8

• Противолежащие углы равнобедренной трапеции являются дополнительными.

Пример:

Равнобедренная трапеция ARTS. Являются ли ∠R и ∠S дополнительными? Да, потому что по теореме 8 противолежащие углы равнобедренной трапеции являются дополнительными.

∠T и ∠A дополнительны? Да, потому что по теореме 8 противолежащие углы равнобедренной трапеции являются дополнительными.

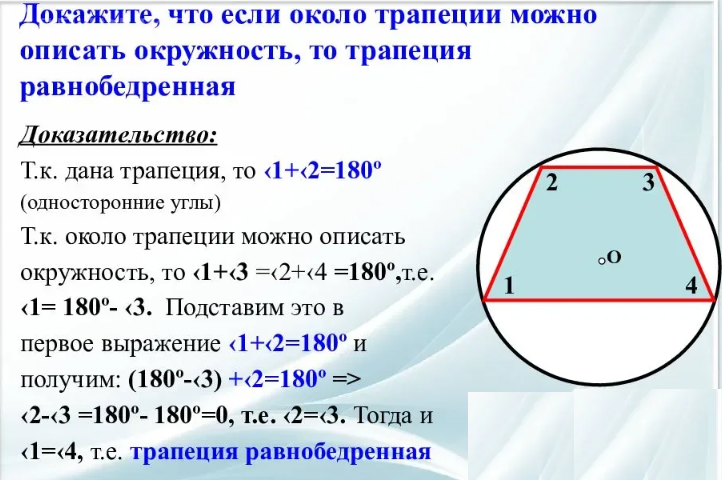
Теорема 9

• Диагонали равнобедренной трапеции равны.

Пример:

Равнобедренная трапеция ROMA. Является ли RM ≅ АО? Да, потому что по теореме 9 диагонали равнобедренной трапеции равны.