Синус, косинус и тангенс угла
Похожие презентации:
Синус, косинус и тангенс угла
Синус, косинус, тангенс, котангенс
Синус, косинус и тангенс угла
Синус, косинус и тангенс угла
Синус, косинус и тангенс угла
Синус, косинус и тангенс угла
Синус, косинус, тангенс угла
Синус, косинус и тангенс углов от 0⁰ до 180 ⁰
Синус, косинус, тангенс и котангенс угла прямоугольного треугольника
Градусная и радианная меры угла. Вращательное движение. Синус, косинус, тангенс и котангенс
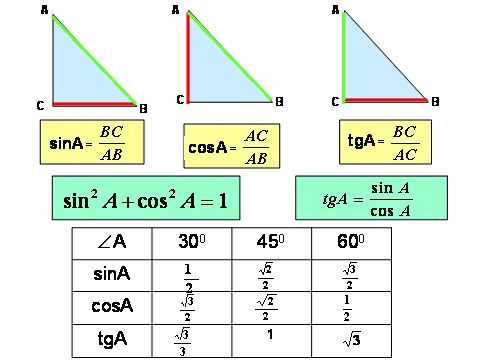
Синусом острого угла прямоугольного треугольника
называется отношение противолежащего катета к
гипотенузе.
В
ВС
sin А
АВ
АС
cos А
АВ
Косинусом острого угла прямоугольного
треугольника называется отношение
прилежащего катета к гипотенузе.
Тангенсом острого угла прямоугольного
треугольника называется отношение
противолежащего катета к прилежащему.
С
А
ВС
tgА
АС
единичной, если ее центр находится в начале
координат, а радиус равен 1.
y
h
C (0; 1)
M (x; y)
B (-1; 0)
O
y
x
D A(1; 0)
x
∆OMD — прямоугольный
y
h
sin =
C (0; 1)
M (x; y)
MD
OM
sin = y
MD = y
OM = 1
B (-1; 0)
0
x
y
Синус угла – ордината у точки М
cos = OM
OD
D A(1; 0) x
cos = x
OD = x
OM = 1
Косинус угла – абсцисса х точки М
tg =
MD
OD
MD = y = sin
OD = x = cos
tg
sin
cos
y
h
C (0; 1)
M (x; y)
B (-1; 0)
0
x
y
Так как координаты (х; у) заключены
в промежутках
0 ≤ у ≤ 1, — 1 ≤ х ≤ 1,
то для любого из промежутка
0 ≤ ≤ 180
D A(1; 0) x
справедливы неравенства:
0 ≤ sin ≤ 1,
— 1≤ cos ≤ 1
y
h
C (0; 1)
M (x; y)
B (-1; 0)
0
x
y
D A(1; 0) x
Так как точки А, С и B имеют
координаты
А (1; 0), С (0; 1), В (-1; 0), то
00
900
1800
sin
0
1
0
cos
1
0
-1
tg
0
—
0
y
h
C (0; 1)
M (x; y)
B (-1; 0)
0
x
х2 + у2 = 1 — уравнение окружности
sin = y, cos = x
y
D A(1; 0) x
для любого из промежутка 0 ≤ ≤ 180
sin 1 cos
2
cos 1 sin
2
sin (90 — ) = cos
при 0 ≤ ≤ 90
cos (90 — ) = sin
sin (180 — )= sin
cos (180 — ) = — cos
при 0 ≤ ≤ 180
А (x; y) – произвольная точка
y
A (x; y)
М (сos α; sin α)
M (cos α; sin α) OM cos ; sin
OA x; y
O
OA OA OM
x
x = ОА ∙ cos
y = OA ∙ sin
Найдите по рисунку синус, косинус и тангенс угла:
sin y
АОМ ; АОК ; АОС.
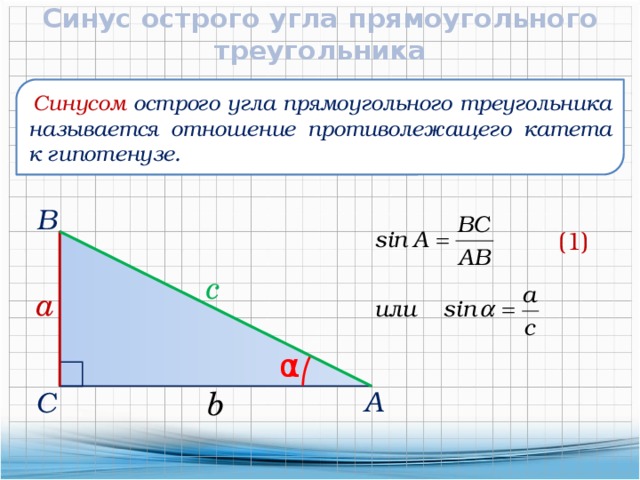
sin АОМ 0,6;
sin АОК 0,8;
cos
АОМ
АОМ 0,8;
cos
АОК
АОК 0,6;
3
3
tg АОМ
4
К
С(-1;0)
cos x
sin АОС 0;
В (0;1)
М
О
А (1;0)
cos
АОС 1;
АОС
tg АОМ 0
Х
Найдите sinα:
sin 1 cos2
1
cos
2
1
sin 1
4
2
cos
5
2 2
4
21
sin 1 ( ) 1
5
25
5
cos 1
sin 1 ( 1) 1 1 0
cos 0
sin 1 02 1 1
3
3
4
2
2
Найдите cosα:
3
sin
2
cos 1 sin 2
3
cos 1
4
1
1
4
2
1
sin
4
1
15
15
cos 1
16
16
4
sin 1
cos 1 12 0
English Русский Правила
Касательные и уклоны
Касательные и уклоныОпределение касательной
Синус и косинус — не единственные тригонометрические функции, используемые в тригонометрии. Многие другие использовались на протяжении веков.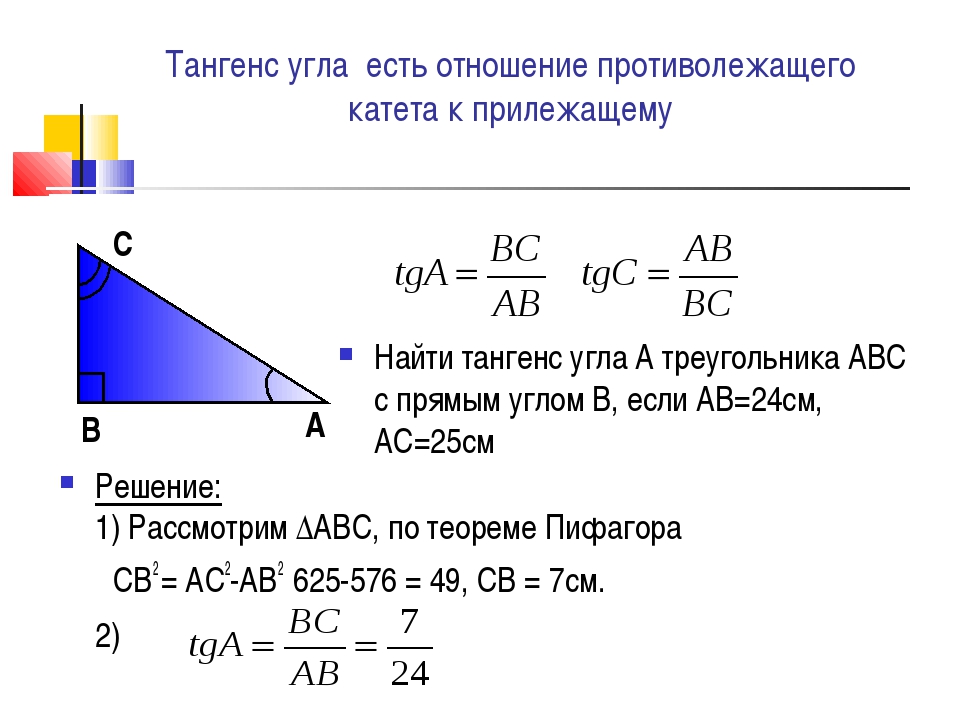
Наиболее полезным из них является тангенс. С точки зрения диаграммы единичного круга, касательная — это длина вертикальной линии ED , касательной к окружности от точки касания E до точки D , где эта касательная пересекает луч 9.0007 AD формирование угла.Тангенс относительно синуса и косинуса
Поскольку два треугольника ADE и ABC подобны, имеемНо ED = tan A, AE = 1, CB = sin A, и AC = cos AB. Таким образом, мы получили фундаментальное тождество
| тан А = | sin A cos A |
Касательные и прямоугольные треугольники
Точно так же, как синус и косинус можно найти как отношение сторон прямоугольного треугольника, можно найти и тангенс.
| тан = | опп прил |
Наклоны линий
Одна из причин, по которой касательные так важны, заключается в том, что они дают наклоны прямых линий. Рассмотрим прямую линию, проведенную в x-y координатная плоскость. Точка B находится там, где линия пересекает ось y . Мы можем принять координаты B равными (0, b ), так что b, , называемая точкой пересечения y , указывает, насколько выше оси x лежит B .
(Эти обозначения противоречат обозначению сторон треугольника a, b, и c, , поэтому не будем сейчас обозначать стороны.)
Вы можете видеть, что точка на 1 единицу вправо от начала координат помечена 1, и ее координаты, конечно же, (1,0). Пусть C будет точкой, в которой эта вертикальная линия пересекает горизонтальную линию через B. Тогда C имеет координаты (1, b ).
Точка A находится там, где вертикальная линия выше 1 пересекает исходную линию. Пусть м обозначает расстояние, на котором А выше С. Тогда A имеет координаты (1, b + m ). Это значение м называется уклоном линии. Если вы переместитесь вправо на одну единицу в любом месте по линии, то вы переместитесь вверх на
Теперь рассмотрим угол СВА. Назовем это углом наклона . Его касательная равна CA/BC = м /1 = м.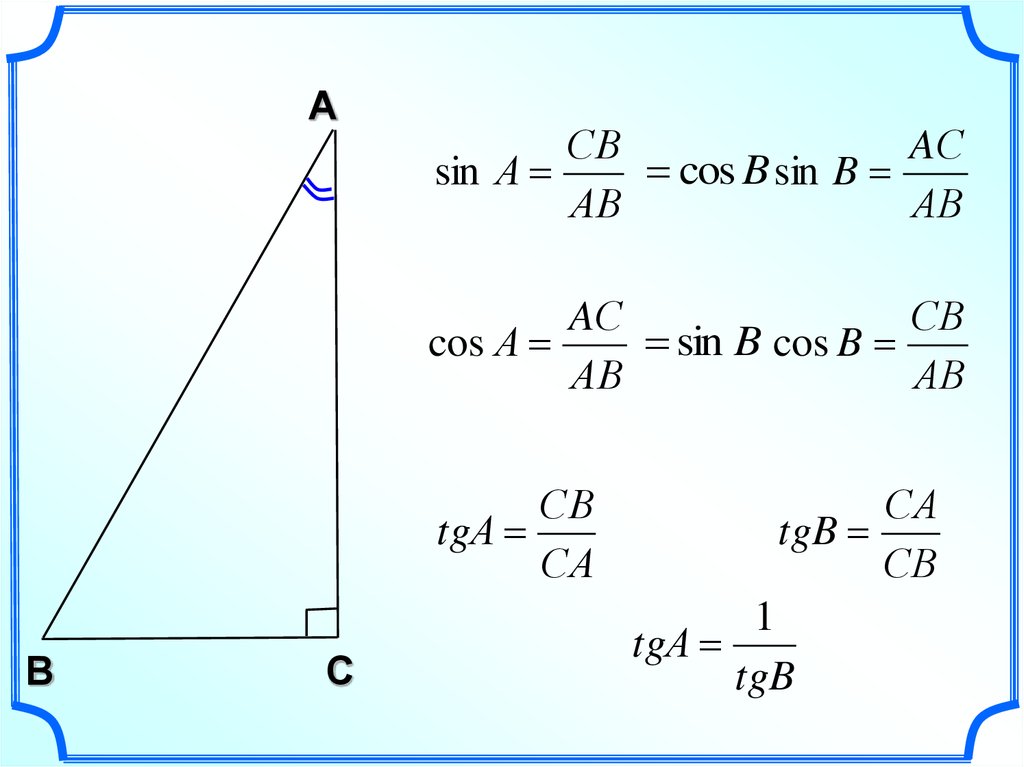
Таким образом, наклон представляет собой тангенс угла наклона.
Углы возвышения и депрессии
Термин «угол места» относится к углу над горизонталью от зрителя. Если вы находитесь в точке А, AH и AH , то угол места B над горизонтом равен углу BAH. Точно так же «угол депрессии» к точке C ниже горизонта составляет угол CAH.
Касательные часто используются для решения задач, связанных с углами возвышения и депрессии.
Снова общие углы
Мы можем расширить нашу таблицу синусов и косинусов общих углов до тангенсов. Вам не нужно запоминать всю эту информацию, если вы можете просто запомнить отношения сторон треугольника 45°-45°-90° и треугольника 30°-60°-90°. Отношения являются значениями триггерных функций. Обратите внимание, что тангенс прямого угла указан как бесконечность. Это потому, что по мере увеличения угла до 90°, его касательная неограниченно растет.
Может быть, лучше сказать, что касательная 90 ° не определена, поскольку, используя определение окружности, луч, исходящий из начала координат под углом 90 °, никогда не пересекается с касательной.| Angle | Degrees | Radians | cosine | sine | tangent |
|---|---|---|---|---|---|
| 90° | /2 | 0 | 1 | infinity | |
| 60° | /3 | 1/2 | 3 / 2 | 3 | |
| 45° | /4 | 2 / 2 | 2 / 2 | 1 | |
| 30° | /6 | 3 / 2 | 1/2 | 1/3 | |
| 0° | 0 | 1 | 0 | 0 |
Упражнения
29. В прямоугольном треугольнике a = 30 ярдов и загар A = 2.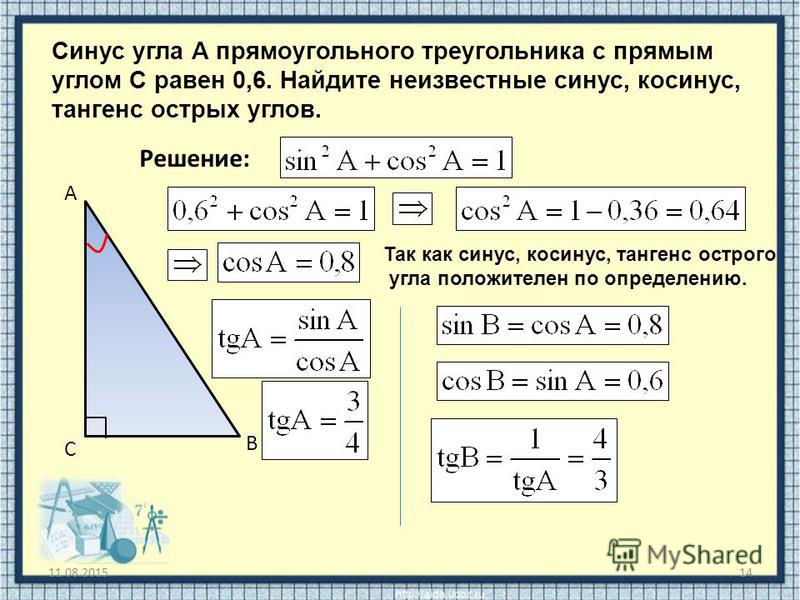
Найдите b и c.
49. cos t = 2 tan t. Найти значение sin t.
Примечание: В следующих задачах расстояние означает расстояние по горизонтали, если не указано иное; под высотой объекта понимается его высота над горизонтальной плоскостью через точку наблюдения. Высота глаза наблюдателя не должна приниматься во внимание, если это специально не оговорено. В задачах, связанных с тенью объекта, предполагается, что тень падает на горизонтальную плоскость через основание объекта, если не указано иное.
151. Угол возвышения дерева на расстоянии 250 футов составляет 16° 13′. Найдите высоту.
152. Найдите высоту колокольни, удаленной на 321 фут, угол возвышения 35°16′.
153. С корабля угол возвышения вершины маяка на высоте 200 футов над водой составляет 2° 20′. Найдите расстояние.
154. С вершины маяка на высоте 165 футов над водой угол депрессии корабля составляет 3° 50′.
Найдите расстояние.
159. Найдите высоту башни на расстоянии 186 футов, угол возвышения 40° 44′.
160. С одной стороны ручья шест высотой 50 футов имеет с противоположной точки угол возвышения 5° 33′. Найдите ширину потока.
164. От одного холма вершина другого на 128 футов выше имеет угол возвышения 2° 40′. Найдите расстояние.
165. От одного холма до вершины другого на расстоянии 6290 футов имеет угол возвышения 4° 9′. Найдите, на сколько высота второго холма больше высоты первого.
189. Фронтон крыши имеет ширину 40 футов у основания и 26 футов от основания до конька. Под каким углом наклон стропил?
Советы
Общий совет для всех этих упражнений: сначала нарисуйте фигуру.29. Поскольку вы знаете a и tan A, вы можете найти b. Затем вы можете определить c по теореме Пифагора, или с помощью синусов, или с помощью косинусов.
49. Вам понадобятся две личности.
Во-первых, tan t = sin t /cos t. Во-вторых, тождество Пифагора, sin 2 t + cos 2 t = 1. Тогда вам нужно будет решить квадратное уравнение.
151. Помните, что тангенс угла прямоугольного треугольника равен противолежащей стороне, деленной на прилежащую сторону. Вы знаете соседнюю сторону (расстояние до дерева) и угол (угол возвышения), поэтому можете использовать касательные для нахождения высоты дерева.
152. Вы знаете угол (опять же, угол возвышения) и примыкающую сторону (расстояние до шпиля), поэтому используйте касательные, чтобы найти противоположную сторону.
153. Используя угол и противоположную сторону, используйте тангенс, чтобы найти соседнюю сторону.
154. Та же подсказка, что и в 153.
159. Та же подсказка, что и в 152.
160. Та же подсказка, что и в 153.
164. Та же подсказка, что и в 153.
165. Та же подсказка, что и в 152.
189. Фронтон крыши представляет собой равнобедренный треугольник. Если провести перпендикулярную линию от хребта, то получится два конгруэнтных прямоугольных треугольника. Вы знаете две стороны треугольников, поэтому можете определить угол наклона стропил с помощью арктангенса.
Ответы
29. b = a /tan A = 30/2 = 15 ярдов. c = 33,5 ярда.
49. Поскольку COS T = 2 TAN T, Следовательно, COS T = 2 SIN T /COS T, SO COS 2 T = 2 SIN T, и, по Пифагорейское тождество: 1 sin 2 t = 2 sin t. Это дает вам квадратное уравнение sin 2 t + 2 sin t 1 = 0. Решения таковы: sin t = 1 ± 2. Из этих двух решений единственно допустимым является грех t = 2 1.
151. Высота = 250 tan 16°13′ = 72,7′ = 72’9″.
152. Высота = 321 тан 35°16′ = 227 футов.
153. Расстояние = 200/тангенс 2°20′ = 4908 футов, почти миля.
154. Расстояние = 165/тангенс 3°50′ = 2462 фута, почти полмили.
159. Высота = 186 тан 40°44′ = 160 футов.
160. Расстояние = 50/тангенс 5°33′ = 515 футов.
164. Расстояние = 128/тангенс 2°40′, около 2750 футов, чуть больше полумили.
165. Высота = 6290 tan 4°9′ = 456,4 фута.
189. тангенс А = 26/20, поэтому А = 52°.
Оглавление. | Вернемся к косинусам. | К прямоугольным треугольникам.
© 1996, 1997, 1999.
Дэвид Э. Джойс
Кафедра математики и информатики
Университет Кларка
Вустер, Массачусетс, 01610
Электронная почта: [email protected]
Краткий триггерный курс Дейва находится по адресу http://aleph0.clarku.edu/~djoyce/java/trig.
Использование функции касательной для нахождения угла (ключевой этап 3)
Урок
Функция тангенса связывает заданный угол с противолежащей стороной и прилежащей стороной прямоугольного треугольника.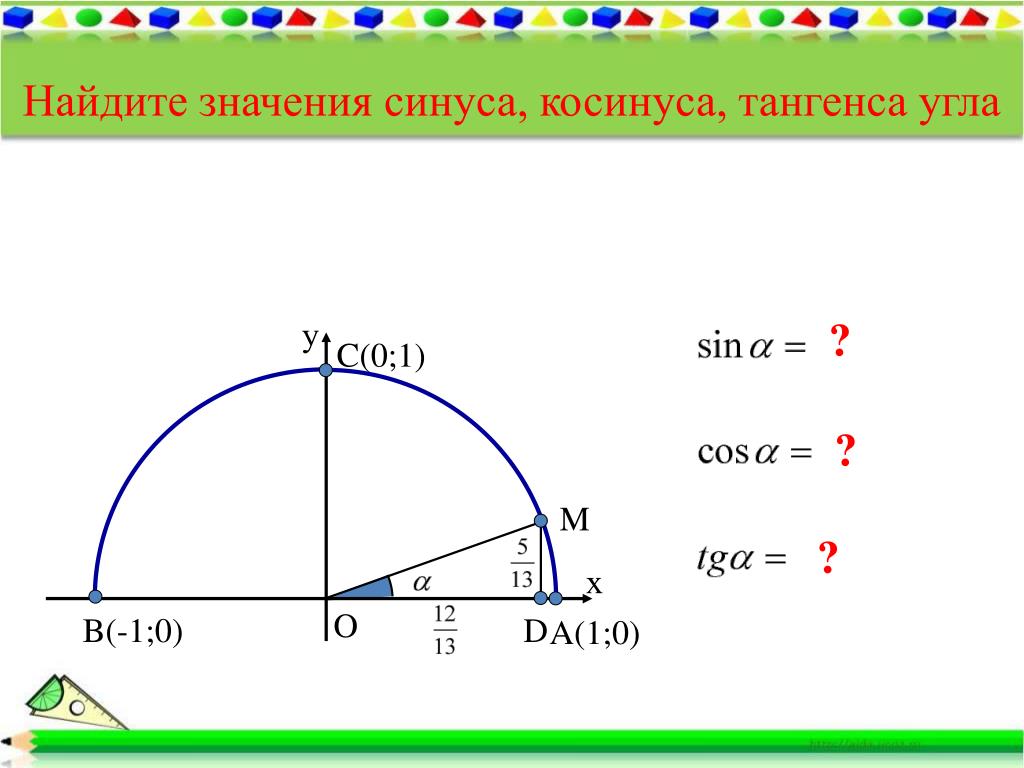
Угол (обозначенный θ) определяется по следующей формуле:
В этой формуле θ — это угол прямоугольного треугольника, противоположная сторона — это длина стороны, противоположной углу, а прилежащая — это длина стороны, следующей за углом. загар −1 — функция арктангенса (см. , примечание ). На изображении ниже показано, что мы имеем в виду:
Как использовать функцию касательной для нахождения угла прямоугольного треугольника
Найти угол прямоугольного треугольника легко, если мы знаем противоположный и прилежащий.
Чему равен угол прямоугольного треугольника, изображенного ниже?
Пошагово:
Начните с формулы:
θ = tan −1 (напротив / рядом)
Не забывайте: tan −1 — функция арктангенса (применяется ко всему в скобках) и / означает ÷
Подставляем в формулу длину противоположного и длину прилежащего.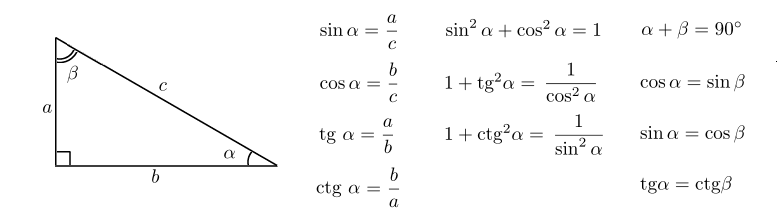
В нашем примере противолежащее 5 см и соседнее 5 см.
θ = тангенс −1 (5/5) θ = загар −1 (5 ÷ 5) θ = тангенс −1 (1) θ = 45°
Ответ:
Угол прямоугольного треугольника с противолежащим 5 см и прилежащим 5 см равен 45°.
Вспоминая формулу
Часто самая сложная часть поиска неизвестного угла — это вспомнить, какую формулу использовать. Всякий раз, когда у вас есть прямоугольный треугольник, в котором вы знаете две стороны и должны найти неизвестный угол… ……подумайте о тригонометрии… ……………подумайте о синусе, косинусе или тангенсе… …………………………..думаю SOH CAH TOA .
Глядя на приведенный выше пример, мы знаем O pposite и A djacent.
Две буквы, которые мы ищем, это OA , которые входят в TOA в SOH CAH TOA .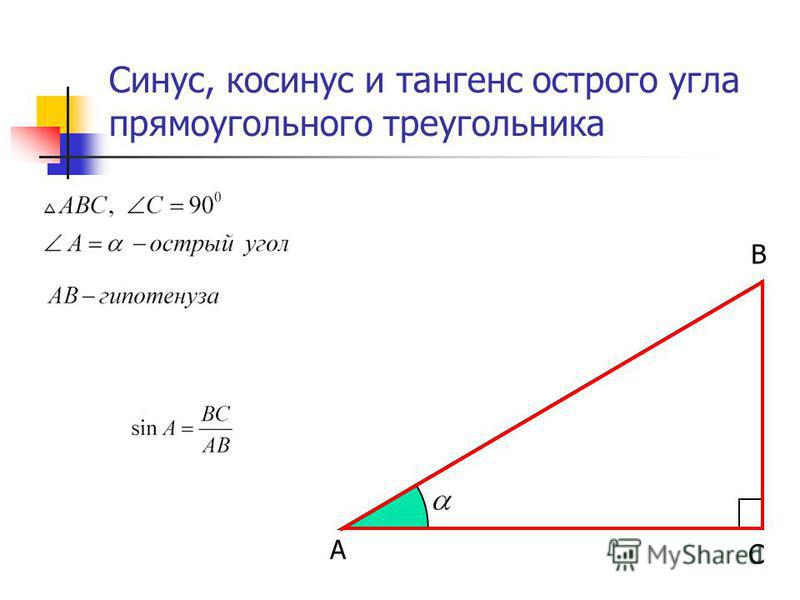
Это напоминает нам уравнение:
T ан θ = O ппоз. / A djacent
Нам нужен угол θ, а не тангенс угла, tan θ. Для этого нам нужно взять арктангенс, тангенс -1 (см. Примечание ).
θ = T и −1 ( O точка / A точка)
Слайды урока
Ползунок ниже дает еще один пример нахождения угла прямоугольного треугольника (если известны противоположный и прилежащий). Откройте слайдер в новой вкладкеИнтерактивный виджет
Вот интерактивный виджет, который поможет вам узнать о функции касательной к прямоугольному треугольнику.
Что такое функция арктангенса?
Функция арктангенса является противоположностью функции тангенса. Функция тангенса принимает угол и дает отношение противоположного к прилежащему:
Функция арктангенса, tan &mius;1 , работает в другом направлении.