Определить точки пересечения с осями координат. Координаты точки пересечения графиков функций. Случай двух линейных функций
- Чтобы найти координаты точки пересечения графиков функций нужно приравнять обе функции друг к другу, перенести в левую часть все члена, содержащие $ x $, а в правую остальные и найти корни, полученного уравнения.
- Второй способ заключается в том, что нужно составить систему уравнений и решить её путём подстановки одной функции в другую
- Третий способ подразумевает графическое построение функций и визуальное определение точки пересечения.
Случай двух линейных функций
Рассмотрим две линейные функции $ f(x) = k_1 x+m_1 $ и $ g(x) = k_2 x + m_2 $. Эти функции называются прямыми. Построить их достаточно легко, нужно взять любые два значения $ x_1 $ и $ x_2 $ и найти $ f(x_1) $ и $ (x_2) $. Затем повторить тоже самое и с функцией $ g(x) $. Далее визуально найти координату точки пересечения графиков функций.
Следует знать, что линейные функции имеют только одну точку пересечения и только тогда, когда $ k_1 \neq k_2 $.
Иначе, в случае $ k_1=k_2 $ функции параллельны друг другу, так как $ k $ — это коэффициент угла наклона. Если $ k_1 \neq k_2 $, но $ m_1=m_2 $, тогда точкой пересечения будет $ M(0;m) $. Это правило желательно запомнить для ускоренного решения задач.
| Пример 1 |
| Пусть даны $ f(x) = 2x-5 $ и $ g(x)=x+3 $. Найти координаты точки пересечения графиков функций. |
| Решение |
Как это сделать? Так как представлены две линейные функции, то первым делом смотрим на коэффициент угла наклона обеих функций $ k_1 = 2 $ и $ k_2 = 1 $. Замечаем, что $ k_1 \neq k_2 $, поэтому существует одна точка пересечения. Найдём её с помощью уравнения $ f(x)=g(x) $: $$ 2x-5 = x+3 $$ Переносим слагаемые с $ x $ в левую часть, а остальные в правую: $$ 2x — x = 3+5 $$ Получили $ x=8 $ абциссу точки пересечения графиков, а теперь найдём ординату. Для этого подставим $ x = 8 $ в любое из уравнений хоть в $ f(x) $, либо в $ g(x) $: $$ f(8) = 2\cdot 8 — 5 = 16 — 5 = 11 $$ Итак, $ M (8;11) $ — является точкой пересечения графиков двух линейных функций. $ M (0;1) $ — точка пересечения графиков функций |
| Ответ |
| $$ M (0;1) $$ |
2-2\cdot 0 + 1 = 1 $$В июле 2020 года NASA запускает экспедицию на Марс. Космический аппарат доставит на Марс электронный носитель с именами всех зарегистрированных участников экспедиции.
Если этот пост решил вашу проблему или просто понравился вам, поделитесь ссылкой на него со своими друзьями в социальных сетях.
Один из этих вариантов кода нужно скопировать и вставить в код вашей веб-станицы, желательно между тегами
и или же сразу после тега . По первому варианту MathJax подгружается быстрее и меньше тормозит страницу. Зато второй вариант автоматически отслеживает и подгружает свежие версии MathJax. Если вставить первый код, то его нужно будет периодически обновлять. Если вставить второй код, то страницы будут загружаться медленнее, зато вам не нужно будет постоянно следить за обновлениями MathJax.
Подключить MathJax проще всего в Blogger или WordPress: в панели управления сайтом добавьте виджет, предназначенный для вставки стороннего кода JavaScript, скопируйте в него первый или второй вариант кода загрузки, представленного выше, и разместите виджет поближе к началу шаблона (кстати, это вовсе не обязательно, поскольку скрипт MathJax загружается асинхронно). Вот и все. Теперь изучите синтаксис разметки MathML, LaTeX и ASCIIMathML, и вы готовы вставлять математические формулы на веб-страницы своего сайта.
Очередной канун Нового Года… морозная погода и снежинки на оконном стекле… Все это побудило меня вновь написать о… фракталах, и о том, что знает об этом Вольфрам Альфа. По этому поводу есть интересная статья , в которой имеются примеры двумерных фрактальных структур. Здесь же мы рассмотрим более сложные примеры трехмерных фракталов.
Фрактал можно наглядно представить (описать), как геометрическую фигуру или тело (имея ввиду, что и то и другое есть множество, в данном случае, множество точек), детали которой имеют такую же форму, как и сама исходная фигура.
То есть, это самоподобная структура, рассматривая детали которой при увеличении, мы будем видеть ту же самую форму, что и без увеличения. Тогда как в случае обычной геометрической фигуры (не фрактала), при увеличении мы увидим детали, которые имеют более простую форму, чем сама исходная фигура. Например, при достаточно большом увеличении часть эллипса выглядит, как отрезок прямой. С фракталами такого не происходит: при любом их увеличении мы снова увидим ту же самую сложную форму, которая с каждым увеличением будет повторяться снова и снова.
Бенуа Мандельброт (Benoit Mandelbrot), основоположник науки о фракталах, в своей статье Фракталы и искусство во имя науки написал: «Фракталы — это геометрические формы, которые в равной степени сложны в своих деталях, как и в своей общей форме. То есть, если часть фрактала будет увеличена до размера целого, она будет выглядеть, как целое, или в точности, или, возможно, с небольшой деформацией».
В практике и в учебниках наиболее распространены нижеперечисленные способы нахождения точки пересечения различных графиков функций.
2+4х-1:
а) на отрезке [-1;0]
Решение: 1) Точки пересечения = корни квадратного уравнения.
Х1 = — 2 и Х2 = +6 — видно на графике.
2) Экстремумы функции
У(-1) = -3 — минимум У(0) = -1 — максимум в заданном интервала.
1. Постройте график функции:. у=-4х+6
2 Не выполняя построений, найдите координаты точек пересечения графика функции у=6х-11 с осями координат.
3 Постройте график функции у=-0,5х ; найдите координаты точки пересечения этого графика с прямой у=1.
4 График прямой пропорциональности проходит через точку А. Проходит ли он через точку В, если А (1,5; -3), В (-11; 22)?
Решение: ⇒
1) у=-4х+6
график прямая, для построения достаточно двух точек
х= 0 1
у= 6 2
отмечаем точки в системе координат, чертим прямую
2) с осью ОХ (х;0) -4х+6=0; -4х=-6; х=3/2 =1,5 ⇒ (1,5; 0)
с осью ОУ (0; у) у=6 ⇒ (0; 6)
3) у=-0,5 х
график прямая, проходящая через начало координат
х= 0 -2
у= 0 1
отмечаем точки в системе координат, чертим прямую
у=-0,5х и у=1 точка пересечения графиков (-2; 1)
4) А(1,5; -3) В(-11; 22)
прямая пропорциональность у=кх
-3 = 1,5к ; к=-2 ⇒ у=-2х -данная функция
подставим точку В
22=-2*(-11)
22=22 верно
ответ: да, график проходит через точку В
Не выполняя построение, найдите координаты точек пересечения графика функции y=0,8x+4 с осями координат.
Решение: Оу: х=о
у=4
Ох: у=о
х=-4/0.8
Чтобы найти координаты пересечения графика функции с осями координат, нужно сначала вместо х подставить 0 в уравнение у=0,8х+4, получим у=0,8*0+4=4, значит точка с координатами (0;4) будет точкой пересечения графика функции с осью ординат. Теперь вместо у подставляем 0 в уравнение у=0,8х+4, получим 0=0,8х+4, отсюда х=-5, значит точка с координатами (-5;0) будет точкой пересечения графика функции с осью абсцисс.
Ответ: (0;4) и (-5;0).
Линейная функция задана формулой y=2x+3. Найдите значение функции, если значение аргумента равно 0.
Линейная функция задана формулой y=3х-5. Найдите значение функции, если значение функции равно 1.
Не выполняя построения графиков, укажите координаты точек пересечения графиков
у=16х+15.
Не выполняя построений, найдите координаты точек пересечения графика функции
у= -2х+2 с осями координат.
Решение: 1) y=2x+3
x=0 y=2*0+3=3
Ответ: 3
2) у=3х-5
х=1 у=3*1-5= -2
Ответ: -2
3) у=16х+15
с осью ОХ: у=0 0=16х+5
-5=16х
х= -5/16
(-5/16; 0) — точка пересечения графика с осью ОХ.
с осью ОУ: х=0 у=16*0+5
у=5
(0; 5) — точка пересечения графика с осью ОУ.
4) у= -2х+2
с осью ОХ: у=0 0= -2х+2
-2= -2х
х=1
(1; 0) — точка пересечения графика с осью ОХ.
с осью ОУ: х=0 у= -2*0+2
у=2
(0; 2) — точка пересечения графика с осью ОУ.
Найдите координаты точек пересечения графика линейной функции y= -2,4x+7,2 с осями координат
Решение: Y=-2.4x+7.2при пересечении с осью Оу х=0, значит у=7,2 координаты точки пересечения(0;7,2) при пересечении с осью Ох у=0, значит 2,4х=7,2 х=3 координаты точки пересечения (3;0)
При х=0 у=7.2 >>> точка пересеч с Оу с координатами (0; 7.2)
при у=0 х=3 >>> точка пересеч с Оx с координатами (3;0)
Найдите координаты точек пересечения графика линейной функции y=1.2x-5.7 с осями координат
Решение: Y=1.2x-5.7 — линейная функция, проходящая через 2 точки.
будет пересекать ось x и y в 2-ух точках, по одной на каждой оси:)y-ось y
x- ось x
функция пересечет ось x, когда y=0
функция пересечет ось y, когда x=0
подставляем:
y=0
0=1.2x-5.7
1.2x=5.7
x=4.75
x=0
y=0-5.7
y=-5.7
2 точки пересечения:
x=4.75 y=0
x=0 y=-5.7
Не выполняя построений найдите координаты точек пересечения графика заданной функции с осями координат
1) у=0,2х+2 2) у=-0,3х+3
Решение: Чтобы найти координаты точек пересечения с осями Ох и Оу, нужно подставить y=0 и x=0 соответственно. То есть:
1) для первой функции y=0,2x+2. Находим координаты точки пересечения с осью Ох: подставляем y=0 и получаем точку с координатами (-10;0). Находим координаты точки пересечения с осью Оу: подставляем x=0 и получаем точку с координатами (0;2).
2) для второй функции y=-0,3x+3. Аналогично. С осью Ох: точка с координатами (10;0). С осью Оу: точка с координатами (0;3)
Не выполняя построений, найдите координаты точек пересечения
графика заданной функции с осями координат:
1) y = −0,7x +42;
2) y = 5x −3,5.
Решение: 1) Y = — 0,7х + 42 ; Y = 0 ; — 0,7x = — 42 ; X = 60 ; X = 0 ; Y = 42 Ответ ( 0 ; 42 ) ; ( 60 ; 0 ) 2) y = 5x — 3,5 ; Y = 0 ; 5x = 3,5 ; X = 0,7 ; X = 0 ; y = — 3,5 ; Ответ ( 0 ; — 3,5 ) ; ( 0,7 ; 0 )
Х=0 пересечение с ОУ
у=-0,7*0+42=42 (0;42)
у=0 пересечение с ОХ
0=-0,7х+42
х=60 (60;0)
у=5х-3,5
х=0 пересечение с ОУ
у=5*0-3,5=-3,5 (0;-3,5)
у=0 пересечение с ОХ
0=5х-3,5
х=0,7 (0,7;0)
Не вополняя построения. Найдите координаты координаты точек пересечения графика функции у=0,24х + 6 с осями координат.
если Вам не трудно объясните как это решать вообще ?
И вот ещё :
покажите как примерно расположен в координатной плоскости график функции :
а.) у= — 0,9х + 4
б.) у=2,3х
Решение: нужно просто вместо х поставить ноль
у=0,24*0+6=6
( х=0 у=6 )
потом вместо у
(у=0 х=-25)
( х=0 у=6 ) и ( у=0 х=-25) — это и есть точки пересечения
а) у=- 0,9х + 4 — прямая,
при х=1, у=3,1; при х=2, у=2,2 — по этим точкам (1; 3,1) и (2; 2,2) строите прямую
Под б) так же:
у=2,3х — прямая, при х=1, у=2,3; при х =2, у=4,6 (1; 2,3) и (2; 4,6)
Дана функция у=5х+1.
Найдите координаты точек пересечения графика данной функции с осями Решение: ОУ — (0;1)
OX — (-0.2;0)
1) Чтобы найти точки пересечения с осью OУ, надо подставить вместо х — 0
y=5*0+1(подставлять надо во всех уравнениях)
y=1
(0;1)
2) Чтобы найти точки пересечения с осью OХ, надо подставить вместо у — 0
0=5x+1(подставлять надо во всех уравнениях)
5x+1=0
5x=-1
x=-0.2
(-0.2;0)
—
456 7 8 > >>
Как найти точки пересечения графиков функций — алгоритмы и примеры правила и методики
Существует определенный класс задач по дисциплине «Алгебра и начало анализа», в которых нужно найти точки пересечения графиков функций без их построения. Решать такие задания довольно просто, когда известна определенная методика нахождения координат по оси абсцисс и ординат. Однако для этого необходимо научиться правильно находить корни уравнений различных типов.
Содержание
- Общие сведения
- Классификация уравнений
- Равносильные тождества
- Математические преобразования
- Разложение на множители
- Методики нахождения точек
- Первой и второй степени
- Кубические и биквадратные
- Пример решения
Общие сведения
Функция — некоторое выражение, описывающее зависимость между двумя величинами. Следует отметить, что последних может быть несколько. Параметр, который не зависит от других элементов, называется аргументом, а зависимое тождество — значением функции.
Точка пересечения графиков означает, что у системы уравнений существует общее решение. Следует отметить, что для их нахождения можно воспользоваться графическим и аналитическим методом. Первый подразумевает построение графического представления выражения с переменной.
Чтобы найти пересечение графиков функций аналитическим способом, необходимо решить уравнение, корни которого являются искомыми точками.
2+St+U=0).
Равносильные тождества
При выполнении математических операций каждое выражение может быть заменено на эквивалентное, т. е. равносильное. Иными словами, равносильными называются уравнения, различные по составляющим их элементам, но имеющие одинаковые корни. Следует отметить, что ими являются также выражения, не имеющие решений. Математики выделяют три свойства: симметричность, транзитивность и разложение на множители.
Формулировка первого: когда I уравнение равносильно II, то значит, и II равносильно I. Суть транзитивности состоит в том, что если I равносильно II, а II — III, то значит I эквивалентно III. Второе свойство имеет такую формулировку: произведение двух элементов, содержащих переменные, равное нулевому значению, эквивалентно двум выражениям, которые можно приравнять к 0. Математическая запись утверждения имеет такой вид: R(t)*S(t)=0 {R(t)=0 и S(t)=0}.
Математические преобразования
Для решения уравнения необходимо выполнить некоторые математические преобразования.
2 -9 не заканчиваются, поскольку его можно представить в виде разности квадратов, т. е. (s+2-9)(s+2+9)=(s-7)(s+11). Кроме того, формулы сокращенного умножения рекомендуется применять при понижении степени.
Методики нахождения точек
Чтобы узнать, пересекаются ли графики функций, нужно приравнять соответствующие тождества, а затем решать уравнение. Однако при такой операции могут получиться различные равенства с неизвестными. В этом случае требуется обратить внимание на нижеописанные методики решения для каждого вида.
Первой и второй степени
Уравнение первой степени, или линейное, решается очень просто. Для этого необходимо перенести переменные величины в одну, а известные — в другую сторону. Методика решения имеет следующий вид:
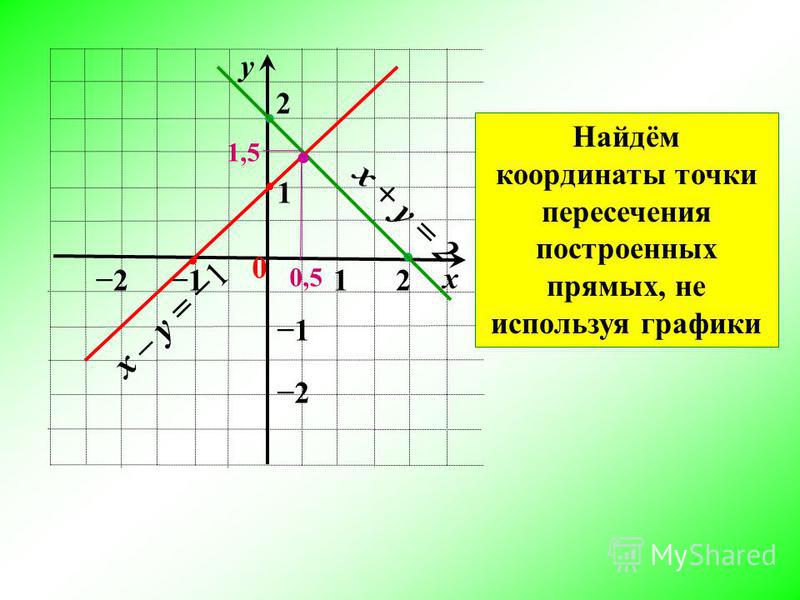(1/2)]/2P, где t1 и t2 — точки пересечения с осью абсцисс.Если коэффициент при второй степени (P) эквивалентен 1, то дискриминант можно не высчитывать, а воспользоваться сокращенным вариантом решения — теоремой Виета. Суть ее заключается в подборе корней по таким формулам: t1+t2=-S и t1*t2=U. Иногда для реализации этой методики нужно сократить обе части на коэффициент Р. Алгоритм решения квадратных уравнений имеет следующий вид:
Следует отметить, что распространенная ошибка новичков — отсутствие проверки. В результате неправильных действий образуются ложные корни, а оценка на контрольной, зачете или экзамене существенно снижается.
Кубические и биквадратные
Решение тождеств кубического и биквадратного типов с неизвестными осуществляется двумя способами.
К ним относятся:
В первом случае необходимо выполнить преобразования, которые позволят применить одну из формул сокращенного умножения. Однако этот метод применяется довольно редко, поскольку математики отдают предпочтение второму способу. Для его реализации вводится дополнительная переменная, обладающая более низкой степенью и существенно упрощающая выражение. Алгоритм имеет такой вид:
Для проверки рекомендуется воспользоваться онлайн-приложениями, позволяющими вычислить корни, а также построить графики функций.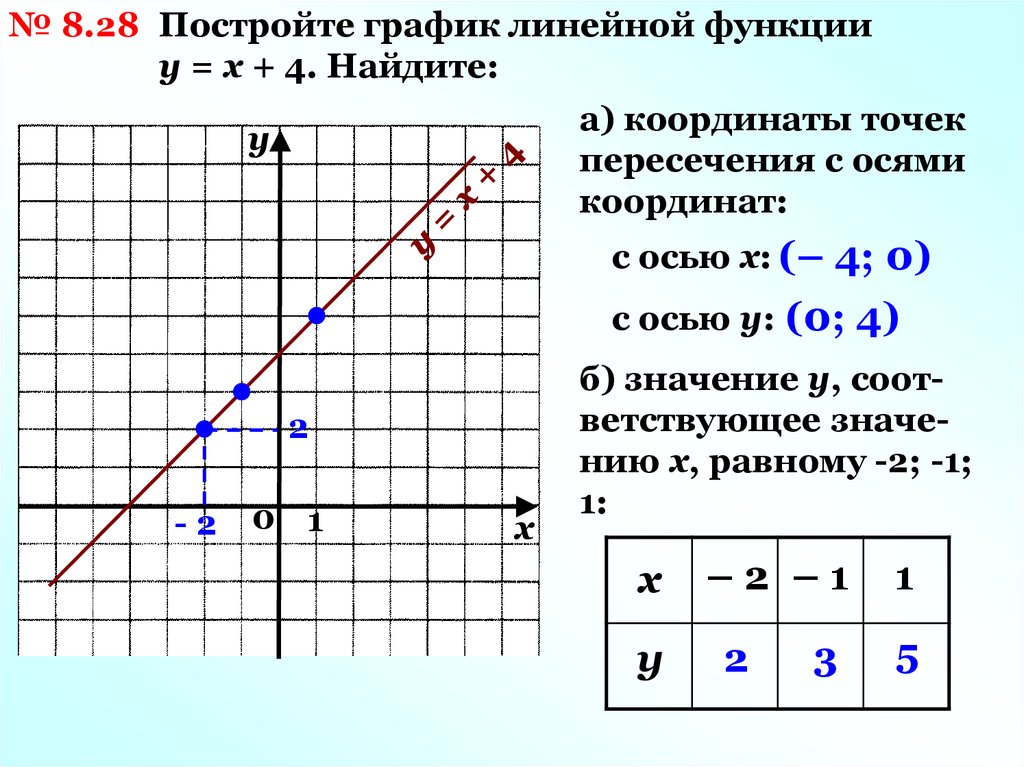
3 +km+l=0.
Следует отметить, что важным пунктом методики является правильный выбор выражения замены, а затем верное выполнение математических преобразований.
Пример решения
Для закрепления знаний необходимо перейти к практическому решению заданий.Одной из простых задач является следующая: найдите координаты точки пересечения графиков линейных функций z=2t+7 и z=t-1. Решается задача по такому алгоритму:
В четвертом пункте нужно подставить координату по оси абсцисс в любое из уравнений для получения второй составляющей, необходимой для точки. Следует отметить, что в этой задаче нет необходимости проводить математические преобразования. Однако существуют и более сложные задания, в которых необходимо решать квадратные уравнения, а также раскрывать скобки.
Таким образом, для определения точки пересечения графиков необходимо уметь находить корни уравнения, а также выполнять алгебраические преобразования.
Предыдущая
АлгебраДеление многочлена на многочлен – правило и примеры
Следующая
АлгебраНеполное квадратное уравнение — виды, примеры и способы решения
Mathscene — Функции 1 — урок 4
Mathscene — Функции 1 — урок 4| 2007 Расмус Эф и Джанн Сак | Функции я | Печать |
Урок 4
Рациональные функции
Рациональный функции имеют следующий вид:
| или |
Где f(x) и g(x) являются полиномами, а
знаменатель, g(x) имеет степень по крайней мере один ( содержит x ).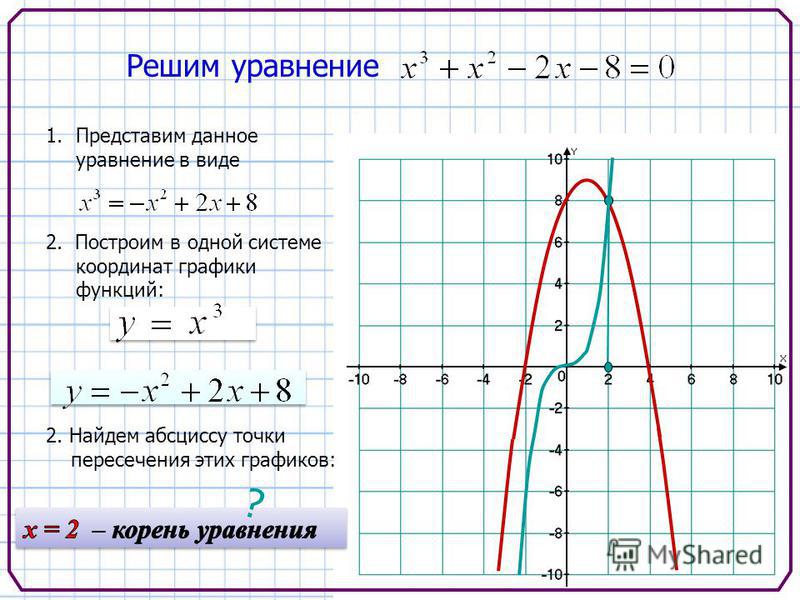
Теперь мы рассмотрим несколько примеров рационального функции и их графики.
Пример 1
Первый взгляд на
Если мы начнем делать стол значений, мы сразу видим, что x не может принимать значение 0, так как это означало бы деление на 0,
По мере того, как х становится все ближе и ближе до значения 0, но остается положительным ( x = 0,1 , x = 0,01 и так далее..)
мы видим, что значение функции ( значение y ) становится больше и больше (x = 0,01 дает нам y = 100).
По мере того, как x становится все ближе и ближе к 0, но отрицательный ( х = -0,1, x = − 0,01 и т. д.).
значение функции принимает все большее и большее отрицательное значение ( x = −0,01 дает нам y = −100).
График функции кажется почти параллельным оси y вблизи того места, где x равно 0
В этом случае Говорят, что функция имеет вертикаль асимптота.
Уравнение асимптота х = 0,
Пример 2
Далее мы рассмотрим функция
Мы видим, что значение функция становится все больше и больше по мере того, как x приближается к 0 справа ( x > 0 ) и слева ( х < 0 )
Снова ось Y
вертикальная асимптота.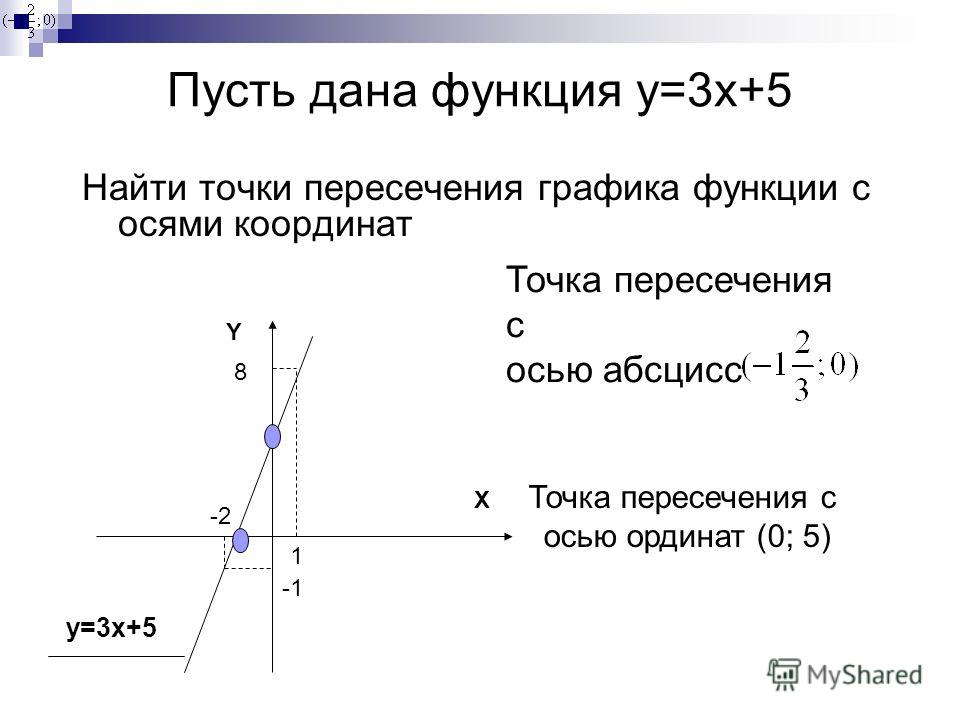
Мы также замечаем, что график не пересекает ни ось x, ни ось y.
Мы можем попытаться вычислить эти точки пересечения и посмотреть, что произойдет.
Находим где график пересекает ось y, вычисляя f(0) как координату x всех точек на ось y равна 0,
Чтобы вычислить это, мы должны разделить на 0, что невозможно.
Найти где график пересекает ось x, мы должны решить уравнение f(x) = 0 или y = 0, потому что все точки на оси x имеют y координата 0.
| = 0 |
1 = 0x 2
Снова получаем уравнение, которое нельзя решить. Отсюда можно сделать вывод, что график не пересекает координатные оси.
Пример 3
Посмотрите на функцию
И вычислить, где график пересекает оси.
Если x = 1 мы будем делить
на 0 поэтому x ≠ 1 . По мере того, как x становится все ближе и ближе к 1, значение y становится равным
больше и больше, положительное, если x>1, и отрицательное, если x<1.
На этот раз график кажется близким к
линия через
x = 1, растет, когда x > 1 и
вниз, когда x < 1.
Найти где график пересекает ось y, мы вычисляем f(0), так как x = 0 на оси y.
Найти где график пересекает ось x, мы решаем уравнение f(x) = 0 или y = 0, так как все точки на оси x имеют y = 0,
1 = 0 (х — 1) = 0
Снова получаем уравнение не имеет решения, поэтому заключаем, что график не пересекает x ось.
Пример 4
Посмотрите на функцию
И найти любые точки пересечение с осями координат.
Мы видим, что x ≠ 2 как тогда у нас будет 0 в знаменателе. Когда x приближается к 2 справа, значение функции становится все больше и больше, и график идет вверх. Когда x приближается к 2 слева функция принимает все большее и большее отрицательное значение, а график идет вниз.
Таким образом, граф имеет
вертикальная асимптота x = 2.
График пересекает ось Y когда х = 0
График пересекает ось Y
когда f(x)
= 0. Нам нужно решить
уравнение:
| Когда умножаем на (х — 2) получаем уравнение не имеющее решения. |
Как уравнение f(x) = 0 решения не имеет, график не пересекает ось абсцисс.
Приведенные выше примеры показывают, что рациональная функция почти всегда имеет вертикальную асимптоту в точке, где знаменатель нуль. (Единственными исключениями являются случаи, когда мы можем разложить дробь на множители и сократить знаменатель). Функцию можно вычислить для всех остальных значений x.
Пример 5
Наконец мы разберемся функция
найти вертикальная асимптота и точки, в которых график пересекает x и y оси.
Сначала рассмотрим, для чего x
значений мы не можем вычислить f(x). Знаменатель равен нулю, когда x
− 1 = 0, т.
е. когда
х = 1,
Вертикальная асимптота где x = 1 и функция действительна для всех значений x, кроме x = 1. Использование Установите обозначение, которое мы можем написать
{х Р| х 1} или R \ {1}
Затем найдите точку пересечения y вычисление f(0).
f(0) = (0 − 0)/(0 − 1) = 0
График пересекает y ось в (0, 0).
Найти где график пересекает ось x, мы должны решить уравнение f(x) = 0,
х 2 − 2x = 0∙(x − 1) = 0
х (х — 2) = 0
х = 0 или 2
График пересекает x ось, где x = 0 и x = 2.
Попробуйте пройти тест 4 по функциям I.
Не забывайте использовать контрольный список, чтобы отслеживать свою работу.
Как найти пересечение с осью Y. То есть точка пересечения параболы с осью OY имеет координаты (0;с)
Задачи на поиск точки пересечения любые фигуры идеологически примитивны.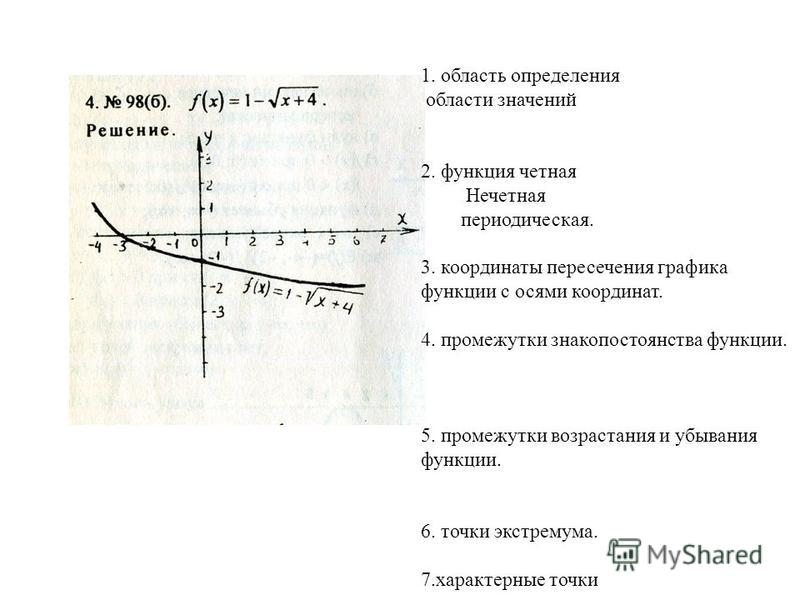
Сложности в них только из-за арифметики, ведь именно в ней делаются различные опечатки и ошибки. 92+(б-к)х+с-ч=0. Теперь осталось решить полученное квадратное уравнение.
5. Все обнаруженные «иксы» еще не являются результатом задачи, так как точка на плоскости характеризуется двумя действительными числами (x, y). Для полного вывода решения необходимо рассчитать соответствующие «игры». Для этого необходимо подставить «иксы» либо в функцию f(x), либо в функцию g(x), чай для точки пересечений правильных: y=f(x)=g(x) . Позже вы найдете все универсальные точки параболы и 92-5х+6=0. Корни этого квадратного уравнения: x1=2, x2=3. Теперь найдите соответствующих «игроков»: y1=g(x1)=1, y2=g(x2)=3. Таким образом, всего найдено точек пересечения : (2,1) и (3,3).
Точка пересечений прямых линий можно приблизительно определить по графику. Однако часто нужны точные координаты этой точки, или не нужно строить график, тогда можно найти точку пересечений зная только уравнения прямых.
Инструкция
1. Пусть две прямые заданы общими уравнениями прямой: A1*x + B1*y + C1 = 0 и A2*x + B2*y + C2 = 0. Точка пересечения принадлежит одной прямой, а другой . Выразим из первого уравнения прямой x, получим: x = -(B1*y + C1)/A1. Подставляем полученное значение во второе уравнение: -A2*(B1*y + C1)/A1 + B2*y + C2 = 0 A1C2)/(A1B2 – A2B1). Подставим полученное значение в уравнение первой прямой: A1*x + B1(A2C1 – A1C2)/(A1B2 – A2B1) + C1 = 0,A1(A1B2 – A2B1)*x + A2B1C1 – A1B1C2 + A1B2C1 – A2B1C1 = 0(A1B2 – A2B1)*x – B1C2 + B2C1 = 0 Тогда x = (B1C2 – B2C1)/(A1B2 – A2B1).
2. В школьном курсе математики прямые часто задаются уравнением с угловым показателем, рассмотрим этот случай. Пусть так заданы две прямые: y1 = k1*x + b1 и y2 = k2*x + b2. Очевидно, в точке пересечений y1 = y2, тогда k1*x + b1 = k2*x + b2. Получаем, что ордината точки пересечений x = (b2 – b1)/(k1 – k2). Подставим x в любое уравнение прямой и получим y = k1(b2 – b1)/(k1 – k2) + b1 = (k1b2 – b1k2)/(k1 – k2).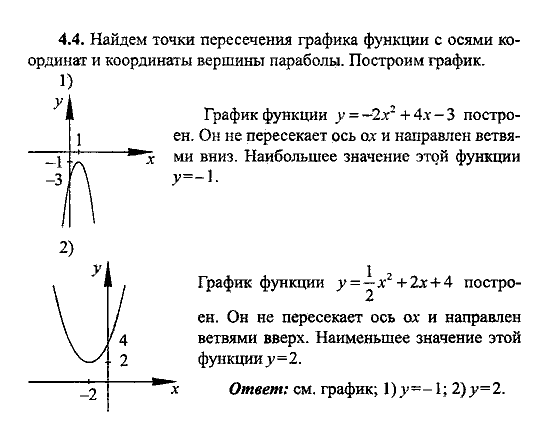
2. По ее виду можно сделать вывод, что она растет как при правильных, так и при отрицательных значениях аргумента x. Точка, в которой x=0, и в то же время y=0, считается точкой минимума функции. 94. В таких случаях x=const, а y резко возрастает. Однако это относится только к четным функциям. Графики парабол часто присутствуют в физических задачах, скажем, полет тела описывает линию, похожую на параболу. Также вид параболы имеет продольный разрез отражателя фары, лампы. В отличие от синусоиды, этот график непериодический и прогрессивный.
Задание на построение точки пересечения прямой с плоскостью является классической в курсе инженерной графики и выполняется с использованием методов начертательной геометрии и их графического решения на чертеже.
Инструкция
1. Рассмотрим определение точки пересечения прямой с частной локационной плоскостью (рис. 1). Прямая l пересекает плоскость фронтальной проекции?.
Точка их пересечения принадлежит К и прямой и плоскости, поэтому общая проекция К2 лежит на ?2 и l2. То есть K2= l2??2, а его горизонтальная проекция K1 определяется на l1 с помощью проекционной соединительной линии. Таким образом, искомая точка пересечений K(K2K1) строится свободно без использования вспомогательных плоскостей. Точки определяются аналогично пересечений прямых со всякими частными плоскостями.
2. Рассмотрим определение точки пересечения прямой с общей плоскостью. На рисунке 2 дана произвольно расположенная в пространстве плоскость? и прямая л. Для определения точки пересечения прямой с плоскостью общего расположения используется метод вспомогательных секущих плоскостей в следующем порядке:
3. Через прямую l? проведена вспомогательная секущая плоскость. Для облегчения строительства это будет плоскость проектирования.
5. Точка К отмечена пересечениями прямой л и построенной линией пересечений МН.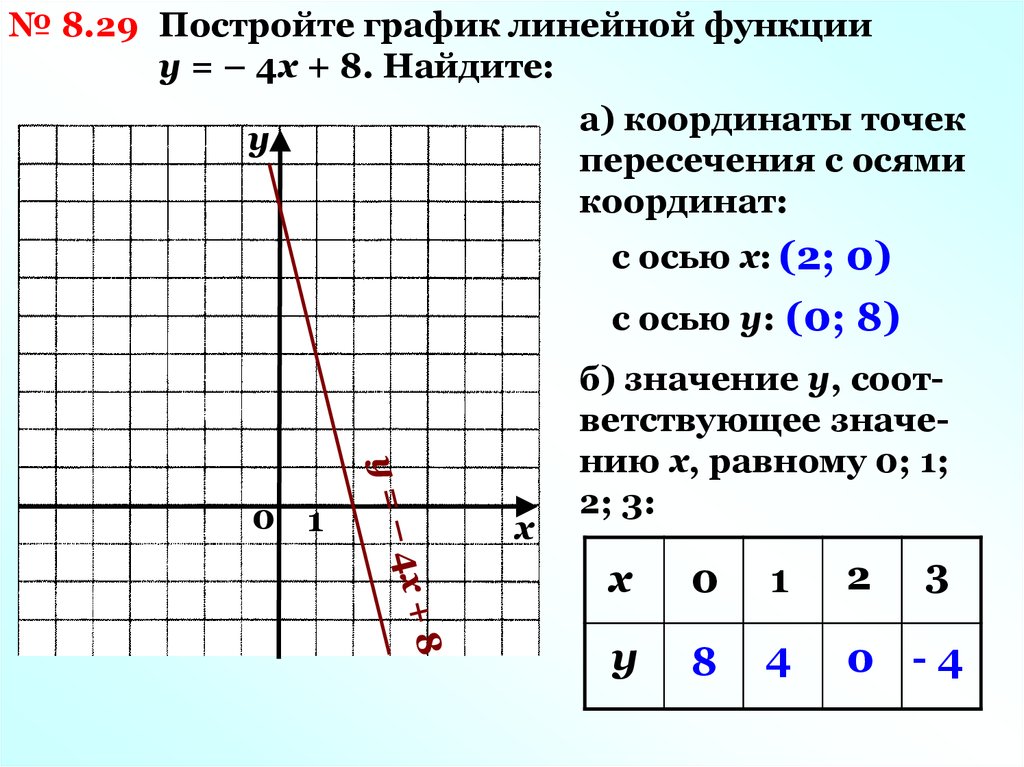
Она искомая точка пересечений прямых и плоскостей.
6. Применим это правило для решения конкретной задачи на сложном чертеже. Пример. Определите пункт пересечений прямых л с плоскостью общего расположения, заданной треугольником АВС (рис. 3).
7. Через линию l проведена вспомогательная секущая плоскость, перпендикулярная проекции плоскости?2. Его проекция ?2 совпадает с проекцией прямой l2.
8. Строится линия MN. Самолет? пересекает AB в точке M. Его общая проекция M2= ?2?A2B2 и горизонталь M1 на A1B1 отмечены по линии соединения проекций. Самолет? пересекает сторону AC в точке N. Его общая проекция N2=?2?A2C2, горизонтальная проекция N1 на A1C1. Линия MN принадлежит обеим плоскостям одновременно и, следовательно, является их линией перекрестков .
9. Точка К1 определяется пересечениями л1 и М1Н1, после чего строится точка К2 с опорой на линию связи. Получается, что К1 и К2 являются проекциями искомой точки пересечений К прямых л и плоскостей? АВС:К(К1К2)=1(1112)? ? АВС(А1В1С1, А2В2С2).
По конкурирующим точкам М,1 и 2,3 определяется видимость по прямой л относительно данной плоскости? азбука.
Похожие видео
Внимание!
Используйте вспомогательную плоскость при решении задачи.
Полезный совет
Выполнить расчеты по подробным чертежам, соответствующим требованиям задачи. Это поможет вам быстро сориентироваться в решении.
Две прямые, если они не параллельны и не совпадают, строго пересекаются в одной точке. Нахождение координат этого места означает вычисление точек пересечений прямой. Две пересекающиеся прямые всегда лежат в одной плоскости, поэтому достаточно увидеть их в декартовой плоскости. Давайте рассмотрим пример того, как найти универсальную точку прямых.
Инструкция
1. Возьмем уравнения 2-х прямых, помня, что уравнение прямой в декартовой системе координат, уравнение прямой имеет вид ах + ву + с = 0, а а, Ь, с — обыкновенные числа, а х и у — координаты точек.
Например, найти точек пересечений прямых 4x+3y-6=0 и 2x+y-4=0. Для этого найдите решение системы этих двух уравнений.
2. Чтобы решить систему уравнений, измените любое из уравнений так, чтобы перед y стоял такой же показатель степени. Поскольку в одном уравнении показатель степени перед y равен 1, то примитивно умножьте это уравнение на число 3 (показатель степени перед y в другом уравнении). Для этого умножаем каждый элемент уравнения на 3: (2х*3)+(у*3)-(4*3)=(0*3) и получаем обыкновенное уравнение 6х+3у-12=0. Если бы показатели степени перед y были отличны от единицы в обоих уравнениях, то оба равенства пришлось бы перемножать.
3. Вычтите из одного уравнения другое. Для этого вычтите из левой части одной левую часть другой и проделайте то же самое с правой. Получите такое выражение: (4х+3у-6)-(6х+3у-12)=0-0. Поскольку перед скобкой стоит знак «-», замените все знаки в скобках на противоположные. Получите такое выражение: 4x + 3y-6 — 6x-3y + 12 = 0.
Упростите выражение, и вы увидите, что переменная y исчезла. Новое уравнение выглядит так: -2x+6=0. Перенесите число 6 в другую часть уравнения, и из полученного равенства -2х=-6 выразите х: х=(-6)/(-2). Итак, вы получили х=3.
4. Подставим значение x=3 в любое уравнение, скажем, во второе и получим следующее выражение: (2 * 3) + y-4 = 0. Упростим и выразим y: y=4-6=-2.
5. Полученные значения x и y записать как координаты точек (3;-2). Это будет решение проблемы. Проверьте значение, полученное путем подстановки в оба уравнения.
6. Если линии заданы не уравнениями, а заданы примитивно на плоскости, найти координаты точек пересечений графически. Для этого продлите линии так, чтобы они пересекались, затем опустите перпендикуляры на оси x и y. Пересечение перпендикуляров с осями х и у будет координатами этих точек , посмотрите на рисунок и вы увидите, что координаты точек пересечения х = 3 и у = -2, то есть , точка (3;-2) — решение задачи.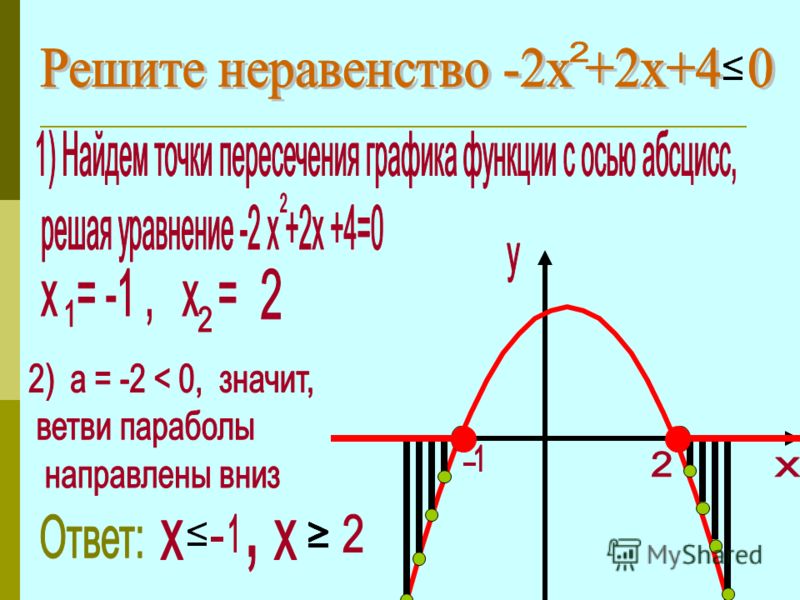
Похожие видео
Парабола — это каноническое уравнение плоской кривой второго порядка, которое в декартовой системе координат имеет вид y?=2px. Где p — фокальный параметр параболы, равный расстоянию от фиксированной точки F, называемой фокусом, до фиксированной линии D в той же плоскости, называемой директрисой. Вершина такой параболы проходит через предисловие координат, а сама кривая симметрична относительно оси абсцисс Ох. В школьном курсе алгебры принято рассматривать параболу, ось симметрии которой совпадает с осью ординат Оу: х?=2ру. А уравнение записывается несколько наоборот: y=ax?+bx+c, a=1/(2p). Начертить параболу можно несколькими методами, которые условно можно назвать алгебраическими и геометрическими.
Инструкция
1. Алгебраическое построение параболы. Узнайте координаты вершины параболы. Рассчитаем координату по оси Ох по формуле: x0=-b/(2a), а по оси Oy: y0=-(b?-4ac)/4a или подставим полученное значение x0 в уравнение параболы y0 =ax0?+bx0+c и вычислить значение.
2. На координатной плоскости построить ось симметрии параболы. Его формула совпадает с формулой для координаты x0 вершины параболы: x=-b/(2a). Определите, куда направлены ветви параболы. Если а>0, то оси направлены вверх, если а
3. Возьмем произвольно 2-3 значения параметра x так, чтобы: x0
4. Расположите точки 1′, 2′ и 3′ так, чтобы они были симметричны точкам 1, 2, 3 относительно оси симметрии.
5. Соедините точки 1′, 2′, 3′, 0, 1, 2, 3 плавной наклонной линией. Продолжайте линию вверх или вниз, в зависимости от направления параболы. Парабола построена.
6. Геометрическое построение параболы. Этот метод основан на определении параболы как совокупности точек, равноудаленных как от фокуса F, так и от направляющей D. Поэтому сначала найдем фокальный параметр данной параболы p=1/(2a).
7. Построить ось симметрии параболы, как описано в шаге 2. На ней поставить точку F с координатой по оси Оу равной y=p/2 и точку D с координатой y=-p/ 2.
8. С помощью угольника постройте прямую, проходящую через точку D, перпендикулярную оси симметрии параболы. Эта линия является направляющей параболы.
9. Возьмите нить по длине, равной одной из сторон квадрата. Закрепите один конец нити пуговицей в верхней части квадрата, к которому примыкает эта ножка, а 2-й конец в фокусе параболы в точке F. Положите линейку так, чтобы ее верхний край совпадал с направляющей D. Поместите квадрат на линейке, свободный от пуговицы с ножкой.
10. Установите карандаш так, чтобы он своим кончиком прижимал нить к ножке квадрата. Переместите квадрат по линейке. Карандаш нарисует нужную вам параболу.
Похожие видео
Внимание!
Не изображайте вершину параболы в виде угла. Его ветви сходятся друг с другом, плавно закругляясь.
Полезный совет
При построении параболы геометрическим методом следите за тем, чтобы нить всегда была натянута.
Прежде чем приступить к поиску поведения функции, необходимо определить область метаморфозы рассматриваемых величин.
Предположим, что переменные относятся к множеству действительных чисел.
Инструкция
1. Функция — это переменная, зависящая от значения аргумента. Аргумент является независимой переменной. Пределы изменения аргумента называются областью возможных значений (ROV). Поведение функции рассматривается в рамках ОДЗ, поскольку в этих пределах связь между двумя переменными не является хаотичной, а подчиняется определенным правилам и может быть записана в виде математического выражения.
2. Рассмотрим произвольную функциональную связность F=?(x), где? является математическим выражением. Функция может иметь точки пересечения с осями координат или с другими функциями.
3. В точках пересечения функции с осью x функция становится равной нулю: F(x)=0. Решите это уравнение. Вы получите координаты точек пересечения заданной функции с осью OX. Таких точек будет столько, сколько корней уравнения на данном участке метаморфозы рассуждения.
4. В точках пересечения функции с осью Y значение аргумента равно нулю. Следовательно, задача превращается в нахождение значения функции при x=0. Точек пересечения функции с осью OY будет столько, сколько значений данной функции с нулевым аргументом.
5. Чтобы найти точки пересечения данной функции с другой функцией, нужно решить систему уравнений: F=?(x)W=?(x). , точки пересечения, с которыми необходимо обнаружить данную функцию. Судя по всему, в точках пересечения обе функции принимают одинаковые значения при одинаковых значениях аргументов. Универсальных точек для 2-х функций будет столько, сколько решений системы уравнений в данной области изменения аргумента.
Видео по теме
В точках пересечения функции имеют одинаковые значения при одинаковом значении аргумента. Найти точки пересечения функций — значит определить координаты точек, универсальных для пересекающихся функций.
Инструкция
1.
В общем случае задача нахождения точек пересечения функций одного аргумента Y=F(x) и Y?=F?(x) на плоскости XOY сводится к решению уравнения Y= Y?, из того, что при универсальная точка функции имеют равные значения. Значения x, удовлетворяющие равенству F(x)=F?(x), (если они существуют) являются абсциссами точек пересечения заданных функций.
2. Если функции заданы простым математическим выражением и зависят от одного аргумента x, то задачу нахождения точек пересечения можно решить графически. Графики функций графика. Определить точки пересечения с осями координат (x=0, y=0). Задайте еще несколько значений аргументов, найдите соответствующие значения функций, добавьте полученные точки на графики. Чем больше точек будет использовано для построения, тем точнее будет график.
3. Если графики функций пересекаются, определить координаты точек пересечения по чертежу. Для проверки подставьте эти координаты в формулы, определяющие функции. Если математические выражения оказываются объективными, то точки пересечения находятся положительно.
Если графики функций не пересекаются, попробуйте масштабирование. Сделайте больший шаг между точками построения, чтобы определить, в какой части числовой плоскости сходятся линии графиков. После этого на выявленном участке пересечения построить более подробный график с мелким шагом для точного определения координат точек пересечения.
4. Если необходимо найти точки пересечения функций не на плоскости, а в трехмерном пространстве, то можно увидеть функции 2-х переменных: Z=F(x,y) и Z?=F?( х, у). Для определения координат точек пересечения функций необходимо решить систему уравнений с двумя неизвестными x и y при Z=Z?.
Видео по теме
Итак, основные параметры графика квадратичной функции представлены на рисунке:
Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, как задана квадратичная функция, можно выбрать наиболее удобную.
1 . Функция задается формулой .
Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции
1 .
Направление ветвей параболы.
Так как ветви параболы направлены вверх.
2 . Найдите дискриминант квадратного трехчлена
Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью OX.
Чтобы найти их координаты, решаем уравнение:
,
3 . Координаты вершин параболы:
4 . Точка пересечения параболы с осью OY: (0;-5), и она симметрична относительно оси симметрии параболы.
Поместим эти точки на координатную плоскость и соединим их плавной кривой:
Этот способ можно несколько упростить.
1. Найдите координаты вершины параболы.
2. Найдите координаты точек справа и слева от вершины.
Воспользуемся результатами построения графика функции
Вершины параболы
Ближайшие к вершине точки, расположенные левее вершины, имеют абсциссы соответственно -1; -2; -3
Ближайшие к вершине точки, расположенные справа, имеют абсциссы соответственно 0; 1; 2
Подставим значения x в уравнение функции, найдем ординаты этих точек и занесем в таблицу:
Положим эти точки на координатную плоскость и соединим их плавной линией:
2 .
Уравнение квадратичной функции имеет вид — в этом уравнении — координаты вершины параболы
или в уравнении квадратичной функции , а второй коэффициент является четным числом.
Например, построим график функции .
Вспомним графики функций линейных преобразований. Для построения функции необходимо
§ сначала построить функцию ,
§ затем умножить все точки графика на 2,
§ затем сдвинуть его по оси ОХ на 1 единицу вправо,
§ а затем по ось OY на 4 шт. больше:
Теперь давайте посмотрим на график функции. В уравнении этой функции второй коэффициент является четным числом.
3.2: Пересечения — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 63370
Во многих задачах интегрального исчисления вам придется находить площадь, заключенную между несколькими функциями или между ними.
В рамках нахождения площади вам нужно будет определить, где функции пересекаются друг с другом, то есть пары координат \((x,y)\), где пересекаются кривые. точки пересечения двух функций, \(f(x)\) и \(g(x)\), представляют собой \((x,y)\) пары координат, для которых входные данные, \(x\ ), приводит к одинаковому выходному значению обеих функций. В этом разделе мы рассмотрим три различных метода нахождения точек пересечения двух графиков. Первые два метода, которые мы обсудим, в значительной степени зависят от навыков, которые вы приобрели в предыдущем разделе, где узнали, как вычислять переменные.
Обратите внимание, что, хотя мы в основном использовали обозначение функции, такое как \(f(x)\), здесь мы часто будем указывать вывод функции как \(y\). Одна из причин, по которой мы используем \(y\) здесь, заключается в том, что некоторые из наших функций будут определены неявно . Когда функция определена неявно, это означает, что вывод функции не изолирован; мы видели это раньше с точечной формой наклона линии.
Когда выход изолирован, мы говорим, что наша функция определена явно , как в форме перехвата наклона.
3.2.1 Замена
Замена чаще всего используется, когда одна или обе функции определены неявно или когда обе функции имеют общий термин. С помощью этого метода мы решим одно уравнение для одной из переменных, а затем подставим решение во второе уравнение и решим для оставшейся переменной. В этом курсе нас интересуют только решения действительных чисел. Здесь это вопрос личных предпочтений при выборе, с какой функцией работать изначально и для какой переменной решать. Однако мы рекомендуем начать с уравнения, которое является «более простым»; если одно уравнение линейное, а другое квадратичное, обычно проще начать с линейной функции. Давайте посмотрим на пример. 92=4\) квадратично как по \(x\), так и по \(y\), но второе уравнение \(y-1=2(x-1)\) линейно по обоим \(x\) и в \(у\). Поэтому мы начнем нашу работу со второго уравнения.
Кроме того, во втором уравнении \(y\) уже почти изолировано, поэтому мы сначала изолируем \(y\) в этом уравнении.
\[\begin{align}\begin{align}\begin{split} y-1 & = 2(x-1) \\ y & = 2(x-1)+1 \\ & = 2x-2 +1 \\ & = 2x-1 \end{split}\end{align}\end{align}\]
92-4(8)(-3)}}{2(8)} \\[6pt] & = \frac{4 \pm \sqrt{16+96}}{16} \\[6pt] & = \ frac{4\pm \sqrt{112}}{16} \\[6pt] & = \frac{4 \pm 4 \sqrt{7}}{16} \\[6pt] & = \frac{1 + \ sqrt{7}}{4}, \frac{1 — \sqrt{7}}{4} \end{split}\end{aligned}\end{align}\]Это дает нам только \(x \) координаты; нам также нужны координаты \(y\). Чтобы получить соответствующие координаты \(y\), мы будем использовать линейное уравнение, где мы уже решили для \(y\) через \(x\). Мы могли бы использовать более раннюю форму этого уравнения или даже квадратное уравнение, но любое из них потребовало бы дополнительной работы. Первая координата \(y\):
\[\begin{align}\begin{align} y&=2x-1 \\ &=2\left(\frac{1+\sqrt{7}}{4}\right)-1 \\ &= \frac{1+\sqrt{7}}{2}-\frac{2}{2} \\ &=\frac{-1+\sqrt{7}}{2}\end{выровнено}\end{ align}\]
Вторая координата \(y\): \[\begin{align}\begin{aligned}\begin{split} y & = 2x -1 \\ & = 2\Bigg(\frac{ 1 — \sqrt{7}}{4}\Bigg) -1 \\[6pt] & =\frac{1 — \sqrt{7}}{2} — \frac{2}{2} \\[6pt ] & = \frac{-1 — \sqrt{7}}{2} \end{split}\end{aligned}\end{align}\]
Теперь у нас есть обе точки пересечения:
\[\left(\frac{1+\sqrt{7}}{4},\frac{-1+\sqrt{7}}{2}\right)\text{ и }\left(\frac {1-\sqrt{7}}{4},\frac{-1-\sqrt{7}}{2}\right)\]
Иногда мы можем проявить творческий подход к использованию замены.
В зависимости от уравнений, с которыми вы работаете, иногда может быть быстрее решить , а не для переменной полностью, а скорее для члена, который появляется в обоих уравнениях. Давайте посмотрим на пример.
Пример \(\PageIndex{2}\): точки пересечения: замена 92\). Здесь это дает нам воображаемый ответ для \(y\), так что мы не получаем дополнительную точку пересечения. Единственной точкой пересечения этих уравнений является
\[(4,0)\]
3.2.2 Приравнивание функций
Следующий метод, который мы обсудим, хорошо работает, когда обе функции явные или заданы в виде функций. Для этого метода мы сначала решим каждое уравнение для одной и той же переменной, установим два равными для каждого и решим.
Пример \(\PageIndex{3}\): Точки пересечения: равенство 92 -x &= 0 \\ x(x-1)&=0 \\ x&= 0,1 \end{split}\end{aligned}\end{align}\]
Теперь осталось найти координаты \(у\). Для этого мы можем использовать \(f(x)\) или \(g(x)\); \(g(x)\) проще, поэтому мы будем использовать его.
Получаем, что \(g(0) = 1\) и \(g(1)=2\). Таким образом, у нас есть две точки пересечения:
\[(0,1)\text{ и }(1,2)\]
3.2.3 Исключение
Третий метод, который мы обсудим, немного отличается от первого. другие методы, которые мы видели. Этот метод также требует сильных навыков алгебры. Основное преимущество этого метода не будет очевидным до следующего раздела этой книги, потому что он наиболее полезен, когда у нас есть система из двух или более линейных уравнений. Здесь мы покажем, как использовать его только с двумя переменными, но идея расширяется (это означает, что этот метод легко адаптировать к другим, более сложным ситуациям). Для исключения мы возьмем каждое уравнение, умножим все уравнение на константу и сложим уравнения вместе таким образом, чтобы исключить одну переменную.
Пример \(\PageIndex{4}\): Точки пересечения: Исключение
Найти все точки пересечения \(2x+3y=2\) и \(-x+y=4\).
Решение
Сначала попробуем исключить \(x\) из обоих уравнений.
Первое уравнение имеет \(2x\), а второе имеет \(-x\). Если мы умножим второе уравнение на \(2\) и добавим его к первому, члены \(x\) сократятся:
\[\begin{align}\begin{align}2x+3y&=2 \ \ +2(-x+y&=4)\end{выровнено}\end{выровнено}\]
или:
\[\begin{align}\begin{aligned}2x+3y&=2 \\ +(-2x+2y&=8) \\ \hline 5y&=10\end{align}\end{align }\]
Обратите внимание, что мы выровняли наши переменные и обработали это как большую задачу сложения. Упорядочивание переменных упрощает нашу работу.
Теперь мы можем взять результат и легко найти \(y\), получив \(y=2\). Теперь мы можем использовать \(y\), чтобы найти \(x\). Подойдет любое уравнение, но мы будем использовать второе: \(-x+(2) = 4\) или \(x=-2\). Это дает использование одной точки пересечения на
\[(-2,2)\]
Исключение — особенно гибкий метод. Чтобы проиллюстрировать это, мы снова решим задачу, но на этот раз сначала исключим \(y\).
Пример \(\PageIndex{5}\): Точки пересечения: Исключение
Найти все точки пересечения \(2x+3y=2\) и \(-x+y=4\).
Решение
Первое уравнение имеет \(3y\), а второе имеет \(y\). Умножим первое уравнение на \(-\frac{1}{3}\) и добавим его ко второму уравнению:
\[\begin{align}\begin{aligned}-\frac{1}{3}(2x+3y&=2) \\ +\quad (-x+y&=4) \\ \hline -\frac {5}{3}x&=\frac{10}{3}\end{aligned}\end{align}\]
Решение \(-\frac{5}{3}x = \frac{10}{ 3}\) дает нам \(x=-2\), а подстановка в любое уравнение дает нам \(y=2\). Мы получаем ту же точку пересечения:
\[(-2,2)\]
Кроме того, мы могли бы умножить второе уравнение, \(-x+y=4\), на \(3\) и вычесть из первого, чтобы исключить \(y\) первым. При исключении лучше немного спланировать, чтобы выяснить, какую переменную проще всего исключить в первую очередь и какие комбинации сохранят числа простыми.
3.2.4 Графики
Теперь мы кратко обсудим распространенный метод, используемый студентами: построение графиков. Хотя построение графика — отличный способ определить количество существующих точек пересечения и приблизительные координаты, он не даст вам точного набора координат, если только вы не используете калькулятор или компьютер.