Построение геометрических фигур в текстовом редакторе / Открытый урок
Цели и задачи:
1. Научить строить геометрические фигуры в текстовом редакторе Word.
2. Развивать аккуратность в строениях и воспитывать некоторые правила поведения.
Требования к знаниям и умениям:
Учащиеся должны знать:
— что такое прикладные программы, текстовый редактор, назначение, возможности текстового редактора Word.
— понятие редактирования и форматирования текста.
— геометрические фигуры на плоскости.
— фигуры в пространстве.
Учащиеся должны уметь:
— вычислять объёмы фигур на плоскости;
— вычислять объёмы фигур в пространстве.
Программно-дидактическое обеспечение: ПК,презентация к уроку в программе Power Point.
Ход урока
Слайд 1
Слайд 2
Цели и задачи урока
Слайд 3
Геометрические фигуры на плоскости
Слайд 4
Рисование фигур средствами компьютерной графики
Понятие растровой и векторной графики доклад ученицы 11 А класса Капустник Елены
Слайд 5
Построение геометрических фигур в текстовом редакторе Word
Для вставки новой фигуры, или графического объекта,
в документ необходимо:
1.
Выбрать на панели Рисование фигуру (например, овал, прямоугольник).
2. Щёлкнуть на одной из выбранных фигур.
3. Выбрать из базовых форм, нажав Автофигуры.
После щелчка на выбранной фигуре курсор принимает форму перекрестья +
Слайд 6
4. Появляется зона для создания рисунка.
Устанавливаем курсор в нужном месте в документе и, нажав Левую кнопку мыши рисуем фигуру, определив тем самым её размеры, местоположение и пропорции.
5. Для того, чтобы закрасить фигуру
необходимо её выбрать.
6. На панели Рисование выбираем значок Цвет заливки
Слайд 7
Вопрос к ученикам: Какие фигуры в пространстве вы знаете?
Слайд 8
Пирамиды вокруг нас
Слайд 9
Рисование объёмных фигур
Для того, чтобы придать фигуре объём, необходимо
1.
2. На панели Рисование
выбрать значок меню Объёма
3. Фигура обрела выбранный объём
Слайд 10
Для того, чтобы в фигуру вписать текст необходимо:
1. Выбрать фигуру
2. Щёлкнуть Правой кнопкой мыши внутри фигуры, чтобы открыть контекстное меню и выбрать строку Добавить текст
3. Внутри фигуры появляется курсор, добавляем текст
Учащиеся решают задачи:
- На вычисление объёма воздуха в автобусе с пассажирами.
- Вычисление объёма жидкости в бутылке.
Слайд 11
Показ драгоценных камней с гранями, пример из песни «Лучшие друзья девушек – это бриллианты».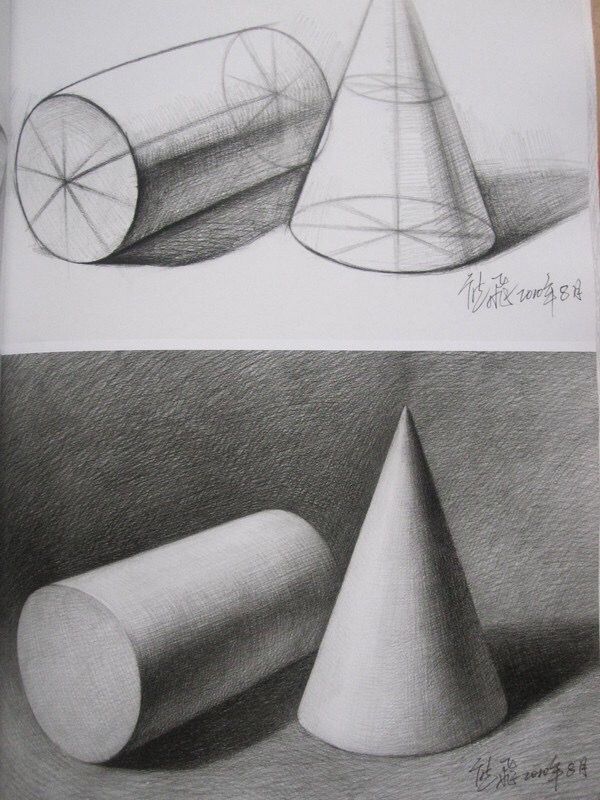
Слайд 12
Выполнение практической работы на построение фигур в текстовом редакторе Word. (15 мин).
Закрепление изученного
Ответы на вопросы, поставленные в начале урока.
Слайд 13
Слайд 14
Проверь себя!
Тест по пройденной теме.
1. Текстовый редактор Word — это
2. Чтобы нарисовать геометрическую фигуру необходимо:
3. Чтобы закрасить геометрический объект необходимо:
4. Чтобы придать объём геометрической фигуре необходимо:
Итоги урока
Оцениваем работу класса и называем учащихся, отличившихся на уроке.
Домашнее задание
Придумать рисунок, используя геометрические фигуры текстового редактора.
Вычислить объём построенных фигур.
Скачать публикацию
Линейное и тоновое изображение трехмерных геометрических тел (Методы построения геометрических фигур в пространстве) [Реферат №593]
Содержание:
Введение
Актуальность.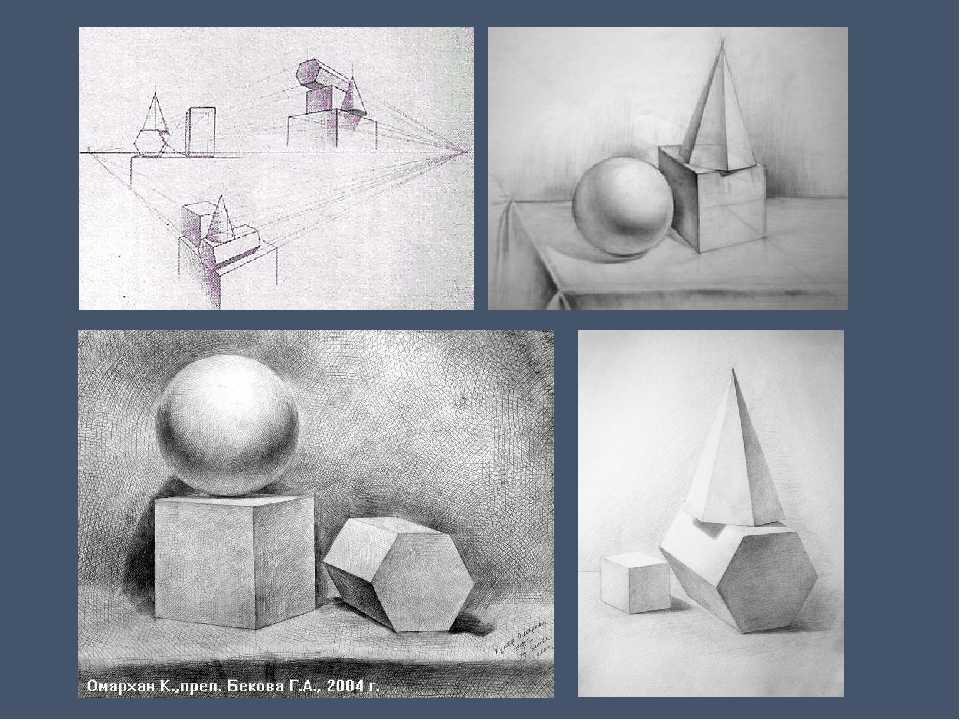
Рисунок – это база изобразительных искусств, поэтому он глубоко изучается художниками, скульпторами и архитекторами в дисциплине «академический рисунок». Рисунки и наброски создаются с натуры при поиске композиционных решений графических, живописных и скульптурных произведений, а так же при разметке живописной картины.
Цель работы – Обосновать линейное и тоновое изображение трехмерных геометрических тел.
Задачей является изучение основных правил и норм построения геометрических тел, а так же научится выполнять чертежи, эскизы, наглядные изображения.
Тела вращения характеризуются осью, радиусом основания и точками образующей поверхности тел.
Рассмотрев и изучив окружности и их изменения, можно перейти к способам и приемам изображения окружностей на плоскости.
Рисунок образует в европейском искусстве отдельный вид графики. Под категорию станкового рисунка подпадают исторически известные рисунки значительной эстетической ценности. С живописью рисунок объединяет его уникальность, тогда как такие произведения печатной графики, как гравюры, могут распространяться во множестве равноценных экземпляров.
Выделяют элементы рисунка создающие иллюзию объема изображения. Это свет, тень (собственная и отбрасываемая, полутени, рефлекс, блик).
С помощью графики рисунка можно передать не только, но и «передать» цвет, — посредством черно-белого оттенка.
Исполняются рисунки в подавляющем большинстве случаев на бумаге. В станковом рисунке используется весь спектр графических материалов: «мягкие материалы» (такие, как уголь, соус, сангина, разнообразные мелки, техника сухая кисть), краски, наносимые кистью и пером (тушь, чернила, бистр), карандаши, капиллярные и прочие пишущие узлы. В учебном рисунке в настоящее время наиболее употребимы графитный карандаш и уголь.
1.2 Методы построения геометрических фигур в пространствепостроение геометрического рисунка в пространстве
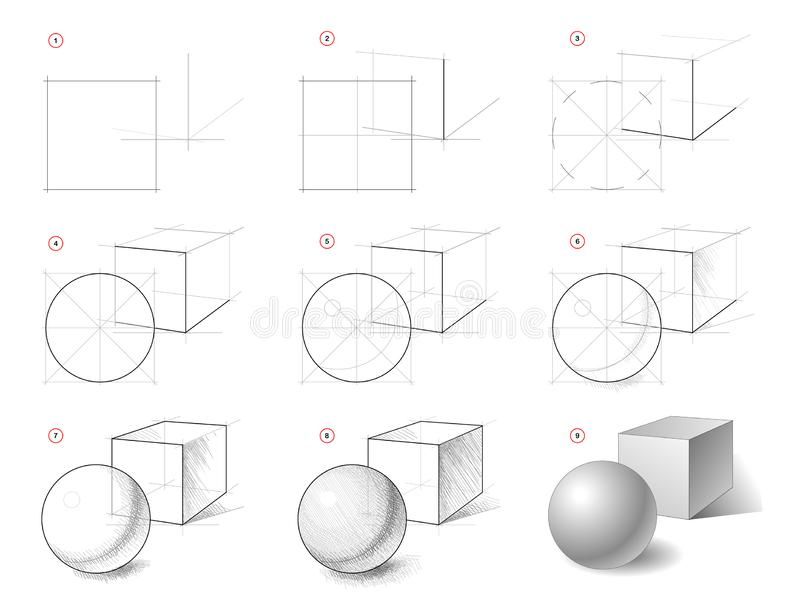
Куб
Куб является самой важной геометрической фигурой. Лучшей модели для развития объемно-пространственного мышления не существует. Рисунок куба формирует видение перспективы, является источником знаний и умений рисования.
В основе будущих проектных решений дизайнера всегда лежит куб или комбинация из кубов.
Главное в рисунке куба — трехмерность, построить его основание с учетом перспективного сокращения и ракурса. А далее просто построить все грани, по пропорциям и перспективных параллельностей линий, сходящихся в точке на линии горизонта. Конечно, для того, чтобы все это выполнить, рисунок куба должен выглядеть прозрачным каркасом. Итак, рисуем каркас куба.
К сожалению, для некоторых начинающих куб является неким неинтересным, простым и бесполезным для рисования предметом. Позже часть таких художников осознает объем собственной трагедии и будет затрачивать колоссальное количество энергии, чтобы заново научиться видеть законы перспективы.
Шестигранная призма
Шестигранная призма — это геометрическое тело. Выполнить конструктивный рисунок в пространстве очень сложно, если не увидеть в его конструктивной основе четырехгранную призму, так называемый «кирпич» , конструкция которой схожа с кубом и которую вы уже умеете рисовать.
Обращаем внимание на то, что мы уже стараемся понять его конструкцию, как сумму более простых примитивов, а именно как четырехгранная призма и две трехгранных призмы. Если «не увидеть» правильное построение рисунка, то построить чертеж будет практически невозможно без знаний и представлений о геометрическом теле.
Для начала нужно выполнить каркасный рисунок «кирпича» в пространстве, соблюдая пропорции, отношения высоты, ширины и глубины. На торцевых поверхностях нужно провести диагонали. В месте пересечения диагоналей мы получим две точки, которые будут находиться в центре торцевых поверхностей и через которые мы сможем построить перпендикулярное сечение. Оно будет проходить через фигуру четырехгранной призмы.
Далее, мы проводим отрезки из вершин четырехгранной призмы, практически повторяющие направление диагоналей, до пересечения с секущей плоскостью и получим еще четыре вершины шестигранной призмы. После всех проделанных действий, мы соединяем вершины между собою при помощи линий и получаем конструктивный (или, как его еще называют, каркасный) рисунок шестигранной призмы.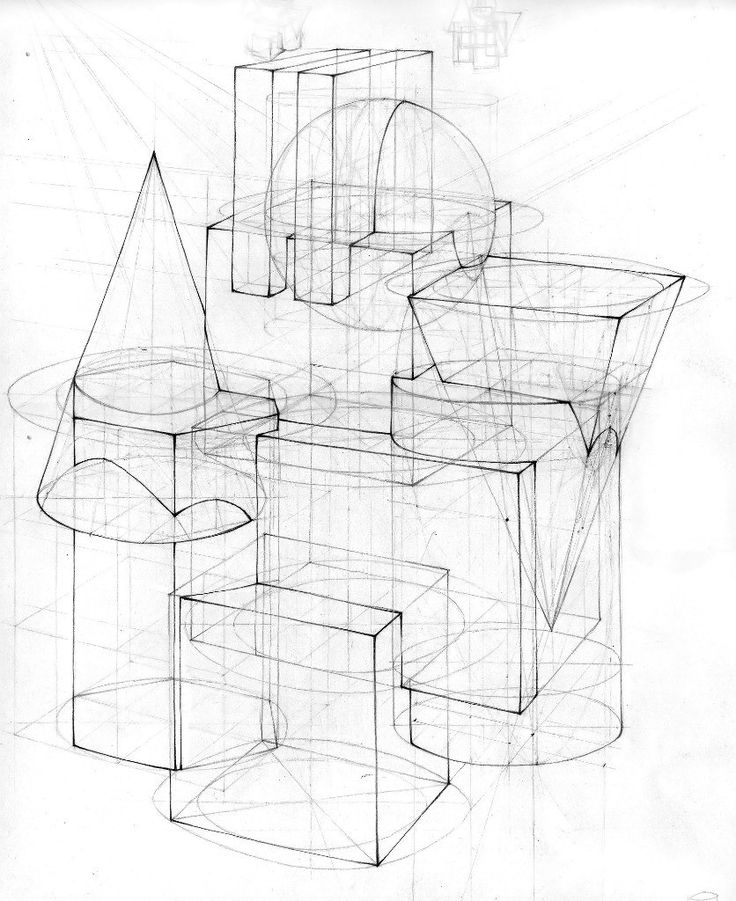
Если рисунок окажется не совсем верным, то стоит искать причину в пропорциональных отношениях сторон у четырехгранной призмы.
Шар
Шар – это объемная фигура, геометрический примитив. Он трехмерен, имеет все стороны трехмерного пространства, с легкостью вписывается в куб. Вершины шара, вписанного в куб, находятся в центре поверхностей сторон куба, иными словами, точка касания стороны шара к стороне куба является центром этой стороны куба.
Самый примитивный способ конструктивного построения шара выполняется следующим образом: проводим две осевые линии, одну вертикальную и одну горизонтальную. От центра пересечения осевых линий мы откладываем одинаковые отрезки на осевых линиях и строим окружность.
Получится двухмерная поверхность в виде круга, но она, пока что, не является шаром, потому что у нее отсутствует третье измерение, иными словами, объем. Чтобы создать объем, надо горизонтальную осевую линию раскрыть до состояния квадратной плоскости в перспективе.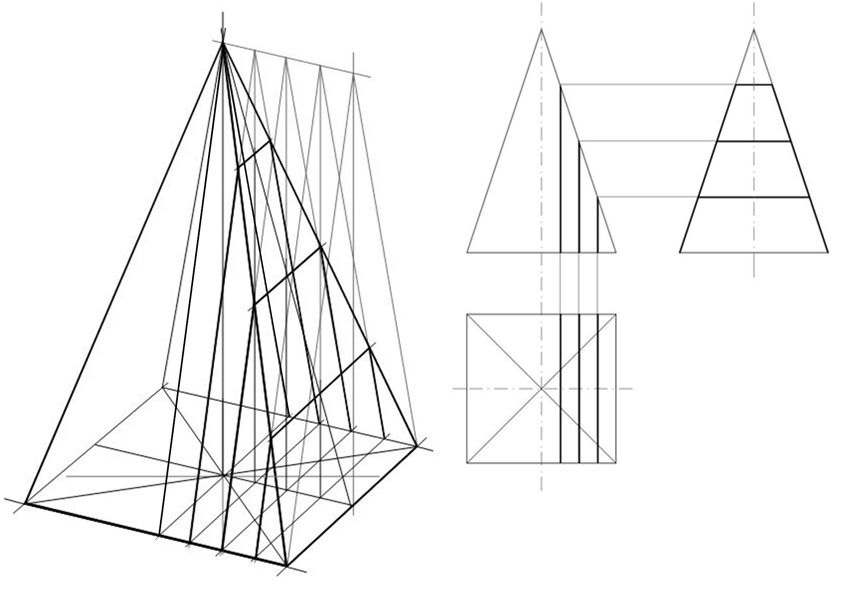
К примеру, оси х, у и z находятся в объеме, то есть, в пространстве. На каждой из оси мы откладываем одинаковые расстояния и помечаем их точками. Далее, мы соединяем эти точки и воссоздаем трехмерную фигуру куба. От фигуры куба мы создаем шар, так как выше сказано, что сторона шара – это середина одной из стороны куба.
Цилиндр
Цилиндр еще один геометрический примитив. Форма цилиндра образуется прямоугольным сечением, повернутым в пространстве на 360 градусов вокруг оси. Иными словами, цилиндр – это тело вращения. Функцию оси выполняет одна из сторон этого прямоугольного сечения. Если рассмотреть формы сечения цилиндра (а их ровно две), то одна из них представляет собой прямоугольник, а другая — круг. То есть, если мы посмотрим на цилиндр со стороны, мы увидим в нем прямоугольник, но если мы посмотрим на него сверху, мы увидим, что часть его составляющей, это круг.
Чтобы построить цилиндр стоящий вертикально, надо провести вертикальную осевую линию, отложить на осевой пропорциональный отрезок, равный высоте цилиндра.
Затем через крайние точки отрезка провести две горизонтальные осевые параллельные линии, строго перпендикулярные вертикальной. На горизонтальных осевых линиях отложите пропорциональные, равные между собой, отрезки, равные ширине цилиндра. Соедините точки горизонтальных отрезков между собой. Получите двухмерную прямоугольную фигуру с отношениями сторон, как стороны цилиндра.
Создадим третье измерение. Построим две окружности в перспективе через четыре точки. Верхний эллипс будет нижнего эллипса, так как находится он в большем перспективном сокращении.
Самая частая проблема при построении цилиндра состоит не в создании эллипсов, а в их осевых линиях, потому что к их построению серьезно не относятся. Нарушение в построении вертикальной осевой линии приводит к асимметрии и неустойчивости формы цилиндра, Иными словами, цилиндр получается кривой, фигура как будто «дрожит» и «не стоит на месте». Нарушение же в построении горизонтальной осевой линии приводит к невозможности нарисовать правильный эллипс.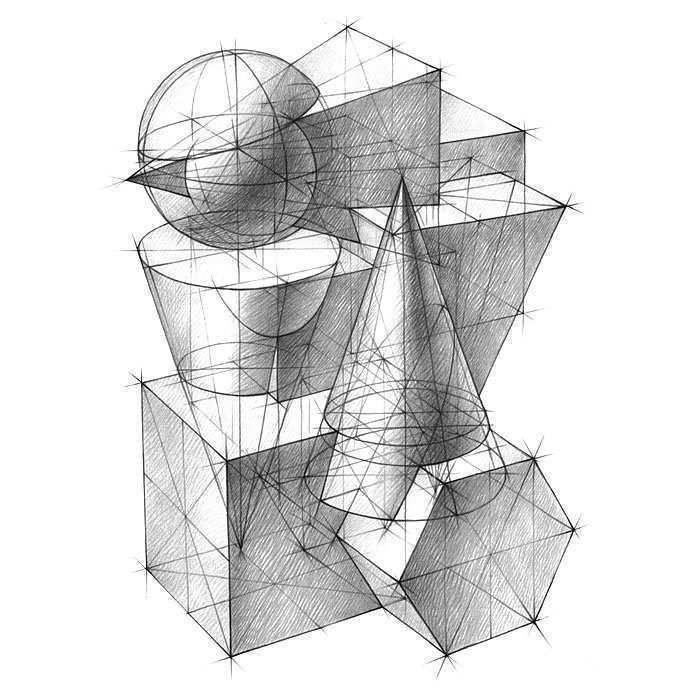
А ведь все просто: вертикальная осевая линия рисунка соответствует вертикальной стороне листа рисунка, то же можно сказать и про горизонтальные осевые линии.
Особую сложность в конструктивном построении представляет форма цилиндра, лежащего на боковой поверхности. Круглое сечение цилиндра вписывается в квадрат (который относительно легко можно построить в пространстве) по четырем точкам. Значит, нам легче сначала построить в пространстве четырехгранную призму, соответствующую пропорциональным отношениям сторон цилиндра, а затем вписать в нее цилиндр.
Как найти осевую линию, равную ширине цилиндра, в этом ракурсе? Построив в пространстве четырехгранную призму, найдите в ней срединную линию, проведите линию под прямым углом к срединной линии через центр боковой поверхности. На этой прямой находится отрезок, равный ширине цилиндра в этом ракурсе. Получается, что боковая поверхность цилиндра строится по шести точкам.
Почему мы так много говорим о построении цилиндра? Потому что вы с ним будете сталкиваться на каждом шагу, будет ли это предмет быта, драпировка, голова человека или фигура человека.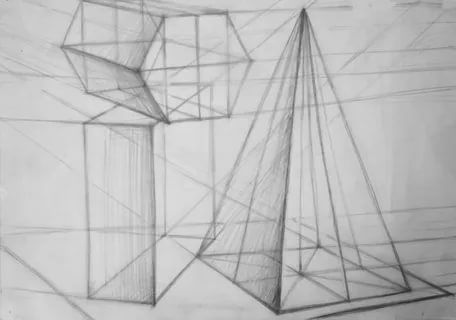
Несмотря на все возрастающую сложность заданий по рисунку, вам придется абстрагировать сложные пластические формы до простых понятий, если вы, конечно, хотите их передать в рисунке.
Продолжаем тему конструктивного рисунка натюрморта из геометрических тел. Первое, что надо построить в рисунке натюрморта после создания композиции листа — это плоскость, на которой находятся предметы натюрморта. От того, как правильно вы нарисуете положение плоскости в пространстве, зависит успех всего рисунка. На плоскости создаются как бы следы предметов, и только после того, как вы убедитесь, что они действительно лежат на этой плоскости, приступайте к дальнейшему построению, то есть возводите каркас.
В большинстве натюрмортов некоторые геометрические предметы находятся на втором уровне. Это значит, что куб находится на плоскости стола, а на нем стоит конус. Пока вы не определите положение куба на плоскости стола, конус на кубе не построить. Типичной ошибкой является плоскость, опрокинутая на нас — предметы натюрморта, врезанные в плоскость стола (а на старших курсах — человеческие фигуры), будто скатываются с горки.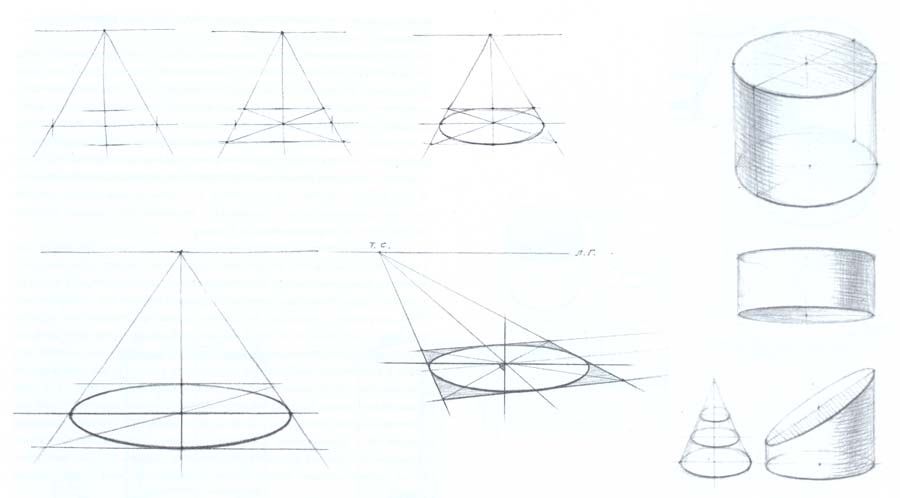
Все дальнейшие построения предметов натюрморта выполняются с помощью методов, приведенных выше.
Конструктивное построение дает ясное понимание объема предметов натюрморта в пространстве и выполняется при помощи линий. Нарисованные предметы выглядят прозрачными каркасами.
Частичное включение тона. Передача объема.
Введите легкий тон в тени собственные и падающие; решите тональные отношения между тенями: тени на первом плане должны быть темнее. Введите светотени. Граница света и тени темнее, чем сама тень, поэтому при введении светотени тень приобретает признаки рефлекса.
У куба светотень жесткая; цилиндр имеет мягкую светотень. У шара светотень приобретает, кроме мягкости, еще и воздушность, она, как эллипс, располагается в пространстве. Проверьте еще раз плановость, то есть состояние воздушной перспективы линий, теней и светотеней. И рисунок закончен!
Конструктивный рисунок натюрморта не включает в себя понятия тональных отношений. Все предметы в натюрморте как бы одного окраса, потому что задача конструктивного рисунка — построить объем в пространстве при помощи линии и света.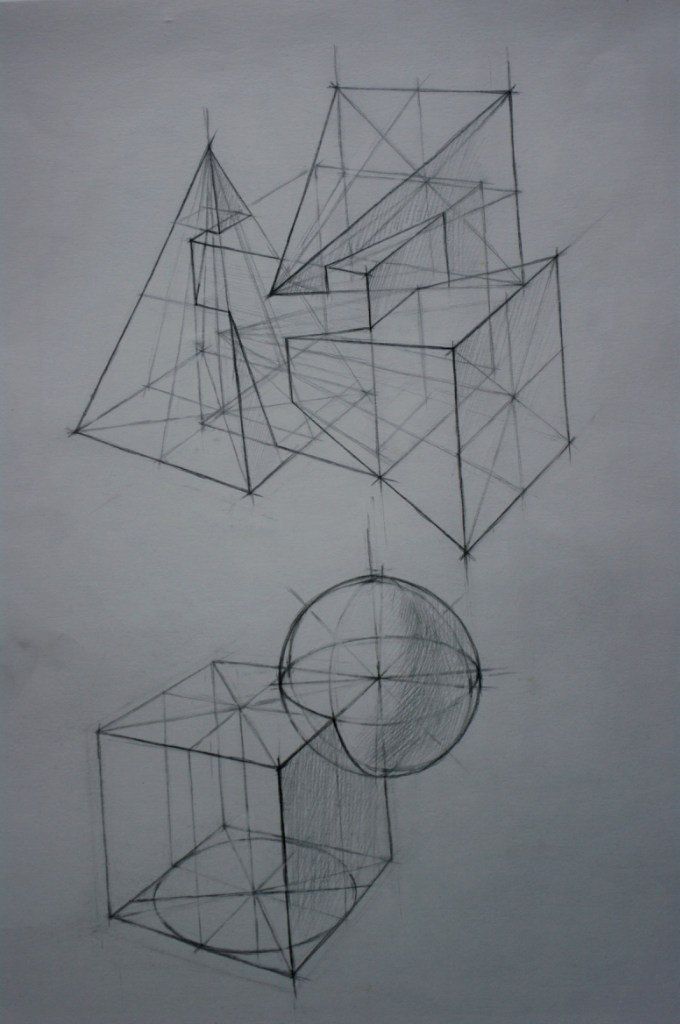
Конструктивный рисунок — это основа рисунка вообще, его база. Только опираясь на эту базу, можно переходить к следующим задачам, таким как тональные отношения, материальность и так далее.
Что такое рисунок?
Что вспоминается в первую очередь, когда спрашивают, что такое рисунок? «Это основа всех видов изобразительного искусства». Так — просто, без дальнейших разъяснений — начинаются многие учебные издания по рисунку. Потому что за разъяснениями нужно будет погрузиться в основы всех видов изобразительного искусства, понять их конструкцию, понять, какую долю в ней составляет рисунок (что является делом конкретным, а не литературным излиянием). После чего совершенно ясно будет видно, что рисунок — ядро, вокруг которого и формируются все виды изобразительного искусства, главный элемент их конструкции.
Почему мы говорим, что карандашом — рисуем, а красками — пишем? В чем разница? Анатомическое строение человека не меняется из-за одежд, которыми оно укрыто — меняется функция и образ оболочек.
Так и рисунок является не образной оболочкой, а главной формой. Рисунок — это намного больше, чем мы представляли себе раньше или можем представить сейчас. Почему большинство художников-живописцев не может теоретически объяснить свой вид деятельности? Потому что цвет и технические приемы не есть живопись, а всего лишь элементы основы, которой и является рисунок.
Данное учебное пособие предназначено для самого широкого круга пользователей, но особенно оно будет полезно для студентов факультетов дизайна, архитектуры, а также для студентов художественно-графических факультетов, которым необходимо знать теорию и методику преподавания рисунка.
Развитие объемно-пространственного мышления, такого необходимого для этих специальностей, начинается с уроков рисунка. Если вы знакомы с программами подготовки дизайнеров в старейшем и уважаемом российском учебном заведении, каким является Художественно-промышленный университет им. Строганова, то вы можете обратить внимание, что дисциплина «Рисунок» равна по количеству часов (по времени подготовки специалистов) дисциплине «Проектирование».
Пластика совершенных творений природы является кладезем для дизайнера и архитектора. Одно из таких творений — человек. Не даром в программных заданиях по рисунку есть так много постановок, связанных с человеком. Так же этим объектом занимается такая наука, как бионика.
Метод проектирования в дизайне и архитектуре (функциональный анализ) очень схож с методом конструктивного анализа в рисунке. Получить полную информацию об объекте, научиться видеть простое в сложном, а затем вести рисунок (или процесс проектирования) по пути «от простого к сложному» — это один из основных методов работы как над рисунком, так и над проектом. Поэтому рисунок как предмет в подготовке дизайнера и архитектора играет весомую роль.
Существует большая проблема, которая связана с отсутствием учебной литературы по рисунку, а особенно — с отсутствием в этой литературе вопросов конструктивного рисунка как базы или фундамента рисунка вообще.
Почти все уважаемые теоретики рисунка упоминают в своих трудах о конструктивном анализе в рисунке.
Но удивляет всегда одно и то же. Откройте некоторые учебные пособия: после темы построения осевых линий в рисунке головы или фигуре человека всегда следует тема построения теней и тоновая проработка. Хотя вас всячески и убеждают обратить внимание на конструкцию предмета, то есть формы.
Понимая важность конструкции в рисунке, тем не менее, вам никто не покажет и не расскажет, что это такое (за исключением нескольких иллюстраций рисунков, которые выполнили еще художники эпохи Возрождения, и изданий художественно-промышленного вуза). Поэтому большинство учебных пособий по рисунку, включая и некоторые академические, выглядят довольно странно. Странность заключается в том, что возникает ощущение, будто из этих изданий изъяли часть страниц. Мол, вот вам первый этап рисунка с массой и основными осевыми линиями — а вот вам уже завершающий этап и дедушка с усами, как живой.
В программе обучения студентов рисунку блок заданий «Конструктивный анализ» следует после блока заданий «Рисунок натюрморта».
Это связано с тем, что знания для рисунка натюрморта закладываются с детства в традиционной манере срисовывания, в следствие чего задания по этому рисунку выполняются студентами с определенной долей инерции, обусловленной особенностями мышления.
Между заданиями «Рисунок натюрморта» и «Рисунок головы человека» существует граница, переступив которую студент попадает в область иного для него объемно-пространственного мышления, опирающегося на конструктивный анализ.
Неподготовленность к осознанному рисованию вызывает болезненное состояние, сильно затормаживая процесс познания рисунка. Научить студента хорошо рисовать за период обучения в институте невозможно. Но научить его мыслить категориями рисунка и, тем более, основам конструктивного анализа — можно. Это станет его путеводной нитью, а особенно — в дизайне.
Самое главное, что рисунок как форма — конечен. Конструкция формы рисунка известна, в ней, как и в музыке, «семь нот и бесконечность возможностей». Без конструктивного анализа формы не существует рисунка вообще, как и не существует архитектурного сооружения без фундамента.
Овладение методикой конструктивного анализа в рисунке является задачей номер один. Вот только процесс этот довольно-таки специфичный, потому что требует как от преподавателя, так и от студента творческого подхода.
Понимание конструкции рисуемого предмета всегда опирается на собственный опыт. Без опыта данное преподавателем конструктивное понимание формы предмета может превратиться в шаблон или схему. Вот почему здесь так необходимы навыки преподавателя с развитым объемно-пространственным мышлением, владеющего основами конструктивного рисунка.
Конструкция (лат. constructio) — построение, сложение.
Нас окружает мир, в котором все построено по единым законам, в том числе и мы. А мы — маленькая часть этого большого мира, который окружает нас бесконечным количеством предметов. Предметы, в свою очередь, сложены из большого количества форм. Познать суть предмета, его формообразование — дело не простое, но возможное.
Чтобы познать мир, надо познать его конструкцию. Причем, познав часть, можно познать и целое.
Ведь, как мы уже говорили, все построено по единым законам. Термин «сложение» входит в понятие «композиция». Ведь недаром композиционный строй картины мы называем ее конструкцией, а формообразующий строй предмета — конструкцией формы.
Фигура — это произвольное множество точек на плоскости. Точка, прямая, отрезок, луч, треугольник, круг, квадрат и так далее — всё это примеры геометрических фигур.
Основными геометрическими фигурами на плоскости являются точка и прямая. Этим фигурам в геометрии не даётся определений.
Неопределяемыми геометрическими фигурами на плоскости являются точка и прямая.
Точки принято обозначать прописными латинскими буквами: А, В, С, D …. Прямые обозначаются строчными латинскими буквами: а, b, с, d ….
Фигуры, изучаемые планиметрией:
1. Точка
2. Прямая
3. Параллелограмм (частные случаи: квадрат, прямоугольник, ромб)
4. Трапеция
5. Окружность
6. Треугольник
7.
Многоугольник
1) Точка:
В геометрии, топологии и близких разделах математики точкой называют абстрактный объект в пространстве, не имеющий ни объёма, ни площади, ни длины, ни каких-либо других аналогичных характеристик больших размерностей. Таким образом, точкой называют нульмерный объект. Точка является одним из фундаментальных понятий в математике.
Точка — это одно из фундаментальных понятий геометрии, поэтому «точка» не имеет определения. Евклид определил точку как то, что нельзя разделить.
Также в геометрии нет определения «прямой» (имеется в виду прямая линия).
2) Прямая:
Прямая — одно из основных понятий геометрии.
Геометрическая прямая (прямая линия) — незамкнутый с двух сторон, протяженный не искривляющийся геометрический объект, поперечное сечение которого стремится к нулю, а продольная проекция на плоскость даёт точку.
При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии.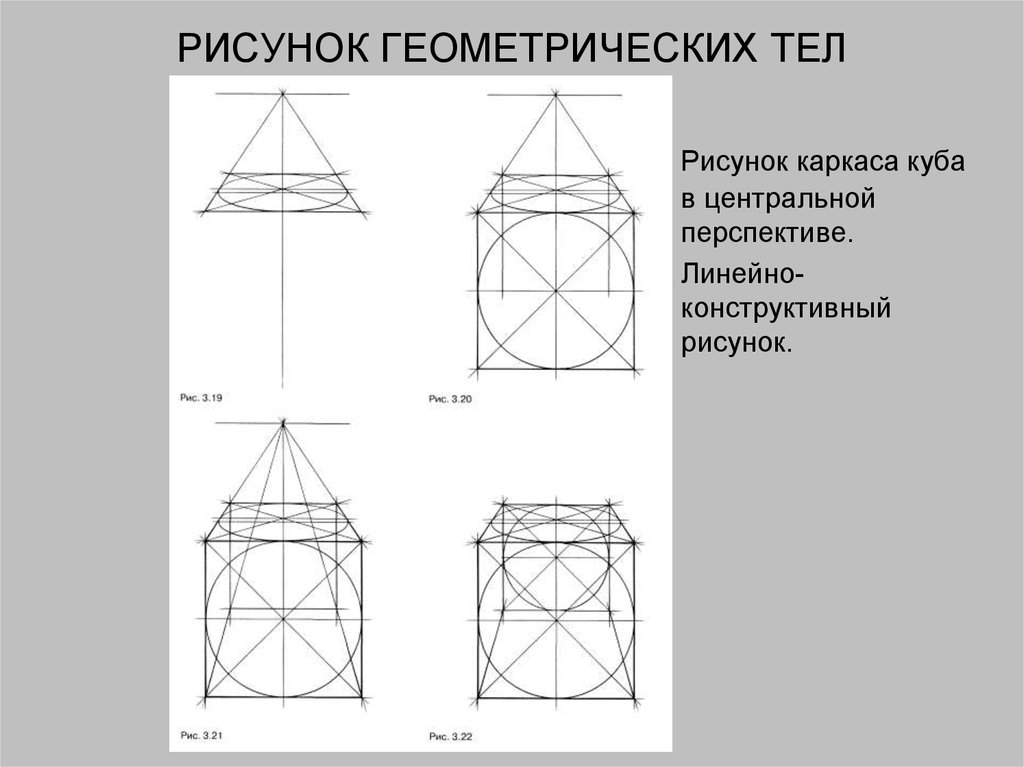
Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками.
3) Параллелограмм
Параллелограмм— это четырёхугольник, у которого противолежащие стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
Частные случаи:
Квадрат — правильный четырёхугольник или ромб, у которого все углы прямые, или параллелограмм, у которого все стороны и углы равны.
Квадрат может быть определён как:
§ прямоугольник, у которого две смежные стороны равны
§ ромб, у которого все углы прямые (любой квадрат является ромбом, но не любой ромб является квадратом).
Прямоугольник — это параллелограмм , у которого все углы прямые (равны 90 градусам).
Ромб — это параллелограмм, у которого все стороны равны. Ромб с прямыми углами называется квадратом.
4) Трапеция
Трапеция — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна.
Иногда трапеция определяется как четырёхугольник, у которого пара противолежащих сторон параллельна (про другую не уточняется), в этом случае параллелограмм является частным случаем трапеции. В частности, существует понятие как криволинейная трапеция.
Прямоугольная трапеция
5) Окружность
Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом.
6) Треугольник
Треугольник — простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, и тремя отрезками, попарно соединяющими эти точки.
Если все три точки треугольника лежат на одной прямой, он называется вырожденным.
7) Многоугольник
Многоугольник — это геометрическая фигура, определяется как замкнутая ломаная. Существуют три различных варианта определения:
§ Плоские замкнутые ломаные;
§ Плоские замкнутые ломаные без самопересечений;
§ Части плоскости, ограниченные ломаными.
Вершины ломаной называются вершинами многоугольника, а отрезки — сторонами многоугольника.
Тон в изображении чертежа.
Тоновое и линейное изображение чертежа создано для того, чтобы показать тени, объемы изображаемых фигур на бумаге, частично, передать их форму и структуру. Тоновое и линейное изображение выделяет конкретную фигуру от остальных фигур в чертеже. Это сделано не сколько для удобства, сколько для аккуратности и подачи чертежа.
Изображение тона появилось в момент создания самого рисунка и до сих пор не теряет свою функцию и уникальность. Ведь, с помощью тона достаточно легко передать то, что не удается прочертить или написать на чертеже.
В изобразительном искусстве тон играет огромную роль для рисунка. С неправильной подачей тона и тени, рисунок теряет свою уникальность и «правильность» в исполнении. Но прежде чем приступить к изображению тона, нужно сначала научиться изображать сам рисунок, то есть, грубо говоря, его чертеж. Когда ребенок берет в первый раз карандаш в руки, он сначала учиться передавать форму, фигуру, сам объект, а потом уже и тенеотдачу.
Заключение
Важнейшей задачей преподавания изобразительного искусства в современной школе является развитие личности учащегося путем формирования его сложного внутреннего мира. Происходит получение научных знаний об объективном мире вокруг (цель абсолютного большинства школьных дисциплин) и развитие эстетических вкусов, творческого восприятия этого объективного мира. Интеллектуальное и духовное развитие — это сложный, многогранный процесс, и в нем немалую роль играют уроки эстетического цикла, ИЗО в том числе. Уроки рисунка не только развивают уровень познания, но и формируют психический мир личности, они также помогают включить субъективные эстетические ценности в формирующиеся общественно-значимые ценности, а это — основная задача личностно-ориентированного обучения. Исходя из вышесказанного, следует отметить, что уроки рисования являются замечательной площадкой для развития патриотизма и любви к Родине. Нет ничего лучше чем развивать у ребенка видение красоты русской природы, русского человека его быта и традиций.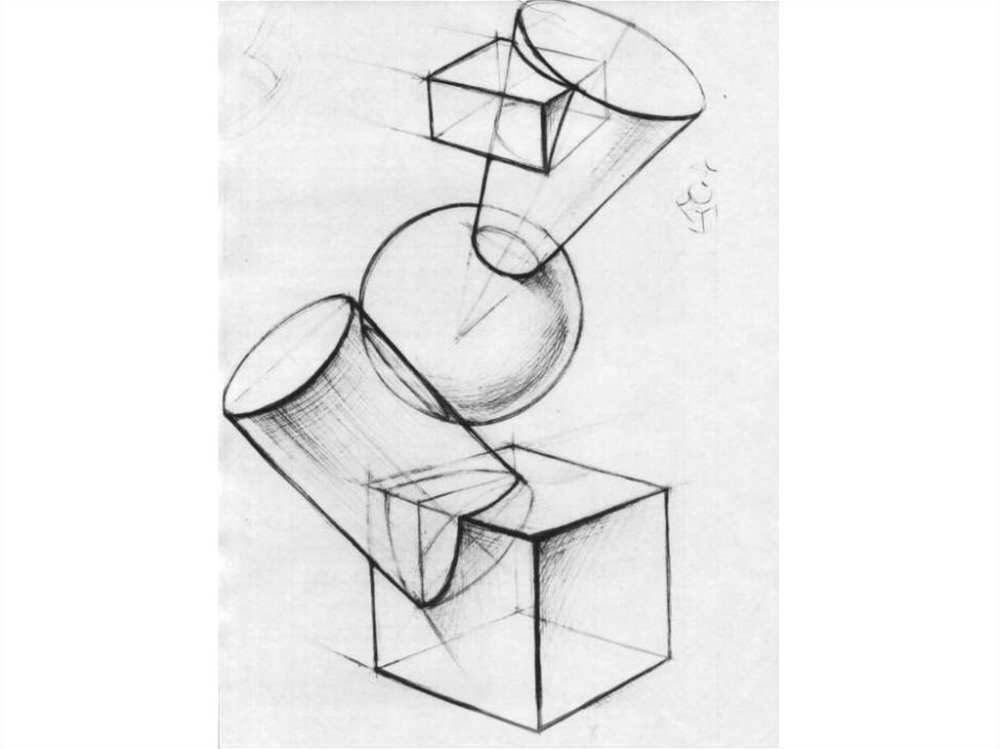
Для правильного изображения натурной модели ученикам необходимо еще раз напомнить о необходимости приучить себя всегда анализировать натуру, ясно представлять ее внешнее и внутреннее строение. К сожалению, как показывает практика, многие учащиеся ограничиваются лишь поверхностным впечатлением, не углубляясь в суть строения формы предмета. В искусстве, как и в любой науке, к изучению натурного предмета необходимо подходить с научной точки зрения. Подходить к работе следует осознанно, не довольствуясь копированием внешних форм, которые видит глаз. Такое рисование не будет способствовать успешному выполнению работ по изображению как простых, так и сложных форм.
Для основательного изучения геометрические формы лучше всего следует рассматривать в виде прозрачных каркасных моделей. Это позволяет лучше проследить, понять и усвоить основы пространственного построения конструкций и перспективного сокращения форм геометрических тел: куба, пирамиды, цилиндра, шара, конуса и призмы. Вместе с тем, такой прием в значительной степени облегчает построение рисунка, в котором отчетливо прослеживаются все пространственные углы, ребра, грани тела, независимо от их поворотов в пространстве и в перспективном сокращении.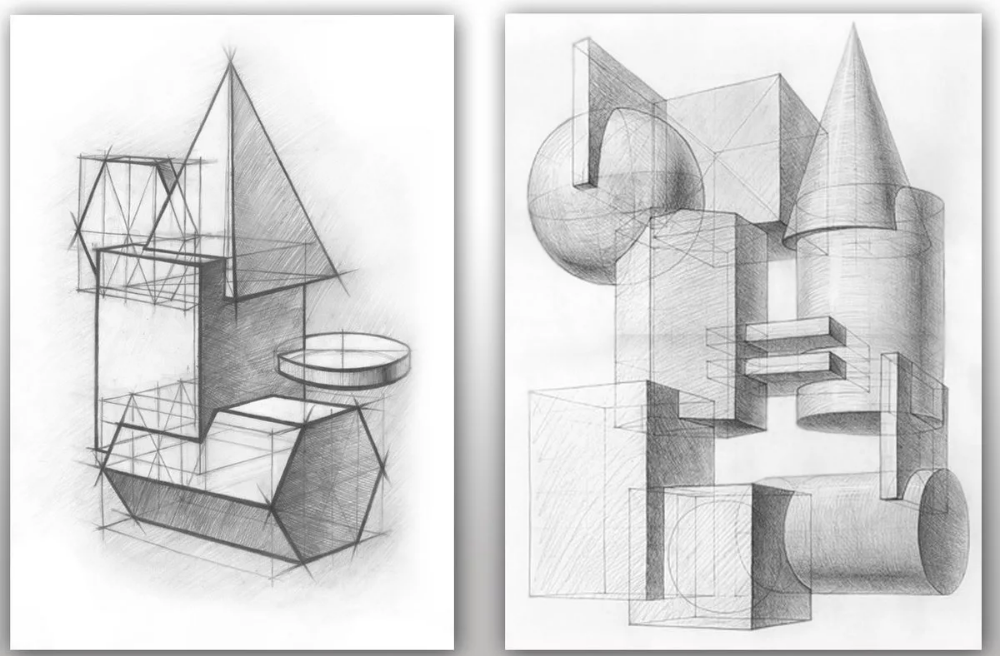
Каркасные модели позволяют развить у учащихся объемно-пространственное мышление, тем самым способствуя правильному изображению геометрической формы на плоскости бумаги.
Итог работы заключается в том,что рассмотрено несколько основных геометрических тел вращения, их особенности, элементы, и наглядные примеры.
Список использованной литературы
1. Тихонов С.В. Рисунок. Учебник. М. 1983. Архитектурный рисунок: современные требования: Учеб. пособие. Екатеринбург, 2005.
2. Тюрин Н.П. Рисование архитектурного сооружения. Учебное пособие. М. 1980 г.
3. Чивиков Е.К. Журнал «Юный художник», ст. «Почему я рисую городской пейзаж?», М. 2004, №7.
4. Короев Ю.И. Построение широкоугольных архитектурных перспектив. Метод. пособие, М. 1970.
5. Раушенбах Б.В. Пространственные построения в живописи. М., Наука, 1980.
6. Токарев В.А. Методические основы рисунка по памяти и по представлению. М. 1984.
7. Федоров Н.В. Рисунок и перспектива. М., Искусство, 1960.
8. Чернихов Я. Искусство начертания.
9.. Г. Баммес, «Образ человека», ООО «Дитон», 2011 г.
10. Ф. Готтенрот, «Иллюстрированная история материальной культуры», «Полигон», 2001г.
11. Козлинский В.И., Фрезе Э.П., «Художник и театр», «Советский художник», 1975г.
12. Лилиана и Фред Функен, «Энциклопедия вооружения и военного костюма», Москва, «Астрель-АСТ», 2007г.
13. «Традиции школы рисования» Художественно-промышленная Академия имени А.Л.Штиглица под редакцией В.В.Пугина, 2009г.
14. «Искусство рисунка» Б.А.Соловьева, 1989 г.
15. «Учебный рисунок» издательство Изобразительное искусство под редакцией В.А.Королева, 1981 г.
16. «Рисунок с натуры» Т.Б.Смирнов, 1960 г.
17. «Наброски и зарисовки» В.Ф.Кузин, 1981 г.
Цилиндр и другие тела на рисунке. Как рисовать геометрические фигуры карандашом
Умение строить геометрические фигуры – это основа основ рисования в целом. Без этой базы вы не сможете продвинуться дальше и начать изображать более сложные фигуры и предметы.
Любые объекты состоят из геометрических тел, и их нужно уметь увидеть и правильно передать на бумаге.
Геометрические фигуры учат понимать законы перспективы, изображать объем и выявлять правильность форм и композиции.
Каждый художник, желающий стать профессионалом, должен в совершенстве владеть навыками построения линейно-конструктивного рисунка, уметь наложить штриховку, создать объем и сделать изображение выразительным и убедительным.
Одной из базовых фигур, наряду с шаром и кубом, является цилиндр.
Приступая к работе
Цилиндр мы будем изображать карандашом. Для начального этапа нам нужны твердые или твердо-мягкие карандаши (T (можно TM) или H (HB)) для того, чтобы изображение цилиндра получилось более точным.
Чтобы лист не протерся после неоднократной работы ластиком, выбирайте плотную чертежную бумагу. Используйте мягкий ластик, который не повредит текстуру бумаги. Вам также может пригодиться формопласт для облегчения тона рисунка.
Измерения пропорций цилиндра
При рисовании цилиндра с натуры можно произвести нужные измерения объекта при помощи карандаша.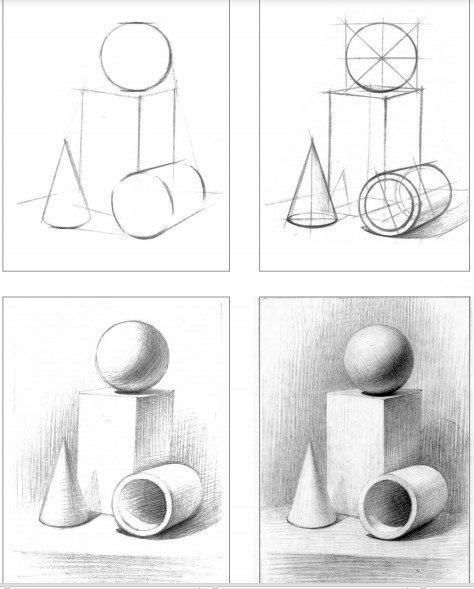
Для этого его нужно держать на расстоянии вытянутой руки. Кончик грифеля – начальная точка измерения. Большим пальцем зажмите отметку, где проходит нижняя граница объекта. Таким же образом измеряем цилиндр по ширине. Такой прием поможет вам соблюсти правильные пропорции изображаемого предмета.
Создание основы цилиндра
Рисуя с натуры на начальном этапе, лучше всего выбрать положение прямо напротив цилиндра. Таким образом, вы избежите искажения перспективы, а, соответственно, и искажения размеров и формы.
Основой любого изображаемого объекта является центральная ось. Именно она будет служить нам ориентиром для дальнейшего построения цилиндра. Теперь рисуем две перпендикулярные линии, которые будут служить ориентиром для нижнего и верхнего оснований будущей фигуры.
На равном расстоянии от центральной оси рисуем по одной параллельной линии с каждой стороны. Они определяют ширину фигуры. Благодаря таким ориентирам нам будет просто определить границы будущего цилиндра и не исказить его пропорции.
Построение эллипсов
Вертикально расположенное геометрическое тело в горизонтальной плоскости нужно начинать создавать с его основания. Тут нам поможет метод линейно-конструктивного построения изображения.
Эллипсы проще всего нанести двумя дугами, переходящими одна в другую. Для ровного построения окружностей требуется определенная тренировка. На начальном этапе линии могут получиться волнистыми.
Еще один способ – вписывание окружности в квадрат. Точки соприкосновения линий должны находиться в середине каждой стороны четырехугольника.
Центральная ось цилиндра должна оставаться перпендикулярной плоскостям окружностей.
Следите за искажением пропорций вследствие изменения перспективы. В разных частях рисунка эллипсы будут иметь разную форму. Это зависит от того, под каким углом вы смотрите на фигуру. Со временем вам понадобиться все меньше вспомогательных линий для создания правильного цилиндра.
Грани
Теперь нам нужно немного ослабить нарисованные линии.
На этом этапе делим наш цилиндр, отделяя передний план от заднего. Для этого мы прорисовываем более толстые линии видимых частей фигуры. Причем более толстые линии мы проводим по нижним и верхним дугам. Заднюю видимую часть эллипса вверху фигуры выделяем не так жирно, но она должна оставаться четкой.
То есть у нас появляются три типа линий по толщине: толстые линии переднего плана, тонкая линяя заднего плана и едва заметные вспомогательные линии.
Окружности основания цилиндра прорисовывайте насквозь, на этапе штрихования внутренние (невидимые линии) удаляются. Таким образом, вы сможете проследить различия размеров верхнего и нижнего оснований.
Следующий этап: штриховка
При помощи мягкого карандаша мы будем накладывать тон на получившееся изображение, постепенно создавая объем. На начальном этапе лучше всего воспользоваться так называемой диагональной штриховкой. Начинать штриховать цилиндр следует с самых темных участков.
Элементы светотени, которые встретятся в процессе выполнения работы, включают в себя блики, полутени, тени, рефлексы и свет.
Самым светлым участком будет блик. Здесь наложения тона не требуется. Следующий участок – это свет, здесь штрих должен быть еле заметным. Зона полутени – это основной тон цилиндра. В области тени мы накладываем самую темную и плотную штриховку. В районе кромки предмета находится рефлекс, тон практически равен полутени. Работать стоит аккуратно, нанося равномерную штриховку.
Свет строит форму геометрического тела. От правильности выполнения зависит его итоговый объем. От самого яркого участка (блика) свет расходится по округлой поверхности, переходя в полутень. Цилиндрическая форма помогает рисовальщику понять последовательность распределения светотени.
Сложность задачи состоит в том, чтобы сделать переходы между участками плавными и незаметными. На каждом этапе следите за правильной передачей пропорций и градациями тона.
Фон мы не оставляем нетронутым. Он также играет важную роль в восприятии объема и построении пространства. При помощи штриховки тона мы можем передать освещенность.
После того, как вы закончили создавать цилиндр, следует проверить наличие ошибок. Отойдите на расстояние в несколько метров от мольберта, так чтобы изображение было отчетливо видно. То есть, чем больше рисунок, тем дальше нужно от него отдалиться. С такого ракурса видны ошибки в построении. После исправления проверьте правильность выполнения еще раз.
Развитие навыков
Это был самый простой вариант расположения геометрического тела. Когда вы его освоите, то можете переходить к более сложным вариациям: цилиндр в пространстве, в горизонтальном или наклонном положении.
В художественной студии К.Э. Арутюновой вы сможете обучиться азам рисования. Вы научитесь строить не только цилиндр, но и любые геометрические тела в разных положениях. С развитием навыков вы будете переходить к новым этапам, и сможете развить свои художественные способности. Со временем вам не понадобится такое множество вспомогательных линий, и вы с легкостью сможете начать изображать на бумаге сложные элементы.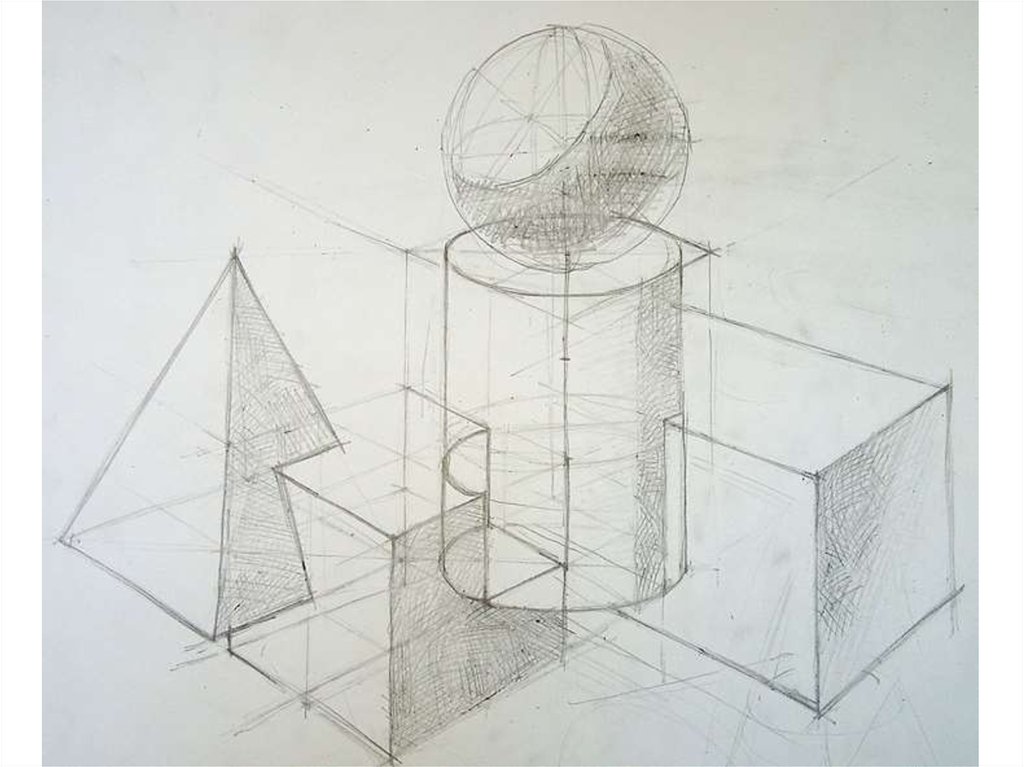
Похожие записи
Как нарисовать человеческую фигуру Роберта Барретта
Поделиться:
Следующая статья о рисовании человеческой фигуры появилась в выпуске The Artist’s Magazine за май 2009 года, который доступен для заказа в виде цифровой загрузки. Кликните сюда, чтобы узнать больше. Бонус: получите бесплатную загрузку о том, как рисовать людей!
Усовершенствовав базовые структуры до более мелких единиц, вы сможете точно визуализировать тело.
Роберт Барретт
Для рисования Лежащей фигуры (пастель, 22х28) использовались геометрические фигуры, средние линии и принцип прорисовки). Самый эффективный способ упростить рисование фигуры человека — свести ее сложные формы к фундаментальным. В этой статье я расскажу, как использовать различные аспекты геометрических фигур, средних линий и рисования жестами, а также принцип сквозного рисования. Использование геометрических фигур, срединных линий и принципа сквозного рисования помогло мне точно передать эту фигуру в ракурсе.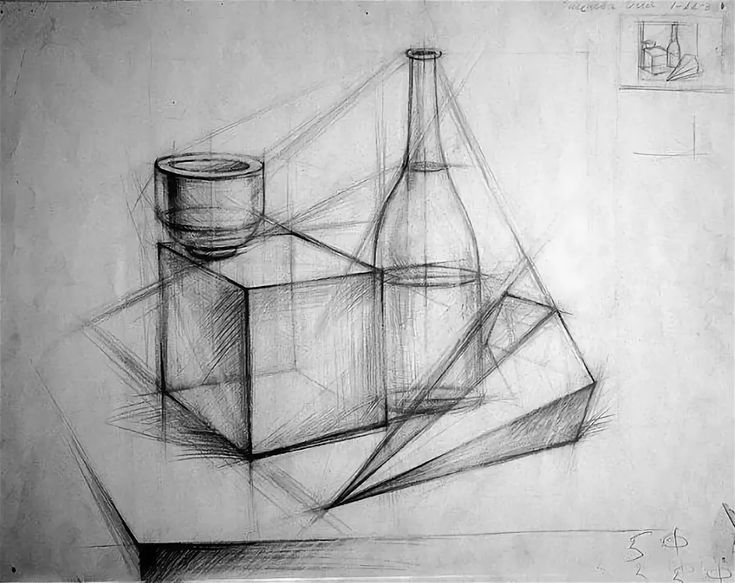
1. Начните с основных структур
Фигура представляет собой трехмерный объект, который имеет объем и занимает пространство. Важно думать о человеческой фигуре с точки зрения фундаментальных форм, поскольку именно эти формы создают основные массы, влияющие как на внутренний жест, так и на внешнюю форму вещей. Меньшие части важны, но они должны быть подчинены большим. Когда вы разбиваете основные единицы на все более мелкие, эти единицы также становятся важными формами, из которых вы можете развивать и совершенствовать более конкретные формы.
Сокращая фигуру до геометрических фигур, можно создать убедительный ракурс. Этот подход также помогает вам понять большие формы и то, как одна из них строится поверх другой.
2. Создайте на основе жеста каркас
Как и в случае любого рисунка, создайте фигуру, набросав жесты. Эскиз свободного жеста поможет вам уловить общую суть фигуры. Продолжайте «наполнять» фигуру, добавляя массу и вес с помощью геометрических форм (см.
рисунок на противоположной странице справа). Важно, чтобы фигура была плавной и жестикулированной; в противном случае вы можете забыть действие фигуры и сделать ее слишком жесткой или тугой. Постарайтесь почувствовать действие позы, когда вы развиваете твердость форм. Помните, что фигура размерна — у нее есть высота, ширина и глубина.
3. Двигайтесь от известного к неизвестному
Такие фигуры, как сферы, кубы, цилиндры и конусы, помогут вам понять сложные структуры фигур, потому что их легко рисовать. Когда вы понимаете известную величину, такую как куб, вам будет легче понять и оценить неизвестную величину, такую как таз.
Чтобы создать измененную форму фигуры, нарисуйте ноги, руки и туловище в основном в виде цилиндров и уменьшите голову до сферы, а руки и ступни предложите в форме клина или куба.
Рисуйте (формы) насквозь, то есть рисуйте так, как если бы тело было прозрачным.
4. Понимание дизайна структур
Процесс восприятия сложных структур как простых форм имеет решающее значение для понимания дизайна как простой, так и сложной анатомии. По мере того, как вы будете участвовать в процессе разбиения сложных структур на более простые, вы обнаружите, что ваше понимание устройства структур резко возрастет.
5. Уточните, определите и измените
По мере того, как рисунок будет продвигаться от первоначального наброска жестов, уточните голову в сферу, а туловище в основные цилиндры. Измените руки и ноги из симметричных цилиндров в конические цилиндры.
Добавьте прямую линию или стержень — среднюю линию — вниз по центру руки или ноги, чтобы помочь определить и уточнить внешние — и более тонкие — контуры каждого соответствующего придатка.
Художник, монументалист и иллюстратор Роберт Барретт также является профессором кафедры визуальных искусств Университета Бригама Янга в Прово, штат Юта. Он является членом Общества иллюстраторов, Американского общества пастели, Американского портретного общества и Клуба Салмагунди.
Эта статья взята из его книги «Рисунок с жизни: как точно и выразительно изобразить фигуру».
Эта статья появилась в выпуске The Artist’s Magazine за май 2009 г., который доступен для заказа в виде цифровой загрузки. Кликните сюда, чтобы узнать больше.
Бесплатный предварительный просмотр на сайте artistnetwork.tv
Нажмите здесь, чтобы посмотреть бесплатный предварительный просмотр видео-семинара «Рисуем и раскрашиваем собак пастельными карандашами» с Колином Брэдли.
ДОПОЛНИТЕЛЬНЫЕ РЕСУРСЫ ДЛЯ ХУДОЖНИКОВ
- Смотрите художественные мастер-классы по запросу на ArtistsNetwork. ТВ
- Онлайн-семинары для художников
- Мгновенная загрузка журналов по изобразительному искусству, книг, видео и многого другого
- Подпишитесь на электронную рассылку новостей Artist’s Network и получите БЕСПЛАТНУЮ электронную книгу
Поделиться:
Категории: Среды искусства, Предметы искусства, Техники и навыки искусства, Журнал художников, Рисование, Портреты и изобразительное искусство
Что такое геометрический рисунок? — Улучшение чертежа
Что такое геометрический рисунокВведение в геометрический рисунок?
Вы слышали об этом раньше, но это не всегда относится к механическому рисованию, как вы скоро узнаете.
Геометрический рисунок для среднего художника имеет прямое отношение к техническим формам, которые свободно вращаются вокруг основных математических принципов.
Примеры базовых рисунков
Вы будете удивлены простотой геометрического искусства, так как оно не требует тонкого прикосновения к рисованию от руки. Большинство основных рисунков, которые вы можете создать с помощью геометрического искусства, представляют собой прямые линии, проведенные с помощью обычной линейки.
Единственная загвоздка в том, чтобы создать изображение, состоящее в основном из линий. Эти линии могут быть длинными или короткими и часто повторяются, как зеркало, создавая законченное изображение, такое как животное или лицо.
Какую бы форму вы ни выбрали, каждая нарисованная линия не обязательно должна быть одинаковой длины, если вы создаете зеркальное отражение.
Подобно работе с детскими конструкторами, они формируют изображение, используя простые формы строительных блоков, включая треугольники, квадраты и прямоугольники.
Воспользуйтесь этой ссылкой, чтобы получить доступ к курсам рисования в «Доместике». Январские распродажи в «Доместике» со скидкой до 75 %.
Рисунки «точка-точка»
Это правда, рисунки «точка-точка» — это именно то, о чем вы могли бы подумать, если бы угадывали эти глупые картинки «точка-точка» в детских тетрадях. Но действительно ли это то, что означают точечные рисунки?
Реальность этих рисунков включает в себя серию точек или «точек», которые создают изображение, в котором используется одна соединенная линия для соединения точек. С базовым рисованием использование метода «точка-точка» похоже на ту старую песню о построении скелета.
Некоторые художники будут использовать этот метод для создания формы скелета, используя общие контрольные точки для построения базовой системы точек. Бедренная кость соединена с костью голени и так далее.
Это ускоряет процесс, который в противном случае занял бы больше времени, чтобы нарисовать форму или фигуру вручную, поэтому для соединения этих точек соединения используются только практические точки.
Как нарисовать куб
Как нарисовать куб
Пожалуйста, включите JavaScript
Похожие посты:
- Перспектива трудна?
- Как нарисовать городскую улицу в перспективе
- Как затенять городскую улицу в перспективе
- Как нарисовать в 3D
- Как нарисовать с перспективой
Geometric Геометрический штриховой рисунок
Геометрический штриховой рисунок очень похож на рисование точка-точка, поскольку вы можете использовать разнесенные точки для построения начала и конца ваших линий. То, что ставится вместо рисования от руки, затем заменяется геометрическими фигурами. Так что это действительно больше похоже на рисование в стиле «точка-точка».
Фигура может состоять из отдельных геометрических фигур, связанных и соединенных друг с другом, образуя изображение, которое вы хотите создать.
Исключением являются определенные формы, которые можно изменить из основных строительных блоков, включая треугольники, квадраты и прямоугольники.
Их можно растягивать и деформировать по своему желанию, поэтому окончательная форма будет иметь точную геометрическую форму.
Чтобы создать иллюзию изогнутых линий, края и углы имеют отдельные точки соединения в пределах трех-четырехточечного соединения, создавая дополнительные точки соединения, чтобы сделать их пяти- или шеститочечными. Они по-прежнему выглядят как важный строительный блок с добавленными углами, чтобы они лучше вписывались в ваш геометрический рисунок.
Пожалуйста, посмотрите этот видеокурс рисования и набросков , который я создал . Воспользуйтесь этой ссылкой.
Рисование геометрических фигур:
Не все геометрические фигуры являются простыми блоками и имеют отдельные имена блоков, которые можно использовать в вашем геометрическом рисунке. Некоторые из них вы уже знаете, а другие представляют собой индивидуальные формы.
Эти сложные формы не всегда лучше включать в свой рисунок, но если проявить немного воображения, они найдут способ вписаться в ваш образ, если вы будете использовать их художественно.
Изометрический куб
Изометрические чертежиИзометрический куб — это просто квадрат, нарисованный в 3D, поэтому вы можете увидеть сам куб в трех четвертях. У него всегда будут видны три стороны. Как будто вы смотрите на квадратный блок сверху или снизу.
Каждая из линий будет одинаковой и расположена под углом 30 градусов друг к другу только из соображений перспективы. Эти кубики можно складывать друг на друга, чтобы создать любое количество блочных изображений, как в Minecraft.
В качестве альтернативы изометрические кубы должны следовать двухточечной перспективе, когда они сложены вместе, чтобы все они соответствовали чертежу в перспективе.
Это означает, что он включает в себя линию горизонта и две отдельные точки схода под углом около 30 градусов, чтобы сделать ваше блочное изображение более естественным.
Плоский круг
При рисовании плоского круга на геометрическом чертеже используется тот же принцип, что и при рисовании в перспективе.
Используя заданный горизонт на бумаге, вам нужно нарисовать плоский квадрат на вашем ландшафте. На данный момент края квадрата не являются трехмерными.
Все, что вы делаете, это создаете базовую квадратную форму в соответствии с точкой схода и равными сторонами вашего квадрата на картинке.
Затем вы поместите свой круг внутри этого квадрата в зависимости от формы квадрата. Ваш круг будет казаться более овальным, когда он вписывается в эту размерную версию плоского квадрата.
Теперь у вас есть плоский круг, которому впоследствии можно придать любую нужную форму.
Квадраты
Независимо от того, как вы хотите назвать эту фигуру, квадрат может быть кубом, блоком, кубиком или коробкой. Этот базовый строительный блок будет широко распространен в геометрических формах, а также будет соответствовать объемному изображению. Поскольку у квадрата 4 равные стороны, поместить его на плоскость достаточно просто, но правила сразу же меняются, когда вы применяете его к рисунку в перспективе.
Вам всегда нужно будет определять горизонт и угол обзора вашего квадрата.
Это позволяет квадрату принимать форму куба, блока, прямоугольника или игральной кости. Добавление большего количества квадратов на ваш квадрат или соединение с ним — это всего лишь вопрос укладки одной и той же формы на каждую часть, следуя тем же правилам, что и выше.
Треугольник
Треугольник имеет три равные стороны независимо от того, какой формы вы удлиняете линии, соединяющие все три точки соединения. Растянутый треугольник может мгновенно создать прямоугольник на плоской поверхности, когда изображение перевернуто и перевернуто, что делает треугольник очень универсальным.
Сам по себе, с равными сторонами, треугольник становится практичной формой, когда геометрические изображения плотно прилегают друг к другу и создают иллюзию округления, когда они растягиваются и складываются.
Если вы новичок в геометрическом рисовании, вы не ошибетесь, используя треугольные формы, поскольку они помогут совместить почти любой узор или рисунок, используя треугольники разного размера, которые все стыкуются «хорошо и аккуратно».
Полукруг
Давайте назовем это как есть, это полукруг, и для этого потребуется половина нарисованного круга, верно? Не совсем в этом случае, если вы решите сделать полукруг на чертеже в перспективе.
Вам нужно начать с простого квадрата, чтобы поместить в него свой круг, а после того, как вы закончите, вы можете разделить свой круг на половину. Это займет больше времени, но, по крайней мере, вы получите размерные результаты, необходимые для того, чтобы все выглядело правильно.
На абсолютно плоской поверхности нарисовать полукруг очень просто, используя инструмент окружности, чтобы получить круг нужного размера и провести линию по центру. В зависимости от необходимого вам размера. Также можно заменить окружность на круглую чашку или крышку от банки.
Прямоугольник
Все прямоугольники имеют четыре стороны, две из которых длиннее или шире и идут параллельно. Плоские прямоугольники всегда легко рисовать, когда они одномерные, но, как и квадрат, нарисованный внутри перспективных поверхностей рисования, вам нужно будет придать этой форме соответствующие размерные угловые края.
Прямоугольники также можно очень быстро разделить на вытянутые треугольники.
Вы просто проводите линию от левой стороны одной передней кромки к правой стороне нижней кромки. Это изменяет внешний вид прямоугольника и помогает замаскировать его в геометрическом рисунке.
Параллелограмм
Для большинства из нас, не разбирающихся в математических уравнениях, параллелограмм выглядит как прямоугольник, наклоненный в одну сторону. Фактическое определение того, как работает параллелограмм, будет включать 2 пары параллельных противоположных сторон.
Другой способ помочь определить это дальше, это сказать, что у него есть 2 пары равных сторон, которые совпадают и идут параллельно противоположным сторонам. Таким образом, каждая делящая сторона, расположенная под углом к одной стороне, соответствует другой.
Как бы то ни было, нарисовать параллелограмм в перспективе будет сложнее, если только вы не нарисуете фигуру такой, какой ее следует видеть, а не ошибочно приметите за прямоугольник, видимый под странным углом.
Ромб
В отличие от ромба, который появляется в форме воздушного змея, ромб имеет четыре равные стороны одинаковой длины. У ромба есть две совпадающие стороны: верхняя и более короткая половина, а нижняя половина длиннее.
Ромб — это виртуальное зеркальное отражение самого себя, если разделить его пополам и быстро превратиться в треугольник. Даже после деления пополам у самого треугольника будут три стороны одинаковой длины.
Если провести линию от одного угла к другому внутри ромба, а противолежащая линия образует букву x внутри ромба, у вас получится 4 разделенных треугольника. Они не будут одинаковой длины из-за такого деления, но и не сделают ваш ромб непривлекательным.
Трапеция
Трапеция может быть похожа на анкер бетонного настила, но ее форма основана на строгом наборе углов для определения окончательной формы. Дно плоское с двумя смежными сторонами, которые наклонены внутрь под углом 65 градусов.
Суммарный градус для обеих сторон составляет 180 градусов.
Стороны, обращенные внутрь, всегда вдвое короче основания. Оставшаяся часть, закрывающая верхнюю часть, на четверть больше угловых сторон.
По сути, ваша трапеция может быть разделена на два треугольника на каждом конце, с прямоугольником в середине.
Используется ли геометрия в чертеже?
Независимо от того, знаете вы этот маленький факт или нет, широко распространено, что в рисовании постоянно используются математика и геометрия. Это не вопрос обработки чисел, как вы видите в бухгалтерии, а более или менее молчаливый партнер для выполнения простых расчетов.
Часто эти расчеты используются для определения масштаба и относительного размера объектов или пропорций тела. И хотя их часто называют формулами рисования, они используют геометрию и математику.
Рисование фигуры
Основы рисования фигуры в значительной степени основаны на пропорциональных примерах того, как построены скелет и человеческая форма. Узнаете ли вы, что общий рост человека составляет примерно 7 голов, но это приблизительная оценка фактического роста.
Пропорции используют математику и предустановленные расчеты, чтобы получить правильный масштаб в соответствии с установленными формулами. Фактическое использование геометрии в рисовании фигур упрощается с помощью блочных форм для имитации человеческого тела.
Портретный рисунок
Геометрические портреты стали очень популярными с годами и придают другой вид рисованию в целом. Человеческое лицо разбито на секции, которые начинают принимать множество геометрических форм.
Эти формы часто следуют существующим теневым линиям, но настоящая хитрость заключается в создании трехмерной кривизны линий, видимых по всему лицу и голове.
Вам не нужно следовать определенным математическим правилам, но имеет смысл следовать линиям кривизны, которые превращаются в углы и сложные треугольники. Это придает больше реализма, как будто изображение полностью создано из трехмерных геометрических фигур, образующих человеческое лицо.
Базовый натюрморт
Для натюрморта используется формула, определяющая, как должны располагаться объекты.
Это связано с пропорциями и визуальным расстоянием. Вы же не хотите, чтобы рисунок натюрморта превратился в вечеринку с сосисками для нежной орхидеи, поэтому важно правильное расстояние для реквизита!
После этого вы можете использовать любое количество геометрических фигур для замены вашего реквизита. Размещение этих реквизитов и используемые интервалы будут дополнять используемые вами геометрические формы.
В чем используется геометрия?
Несколько других известных торговых навыков часто используют геометрию для создания сложных фигур и форм. Некоторые художники, у которых есть явные способности к математике и математическим формулам, поймут, насколько ценными могут быть эти навыки.
Эти навыки также переносятся в традиционное схематическое искусство и архитектуру. Вот три примера того, как многие профессионалы используют геометрию для создания определенных произведений искусства.
Технический чертеж
То, что раньше называлось техническим чертежом или механическим чертежом, теперь обычно называют техническим чертежом.
Это то же самое, и вместо того, чтобы рассчитывать на бумаге, эти профессионалы используют компьютерное программное обеспечение для выполнения работы.
Инновации CAD и AutoCAD устранили необходимость рисовать технические схемы на бумаге. Он также сохраняется и математически корректируется на компьютере, поэтому ошибки не допускаются.
Те, кто изучил основы изучения технической информации и математических особенностей, могут оценить, насколько трудна эта работа.
Изометрия
Это особый навык рисования, который помогает проиллюстрировать, как объекты сочетаются друг с другом или могут быть расположены. Это упрощенная версия блочного рисунка, в котором используются геометрические фигуры для создания изометрических проекций.
Они созданы не для того, чтобы выглядеть трехмерными, а скорее для двухмерного объекта, видимого без нарушения трехмерной перспективы. Если вы когда-либо играли в Farmville или другие игры для смартфонов, посвященные строительству деревень, то это прекрасный пример изометрии.
Перспектива
Вы уже знаете, что перспективный рисунок использует простую перспективную плоскость для определения горизонта и точек схода. Помещение геометрических фигур в эту перспективу основано на тех же правилах, чтобы сделать любой геометрический объект в трехмерном пространстве реалистичным.
Угол, под которым вы видите эти объекты, соответствует традиционным правилам и может иметь две точки схода, чтобы сделать эти геометрические формы более определенными.
Как называется геометрическое искусство?
Геометрический рисунокОдним из наиболее часто используемых выражений, которые называют геометрическим искусством, является геометрическая абстракция. Если вы когда-нибудь видели много картин Пикассо, в которых используется геометрия, он любит называть это кубизмом.
Во Франции есть слово, которое также описывает геометрическое искусство и называется Le Neoplastimime. Голландцы, любящие тюльпаны, также претендуют на этот стиль, называя его «De Stijl» (Стиль) при описании геометрического искусства.
Независимо от того, из какой части мира вы приехали, всегда найдется другое слово для описания этого вида искусства. Достаточно ли называть это абстрактным? В каком-то смысле использование геометрических фигур делает искусство, построенное из строительных блоков, довольно абстрактным, но это организованный хаос.
Причина, по которой он называется абстрактным, связана с блочной природой его внешнего вида.
Сколько существует типов геометрического рисунка?
Есть только два типа геометрических фигур, когда дело доходит до их рисования на бумаге. Первый — это 2D, который представляет собой заурядную плоскую форму любой геометрической формы. Затем есть 3D-версия, которая придает геометрической форме большую четкость и реалистичность. Если вам нужно задать вопрос, сколько на самом деле существует геометрических фигур, список довольно исчерпывающий. Вот полный список основных геометрических фигур .
В чем важность геометрического рисунка?
Геометрический рисунок так же необходим в повседневной жизни, как воздух, которым можно дышать! Может показаться сложным отказаться от иронического и саркастического представления о том, что геометрия является основным строительным блоком самого нашего общества.
Без механического черчения не было бы зданий и сооружений, которые просуществовали бы очень долго. Геометрия используется для разработки новых продуктов, конструкций и машин, которые мы используем каждый день.
Геометрический рисунок помогает нам решать проблемы с помощью вековых инженерных навыков, используя эти чертежи в качестве чертежей, чтобы воплотить их в жизнь. Геометрические чертежи также используются для проектирования электроники, которая заставляет работать каждое электронное устройство.
Удивительно, почему маленьким детям в таком раннем возрасте дают играть с геометрическими кубиками? Мы используем геометрическое рисование в его простейшей форме для решения проблем больше, чем вы думаете, поскольку это навык, к которому мы все можем относиться.
Отрицание представления о том, что такое геометрический рисунок, равнозначно сравнению с чем-либо еще, что мы принимаем как должное в этом мире. Мы не можем жить без геометрии по той простой причине, что мы, как вид, постоянно движемся вперед, используя технологии, которые являются частью нашего древнего прошлого.
Тот факт, что геометрическое искусство обычно используется чаще, чем ему приписывают, является причиной того, что многие художники часто забывают, насколько важны эти навыки.
Создавайте рисунки с помощью моих любимых ресурсов для рисования
Общие курсы рисования. Мне нравится Udemy, если вы хотите развить свои знания в области техники рисования. Udemy — отличный выбор благодаря широкому выбору творческих курсов и отличной политике возврата средств. У них часто есть ежемесячные скидки для новых клиентов, которые вы можете проверить здесь. Используйте мою ссылку .
Эскиз и коллаж. Посмотрите на этот ресурс для рисования, который я создал. Используйте эту ссылку .
Проко. – один из моих любимых учителей, превосходно преподающий анатомию и рисование фигур. Курс Prokos разбивает рисунок человеческого тела на простые для понимания компоненты, помогая новичку быстро прогрессировать.
За это мне очень нравится Proko.
Мольберты . Один из моих любимых способов рисования — использование мольберта, который развивает навык рисования на вертикальной поверхности. Мольберт с H-образной рамой – отличный вертикальный способ внести разнообразие в стиль и тип рисунков, которые вы создаете, используя чертежную доску.
Чтобы увидеть все мои самые актуальные рекомендации, просмотрите этот ресурс , который я сделал для вас.
Геометрические построения. Шаги и решенные примеры
В этом мини-уроке мы познакомимся с миром геометрических построений в математике. Вы узнаете о способах построения биссектрисы перпендикуляра, биссектрисы угла, параллельных прямых и других интересных фактах по этой теме. Вы можете попробовать свои силы в решении нескольких интересных практических вопросов в конце страницы.
Остин — инженер-строитель.
Ему нужна точная карта, чтобы построить здание и спроектировать инструменты.
Для рисования таких фигур он использует некоторые основные геометрические инструменты, такие как градуированная шкала, пара квадратов, делитель, циркуль и линейка.
Мы не хотим, чтобы вы волновались, и приготовьте свои геометрические инструменты, поскольку мы в Cuemath здесь, чтобы помочь вам понять геометрические построения ясным образом.
В этом коротком уроке мы познакомимся с некоторыми основными геометрическими построениями.
План урока| 1. | Что такое геометрическая конструкция? |
| 2. | Важные замечания по геометрическому построению |
| 3. | Решенные примеры геометрического построения |
| 4. | Советы и рекомендации по геометрическому построению |
| 5. | Интерактивные вопросы по геометрическому построению |
Геометрическое построение – это процесс построения геометрической фигуры с использованием двух геометрических инструментов, циркуля и линейки.
Мы используем циркуль, чтобы чертить дуги и окружности и отмечать равные длины.
Мы используем линейку для рисования отрезков и измерения их длины.
Как построить биссектрису?
Для выполнения этого построения мы будем использовать тот факт, что любая точка на серединном перпендикуляре к отрезку равноудалена от двух концов отрезка.
Предположим, у нас есть отрезок \(\overline{AB}\).
Этапы строительства описаны ниже.
Шаг 1: Взяв A и B за центры и радиус более половины \(\overline{AB}\), нарисуйте дуги по обеим сторонам \(\overline{AB}\) для пересечения друг друга, как показано ниже.
Причина, по которой вам требуется, чтобы радиус ваших дуг был больше половины \(\overline{AB}\), заключается в том, что если радиус меньше половины \(\overline{AB}\), дуги не будут пересекаться (попробуйте!).
Шаг 2: Пусть две точки пересечения, полученные таким образом, будут P и Q.
Проведите прямую через P и Q. Это искомый серединный перпендикуляр.
Здесь POQ — серединный перпендикуляр к \(\overline{AB}\).
Вы можете визуализировать эти шаги в симуляции ниже, нажав кнопку «GO».
Этапы построения параллельных линий
Разве не интересно осознавать тот факт, что эти оранжевые и зеленые линии будут продолжаться вечно, но никогда не пересекутся?
Эти две линии параллельны друг другу.
Мы научимся строить параллельные линии с помощью линейки и циркуля.
Пусть \(\overleftrightarrow{AB}\) – прямая, а P – точка вне линии \(\overleftrightarrow{AB}\).
Шаг 1: Проведите секущую через точку P, пересекающую прямую \(\overleftrightarrow{AB}\), скажем, в точке X.
центра и любого радиуса, нарисуйте дугу, пересекающую отрезок \(\overline{PX}\) в точке M и \(\overleftrightarrow{AB}\) в точке N.
P в качестве центра и того же радиуса, нарисуйте дугу EF, пересекающую отрезок \(\overline{PX}\) в точке Q.
Шаг 4: Приняв Q в качестве центра и того же радиуса, нарисуйте дугу, пересекающую дугу EF в точке R.
Шаг 5: сторон, чтобы нарисовать линию \(\overleftrightarrow{CD}\).
Здесь прямая \(\overleftrightarrow{CD}\) параллельна прямой \(\overleftrightarrow{AB}\).
Поэкспериментируйте с симуляцией ниже, чтобы визуализировать этот процесс, нажав кнопку «GO».
Как построить биссектрису угла?
Предположим, у нас есть \(\угол PQR\), и мы хотим разделить этот угол пополам.
Следуйте шагам построения, указанным ниже:
- Пусть Q будет центром и с любым радиусом нарисуйте дугу, пересекающую луч \(\overrightarrow{QP}\) и \(\overrightarrow{QR} \), скажем, в точках E и D соответственно.
- Теперь, взяв D и E за центры и одинаковый радиус, нарисуйте дуги, пересекающие друг друга, скажем, в точке F.
- Нарисуйте луч \(\overrightarrow{QF}\).
Здесь \(\overrightarrow{QP}\) — биссектриса угла \(\angle PQR\).
Используйте симуляцию ниже, чтобы визуализировать этапы построения биссектрисы угла, нажав кнопку «GO».
Важные примечания
Параллельные линии никогда не пересекаются друг с другом и не встречаются ни в одной точке.
Биссектриса проходит через середину данного отрезка.
Если луч делит угол на два равных угла, то он является биссектрисой угла.
| Пример 1 |
Зеленая и синяя линии параллельны, а M и N являются точками на зеленой и синей линиях соответственно.
Если кратчайшее расстояние от М до синей линии составляет 6 единиц.
Каким будет кратчайшее расстояние от N до зеленой линии?
Решение
Данные прямые параллельны, значит, они на всем протяжении равноудалены.
Это означает, что расстояние по перпендикуляру от M до синей линии равно расстоянию по перпендикуляру от N до зеленой линии. Следовательно, это расстояние равно 6 единицам.
На самом деле кратчайшее расстояние между двумя линиями — это перпендикулярное расстояние между ними.
| Итак, кратчайшее расстояние от N до зеленой линии составляет 6 единиц. |
| Пример 2 |
Райан запускает воздушного змея.
Воздушный змей имеет два угла, разделенных пополам, как показано ниже.
Сможете ли вы найти величины углов \(\угол EKI\) и \(\угол ITE\)?
{\circ}\). Мисс Эми попросила Мию обосновать построение серединного перпендикуляра к отрезку. Можете ли вы помочь ей обосновать это? Решение В \(\Delta PAQ\) и \(\Delta PBQ\): 1. PA = PB (дуги равного радиуса) 2. QA = QB (опять же, дуги равного радиуса) радиус) 3. PQ = PQ (общий) По критерию SSS два треугольника конгруэнтны, что означает, что \(\угол APO\) = \(\угол BPO\). В \(\Delta APO\) с \(\Delta BPO\): 1. PA = PB (дуги одинакового радиуса) 2. \(\угол APO\) = \(\угол BPO\ ) (только что показано) 3. PO = PO (общий) По критерию SAS два треугольника конгруэнтны, что означает, что AO = BO, а также: \(\угол AOP\) = \( \угол BOP\) = \(\dfrac{1}{2}180^0 = 90\) Это означает, что \(\angle PQT=\angle TQR\). Будьте осторожны при выполнении геометрических построений. Вот несколько советов и рекомендаций, которым вы можете следовать при строительстве. Советы и рекомендации Вот несколько заданий для практики. Выберите/введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат. Мини-урок был посвящен увлекательной концепции геометрических построений. Математическое путешествие вокруг геометрических построений начинается с того, что ученик уже знает, и продолжается творческим созданием новой концепции в юных умах. Сделано таким образом, что это не только понятно и легко для понимания, но и останется с ними навсегда. В этом заключается магия Cuemath. В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов! Благодаря интерактивному и увлекательному подходу «обучение-преподавание-обучение» учителя изучают тему со всех сторон. Будь то рабочие листы, онлайн-классы, сеансы сомнений или любая другая форма отношений, мы в Cuemath верим в логическое мышление и разумный подход к обучению. . Что такое параллельные линии? Параллельные прямые — это пара прямых, которые никогда не пересекаются и не пересекаются, и лежат в одной плоскости. Пример 3 \(\следовательно\), POQ — серединный перпендикуляр к AB. 
{\circ}\end{align}\] 9{\circ}\end{align}\] Итак, луч QT является биссектрисой угла \(\угол PQR\).
Интерактивные вопросы 
Подведем итоги 