Как найти точки пересечения: Как найти координаты точки пересечения графиков функций?

Пересечение прямых. Точка пересечения двух прямых

Пересечение прямых. Точка пересечения двух прямых

Навигация по странице:

• Определение точки пересечения прямых
• Точка пересечения двух прямых на плоскости
  
• Точка пересечения двух прямых в пространстве
  

Онлайн калькулятор. Точка пересечения двух прямых

Определение. Две прямые называются пересекающимися, если они имеют одну общую точку.

Определение. Точка, в которой пересекаются две прямые, называется точкой пересечения этих прямых.

Если точка M, является точкой пересечения двух прямых, то она должна принадлежать этим прямым, а ее координаты удовлетворять уравнения этих прямых.

Точка пересечения двух прямых на плоскости

Методы решения. Существует два метода решения плоских задач на определение координат точки пересечения прямых:

• графический
• аналитический

Графический метод решения.

Используя уравнения, начертить графики прямых и с помощью линейки найти координаты точки пересечения.

Аналитический метод решения. Необходимо объединить уравнения прямых в систему, решение которой, позволит определить точные координаты точки пересечения прямых.

Если система уравнений:

• имеет единственное решение, то прямые пересекаются;
• имеет бесконечное множество решений, то прямые совпадают;
• не имеет решений, то прямые не пересекаются (прямые параллельны между собой)

Пример 1. Найти точку пересечения прямых y = 2x — 1 и y = -3x + 1.

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:

y = 2x — 1y = -3x + 1

Вычтем из первого уравнения второе

y — y = 2x — 1 — (-3x + 1)y = -3x + 1     =>     0 = 5x — 2y = -3x + 1

Из первого уравнения найдем значение x

5x = 2y = -3x + 1     =>     x = 25 = 0. 4y = -3x + 1

Подставим значение x во второе уравнение и найдем значение y

x = 0.4y = -3·(0.4) + 1 = -1.2 + 1 = -0.2

Ответ. Точка пересечения двух прямых имеет координаты (0.4, -0.2)

Пример 2. Найти точку пересечения прямых y = 2x — 1 и

x = 2t + 1y = t

.

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:

y = 2x — 1x = 2t + 1y = t

В первое уравнение подставим значения x и y из второго и третьего уравнений.

t = 2·(2t + 1) — 1x = 2t + 1y = t     =>     t = 4t + 1x = 2t + 1y = t     =>    

-3t = 1x = 2t + 1y = t     =>     t = -13x = 2t + 1y = t

Подставим значение t во второе и третье уравнение

t = -13x = 2·(-13) + 1 = -23 + 1 = 13y = -13

Ответ. Точка пересечения двух прямых имеет координаты (13, -13)

Пример 3 Найти точку пересечения прямых 2x + 3y = 0 и

x — 23

=

y4

.

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:

2x + 3y = 0x — 23 = y4

Из второго уравнения выразим y через x

2x + 3y = 0y = 4·x — 23

Подставим y в первое уравнение

2x + 3·4·x — 23 = 0y = 4·x — 23     =>     2x + 4·(x — 2) = 0y = 4·x — 23     =>    

2x + 4x — 8 = 0y = 4·x — 23     =>     6x = 8y = 4·x — 23     =>    

x = 86 = 43y = 4·x — 23     =>     x = 86 = 43y = 4·4/3 — 23 = 4·-2/3 3 = -89

Ответ. Точка пересечения двух прямых имеет координаты (43, -89)

Пример 4. Найти точку пересечения прямых y = 2x — 1 и y = 2x + 1.

Решение: Обе прямые заданы уравнениями с угловым коэффициентом. Так как k₁ = k₂ = 2, то прямые параллельны. Так как эти прямые не совпадают то точек пересечения нет.

Решим также эту задачу используя систему уравнений:

y = 2x — 1y = 2x + 1

Вычтем из первого уравнения второе

y — y = 2x — 1 — (2x + 1)y = -3x + 1     =>     0 = -2y = -3x + 1

В первом уравнении получили противоречие (0 ≠ -2), значит система не имеет решений — отсутствуют точки пересечения прямых (прямые параллельны).

Ответ. Прямые не пересекаются (прямые параллельны).

Пример 5. Проверить является ли точка N(1, 1) точкой пересечения прямых y = x и y = 3x — 2.

Решение: Подставим координаты точки N в уравнения прямых.

1 = 1

1 = 3·1 — 2 = 1

Ответ. Так как оба уравнения превратились в тождества, то точка N — точка пересечения этих прямых.

Точка пересечения двух прямых в пространстве

Метод решения. Для определение координат точки пересечения прямых в пространстве, необходимо объединить уравнения прямых в систему, решение которой, позволит определить точные координаты точки пересечения прямых.

Если система уравнений:

• имеет единственное решение, то прямые пересекаются;
• имеет бесконечное множество решений, то прямые совпадают;
• не имеет решений, то прямые не пересекаются (прямые параллельны или скрещиваются между собой)

Пример 6.

Найти точку пересечения прямых x — 1 = y — 1 = z — 1 и

x — 3-2

= 2 — y = z.

Решение: Составим систему уравнений

x — 1 = ay — 1 = az — 1 = ax — 3-2 = b2 — y = bz = b   =>   x = a + 1y = a + 1z = a + 1x — 3-2 = b2 — y = bz = b   =>  

Подставим значения x, y, z из 1, 2, 3 уравнений в 4, 5, 6 уравнения

x = a + 1y = a + 1z = a + 1a + 1 — 3-2 = b2 — (a + 1) = ba + 1 = b   =>   x = a + 1y = a + 1z = a + 1a — 2-2 = b1 — a = ba + 1 = b

К шестому уравнению добавим пятое уравнение

x = a + 1y = a + 1z = a + 1a — 2-2 = b1 — a = ba + 1 + (1 — a) = b + b   =>   x = a + 1y = a + 1z = a + 1a — 2-2 = b1 — a = bb = 1

Подставим значение b в четвертое и пятое уравнения

x = a + 1y = a + 1z = a + 1a — 2-2 = 11 — a = 1b = 1   =>   x = a + 1y = a + 1z = a + 1a — 2 = -2a = 0b = 1   =>  

x = a + 1y = a + 1z = a + 1a = 0a = 0b = 1   =>   x = 0 + 1 = 1y = 0 + 1 = 1z = 0 + 1 = 1a = 0a = 0b = 1

Ответ. Прямые пересекаются в точке с координатами (1, 1, 1).

Замечание. Если уравнения прямых заданы параметрически, и в обоих уравнениях параметр задан одной и той же буквой, то при составлении системы в одном из уравнений необходимо заменить букву отвечающую за параметр.

Пример 7. Найти точку пересечения прямых

x = 2t — 3y = tz = -t + 2

и

x = t + 1y = 3t — 2z = 3

.

Решение: Составим систему уравнений заменив во втором уравнении параметр t на a

x = 2t — 3y = tz = -t + 2x = a + 1y = 3a — 2z = 3

Подставим значения x, y, z из 1, 2, 3 уравнений в 4, 5, 6 уравнения

x = 2t — 3y = tz = -t + 22t — 3 = a + 1t = 3a — 2-t + 2 = 3

  =>  

x = 2t — 3y = tz = -t + 22t = a + 4t = 3a — 2t = -1

  =>  

Подставим значение t из шестого уравнения в остальные уравнения

x = 2·(-1) — 3y = (-1)z = -(-1) + 22·(-1) = a + 4-1 = 3a — 2t = -1   =>   x = -5y = -1z = 3a = -6a = 13t = -1

Ответ. Так как -6 ≠ 13, то прямые не пересекаются.

Онлайн калькуляторы. Аналитическая геометрия. Декартовые координаты

Координаты точки пересечения двух прямых

Для того, чтобы решить геометрическую задачу методом координат, необходима точка пересечения, координаты которой используются при решении. Возникает ситуация, когда требуется искать координаты пересечения двух прямых на плоскости или определить координаты тех же прямых в пространстве. Данная статья рассматривает случаи нахождения координат точек, где пересекаются заданные прямые.

Точка пересечения двух прямых – определение

Необходимо дать определение точкам пересечения двух прямых.

Раздел взаимного расположения прямых на плоскости показывает, что они могут совпадать , быть параллельными, пересекаться в одной общей точке или скрещивающимися. Две прямые, находящиеся  в пространстве, называют пересекающимися, если они имеют одну общую точку.

Определение точки пересечения прямых звучит так:

Определение 1

Точка, в которой пересекаются две прямые, называют их точкой пересечения. Иначе говоря, что точка пересекающихся прямых и есть точка пересечения.

Рассмотрим на рисунке, приведенном ниже.

Нахождение координат точки пересечения двух прямых на плоскости

Перед нахождением координат точки пересечения двух прямых, необходимо рассмотреть предлагаемый ниже пример.

Если на плоскости имеется система координат Оху, то задаются две прямые a и b. Прямой a соответствует общее уравнение вида A1x+B1y+C1=0, для прямой b — A2x+B2y+C2=0. Тогда M0(x0, y0) является некоторой точкой плоскости необходимо выявить , будет ли точка М0 являться точкой пересечения этих прямых.

Чтобы решить поставленную задачу, необходимо придерживаться определения. Тогда прямые должны пересекаться  в точке, координаты которой  являются решением заданных уравнений A1x+B1y+C1=0 и A2x+B2y+C2=0. Значит, координаты точки пересечения подставляются во все заданные уравнения. Если они при подстановке дают верное тождество, тогда M0(x0, y0) считается их точкой пересечения.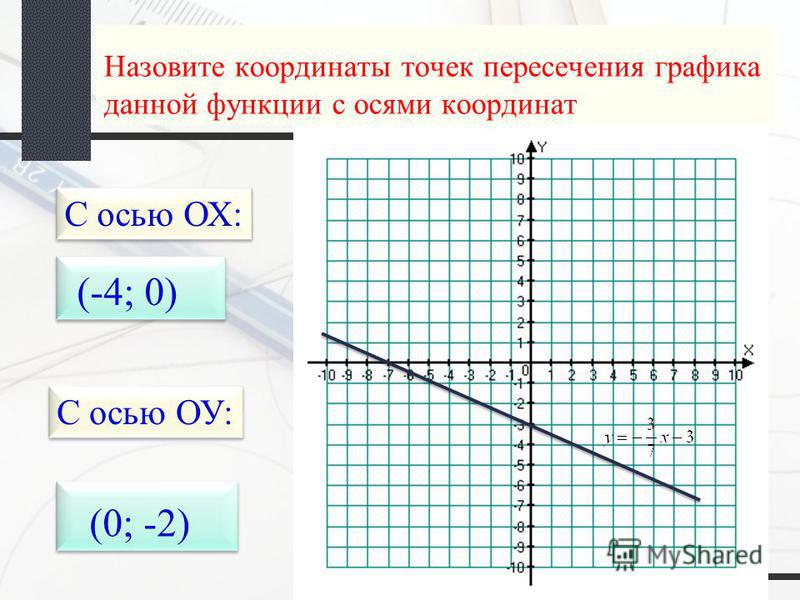

Пример 1

Даны две пересекающиеся прямые 5x-2y-16=0 и 2x-5y-19=0. Будет ли точка М0 с координатами (2,-3) являться точкой пересечения.

Решение

Чтобы пересечение прямых было действительным, необходимо, чтобы координаты точки М0 удовлетворяли уравнениям прямых. Это проверяется при помощи их подстановки. Получаем, что 

5·2-2·(-3)-16=0⇔0=02·2-5·(-3)-19=0⇔0=0

Оба равенства верные, значит М0 (2, -3) является точкой пересечения заданных прямых.

Изобразим данное решение на координатной прямой рисунка, приведенного ниже.

Ответ:  заданная точка с координатами (2,-3) будет являться точкой пересечения заданных прямых.

Пример 2

Пересекутся ли прямые 5x+3y-1=0 и 7x-2y+11=0 в точке M0 (2, -3)?

Решение

Для решения задачи необходимо подставить координаты точки во все уравнения. Получим, что

5·2+3·(-3)-1=0⇔0=07·2-2·(-3)+11=0⇔31=0

Второе равенство не является верным, значит, что заданная точка не принадлежит прямой 7x-2y+11=0. Отсюда имеем, что точка М0 не точка пересечения прямых.

Чертеж наглядно показывает, что М0_{— это не точка пересечения прямых. Они имеют общую точку с координатами (-1,2).}

Ответ: точка с координатами (2,-3) не является точкой пересечения заданных прямых.

Переходим к нахождению координат точек пересечения двух прямых при помощи заданных уравнений на  плоскости.

Задаются две пересекающиеся прямые a и b уравнениями вида A1x+B1y+C1=0 и A2x+B2y+C2=0, расположенных в Оху. При обозначении точки пересечения М0 получим, что следует  продолжить поиск координат по уравнениям A1x+B1y+C1=0 и A2x+B2y+C2=0.

Из определения очевидно, что М0 является общей точкой пересечения прямых. В этом случае ее координаты должны удовлетворять уравнениям A1x+B1y+C1=0 и A2x+B2y+C2=0. Иными словами это и есть решение полученной системы A1x+B1y+C1=0A2x+B2y+C2=0.

Значит, для нахождения координат точки пересечения , необходимо все уравнения добавить в систему и решить ее.

Пример 3

Заданы две прямые x-9y+14=0 и 5x-2y-16=0 на плоскости. необходимо найти их пересечение.

Решение

Данные по условию уравнения необходимо собрать в систему, после чего получим x-9y+14=05x-2y-16=0. Чтобы решить его, разрешается первое уравнение относительно x, подставляется выражение во второе:

 

x-9y+14=05x-2y-16=0⇔x=9y-145x-2y-16=0⇔⇔x=9y-145·9y-14-2y-16=0⇔x=9y-1443y-86=0⇔⇔x=9y-14y=2⇔x=9·2-14y=2⇔x=4y=2

Получившиеся числа являются координатами, которые необходимо было найти.

Ответ: M0 (4, 2) является точкой  пересечения прямых x-9y+14=0 и 5x-2y-16=0.

Поиск координат сводится к решению системы линейных уравнений. Если по условию дан другой вид уравнения, тогда следует привести его к нормальному виду.

Пример 4

Определить координаты точек пересечения прямых x-5=y-4-3 и x=4+9·λy=2+λ, λ∈R.

Решение

Для начала необходимо привести уравнения к общему виду.  Тогда получаем, что x=4+9·λy=2+λ, λ∈R преобразуется таким образом:

x=4+9·λy=2+λ⇔λ=x-49λ=y-21⇔x-49=y-21⇔⇔1·(x-4)=9·(y-2)⇔x-9y+14=0

После чего беремся за уравнение канонического вида x-5=y-4-3 и преобразуем. Получаем, что 

x-5=y-4-3⇔-3·x=-5·y-4⇔3x-5y+20=0

Отсюда имеем, что координаты – это точка пересечения

x-9y+14=03x-5y+20=0⇔x-9y=-143x-5y=-20

Применим метод Крамера для нахождения координат:

∆=1-93-5=1·(-5)-(-9)·3=22∆x=-14-9-20-5=-14·(-5)-(-9)·(-20)=-110⇒x=∆x∆=-11022=-5∆y=1-143-20=1·(-20)-(-14)·3=22⇒y=∆y∆=2222=1

Ответ: M0 (-5, 1).

Имеется еще способ для нахождения координат точки пересечения прямых, находящихся на плоскости. Он применим, когда одна из прямых задается параметрическими уравнениями, имеющими вид x=x1+ax·λy=y1+ay·λ, λ∈R. Тогда вместо значения x подставляется x=x1+ax·λ и y=y1+ay·λ, где получим λ=λ0, соответствующее точке пересечения, имеющей координаты x1+ax·λ0, y1+ay·λ0.

Пример 5

Определить координаты точки пересечения прямой x=4+9·λy=2+λ, λ∈R и x-5=y-4-3.

Решение

Необходимо выполнить подстановку в x-5=y-4-3 выражением x=4+9·λ, y=2+λ, тогда получим:

4+9·λ-5=2+λ-4-3

При решении получаем, что λ=-1. Отсюда следует, что имеется точка пересечения между прямыми x=4+9·λy=2+λ, λ∈R и x-5=y-4-3. Для вычисления координат необходимо подставить выражение λ=-1 в параметрическое уравнение. Тогда получаем, что x=4+9·(-1)y=2+(-1)⇔x=-5y=1.

Ответ: M0 (-5, 1).

Для полного понимания темы, необходимо знать некоторые нюансы.

Предварительно необходимо понять расположение прямых. При их пересечении мы найдем координаты, в других случаях решения существовать не будет. Чтобы не делать эту проверку, можно составлять систему вида A1x+B1y+ C1=0A2x+B2+C2=0 При наличии решения делаем вывод о том, что прямые пересекаются. Если решение отсутствует, то они параллельны. Когда система имеет бесконечное множество решений, тогда говорят, что они совпадают.

Пример 6

Даны прямые x3+y-4=1 и y=43x-4. Определить, имеют ли они общую точку.

Решение

Упрощая заданные уравнения, получаем 13x-14y-1=0 и 43x-y-4=0.  

Следует собрать уравнения в систему для последующего решения:

13x-14y-1=013x-y-4=0⇔13x-14y=143x-y=4

Отсюда видно, что уравнения выражаются друг через друга, тогда получим бесконечное множество решений. Тогда уравнения x3+y-4=1 и y=43x-4 определяют одну и ту же прямую. Поэтому нет точек пересечения.

Ответ: заданные уравнения определяют одну и ту же прямую.

Пример 7

Найти координаты точки пересекающихся прямых 2x+(2-3)y+7=0 и 23+2x-7y-1=0.

Решение

По условию возможно такое, прямые не будут пересекаться. Необходимо составить систему уравнений и решать. Для решения необходимо использовать метод Гаусса, так как с его помощью есть возможность проверить уравнение на совместимость. Получаем систему вида:

2x+(2-3)y+7=02(3+2)x-7y-1=0⇔2x+(2-3)y=-72(3+2)x-7y=1⇔⇔2x+2-3y=-72(3+2)x-7y+(2x+(2-3)y)·(-(3+2))=1+-7·(-(3+2))⇔⇔2x+(2-3)y=-70=22-72

Получили неверное равенство, значит система не имеет решений. Делаем вывод, что прямые являются параллельными. Точек пересечения нет.

Второй способ решения.

Для начала нужно определить наличие пересечения прямых.

n1→=(2, 2-3) является нормальным вектором прямой 2x+(2-3)y+7=0, тогда вектор n2→=(2(3+2), -7 — нормальный вектор для прямой 23+2x-7y-1=0.

Необходимо выполнить проверку коллинеарности векторов n1→=(2, 2-3) и n2→=(2(3+2), -7). Получим равенство вида 22(3+2)=2-3-7. Оно верное, потому как 223+2-2-3-7=7+2-3(3+2)7(3+2)=7-77(3+2)=0. Отсюда следует, что векторы коллинеарны. Значит, прямые являются параллельными и не имеют точек пересечения.

Ответ: точек пересечения нет, прямые параллельны.

Пример 8

Найти координаты пересечения заданных прямых 2x-1=0 и y=54x-2.

Решение

Для решения составляем систему уравнений. Получаем

2x-1=054x-y-2=0⇔2x=154x-y=2

Найдем определитель основной матрицы. Для этого 2054-1=2·(-1)-0·54=-2. Так как он не равен нулю, система имеет 1 решение. Отсюда следует, что прямые пересекаются. Решим систему для нахождения координат точек пересечения:

2x=154x-y=2⇔x=1245x-y=2⇔x=1254·12-y=2⇔x=12y=-118

Получили, что точка пересечения заданных прямых имеет координаты M0(12, -118).

Ответ: M0(12, -118).

Нахождения координат точки пересечения двух прямых в пространстве

Таким же образом находятся точки пересечения прямых пространства.

Когда заданы прямые a и b в координатной плоскости Охуz уравнениями пересекающихся плоскостей, то имеется прямая a , которая  может быть определена при помощи заданной системы A1x+B1y+C1z+D1=0A2x+B2y+C2z+D1=0 а прямая b — A3x+B3y+C3z+D3=0A4x+B4y+C4z+D4=0.

Когда точка М0 является точкой пересечения прямых, тогда ее координаты должны быть решениями обоих уравнений. Получим линейные уравнения в системе:

A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0A3x+B3y+C3z+D3=0A4x+B4y+C4z+D4=0

Рассмотрим подобные задания на примерах.

Пример 9

Найти координаты точки пересечения заданных прямых x-1=0y+2z+3=0 и 3x+2y+3=04x-2z-4=0

Решение

Составляем систему x-1=0y+2z+3=03x+2y+3=04x-2z-4=0 и решим ее. Чтобы найти координаты, необходимо решать через матрицу. Тогда получим основную матрицу вида   A=10001232040-2 и расширенную T=1001012-340-24. Определяем ранг матрицы по Гауссу.

Получаем, что

1=1≠0, 1001=1≠0, 100012320=-4≠0, 1001012-3320-340-24=0

Отсюда следует, что ранг расширенной матрицы имеет значение 3. Тогда система уравнений  x-1=0y+2z+3=03x+2y+3=04x-27-4=0 в результате дает только одно решение.

Базисный минор имеет определитель 100012320=-4≠0, тогда последнее уравнение не подходит. Получим, что x-1=0y+2z+3=03x+2y+3=04x-2z-4=0⇔x=1y+2z=-33x+2y-3 . Решение системы x=1y+2z=-33x+2y=-3⇔x=1y+2z=-33·1+2y=-3⇔x=1y+2z=-3y=-3⇔⇔x=1-3+2z=-3y=-3⇔x=1z=0y=-3.

Значит, имеем, что точка пересечения x-1=0y+2z+3=0 и 3x+2y+3=04x-2z-4=0   имеет координаты (1, -3, 0).

Ответ: (1, -3, 0).

Система вида A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0A3x+B3y+C3z+D3=0A4x+B4y+C4z+D4=0 имеет только одно решение. Значит, прямые a и b пересекаются.

В остальных случаях уравнение не имеет решения, то есть и общих точек тоже. То есть невозможно найти точку с координатами, так как ее нет.

Поэтому система вида A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0A3x+B3y+C3z+D3=0A4x+B4y+C4z+D4=0 решается методом Гаусса. При ее несовместимости прямые не являются пересекающимися. Если решений бесконечное множество, то они совпадают.

Можно произвести решение при помощи вычисления основного и расширенного ранга матрицы, после чего применить теорему Кронекера-Капелли. Получим одно, множество или полное отсутствие решений.

Пример 10

Заданы уравнения прямых x+2y-3z-4=02x-y+5=0 и x-3z=03x-2y+2z-1=0. Найти точку пересечения.

Решение

Для начала составим систему уравнений. Получим, что x+2y-3z-4=02x-y+5=0x-3z=03x-2y+2z-1=0 . решаем ее методом Гаусса:

12-342-10-510-303-221~12-340-56-130-20-40-811-11~~12-340-56-1300-125650075-1595~12-340-56-1300-1256500031110

Очевидно, что система не имеет решений, значит прямые не пересекаются. Точки пересечения нет.

Ответ: нет точки пересечения.

Если прямые заданы при помощи кононических или параметрических уравнений, нужно привести к виду уравнений пересекающихся плоскостей, после чего найти координаты.

Пример 11

Заданы две прямые x=-3-λy=-3·λz=-2+3·λ, λ∈R и x2=y-30=z5 в Охуz. Найти точку пересечения.

Решение

Задаем прямые уравнениями двух пересекающихся плоскостей. Получаем, что

x=-3-λy=-3·λz=-2+3·λ⇔λ=x+3-1λ=y-3λ=z+23⇔x+3-1=y-3=z+23⇔⇔x+3-1=y-3x+3-1=z+23⇔3x-y+9=03x+z+11=0x2=y-30=z5⇔y-3=0x2=z5⇔y-3=05x-2z=0

Находим координаты 3x-y+9=03x+z+11=0y-3=05x-2z=0, для этого посчитаем ранги матрицы. Ранг матрицы равен 3, а базисный минор 3-10301010=-3≠0, значит, что из системы необходимо исключить последнее уравнение. Получаем, что

3x-y+9=03x+z+11=0y-3=05x-2z=0⇔3x-y+9=03x+z+11=0y-3=0

Решим систему методом Крамер. Получаем, что x=-2y=3z=-5. Отсюда получаем, что пересечение заданных прямых дает точку с координатами (-2, 3, -5).

Ответ: (-2, 3, -5).

Поиск точки пересечения двух прямых с помощью Python

В линейной алгебре говорят, что две прямые пересекаются только в одной точке, если они не равны и не параллельны. Единственная точка пересечения также называется решением двух линейных уравнений. Python можно использовать для поиска решения этих двух линейных уравнений. Линии могут быть представлены в различных форматах. Решение X и Y может быть получено в каждом формате. Можно описать функцию Python, в которой X и Y можно найти напрямую, используя формулы, полученные для каждого формата. В этой статье рассказывается о двух разных форматах линейного уравнения и о том, как реализовать функцию для их получения.

Чтобы найти пересечение точки с помощью двух линий, ручной метод продвигается вперед, приравнивая оба уравнения к одной переменной. Он преобразует уравнение в уравнение с одной переменной. Далее с помощью простых математических расчетов находится единственная переменная, и ее значение подставляется в одно из предыдущих уравнений для получения второй координаты точки пересечения. Это хорошо проиллюстрировано в статье ниже и будет пояснено примерами и выводами. 9В этой статье используются два формата линейных уравнений: 2

Должно быть отмечено, что в этой статье NumPy не используется для реализации поиска точки пересечения двух линий. Здесь класс был реализован индивидуально и функция для работы с этим классом. Пожалуйста, обратитесь к этой статье, чтобы узнать больше о линейной алгебре NumPy.

Для облегчения понимания темы также используется графический анализ. Чтобы реализовать весь код как есть, необходимо импортировать Matplotlib.pyplot. Это можно сделать следующим образом, до начала кода:

 import matplotlib.pyplot as plt
 

Поиск точки пересечения с линейным уравнением как y=mx+c

Это самый простой формат линейных уравнений. Чаще всего он используется в линейной алгебре и графическом анализе. Здесь m — наклон уравнения, а c — константа уравнения. Здесь будут рассмотрены два линейных уравнения в одном и том же формате. Во-первых, будет выполнен вывод X и Y. На основе полученных формул будет создана функция в Python. Вывод следующий:

Первое уравнение в форме y=mx+cВторое уравнение в форме y=mx+cВывод X и Y из линейного уравнения y=mx+c

Из приведенного выше вывода видно, что переменную x можно легко найти из два линейных уравнения по формуле:

x=(c ₁ -c ₂ )/(m ₂ -m ₁ ) 9 0003

Вышеприведенная формула может быть легко закодирована в функция Python. Но перед созданием функции необходимо создать класс Line, который инкапсулирует Line в уравнении y=mx+c. Это показано ниже:

 класс Строка:
  def __init__(я, наклон, константа):
    self.m=наклон
    self.c=const
 

В приведенном выше объявлении класса также есть конструктор, описанный с помощью функции __init__(). Он принимает два входа: наклон уравнения и константу уравнения. В классе есть две переменные, m и c. Переменной m присваивается значение наклона, а переменной c присваивается значение константы. Теперь, когда класс объявлен, можно определить функцию, которая принимает две линии в качестве входных данных и показывает точку их пересечения в качестве выходных данных. Это показано в коде ниже:

 по определению findSolution(L1,L2):
  х=(L1.c-L2.c)/(L2.m-L1.m)
  у=L1.m*x+L1.с
  X=[x для x в диапазоне (-10,11)]
  Y1=[(L1.m*x)+L1.c для x в X]
  Y2=[(L2.m*x)+L2.c для x в X]
  plt.plot(X,Y1,'-r',label=f'y={L1.m}x+{L1.c}')
  plt.plot(X,Y2,'-b',label=f'y={L2. m}x+{L2.c}')
  plt.legend(loc='вверху справа')
  plt.show()
  возврат (х, у)
 

В приведенной выше функции findSolution() принимает на вход две строки. Сначала он присваивает переменную x в соответствии с формулой, полученной выше. Оператор точки (‘.’) в Python позволяет объекту класса получить доступ к его общедоступным переменным, в данном случае m и c. После нахождения переменной x переменная y просто назначается путем помещения переменной x в уравнение первой строки. Остальная часть кода строит линейный график двух уравнений в диапазоне (-10,10). В этой статье четко объясняется, как отображать легенды на графике и разные цвета для разных линий на одном графике. Функция возвращает кортеж с двумя значениями: координатами X и Y точки пересечения. Теперь давайте проверим работу функции на двух линиях с уравнениями y=3x+5 и y=2x+3 соответственно.

 L1=Линия(3,5) #Уравнение прямой y=3x+5
L2=Line(2,3) #Уравнение прямой y=2x+3
sol=найтирешение(L1,L2)
печать (соль)
 

При выполнении приведенного выше фрагмента кода генерируется следующий вывод:

Вывод функции, находящей решение с y=mx+c

Приведенная выше функция сообщает, что координаты (-2,-1) находятся в точке пересечения двух линий. Это можно проверить, подставив значения в уравнения. Вышеприведенный график также доказывает функцию, так как это место пересечения двух графиков.

Поиск точки пересечения с линейным уравнением как ay=bx+c

Этот формат линейных уравнений обычно используется в линейной алгебре. Здесь переменная y также имеет коэффициент. В этом случае наклон уравнения становится равным b/a , а константа становится c/a . Эти значения можно подставить в формулу x, выведенную ранее, или провести новый вывод для этого формата уравнений. Новый вывод будет следующим:

Первое уравнение в форме ay=bx+cВторое уравнение в форме ay=bx+cВывод X и Y из уравнения в форме ay=bx+c

Выше полученная формула для x, ее можно легко закодировать в функции Python. Но то же определение класса, которое использовалось для более раннего формата, не будет работать для этого формата. Требуется новое объявление класса. Это показано во фрагменте кода ниже:

 class Строка:
  def __init__(self,ycoeff,xcoeff,const):
    self. a=ycoeff
    self.b=xcoeff
    self.c=const
 

Эта реализация Class Line отличается от приведенной выше реализации. Здесь есть три входных параметра в функции-конструкторе. Первый параметр — это коэффициент y или «a» в формате уравнения. Второй — это x-коэффициент или «b» в формате уравнения. Последняя является константой или «c» в формате Equation. Класс состоит из трех переменных a,b и c для формирования уравнения формата ay=bx+c

Следующая функция findSolution() находит решение двух линейных уравнений формата ay=bx+c, используя формулу для вывода x и помещая значение x в одно линейное уравнение, чтобы найти y. Это показано в коде ниже:

 def findSolution(L1,L2):
  х=((L1.a*L2.c)-(L2.a*L1.c))/((L2.a*L1.b)-(L1.a*L2.b))
  y=(L1.b*x+L1.c)/L1.a
  X=[x для x в диапазоне (-10,11)]
  Y1=[((L1.b*x)+L1.c)/(L1.a) для x в X]
  Y2=[((L2.b*x)+L2.c)/(L2.a) для x в X]
  plt.plot(X,Y1,'-r',label=f'{L1.a}y={L1.b}x+{L1.c}')
  plt.plot(X,Y2,'-b',label=f'{L2.a}y={L2.b}x+{L2. c}')
  plt.legend(loc='вверху справа')
  plt.show()
  возврат (х, у)
 

Здесь функция принимает на вход линии L1 и L2, находит точку пересечения и возвращает ее в виде кортежа. Он использует производную формулу для x. Он также отображает две линии на графике для лучшей визуализации и понимания. Давайте проверим функцию на двух уравнениях как 3y=4x+6 и 2y=5x+3 .

 L1=Line(3,4,6) #Уравнение для строки 3y=4x+6
L2=Line(2,5,3) #Уравнение для строки 2y=5x+3
sol=найтирешение(L1,L2)
печать (соль)
 

Вывод приведенного выше фрагмента кода выглядит следующим образом:

Вывод функции, находящей решение с ay=bx+c

В приведенном выше выводе функция обеспечивает точку пересечения в виде (0.428,2.571), удовлетворяющую двум уравнениям, заданным в качестве входных данных. График двух уравнений, как показано выше, поддерживает вывод функции. ]

Эта статья посвящена простой реализации поиска пересечения двух точек. Для получения дополнительных реализаций линейной алгебры в Python настоятельно рекомендуется обратиться к документации NumPy Linalg.

Код для справки

Вот полный код реализации условия задачи.

Код для y=mx+c Line Equation:

 импортировать matplotlib.pyplot как plt
Линия класса:
  def __init__(я, наклон, константа):
    self.m=наклон
    self.c=const
деф найтиРешение(L1,L2):
  х=(L1.c-L2.c)/(L2.m-L1.m)
  у=L1.m*x+L1.с
  X=[x для x в диапазоне (-10,11)]
  Y1=[(L1.m*x)+L1.c для x в X]
  Y2=[(L2.m*x)+L2.c для x в X]
  plt.plot(X,Y1,'-r',label=f'y={L1.m}x+{L1.c}')
  plt.plot(X,Y2,'-b',label=f'y={L2.m}x+{L2.c}')
  plt.legend(loc='вверху справа')
  plt.show()
  возврат (х, у)
L1=Line(3,5) #Уравнение прямой y=3x+5
L2=Line(2,3) #Уравнение прямой y=2x+3
sol=найтирешение(L1,L2)
печать (соль)
 

Код для ay=bx+c Уравнение строки:

 импортировать matplotlib.pyplot как plt
Линия класса:
  def __init__(self,ycoeff,xcoeff,const):
    self.a=ycoeff
    self.b=xcoeff
    self.c=const
деф найтиРешение(L1,L2):
  х=((L1. a*L2.c)-(L2.a*L1.c))/((L2.a*L1.b)-(L1.a*L2.b))
  y=(L1.b*x+L1.c)/L1.a
  X=[x для x в диапазоне (-10,11)]
  Y1=[((L1.b*x)+L1.c)/(L1.a) для x в X]
  Y2=[((L2.b*x)+L2.c)/(L2.a) для x в X]
  plt.plot(X,Y1,'-r',label=f'{L1.a}y={L1.b}x+{L1.c}')
  plt.plot(X,Y2,'-b',label=f'{L2.a}y={L2.b}x+{L2.c}')
  plt.legend(loc='вверху справа')
  plt.show()
  возврат (х, у)
L1=Line(3,4,6) # Уравнение для строки 3y=4x+6
L2=Line(2,5,3) #Уравнение для строки 2y=5x+3
sol=найтирешение(L1,L2)
печать (соль)
 

Пересечение двух линейных прямых линий в Excel

Точки пересечения могут быть полезны для понимания данных, поскольку пересечения дают одинаковые значения для разных наборов данных. Excel может помочь автоматизировать задачу поиска точки пересечения двух линий, используя функции =slope() и =intersection() и заменяя их значения заданными уравнениями. В этой статье мы узнаем, как найти точку пересечения двух прямых в Excel.

Процедура поиска пересечения

Пересечение — это точка, в которой две кривые имеют одинаковые координаты. Уравнение прямой линии можно записать как y = mx + c, где м — это наклон , а c — точка пересечения прямой. Например, вам даны две строки строка1: y = m ₁ x + c ₁ и строка 2: y ₁ = m ₂ x + c _{2 9003 7 где 1 , в 1 — наклон и пересечение линии 1 и m 2, c 2 — наклон и пересечение линии 2 . Считая точку пересечения (a, b) .}

Ниже приведены шаги

Шаг 1: As, (a, b) точка пересечения двух прямых, что означает, что (a, b) удовлетворяет уравнению обеих прямых b = m ₁ а + с ₁ т. е. и b = m ₂ а + с ₂ .

Шаг 2: Приравнивая значения b , найти значение a ,m ₁ a+ c ₁ = m _{2 +} c 900 36 2. .

Шаг 3: После преобразования уравнения значение a получается равным ,.

Шаг 4: Теперь подставьте значение на в любое из уравнений, чтобы найти значение b ,b = m ₁ + c ₁ .

Функции Excel, используемые при расчете пересечения

Есть две функции Excel, которые помогают вычислить точку пересечения линии.

=НАКЛОН(значения_у, значения_х)

Функция наклон вычисляет средний наклон набора данных. Функция наклона принимает два аргумента, первый аргумент — значения y, , а второй аргумент — значения x .

=INTERCEPT(y_values, x_values)

Функция перехвата вычисляет средний перехват набора данных. Функция перехвата принимает два аргумента, первый аргумент — значения y , а второй аргумент — значения x .

Расчет пересечения линий в Excel

Как правило, уравнение линий не дается, но даются точки данных уравнения. Мы рассчитаем пересечение, используя ту же процедуру, что описана выше. Например, «Аруши» — аналитик данных, и ей дали 9 баллов.0009 два набора данных , каждый из которых содержит значения x и y . «Аруши» нарисовала график из двух линий, и она хотела найти пересечение линий, проведенных из заданного набора данных.

Ниже приведены шаги

Шаг 1: Во-первых, нам нужно найти наклон и пересечение обеих линий. Для этого сделайте четыре столбца A9:A12 , указав имя точки пересечения и наклон каждой линии.

Шаг 2: Ячейка C9 должна быть заполнена наклоном линии 1 . Используйте функцию =НАКЛОН() для расчета среднего наклона заданных точек данных, т. е. =НАКЛОН(B4:B6, A4:A6) .

Шаг 3: Нажмите Введите . Наклон линии 1 равен 1 .

Шаг 4: Ячейка C10 должна быть заполнена наклоном линии 2 . Используйте =НАКЛОН() функция для расчета среднего наклона заданных точек данных, т. е. =НАКЛОН(E4:E6, D4:D6).

Шаг 5: Нажмите Введите . Наклон линии2 равен 2 .

Шаг 6: Ячейка C11 должна быть заполнена точкой пересечения строки 1 . Используйте функцию =INTERCEPT() для вычисления среднего значения пересечения заданных точек данных, т. е. =INERCEPT(B4:B6, A4:A6) .

Шаг 7: Нажмите Введите . Точка пересечения линии 1 равна 0 .

Шаг 8: Ячейка C12 должна быть заполнена точкой пересечения строки 2 . Используйте функцию =INTERCEPT() для вычисления среднего значения пересечения заданных точек данных, т. е. =INERCEPT(E4:E6, D4:D6).

Шаг 9: Нажмите Введите . Точка пересечения линии 2 равна -1 .

Шаг 10: Теперь у нас есть наклон и пересечение обеих линий. Теперь нам нужно найти точку пересечения двух прямых. Для этого сделайте две колонки A15:A16 , указав название точки координат пересечения.

Шаг 11: Ячейка B15 должна быть заполнена координатой x пересечения линий. Используйте формулу, как описано выше, чтобы вычислить координату x пересечения линий.

Шаг 12: Нажмите Введите . Координата x точки пересечения равна 1 .