Как найти x0 формула: Вершина параболы — урок. Алгебра, 8 класс.

Формула Лейбница

В заключение этого раздела приведем формулу Лейбница, которая позволяет вычислить производную или дифференциал n-го порядка от произведения 2-х функций.

y=uv

y=uv+vu

y=uv+2uv+vu

y=uv+3uv+3uv+vu

…..

Отсюда вытекает общее формальное правило:

Чтобы найти производную (дифференциал) от (uv)⁽ⁿ⁾ надо по формуле бинома Ньютона разложить n-ю степень суммы (u+v)ⁿ и затем заменить показатели степеней u и v

указателями порядка производных, причем нулевые степени (u⁰ и v⁰), входящие в крайние члены разложения заменить самими функциями u и v (то есть, «производными нулевого порядка»).

Для дифференциала n-го порядка справедлива формула

dⁿ(uv)=(uv)⁽ⁿ⁾dxⁿ

dy=vdu+udv

d²y=vd²u+2dudv+ud²v

d³y=vd³u+3d²udv+3dud²

v +ud³v и т.п.

Применение производных к исследованию свойств функций.

Возрастание и убывание функций.

Экстремум.

Определение1. Функция y=f(x) называется возрастающей в промежутке (a,b), если для любых x₁, x₂(a,b) большему из них соответствует и большее значение функции.

x₁(a,b), x₂(a,b), x₂>x₁  f(x₂)>f(x₁)

Определение 2. Функция y=f(x) называется убывающей на

(a,b), если для любых x₁, x₂(a,b) большему x соответствует меньшее значение f(x).

x₁(a,b), x₂(a,b), x₂>x₁  f(x₂)<f(x₁)

Из этих определений следует, что для возрастающих функции sign(y)=sign(x), в силу чего их отношение положительно:

Для убывающей функции sign(y)=-sign(x) 

Если функция на переходит от возрастания к убыванию, или наоборот, ее называют колеблющейся на (a,b).

Значения x, при которых f(x) достигает своих наибольших или наименьших значений по сравнению с соседними, называют точками максимума и минимума.

Определение 3. x=x₀ — точка максимума f(x), а f(x₀) — максимум функции, если существует некоторая окрестность x₀ (т.е. x₀—, x₀+) такая, что значение функции в любой точке x₁(x₀—, x₀+) будет меньше , чем ее значение в x₀, то есть меньше, чем максимум f(x₀

)

f(x₀+x)<f(x₀) при любом |x|<

Аналогично определяются точки максимума и минимума функции

f(x₀+x)>f(x₀) при любом |x|<

Дать графические примеры.

Точки минимума и максимума объединяются под общим названием – точки экстремума (экстремальные точки), а минимум и максимум функции – экстремумы функции.

Экстремумы функции, определенные выше, часто называют строгими экстремумами, в отличие нестрогих

f(x₀+

x)f(x₀) и f(x₀+x)f(x₀)

Из определения вытекает, что вне -окрестности x₀ значения f(x) могут быть любыми, по отношению к f(x₀).

Например за пределами (x₀—, x₀+), f(x+x)>f(x₀) – где x₀ — точка максимума, и аналогично f(x+x)<f(x₀), если x₀ — точка минимума f(x).

Таким образом понятия максимальной и минимальной функции носят локальный (местный) характер. Далее мы установим признаки возрастания и убывания функций и признаки экстремума функций, основанные на понятии производной.

Теоремы Ферма, Ролля, Лагранжа и Коши.

Теорема Ферма. Если f(x) непрерывна на (a,b) и в x₀(a,b) достигает максимума (минимума) и дифференцируема в x₀, то ее производная в этой точке равна 0:

f(x₀)=0

Доказательство. Допустим, что f(x₀) – максимум (минимум) функции. При достаточно малых x, точка x₀+x независимо от знака 

x.

1. Пусть x>0  , переходя к пределу при x+0 получим: , как предел неположительной величины.

b) x<0 

Так как для дифференцируемой в x₀ функции производная слева равна производной справа  f(x₀)=0, теорема доказана.

Аналогично проводится доказательство и для x₀ — точки минимума, и для случая строгих неравенств.

Геометрический смысл очевиден: касательная к графику f(x) в точке экстремума, в которой f(x) дифференцируема, параллельна оси OX.

рисунок

Теорема Ролля. Если f(x)

непрерывна на [a,b] и дифференцируема в (a,b), а на концах [a,b] принимает равные значения: f(a)=f(b)=c, то в промежутке (a,b) найдется точка x₀ (по крайней мере одна), в которой f(x₀)=0.

Доказательство. Рассмотрим случай f(x)c, x[a,b], удовлетворяющий условиям теоремы:  f(x)=(c)=0 для любых x₀.

Если же f(x)c будучи непрерывной на

[a,b], она достигает своих наибольших и наименьших значений – M и m (см. свойства непрерывной функции). При этом возможны 3 случая:

a) f(a)=f(b)=m,  f(x) достигнет наибольшего M в x₀(a,b), то есть внутренней точке [a,b]. В точке x₀ функция дифференцируема и тогда по теореме Ферма  f(x₀)=0.

b) f(a)=f(b)=M,  f(x) достигнет минимума в некоторой

x₀(a,b), и снова, по теореме Ферма  f(x₀)=0.

c) Пусть теперь f(x) такова, что f (x₀)=M и  f (x₀)=m, x₀,x₀(a,b),  f(x₀)=0 и f( x₀)=0 по теореме Ферма.

Геометрический смысл теоремы Ролля: при выполнении условий теоремы Ролля на графике f(x) найдется хотя бы одна точка x₀, касательная в которой будет параллельна оси ОХ.

Нарушение хотя бы одного из условий ведет к нарушению вывода из теоремы.

Рисунок Рисунок Рисунок

В частном случае, когда f(a)=f(b)=0 теорема Ролля имеет очень полезное для приложений толкование: Между двумя нулями дифференцируемой функции всегда заключен по крайней мере один нуль ее производной, то есть эта точка может оказаться max или min.

Теорема Коши. Если f(x) и (x) непрерывны на [a,b] и дифференцируемы в (a,b), при чем (x)0 на (a,b), то отношение конечных приращений этих функций на отрезке [a,b] равно отношению их производных в некоторой точке, которая может быть не единственной:

(b)(a) т. к. (x) 0 на (a,b)  т.Ролля.

Доказательство. Введем вспомогательную F(x)=f(x)-(x), где =const. Выберем теперь  такое, чтобы F(x) удовлетворяла условиям теоремы Ролля. Достаточно потребовать, чтобы F(a)=F(b). Другими словами:

F(a)-(a)=f(b)-(b) 

— конечное значение, т.к. (b)(a)

Тогда хотя бы в одной точке c(a,b) F(c)=0  

Теорема доказана.

Теорема Лагранжа (частный случай теоремы Коши). Пусть f(x) непрерывна на [a,b] и дифференцируема в (a,b). Тогда конечное приращение f(x) на [a,b] равно произведению длины отрезка [a,b] на значение производной в некоторой внутренней точке (a,b):

f(a)-f(b)=f(c)(b—a)

Полагая в теореме Коши (x)=x получим: (b)-(a)=b—a, (x)1  (c)=1

Поэтому

(*) т.е.

f(b)-f(a)=f(c)(b-a)

Геометрический смысл теоремы Лагранжа определяется формулой (*) . В ней левая часть есть угловой коэффициент хорды MN, соединяющей концы графической функции

РИСУНОК

Правая часть формулы – угловой коэффициент в точке P с абсциссой x=c(a,b)

f(c)=tg   tg =tg , то есть хорда и касательная параллельны.

Таким образом, на произвольной дуге графика дифференцируемой функции всегда найдется хотя бы одна точка, в которой касательная будет параллельна хорде, стягивающей концы дуги.

Тот же геометрический смысл можно придать и теореме Коши, если рассматривать y=f(t) и x=(t) как параметрические уравнения кривой в плоскости XOY, а x считать параметром этой кривой.

Раскрытие неопределенностей.

Правило Бернулли-Лопиталя.

Раскрытием неопределенности в математическом анализе называют нахождение предела , когдаf(x) непрерывна вблизи a, но не определена в самой этой точке, а непосредственная подстановка в функцию x=a приводит к выражению неопределенного вида

, , 0, —, 1^,0^,⁰.

Опираясь на теорему Коши, выведем правило Бернулли-Лопиталя для раскрытия неопределенностей, используя производные.

Основными видами неопределенностей являются две:

и ,

раскрытие которых сводится к нахождению предела отношения двух бесконечно малых или бесконечно больших величин. Остальные виды сводятся к двум последним.

1. Рассмотрим неопределенность (приxa), требуется найти , когда и . Примем f(a)=(a)=0. Тогда f(x) и (x) будут непрерывными в x=a. Предположим также, что f(x) и (x) дифференцируемы вблизи x=a причем (a)0. В этом случае:

, (L — конечно или нет)

Доказательство. Применим к f(x) и (x) теорему Коши на отрезке [x₀,a), где x₀ окрестности a, в которой f и  непрерывны и дифференцируемы (может за исключением a). Тогда

В силу того, что f(a)=(a)=0 

, где c(x₀,a)

Если теперь x₀a,  и ca, поэтому

Теперь, если положить x₀=x, c=x 

то есть в данном случае правило Бернулли-Лопиталя выполняется.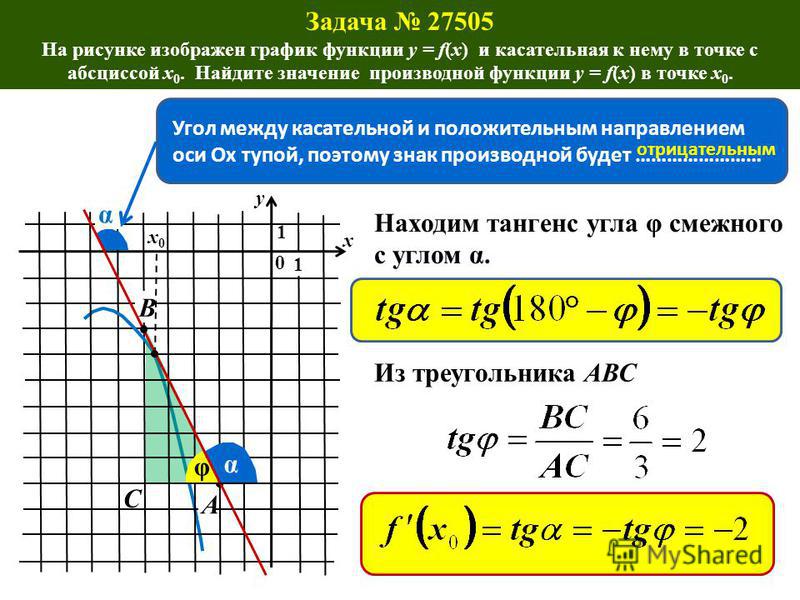

Примеры:

2. Неопределенность (x). Докажем справедливость правила Бернулли-Лопиталя и в этом случае.

Итак требуется найти , еслии .

Предположим, что для достаточно больших x (|x|>M) обе функции дифференцируемы, (x)0 и что существует (конечный или бесконечный) .

Докажем, что

Доказательство. Перейдем к новому аргументу . Тогда, x  u0. Нетрудно видеть, что к отношению правило Бернулли-Лопиталя применимо: в окрестности u=0 f и  дифференцируемы, а и существует

Тогда, принимая правило Бернулли-Лопиталя, получим

Возвращаясь к x, получим:

Правило остается в силе при x+ или x—.

Пример. .

3. Неопределенность (xa). Пусть теперь нужно найти , если .

Как и в случае 1., пусть f и  дифференцируемы вблизи a, и (x)0.

Тогда, если существует (конечный или бесконечный) , то

Доказательство. Пусть x₁ и x₂  окрестности x=a, и пусть x₁<x₂<a, если точки берутся слева от a, или x₁>x₂>a — если справа. Тогда на отрезке [x₁,x₂] или [x₂,x₁]) к отношению f(x) и (x) применима теорема Коши:

c[x₁,x₂]

Далее пусть

Зададим теперь >0 и найдем ()>0 такое, что при |x—a|<() 

(*)

Выберем теперь x так, чтобы |x₁—a|<() и зафиксируем его. Тогда, согласно условию выбора x₂  |x₂—a|<() и |c—a|<(), так как c[x₁,x₂]. Поэтому, в силу (*) будем иметь:

или

Заменяя в этом неравенстве отношение производных отношением конечных приращений функций, получим



(1)

Если теперь x₂a, не изменяя x₁, то, так как ,

другими словами при заданном , найдется ₁(), что при |x₂—a|<₁() 

или

Перемножая теперь почленно неравенства (1) и (2) (что возможно , так как все члены неравенства (2) положительны), получим

и

Другими словами разность между и постоянной A будет бесконечно малой величиной.

Следовательно и следовательно

(3)

Пусть теперь . Тогда f(x)0 в некоторой малой окрестности a (иначе не было бы бесконечно большой величиной). С другой стороны, а поэтому к обратному отношению применимо предыдущее правило:

Из последней формулы вытекает справедливость и формулы (3).

Пример.

4. Неопределенность (x). Правило применимо, если f(x) и (x) дифференцируемы при любом x, |x|<M, причем (x)0 и при условии, что существует (конечный или бесконечный) .

Для доказательства достаточно перейти к новому * и использовать правило для случая 3.

Пример. .

Правило Бернулли-Лопиталя иногда приходится применять несколько раз, если появляется неопределенность в отношении . Для этого необходимо соблюдение условий применимости теоремы Коши к производной

.

Примеры 1) 3 раза правило Бернулли-Лопиталя

2) . n раз правило Бернулли-Лопиталя

Примение правила Лопиталя к раскрытию неоределенности

0, —, 1^,0^,⁰ покажем на примерах. Идея — эти неопределенности сводятся в виду или, а в последних 3-х случаях с применением логарифмирования.

Пример 1.

Представим в виде: (x^k – бесконечно малая величина,  — бесконечно большая величина)  . x0

Пример 2.  —, но

, применяя правило Лопиталя, получим:

Пример 3.

Пример 4.

Правило Лопиталя не применимо, если не существует . Однако это еще не означает, что не существует. Просто в этом случае правило Лопиталя нельзя использовать.

Пример. , тогда как .

Признаки возрастания и убывания функций.

Определения возрастания и убывания функций было дано ранее.

Теорема 1) Если f(x), дифференцируемая на отрезке [a,b], возрастает на этом отрезке, то f(x) неотрицательна на [a,b], то есть

f(x)0, x[a,b], если f(x),

2) Если f(x)непрерывна на[a,b]и дифференцируема в(a,b), причемf(x)>0, x(a,b),  f(x)возрастает на[a,b].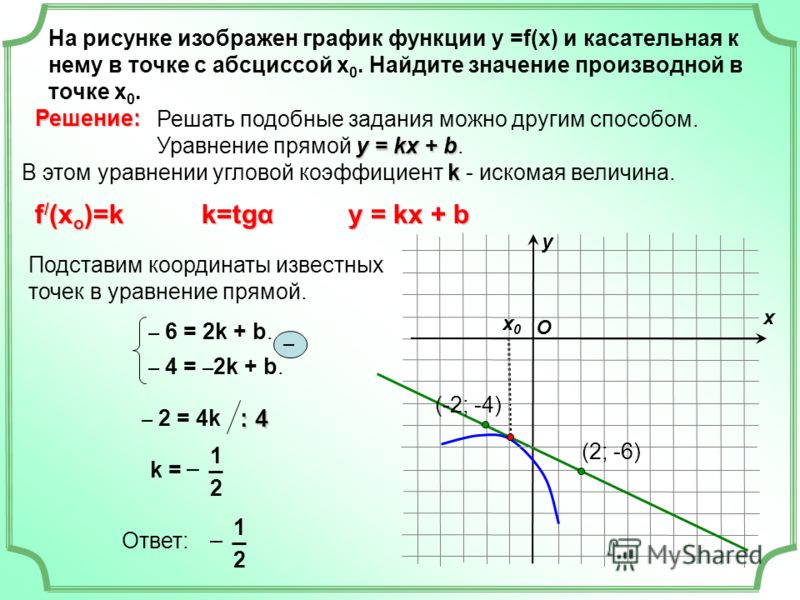

Исчисление I — метод Ньютона

Онлайн-заметки Пола
Главная / Исчисление I / Применение производных / Метод Ньютона

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.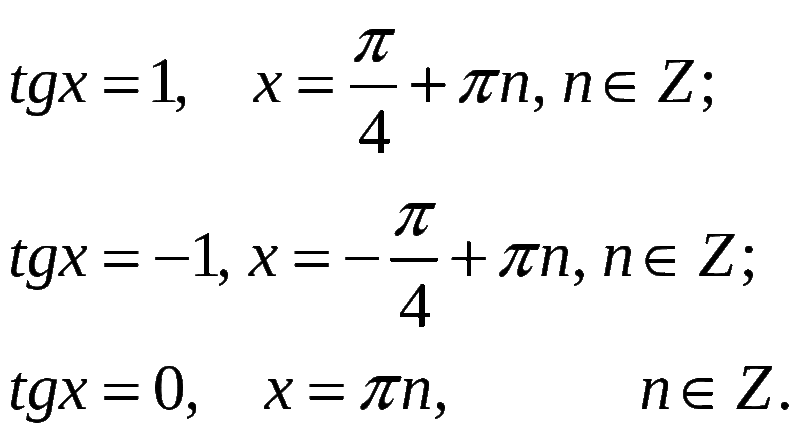

Раздел 4.13: Метод Ньютона

Следующее приложение, которое мы рассмотрим в этой главе, является важным приложением, которое используется во многих областях. Если вы дочитали главу до этого места, вполне возможно, что у вас сложилось впечатление, что многие приложения, которые мы рассмотрели, созданы нами только для того, чтобы заставить вас работать. Это прискорбно, потому что все приложения, которые мы рассмотрели до этого момента, являются реальными приложениями, которые действительно используются в реальных ситуациях. Проблема часто заключается в том, что для работы с более содержательными примерами приложений нам потребуется больше знаний, чем мы обычно имеем, о науке и/или физике, стоящей за проблемой. Без этих знаний мы застряли на некоторых довольно упрощенных примерах, которые часто не кажутся очень реалистично, и из-за этого трудно понять, что приложение, на которое мы смотрим, является реальным приложением.

В этом разделе это изменится. Это приложение, которое мы все можем понять, и мы все можем понять, что его нужно делать время от времени, даже если мы не понимаем физику / науку, стоящую за реальным приложением.

В этом разделе мы рассмотрим метод аппроксимации решений уравнений. Мы все знаем, что иногда приходится решать уравнения, и на самом деле мы сами решили довольно много уравнений до этого момента. Во всех примерах, которые мы рассмотрели к этому моменту, мы действительно смогли найти решения, но не всегда возможно сделать это точно и/или выполнить работу вручную. Вот где это приложение вступает в игру. Итак, давайте посмотрим, что представляет собой это приложение.

Предположим, что мы хотим приблизить решение к \(f\left( x \right) = 0\), а также предположим, что мы каким-то образом нашли начальное приближение к этому решению, скажем, \({x_0}\) . Это начальное приближение, вероятно, не так уж хорошо, на самом деле это может быть не более чем быстрое предположение, которое мы сделали, и поэтому мы хотели бы найти лучшее приближение. Это достаточно легко сделать. Во-первых, мы получим касательную к \(f\left( x \right)\)в \({x_0}\).

\[y = f\left( {{x_0}} \right) + f’\left( {{x_0}} \right)\left( {x — {x_0}} \right)\]

Теперь взгляните на график ниже.

Синяя линия (если вы все равно читаете это в цвете…) — это касательная в точке \({x_0}\). Мы можем видеть, что эта линия будет пересекать ось \(x\) гораздо ближе к фактическому решению уравнения, чем \({x_0}\). Давайте назовем эту точку, где касательная в \({x_0}\) пересекает \(x\)-ось \({x_1}\), и мы будем использовать эту точку как наше новое приближение к решению.

Итак, как нам найти эту точку? Ну, мы знаем его координаты, \(\left( {{x_1},0} \right)\), и мы знаем, что он находится на касательной, поэтому подставьте эту точку к касательной и найдите \({x_1}\ ) следующим образом,

\[\begin{align*}0 & = f\left( {{x_0}} \right) + f’\left( {{x_0}} \right)\left( {{x_1} — {x_0}} \ справа)\\ {x_1} — {x_0} & = — \frac{{f\left( {{x_0}} \right)}}{{f’\left( {{x_0}} \right)}}\ \ {x_1} & = {x_0} — \frac{{f\left( {{x_0}} \right)}}{{f’\left( {{x_0}} \right)}}\end{align* }\]

Итак, мы можем найти новое приближение, если производная не равна нулю в исходном приближении.

Теперь мы повторяем весь процесс, чтобы найти еще лучшее приближение. Мы формируем касательную к \(f\left( x \right)\)в \({x_1}\) и используем ее корень, который мы назовем \({x_2}\), как новое приближение к фактическое решение. Если мы это сделаем, то придем к следующей формуле.

\[{x_2} = {x_1} — \frac{{f\left( {{x_1}} \right)}}{{f’\left( {{x_1}} \right)}}\]

Эта точка также показана на графике выше, и из этого графика видно, что если мы продолжим следовать этому процессу, то получим последовательность чисел, которые очень близки к фактическому решению. Этот процесс называется методом Ньютона.

Вот общий метод Ньютона

Метод Ньютона

Если \({x_n}\) является приближенным решением \(f\left( x \right) = 0\) и если \(f’\left ( {{x_n}} \right) \ne 0\) следующее приближение дается выражением,

\[{x_{n + 1}} = {x_n} — \frac{{f\left( {{x_n}} \right)}}{{f’\left( {{x_n}} \right)}} \]

Это должно привести к вопросу, когда мы остановимся? Сколько раз мы проходим через этот процесс? Одной из наиболее распространенных точек остановки в процессе является продолжение до тех пор, пока два последовательных приближения не согласуются с заданным числом знаков после запятой.

Прежде чем работать с любыми примерами, мы должны решить две проблемы. Во-первых, нам действительно нужно решить \(f\left( x \right) = 0\), чтобы можно было применить метод Ньютона. На самом деле это не такая уж большая проблема, но нам нужно убедиться, что уравнение находится в этой форме, прежде чем использовать метод.

Во-вторых, нам нужно каким-то образом получить начальное приближение к решению ( т.е. нам как-то нужно \({x_0}\)). Один из наиболее распространенных способов получить в свои руки \({x_0}\) — это набросать график функции и использовать его для получения оценки решения, которое мы затем используем как \({x_0}\). Другой распространенный метод: если мы знаем, что есть решение функции в интервале, мы можем использовать среднюю точку интервала как \({x_0}\).

Давайте рассмотрим пример метода Ньютона.

Пример 1 Используйте метод Ньютона, чтобы определить приближение к решению \(\cos x = x\), которое лежит в интервале \(\left[ {0,2} \right]\). Найдите приближение к шести знакам после запятой.

Показать решение

Во-первых, обратите внимание, что нам не давали первоначального предположения. Однако нам дали интервал для поиска. Мы будем использовать это, чтобы получить наше первоначальное предположение. Как отмечалось выше, общее эмпирическое правило в этих случаях состоит в том, чтобы принять за начальное приближение середину интервала. Итак, мы будем использовать \({x_0} = 1\) в качестве нашего первоначального предположения.

Далее, напомним, что мы должны иметь функцию в виде \(f\left( x \right) = 0\). Поэтому мы сначала перепишем уравнение как

\[\cos х — х = 0\]

Теперь мы можем записать общую формулу метода Ньютона. Это часто немного упрощает работу, поэтому, как правило, это неплохая идея.

\[{x_{n + 1}} = {x_n} — \frac{{\cos x_{n} — x_{n}}}{{ — \sin x_{n} — 1}}\]

Давайте теперь получим первое приближение.

\[{x_1} = 1 — \frac{{\cos \left( 1 \right) — 1}}{{ — \sin \left( 1 \right) — 1}} = 0,7503638679\]

В этом месте мы должны отметить, что фраза «шесть знаков после запятой» не означает просто получить \({x_1}\) до шести знаков после запятой, а затем остановиться. Вместо этого это означает, что мы продолжаем до тех пор, пока два последовательных приближения не согласуются с шестью десятичными знаками.

Учитывая это условие остановки, нам явно нужно сделать как минимум еще один шаг.

\[{x_2} = 0,7503638679 — \frac{{\cos \left( 0,7503638679 \right) — 0,7503638679}}{{ — \sin \left( {0,7503638679} \right) — 1}} = 0,7391128909\]

Хорошо, мы продвигаемся вперед. У нас есть приближение к 1 знаку после запятой. Давайте сделаем еще один, оставив детали вычислений вам.

\[{x_3} = 0,7390851334\]

С точностью до трех знаков после запятой. Нам понадобится еще один.

\[{x_4} = 0,7390851332\]

Теперь у нас есть два приближения, которые согласуются с точностью до 9 знаков после запятой, так что мы можем остановиться. Будем считать, что решение приблизительно равно \({x_4} = 0,7390851332\).

В этом последнем примере мы увидели, что нам не нужно делать слишком много вычислений, чтобы метод Ньютона дал нам приближение в желаемом диапазоне точности. Так будет не всегда. Иногда требуется много итераций процесса, чтобы достичь желаемой точности, а иногда он может полностью выйти из строя.

Следующий пример немного глуповат, но он показывает, что метод не работает.

Пример 2 Используйте \({x_0} = 1\), чтобы найти приближение к решению \(\sqrt[3]{x} = 0\).

Показать решение

Да, глупый пример. Ясно, что решение \(x = 0\), но оно имеет очень важное значение. { — \frac{2}{3}}}} = {x_n} — 3{x_n} = — 2{x_n}\]

На самом деле здесь нам не нужно делать никаких вычислений. Эти вычисления уходят все дальше и дальше от решения \(x = 0\) с каждой итерацией. Вот пара вычислений, чтобы прояснить ситуацию.

\[\begin{align*}{x_1} & = — 2\\ {x_2} & = 4\\ {x_3} & = — 8\\ {x_4} & = 16\\ & etc. \end{align* }\]

Итак, в этом случае метод терпит неудачу, и терпит неудачу эффектно.

Итак, нам нужно быть немного осторожными с методом Ньютона. Обычно он быстро находит приближение к уравнению. Однако бывают случаи, когда это потребует много работы или когда это не сработает вообще.

6.3 Метод Ньютона

Предположим, у вас есть функция $f(x)$, и вы хотите найти как можно точнее возможно там, где он пересекает ось $x$; Другими словами, вы хотите решить $f(x)=0$. Предположим, вы не знаете способа найти точное решение любым алгебраическая процедура, но вы можете использовать приближение, при условии, что его можно сделать достаточно близким к истинному значению. Метод Ньютона — это способ найти решение уравнение до любого количества знаков после запятой. Это то, что называется «итеративная процедура», означающая, что ее можно повторять снова и снова, чтобы получить ответ все большей и большей точности. Итерационные процедуры, такие как Метод Ньютона хорошо подходит для программирования компьютер. метод Ньютона использует тот факт, что касательная к кривая является хорошим приближением к кривой вблизи точки касания. 92-3$. Мы начинаем с угадывания что-то достаточно близкое к истинному значению; обычно это легко делать; давайте использовать $\ds\sqrt3\приблизительно2$. Теперь используйте касательную к кривой когда $x=2$ как приближение к кривой, как показано на рисунок 6.3.1. Поскольку $f'(x)=2x$, наклон этого касательная равна 4, а ее уравнение $y=4x-7$. Касательная линия довольно близко к $f(x)$, поэтому он пересекает ось $x$ вблизи точки которую пересекает $f(x)$, т.е. вблизи $\ds\sqrt3$. Легко найти, где касательная пересекает ось $x$: решите $0=4x-7$, чтобы получить $х=7/4=1,75$. 2+3)/(7/2)=97/56\приблизительно 1,73214$, $\ds x_3\приблизительно 1,73205$ и так далее на. Вручную это все еще немного утомительно, но с калькулятором или, даже лучше, хорошая компьютерная программа, ее довольно легко достать, много приближений. Мы уже можем догадаться, что $1,73205$ — это точно. до двух знаков после запятой, а на деле оказывается, что с точностью до 5 мест. $\квадрат$

Вы можете перетащить точку $x_0$, чтобы изменить начальное значение. Перетащите его в правую часть графика, затем перетащите его на $1$ и $0,5$. Здесь вы можете изменить функцию, например, на Math.sin(x) или Math.exp(x) или Math.pow(2,x) или 1-2/(х*х).
$x_{final}=$

Рисунок 6.3.1. Метод Ньютона.

Давайте подумаем об этом процессе в более общих чертах. Мы хотим аппроксимировать решение $f(x)=0$. Мы начинаем с приблизительного предположения, которое мы называем $\ds x_0$. Мы используем касательную линию к $f(x)$, чтобы получить новое приближение, которое, как мы надеемся, будет ближе к истинному значению. Чему равно уравнение касательной, когда $\ds ​​х=x_0$? Наклон $\ds f'(x_0)$ и линия проходит через $\ds(x_0,f(x_0))$, поэтому уравнение прямой $$ y=f'(x_0)(x-x_0)+f(x_0).$$ Теперь найдем, где это пересекает ось $x$, подставив $y=0$ и решение для $x$: $$x={x_0f'(x_0)-f(x_0)\over f'(x_0)} = x_0 — {f(x_0)\over f'(x_0)}.$$ Обычно мы хотим вычислить более одного из этих улучшенных приближения, поэтому нумеруем их последовательно; из $\ds x_0$ имеем вычислено $\ds x_1$: $$x_1={x_0f'(x_0)-f(x_0)\над f'(x_0)} = x_0 — {f(x_0)\над f'(x_0)},$$ и вообще из $\ds x_i$ мы вычисляем $\ds x_{i+1}$: $$x_{i+1}={x_if'(x_i)-f(x_i)\over f'(x_i)} = x_i — {f(x_i)\over f'(x_i)}.$$ 92+3)/(2x_i)$, как до. $\квадрат$

На практике, то есть, если вам нужно аппроксимировать значение в в ходе проектирования моста, здания или планера вы потребуется некоторая уверенность в том, что приближение, на котором вы остановились, достаточно точно. Как правило, после определенного количества десятичные разряды перестают меняться от одного приближения к другому вероятно, что эти десятичные знаки верны. Тем не менее, это может быть не достаточно уверенности, и в этом случае мы можем проверить результат на точность. 92 x_i — 2}.$$ Из графика на рисунке 6.3.2 мы предполагаем $\ds x_0=1$ в качестве отправной точки, затем, используя формулу, мы вычислить $\ds x_1=1,310478030$, $\ds x_2=1,223929096$, $\ds x_3=1,176050900$, $\ds ​​x_4=1,165926508$, $\ds x_5=1,165561636$. Итак, мы предполагаем, что первый правильно три места, но это не то же самое, что сказать $1,165$ правильно до трех знаков после запятой — $1,166$ может быть правильным, округленное приближение. Как мы можем сказать? Мы можем заменить $ 1,165 $, $1,1655$ и $1,166$ в $\tan x — 2x$; этот дает -0,002483652$, -0,000271247$, 0,0019$48654$. С момента первого два отрицательны, а третий положителен, $\tan x — 2x$ пересекает Ось $x$ между $1,1655$ и $1,166$, поэтому правильное значение равно трем места составляет $ 1,166 $.