Вычисление значений тригонометрических функций с помощью формул приведения и единичной окружности. 10-й класс
Цели и задачи:
- Образовательная: формирование умений и навыков применения формул приведения и единичной окружности для вычисления значений синуса, косинуса, тангенса углов, использование мнемонического правила для этих формул к преобразованию тригонометрических выражений
- Развивающая: учить анализировать, сравнивать, строить аналогии, обобщать и систематизировать, доказывать и опровергать.
- Воспитательная: воспитание добросовестного отношения к труду и положительного отношения к знаниям.
- Здоровьесберегающая: создание комфортного психологического климата на уроке, атмосферы сотрудничества: ученик – учитель.
Тип урока: комбинированный
Ход урока
I.
 Организационный момент
Организационный момент
Приложение 1 (Слайд 1), Приложение 2
Здравствуйте, ребята!
“Однажды царь решил выбрать из своих придворных первого помощника. Он подвёл всех к огромному дверному замку. «Кто откроет, тот и будет первым помощником.» Никто не притронулся даже к замку. Лишь один визирь подошёл и толкнул замок, который открылся. Он не был закрыт на ключ.
Тогда царь сказал: «Ты получишь эту должность, потому что полагаешься не только на то, что видишь и слышишь, но надеешься, на собственные силы и не боишься сделать попытку”.
Сегодня на уроке мы будем полагаться не только на то, что видим и слышим, но и на собственные силы и не будем бояться сделать попытку.
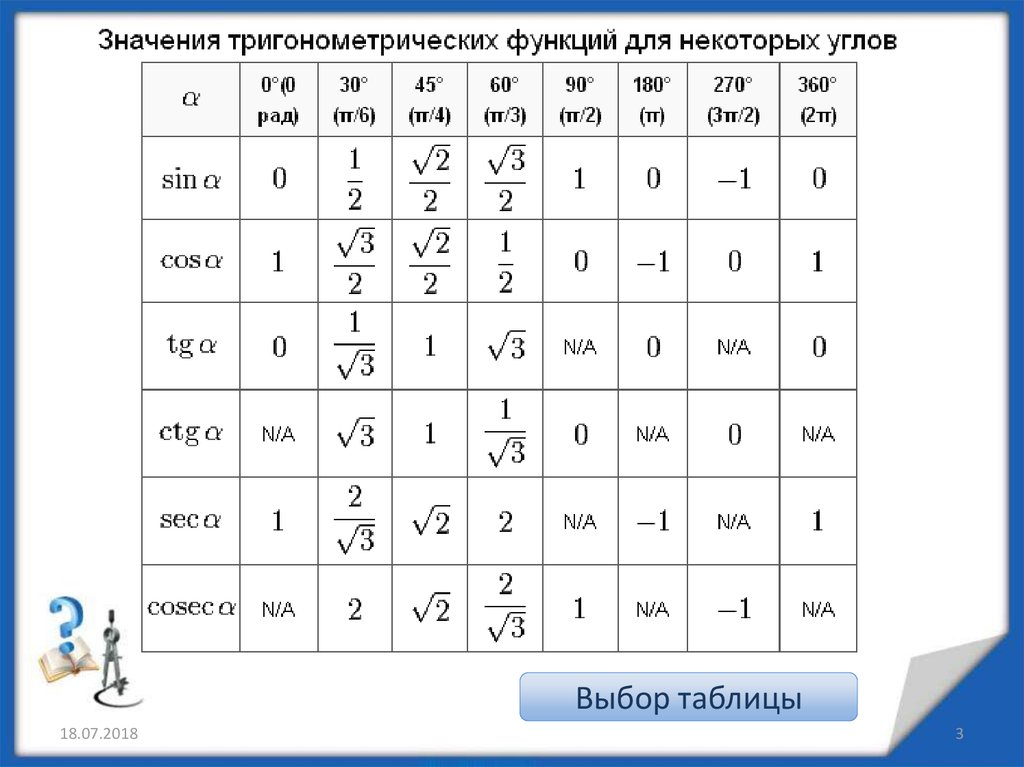
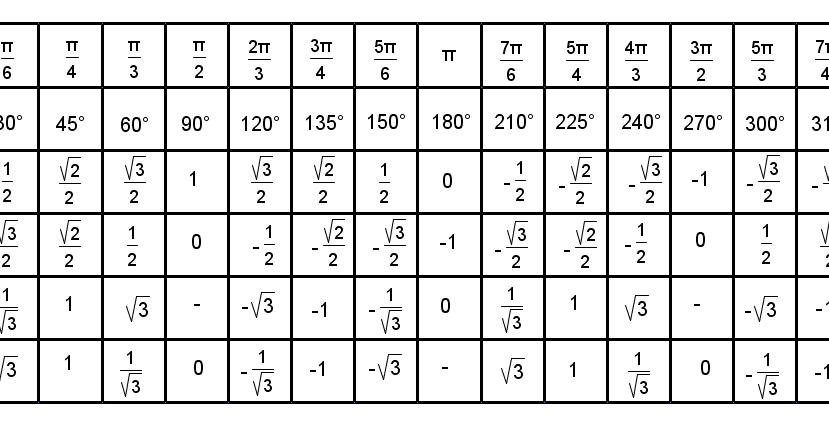
II. Повторение табличных значений
тригонометрических функций для углов 0°, 30°, 45°,
60°, 90°
Изучая раздел “Тригонометрия” мы часто
пользуемся табличными значениями
тригонометрических функций для углов 0°, 30°, 45°,
60°, 90°.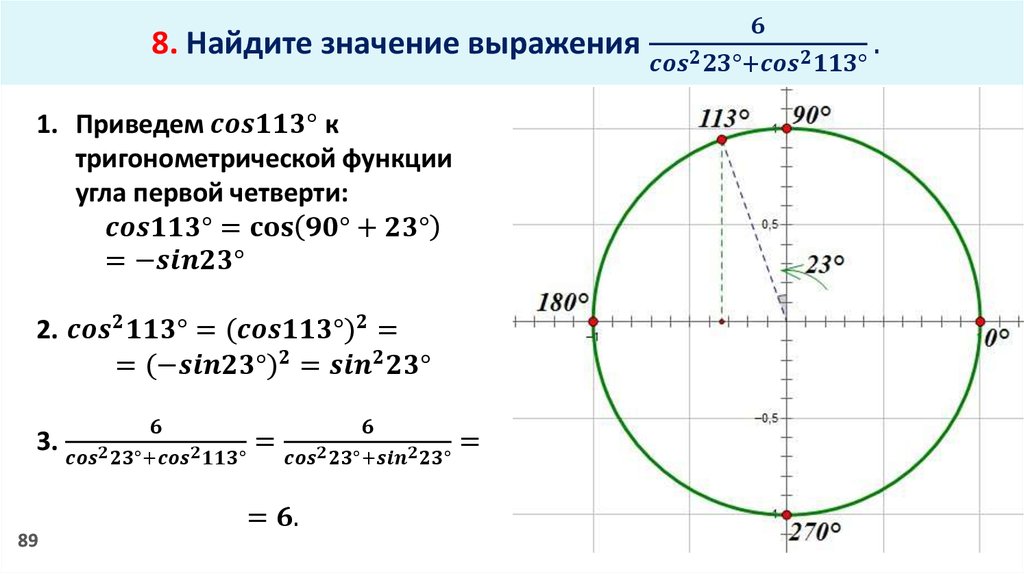
Но как быть, если какое-нибудь значение забудется? К уроку вам было дано задание найти способ или правило быстрого запоминания этих значений.
“Тригонометрия на ладони” Мнемоническое правило (объясняет ученик) (Слайд 2)
В этом случае нам поможет наша рука. На экране вы видите изображение руки и формулу где n – номер пальца.
Давайте внимательно посмотрим на нашу руку. Если провести линии через мизинец и большой палец, то они пересекутся в точке, называемой “лунный бугор”. Образуется угол 90°. Линия мизинца образует угол 0°. Проведя лучи из “лунного бугра” через безымянный, средний, указательный пальцы, получаем углы соответственно 30°, 45°, 60°. Подставляя вместо n, 0, 1, 2, 3, 4, получаем значения sin, для углов 0°, 30°, 45°, 60°, 90°. Давайте попробуем.
, , , ,
Для cos отсчет происходит в обратном порядке.
III. Этап подготовки учащихся к активному и
сознательному усвоению и закреплению материала:
А как вы думаете, можно ли вычислить значения тригонометрических функций для тупых углов? Конечно можно, и в этом нам помогут формулы приведения, которые приводят значения тригонометрических функций остальных углов к значениям тригонометрических функций для острых углов.
Формулами приведения называют формулы, которые сводят значения тригонометрических функций для углов вида к значениям острых углов. (Слайд 3
)На прошлом уроке мы с вами с помощью формул сложения вывели и доказали эти формулы, сейчас вы видите их перед вами.
Формул приведения много, а точнее 32. (Слайд 4) И
все формулы надо знать. К счастью существует
простое мнемоническое правило, позволяющее
быстро воспроизвести любую формулу приведения.
Правда для этого надо хорошо знать основы
тригонометрии – единичную окружность и способы
работы с ней.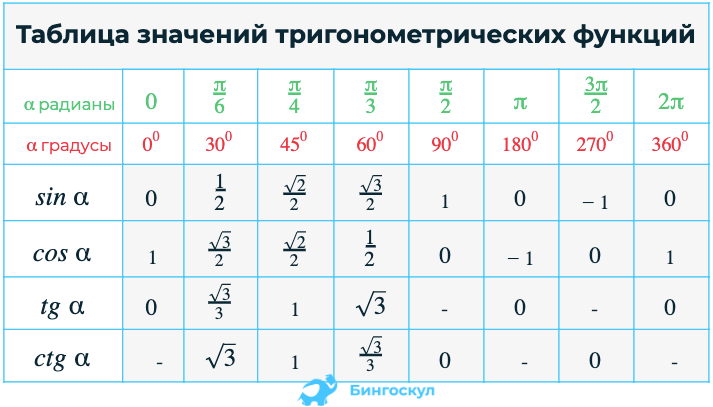
IV. Мнемоническое правило
Давайте внимательно посмотрим на эти формулы и выявим сходство и различия в них.
Каждая формула связывает между собой либо синус с косинусом, либо тангенс с котангенсом. Причём, первая функция либо меняется на вторую, либо нет.
В левой части формулы аргумент представляет собой сумму или разность одного из “основных координатных углов”: и острого угла , а в правой части аргумент
В правой части знак перед функцией либо “плюс”, либо “минус”.
Достаточно задать себе два вопроса: (Слайд 5)
1. Меняется ли функция?
Ответ: Если в формуле присутствуют углы или – это углы
вертикальной оси (рабочие), киваем головой по
вертикали и сами себе отвечаем: “Да”, если же
присутствуют углы горизонтальной оси или (спящие), то
киваем головой по горизонтали и получаем ответ:
“Нет”.
2. Какой знак надо поставить в правой части формулы?
Ответ: Знак определяем по левой части. Смотрим, в какую четверть попадает угол, и вспоминаем, какой знак в этой четверти имеет функция, стоящая в левой части.
Например:
1) “Меняется функция или нет?”
– угол вертикальной оси, киваем головой по вертикали: “Да, меняется”. Значит, в правой части будет cos .
2) “Знак?”
Угол попадает в ІV ч. sin в ІV ч. имеет знак “минус”. Значит, в правой части ставим знак “минус”.
Итак, получили формулу,
Где же применяются формулы приведения?
Одно из применений – нахождение значений тригонометрических функций различных углов с помощью приведения к углу 1-ой четверти.
Например: (Слайд 6)
I способ:
II способ:
Решение упражнений с комментированием учащихся с места:
Верна ли запись?
tg
Второе применение – упрощение
тригонометрических выражений. Но об этом мы
поговорим на следующем уроке.
Но об этом мы
поговорим на следующем уроке.
V. Работа с единичной окружностью
Значения тригонометрических функций для углов больших 90 градусов удобно находить с помощью единичной окружности. (Слайды 7-9) (Комментирует учитель).
VI. Практическая работа
1 вариант проходит к компьютерам и выполняет тест, 2 вариант вычисляет значения тригонометрических функций с помощью единичной окружности. Поднимите руки, у кого за тест 5 и 4. Молодцы, справились с заданием. Теперь поменяйтесь местами.
Выставление оценок.
V. Итог урока:
Сегодня на уроке мы рассмотрели только 3 приёма:
быстрого запоминания тригонометрических
значений, формул приведения, вычисления
тригонометрических функций с помощью единичной
окружности. Какой приём вам больше понравился?
Применение различных приёмов и способов в
математике развивает познавательную
деятельность и помогает добиться лучших
результатов.
VI. Домашнее задание
(Слайд 10)
С помощью единичной окружности выполнить №155,
формул приведения №157 стр. 296.
Спасибо за урок!
Значение тригонометрических функций
Кому-то тригонометрия покажется слишком мудреной – сплошные синусы и косинусы. Но стоит в ней поглубже разобраться и все становится проще простого, некоторым она даже понравится.
Так с чего же начать? А начнем мы с того, что науке этой не одна сотня лет, двадцать веков люди колдуют над ней. В переводе с латыни на современный лад тригонометрия означает решение треугольников или выведение всех его сторон, углов и прочих элементов на основании имеющихся данных. Само слово «тригонометрия» созвучно уже c хорошо знакомой всем геометрией. Оказывается они похожи не только на слух, но и напрямую связаны. Но, все по порядку…
Для наглядности изобразим прямоугольный треугольник, в котором стороны обозначим а, в, с и выберем один из острых углов – х:
В прямоугольном треугольнике, как вы помните, стороны, образующие прямой угол, называются катетами, в нашем случае это а и в, третья сторона с – это гипотенуза.
Так вот, еще в древности люди заметили любопытную вещь. Проследим их действия. Сперва измерим сторону в, допустим она будет 4см. Теперь а – пусть ее длина 3см. Ну а теперь разделим длины сторон а и в, т.е. возьмем их отношение и получим а/в = 3/4.
Если хотите, сделайте наоборот, разделите в на а — особой роли это не играет. Получаем 4/3. Можно и в разделить на с, но тогда надо точно знать длину гипотенузы. В общем, подойдет любой вариант.
Теперь возьмем и увеличим наш треугольник, но только так, чтобы угол х не менялся и треугольник оставался прямоугольным. Изменившиеся стороны а, в и с обозначим соответственно m, n, k.
Стороны треугольника изменились, а вот их отношения – нет!
Было а/в = 3/4, получилось m/n = 6/8 = 3/4. Это же справедливо и для других сторон. Можно свободно изменять длину сторон в прямоугольном треугольнике — уменьшать, увеличивать, но обязательно оставлять неизменным угол х – отношения сторон не изменятся. Вот такую вот закономерность и заметили древние математики. Любопытно, не правда ли?
Любопытно, не правда ли?
Но как только мы затронем угол х, сразу все отношения сторон меняются. И это имеет большое значение.
Таким образом, в прямоугольном треугольнике при неизменном угле отношения сторон не зависят от длин этих сторон, но резко становятся зависимы от этого самого угла!
Вот здесь нам предстоит первое знакомство.
Синусом угла хназывается отношение противолежащего (дальнего) катета к гипотенузе:
sin x = а/с
Косинусом угла хназывается отношение прилежащего (ближнего) катета к гипотенузе:
cos x= в/с
Тангенсом угла хназывается отношение противолежащего (дальнего) катета к прилежащему:
tg x = а/в
Котангенсом угла хназывается отношение прилежащего (ближнего) катета к противолежащему:
ctg x = в/а
Чтобы легче было запомнить, отметим для себя, что в тангенсе и котангенсе заложены отношения катетов, а в синусе и косинусе еще и гипотенуза появляется.
Как видите – ничего сложного. Все эти непонятные синусы, косинусы, тангенсы и котангенсы – это просто некоторые безразмерные числа. Для каждого угла – свои.
Кстати, может вы заметили – мы не трогали отношения гипотенузы к катетам, потому как в школьной программе они не рассматриваются и мы не станем, хотя называются они не менее мудрено — секанс и косеканс.
Если собрать в кучу все наши синусы, косинусы, тангенсы и котангенсы мы получим так называемые тригонометрические функции.
Каждое из определений всех тригонометрических функций надо знать назубок, потому что они понадобятся нам в дальнейшем для решения разного рода задач.
И еще один немаловажный момент — угол и его тригонометрические функции крепко-накрепко связаны друг с другом. Это значит, что каждому углу соответствуют свои синус и косинус, и почти каждому — свой тангенс и котангенс. Принято считать, что если у нас есть угол, то его синус, косинус, тангенс и котангенс автоматически становятся известны! Это же утверждение выполняется и в обратном порядке — дан синус, косинус или еще какая-нибудь тригонометрическая функция – значит, известен и угол. Для каждого угла создали специальные таблицы, в которых разложены его тригонометрические функции. Называются они — таблицы Брадиса, причем составлены они еще до появления компьютеров, и даже калькуляторов.
Для каждого угла создали специальные таблицы, в которых разложены его тригонометрические функции. Называются они — таблицы Брадиса, причем составлены они еще до появления компьютеров, и даже калькуляторов.
Знать тригонометрические функции всех углов совсем необязательно, да и вряд ли кому по силам, а вот для определенных запомнить все же придется.
Рассмотрим первый пример.
Из условий задачи дан только рисунок:
И больше ничего. Требуется найти длину короткого катета ВС.
Все-таки кое-какую информацию все же еще можно выудить. Сетка явно нам для чего-то дана, вот к ней и привяжемся. Как видим – гипотенуза занимает 8клеток.
Вот здесь вспоминаем магическое заклинание «мне известен угол – значит мне известны его тригонометрические функции». Но какую из них выбрать? Нам надо найти прилежащий катет. Вспоминаем, в каком из определений он упоминается. Конечно же – косинус. Вот его то и будем использовать. Итак, исходя из определения косинуса:
Cos602 = ВС/AC
Примем АС длиной в 8 клеток, получим:
Cos600=ВС/8 = 1/2 (это одно из табличных значений, которые надо знать)
Получаем ВС = 4.
Как видим все очень просто. До поры, до времени…
А что, если наш угол х (смотрим рисунок выше) сделать тупым? Сразу пропадут и катеты, и гипотенуза. Откуда брать синус? Если бы выход из этого положения не был бы найден, мы так и продолжали бы сидеть в средневековье и не узнали бы всех прелестей радио и телевидения, не существовало бы понятия интернет, да что там говорить – сидели бы при факелах и свечках – электричества-то тоже бы не было. А все потому, в основе всех этих благ цивилизации лежат уже знакомые нам тригонометрических функции. Но мы с вами общаемся, значит предки все-таки постарались. Как же им это удалось? Значение тригонометрических функций понимаешь только тогда, когда погружаешься в тонкости той или иной области нашей жизни. Если сказать на молодежном сленге – математика «рулит»!
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
В гараже в одном ряду было 25 машин,а в другом -32.Уехало 20 машин. Сколько машин осталось в гараже? Реши задачу 3 мя способами.
Решено
Помогите решить задачу В парке…
Задача
решение задачи
Пользуйтесь нашим приложением
Найти значение любой из шести тригонометрических функций
Все ресурсы для предварительного исчисления
12 диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
Precalculus Help » Тригонометрические функции » Тригонометрические функции » Найдите значение любой из шести тригонометрических функций
Решите следующее:
Возможные ответы:
Правильный ответ:
Объяснение:
Переписать в терминах функций синуса и косинуса.
Поскольку эти углы являются особыми углами от единичной окружности, значения каждого члена могут быть определены из точек координат x и y под заданным углом.
Решите каждый член и упростите выражение.
Сообщить об ошибке
Найдите значение .
Возможные ответы:
Правильный ответ:
Пояснение:
Используя тригонометрические соотношения, можно составить уравнение
.
Решение для ,
Таким образом, ответ равен 29.
Сообщить об ошибке
Найдите значение .
Возможные ответы:
Правильный ответ:
Пояснение:
Используя тригонометрические соотношения, можно составить уравнение
.
Подставив значения, указанные на картинке, мы получим уравнение
.
Решение для ,
.
Таким образом, ответ равен 106.
Сообщить об ошибке
Найдите все углы , которые удовлетворяют следующему уравнению:
Возможные ответы:
Правильный ответ:
ИЛИ
Объяснение:
Значения , соответствующие этому уравнению, будут следующими:
и
, потому что эти углы находятся в QI и QII, где sin положителен и где
.
Вот почему ответ
неверен, потому что он включает в себя входные данные, которые дают отрицательные значения, такие как:
Таким образом, ответом будет каждое кратное и, что даст следующие уравнения:
ИЛИ
Сообщить об ошибке
Оценка:
Возможные ответы:
Правильный ответ:
5
5
Объяснение: Чтобы оценить, разбейте каждый термин на 3 части и оцените каждый термин по отдельности.
Упростите, объединив три термина.
Сообщить об ошибке
Каково значение ?
Возможные ответы:
Правильный ответ:
Объяснение:
Преобразовать в виде синуса и косинуса.
Поскольку тета – это радианы, значение – это значение y точки на единичной окружности в радианах, а значение соответствует значению x для этого угла.
Точка на единичной окружности в радианах.
Следовательно и . Подставьте эти значения и решите.
Сообщить об ошибке
Решить:
Возможные ответы:
Правильный ответ:
Объяснение:
Сначала найдите значение .
На единичной окружности координата в радианах равна . Значение синуса – это значение Y, т. е. . Подставьте это значение обратно в исходную задачу.
Рационализируйте знаменатель.
Сообщить об ошибке
Найдите точный ответ для:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы оценить , решите каждое условие отдельно.
относится к значению x координаты в 60 градусах от начала координат. Значение x этого специального угла равно .
относится к значению Y координаты на 30 градусов. Y-значение этого специального угла .
относится к значению x координаты при 30 градусах. Значение x равно .
Объедините условия, чтобы решить .
Сообщить об ошибке
Найдите значение
.
Возможные ответы:
Правильный ответ:
Объяснение:
Значение относится к значению Y координаты, расположенной в четвертом квадранте.
Этот угол также от исходной точки.
Поэтому мы оцениваем .
Сообщить об ошибке
Упростите следующее выражение:
Возможные ответы:
Правильный ответ:
Объяснение:
Упростите следующее выражение:
Начните с определения угла на единичной окружности. -270 должно лежать в том же месте, что и 90. Мы доберемся туда, начав с 0 и вращая по часовой стрелке
Итак, мы знаем, что
А поскольку мы знаем, что sin относится к значениям y, мы знаем, что
Таким образом, наш ответ должен быть 1
Сообщить об ошибке
← Предыдущий 1 2 3 Следующий →
Уведомление об авторских правах
Все ресурсы Precalculus 12 диагностических тестов
380 практических тестов
Вопрос дня
Карточки
Learn by Concept
Поиск значений тригонометрических функций
Вопросы с ответами о том, как найти точные значения тригонометрических функций. Вам может понадобиться таблица значений тригонометрических функций для специальных углов.
Вам может понадобиться таблица значений тригонометрических функций для специальных углов.
Во всех приведенных ниже вопросах от вас требуется найти точные значения, если это возможно, заданных тригонометрических функций.
Вопрос 1:
грех (-π/4)
Вопрос 2:
тан ( — 3 π / 4)
Вопрос 3:
сек ( 5 π / 3)
Вопрос 4:
детская кроватка (- 5 π/3)
Вопрос 5:
соз ( 25 π / 3)
Вопрос 6:
csc ( 15 π / 6)
Вопрос 7:
грех( 17 π / 4 )
Вопрос 8:
сек ( π / 2 )
Вопрос 9:
тан ( 5 π / 6)
Вопрос 10:
csc ( 15 π / 2)
Ответы на вышеуказанные вопросы:
Примечание: sqrt означает квадратный корень.
вопрос 1: — sqrt ( 2 ) / 2
вопрос 2: 1
вопрос 3: 2
вопрос 4: sqrt(3) / 3
вопрос 5: 1 / 2
вопрос 6: 1
вопрос 7: sqrt(2) / 2
вопрос 8: не определен
вопрос 9: — sqrt(3) / 3
вопрос 10: -1
Больше страниц, посвященных математическим задачам и онлайн-тестам для самопроверки. и как найти точные значения тригонометрических функций; вопросы с ответами и подробными решениями.
Тригонометрические функции и прямоугольные треугольникиугол 0 градусов) в тригонометрии самое важное, что нужно понять, это то, что независимо от размера треугольника отношение
длин сторон остается неизменным. Таким образом, вполне естественно давать имена этим отношениям — и вот откуда берутся определения прямоугольных треугольников тригонометрических функций! В приведенном выше треугольнике прямой угол отмечен маленьким квадратом. Два других угла являются острыми углами (имеют размеры менее 90 градусов). Любой из них может быть интересующим нас углом, поскольку триггерные функции будут зависеть от того, какая сторона находится рядом (прилегает) к нашему углу, а какая сторона противоположна нашему углу. Поэтому важно обращать внимание на то, какой угол представляет интерес каждый раз, когда вы работаете с этими определениями.
Два других угла являются острыми углами (имеют размеры менее 90 градусов). Любой из них может быть интересующим нас углом, поскольку триггерные функции будут зависеть от того, какая сторона находится рядом (прилегает) к нашему углу, а какая сторона противоположна нашему углу. Поэтому важно обращать внимание на то, какой угол представляет интерес каждый раз, когда вы работаете с этими определениями.
реклама
Определения
Учитывая угол \(\theta\) (theta), как на картинке выше, мы определим шесть тригонометрических функций как:
\(\ sin(\ theta) = \dfrac{\textrm{напротив}}{\textrm{гипотенуза}}\)
\(\cos(\theta) = \dfrac{\textrm{смежный}}{\textrm{гипотенуза}}\)
\(\ tan (\ theta) = \ dfrac {\ textrm {напротив}} {\ textrm {смежный}} \)
\(\csc(\theta) = \dfrac{\textrm{гипотенуза}}{\textrm{напротив}}\)
\(\ sec (\ theta) = \ dfrac {\ textrm {гипотенуза}} {\ textrm {смежный}} \)
\(\ кроватка (\ тета) = \ dfrac {\ textrm {смежный}} {\ textrm {напротив}} \)
При изучении тригонометрии абсолютно необходимо запомнить эти определения! К счастью, вы можете щелкнуть здесь, чтобы прочитать о хорошем трюке, который вам поможет.
Применение определений
Давайте посмотрим, как определения работают на реальном примере.
Пример
Рассмотрим треугольник ниже.
Найдите точные значения шести тригонометрических функций угла \(\theta\).
Решение
Когда написано «точное значение», это означает, что вы не должны давать десятичную аппроксимацию. Это означает, что как только вы получите упрощенную дробь, вы оставите ответ как есть.
Глядя на треугольник, сторона, противоположная углу тета, имеет длину 2, а прилежащая сторона имеет длину 1. Кроме того, гипотенуза имеет длину \(\sqrt{5}\).
Это все, что нужно для расчета значений всех триггерных функций. Итак, начните подключать их и упрощайте!
\(\begin{align}\sin(\theta) &= \dfrac{\textrm{напротив}}{\textrm{гипотенуза}}\\ &= \dfrac{2}{\sqrt{5}}\end{ выровнять}\)
\(\begin{align}\cos(\theta) &= \dfrac{\textrm{adjacent}}{\textrm{гипотенуза}}\\ &= \dfrac{1}{\sqrt{5}}\end{ выровнять}\)
\(\begin{align}\tan(\theta) &= \dfrac{\textrm{напротив}}{\textrm{смежный}}\\ &= \dfrac{2}{1}\\ &= 2\end {выровнять}\)
\(\begin{align}\csc(\theta) &= \dfrac{\textrm{гипотенуза}}{\textrm{напротив}}\\ &= \dfrac{\sqrt{5}}{2}\end{ выровнять}\)
\(\begin{align}\sec(\theta) &= \dfrac{\textrm{гипотенуза}}{\textrm{adjacent}}\\ &= \dfrac{\sqrt{5}}{1}\\ & = \sqrt{5}\конец{выравнивание}\)
\(\begin{align}\cot(\theta) &= \dfrac{\textrm{adjacent}}{\textrm{opposite}}\\ &= \dfrac{1}{2}\end{align}\)
Некоторые учебники и курсы требуют от вас «рационализации» знаменателя. Это означает, что везде, где есть корень в знаменателе, такой как \(\sin(\theta)\) и \(\cos(\theta)\) выше, вы должны умножить верх и низ дроби на этот корень в чтобы исключить его из знаменателя. Опять же, это не всегда требуется, но если мы сделаем это здесь:
Это означает, что везде, где есть корень в знаменателе, такой как \(\sin(\theta)\) и \(\cos(\theta)\) выше, вы должны умножить верх и низ дроби на этот корень в чтобы исключить его из знаменателя. Опять же, это не всегда требуется, но если мы сделаем это здесь:
\(\begin{align}\sin(\theta) &= \dfrac{2 \times \sqrt{5}}{\sqrt{5} \times \sqrt{5}}\\ &= \dfrac{2\ sqrt{5}}{5}\end{align}\)
\(\begin{align}\cos(\theta) &= \dfrac{1 \times \sqrt{5}}{\sqrt{5 \times \sqrt{5}}}\\ &= \dfrac{\sqrt {5}}{5}\конец{выравнивание}\)
Важно! – Эти рационализированные ответы математически такие же, как ответы над ними. Это просто другой способ написания ответов.
А что, если вам даны только две длины треугольника? Означает ли это, что мы не можем найти другие длины? Нисколько. На самом деле вам нужно только два элемента любой длины, как показано в следующем примере.
Пример
Прямоугольный треугольник имеет гипотенузу длины 10 и катет длины 6. Найдите точные значения шести тригонометрических функций угла \(\theta\), если \(\theta\) примыкает к катету длины 6.
Найдите точные значения шести тригонометрических функций угла \(\theta\), если \(\theta\) примыкает к катету длины 6.
Решение
Чтобы найти эти значения, первое, что вам нужно сделать, это определить длину стороны отсутствующей ноги. Здесь поможет теорема Пифагора. Он говорит, что если \(a\) и \(b\) катет прямоугольного треугольника и если \(c\) гипотенуза, то: 92 &= 100 – 36 = 64\\b &= \sqrt{64}\\ &= 8\end{align}\)
Теперь вспомним, что в задаче сказано: «\(\theta\) примыкает к отрезку длины 6». Это означает, что теперь вы можете нарисовать свой треугольник:
Используя это:
\(\begin{align} \sin(\theta) &= \dfrac{\textrm{напротив}}{\textrm{гипотенуза}} \\ &= \dfrac{8}{10}\\ &= \dfrac{ 4}{5}\конец{выравнивание}\)
\(\begin{align}\cos(\theta) &= \dfrac{\textrm{adjacent}}{\textrm{гипотенуза}}\\ &= \dfrac{6}{10}\\ &= \dfrac{ 3}{5}\конец{выравнивание}\)
\(\begin{align} \tan(\theta) &= \dfrac{\textrm{напротив}}{\textrm{смежный}}\\ &= \dfrac{8}{6}\\ &= \dfrac{ 4}{3}\конец{выравнивание}\)
\(\begin{align}\csc(\theta) &= \dfrac{\textrm{гипотенуза}}{\textrm{напротив}}\\ &= \dfrac{10}{8}\\ &= \dfrac{ 5}{4}\конец{выравнивание}\)
\(\begin{align}\sec(\theta) &= \dfrac{\textrm{гипотенуза}}{\textrm{adjacent}}\\ &= \dfrac{10}{6}\\ &= \dfrac{ 5}{3}\конец{выравнивание}\)
\(\begin{align}\cot(\theta) &= \dfrac{\textrm{adjacent}}{\textrm{opposite}}\\ &= \dfrac{6}{8}\\ &= \dfrac{ 3}{4}\конец{выравнивание}\)
Как видите, правильное изображение было важной частью решения этой проблемы.



Вопросы с ответами о том, как найти точные значения тригонометрических функций. Во всех приведенных ниже вопросах от вас требуется найти точные значения, если это возможно, заданных тригонометрических функций. Вопрос 1: грех (-π/4) Вопрос 2: тан ( — 3 π / 4) Вопрос 3: сек ( 5 π / 3) Вопрос 4: детская кроватка (- 5 π/3) Вопрос 5: соз ( 25 π / 3) Вопрос 6: csc ( 15 π / 6) Вопрос 7: грех( 17 π / 4 ) Вопрос 8: сек ( π / 2 ) Вопрос 9: тан ( 5 π / 6) Вопрос 10: csc ( 15 π / 2) Ответы на вышеуказанные вопросы: Примечание: sqrt означает квадратный корень. вопрос 1: — sqrt ( 2 ) / 2 вопрос 2: 1 вопрос 3: 2 вопрос 4: sqrt(3) / 3 вопрос 5: 1 / 2 вопрос 6: 1 вопрос 7: sqrt(2) / 2 вопрос 8: не определен вопрос 9: — sqrt(3) / 3 вопрос 10: -1 Больше страниц, посвященных математическим задачам и онлайн-тестам для самопроверки. и как найти точные значения тригонометрических функций; вопросы с ответами и подробными решениями. |
 Два других угла являются острыми углами (имеют размеры менее 90 градусов). Любой из них может быть интересующим нас углом, поскольку триггерные функции будут зависеть от того, какая сторона находится рядом (прилегает) к нашему углу, а какая сторона противоположна нашему углу. Поэтому важно обращать внимание на то, какой угол представляет интерес каждый раз, когда вы работаете с этими определениями.
Два других угла являются острыми углами (имеют размеры менее 90 градусов). Любой из них может быть интересующим нас углом, поскольку триггерные функции будут зависеть от того, какая сторона находится рядом (прилегает) к нашему углу, а какая сторона противоположна нашему углу. Поэтому важно обращать внимание на то, какой угол представляет интерес каждый раз, когда вы работаете с этими определениями. реклама

 Это означает, что везде, где есть корень в знаменателе, такой как \(\sin(\theta)\) и \(\cos(\theta)\) выше, вы должны умножить верх и низ дроби на этот корень в чтобы исключить его из знаменателя. Опять же, это не всегда требуется, но если мы сделаем это здесь:
Это означает, что везде, где есть корень в знаменателе, такой как \(\sin(\theta)\) и \(\cos(\theta)\) выше, вы должны умножить верх и низ дроби на этот корень в чтобы исключить его из знаменателя. Опять же, это не всегда требуется, но если мы сделаем это здесь:Важно! – Эти рационализированные ответы математически такие же, как ответы над ними. Это просто другой способ написания ответов.
 Найдите точные значения шести тригонометрических функций угла \(\theta\), если \(\theta\) примыкает к катету длины 6.
Найдите точные значения шести тригонометрических функций угла \(\theta\), если \(\theta\) примыкает к катету длины 6.

 .. — Учеба и наука
.. — Учеба и наука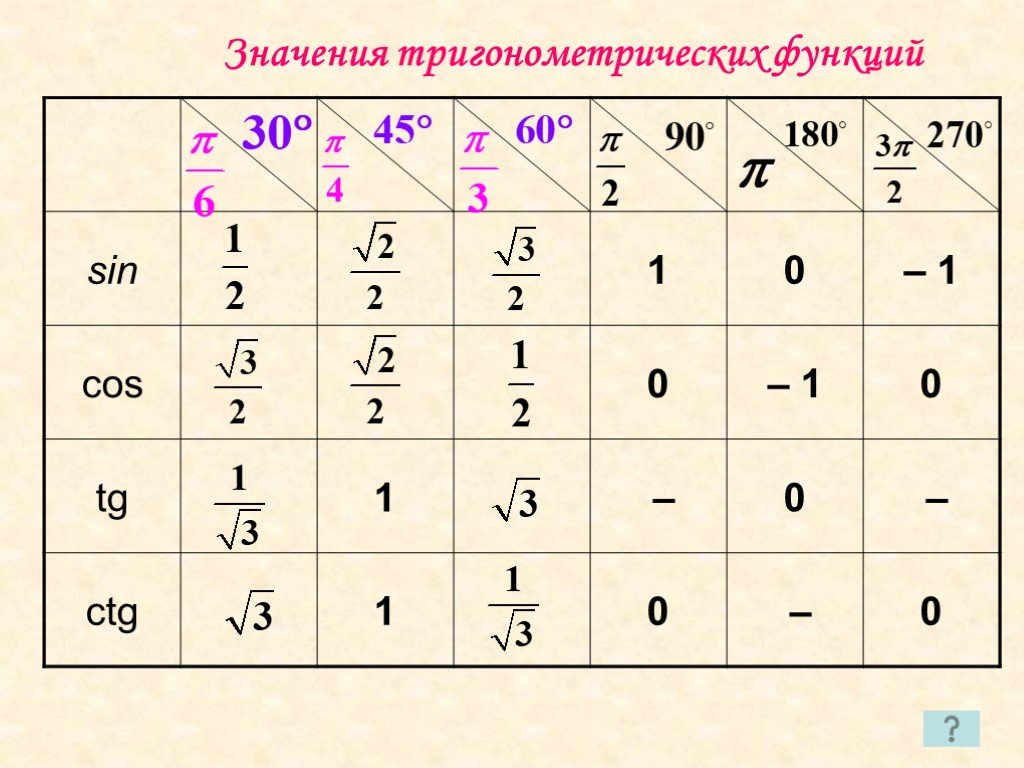 06.14
06.14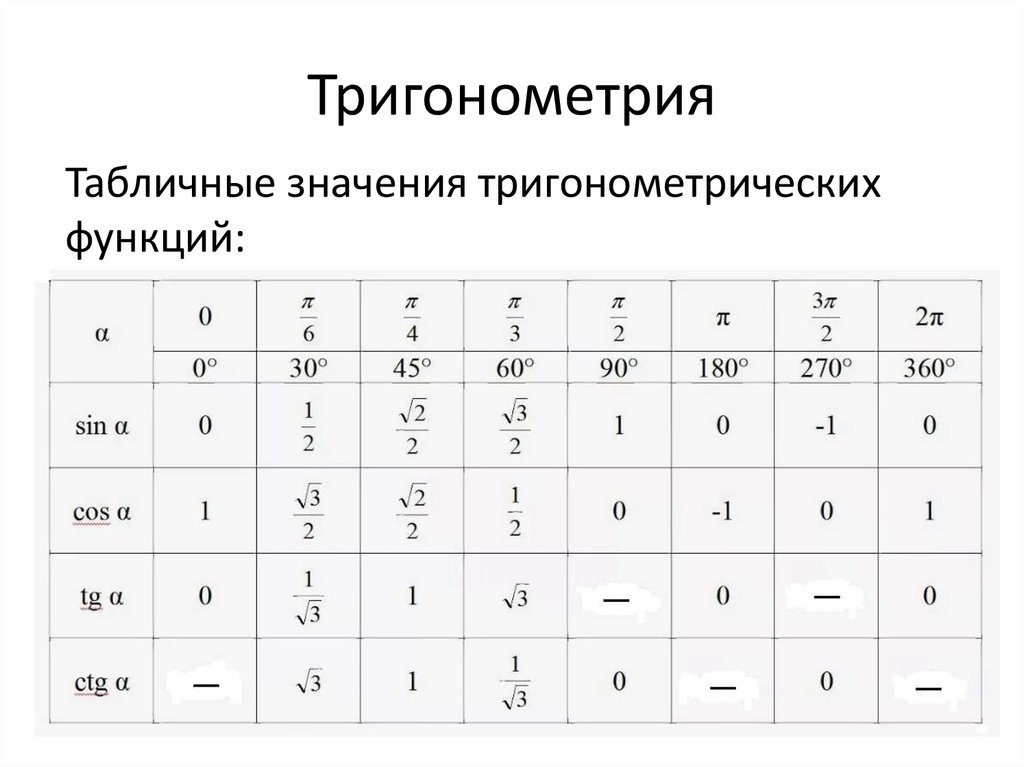
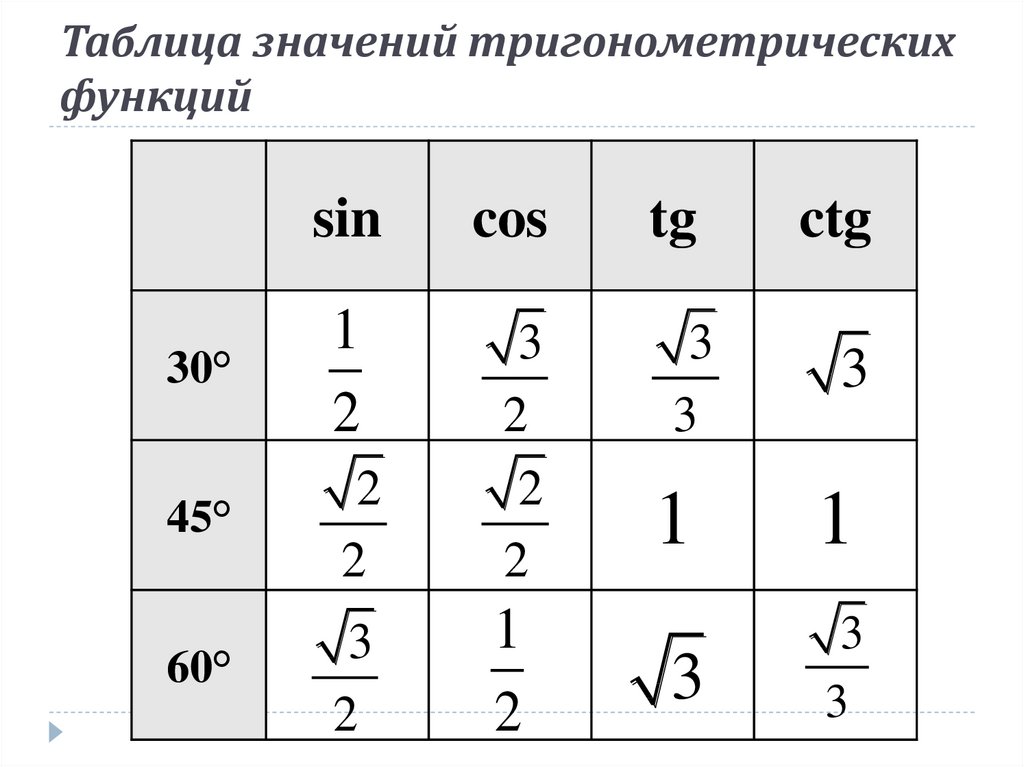
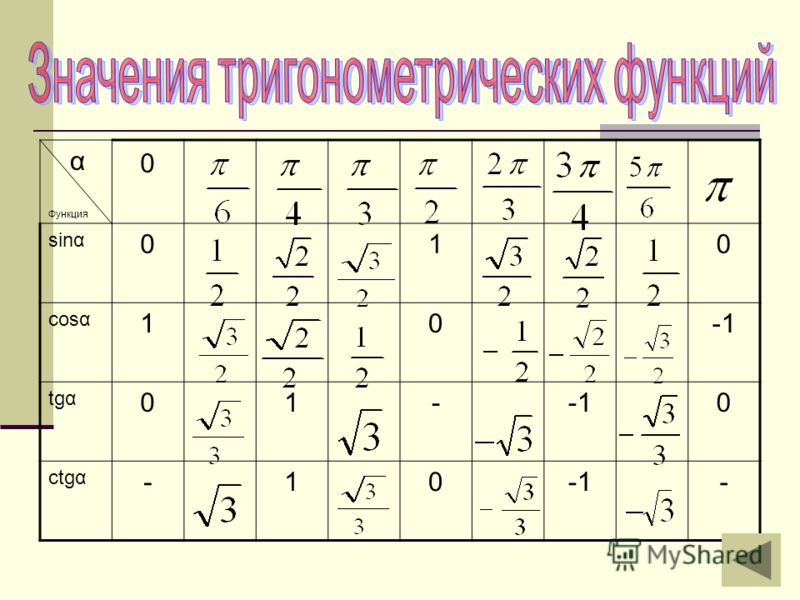
 Вам может понадобиться таблица значений тригонометрических функций для специальных углов.
Вам может понадобиться таблица значений тригонометрических функций для специальных углов.