Как называются эти фигуры ? презентация, доклад
ThePresentationru
- Регистрация |
- Вход
- Загрузить
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Страхование
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
- 1. Как называются эти фигуры ?
- 2. Как можно называть эту фигуру ?
- 3. Гладкова Ольга
-
4.
- 6. Овал
- 7. Треугольник
-
8.
Квадрат Ромб
- 9. Гладкова Ольга
- 10. Прямоугольник
-
11.
Гладкова Ольга
- 12. Гладкова Ольга
- 13. Гладкова Ольга
-
14.Гладкова Ольга
- 15. Гладкова Ольга
- 16. Гладкова Ольга
-
17.
Молодцы Гладкова
Квадрат Ромб
Гладкова Ольга
Молодцы Гладкова
Как можно называть эту фигуру ? Четырёхугольник Многоугольник Квадрат Прямоугольник ✓ ✓ ✓ Гладкова Ольга Владимировна учитель начальных классов Гимназии № 54 город
Слайд 1Как называются эти фигуры ?
Гладкова Ольга
Владимировна учитель начальных классов Гимназии № 54 город Краснодар
Слайд 2Как можно называть эту фигуру ?
Четырёхугольник
Многоугольник
Квадрат
Прямоугольник
✓
✓
✓
Гладкова Ольга Владимировна учитель начальных классов Гимназии № 54 город Краснодар
Слайд 3 Гладкова Ольга Владимировна учитель начальных классов
Гимназии № 54 город Краснодар
Что такое квадрат ?
Квадрат – это прямоугольник у которого все стороны равны
Сколько на чертеже прямоугольников?
Гладкова Ольга Владимировна
учитель начальных классов Гимназии № 54 город Краснодар
Какие геометрические фигуры вы узнали на рисунке?
Гладкова Ольга Владимировна учитель начальных классов Гимназии № 54 город Краснодар
Гладкова Ольга Владимировна учитель начальных классов
Гимназии № 54 город Краснодар
Гладкова Ольга Владимировна учитель начальных классов
Гимназии № 54 город Краснодар
Гладкова Ольга Владимировна учитель начальных классов
Гимназии № 54 город Краснодар
Слайд 9 Гладкова Ольга Владимировна учитель начальных классов
Гимназии № 54 город Краснодар
Трапеция
Гимназии № 54 город Краснодар
Слайд 11 Гладкова Ольга Владимировна учитель начальных классов
Гимназии № 54 город Краснодар
Круг
Слайд 12 Гладкова Ольга Владимировна учитель начальных классов
Гимназии № 54 город Краснодар
Назовите формулу нахождения периметра прямоугольника
a + b + a + b
(a + b) ● 2
a ● b
✓
✓
Слайд 13 Гладкова Ольга Владимировна учитель начальных классов
Гимназии № 54 город Краснодар
Как называются эти углы?
А
В
С
Слайд 14 Гладкова Ольга Владимировна учитель начальных классов
Гимназии № 54 город Краснодар
МОЛОДЕЦ !
Слайд 15 Гладкова Ольга Владимировна учитель начальных классов
Гимназии № 54 город Краснодар
ПОДУМАЙ !
Слайд 16 Гладкова Ольга Владимировна учитель начальных классов
Гимназии № 54 город Краснодар
Покажи у фигуры прямой угол
D
А
С
В
Слайд 17Молодцы
Гладкова Ольга Владимировна учитель начальных классов
Гимназии № 54 город Краснодар
Скачать презентацию
Обратная связь
Если не удалось найти и скачать презентацию, Вы можете заказать его на нашем сайте.
Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Email: Нажмите что бы посмотреть
Что такое ThePresentation.ru?
Это сайт презентаций, докладов, проектов, шаблонов в формате PowerPoint. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами с другими пользователями.
Для правообладателей
Как называются пространственные геометрические фигуры?
содержание
Что такое пространственные геометрические фигуры?
Примеры пространственных фигур: пирамида, призма, куб, сфера, цилиндр и др.
Сколько пространственных геометрических фигур?
Пространственные геометрические фигуры# Пространственная геометрия изучает различные геометрические тела, среди основных у нас есть: цилиндр, куб, конус, сфера, параллелепипед и пирамида.
Как называются все геометрические фигуры?
Кроме того, у каждого из них есть несколько сторон.
- Треугольник — 3 стороны.
- Четырехугольник – 4 стороны.
- Пентагон – 5 сторон.
- Шестиугольник — 6 сторон.
- Гептагон – 7 сторон.
- Октагон – 8 сторон.
- Эннеагон – 9 сторон.
- Декагон – 10 сторон.
Что такое космические фигуры?
Пространственные фигуры необходимо определять в трехмерных пространствах, так как они имеют глубину в дополнение к длине и ширине. Кубы, призмы, цилиндры, конусы и сферы, например, являются фигурами, которые могут быть определены только в трехмерном пространстве.
Что такое пространственные геометрические фигуры 2 основного года?
Космические геометрические фигуры, называемые также геометрическими телами, — это те, которые имеют три измерения: длину, ширину и глубину.
Какие плоские фигуры образуют пространственную фигуру?
Поэтому любая фигура, для построения и определения которой необходимы три измерения, называется пространственной геометрической фигурой.
Примеры пространственных фигур: куб, призма, параллелепипед, пирамида, конус, цилиндр, сфера и др.
Что касается названия шестиугольной призмы и пространственной формы?
Шестиугольная призма: основание образовано шестиугольником. Семиугольная призма: основание образовано семиугольником.
Какие 4 основные геометрические фигуры?
Треугольники, квадраты, прямоугольники и пятиугольники являются примерами плоских геометрических фигур. Неплоские (пространственные) геометрические фигуры имеют ширину, длину и толщину, будучи трехмерными. Эти формы делятся на многогранники и не-многогранники (круглые тела).
Какие 4 геометрические фигуры?
плоские геометрические фигуры
| Количество сегментов линии | Классификация |
|---|---|
| 4 | четырехугольник |
| 5 | пятиугольник |
| 6 | Гексагоно |
| 7 | Семиугольник |
Что такое плоские геометрические фигуры?
Основными плоскими фигурами являются треугольник, круг, квадрат, прямоугольник, ромб и трапеция, и каждая из них имеет формулу вычисления площади.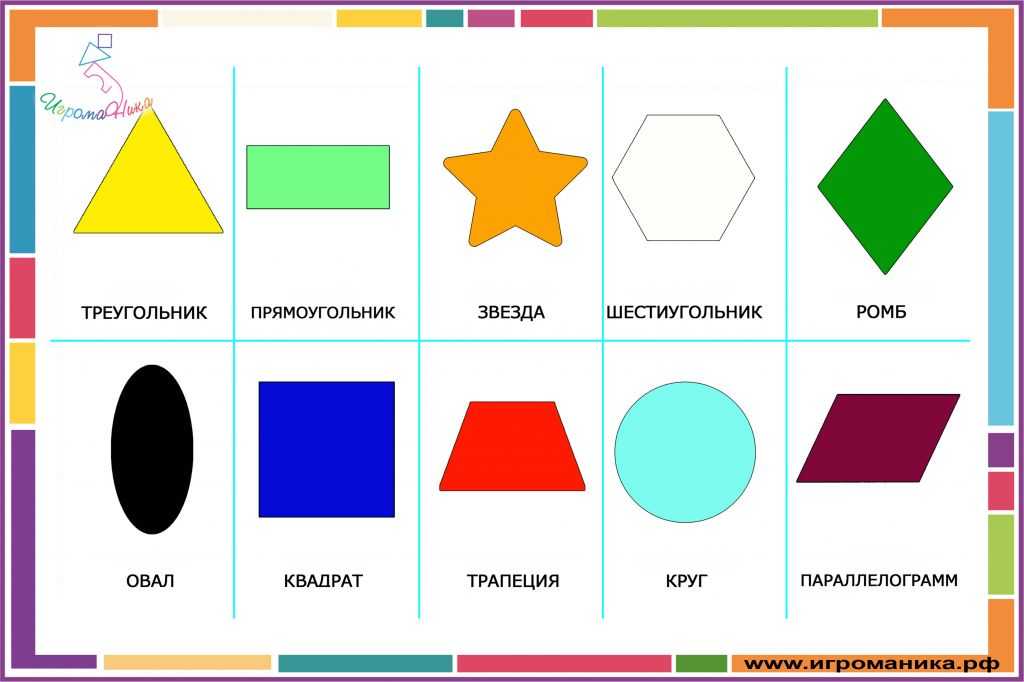
Стоит отметить, что область изучается в планиметрии, геометрии для двухмерных объектов.
Как сделать пространственную геометрию?
Тетраэдр – это правильная пирамида с четырьмя конгруэнтными гранями, причем треугольники граней равносторонние. Поскольку площадь равностороннего треугольника определяется как Ab = (a²*√3)/4, а высота определяется как h = (a*√6)/3, мы имеем: V = Ab*h/3 = (а²* √3)*(а*√6)/3*4*3 = а³*√2/12.
Чем отличаются плоские геометрические фигуры от пространственных?
Планиметрия — это изучение фигур в двух измерениях, таких как квадраты, круги, прямоугольники и треугольники. В то время как пространственная геометрия изучает фигуры в трех измерениях, то есть кубы, сферы, параллелепипеды и пирамиды.
Что такое 6 пространственных геометрических фигур?
Особенности пространственной геометрии
- призма.
- Куб.
- брусчатка.
- пирамида.
- конус.
- цилиндр.
- мяч.
Является ли это пространственной геометрической фигурой, у которой все грани квадратные?
Также известный как шестигранник, куб представляет собой геометрическое тело, все грани которого образованы квадратами. У него 6 граней, 12 ребер и 8 вершин. Куб представляет собой шестигранный многогранник, все грани которого квадратные.
Что такое 4-летние пространственные геометрические фигуры?
ПРОСТРАНСТВЕННЫЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ ИЛИ ГЕОМЕТРИЧЕСКИЕ ТЕЛА ЯВЛЯЮТСЯ ТЕ, КОТОРЫЕ ПРОИСХОДЯТ В ПРОСТРАНСТВЕ, В СВЯЗИ С ИХ ТРЕХМЕРНОСТЬЮ, Т.Е. ИМЕЮТ ТРИ ИЗМЕРЕНИЯ (ВЫСОТУ, ШИРИНУ И ДЛИНУ).
Какие из приведенных ниже пространственных геометрических фигур являются многогранниками?
На основе примитивных элементов разрабатываются геометрические тела, главными из которых являются многогранники: параллелепипеды, кубы и другие призмы, помимо так называемых платоновских тел; и круглые тела: конус, цилиндр и сфера.
Являются ли они неплоскими космическими фигурами?
Неплоские или пространственные геометрические фигуры — это фигуры, расположенные в пространстве. Эти фигуры расположены в трех измерениях: длина, ширина и высота.
Как называются все призмы?
четырехугольная призма: имеет каждое из оснований в форме четырехугольника; пятиугольная призма: имеет каждое из оснований в форме пятиугольника; шестиугольная призма: имеет каждое из оснований в форме шестиугольника; восьмиугольная призма: имеет каждое из оснований в форме восьмиугольника.
Что такое специальные призмы?
3. Пирамиды и специальные призмы. Особой призмой, например, является куб: это призма с квадратными основаниями и равными боковыми гранями, то есть фигура имеет шесть равных граней, образованных квадратами.
Как называется геометрическая фигура, имеющая 8 граней?
Октаэдр имеет 8 конгруэнтных треугольных граней и 6 конгруэнтных тетраэдрических углов.
Что такое пространственные геометрические фигуры и как они образуются?
Пространственные геометрические фигуры – это те, которые имеют три измерения: длину, высоту и ширину. Эти фигуры делятся на две группы: круглые тела (ограниченные какой-либо округлой поверхностью) и многогранники (поверхности, ограниченные плоскими геометрическими фигурами).
Как называются все многоугольники?
Поэтому по отношению к числу сторон многоугольникам можно давать следующие названия:
- 3 стороны → треугольник или трехугольник.
- 4 стороны → квадрат или четырехугольник.
- 5 сторон → пятиугольник или пятиугольник.
- 6 сторон → шестиугольник или шестигранник.
- 7 сторон → семиугольник или семиугольник.
- 8 сторон → восьмиугольник или восьмиугольник.
Что такое плоские и неплоские геометрические фигуры?
Неплоские геометрические фигуры (куб, прямоугольный блок, пирамида, конус, цилиндр и сфера): распознавание и характеристика.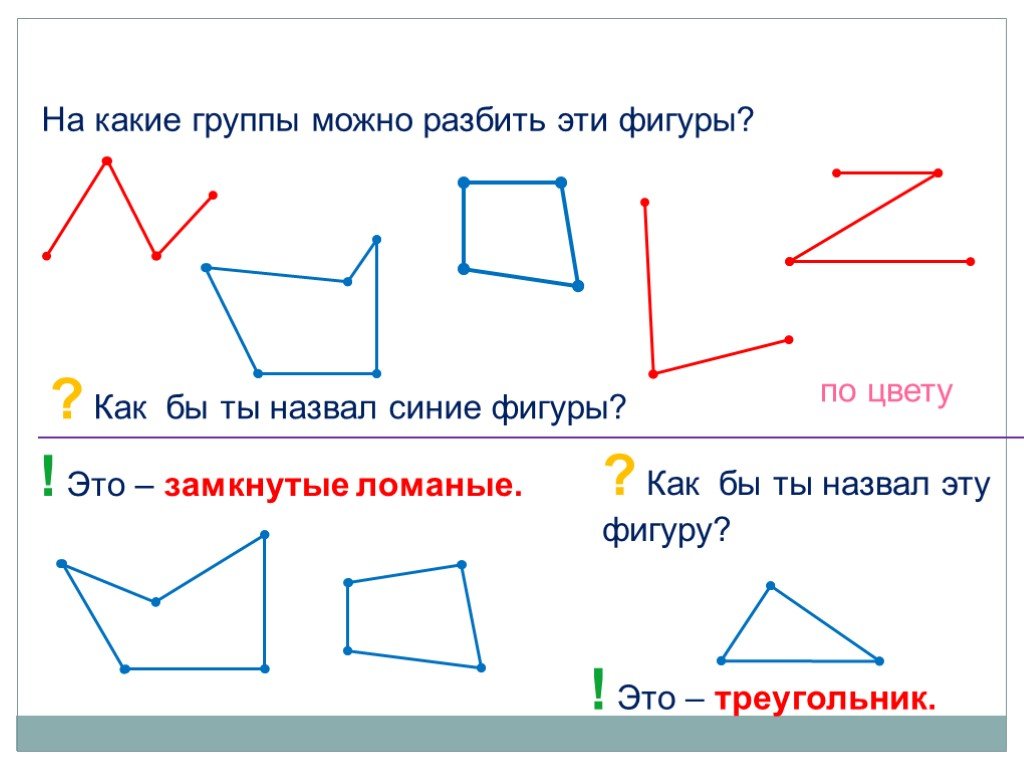
Плоские геометрические фигуры (круг, квадрат, прямоугольник и треугольник): распознавание и характеристика.
Что такое плоские фигуры?
Мы называем плоской фигурой любую фигуру, имеющую два измерения. Нас окружают плоские фигуры, такие как квадраты, круги, треугольники и другие формы. Плоские фигуры имеют два измерения. Плоские фигуры присутствуют во все времена в быту.
Сколько и какие полигоны?
Посмотрите названия различных типов многоугольников в зависимости от количества их сторон.
Типы полигонов.
| количество сторон | имя |
|---|---|
| 4 | четырехугольник |
| 5 | пятиугольник |
| 6 | Гексагоно |
| 7 | Семиугольник |
Как называется фигура, у которой 5 сторон?
J. 2 полигона
| четырехугольник | 4 | 4 |
| пятиугольник | 5 | 5 |
| Гексагоно | 6 | 6 |
| Семиугольник | 7 | 7 |
| восьмиугольник | 8 | 8 |
Сколько граней у призмы?
У него 8 вершин, 12 ребер и 6 граней, две из которых являются основаниями, а остальные прямоугольными.
Сколько граней у параллелепипеда?
Параллелепипед – это геометрическое тело, грани которого образованы параллелограммами. Он состоит из 8 вершин, 12 ребер и 6 граней. Он классифицируется как прямой, если его края перпендикулярны, и как косой, если его края не перпендикулярны.
Что такое круглое тело?
Цилиндр, конус и сфера являются круглыми телами. Мы называем круглыми телами геометрические тела, имеющие криволинейные поверхности. Они также известны как тела вращения, потому что они построены путем вращения плоской фигуры.
Кто создал геометрию?
Евклид, великий математик и писатель, жил, вероятно, в XNUMX веке до нашей эры и считается отцом геометрии. Он первым собрал всю геометрию в единое произведение под названием «Элементы». Этот математик основывал планиметрию на пяти постулатах.
Что еще относится к пространственной геометрии?
Наиболее часто повторяющейся темой в тестах, связанных с пространственной геометрией, является расчет объема геометрических тел.
Помимо расчета объема часто возникают вопросы по идентификации геометрических тел, их характеристикам и свойствам.
Что такое геометрические объекты?
Геометрические тела — это трехмерные объекты, заданные в пространстве. Некоторые примеры геометрических тел: кубы, пирамиды, призмы, цилиндры и сферы. Совокупность всех геометрических тел принято делить на три большие группы: многогранники, круглые тела и другие.
Каковы пространственные различия?
Таким образом, пространственная дифференциация была бы просто географическим соответствием, т. е. различием, существенным, имманентным условием, выраженным в пространстве, так как она видна как в природных условиях (почва, растительность, климат), так и в аспектах социальных (экономика, политика, культура).
Где используется пространственная геометрия?
Куб, цилиндр, конус, пирамиды и другие являются объектами изучения космической геометрии. С помощью пространственной геометрии можно обнаружить характеристики и свойства геометрических тел, а также разработать формулы для расчета объема и площади этих тел.
Чем отличаются плоские фигуры от пространственных?
Планиметрия — это изучение фигур в двух измерениях, таких как квадраты, круги, прямоугольники и треугольники. В то время как пространственная геометрия изучает фигуры в трех измерениях, то есть кубы, сферы, параллелепипеды и пирамиды.
Какую группу я могу рассматривать как плоские фигуры и пространственные геометрические фигуры?
Аннотация о плоских фигурах
- Это фигуры, имеющие два измерения.
- Основные из них: треугольник; площадь;
- Плоские фигуры всегда двухмерны. Когда есть трехмерные фигуры, они известны как пространственные.
- На основных плоских рисунках у каждого из них есть определенная формула для расчета его площади.
Как сделать пространственную геометрию?
Тетраэдр – это правильная пирамида с четырьмя конгруэнтными гранями, причем треугольники граней равносторонние. Поскольку площадь равностороннего треугольника определяется как Ab = (a²*√3)/4, а высота определяется как h = (a*√6)/3, мы имеем: V = Ab*h/3 = (а²* √3)*(а*√6)/3*4*3 = а³*√2/12.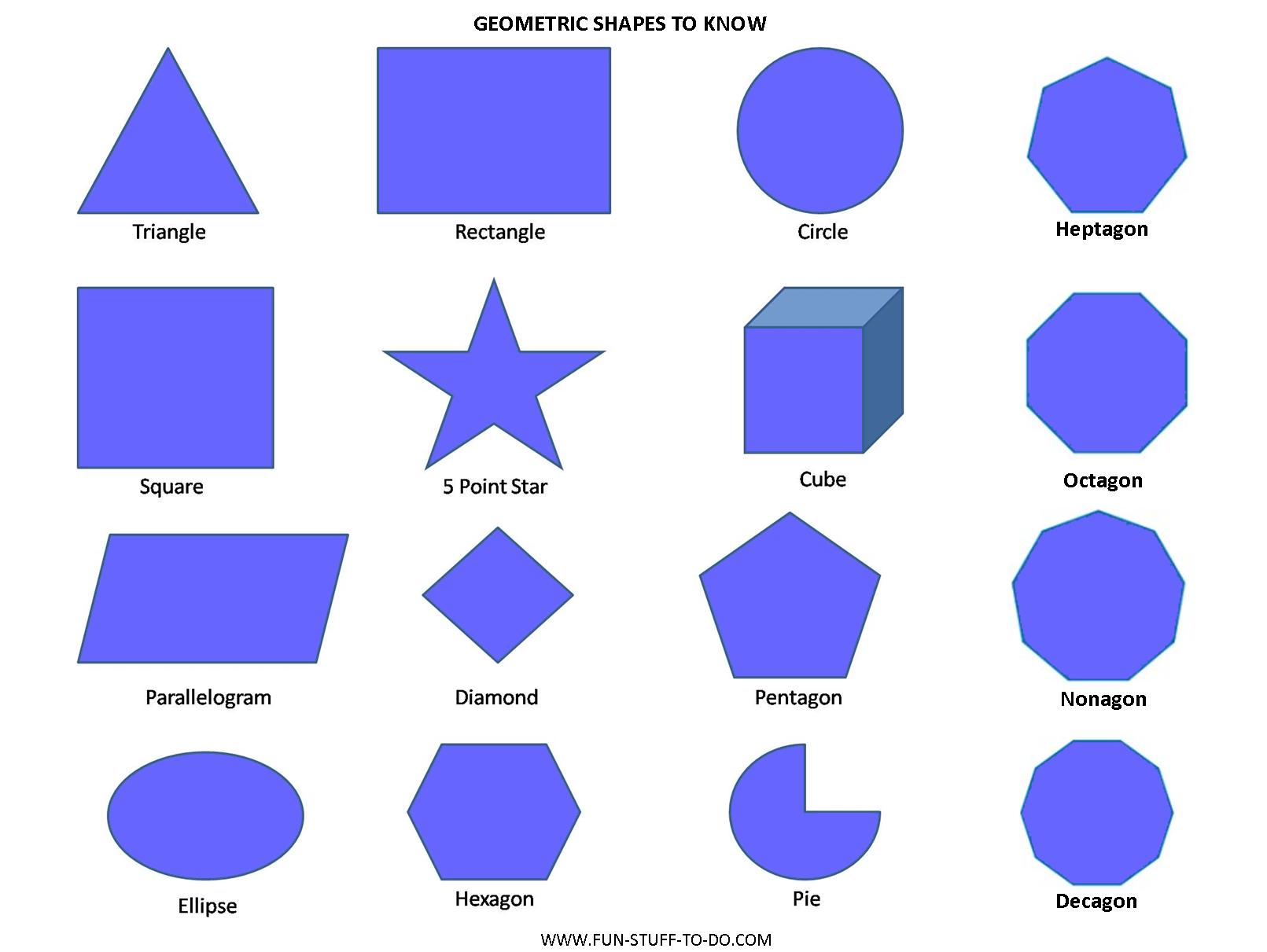
Определение, типы, список, решенные примеры, факты
Что такое формы?
В геометрии форма может быть определена как форма объекта или его контур, внешняя граница или внешняя поверхность.
Все, что мы видим в окружающем нас мире, имеет форму. Мы можем найти различные основные формы, такие как двухмерный квадрат, прямоугольник и овал или трехмерную прямоугольную призму, цилиндр и сферу, в объектах, которые мы видим вокруг нас. Эти геометрические формы появляются в объектах, которые мы видим, таких как кредитные карты, банкноты и монеты, перстни, фоторамки, доски для игры в дартс, хижины, окна, волшебные палочки, высокие здания, цветочные горшки, игрушечные поезда и воздушные шары.
Связанные игры
Различные типы фигур
Фигуры можно разделить на открытые и замкнутые.
| В геометрии незамкнутая форма может быть определена как форма или фигура, сегменты линий и/или кривые которых не пересекаются.  Они не начинаются и не заканчиваются в одной и той же точке. | В геометрии замкнутая фигура может быть определена как замкнутая форма или фигура, сегменты линий и/или кривые которых соединены или пересекаются. Они начинаются и заканчиваются в одной и той же точке. |
Замкнутые геометрические формы можно разделить на две широкие категории, а именно двухмерные формы и трехмерные формы.
| Плоская двухмерная форма. | Трехмерная форма — это твердая форма. |
| Он имеет два измерения, то есть длину и ширину. | Он имеет два измерения: длину, ширину и глубину. |
Вот список двухмерных или двухмерных фигур с их названиями и изображениями:
| Двумерные геометрические формы |
Здесь Список 3-D или трехмерные формы с их названиями и картинками:
Трехэ. |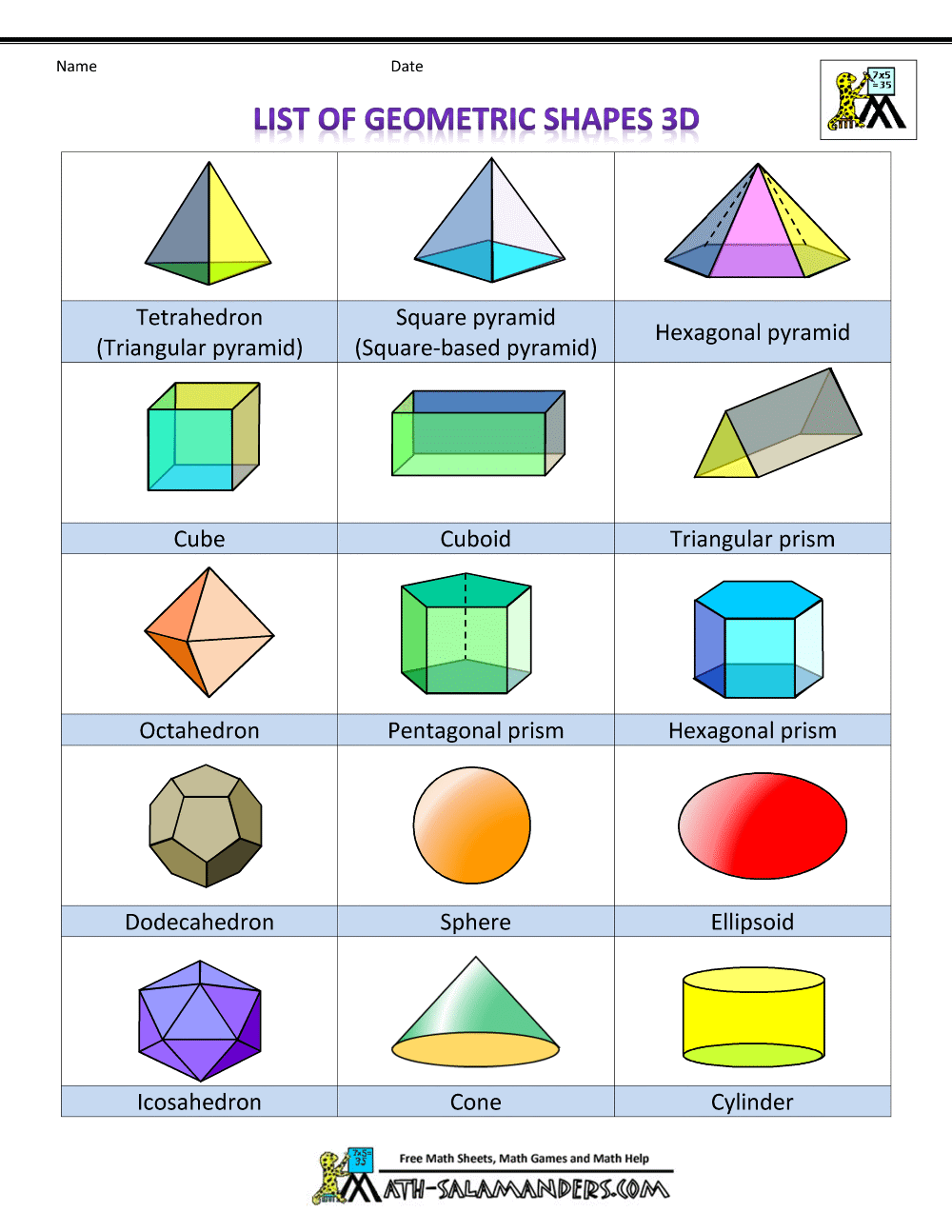
Цвет, общий размер и ориентация, называемые неопределяющими атрибутами двухмерной или трехмерной формы, никак не определяют форму и не влияют на нее. Эти атрибуты могут изменяться без какого-либо влияния на форму.
С другой стороны, определение таких атрибутов, как количество сторон (параллельных или непараллельных, прямых или изогнутых), вершин, ребер и граней формы, открытость формы или замкнутость, а также угловые меры определяют форма двухмерного или трехмерного объекта. Любое изменение этих определяющих атрибутов изменит форму.
Связанные рабочие листы
Решенные примеры фигур
Пример 1: Назовите фигуры.
- Многоугольник с 6 сторонами.
- Контур двери.
- При складывании квадрата угол в угол.
- Квадрат и треугольник поверх него.
Решение:
- Шестиугольник
- Прямоугольник или четырехугольник
- Треугольник
- Пентагон
Пример 2: Классифицируйте данные буквы как открытые или закрытые.
C, D, L, M, O, S, U, V, Z
Решение:
Незамкнутая форма: C, L, M, S, U, V, Z
Замкнутая форма: D, O
Пример 3: Определите объемную форму данных объектов.
- Глобус
- Книга
- Банка для холодных напитков
- Кости
Решение:
- Сфера
- Прямоугольный
- Цилиндр
- Куб
Пример 4: Почему луна в форме полумесяца не является многоугольником?
Решение:
Луна в форме полумесяца не является многоугольником, поскольку имеет изогнутые линии.
Практические задачи на фигурах
1
Как называется 8-сторонний многоугольник?
шестиугольник
семиугольник
восьмиугольник
четырехугольник
Правильный ответ: восьмиугольник
Многоугольник с 8 сторонами известен как восьмиугольник.
2
Сколько измерений имеет твердое тело?
1
2
3
зависит от формы
Правильный ответ: 3
Все объемные формы являются трехмерными.
3
Какое из следующих утверждений неверно?
замкнутые формы могут иметь только прямые стороны.
замкнутые формы имеют определенную площадь.
начальная и конечная точки замкнутой формы совпадают.
Начальная и конечная точки открытой формы разные.
Правильный ответ: замкнутые формы могут иметь только прямые стороны.
Замкнутые фигуры — это фигуры, у которых начальная и конечная точки совпадают. Не обязательно, чтобы он образовывался только прямыми сторонами.
Как называются 2D- и 3D-формы?
Мы объясняем, чем отличаются двухмерные и трехмерные фигуры, когда детей младшего школьного возраста учат называть их и сортировать фигуры в соответствии с их свойствами, а также когда они учатся идентифицировать и рисовать свои собственные сети трехмерных фигур.
или зарегистрируйтесь, чтобы добавить к своим сохраненным ресурсам
Во время обучения в начальной школе дети будут изучать различные 2D (двухмерные) и 3D (трехмерные) формы.
Первое, что им нужно усвоить, это разницу между 2D и 3D формами. Учителя часто говорят о том, что 2D-формы «плоские», а 3D-формы не . Ожидается, что дети смогут назвать эти фигуры, а также обсудить свойства этих фигур.
2D-фигуры| Круг | Square | ||
| Triangle | Rectangle | ||
| Pentagon | Hexagon | ||
| Octagon | Нонагон |
youtube.com/embed/OVItzLoovLc?rel=0″/> Трехмерные формы | Cube | Cuboid | ||
| Sphere | Square-based pyramid | ||
| Cylinder | Triangular prism | ||
| Пятиугольная пирамида | Шестиугольная призма |
2D- и 3D-фигуры в KS1
В 1-й год дети должны уметь распознавать и называть:
- 2D-фигуры, включая прямоугольники, квадраты, круги и треугольники
- 3D-фигуры, включая кубы , пирамиды и сферы
- сортировать, создавать и описывать распространенные 2D- и 3D-формы
В 2-м классе дети должны уметь:
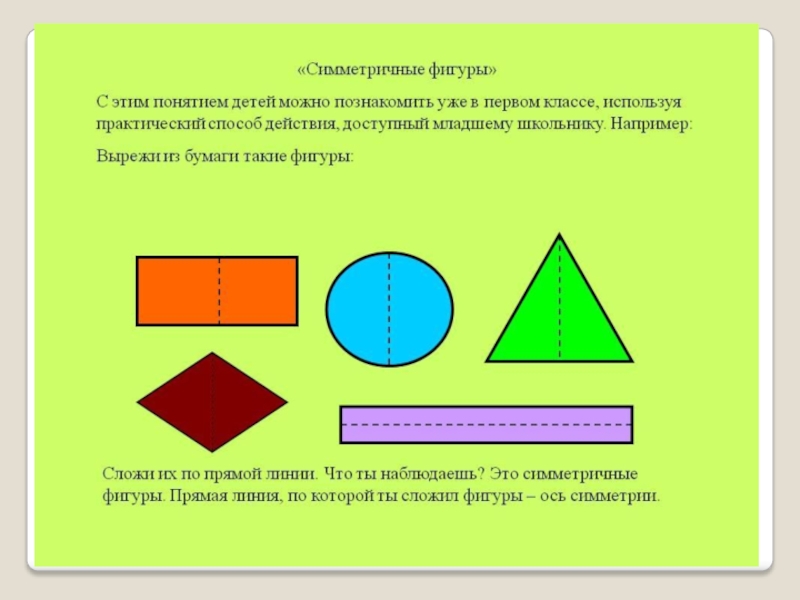
- определять и описывать свойства 2D-фигур, включая симметрию и линейную симметрию
- идентифицировать и описывать 3D-формы, включая количество ребер, вершин и граней
- идентифицировать 2D-фигуры на поверхности 3D-фигур
- сравнивать и сортировать распространенные 2D- и 3D-фигуры
- понимать, что прямой угол — это четверть оборота и знать, по часовой стрелке или против часовой стрелки
2D и 3D фигуры в KS2
В Year 3 дети должны:
- рисовать 2D фигуры и делать 3D фигуры
- определять прямые углы и знать, что два из них делают пол-оборота, три — на три четверти, а четыре — полный оборот необходимо:
- сравнивать четырехугольники и треугольники по их свойствам и размерам
- определять острые и тупые углы, сравнивать и упорядочивать углы
- определять линии симметрии в двумерных фигурах
В 5 классе дети должны:
- определять трехмерные фигуры из двухмерных представлений
- оценивать и сравнивать острые, тупые и обратные углы
- рисовать заданные углы между правильными и неправильными многоугольниками
Дети, изучающие в 6 классе , должны:
- классифицировать 2D и 3D формы, рассказывая о параллельных и перпендикулярных ребрах и гранях
- рисовать двухмерные фигуры, используя заданные размеры и углы
- распознавать, описывать и строить простые трехмерные фигуры, включая создание сетей
- находить неизвестные углы в треугольниках, четырехугольниках и правильных многоугольниках окружности и знать, что диаметр в два раза больше радиуса
Другие термины 2D и 3D форм, используемые в KS2
Равносторонний треугольник: Треугольник с 3 равными сторонами и 3 равными углами. Равнобедренный треугольник: Треугольник с 2 равными сторонами. Разносторонний треугольник: Треугольник с 3 неравными сторонами. Прямоугольный треугольник: Треугольник с прямым углом. Четырехугольник: Четырехсторонняя форма. Ромб: Четырехугольник, у которого обе пары или противоположные стороны параллельны и все стороны имеют одинаковую длину. (Отличается от квадрата тем, что углы НЕ 90˚). Трапеция: Четырехугольник с одной парой параллельных сторон. Параллелограмм: Четырехугольник, у которого обе пары противоположных сторон параллельны и обе пары имеют одинаковую длину. Воздушный змей : Четырехугольник с двумя парами сторон одинаковой длины.
