⌀ — Знак диаметра: U+2300
U+2300
Нажмите, чтобы скопировать и вставить символ
Техническая информация
| Название в Юникоде | Diameter Sign |
| Номер в Юникоде | U+2300 |
| HTML-код | ⌀ |
| CSS-код | \2300 |
| Раздел | Разнообразные технические символы |
| Версия Юникода: | 1. 1 (1993) 1 (1993) |
Значение символа
Диаметр – отрезок (хорда), соединяющий две точки на окружности и проходящий через её центр. Но, обычно, под диаметром подразумевают длину этого отрезка. Равняется двум радиусам. В формулах обозначается латинской буквой «D». Слово «диаметр» происходит от греческого «diametros» (поперечник).
Символ диаметра представляет собой окружность перечёркнутую вышеупомянутым отрезком. Правда, для наглядности, концы отрезка выходят за пределы окружности, что строго говоря неверно. Символ диаметра похож на «о с диагональным штрихом», используемую в некоторых основанных на латинице алфавитах. Кроме того, часто похожим образом пишут цифру «ноль», перечёркивая её, чтобы отличить от буквы «о».
Обычно, знак диаметра используется на чертежах деталей. Символ наносят перед числом на размерной линии: «⌀ 40 см». Диаметр можно указывать, как для цилиндрических деталей, так и для конических. Пример детали с цилиндрической поверхностью – вал.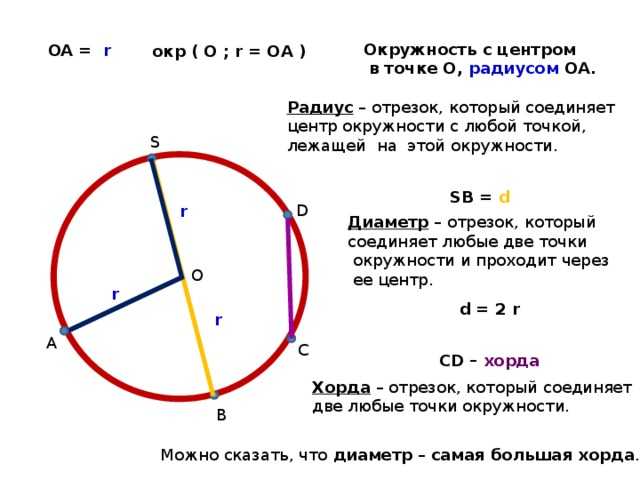
Символ «Знак диаметра» был утвержден как часть Юникода версии 1.1 в 1993 г.
Этот текст также доступен на следующих языках: English;
Свойства
| Версия | 1.1 |
| Блок | Разнообразные технические символы |
| Тип парной зеркальной скобки (bidi) | Нет |
| Композиционное исключение | Нет |
| Изменение регистра | 2300 |
| Простое изменение регистра | 2300 |
Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | E2 8C 80 | 226 140 128 | 14847104 | 11100010 10001100 10000000 |
| UTF-16BE | 23 00 | 35 0 | 8960 | 00100011 00000000 |
| UTF-16LE | 00 23 | 0 35 | 35 | 00000000 00100011 |
| UTF-32BE | 0 0 35 0 | 8960 | 00000000 00000000 00100011 00000000 | |
| UTF-32LE | 00 23 00 00 | 0 35 0 0 | 2293760 | 00000000 00100011 00000000 00000000 |
Наборы с этим символом:
∑
Математические знаки
Равен ее диаметр.
 Разница между радиусом и диаметром
Разница между радиусом и диаметромВ тех случаях, когда требуется указать размер диаметра, используют знак в виде окружности с линией « Ø ». Этот символ наносят перед размерным числом.
Примеры использования знака диаметра:
Знаки диаметра на деталях вращения цилиндрической и конической формы
Размеры наносимые при недостатке места
на размерной линии
Обозначение размеров при недостатке места
для стрелок
Диаметр – это длинна отрезка прямой соединяющей поверхности окружности. Отрезок диаметра, в любом случае проходит только через центр окружности. Обозначают его обычно латинской буквой « D » или знаком « Ø ». Если радиус окружности умножить на два, суммой будет диаметр. Все объемные тела, имеющие сферическую форму, а также те, хотя бы одно из возможных сечений которых представляет собой круг, обозначаются символами диаметра. Слово «
Пример обозначения четырёх отверстий
с указанием диаметра
На технических чертежах диаметры обозначаются символом в виде перечеркнутой окружности « Ø ». Данный знак, ставится перед размерными числами деталей, которые могут быть как цилиндрическими, так и коническими.
Данный знак, ставится перед размерными числами деталей, которые могут быть как цилиндрическими, так и коническими.
В сечение конус представляет собой прямоугольный треугольник, один из катетов которого параллелен или сосен телу вращения. Его параметры имеют следующими обозначениями: « D » – больший диаметр, « d » – меньший диаметр, « L » – длина. На чертеже диаметры конуса обозначаются цифрами, перед которыми ставятся знаки « Ø » а числовое значение длинны без буквенных обозначений.
К наиболее распространенным деталям с цилиндрическими поверхностями, относятся валы различного назначения. Цилиндрические тела, образованные вращением прямоугольника около одной из его сторон обозначаются диаметром. Гладкие валы имеют некоторые конструктивные особенности, и разделяются на разновидности: прямые, ступенчатые односторонние, ступенчатые двусторонние и тяжелые. К примеру, валы асинхронных двигателей, в которых ротор сопрягается с валом методом запрессовки на наибольший его диаметр, а по обеим сторонам имеются ступени под подшипники, вентиляторы, и шкивы.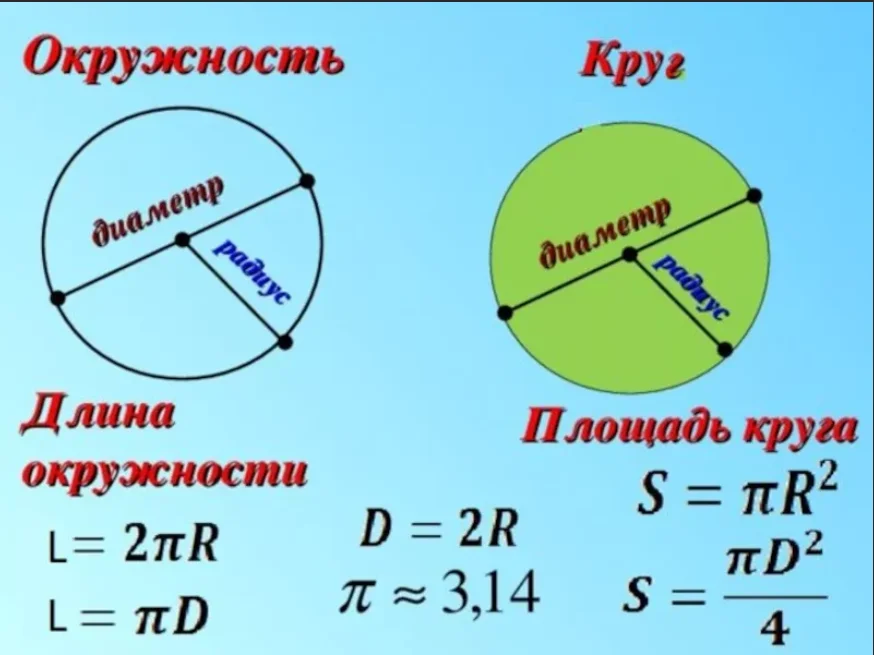 Двусторонние ступенчатые валы можно встретить так же в различных механизмах там, где требуются, какие либо другие конструктивные особенности. Цилиндрические детали, как правило, имеют общую максимальную длину и наружный диаметр. В зависимости от конкретной конфигурации того или иного изделия в её состав могут входить такие элементы как внутренние и наружные канавки, ступени, выточки и др. с различными диаметрами перед значениями которых ставятся знаки « Ø ».
Двусторонние ступенчатые валы можно встретить так же в различных механизмах там, где требуются, какие либо другие конструктивные особенности. Цилиндрические детали, как правило, имеют общую максимальную длину и наружный диаметр. В зависимости от конкретной конфигурации того или иного изделия в её состав могут входить такие элементы как внутренние и наружные канавки, ступени, выточки и др. с различными диаметрами перед значениями которых ставятся знаки « Ø ».
Пример нанесения знака диаметра
на сферической поверхности
К деталям с коническими поверхностями относятся инструментальные переходные втулки, у которых наружная и внутренняя поверхность конические. Такие втулки обеспечивают высокую точность центрирования и быстродействие смены инструмента с достаточной жёсткостью при использовании их на станках. Переходные втулки бывают короткие и длинные.
Конические инструментальные детали данного типа называются «конус Морзе » и делятся на номера. Углы, длины и диаметры переходных втулок можно взять из специальных таблиц. В табличных данных используются буквенные обозначения такие как – « d » меньший диаметр, « D » большой диаметр, « L » длина детали. На чертежах диаметры и длины обозначаются цифровыми значениями, причём перед числами диаметра ставится знак « Ø ».
В табличных данных используются буквенные обозначения такие как – « d » меньший диаметр, « D » большой диаметр, « L » длина детали. На чертежах диаметры и длины обозначаются цифровыми значениями, причём перед числами диаметра ставится знак « Ø ».
«Конус Морзе » – помимо переходных втулок применяется при изготовлении хвостовиков спиральных свёрл, концевых фрез, приспособлений и оправок. Инструментальные конусы фиксируются за счёт упругой и пластической деформации. Для реализации таких соединений в шпинделях фрезерных и токарных станков, предусмотрены конические отверстия для установки вспомогательного инструмента. Кроме того у токарного станка пиноль задней бабки имеет такое же коническое отверстие.
В технике используются большое количество деталей и их элементов для обозначения, которых используется знак диаметра. Для стандартных размеров диаметров используются параметрический ряд, в который входят стандартные размеры. При разработке технических изделий расчётные диаметры округляются до ближайших их величин.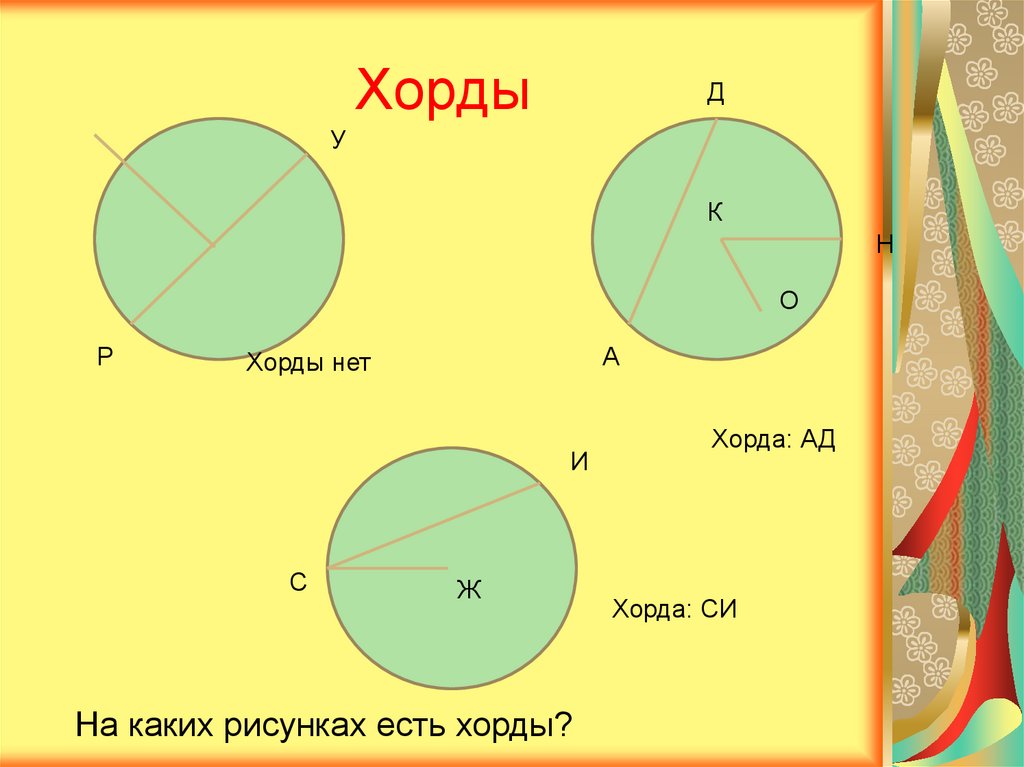
Что такое определение? Что такое центр, радиус, хорда и диаметр окружности?
- класс
- Диаметор-отрезок соеденяющий две точки на окружности и проходящий через центор окружности,
- Окружность геометрическое место точек плоскости, равноудалнных от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое е радиусом
Радиус не только величина расстояния, но и отрезок, соединяющий центр окружности с одной из е точек
Отрезок, соединяющий две точки окружности, называется е хордой. Хорда, проходящая через центр окружности, называется диаметром
Диаметр это хорда (отрезок, соединяющий две точки) на окружности (сфере, поверхности шара) , и проходящий через центр этой окружности (сферы, шара) . Также диаметром называют длину этого отрезка. Диаметр окружности является хордой, проходящей через е центр; такая хорда имеет максимальную длину. По величине диаметр равен двум радиусам.
По величине диаметр равен двум радиусам. - определение опознается по наличию во фразе слова НАЗЫВАЕТСЯ, те это разъяснение некоторого понятия. свойства которого начинают изучать 9 большинство Проходит…. мимо)
окружностью называется
геометрическая фигура. состоящая из точек плоскости. находящихся на одинаковом расстоянии от одной точки. называемой центром окр.
радиус — отрезок. соединяющий центр окружности с любой точкой окружности.
хорда- отрезок. соединяющий 2 точки окружности
диаметр — хорда. проходящая через центр окружности. длина диаметра равна длине 2 радиусов.УЧЕБНИК украли злые люди?
доступ в поиск заблокировали старшие товарищи? - Центр — это точка, все точки окр-сти от которой находятся на одинаковом расстоянии.
радиус — отрезок от центра до любой точки на окр.
Диаметр — отрезок, соединяющий две точки на окружности и проходящий через центр.
Хорда — отрезок, соединяющий две точки окружности. Не обязательно проходит через центр. Удачи! ! Все просто))
Удачи! ! Все просто)) - Домашнее задание (09.02.2016 г.)
Данное домашнее задание необходимо выполнять на формате А4
Прочитать параграф 22 Окружность. Длина окружности.
Записать определение окружности, центра, радиуса и диаметра окружности (используя Интернет или любой справочник по математике).
Начертить рисунок 87(б) стр. 146, со страницы 147 записать две формулы для нахождения длины окружности через радиус и диаметр окружности. Запишите значение числа.
Выполните контрольные задание 2, 3, 4 на странице 153 учебника.
Прочитать параграф 23 Круг. Площадь круга.
Записать определение круга (стр. 153).
Начертить круг, отметить центр, радиус и диаметр круга.
Записать две формулы для нахождения площади круга через радиус и диаметр круга:
;
675(в, г), 676(в, г), 678(в, г. Изображать круг не надо, необходимо найти диаметр и радиус).
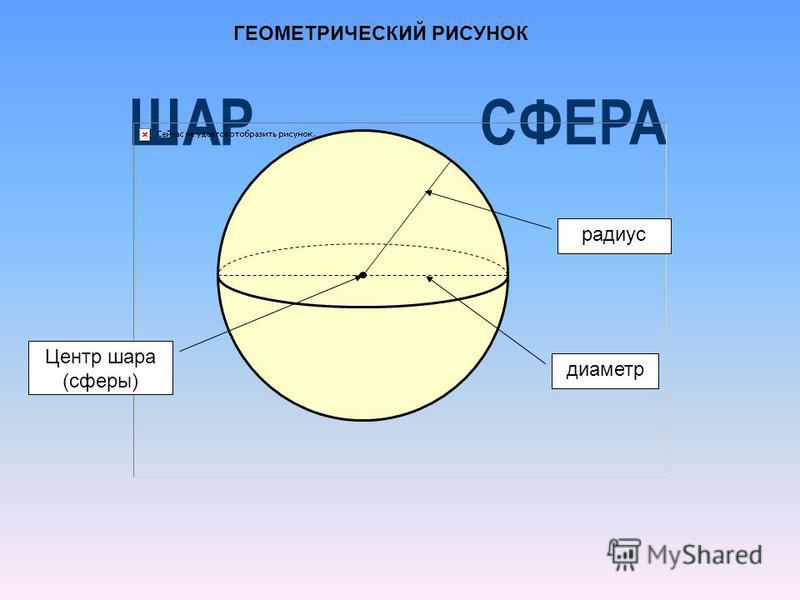
Прочитать параграф 23 Шар. Сфера.
Заполнить таблицуПредметы, имеющие форму сферы
(название и рисунок предмета) Предметы, имеющие форму шара (название и рисунок предмета)
1
2
3Начертить рисунок 103 страница 158, записать формулы для объема шара и площади сферы (страница 158)
690, 691, 692. попробуйте решить
попробуйте решить - ееееееееееееееееееееееееееееееееееее
И в чем ее отличие от круга. Возьмите ручку или цвета и нарисуйте на листке бумаги обычный круг. Закрасьте всю середину полученной фигуры синим карандашом. Красный контур, обозначающий границы фигуры, — это окружность. А вот синее содержимое внутри нее — и есть круг.
Размеры круга и окружности определяются диаметром. На красной линии, обозначающей окружность, отметьте две точки таким образом, чтобы они оказались зеркальным отражением друг друга. Соедините их линией. Отрезок обязательно пройдет через точку в центре окружности. Этот отрезок, соединяющий противоположные части окружности, и называется в геометрии диаметром.
Отрезок, который тянется не через центр окружности, но смыкается с ней противоположными концами, называется хордой. Следовательно, хорда, пролегающая через точку центра окружности, и является ее диаметром.
Обозначается диаметр латинской буквой D. Находить диаметр окружности можно по таким значениям, как площадь, длина и радиус круга.
Расстояние от центральной точки до точки, отложенной на окружности, называется радиусом и обозначается буквой R. Знание величины радиуса помогает вычислить диаметр окружности одним несложным действием:
К примеру, радиус — 7 см. Умножаем 7 см на 2 и получаем величину, равную 14 см. Ответ: D заданной фигуры равен 14 см.
Иногда приходится определять диаметр окружности лишь по ее длине. Здесь необходимо применить специальную формулу, помогающую определить Формула L = 2 Пи * R, где 2 — это неизменная величина (константа), а Пи = 3,14. А так как известно, что R = D * 2, то формулу можно представить и другим способом
Данное выражение применимо и как формула диаметра окружности. Подставив известные в задаче величины, решаем уравнение с одним неизвестным. Допустим, длина равна 7 м. Следовательно:
Ответ: диаметр равен 21,98 метрам.
Если известно значение площади, то также можно определить диаметр окружности. Формула, которая применяется в данном случае, выглядит так:
D = 2 * (S / Пи) * (1 / 2)
S — в данном случае Допустим, в задаче она равна 30 кв. м. Получаем:
м. Получаем:
D = 2 * (30 / 3, 14) * (1 / 2) D = 9, 55414
При обозначенной в задаче величине, равной объему (V) шара, применяется следующая формула нахождения диаметра: D = (6 V / Пи) * 1 / 3.
Иногда приходится находить диаметр окружности, вписанной в треугольник. Для этого по формуле находим радиус представленной окружности:
R = S / p (S — площадь заданного треугольника, а p — периметр, разделенный на 2).
Полученный результат увеличиваем вдвое, учитывая, что D = 2 * R.
Нередко находить диаметр окружности приходится и в быту. К примеру, при определении что равносильно его диаметру. Для этого необходимо обмотать палец потенциального обладателя кольца ниткой. Отметить точки соприкосновения двух концов. Измерить линейкой длину от точки до точки. Полученное значение умножаем на 3,14, следуя формуле определения диаметра при известной длине. Так что, утверждение о том, что познания в геометрии и алгебре в жизни не пригодятся, не всегда соответствует действительности.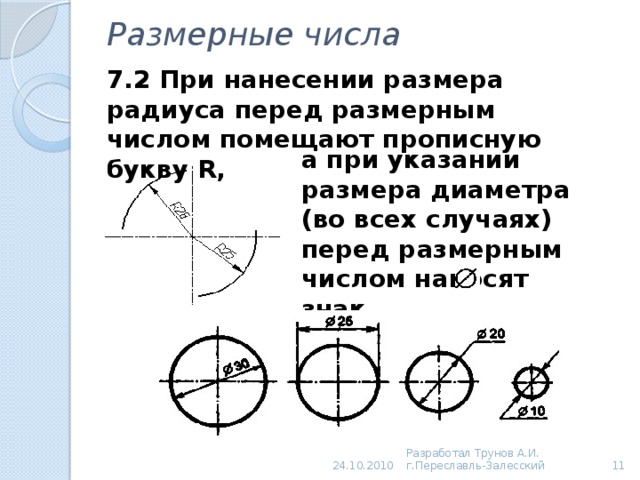 А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.
А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.
Данный урок посвящён изучению окружности и круга. Также учитель научит отличать замкнутые и незамкнутые линии. Вы познакомитесь с основными свойствами окружности: центром, радиусом и диаметром. Выучите их определения. Научитесь определять радиус, если известен диаметр, и наоборот.
Если заполнить пространство внутри окружности, например начертить окружность с помощью циркуля на бумаге или картоне и вырезать, то получим круг (рис. 10).
Рис. 10. Круг
Круг — это часть плоскости, ограниченная окружностью.
Условие: Витя Верхоглядкин начертил в своей окружности (рис. 11) 11 диаметров. А когда пересчитал радиусы, получил 21. Правильно ли он сосчитал?
Рис. 11. Иллюстрация к задаче
Решение: радиусов должно быть в два раза больше, чем диаметров, поэтому:
Витя сосчитал неправильно.
Список литературы
- Математика.
 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / [М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.] — 2-е изд. — М.: Просвещение, 2012. — 112 с.: ил. — (Школа России).
3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / [М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.] — 2-е изд. — М.: Просвещение, 2012. — 112 с.: ил. — (Школа России). - Рудницкая В.Н., Юдачёва Т.В. Математика, 3 класс. — М.: ВЕНТАНА-ГРАФ.
- Петерсон Л.Г. Математика, 3 класс. — М.: Ювента.
- Mypresentation.ru ().
- Sernam.ru ().
- School-assistant.ru ().
Домашнее задание
1. Математика. 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / [М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.] — 2-е изд. — М.: Просвещение, 2012., ст. 94 № 1, ст. 95 № 3.
2. Разгадайте загадку.
Мы живём с братишкой дружно,
Нам так весело вдвоём,
Мы на лист поставим кружку (рис. 12),
Обведём карандашом.
Получилось то, что нужно —
Называется …
3. Необходимо определить диаметр окружности, если известно, что радиус равен 5 м.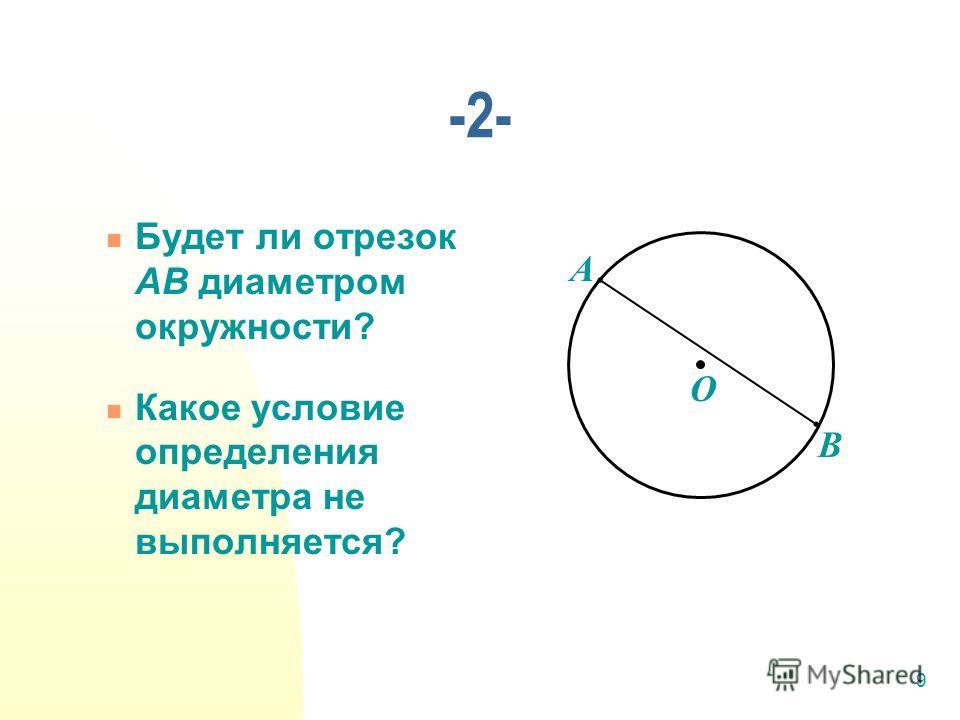
4. * С помощью циркуля начертите две окружности с радиусами: а) 2 см и 5 см; б) 10 мм и 15 мм.
Окружность состоит из множества точек, которые находятся на равном расстоянии от центра. Это плоская геометрическая фигура, и найти ее длину не составит труда. С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты , устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.
Характеристики фигуры
Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.
В пределах окружности имеются точки Х такие , что не изменяется и не равняется единице отношение АХ/ВХ.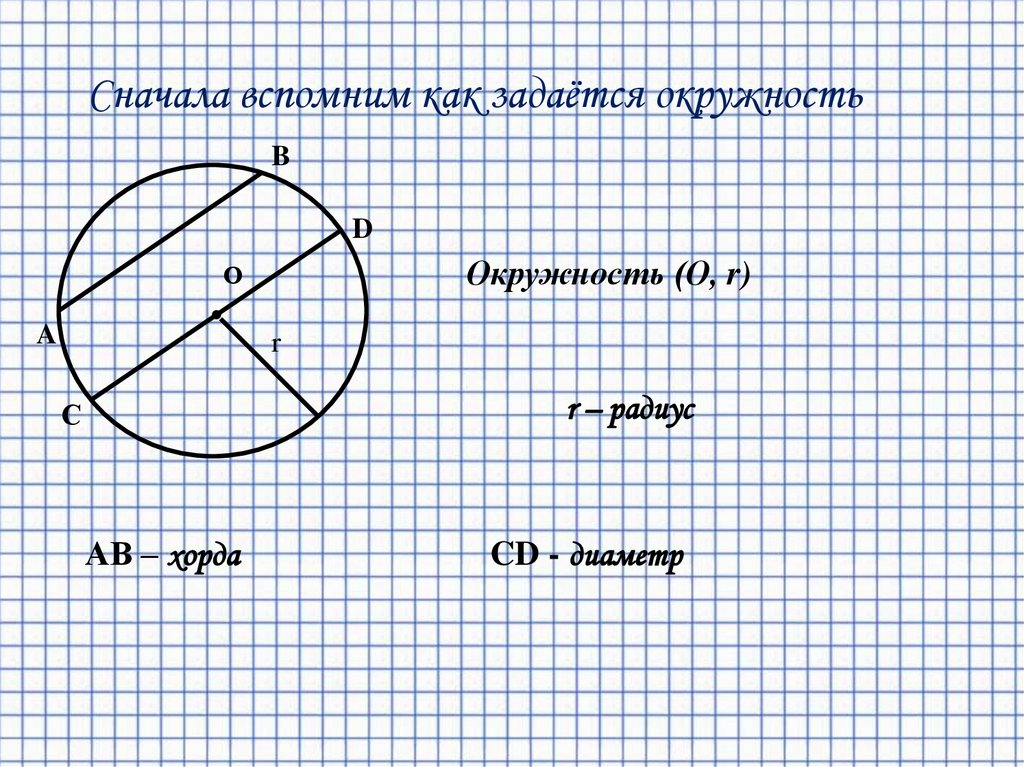 В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.
В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.
Основные термины окружности
Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры — это диаметр, радиус и хорда . Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками , проходящее через центр фигуры.
Основные формулы для вычислений
Параметры используются в формулах вычислений величин окружности:
Диаметр в формулах вычисления
В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы.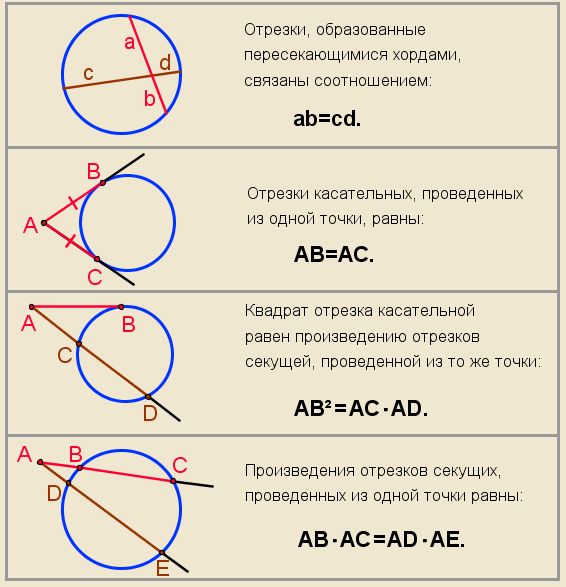 Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.
Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.
Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него. В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.
Расчёты по радиусу
Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С — длина, r — радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.
Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?
Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы. Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.
Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.
Подручные способы вычисления
Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:
- При небольших размерах круглого предмета его длину можно найти с помощью верёвки, обёрнутой вокруг один раз.
- Величину большого предмета измеряют так: на ровной плоскости раскладывают верёвку, и по ней прокатывают круг один раз.
- Современные студенты и школьники для расчётов используют калькуляторы. В режиме онлайн по известным параметрам можно узнавать неизвестные величины.
Круглые предметы в истории человеческой жизни
Первое изделие круглой формы, которое изобрёл человек — это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода.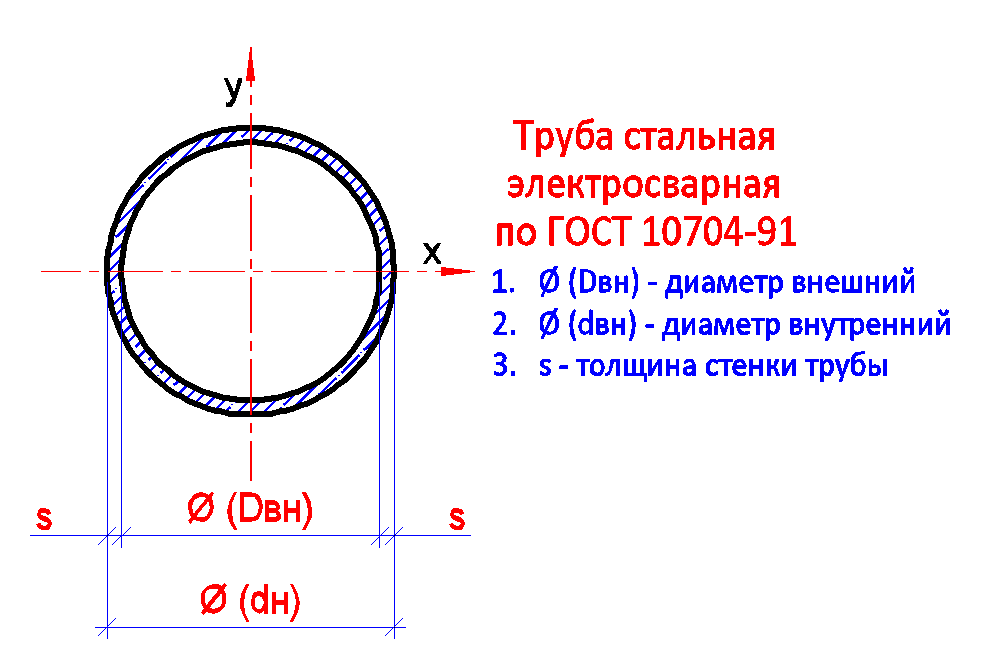 Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.
Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.
Форму колеса имеет гончарный круг , большинство деталей в сложных механизмах, конструкциях водяных мельниц и прялок. Нередко встречаются круглые предметы в строительстве — рамки круглых окон в романском архитектурном стиле, иллюминаторы в суднах. Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.
Какой диаметр? — Learning Street
Какой диаметр? Диаметр — это длина линии, проходящей через центр окружности.
Диаметр всегда в два раза больше длины радиуса окружности.
Когда дети узнают о диаметре? Изучив 2D- и 3D-фигуры в 1-м и 2-м классах, дети познакомятся с различными частями круга в 6-м классе.
Учителя попросят детей измерить радиус и диаметр различных кругов и могут дать веревку, чтобы можно было измерить длину окружности.
Детям также можно давать практические вопросы, в которых им дают радиус круга и просят найти диаметр. Это поможет им узнать, что диаметр равен радиусу, умноженному на 2.
Вот пример практического вопроса:
Каков диаметр окружности, показанной ниже?
Ответ:
Дети должны найти ответ, так как они знают, что диаметр равен радиусу, умноженному на 2 (r²).
6 х 2 = 12 см
Диаметр = 12см.
Зачем детям знать диаметр?
Изучение различных частей круга важно для того, чтобы дети могли вычислять площадь и длину окружности.
Понимание взаимосвязи между диаметром и радиусом важно, когда детям задают практические вопросы.
Учителя могут познакомить детей с формулой для вычисления длины окружности (C = 2 x π x r) и формулой для вычисления площади (A = π x r ²).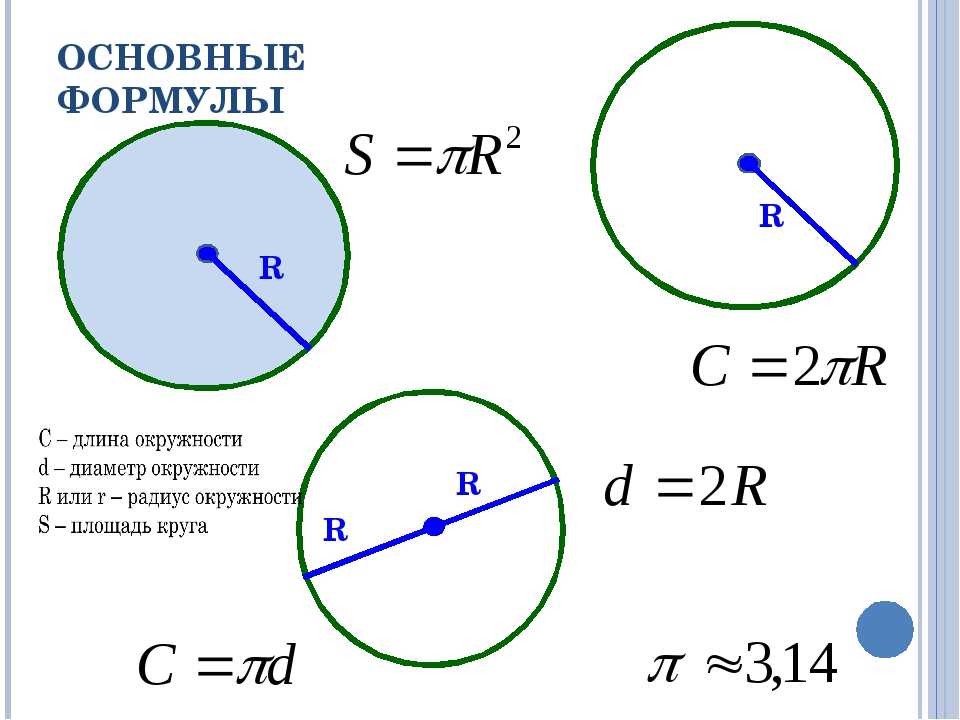 Вот практический вопрос по расчету длины окружности:
Вот практический вопрос по расчету длины окружности:
Тарелка Сэма имеет радиус 12 см. Чему равна окружность пластины?
Ответ:
Во-первых, полезно начертить примерный круг и аннотировать его любыми измерениями, которые дает вопрос.
Нам сказали, что радиус пластины равен 12 см, поэтому теперь мы можем подставить это значение в формулу C = 2 x π x r (где π = 3,14).
2 х 3,14 х 12 = 75,36 см. Окружность тарелки Сэма 75,36 см.
Дети тоже могли бы получить тот же ответ с формулой C = π x d, используя свое знание того, что диаметр в два раза больше радиуса (2 x 12 = 24).
3,14 х 24 = 75,36 см.
Как Learning Street помогает детям с диаметром? Это один из многих случаев, когда наши специализированные математические курсы развивают предыдущую идею, в данном случае радиус, а затем продвигают обучение ребенка, в данном случае к диаметру. Ребенка научат диаметру, попрактикуют его, чтобы обеспечить четкое понимание, а также отредактируют его позже, чтобы он не был забыт.
Тесты могут включать SAT, конкурсные тесты 11 Plus или выборочные экзамены независимой школы.
Наши курсыНажмите, чтобы просмотреть доступные курсы
- Независимая школа 11 Plus Курсы подготовки к экзаменам
- Начальная школа 11 Плюс Курсы подготовки к экзаменам
- Курсы усовершенствования/развития начальной школы
Диаметр
Диаметр окружности — это отрезок, который проходит через центр окружности и имеет конечные точки на окружности.
Отрезок AB вверху является диаметром окружности O, поскольку конечные точки A и B лежат на окружности, а отрезок AB проходит через центр O.
Окружность содержит бесконечно много диаметров. Ниже нарисованы три диаметра окружности О. Пока отрезок прямой проходит через центр и имеет концы на окружности, он является диаметром.
Диаметр и радиусы
Диаметр круга в два раза больше длины радиуса круга.
Два радиуса длины r, показанные выше для окружности, образуют диаметр d.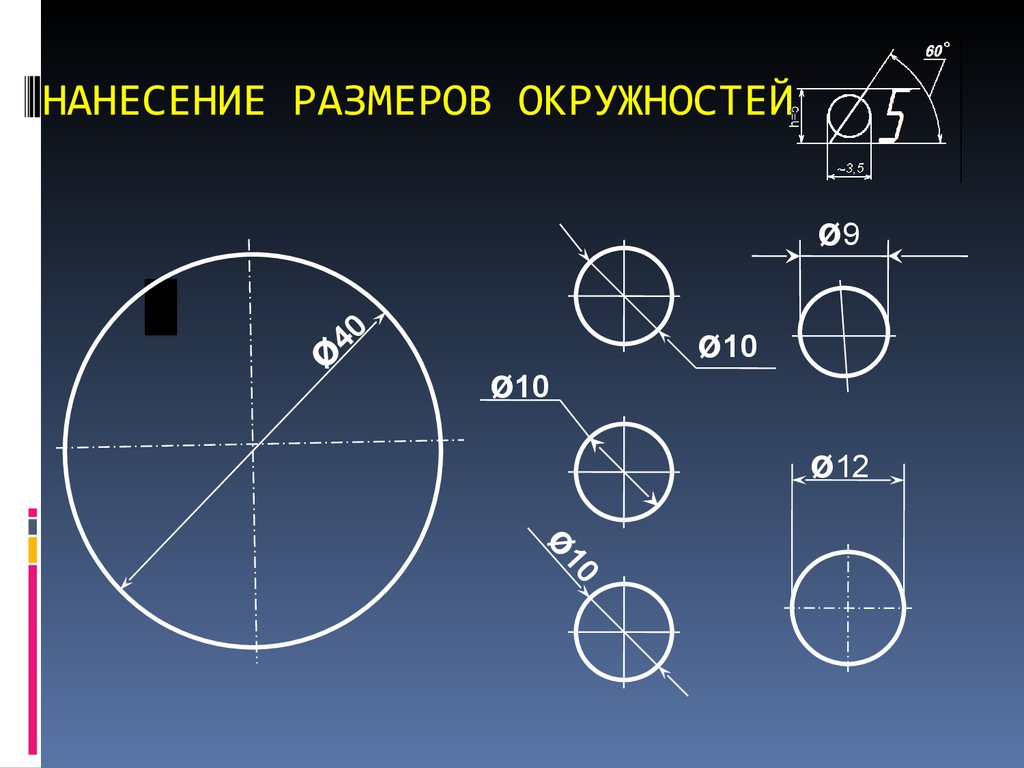 Поскольку каждый радиус окружности имеет одинаковую меру, d = 2r или .
Поскольку каждый радиус окружности имеет одинаковую меру, d = 2r или .
Диаметр и хорды
Хорда — это отрезок, концы которого лежат на окружности. Если хорда содержит центр, она также является диаметром окружности. Диаметр длиннее любой хорды, не содержащей центра (т. е. не являющейся диаметром).
Диаметр AB > хорды CD для окружности O выше, так как хорда CD не содержит центра O.
Диаметр и окружность
Окружность окружности можно сравнить с ее диаметром.
Если окружность окружности выпрямить, чтобы сделать отрезок, показанный выше, его длина будет немного больше, чем длина 3 диаметров окружности. Окружность круга — это его диаметр в масштабе пи (символически записывается как π). Это верно для любого круга любого размера. Пи — математическая константа и иррациональное число, поэтому оно имеет бесконечное количество цифр и не повторяется. Он примерно равен 3,14159..
Диаметр и полуокружности
Дуга окружности, концы которой лежат на концах диаметра окружности, образует полуокружность или полуокружность.
Концы дуги ABC для окружности O, показанной выше, лежат на концах диаметра AB, образуя полуокружность. Кроме того, диаметр делит окружность на две полуокружности, поэтому дуга ниже дуги ABC также является полуокружностью.
Поскольку полукруг охватывает половину всего круга, его длина окружности равна половине длины окружности, или πr, где r — радиус окружности.
Другие свойства и теоремы
Если вершина прямого угла лежит на окружности, то точки пересечения сторон угла и окружности образуют диаметр окружности.
Вершина прямого угла B находится на окружности O, показанной выше. Вписанный угол равен половине длины дуги, на которую опирается. Поскольку угол B является вписанным углом и его градусная мера равна 90°, дуга, на которую опирается этот угол, имеет градусную меру 180°. Таким образом, дуга — это полуокружность, а хорда AC — это диаметр окружности O.
И наоборот, если вершины треугольника лежат на окружности и одна сторона треугольника является диаметром окружности, то угол, противоположный диаметру, является прямым углом, а треугольник является прямоугольным.

 По величине диаметр равен двум радиусам.
По величине диаметр равен двум радиусам.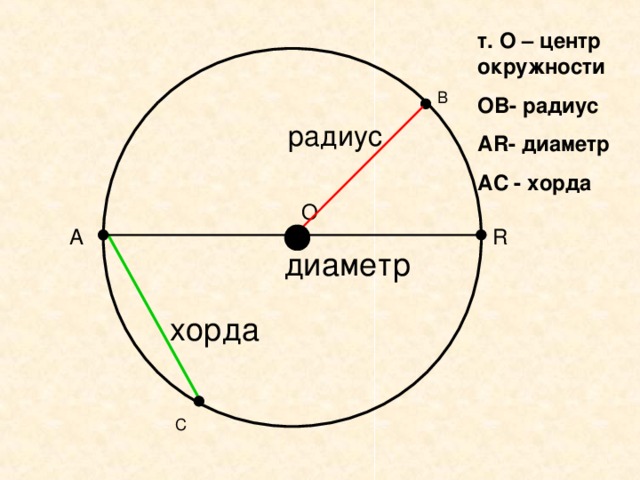 Удачи! ! Все просто))
Удачи! ! Все просто))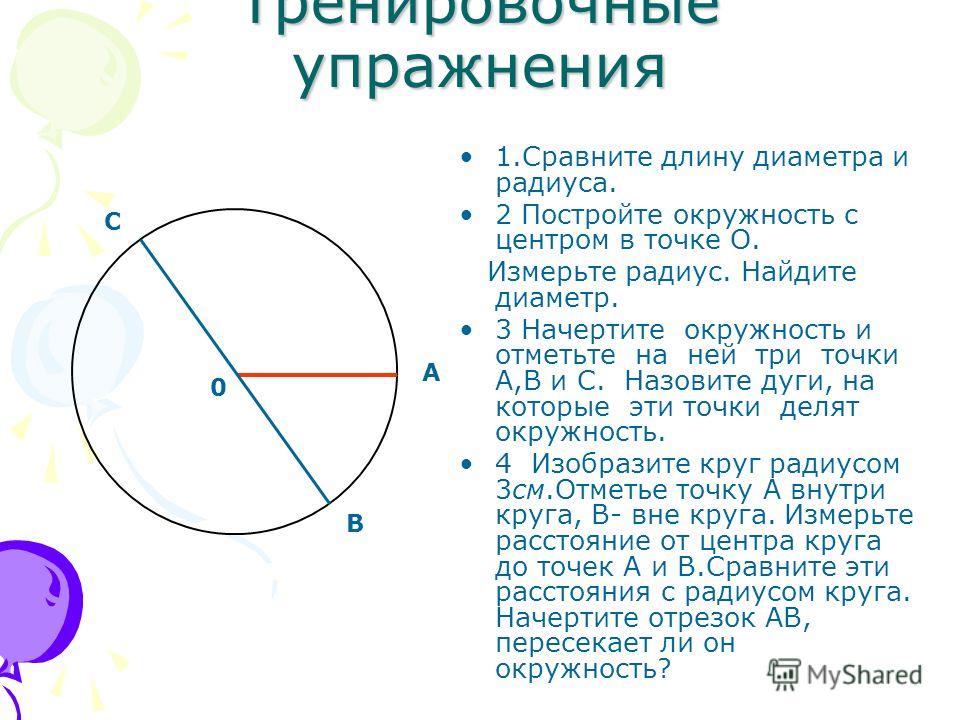 попробуйте решить
попробуйте решить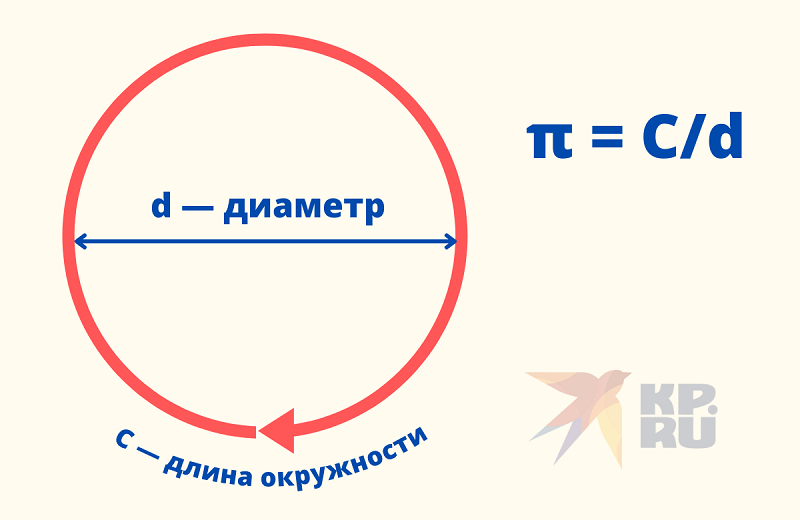 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / [М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.] — 2-е изд. — М.: Просвещение, 2012. — 112 с.: ил. — (Школа России).
3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / [М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.] — 2-е изд. — М.: Просвещение, 2012. — 112 с.: ил. — (Школа России).