Определитель матрицы
Для решения заданий в высшей математике периодически нужно находить определитель матрицы. Встречается он не только в алгебре, но и в геометрии, математический анализ также может его содержать. Следовательно, нужно уметь находить определитель матрицы, так как это необходимо.
Что такое матрица — это таблица прямоугольной формы содержащая в себе различные выражения. Матрица может иметь n столбцов и m строк, ее называют как (m,n) — матрице.
Только квадратная матрица имеет определитель. Который больше всего встречается второго, третьего и четвертого порядка.
Следует запомнить что выражения (числа) стоят сами по себе, значит и вычитать ни чего не нужно, перестановку делать так же нельзя. Иногда можно поменять местами столбцы и строки парами. В результате это даст нам смену знака, но часто этого не требуется. Из чего следует, что в любом данном определителе, не нужно ни чего трогать или менять.
Разберемся в названиях обозначений
— Определитель матрицы обозначается как {A}, реже встречается как D либо ?
— Вычисление определителя — то нахождение числа, которое обозначается знаком вопроса, подразумевая обычное число.
Для того чтобы найти данное неизвестное число определителя нужно знать правила, алгоритмы и формулы. Такие как:
1) Для вычисления определителя второго порядка, нужна формула
Разберем на примере:
2) Для вычисления определителя третьего порядка, существует 8 способов, разберем 2 самых простых.
Разберем на примере:
В использовании данной формулы, нужно быть внимательным что бы не допустить ошибку, так как формула довольно длинная. В избежание допущения ошибок существует еще один вариант решения. Названный как способ Саррюса. Он похож на предыдущий способ, но фишка заключается в том что через матрицу выражений проводятся параллельные линии, вынося за определитель в правую сторону два первых столбца.
Таким образом числа зачеркнутые красным цветом вписываются с положительным знаком, а числа зачеркнутые синим цветом с отрицательным.
Разберем на примере:
Если сравнить оба варианта вычисления, видно что они практически одинаковы, но во втором варианте допущение ошибки сводится к нулю, так как представлены множители.
Затронем еще один способ нормального вычисления, так как он используется в большинстве случаев. Найти определитель можно путем раскрытия его в любом столбце либо строке. Вычисляется путем сложения произведений выражений данного столбца или строки на алгебраические дополнения.
Для наглядности разберем определитель по первой строке.
3) Для вычисления определителя четвертого порядка, нужно действовать так же как и при вычислении третьего порядка, просто таблица буде больше. Приведу пример и разложу на определитель третьего порядка, а потренироваться в решении вы сможете сами. В ответе должно получиться 18.
Это очень познавательно и интересно, главное быть внимательнее!
Определитель матрицы, свойства определителей
Определителем (детерминантом) квадратной матрицы А n-го порядка (или определителем n-го порядка) называется число, которое обозначается через detA, А или |A|, равное алгебраической сумме n! слагаемых, каждое из которых представляет собой произведение n множителей (элементов матрицы), взятых по одному и только одному из каждой строки и столбца, причем знак каждого множителя определяется четностью подстановки составленной из первых и вторых индексов, перемножаемых элементов:
где
— знак перестановки,,
где-
число инверсий перестановки:.
Дадим понятие инверсии. В перестановке два числаисоставляютинверсию, если i<j, но >.
Рассмотрим определитель второго порядка.
В данном случае имеется две перестановки:
и .
Рассмотрим определитель третьего порядка.
3!=1·2·3=6 Следовательно число инверсий равно шести.
, ,,
, ,.
Определитель третьего порядка вычисляется по формуле: (2.1)
(слева на Рис.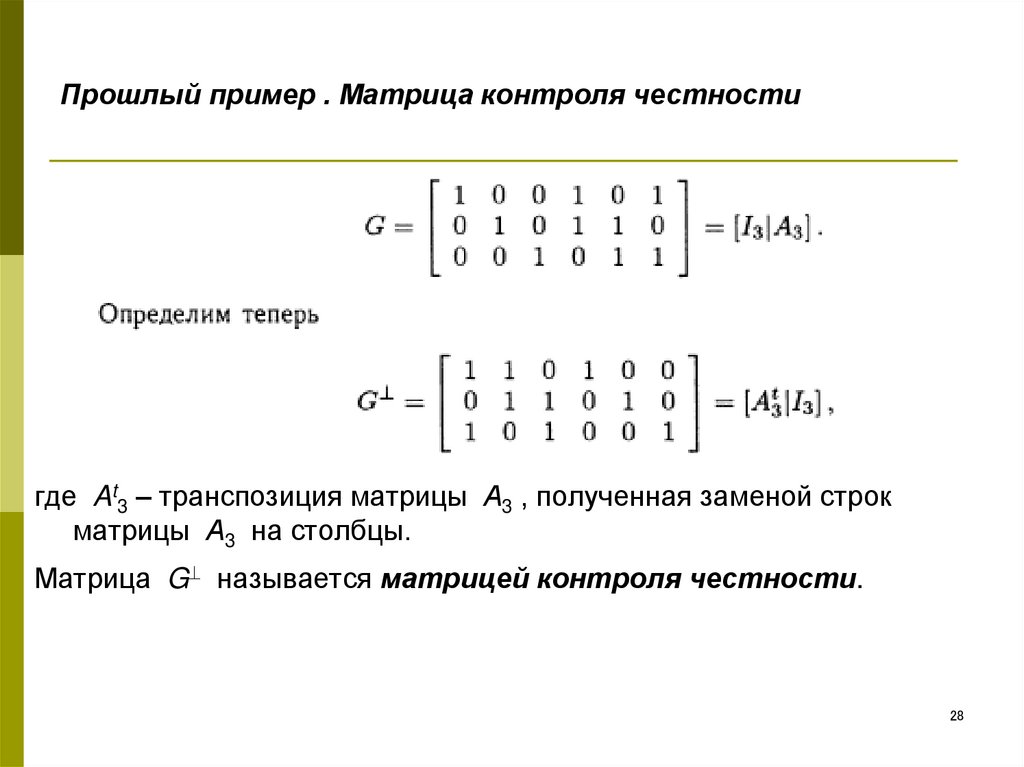 1
дано правило вычисления положительных
членов определителя, а справа –
отрицательных).
1
дано правило вычисления положительных
членов определителя, а справа –
отрицательных).
Пример 2.1:
Сосчитаем определители:
;
Свойства определителей:
Определитель транспонированной матрицы равен определителю исходной матрицы.
Определитель матрицы, содержащей нулевую строку (столбец), равен нулю.
Общий множитель элементов некоторой строки (столбца) матрицы можно вынести за знак определителя, если этот множитель не нулевой.
Если в матрице поменять местами две строки (столбца), то ее определитель изменит только знак.
Определитель матрицы с двумя одинаковыми строками (столбцами) равен нулю.
Две
строки (столбца) матрицы называются пропорциональными,
если одна из них получается умножением
другой на некоторое отличное от нуля
число.
Определитель матрицы с пропорциональными строками равен нулю.
Если к одной строке матрицы прибавить другую ее строку, умноженную на некоторое число, то определитель матрицы не изменится.
Минором Мij элемента aij матрицы n-го порядка называется определитель матрицы (n-1)-го порядка, полученной из исходной матрицы вычеркиванием i-ой строки и j-го столбца.
Например, минором элемента a12 матрицы третьего порядка будет:
.
Каждая матрица n-го порядка имеет n2 миноров (n-1) порядка.
Алгебраическим дополнением Aij элемента aij матрицы n-го порядка называется его минор, взятый со знаком (-1)i+j:
A
ij=(-1)i+j ·Mij, т. е.
алгебраическое дополнение совпадает
с минором, когда сумма номеров строки
и столбца (i+j)
– четное число, и отличатся от минора
знаком, когда (i+j)
– нечетное число.
е.
алгебраическое дополнение совпадает
с минором, когда сумма номеров строки
и столбца (i+j)
– четное число, и отличатся от минора
знаком, когда (i+j)
– нечетное число.
Например, ;.
Теорема Лапласа Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
(разложение по элементам i-ой строки; i=1;2;…;n),
(разложение по элементам j-го столбца; j=1;2;…;n
Данное разложение часто используется для нахождения определителя матрицы 4-го порядка.
Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0, т.
 е..
е..
Объединяя результат теоремы Лапласа и этого свойства, получаем:
Определитель треугольной матрицы равен произведению диагональных элементов.
Определитель произведения двух квадратных матриц равен произведению их определителей: |C|=|A|·|B|, где С=А·В; А и В – матрицы n-го порядка.
Определитель матрицы – объяснение и примеры
Определитель матрицы – это очень важная скалярная величина. С помощью определителя матриц мы можем найти полезную информацию о линейных системах, решить линейные системы, найти , обратную матрицы, и использовать ее в исчислении. Давайте посмотрим на определение определителя:
Определитель матрицы — это скалярная величина, которая получается в результате определенных операций с элементами матрицы.
В этом уроке мы рассмотрим определитель, как найти определитель, формулу определителя матриц $2\times 2$ и $3\times 3$, а также примеры, поясняющие наше понимание определителей . Давайте начнем!
Давайте начнем!
Что такое определитель матрицы?
Определитель матрицы — это одно постоянное значение (или скалярное значение), которое сообщает нам определенные сведения о матрице. Значение определителя получается в результате определенных операций, которые мы делаем с элементами матрицы.
Существует $ 3 $ способов обозначения определителя матрицы . Посмотрите на картинку ниже:
С левой стороны находится Matrix $ A $. Вот так мы пишем матрицу.
В правой части $ 3 $ обозначения для определителей матриц. Мы можем обозначить определитель матрицы $A$, написав $det(A)$, $| А | $, или поместив все элементы матрицы внутрь двух вертикальных полос (как показано). Все эти обозначения $3$ обозначают определитель матрицы .
Как найти определитель матрицы
Так как же найти определитель матрицы?
Прежде всего, мы можем вычислить определитель только для квадратных матриц!
Для неквадратных матриц нет определителя.
Теперь есть формула (алгоритм) для нахождения определителя любой квадратной матрицы. Это выходит за рамки данного урока. Вместо этого мы рассмотрим нахождение определителей матриц $ 2 \times 2 $ и матриц $ 3 \ x 3 $. Формула может быть расширена, чтобы найти определитель $ 4 \times 4 $ матриц, но это слишком сложно и беспорядочно!
Ниже мы рассмотрим формулы для матриц $ 2 \times 2 $ и матриц $ 3 \times 3 $ и посмотрим, как вычислить определитель таких матриц.
Формула определителя матрицы
В этом разделе мы найдем определитель матриц $ 2 \times 2 $ и $ 3 \times 3 $.
Определитель матрицы 2 x 2
Рассмотрим матрицу $ 2 \times 2 $, показанную ниже:
$ A = \begin{bmatrix} { a } & { b } \\ { c } & { d } \ конец {bmatrix} $
Формула для определителя матрицы $ 2 \times 2 $ показана ниже:
$ det( A ) = | А | = \begin{vmatrix} { a } & { b } \\ { c } & { d } \end {vmatrix} = ad – bc $
Примечание. Мы использовали $ 3 $ различных обозначений для обозначения определителя этого matrix
Мы использовали $ 3 $ различных обозначений для обозначения определителя этого matrix
Чтобы найти определитель матрицы $ 2 \times 2 $, мы берем произведение верхнего левого элемента и нижнего правого элемента и вычитаем из него произведение верхнего правого элемента и нижнего левого элемента. вход.
Вычислим определитель матрицы $ B $, показанной ниже:
$ B = \begin{bmatrix} { 1 } & { 3 } \\ { – 3 } & { 2 } \end {bmatrix} $
Используя по только что изученной формуле мы можем найти определитель:
$ det( B ) = | Б | = \begin{vmatrix} { 1 } & { 3 } \\ { – 3 } & { 2 } \end {vmatrix} $
$ = ( 1 ) ( 2 ) – ( 3 ) ( – 3 ) $
$ = 2 + 9 $
$ = 11 $
Определитель матрицы $B$ равен $11$.
Определитель матрицы 3 x 3
Теперь, когда мы научились находить определитель матрицы $ 2 \times 2 $, это пригодится при нахождении определителя матрицы $ 3 x 3 $. Рассмотрим матрицу $ B $, показанную ниже:
$ B = \begin{bmatrix} {a} & {b} & {c} \\ {d} & {e} & {f} \\ {g} & {h } & { i } \end {bmatrix} $
Формула для определителя матрицы $ 3 \times 3 $ показана ниже:
$ det( B ) = | Б | = a \begin{vmatrix} {e} & {f} \\ {h} & {i} \end{vmatrix} — b \begin{vmatrix} {d} & {f} \\ {g} & {i } \end{vmatrix} + c \begin{vmatrix} { d } & { e } \\ { g } & { h } \end{vmatrix} $
Примечание:
- Возьмем $ a $ и умножьте его на определитель матрицы $ 2 \times 2 $, который равен , а не в строке и столбце $ a $
- Затем мы вычитаем произведение $ b $ и определителя $ 2 \ умноженная на 2 $ матрица, равная вместо в строке и столбце $ b $
- Наконец, мы добавляем произведение $ c $ и определитель матрицы $ 2 \times 2 $, который равен , а не в строке и столбце $ c $
Используя формулу определителя матрицы $ 2 \times 2 $, мы можем дополнительно свести эту формулу к следующему виду:
$ det( B ) = | Б | = a ( e i – f h ) – b (di – f g ) + c (d h – e g ) $
Если вы не можете запомнить эту формулу (я знаю, это сложно!), просто запомните пункты $ 3 $, описанные выше. . Кроме того, запомните знаки скалярных величин, на которые вы умножаете каждый определитель. $a$ положительное, $b$ отрицательное и $c$ положительное.
. Кроме того, запомните знаки скалярных величин, на которые вы умножаете каждый определитель. $a$ положительное, $b$ отрицательное и $c$ положительное.
Теперь рассмотрим матрицу $ 3 \times 3 $, показанную ниже:
$ B = \begin{bmatrix} { 1 } & { 2 } & { – 1 } \\ { 0 } & { 3 } & { – 4 } \\ { – 1 } & { 2 } & { 1 } \end {bmatrix} $
Давайте вычислим определитель этой матрицы, используя только что изученную формулу. Как показано ниже:
$ B = \begin{bmatrix} { 1 } & { 2 } & { – 1 } \\ { 0 } & { 3 } & { – 4 } \\ { – 1 } & { 2 } & { 1 } \end {bmatrix} $
$ det( B ) = | Б | = 1 [ ( 3 )( 1 ) – ( – 4 )( 2 ) ] – 2 [ ( 0 )( 1 ) – ( – 4 )( – 1 ) ] + (-1) [ ( 0 )( 2 ) – ( 3 )( – 1 ) ] $
$ = 1 [ 3 + 8 ] — 2 [ 0 — 4 ] + (-1) [ 0 + 3 ] $
$ = 1 [ 11 ] — 2 [ — 4 ] — 1 [ 3 ] $
$ = 11 + 8 – 3 $
$ = 16 $
Определитель матрицы $ 3 \times 3 $ $ B $ равен $ 16 $.
Давайте рассмотрим больше примеров, чтобы лучше понять детерминанты!
Пример 1
Учитывая $ C = \begin{bmatrix} { – 9 } & { – 2 } \\ { 3 } & { – 1 } \end {bmatrix} $, найдите $ | С | $.
Решение
Нам нужно найти определитель матрицы $ 2 \times 2 $, показанной выше. Воспользуемся формулой и найдем определитель. Ниже показано:
$ det( C ) = | С | = \begin{vmatrix} { – 9 } & { – 2 } \\ { 3 } & { – 1 } \end {vmatrix} $
$ = ( – 9 ) ( – 1 ) – ( – 2 ) ( 3 ) $
$ = 9 + 6 $
$ = 15 $
Пример 2 & { 2 } \end {vmatrix} = 34 $.
Решение
Нам уже известен определитель, и нам нужно найти элемент $ x $. Подставим это в формулу и решим для $ x $:
$ \begin{vmatrix} { 1 } & { x } \\ { 8 } & { 2 } \end {vmatrix} = 34 $
$ ( 1 ) ( 2 ) – ( x ) ( 8 ) = 34 $
$ 2 – 8x = 34 $
$ -8x = 34 – 2 $
$ – 8x = 32 $
$ x = – 4 $
Пример 3Рассчитайте 9Определитель 0008
матрицы $ D $ показан ниже:$ D = \begin{bmatrix} { 6 } & { 2 } \\ { – 12 } & { – 4 } \end {bmatrix} $
Решение
Мы будем использовать формулу для вычисления определителя матрицы $D$. Ниже показано:
Ниже показано:
$ det( D ) = | Д | = \begin{vmatrix} { 6 } & { 2 } \\ { – 12 } & { – 4 } \end {vmatrix} $
$ = ( 6 ) ( – 4 ) – ( 2 ) ( – 12 ) $
$ = -24 + 24 $
$ = 0 $
Определитель этой матрицы равен $ 0 $!
Это особый тип матрицы. Это необратимая матрица, известная как сингулярная матрица . Чтобы узнать больше, проверьте здесь.
Практические вопросыНайдите определитель приведенной ниже матрицы:
$ A = \begin{bmatrix} – 5 & – 10 \\ 3 & – 1 \end{bmatrix} $9 9 9 9
Найти $ y $ по $ \begin{vmatrix} { 1 } & { 3 } & { – 1 } \\ { 5 } & { 0 } & { y } \\ { – 1 } & { 2 } & { 3 } \end {vmatrix} = – 60 $
Дана матрица $ A $, матрица размера $ 2 x 2 $. Нам нужно найти его определитель. Мы делаем это, применяя формулу. Процесс показан ниже:
$ det( A ) = | А | = \begin{vmatrix} { – 5 } & { – 10 } \\ { 3 } & { – 1 } \end {vmatrix} $
$ = ( – 5 ) ( – 1 ) – ( – 10 ) ( 3 ) $
$ = 5 + 30 $
$ = 35 $
- Нам уже дан определитель и нужно найти элемент $ y $.
 Подставим его в формулу для определителя матрицы $3\times 3$ и решим относительно $y$:
Подставим его в формулу для определителя матрицы $3\times 3$ и решим относительно $y$:$ \begin{vmatrix} { 1 } & { 3 } & { – 1 } \\ { 5 } & { 0 } & { y } \\ { – 1 } & { 2 } & { 3 } \ end {vmatrix } = – 60 $
$ 1 [ ( 0 ) ( 3 ) – ( y ) ( 2 ) ] – 3 [ ( 5 ) ( 3 ) – ( y ) ( – 1 ) ] + (-1) [ ( 5 ) ( 2 ) – ( 0 )( – 1 ) ] = – 60$
$ 1 [- 2г ] – 3 [ 15 + г ] + (-1) [ 10 ] = – 60 $
$ – 2г – 45 – 3г – 10 = – 60 $
$ – 5y – 55 = – 60 $
$ – 5y = – 60 + 55 $
$ – 5y = – 5 $
$ y = 1 $
Определитель матрицы: определение и формулы
Вы когда-нибудь задумывались, как узнать, имеет ли система одновременных уравнений решение? Вы можете настроить систему уравнений для сравнения сделок по тому, что вы хотите купить, чтобы сравнить несколько факторов в разных вариантах, но как проверить, правильно ли вы настроили систему и есть ли решения для сравнения?
Вы можете сохранить эту систему в матрице, а затем найти определитель этой матрицы, чтобы указать, есть ли у вас доступное решение.
Читайте дальше, чтобы узнать больше о том, как это работает.
Что такое матрица?
Матрица — это массив, используемый для хранения, отображения и вычисления данных. Внутренности называются элементами, а матрица будет иметь \(m\) столбцов и \(n\) строк.
Чтобы понять, что такое определитель и как его применять, мы должны сначала понять, что такое матрица.
Матрица — это способ отображения информации. — например, система одновременных уравнений может быть записана в матричной форме, где столбцы соответствуют переменной, а строки — уравнениям. Затем решения будут формировать вектор-столбец. Матричное представление облегчает выполнение преобразований и решение наборов данных, особенно когда нужно решить более двух уравнений!
Но как решить матрицу? Вот тут-то и появляются определители — мы используем их для решения матриц.
Общее обозначение матрицы состоит в том, что \(m\) обозначает количество столбцов, а \(n\) обозначает количество строк. Тогда внутренние элементы матрицы можно записать как: \[A_{m,n} = \begin{bmatrix}a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\ a_{2,1} & a_{2,2} & \cdots & a_{2,n} \\\vdots & \vdots & \ddots & \vdots \\a_{m,1} & a_{m,2 } & \cdots & a_{m,n} \end{bmatrix}\]
Тогда внутренние элементы матрицы можно записать как: \[A_{m,n} = \begin{bmatrix}a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\ a_{2,1} & a_{2,2} & \cdots & a_{2,n} \\\vdots & \vdots & \ddots & \vdots \\a_{m,1} & a_{m,2 } & \cdots & a_{m,n} \end{bmatrix}\]
Дополнительные сведения и примеры см. в нашей статье о базовых матрицах.
\(2\times 2\) пример матрицы \[A_{2,2}=\begin{bmatrix}3&7\\12&-3\end{bmatrix}\]
\(2\times 3 \) пример матрицы \[A_{2,3}=\begin{bmatrix}2&-4&19\\11&23&5\end{bmatrix}\]
\(4\times 3\) пример матрицы \[A_{ 4,3}=\begin{bmatrix}2&8&4\\-2&-5&-3\\13&9&7\\-7&3&-2\end{bmatrix}\]
Матрицы — это действительно полезный способ отображения и хранения множества информации, и они широко используются в математике, физике и технике на более высоких уровнях этих дисциплин.
Что такое определитель?
Итак, теперь мы знаем общие основы матриц, но что такое определитель и почему он важен?
Определитель — это значение, которое мы можем вычислить для любой квадратной матрицы, а затем использовать для вычисления обратной матрицы. {-1}=I.\] Вы можете думать об обратных матрицах как о обратных величинах матричного мира.
{-1}=I.\] Вы можете думать об обратных матрицах как о обратных величинах матричного мира.
Определитель также сообщает нам , если матрица обратима. Пусть определитель матрицы A обозначается как \(\det{A}.\)
- Если определитель матрицы A задан как \(\det{A} = 0\), то матрица равна s ingular и, следовательно, не имеет обратного. Эта матрица не имеет решения.
- Если определитель матрицы A задан как \(\det{A} \neq 0\), то матрица не-s сингулярная и, следовательно, имеет обратную. У этой матрицы есть решение.
Дополнительную информацию и примеры обращения матрицы см. в нашей статье «Обращение матриц».
Определитель матрицы 2×2
Итак, теперь мы знаем, что такое определитель и для чего он используется, но нам все еще нужно выяснить, как они работают.
Начнем с самой простой формы — определителя матрицы \(2\x 2\). Метод вычисления определителя матрицы \(2\times 2\) в основном объясняется перекрестным умножением, а затем вычитанием этих умноженных значений.
Рассмотрим следующую матрицу: \[A_{2,2} = \begin{bmatrix}a_{1,1} & a_{1,2} \\a_{2,1} & a_{2,2} \end{bmatrix}\]Это обозначение, которое мы использовали ранее, но давайте напишем его с отдельными элементами, чтобы легче было следовать методологии. Следовательно,\[A_{2,2} = \begin{bmatrix}a&b\\c&d\end{bmatrix}\]Наш первый шаг — пересечь умножение- мы умножаем верхний левый, нижний правый, а затем верхний правый, нижний левый- а затем вычесть второе умножение из первого. Следовательно, \[\det{A}=ad-cb\]В наших исходных обозначениях это будет \[\det{A}=a_{1,1}a_{2,2}-a_{1,2} a_{2,1}\]Давайте теперь применим это к примеру.
Найдите определитель матрицы \(A\) ниже и затем определите, является ли матрица обратимой.\[A=\begin{bmatrix}4&9\\-2&8\end{bmatrix}\]
Решение
Шаг 1. Найдите определитель
\[\begin{align} \det{A}&=ad-cb\\&=(4\cdot 8)-(9\cdot -2)\\&=32 -(-18)\\&=50\end{align}\]
Шаг 2. Определите, является ли матрица \(A\) обратимой
\(\det{A} \neq 0\), поэтому матрица \(А\) неособа и поэтому обратима.
мы переходим к изучению того, как найти определитель матрицы \(3\x 3\).
Определитель матрицы 3×3
Теперь мы узнали, как найти определитель матрицы \(2\times 2\), но мы также можем встретить матрицы \(3\times 3\) в дополнительной математике, так что давайте посмотрим на как найти определители этих теперь.
Этот процесс немного сложнее, чем определитель матрицы \(2\times 2\), но следует тем же принципам. Давайте рассмотрим приведенную ниже матрицу: \[A_{3,3}=\begin{bmatrix}a&b&c\\d&e&f\\g&h&i\end{bmatrix}\]Мы вычисляем ее определитель, разбивая его на ряд матриц \(2\times 2\).
Для этого проходим по верхнему ряду и умножаем каждый из элементов там на определитель его минора.
Второстепенные элементы в матрице \(3\x 3\) — это элементы, оставшиеся после вычеркивания строки и столбца, вытекающих из корневого элемента.
Предположим, что наш корневой элемент для начала — это \(a\). Минором будет матрица \(2\times 2\) слева, если мы вычеркнем все значения по горизонтали и вертикали от этого элемента. \[\begin{bmatrix}a&-&-\\|&e&f\\|&h&i\ end{bmatrix}\]Определитель нашей матрицы \(3\times 3\) учитывает все миноры для верхней строки и приводит к приведенной ниже формуле.\[\begin{align}\det{A}&=a \cdot \det{\begin{bmatrix}e&f\\h&i\end{bmatrix}}-b\cdot \det{\begin{bmatrix}d&f\\g&i\end{bmatrix}}+c\cdot \det{\ begin{bmatrix}d&e\\g&h\end{bmatrix}} \\ & =a(ei-fh)-b(di-fg)+c(dh-eg)\end{align} \]
\[\begin{bmatrix}a&-&-\\|&e&f\\|&h&i\ end{bmatrix}\]Определитель нашей матрицы \(3\times 3\) учитывает все миноры для верхней строки и приводит к приведенной ниже формуле.\[\begin{align}\det{A}&=a \cdot \det{\begin{bmatrix}e&f\\h&i\end{bmatrix}}-b\cdot \det{\begin{bmatrix}d&f\\g&i\end{bmatrix}}+c\cdot \det{\ begin{bmatrix}d&e\\g&h\end{bmatrix}} \\ & =a(ei-fh)-b(di-fg)+c(dh-eg)\end{align} \]
Обратите внимание на соглашение о знаках с формулой определителя — это \(+,-,+\).
В приведенном выше совете вы можете видеть, что соглашение о знаках идет \(+,-,+\). Это сомножители для первой строки матрицы \(3\times 3\).
Хотя это несколько выходит за рамки того, с чем вы здесь имеете дело, для каждого элемента матрицы существуют кофакторы.
Это означает, что мы могли бы также найти определитель матрицы, используя строки 2 или 3 в качестве наших корневых элементов, и взять оттуда миноры — для этого нам просто нужно применить правильные кофакторы.
Тем не менее, все, что вам сейчас нужно, это верхняя строка и \(+,-,+\).
Давайте теперь посмотрим, как применить это на примере.
Найдите определитель приведенной ниже матрицы.\[A_{3,3}=\begin{bmatrix}4&8&12\\7&19&2\\0&5&2\end{bmatrix}\]
Решение
Применим нашу формулу для определитель.\[\begin{align}\det{A}&=a(ei-fh)-b(di-fg)+c(dh-eg)\\&=4[(19\cdot 2)- (2\cdot 5)]-8[(7\cdot 2)-(2\cdot 0)]+12[(7\cdot 5)-(19\cdot 0)]\\&=4[(38)-(10)]-8[(14)-(0)]+12[(35)-(0)]\\&=4(28)- 8(14)+12(35)\\&=112-112+420\\&=420 \end{align}\]
Теперь мы переходим к более подробному изучению определителя диагональной матрицы после его определения.
Определитель диагональной матрицы
Чтобы вычислить определитель диагональной матрицы, мы должны сначала понять, что это такое.
Диагональная матрица — это матрица, в которой всех недиагональных элементов равны 0 . Это не означает, что сами диагональные элементы не могут содержать значение 0, но это означает, что любой недиагональный элемент равен 0.
Он принимает вид \[A=\begin{bmatrix}a_{1,1} & 0 &0& \cdots & 0 \\0 & a_{2,2} & 0&\cdots & 0 \\0&0&a_{ 3,3}&\cdots &0\\\vdots & \vdots &\vdots & \ddots & \vdots \\0 & 0 &0& \cdots & a_{m,n} \end{bmatrix}\]
Определитель диагональной матрицы можно найти, перемножая диагональные элементы.
Определитель диагональной матрицы является произведением диагональных элементов . Следовательно, \[\det{A}=a_{1,1}\cdot a_{2,2}\cdot a_{3,3} \cdot \quad \cdots \quad \cdot a_{m,n}\]
Если диагональные элементы не все ненулевые значения, то матрица не может быть невырожденной, так как произведение с \(0\) всегда будет возвращать решение \(0\) и, как мы видели ранее это делает матрицу сингулярной и необратимой.
Давайте посмотрим на это на примере.
Найдите \(\det{A}\), где,\[A_{5,5}=\begin{bmatrix}13&0&0&0&0\\0&-6&0&0&0\\0&0&7&0&0\\0&0&0&-1&0\\0&0&0&0&3\end{bmatrix }\]
Решение
Мы знаем, что определитель диагональной матрицы является произведением диагональных элементов. \[\begin{align} \det{A}&=a_{1,1}\cdot a_{2,2}\cdot a_{3,3}\cdot a_{4,4}\cdot a_{5, 5}\\&=(13)\cdot (-6)\cdot (7)\cdot (-1)\cdot (3)\\&=1638.\end{align}\]
\[\begin{align} \det{A}&=a_{1,1}\cdot a_{2,2}\cdot a_{3,3}\cdot a_{4,4}\cdot a_{5, 5}\\&=(13)\cdot (-6)\cdot (7)\cdot (-1)\cdot (3)\\&=1638.\end{align}\]
Можем ли мы рассчитать определитель обратной матрицы? Ответ: ДА!
Определитель обратной матрицы
Последняя матрица, которую следует учитывать при рассмотрении определителей, — это обратная матрица. 9{-1}}=\frac{1}{\det{A}}.\]
Возьмем следующий пример.
Возьмите приведенную ниже матрицу \(A\) и определите, обратима ли она. Если матрица \(A\) обратима, найдите определитель этой обратной матрицы.
\[A=\begin{bmatrix}6&2\\12&9\end{bmatrix}\]
Решение
Шаг 1. Найдите определитель \(A\)
\[\begin{ align} \det{A}&=ad-cb\\&=(6\cdot 9)-(12\cdot 2)\\&=54-24\\&=30\end{align}\]
9{-1}}&=\frac{1}{\det{A}}\\&=\frac{1}{30}. \end{align}\]Определитель матрицы — основные выводы
- Определитель матрицы \(2\times 2\) определяется выражением,\[\det{A}=ad-bc\]
- определитель матрицы \(3\times 3\) использует элементы верхней строки и определитель их соответствующих миноров для вычисления определителя.


 е..
е.. Подставим его в формулу для определителя матрицы $3\times 3$ и решим относительно $y$:
Подставим его в формулу для определителя матрицы $3\times 3$ и решим относительно $y$: