Что такое радиан? И почему в круге 360 градусов?
Анна Малкова (автор книги для подготовки к ЕГЭ, ведущая годового Онлайн-курса подготовки к ЕГЭ на 100 баллов, руководитель компании «ЕГЭ-студия» (Курсы ЕГЭ))
Это видео — об измерении углов. Почему в круге 360 градусов? Что такое 1 радиан? И как связаны градусы и радианы?
Начнем с градусов. Что за странное число 360? Мы привыкли, что в рубле 100 копеек, в метре 100 сантиметров, в килограмме 1000 граммов. У нас десятеричная система исчисления, потому что на руках у нас по 10 пальцев. Но откуда в нашем языке такие странные слова как дюжина, то есть 12? Почему у нас в часе 60 минут, а не 100? И в минуте 60 секунд. Также и в круге 360 градусов, а не 1000. Дюжина – это 12. 60 делится на 12. Может быть у наших предков было по 12 пальцев на обеих руках? Конечно, нет!
 Так делали самые разные народы: они считали фаланги пальцев. Их всего 12. На видео я показываю, как это сделать.
Так делали самые разные народы: они считали фаланги пальцев. Их всего 12. На видео я показываю, как это сделать.Но чем же число 12 лучше 10? Возможно, оно понравилось древним людям тем, что у числа 12 больше делителей, чем у 10. Число 10 делится на 1, на 2, на 5 и на 10, а число 12 делится на 1, на 2, 3, 4, 6 и 12.
У числа 360 делителей целых 24 делителя. Если в круге 360 градусов, такой круг легко поделить на части разными способами.
Но это не все. Числа 12, 20, 360 имели особое значение для астрономов древности: египтян и шумеров.
Разберемся, почему это так.
Наблюдая за движением Солнца по небу, древние ученые заметили, что в день равноденствия Солнце встает почти точно на востоке и заходит почти точно на западе. При этом оно проходит за день по небу путь в 360 раз больший, чем видимый с Земли диаметр Солнца. Небесную полуокружность разделили на 180 градусов. Угловой диаметр солнца равен примерно 32 угловых минутам, чуть больше, чем полградуса. Он немного меняется в течении года из-за того, что орбита Земли не круговая, а эллиптическая.
Конечно, древние астрономы наблюдали не только за движением Солнца. Они заметили, что яркая планета Юпитер совершает полный оборот вокруг Солнца за 12 лет. Точнее, не 12, а 11,86 лет, но уж очень им хотелось округлить до своего любимого числа.
Да что там Юпитер! Посмотрим на Луну. Юпитер на небе еще и не каждый найдет (а вы сможете?) – зато Луну, особенно полную, трудно не заметить! Месяц – промежуток от полнолуния до полнолуния – равен примерно 29,5 суток. Почти 30, верно? А если у нас в году 12 месяцев, мы получим 360 дней.
Древние астрономы подумали: «Наверное, Боги хотели, чтобы у нас в году было 360 дней, 12 месяцев по 30 дней. Но где-то, вероятно, они ошиблись в расчетах, или кто-то им помешал. А нам никто не помешает, и мы будем делить круг на 360 градусов».
А нам никто не помешает, и мы будем делить круг на 360 градусов».
Обозначается это вот так: 360 и вверху значок градуса. ()
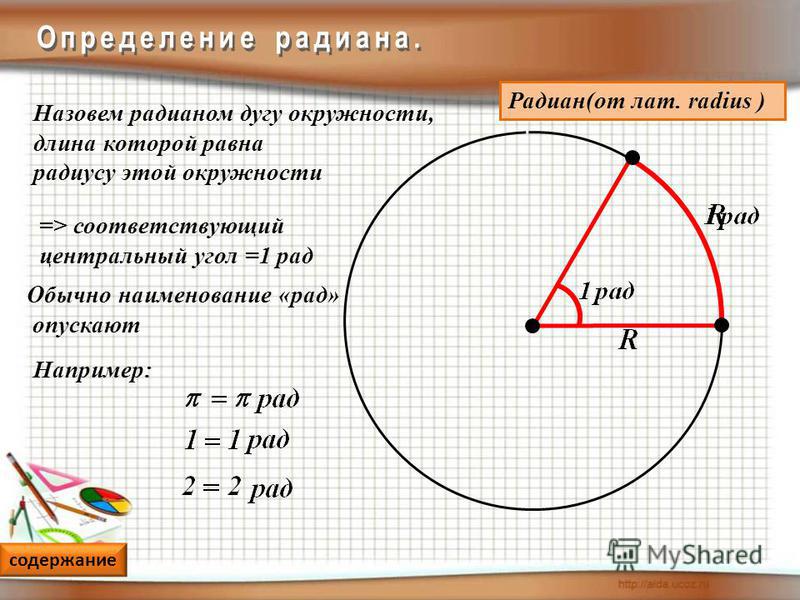
А что же угол в 1 радиан? С радианами все намного проще.
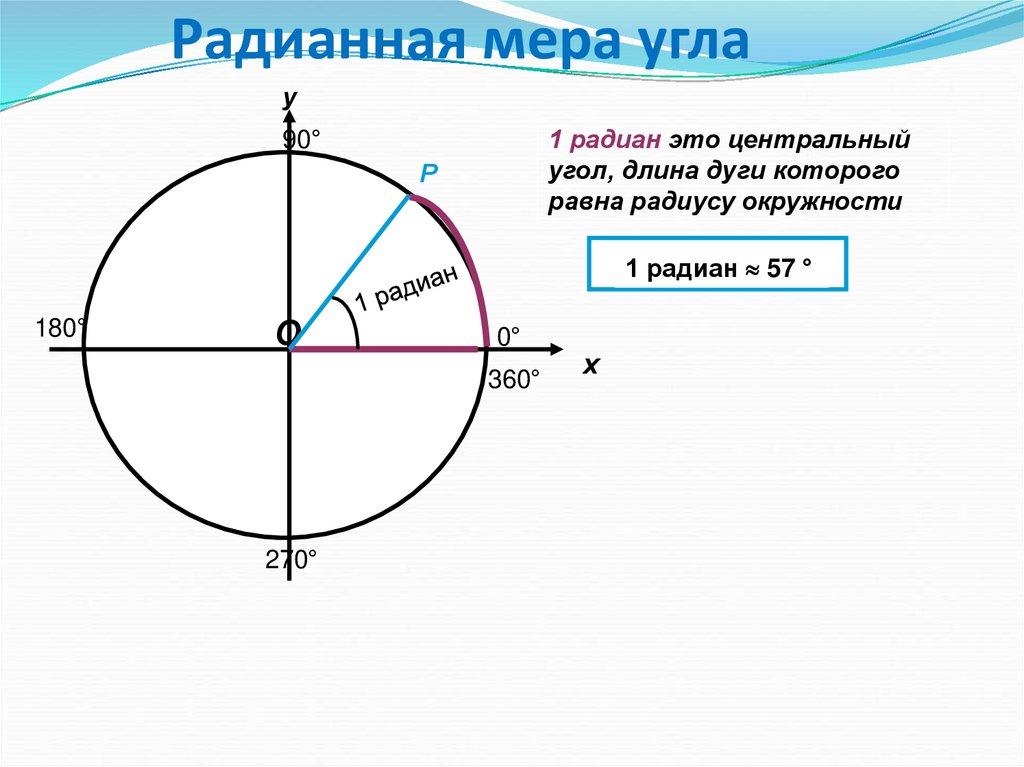
1 радиан – это центральный угол, опирающийся на дугу, длина которой равна радиусу окружности. 1 радиан приблизительно равен 57 градусам.
Как перевести градусы в радианы? Мы сказали, что 1 круг – это 360 градусов. Но чему равна длина всей окружности с радиусом r? Вспоминаем формулу: .
У нас появляется число Пи. Это число известно людям с глубокой древности. С доисторических времен люди рисовали круги. Они видели на небе круглое солнце и круглую полную луну и хотели сделать что-нибудь похожее. Они плели круглые корзины, делали круглые тарелки. И заметили, что отношение длины окружности к ее диаметру всегда одно и то же. Это число немного больше, чем 3, точнее, 3,1415926… Проходили столетия, и число Пи вычисляли со все большей и большей точностью. Отношение длины окружности к ее диаметру – это число Пи.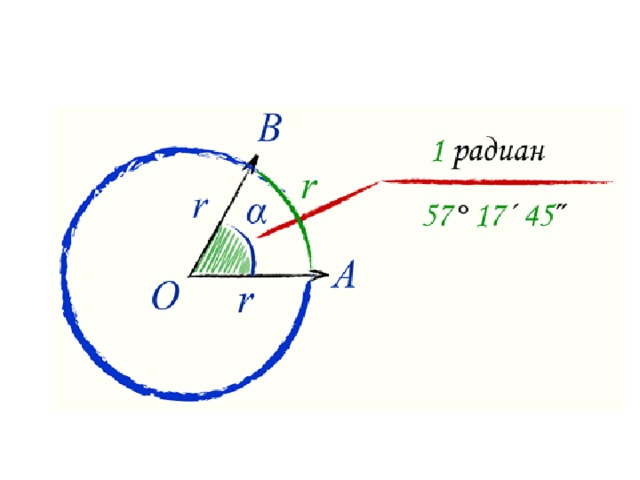
Полный круг – 360 градусов. Длина окружности – .
Наш угол в 1 радиан опирается на дугу окружности, равную r. Мы получаем, что угол в один радиан соответствует дуге окружности, равной r, радиусу окружности. 360 градусов, полный круг, соответствует всей длине окружности, то есть . Во сколько же раз полный круг больше, чем 1 радиан? Очевидно, в раз. 360 градусов соответствует радианам. 180 градусов – радиан, 90 градусов – это радиан.
Теперь вы знаете, что же такое написано на тригонометрическом круге, что такое радианы и почему в круге 360 градусов.
Если у вас есть другие версии, почему именно 360, пишите в комментариях. Присылайте новые интересные вопросы и задачи!
Подписывайтесь на мой канал! Анна Малкова
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Что такое радиан? И почему в круге 360 градусов?» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена: 07.04.2023
как перевести, формула, таблица преобразования
Содержание:
-
Градусы в радианы
- Краткое описание
- В чем можно измерять угол
-
Связь между градусами и радианами
- Мера угла
- Формула соотношения
-
Формулы перевода
- Градусы в радианы
- Радианы в градусы
- Таблица перевода градусов в радианы
- Примеры расчета градусов и минут в радианы
Содержание
-
Градусы в радианы
- Краткое описание
- В чем можно измерять угол
-
Связь между градусами и радианами
- Мера угла
- Формула соотношения
-
Формулы перевода
- Градусы в радианы
- Радианы в градусы
- Таблица перевода градусов в радианы
- Примеры расчета градусов и минут в радианы
Градусы в радианы
Краткое описание
Угол — это два луча, выходящие из одной точки.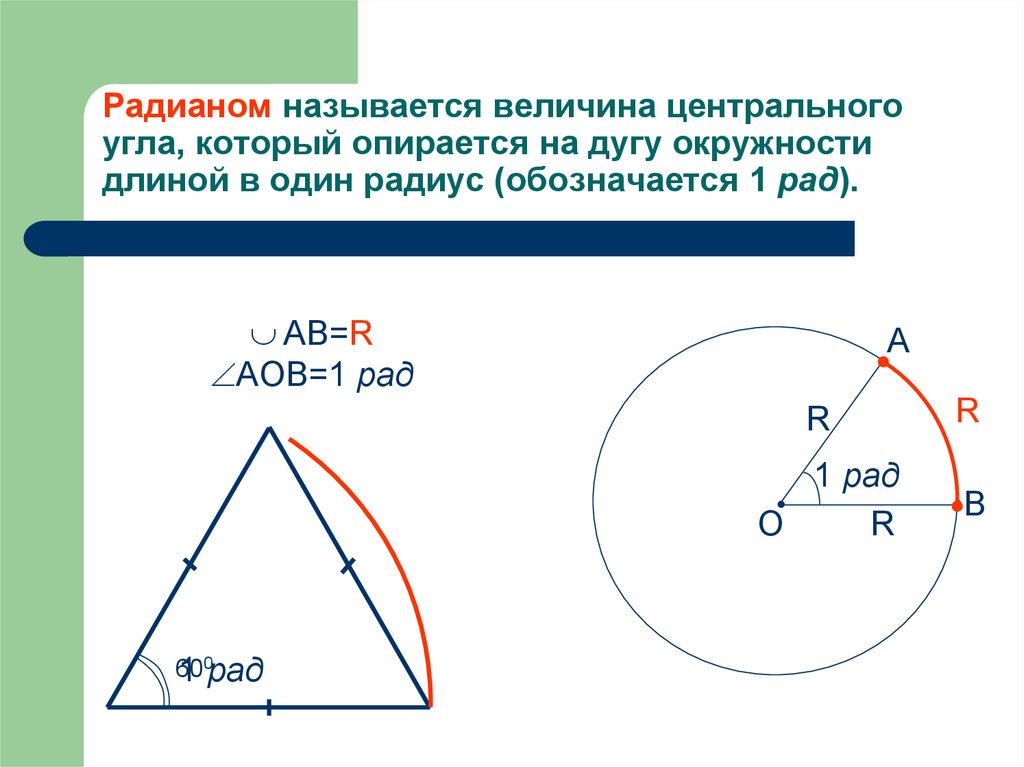
- Величины равных углов равны.
- Величина суммы двух углов равна сумме их величин.
Если ясно, о чем идет речь, вместо «величина угла» говорят просто «угол».
Равные углы с вершиной в центре окружности будут создавать на ней дуги одинаковой длины. Их сумма будет равняться сумме стягиваемых ими дуг. Поэтому единицы измерения углов можно задавать, указывая, какую часть окружности составляет соответствующая дуга.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В чем можно измерять угол
Наиболее распространены две единицы измерения:
- градус, равный дуге в 1/360 всей окружности;
- радиан — центральный угол, высекающий дугу, равную радиусу окружности.
 \circ\;=3,3915\;рад\)
\circ\;=3,3915\;рад\)
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Интуитивное руководство по углам, градусам и радианам – BetterExplained
Очевидно, что круги должны иметь 360 градусов. Верно?
Неправильно. У большинства из нас есть , понятия не имею, , почему в круге 360 градусов. Мы запоминаем магическое число как «размер круга» и приводим себя в замешательство при изучении высшей математики или физики с их так называемыми «радианами».
«Радианы упрощают математику!» эксперты говорят без простой причины, почему (дискуссии, связанные с рядами Тейлора, непросты). Сегодня мы раскроем, что такое радианы на самом деле, и интуитивно понимаем, почему они облегчают математику.
Откуда берутся степени?
До чисел и языка у нас были звезды.
 Древние цивилизации использовали астрономию для обозначения времен года, предсказания будущего и умилостивления богов (принося человеческие жертвы, им лучше быть вовремя
Древние цивилизации использовали астрономию для обозначения времен года, предсказания будущего и умилостивления богов (принося человеческие жертвы, им лучше быть вовремя Какое отношение это имеет к углам? Ну, дружище, загадай мне вот что: не странно ли, что в круге 360 градусов, а в году 365 дней? И не странно ли, что созвездия кружатся по небу в течение года?
В отличие от пиратов, держу пари, вы, сухопутные бабы, не можете определять времена года по ночному небу. Вот Большой Ковш (Большая Медведица), вид из Нью-Йорка в 2008 году (попробуйте любой город):
Созвездия совершают круг каждый день (видео). Если смотреть в одно и то же время каждый день (в полночь), они также будут делать круг в течение всего года. Вот теория о том, как появились степени:
- Люди заметили, что созвездия совершают полный круг каждый год
- Каждый день они немного отклонялись («на градус»)
- Поскольку в году примерно 360 дней, окружность имеет 360 градусов
Но, но… почему бы не 365 градусов по кругу?
Дайте им слабину: у них было солнечных часов , и они не знали, что год должен иметь удобные 365,242199 градусов, как у вас.

360 достаточно близко для работы в правительстве. Он хорошо вписывается в вавилонскую систему счисления с основанием 60 и хорошо делится (на 2, 3, 4, 6, 10, 12, 15, 30, 45, 9).0… ну вы поняли).
Основание математики на Солнце кажется совершенно разумным
Земле повезло: ~360 дней в году очень много. Но это кажется произвольным: на Марсе у нас было бы около 680 градусов по окружности для более длинного марсианского года. А в некоторых частях Европы использовали градианы, когда вы делите круг на 400 частей.
Многие объяснения останавливаются на этом, говоря: «Ну, степень произвольна, но нам нужно выбрать какое-то число ». Не здесь: мы увидим, что вся предпосылка степени задом наперед .
Правило радианов, градусы Слюни
Градус — это то, на сколько мне, наблюдателю, нужно наклонить голову, чтобы увидеть вас, движущегося. Это немного эгоистично, тебе не кажется?
Предположим, вы увидели, как ваш друг бежит по большой дорожке:
«Эй, Билл, как далеко ты ушел?»
«Ну, у меня был очень хороший темп, думаю, я пробежал 6 или 7 миль…»
«Офигеть.
 Как далеко я повернул голову, чтобы увидеть, как ты двигаешься?
Как далеко я повернул голову, чтобы увидеть, как ты двигаешься?«Что?»
«Я буду использовать для вас короткие слова. Я в середине пути. Вы бегали вокруг. Насколько… сильно… я… повернул… голову?
«Придурок».
Эгоистично, верно? Вот как мы занимаемся математикой! Мы пишем уравнения в терминах «Эй, как далеко я повернул голову, чтобы увидеть, что планета/маятник/колесо двигаются?». Бьюсь об заклад, вы никогда не задумывались о чувствах, надеждах и мечтах маятника.
Считаете ли вы, что уравнения физики должны быть упрощены для движущегося или наблюдателя?
Радианы: бескорыстный выбор
Большая часть физики (и жизни!) связана с выходом из системы отсчета и взглядом на вещи с точки зрения другого человека. Вместо того, чтобы задаваться вопросом, как далеко мы наклонили голову, подумайте, как далеко продвинулся другой человек .
Градусы измеряют углы тем, насколько сильно мы наклонили голову.
 Радианы измеряют углы на пройденных расстояний .
Радианы измеряют углы на пройденных расстояний .Но абсолютное расстояние не так полезно, поскольку 10 миль — это разное количество кругов в зависимости от трассы. Итак, мы делим на радиус, чтобы получить нормализованный угол:
Вы часто будете видеть это как
или угол в радианах (тета) это длина дуги (s), деленная на радиус (r).
Окружность имеет 360 градусов или 2pi радиан — полный оборот равен 2 * pi * r / r. Таким образом, радиан составляет около 360/(2 * пи) или 57,3 градуса.
Теперь не уподобляйтесь мне, запоминая эту мысль «Отлично, еще один юнит. 57,3 градуса — это так странно». Потому что это странно, когда ты все еще думаешь о себе!
Перемещение на 1 радиан (единицу) — это совершенно нормальное расстояние. Иными словами, наша идея «чистого, 9Угол 0 градусов» означает, что двигатель проходит очень нечистых единиц pi/2. Подумайте об этом — «Эй, Билл, ты можешь пробежать для меня 90 градусов? Что это такое? О, да, с вашей точки зрения, это пи/2 мили».
 Странность двусторонняя.
Странность двусторонняя.Радианы — это чуткий способ заниматься математикой — переход от наклона головы к точке зрения движущегося.
Что в имени?
Радианы — это количество расстояний в терминах «единиц радиуса», и я думаю, что «радиан» является сокращением для этого понятия.
Строго говоря, радианы — это просто числа, такие как 1,5 или 73, и не имеют единиц измерения (в расчете «радианы = пройденное расстояние / радиус» мы видим, что длина делится на длину, поэтому любые единицы измерения отменяются).
Но с практической точки зрения мы не математические роботы, и полезно думать о радианах как о «расстоянии», пройденном по единичному кругу.
Использование радианов
Я все еще привыкаю думать в радианах. Но мы довольно часто сталкиваемся с понятием «расстояние движителя»:
При измерении определенных скоростей вращения мы используем «обороты в минуту», а не «градусы в секунду». Это сдвиг в сторону точки отсчета двигающегося («Сколько кругов он прошел?») и в сторону от произвольной градусной меры.

Когда спутник вращается вокруг Земли, мы понимаем его скорость в «милях в час», а не в «градусах в час». Теперь разделите на расстояние до спутника, и вы получите орбитальную скорость в радианах в час.
Синус, эта замечательная функция, определяется через радиан как
Эта формула работает только тогда, когда x в радианах! Почему? Что ж, синус в основном связан с пройденным расстоянием , а не с наклоном головы. Но мы оставим это обсуждение на другой день.
Радиан Пример 1: Колеса автобуса
Давайте рассмотрим реальный пример: у вас есть автобус с колесами радиусом 2 метра (это автобус-монстр). Я скажу, как быстро крутятся колеса, а вы скажете, как быстро движется автобус. Готовый?
«Колеса поворачиваются на 2000 градусов в секунду». Вы могли бы подумать:
- Хорошо, колеса вращаются со скоростью 2000 градусов в секунду. Это означает, что он делает 2000/360 или 5 и 5/9 оборотов в секунду.
 Окружность = 2 * pi * r, значит, она движется, гм, 2 * 3,14 * 5 и 5/9… где мой калькулятор…
Окружность = 2 * pi * r, значит, она движется, гм, 2 * 3,14 * 5 и 5/9… где мой калькулятор…
Хорошо. А теперь представьте себе машину с колесами радиусом 2 метра (тоже монстр). «Колеса автомобиля вращаются со скоростью 6 радиан в секунду». Вы могли бы подумать:
- Радианы — это расстояние вдоль единичной окружности — мы просто масштабируем по реальному радиусу, чтобы увидеть, как далеко мы продвинулись. 6 * 2 = 12 метров в секунду. Следующий вопрос.
Вау, в машине разобраться было проще, чем в автобусе! Никаких сумасшедших формул, никакого числа пи — просто умножить на , чтобы преобразовать скорость вращения в линейную скорость. Все потому, что радианы говорят в терминах движителя.
Обратное тоже легко. Предположим, вы едете со скоростью 90 футов в секунду по шоссе (60 миль в час) на своих 24-дюймовых ободах (радиус 1 фут). Как быстро вращаются колеса?
Итак, 90 футов в секунду / 1 фут радиуса = 90 радиан в секунду.
Это было легко.
 Я подозреваю, что рэперы поют о 24-дюймовых дисках именно по этой причине.
Я подозреваю, что рэперы поют о 24-дюймовых дисках именно по этой причине.Радиан Пример 2: sin(x)
Время для более мощного примера. Исчисление связано со многими вещами, и одна из них — это то, что происходит, когда числа становятся очень большими или очень маленькими.
Выберите количество градусов (x) и введите sin(x) в свой калькулятор:
Когда вы сделаете x маленьким, например, 0,01, sin(x) тоже уменьшится. А отношение sin(x)/x примерно равно 0,017 — что это значит? Еще более странно, что значит умножать или делить на степень? У вас могут быть квадратные или кубические градусы?
Радианцы спешат на помощь! Зная, что они относятся к пройденному расстоянию (это не просто отношение!), мы можем интерпретировать уравнение следующим образом:
- х — это расстояние, которое вы прошли по окружности .
- sin(x) — это то, как высоко вы находитесь на круге
Таким образом, sin(x)/x — это отношение того, как высоко вы находитесь, к тому, как далеко вы зашли: количество энергии, направленной «вверх».
 Если вы двигаетесь вертикально, это соотношение равно 100%. Если вы двигаетесь горизонтально, это соотношение равно 0%.
Если вы двигаетесь вертикально, это соотношение равно 100%. Если вы двигаетесь горизонтально, это соотношение равно 0%.Когда что-то движется на небольшую величину, например, от 0 до 1 градуса с нашей точки зрения, это в основном движется прямо вверх. Если вы перейдете на еще меньшую величину, от 0 до 0,00001 градуса, это будет , на самом деле идет прямо вверх. Пройденное расстояние (x) очень близко к высоте (sin(x)).
По мере уменьшения x отношение приближается к 100 % — больше движения прямо вверх. Радианы помогают нам интуитивно понять, почему sin(x)/x приближается к 1, когда x становится крошечным. Мы просто немного подталкиваем в вертикальном направлении. Кстати, это также объясняет, почему sin(x) ~ x для малых чисел.
Конечно, вы можете строго доказать это с помощью исчисления, но интуиция в радианах поможет вам понять это.
Помните, что эти соотношения работают только при измерении углов в радианах. С градусами вы сравниваете свой рост на окружности (sin(x)) с тем, как далеко некоторый наблюдатель наклонил голову (x градусов), и это быстро становится уродливым.

Так в чем смысл?
Степени имеют свое место: в нашей собственной жизни мы являемся фокусом и хотим видеть, как вещи влияют на нас. Как сильно я наклоняю свой телескоп, крутлю сноуборд или поворачиваю руль?
С законами природы мы наблюдатель, описывающий движение других. Радианцы о них, а не о нас. Мне потребовалось много лет, чтобы понять, что:
- Градусов произвольные , потому что они основаны на солнце (365 дней ~ 360 градусов), но они назад , потому что они с точки зрения наблюдателя.
- Поскольку радианы относятся к движителю, уравнения «встают на место». Преобразование скорости вращения в линейную легко, и такие идеи, как sin(x)/x, имеют смысл.
Равные углы можно рассматривать с нескольких точек зрения, а понимание радиан делает математические и физические уравнения более интуитивными. Счастливая математика.
Другие сообщения из этой серии
- Наглядное интуитивное руководство по воображаемым числам
- Интуитивная арифметика с комплексными числами
- Понимание того, почему сложное умножение работает
- Интуитивное руководство по углам, градусам и радианам
- Интуитивное понимание формулы Эйлера
- Интерактивное руководство по преобразованию Фурье
- Интуитивное руководство по свертке
- Интуитивное понимание синусоидальных волн
- Интуитивное руководство по линейной алгебре
- Интуиция программиста для умножения матриц
- Мнимое умножение против мнимых показателей
- Интуитивное руководство по гиперболическим функциям
Радиан — Формула, Определение | Радианы и градусы
Радиан — это единица измерения углов.
 У нас есть две единицы измерения углов: градус и радиан. До этого этапа вы могли использовать градусы для измерения размеров углов. Однако по разным причинам угловые меры в высшей математике часто описываются с использованием системы единиц, отличной от системы градусов. Эта система известна как радианная система. Знаете ли вы, что радиан был дополнительной единицей СИ для измерения углов до 19 века?95? Позже он был изменен на производную единицу.
У нас есть две единицы измерения углов: градус и радиан. До этого этапа вы могли использовать градусы для измерения размеров углов. Однако по разным причинам угловые меры в высшей математике часто описываются с использованием системы единиц, отличной от системы градусов. Эта система известна как радианная система. Знаете ли вы, что радиан был дополнительной единицей СИ для измерения углов до 19 века?95? Позже он был изменен на производную единицу.Приходите, давайте подробно узнаем о формуле радиана, формуле длины дуги и о том, как преобразовать угол из радианов в градусы и из градусов в радианы.
1. Что такое радиан? 2. Формула радиана 3. Преобразование радианов в градусы 4. Различия между радианами и градусами 5. Часто задаваемые вопросы о Radian Что такое радиан?
радиан — это единица СИ, которая используется для измерения углов, а один радиан — это угол, образованный в центре круга дугой, длина которой равна радиусу круга.
 Один радиан, показанный чуть ниже, приблизительно равен 57,296 градусам. Мы используем радианы вместо градусов, когда хотим вычислить угол через радиус. Поскольку «°» используется для обозначения степени, рад или c используется для представления радианов. Например, 1,5 радиана записывается как 1,5 рад или 1,5 c .
Один радиан, показанный чуть ниже, приблизительно равен 57,296 градусам. Мы используем радианы вместо градусов, когда хотим вычислить угол через радиус. Поскольку «°» используется для обозначения степени, рад или c используется для представления радианов. Например, 1,5 радиана записывается как 1,5 рад или 1,5 c .Радиан Определение
Радиан — единица измерения угла. Вот несколько фактов о «радиане»
- Радиан обозначается «рад» или с использованием символа «с» в показателе степени.
- Если угол написан без единиц измерения, то это значит, что он в радианах.
- Некоторые примеры углов в радианах: 2 рад, π/2, π/3, 6 с и др.
Радиан Использование
- Углы обычно измеряются в радианах в исчислении и в большинстве других разделов математики.
- Радиан также широко используются в физике. Они предпочтительнее градусов, когда угловые измерения выполняются в физике.

Радиан Формула
Мы уже узнали, что 1 радиан равен углу, образуемому дугой окружности, длина которой равна радиусу окружности. Таким образом, угол, образуемый дугой в радианах окружности, определяется как отношение длины дуги к радиусу окружности.
Если считать дугу полной окружностью окружности, то длина дуги = 2πr. Кроме того, мы знаем, что угол, образуемый в центре круга его окружностью, равен 360°. Тогда по приведенной выше формуле
Стягиваемый угол = (длина дуги)/(радиус)
360° = (2πr)/r
360° = 2π
Таким образом, формула радианов 2π = 360°.
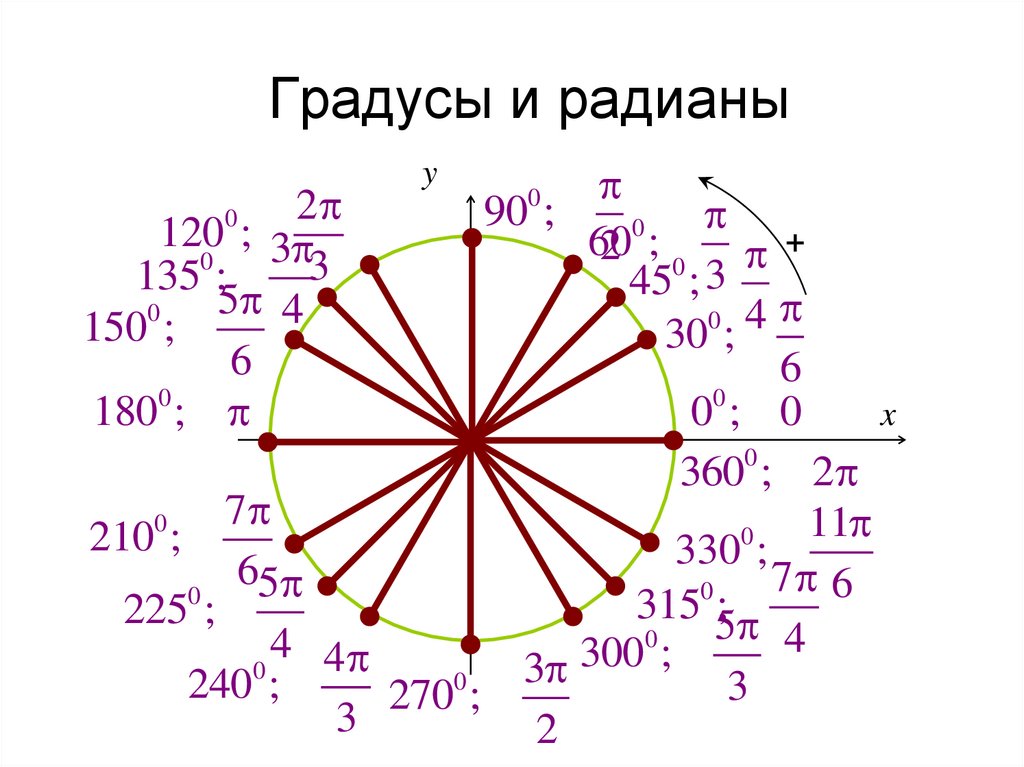
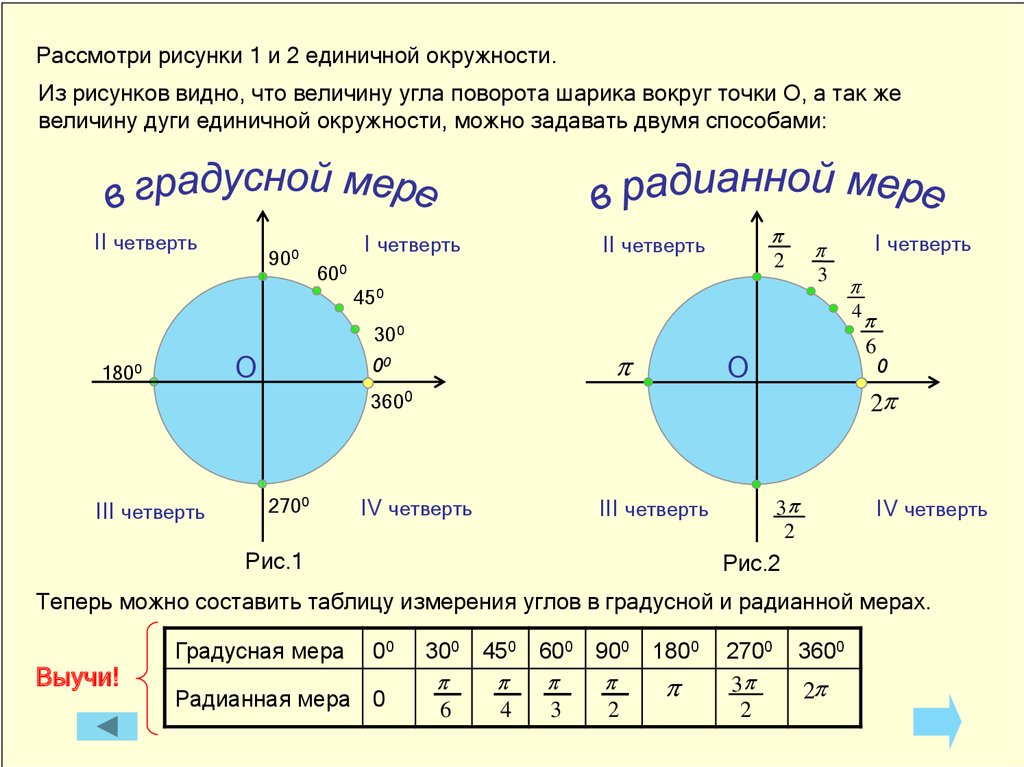
Преобразование радианов в градусы
Угол может быть преобразован из «радианов в градусы» и из «градусов в радианы» в зависимости от необходимости. Мы используем формулу радиана (из предыдущего раздела), 2π = 360 ° для выполнения этих преобразований. Мы можем увидеть, как сделать преобразование между радианами и градусами на рисунке ниже.

Преобразование радианов в градусы
Формула радианов может быть записана как
2π радиан = 360°
Отсюда 1 радиан = 360°/2π (или)
1 радиан = 180°/π.
Таким образом, чтобы преобразовать радианы в градусы, мы умножаем угол на 180°/π.
Примеры преобразования радианов в градусы:
- π/2 = π/2 × 180°/π = 90°
- π/4 = π/4 × 180°/π = 45°
- 7π/6 = 7π/6 × 180°/π = 210°
- 2 рад = 2 × 180°/π ≈ 114,59°
Если мы посмотрим на первые три примера, где угол выражается в виде числа π, то число π сокращается при преобразовании его в градусы. Итак, чтобы преобразовать угол в радианах, выраженный в π, в градусы, просто замените π на 180°. Это трюк для преобразования радианов в градусы. Здесь вы можете увидеть первые три примера использования трюка.
- π/2 = 180°/2 = 90°
- π/4 = 180°/4 = 45°
- 7π/6 = 7(180°)/6 = 210°
Преобразование градусов в радианы
Из формулы для радианов
2π радиан = 360°
Отсюда 1° = (2π радиан)/360°
1° = (π/180) радиан
Таким образом, чтобы преобразовать градусы в радианы, мы умножаем угол на π/180 радиан.

Примеры преобразования градусов в радианы:
- 90° = 90 × π/180 = π/2
- 180° = 180 × π/180 = π
- 210° = 210 × π/180 = 7π/6
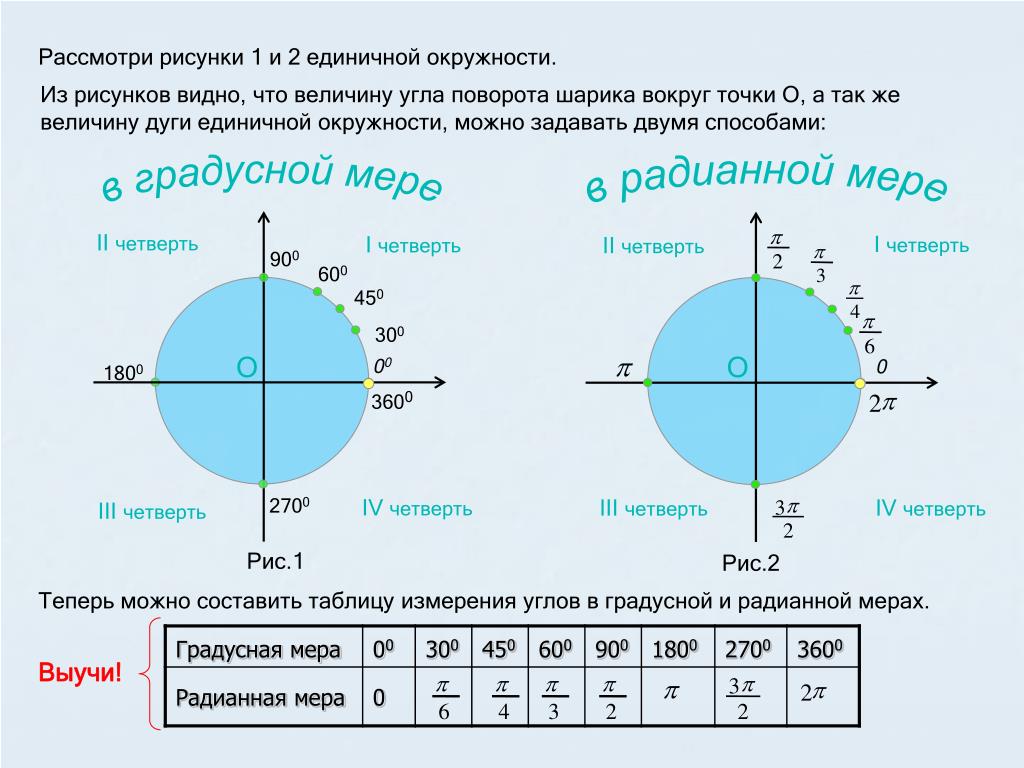
Таблица радианов и градусов
Вот таблица с некоторыми стандартными углами в градусах и соответствующими углами в радианах. Эта таблица помогает узнать эквивалентные углы в радианах (или градусах).
Степень Радиан 30° №/6 45° №/4 60° №/3 90° №/2 180° № 270° 3π/2 360° 2π Различия между радианами и градусами
Радианы и градусы являются измерениями только углов. Вот несколько различий между радианами и градусами.

Радиан Степень Угол, образуемый дугой длины ‘r’ окружности с радиусом ‘r’, известен как 1 радиан. 1/360 th Часть полного угла называется градусом. 1 радиан обозначается как 1 c или иногда просто 1. 1 градус обозначается 1°. Чтобы преобразовать угол из градусов в радианы, умножьте его на π/180. Чтобы преобразовать угол из радианов в градусы, умножьте его на 180/π. Важные примечания по радианам:
- Мы можем преобразовать угол из градусов в радианы, умножив его на π/180.
- Мы можем преобразовать угол из радианов в градусы, умножив его на 180/π.
- Длина дуги = радиус × угол, стягиваемый в центре.
При применении этой формулы угол (если он указан в градусах) следует сначала преобразовать в радианы.
☛ Связанные темы:
- Тригонометрические отношения в радианах 9Калькулятор 0027 градусов в радианы
- Калькулятор радианов в градусы
Часто задаваемые вопросы о Radian
Что такое радиан?
Радиан — это единица измерения углов в системе СИ, основанная на длине дуги и радиусе. 1 радиан равен углу, образуемому дугой в центре окружности, длина которой равна радиусу окружности.
Что такое формула преобразования радианов в градусы?
Чтобы преобразовать радианы в градусы, мы умножаем угол на 180/π. Например, 3π/2 = 3π/2 × 180/π = 270°. Таким образом, градусный эквивалент угла 3π/2 равен 270°.
Что такое градусы в радианах?
Чтобы преобразовать градусы в радианы, мы умножаем угол на π/180. Например, 270° = 270 × π/180 = 3π/2. Таким образом, эквивалентный угол 270° в радианах равен 3π/2.
Сколько радианов в полном круге?
В полном круге угол равен 360°, а по формуле радиана 360° = 2π.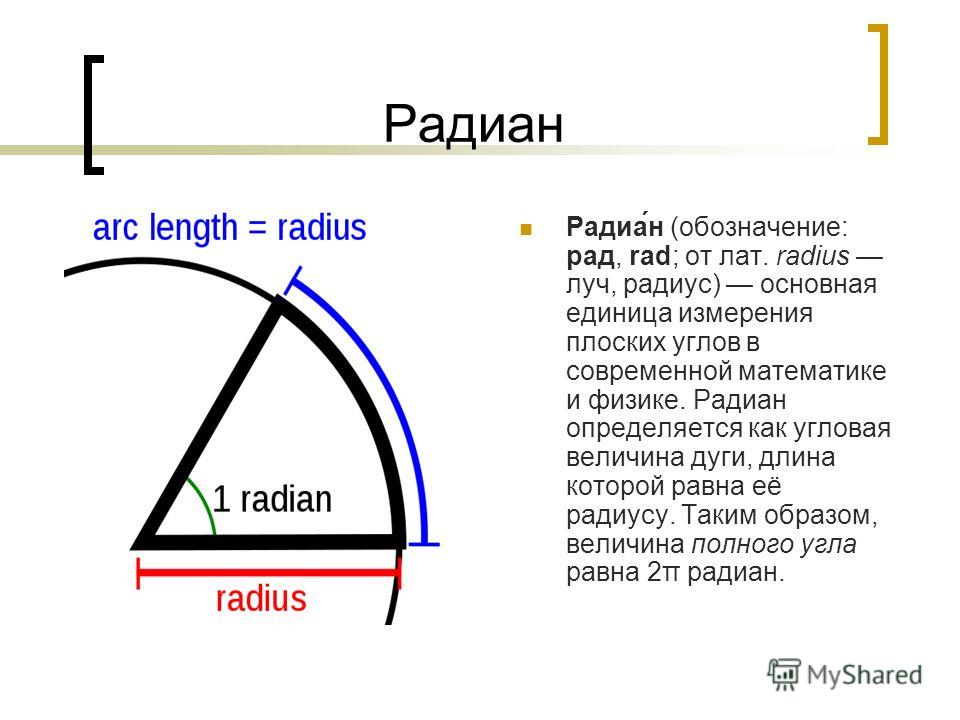 Таким образом, в полном круге 2π радиан.
Таким образом, в полном круге 2π радиан.
Что такое формула длины дуги в радианах?
Длина дуги окружности равна произведению ее радиуса на угол, образуемый дугой, в радианах. то есть длина дуги = радиус × угол в радианах. Если угол задан в градусах, мы сначала должны преобразовать этот угол в радианы, а затем применить формулу длины дуги.
Что такое формула радиана для длины дуги?
Чтобы найти угол, образуемый дугой в радианах, мы просто делим ее длину на радиус окружности. т. е. θ (в радианах) = (длина дуги) / радиус.
Чему равен 1 радиан?
Мы знаем, что 2π радиан = 360°. Разделив это уравнение на 2 с обеих сторон, π радиан = 180°. Разделив это уравнение на π с обеих сторон, 1 радиан = 180°/π. Таким образом, 1 радиан = 57,296°. Это может быть использовано для преобразования любого угла в радианы. Например, 2 радиана в градусах = 2 × 57,296 = 114,592°.
Какова мера 0 радиан в градусах?
Чтобы преобразовать 0 радиан в градусы, мы умножаем его на 180/π.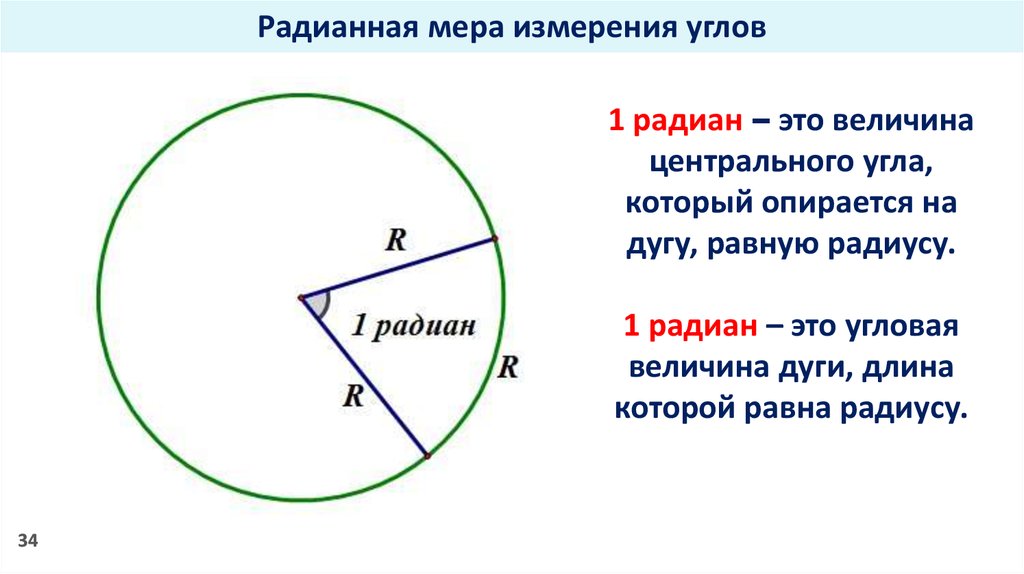

 \circ\;=3,3915\;рад\)
\circ\;=3,3915\;рад\)
 Древние цивилизации использовали астрономию для обозначения времен года, предсказания будущего и умилостивления богов (принося человеческие жертвы, им лучше быть вовремя
Древние цивилизации использовали астрономию для обозначения времен года, предсказания будущего и умилостивления богов (принося человеческие жертвы, им лучше быть вовремя 
 Как далеко я повернул голову, чтобы увидеть, как ты двигаешься?
Как далеко я повернул голову, чтобы увидеть, как ты двигаешься?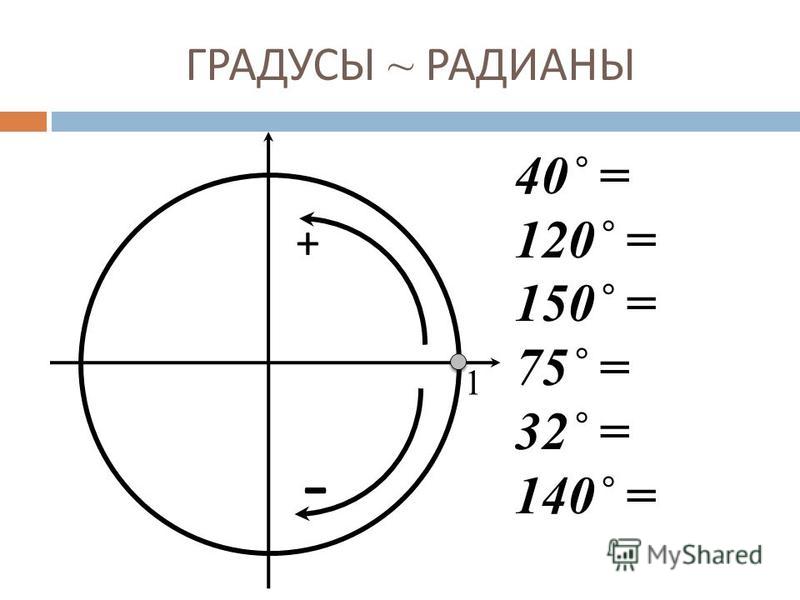 Радианы измеряют углы на пройденных расстояний .
Радианы измеряют углы на пройденных расстояний . Странность двусторонняя.
Странность двусторонняя.
 Окружность = 2 * pi * r, значит, она движется, гм, 2 * 3,14 * 5 и 5/9… где мой калькулятор…
Окружность = 2 * pi * r, значит, она движется, гм, 2 * 3,14 * 5 и 5/9… где мой калькулятор… Я подозреваю, что рэперы поют о 24-дюймовых дисках именно по этой причине.
Я подозреваю, что рэперы поют о 24-дюймовых дисках именно по этой причине. Если вы двигаетесь вертикально, это соотношение равно 100%. Если вы двигаетесь горизонтально, это соотношение равно 0%.
Если вы двигаетесь вертикально, это соотношение равно 100%. Если вы двигаетесь горизонтально, это соотношение равно 0%.
 У нас есть две единицы измерения углов: градус и радиан. До этого этапа вы могли использовать градусы для измерения размеров углов. Однако по разным причинам угловые меры в высшей математике часто описываются с использованием системы единиц, отличной от системы градусов. Эта система известна как радианная система. Знаете ли вы, что радиан был дополнительной единицей СИ для измерения углов до 19 века?95? Позже он был изменен на производную единицу.
У нас есть две единицы измерения углов: градус и радиан. До этого этапа вы могли использовать градусы для измерения размеров углов. Однако по разным причинам угловые меры в высшей математике часто описываются с использованием системы единиц, отличной от системы градусов. Эта система известна как радианная система. Знаете ли вы, что радиан был дополнительной единицей СИ для измерения углов до 19 века?95? Позже он был изменен на производную единицу. Один радиан, показанный чуть ниже, приблизительно равен 57,296 градусам. Мы используем радианы вместо градусов, когда хотим вычислить угол через радиус. Поскольку «°» используется для обозначения степени, рад или c используется для представления радианов. Например, 1,5 радиана записывается как 1,5 рад или 1,5 c .
Один радиан, показанный чуть ниже, приблизительно равен 57,296 градусам. Мы используем радианы вместо градусов, когда хотим вычислить угол через радиус. Поскольку «°» используется для обозначения степени, рад или c используется для представления радианов. Например, 1,5 радиана записывается как 1,5 рад или 1,5 c .