Как обозначаются стороны треугольника: Все о треугольниках. Классификация треугольников.

Треугольник и его виды — PROZNAYKA

Blogerman

Математика

02.12.2019

Просмотров: 4467

(Голосов: 4)

Определение

Треугольник – геометрические фигуры, которые состоят из трех точек, которые не находятся на одной прямой и последовательно соединены отрезками.

Отрезки, соединяющие точки, называются сторонами, а точки – вершинами. Вершины обозначаются большими латинскими буквами, например: A, B, C.

Стороны обозначаются названиями двух точек, из которых они состоят – AB, BC, AC.

Пересекаясь, стороны образуют углы. Нижняя сторона считается основанием фигуры.

Виды треугольников

Треугольники классифицируют по углам и сторонам. Каждый из видов треугольника имеет свои свойства.

Существует три вида треугольников по углам:

• остроугольные;
• прямоугольные;
• тупоугольные.

Виды треугольников

Все углы остроугольного треугольника острые, то есть градусная мера каждого составляет не более 900.

Прямоугольный треугольник содержит прямой угол. Два других угла всегда будут острыми, так как иначе сумма углов треугольника превысит 180 градусов, а это невозможно. Сторона, которая, находится напротив прямого угла, называется гипотенузой, а две другие катетами. Гипотенуза всегда больше катета

.

Тупоугольный треугольник содержит тупой угол.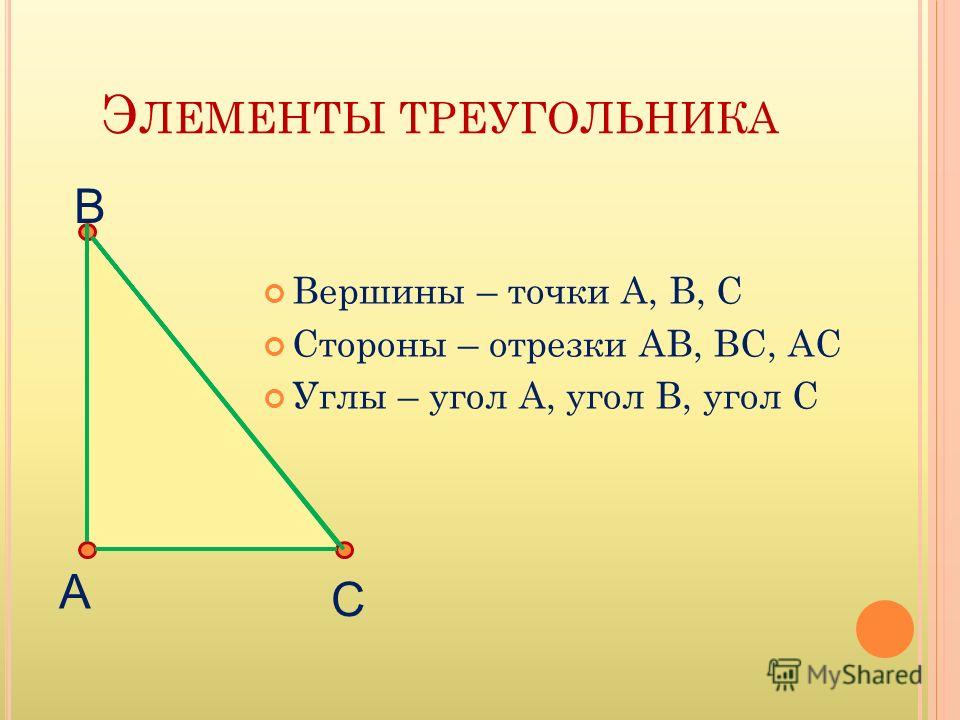 То есть угол, величиной больше 90 градусов. Два других угла в таком треугольника будут острыми.

Пифагоровым треугольником называется прямоугольник, стороны которого равны 3, 4, 5.

Причем, большая сторона является гипотенузой.

Такие треугольники часто используются для составления простых задач в геометрии. Поэтому, запомните: если две стороны треугольника равны 3, то третья обязательно будет 5. Это упростит расчеты.

Виды треугольников по сторонам:

• равносторонние;
• равнобедренные;
• разносторонние.

Виды треугольников.

Равносторонний треугольник – это треугольник, у которого все стороны равны. Все углы такого треугольника равны 600, то есть он всегда является остроугольным.

Равнобедренный треугольник – треугольник, у которого только две стороны равны. Эти стороны называются боковыми, а третья – основанием.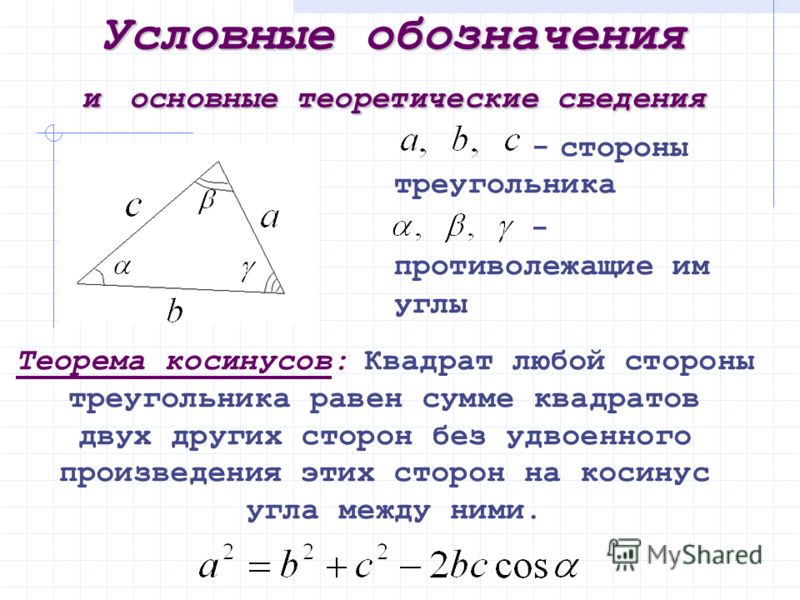 Кроме того, углы при основании равнобедренного треугольника равны и всегда являются острыми.

Разносторонним или произвольным треугольником называется треугольник, у которого все длины и все углы не равны между собой.

Если в задаче нет никаких уточнений по поводу фигуры, то принято считать, что речь идет о произвольном треугольнике.

Сумма всех углов треугольника, независимо от его вида, равна 1800.

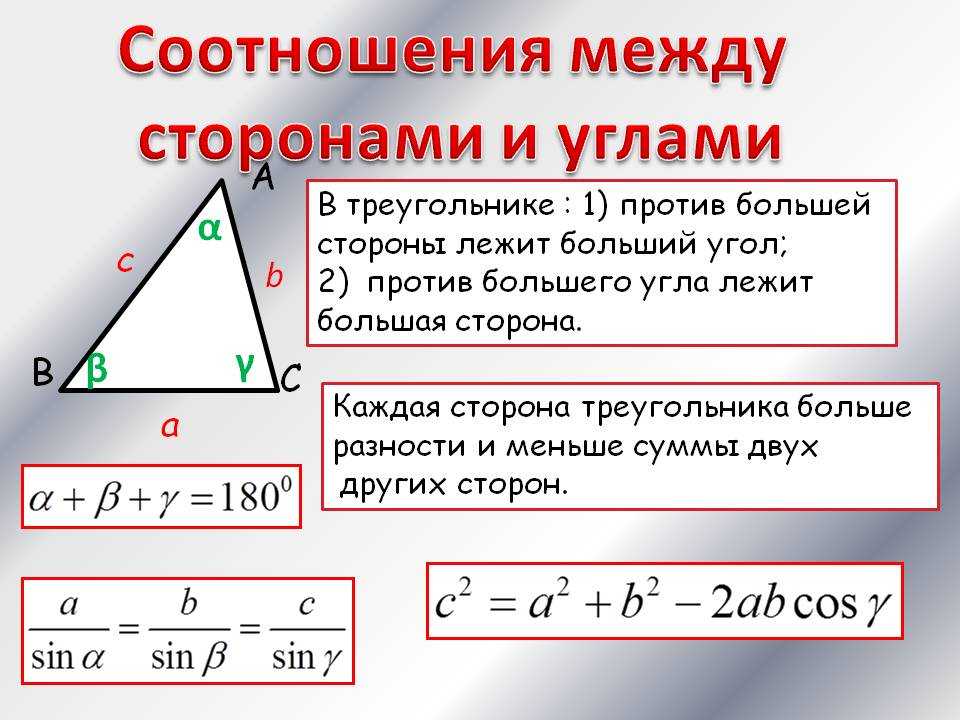
Напротив большего угла находится большая сторона. А также длина любой стороны всегда меньше суммы двух других его сторон. Эти свойства подтверждаются теоремой о неравенстве треугольника.

#образование

#математика

Последнее редактирование: 08 февраля 2023

Blogerman

Урок геометрии для 7 класса «Виды треугольников»

Урок геометрии для 7 класса «Виды треугольников»

 

Цель: научить учащихся определять различные виды треугольников, научить решать задачи, применяя теоретический материал.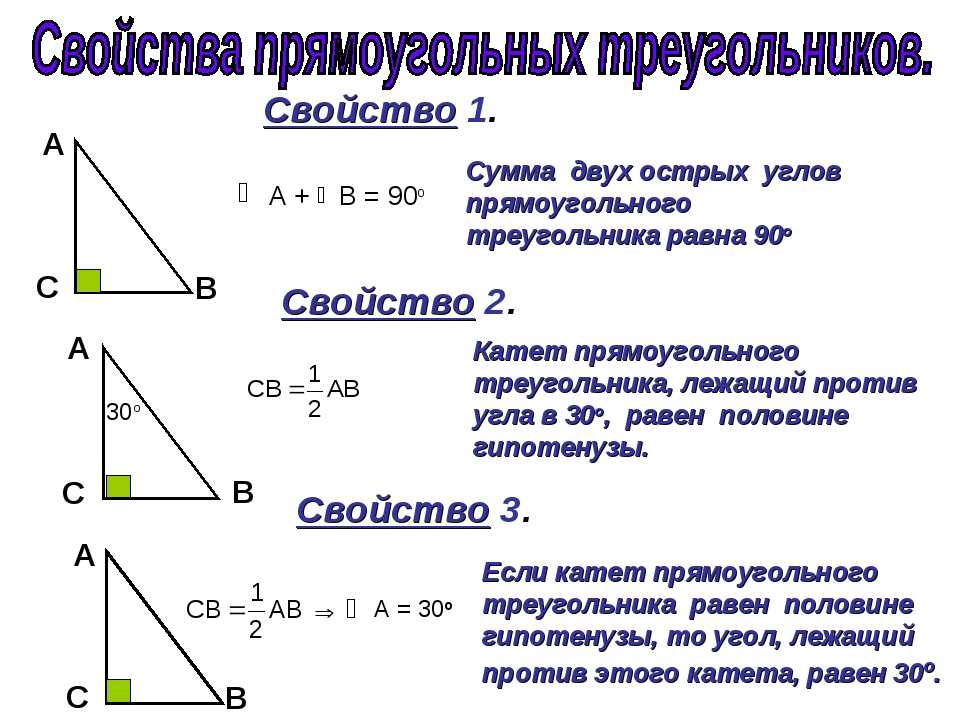

Развивать умения анализировать, сравнивать, обобщать и делать выводы, выступать перед аудиторией.

Воспитывать интеллектуальные, творческие, исследовательские способности, активизировать интерес к математике

Ученик должен знать: определение различных видов треугольников, какими бывают треугольники по длине сторон, по величине углов; названия сторон некоторых видов треугольников.

Ученик должен уметь: обосновывать принадлежность треугольника к определенному виду; классифицировать треугольники по сторонам и по углам; изображать, и находит на рисунках: равносторонние, равнобедренные, прямоугольные треугольники и их элементы;  применять теоретические знания при решении задач.

Тип урока: Урок изучения нового материала.

Технология: Личностно–ориентированная.

Методы:

•                   Наблюдение;
•                   Эвристическая беседа;
•                   Диалог;
•                   Создание ситуации успеха;

Формы: Фронтальный опрос, парная работа, самостоятельная работа, индивидуальная работа.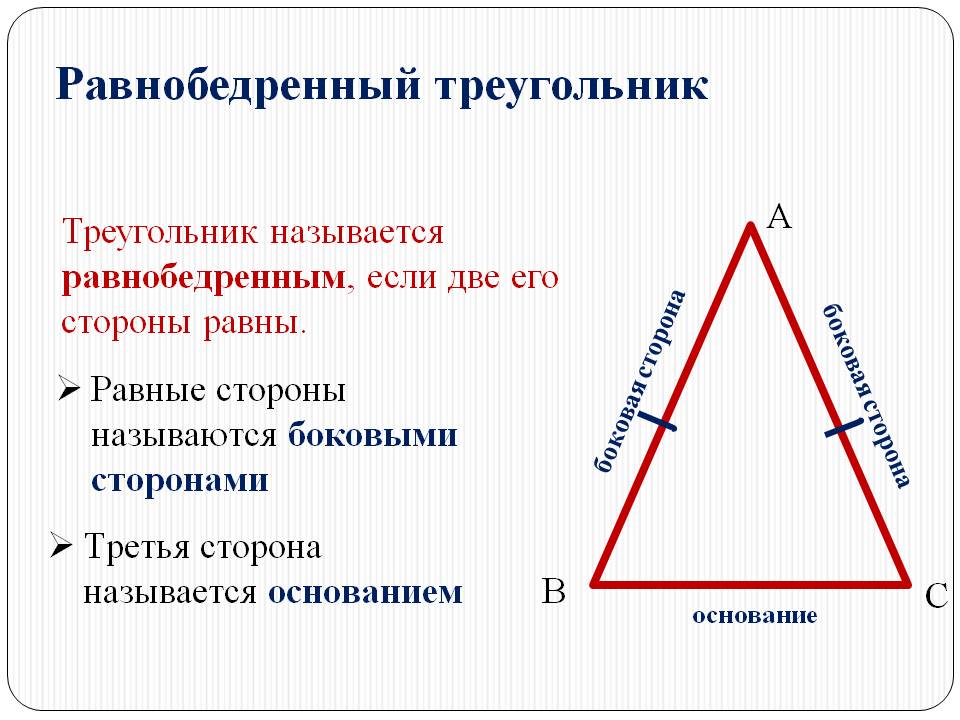

Ход урока

 

I. Организационный момент.

Приветствие учащихся, готовность класса к уроку. Посещаемость. Настрой учащихся на работу. Запись даты урока.

 

II. Проверка домашнего задания.

Собрать тетради.

 

ІIІ.  Мотивация учебной деятельности.

      Хочу вам предложить, определить, о чем сегодня пойдет речь на уроке?

 (Слайд 1 ребус)

Как вы думаете это важная тема в геометрии? Почему? 

(Слайд 2- 5)

 — Жесткость треугольника используют при строительстве железнодорожных мостов,

— опор линий электропередач, башенные краны состоят из треугольников, — стропила домов имеют форму треугольника, а также паруса яхт,

 -дорожные знаки, музыкальные инструменты; оригами изготавливают из треугольных модулей, с помощью треугольной рамки  устанавливаются бильярдные шары перед началом игры, даже в природе некоторые цветы и листья имеют форму треугольника

Вывод:  Треугольник – жесткая фигура (показываю деревянный треугольник, его изготовление).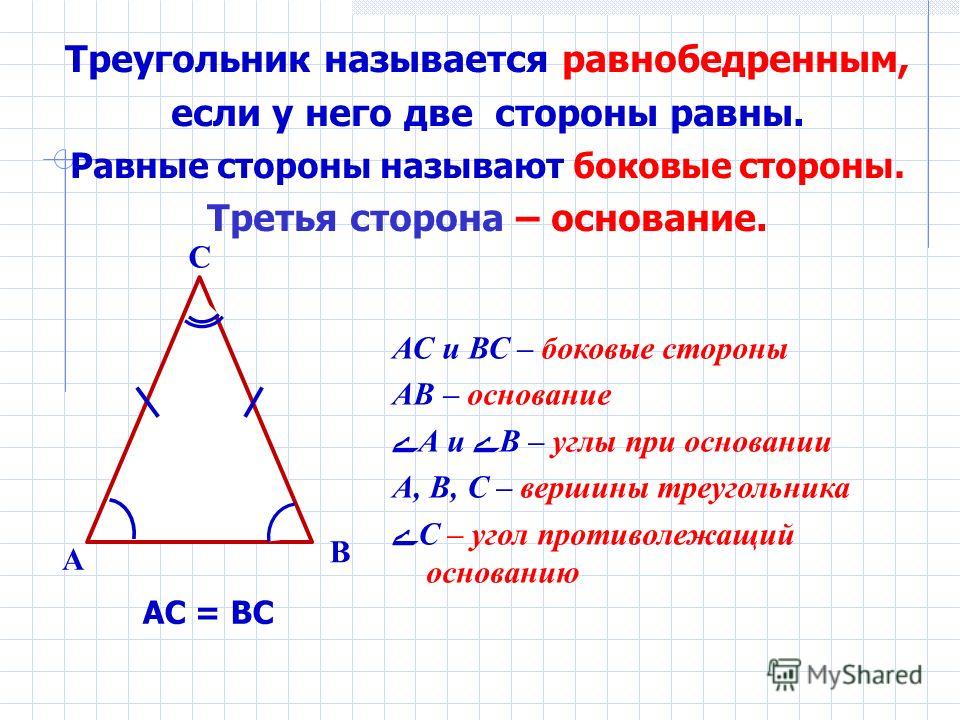

 

Сообщение темы, целей и задач урока:

Тема: Виды треугольников (Слайд 6)

Цель: Научить учащихся определять различные виды треугольников, 

применять теоретические знания при решении задач. 

 

ІV. Изучение нового материала

• Фронтальный опрос:

1. Какую фигуру мы называем треугольником. (Слайд 7) (Треугольник —  это геометрическая фигура, состоящая из трех точек и трех попарно соединяющих отрезков)

 

2. Как называются точки? (Точки называются вершинами треугольника) ЩЕЛЧОК.  Назовите вершины треугольника.

 

3. Как называются отрезки? ( Отрезки — называются сторонами треугольника.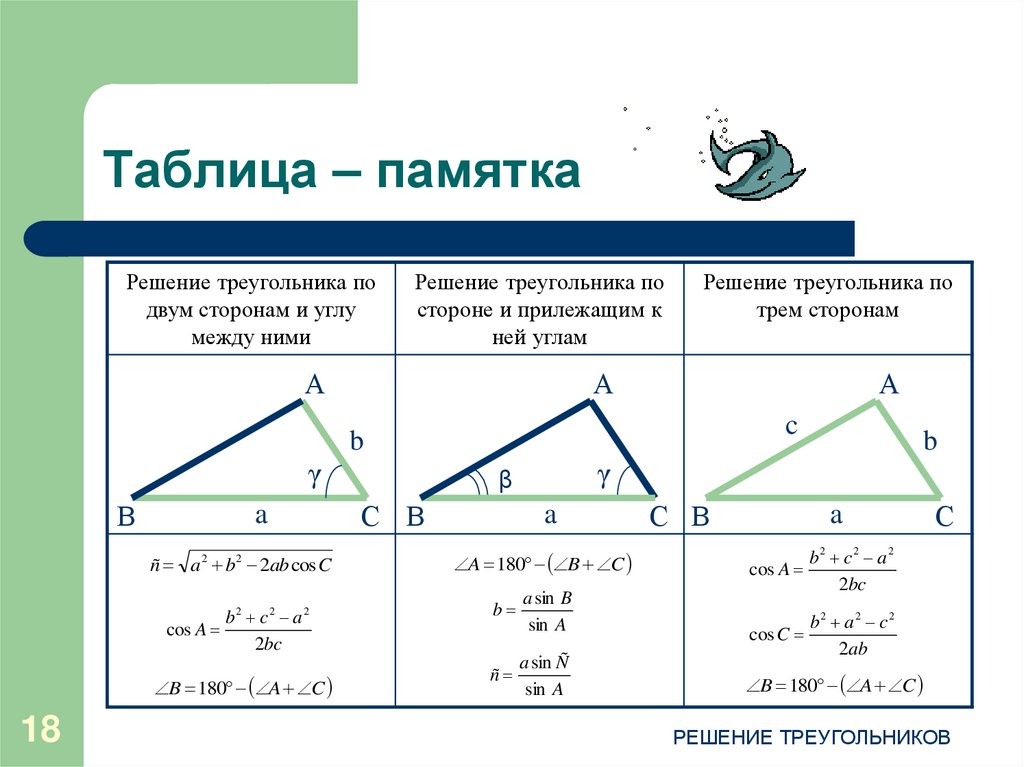 ЩЕЛЧОК.  Назовите стороны треугольника. Какие элементы еще имеет треугольник?  (Углы). Как обозначают треугольник?

 

4. По каким элементам мы различаем треугольники? (По длине сторон и по величине углов)

 

5. Какие  виды треугольников  вам известны?

(ПОКАЗЫВАЮ ТРЕУГОЛЬНИКИ — прямоугольный, остроугольный, тупоугольный треугольник; равносторонний, равнобедренный,  разносторонний треугольник)

 

• Индивидуальные задание учащимся:

— Определить вид треугольника, который лежит у вас на парте, и аргументировать. (Мой треугольник….., потому что….)

И так треугольники различают по сторонам……

Классификация по сторонам.  (Слайд 8)
Учащиеся формулируют определение разностороннего, равнобедренного, равностороннего треугольников. Какой треугольник называют…..

А так же треугольники различают по углам……

Классификация по углам.

  (Слайд 9)
Учащиеся формулируют определение остроугольного, тупоугольного, прямоугольного треугольников. Какой треугольник называют…..

 

• Парная работа

Заполнить таблицу 1: классификация треугольников. Если у вас есть сомнения, не торопитесь, сможете заполнить таблицу, на протяжении урока.

	Остроугольный	Тупоугольный	Прямоугольный
Разносторонний
Равнобедренный
Равносторонний

 

6.

Постройте треугольник, в котором есть прямой угол.  Как называется такой треугольник? (Треугольник, в котором есть прямой угол, называется прямоугольным.) (Слайд 10). Подпишите его. Можно ли построить треугольник с двумя прямыми углами? Почему? 

Элементы прямоугольного треугольника.

Сторона прямоугольного треугольника, лежащая против угла 90⁰,  называется гипотенузой. Остальные две стороны называются катетами.

Назовите гипотенузу и катеты. (АВ, АС и ВС).

 

7. ( Слайд 11).  Какой треугольник изображен на данном слайде? По какому признаку вы это определили? ЩЕЛЧОК.  Какой треугольник называется равнобедренным? Обсуждаются его элементы и свойства, аналогично для прямоугольного треугольника. Равные стороны обозначаются одинаковым количеством черточек.
Ученики строят треугольник и записывают элементы треугольника.

Динамическая пауза.
Давайте проверим промежуточный этап наших знаний. У каждого из вас имеется 3 треугольника. Какой из данных треугольников: прямоугольный, остроугольный и наконец, тупоугольный.  Молодцы!

 

V. Обобщение и систематизация знаний учащихся

 

1) Проверочная работа  в тетрадке

 1. (Слайд 12) Выписать все равнобедренные треугольники и их элементы. (∆ СМN, ∆ ANM, ∆ MAB)

 2. (Слайд 13) Выписать все прямоугольные треугольники и их элементы. (∆ ACB, ∆ ACD, ∆ CDB)

3. У кого были сомнения по заполнению таблицы 1, можете доработать.

 

2) Решение задач по готовым чертежам

Что такое периметр треугольника?

(Слайд14) Найдите периметр данного треугольника

(Слайд15, 16) Найдите неизвестную сторону данного треугольника

 

3) Учебник № 273 ( у доски)

Пусть периметр треугольника х см, тогда 1 сторона х-7см, 2- я х-8 см, 3- я х-9 см. Составляем уравнение:

 х-7 + х – 8 + х – 9 = х,

3х – 24 = х,

3х – х = 24,

2х = 24,

х = 12.

Ответ. 12 см.

 

4) Сколько нас? (Слайд 17)

Часто знает и дошкольник,
Что такое треугольник.
уж вам-то как не знать…
Но совсем другое дело —
Очень быстро и умело
Треугольники считать.
Например, в фигуре этой
Сколько разных? Рассмотри!
Все внимательно исследуй
И «по краю», и «внутри».  (Ответ 9)

 

5) Самопроверка заполнение таблицы 1 (Слайд 18)

 

6)  Найди равные треугольники

Учитель: Каждый из вас в начале урока определял вид своего треугольника, а теперь покажите друг другу треугольники и найдите среди представленных треугольников равные треугольники. Опишите способ нахождения равных треугольников. Как это проверить?

Ученики: наложили треугольники друг на друга.

Учитель: какие треугольники называются равными? ( Равные треугольники — это треугольники, которые можно совместить наложением). 

Учитель: Всегда ли удобно таким образом проверять равенство треугольников? Почему?

Ученики: Нет. Не всегда возможно наложить один треугольник на другой. Размер может влиять.

Учитель: Оказывается, что равенство треугольников можно установить, не накладывая один треугольник на другой, а сравнивая только некоторые их элементы.

Простая это фигура треугольник: три вершины, три стороны, три угла. А задумаешься…, нет, вовсе не простая, мы ещё многое о ней не знаем. Не умеем вычислять площади треугольников, применять теорему косинусов, синусов, не знаем о подобии треугольников, о признаках равенства прямоугольных треугольников и многое ещё осталось загадочным для вас. С этим мы познакомимся с вами на следующих уроках в 7 и старших классах.

 

VI. Итог урока (Слайд 19)

Над какой темой мы работали сегодня на уроке?

Остроугольные треугольники могут быть: разносторонние, равнобедренные, равносторонние.

Прямоугольные треугольники могут быть: равнобедренные, разносторонние.

Тупоугольные треугольники могут быть: равнобедренные, разносторонние.

Продолжите предложение

— Треугольник, у которого все углы острые ……

— Треугольник, в котором есть прямой угол…..

— Равнобедренный треугольник – это……

— Треугольник, у которого все стороны равны…..

— Тупоугольный треугольник – это…..

— Если треугольник имеет все разные стороны, то он называется…..

 

ТЕСТ   Ключ: 1 — Г, 2 – Б,  3 – В,   4 – Г,    5 – А.

 

VII. Домашнее задание.
Учебник § 9 № 271

Провести три отрезка в остроугольном треугольнике так, чтобы получить наибольшее количество треугольников.

 

VIII. Рефлексия (Слайд 20)

Сегодня на уроке я…..

Желаю вам успехов в дальнейшем изучении науки геометрия. Спасибо за внимание!

 

 

ТЕСТ        Класс_____ Фамилия, имя_________________________________________

	Вопрос	Варианты ответов	Ответ
1.	Треугольником называется геометрическая фигура, которая состоит из….	А) трех точек. Б) трех отрезков. В) трех точек и трех отрезков. Г)  трех точек, не лежащих на одной прямой,  трех отрезков попарно соединяющих эти точки
2	По градусной мере углов треугольника определите, какой треугольник является тупоугольным	А) 30 0, 600, 900 Б) 34 0,550, 910       В) 89 0, 530, 380 Г)  72 0, 440, 740
3	Дан треугольник АВС, у которого АВ = 13 см, ВС = 8 см, АС = 8 см. Определите вид треугольника АВС	А) равносторонний. Б) прямоугольный. В) равнобедренный. Г) разносторонний
4	Какое количество треугольников?	А) 7 Б) 8 В) 9 Г) 10
5	Стороны равнобедренного треугольника равны 5 см и 12 см. Найдите его периметр	А) 29 см Б) 36 см В) 22 см Г) 15 см

 

 

Квадраты на сторонах треугольника

Главная » Треугольники » Конгруэнтные треугольники » Квадраты на сторонах треугольника

Последнее обновление: 29 октября 2021 г. от Ido Sarig · Этот веб-сайт получает доход от рекламы и использует файлы cookie · Условия использования · Политика конфиденциальности

Теорема Пифагора показывает нам важное свойство квадратов, построенных на сторонах справа треугольника, а именно, что c ^{2 =} a ² +b ² :

Но есть интересные свойства квадратов, построенных на сторонах любой треугольник , как мы будем исследовать в этой геометрической задаче.

Задача

На сторонах AB и AC треугольника ΔABC построены два квадрата. Покажите, что CE=BD и что CE⊥BD.

Стратегия

Мы решим эту задачу в два этапа: сначала покажем, что отрезки равны, а затем покажем, что они перпендикулярны.

Разделение сложных проблем на более мелкие, управляемые части часто облегчает понимание того, как доказать каждую часть по отдельности.

Доказательство равенства отрезков

В первой части нам нужно показать, что CE=BD, и, как мы это обычно делаем, посмотрим, существуют ли конгруэнтные треугольники, в которых они являются соответствующими сторонами.

Посмотрим на уже приведенные в условии задачи два треугольника, в которых стороны CE и BD, треугольники ΔACE и ΔADB.

Мы построили квадраты на сторонах треугольника ΔABC, а у квадрата все стороны равны. Итак, у нас уже есть две конгруэнтные стороны: AD=AC и AB=AE. Нам нужно доказать, что третья сторона равна (CE=BD), поэтому, очевидно, мы не можем полагаться на нее.

Поищем углы. Поскольку у нас уже есть две конгруэнтные стороны, проще всего будет использовать постулат Сторона-Угол-Сторона, поэтому давайте посмотрим на углы между двумя конгруэнтными сторонами: ∠DAB и ∠CAE.

∠DAB состоит из ∠CAB плюс угол 90° (∠DAC) от квадрата. Точно так же ∠CAE состоит из ∠CAB плюс угол 90 ° (∠BAE) от другого квадрата. Таким образом, оба они равны m∠CAB + 90 и конгруэнтны. Таким образом, треугольники равны, и соответствующие стороны CE=BD.

Доказательство того, что отрезки перпендикулярны

Теперь обратимся ко второй части, показывающей, что прямые перпендикулярны. Для этого нужно будет показать, что один из углов в точке пересечения, Х, равен 90°.

Посмотрим, сможем ли мы добраться туда, используя математику углов. Мы воспользуемся тем, что здесь у нас есть квадраты с прямыми углами.

Обозначим ∠ACE ‘γ’. Мы доказали, что треугольники ΔACE и ΔADB конгруэнтны, поэтому m∠ACE= m∠ADB=γ. Теперь посмотрите на ∠AZD. Это внешний угол к ΔDAZ, поэтому по теореме о внешнем угле он равен сумме двух удаленных друг от друга внутренних углов, поэтому он равен γ+90°.

Но ∠AZD — это , а также внешний угол к ∆ZCX, поэтому по теореме о внешнем угле он равен сумме двух удаленных внутренних углов, поэтому он равен γ+m∠ZXC.

Но если m∠AZD = γ+90° и m∠AZD = γ+m∠ZXC, то m∠ZXC=90° и CE⊥BD.

Proof

(1) AD=AC //Определение квадрата
(2) AB=AE //Определение квадрата
(3) m∠DAC=90° //Определение квадрата
(4) m∠BAE=90° //Определение квадрата
(5) ∠DAB ≅ ∠CAB +∠DAC //Постулат сложения углов
(6) ∠CAE ≅ ∠CAB +∠BAE //Постулат сложения углов
(7) ∠DAB ≅ ∠CAE //(3),(4),(5),(6), транзитивное свойство равенства
( 8) ΔACE ≅ ΔADB //(1), (2), (7), Сторона-Угол-Сторона
(9) CE=DB //(8), Соответствующие стороны в конгруэнтных треугольниках (CPCTC)

Теперь давайте формально доказать вторую часть:
(10) ∠ACE≅∠ADB //(8), Соответствующие стороны в конгруэнтных треугольниках (CPCTC)
(11) m∠ACE= m∠ADB=γ //Определение конгруэнтных углов
( 12) m∠AZD= γ+90° // Теорема о внешнем угле в ΔDAZ
(13) m∠AZD= γ+m∠ZXC //Теорема о внешнем угле в ΔZCX
(14) m∠ZXC=90° //(12), (13) , транзитивность равенства
(15) CE⊥ BD //(14), определение перпендикулярных прямых

Мы будем использовать эти два факта (CE=BD и CE⊥BD) в следующей задаче.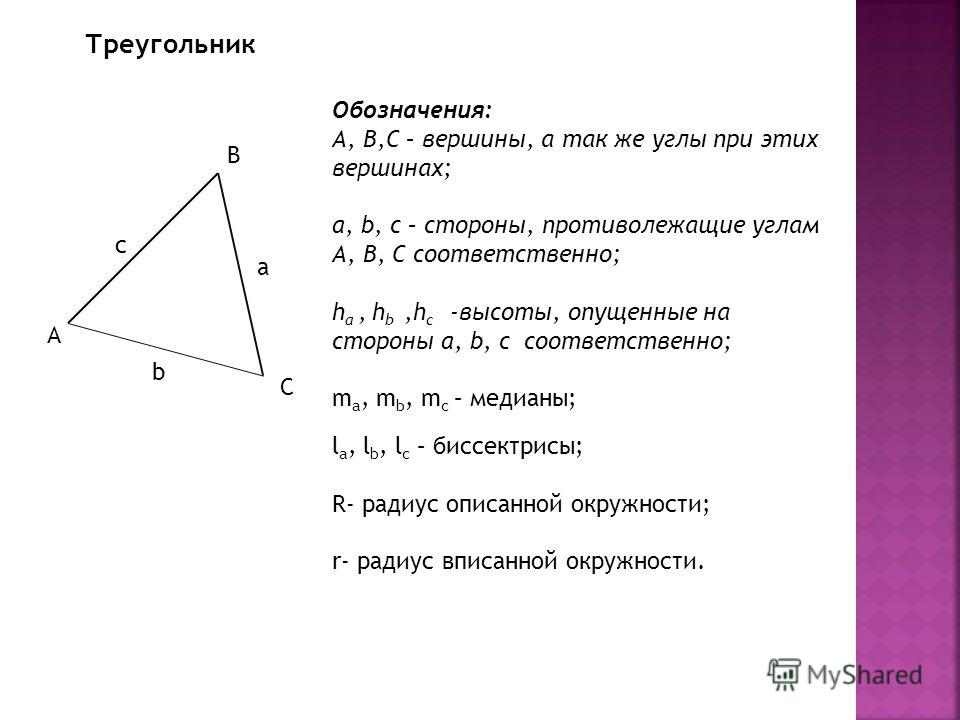

Об авторе

Идо Сариг — руководитель отдела высоких технологий со степенью бакалавра вычислительной техники. Его цель — помочь вам разработать лучший подход к решению геометрических задач. Вы можете связаться с ним по адресу [email protected]

Теорема о неравенстве треугольника — УРОКИ МАТЕМАТИИ КЕЙТ

Длины сторон треугольника Можно ли составить треугольник с любыми тремя длинами сторон? Попробуйте сами и убедитесь. Возьмите 3 карандаша или ручки разной длины. Сможете ли вы сложить их встык, чтобы получился треугольник? На картинке выше из трех карандашей можно составить треугольник. Всегда ли это будет работать? Что, если у вас есть два очень коротких карандаша и один длинный карандаш? Смогут ли два коротких дотянуться до треугольника? На картинке выше вы можете видеть, что два коротких карандаша недостаточно длинные, чтобы образовать треугольник. Бывают случаи, когда треугольник не может быть составлен с тремя заданными длинами сторон. Иногда две самые короткие стороны не будут достаточно длинными, чтобы соприкасаться друг с другом, образуя треугольник. Итак, как мы узнаем, могут ли три заданные длины сторон образовать треугольник (без физической проверки)? Когда вам даны три длины сторон, представьте, что две самые короткие стороны помещены встык, а самая длинная сторона расположена прямо под ними. Если два коротких, соединенных вместе, длиннее, чем самая длинная сторона, они смогут образовать треугольник. Если вы соедините две самые короткие стороны встык, и они не будут такими же длинными, как самая длинная сторона, они не смогут дотянуться, когда вы попытаетесь сформировать треугольник.

Добро пожаловать на уроки математики Кейт! Учителя: обязательно ознакомьтесь с учебными пособиями и заданиями.

Что, если вы поставите две короткие стороны встык, и они будут равны длине самой длинной стороны? Чтобы «выскочить» в треугольник, должно быть немного больше места.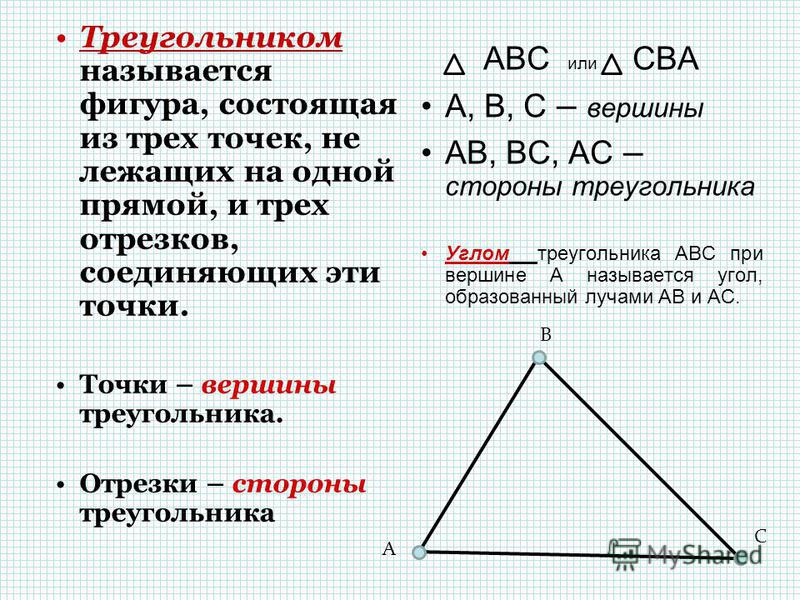 Если они едва касаются концов самой длинной стороны, когда они параллельны самой длинной стороне, у них нет места, чтобы развернуться и образовать треугольник. Две самые короткие стороны, соединенные встык, должны быть на длиннее самой длинной стороны. Если бы вы попытались поставить два самых коротких под углом, они бы очень близко образовали треугольник, но не были бы достаточно длинными.

​Теорема о неравенстве треугольников

Теорема о неравенстве треугольников — это просто более формальный способ описать то, что мы только что обнаружили. Мы обнаружили, что если сложить две короткие стороны встык (это сумма двух самых коротких сторон), они должны быть длиннее самой длинной стороны (поэтому в теореме стоит знак «больше»).

Это всего лишь один из способов сформулировать теорему о неравенстве треугольников. Другой способ сформулировать это — сказать, что сумма длин любых двух сторон треугольника должна быть больше длины третьей стороны.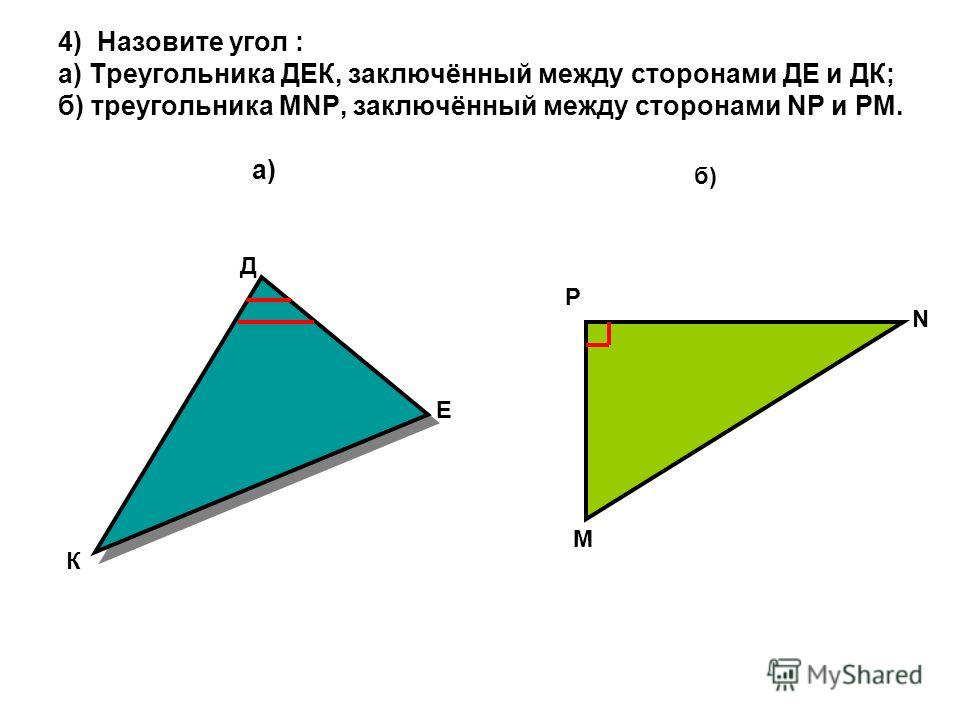

Важно помнить:  
Короткая сторона + Короткая сторона > Самая длинная сторона

Если вы соедините две самые короткие стороны встык, они должны быть длиннее, чем самая длинная сторона, чтобы иметь возможность изогнуться под углом треугольник.

Пример 1

Определите, могут ли заданные длины сторон образовать треугольник:  4, 6 и 8.

Сначала определите две самые короткие стороны: 4 и 6.  Если вы найдете сумму двух самых коротких сторон, больше, чем самая длинная сторона?

Это изображение ниже. Если поставить две самые короткие стороны встык, они будут длиннее самой длинной стороны. Это означает, что они достаточно длинные, чтобы дотянуться, когда вы поворачиваете их под углом, чтобы сформировать треугольник.

​
Пример 2

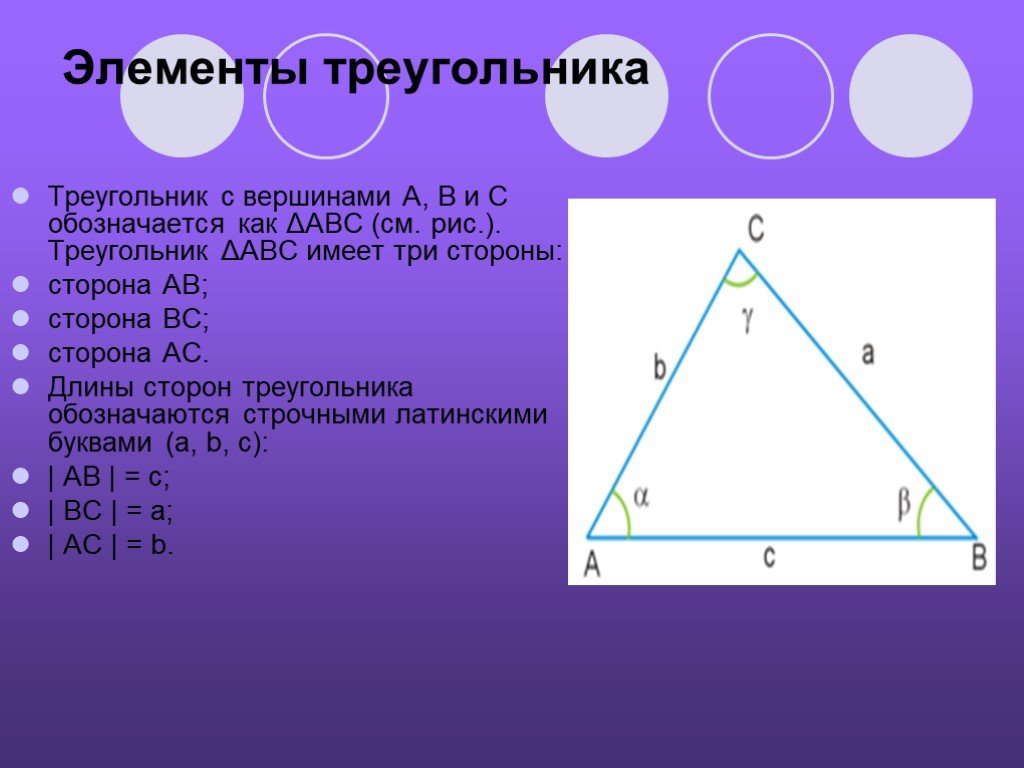
Определите, могут ли заданные длины сторон образовать треугольник:  7, 3 и 2.

​Сначала определите две самые короткие стороны: 3 и 2.