Как определить какой треугольник по сторонам: Выясните, является ли треугольник остроугольным, прямоугольным или тупоугольным, если его стороны равны: 5и 4 и…

Содержание

Существующие Треугольники: Теорема, Докзательство, Признаки

Главная » геометрия

Обновлено 28.02.2022

Содержание

Определение
Теорема
Доказательство теоремы
Следствия из теоремы
Признаки существования треугольника

Определение

Существующие треугольники — это такие треугольники,
существование которых можно доказать с помощью неравенств.

Например существование треугольника, изображенного на рисунке 1,
можно доказать с помощью неравенств: AB + BC > AC, AC + BC > AB, AB + AC > BC
Если эти три неравенства истинны значит треугольник существует,
иначе он не существует.

Также существование того или иного треугольника можно проверить с
помощью одного условия: Если большая сторона треугольника меньше
суммы двух других сторон, значит треугольник существует,
иначе он не существует.

Теорема

Для доказательства того, о чем мы говорили существует теорема под названием неравенство треугольника. Формулировка теоремы:
каждая сторона треугольника меньше суммы двух других сторон.

Докажем, что каждая сторона треугольника, изображенного на рисунке 2, меньше суммы двух других сторон:

Доказательство теоремы

Проведем отрезок CD равный отрезку CB.
△BCD — равнобедренный, значит ∠CBD = ∠CDB.
Рассмотрим △ABD: ∠ABD > ∠CBD, следовательно ∠ABD > ∠CDB, то AB < AD.
Но AD = AC + CD = AC + CB, поэтому AB < AC + CB, ч.т.д.

Следствия из теоремы

Для любых точек А, В, С, не лежащих на
одной прямой справедливы неравенства:
AB < AC + BC
AC < AB + BC
BC < AC + AB
Каждая сторона треугольника меньше суммы двух других сторон.
Внешний угол треугольника равен сумме двух внутренних, не смежных с ним углов.
Теорема о неравенстве треугольника для разности сторон.

Признаки существования треугольника

Если каждая сторона треугольника меньше суммы двух других сторон, значит треугольник существует.
Если большая сторона треугольника меньше суммы двух других сторон,
значит треугольник существует.
Если сумма углов треугольника равна 180°, значит треугольник существует.

Как понять что треугольник остроугольный. Тупоугольный треугольник: длина сторон, сумма углов

Типы треугольников

Рассмотрим три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки (рис. 1).

Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника, а концы отрезков (три точки, не лежащие на одной прямой) – вершинами треугольника.

В таблице 1 перечислены все возможные типы треугольников в зависимости от величины их углов .

Таблица 1 – Типы треугольников в зависимости от величины углов

Признаки равенства прямоугольных треугольников

Рисунок	Тип треугольника	Определение
	Остроугольный треугольник	Треугольник, у которого все углы острые , называют остроугольным
	Прямоугольный треугольник	Треугольник, у которого один из углов прямой , называют прямоугольным
	Тупоугольный треугольник	Треугольник, у которого один из углов тупой , называют тупоугольным

Остроугольный треугольник

Определение:

Треугольник, у которого все углы острые , называют остроугольным

Прямоугольный треугольник

Определение:

Треугольник, у которого один из углов прямой , называют прямоугольным

Тупоугольный треугольник

Определение:

Треугольник, у которого один из углов тупой , называют тупоугольным

В зависимости от длин сторон выделяют два важных типа треугольников.

Таблица 2 – Равнобедренный и равносторонний треугольники

Рисунок	Тип треугольника	Определение
	Равнобедренный треугольник	боковыми сторонами , а третью сторону называют основанием равнобедренного треугольника
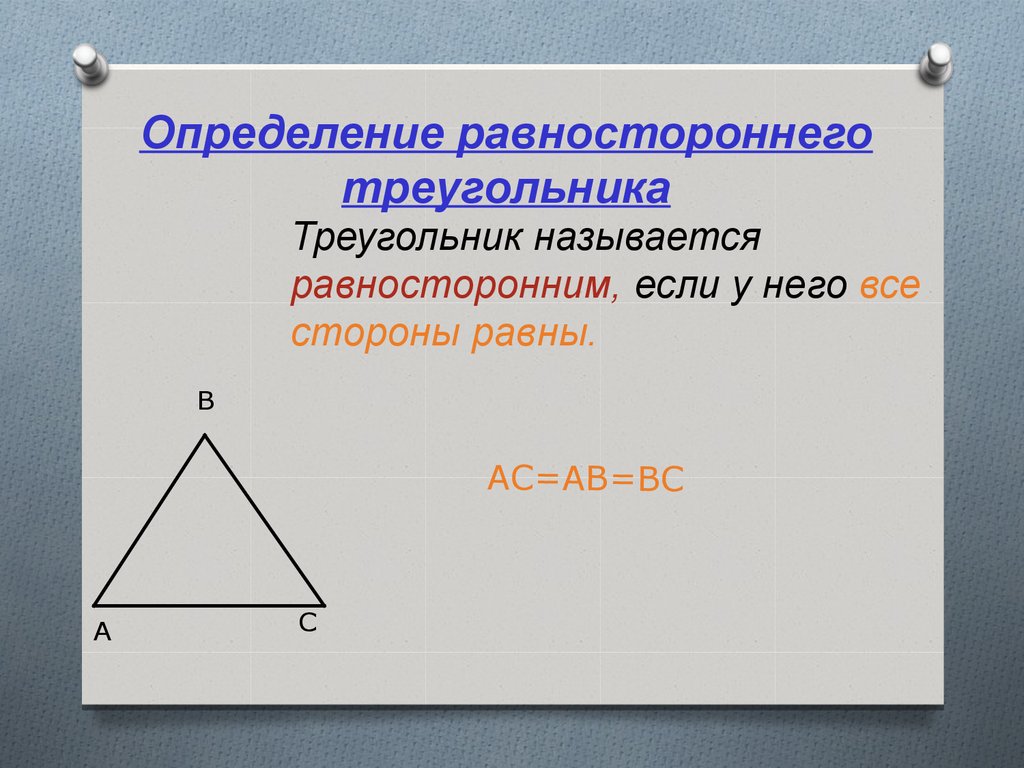
	Равносторонний (правильный) треугольник	Треугольник, у которого все три стороны равны, называют равносторонним или правильным треугольником

Равнобедренный треугольник

Определение:

Треугольник, у которого две стороны равны, называют равнобедренным треугольником. В этом случае две равные стороны называют боковыми сторонами , а третью сторону называют основанием равнобедренного треугольника

Равносторонний (правильный) треугольник

Определение:

Треугольник, у которого все три стороны равны, называют равносторонним или правильным треугольником

Признаки равенства треугольников

Треугольники называют равными , если их можно совместить наложением

В таблице 3 приведены признаки равенства треугольников .

Таблица 3 – Признаки равенства треугольников

Рисунок	Название признака	Формулировка признака
	по двум сторонам и углу между ними
	Признак равенства треугольников по стороне и двум прилежащим к ней углам
	Признак равенства треугольников по трём сторонам

Признак равенства треугольников по двум сторонам и углу между ними

Формулировка признака .
Если две стороны одного треугольника и угол между ними соответственно равны двум сторонам другого треугольника и углу между ними, то такие треугольники равны

Признак равенства треугольников по стороне и двум прилежащим к ней углам

Формулировка признака .

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны

Признак равенства треугольников по трём сторонам

Формулировка признака .
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны

Признаки равенства прямоугольных треугольников

Для сторон прямоугольных треугольников принято использовать следующие названия.

Гипотенузой называют сторону прямоугольного треугольника, лежащую против прямого угла (рис. 2), две другие стороны называют катетами .

Таблица 4 – Признаки равенства прямоугольных треугольников

Рисунок	Название признака	Формулировка признака
	по двум катетам
	Признак равенства прямоугольных треугольников по катету и прилежащему острому углу
	Признак равенства прямоугольных треугольников по катету и противолежащему острому углу	Если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и противолежащему острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники равны
	Признак равенства прямоугольных треугольников по гипотенузе и острому углу	Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники равны
	Признак равенства прямоугольных треугольников по катету и гипотенузе	Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие прямоугольные треугольники равны

Признак равенства прямоугольных треугольников по двум катетам

Формулировка признака .

Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие прямоугольные треугольники равны

Признак равенства прямоугольных треугольников по катету и прилежащему острому углу

Формулировка признака .
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники равны

Признак равенства прямоугольных треугольников по катету и противолежащему острому углу

При изучении математики ученики начинаются знакомиться с различными видами геометрических фигур. Сегодня речь пойдет о различных видах треугольников.

Определение

Геометрические фигуры, которые состоят из трех точек, которые не находятся на одной прямой, называются треугольниками.

Отрезки, соединяющие точки, называются сторонами, а точки – вершинами. Вершины обозначаются большими латинскими буквами, например: A, B, C.

Стороны обозначаются названиями двух точек, из которых они состоят – AB, BC, AC. Пересекаясь, стороны образуют углы. Нижняя сторона считается основанием фигуры.

Рис. 1. Треугольник ABC.

Виды треугольников

Треугольники классифицируют по углам и сторонам. Каждый из видов треугольника имеет свои свойства.

Существует три вида треугольников по углам:

остроугольные;
прямоугольные;
тупоугольные.

Все углы остроугольного треугольника острые, то есть градусная мера каждого составляет не более 90 0 .

Прямоугольный треугольник содержит прямой угол. Два других угла всегда будут острыми, так как иначе сумма углов треугольника превысит 180 градусов, а это невозможно. Сторона, которая, находится напротив прямого угла, называется гипотенузой, а две другие катетами.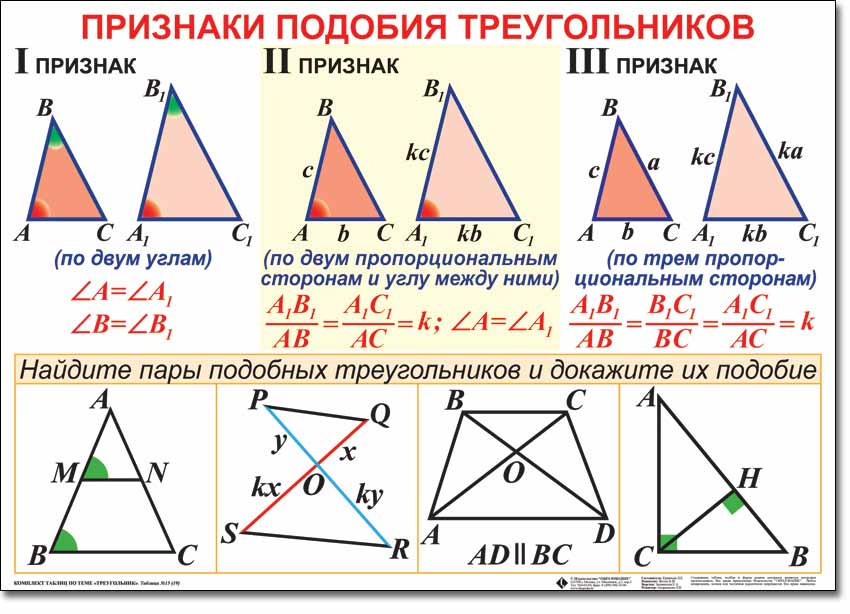

Гипотенуза всегда больше катета.

Тупоугольный треугольник содержит тупой угол. То есть угол, величиной больше 90 градусов. Два других угла в таком треугольника будут острыми.

Рис. 2. Виды треугольников по углам.

Пифагоровым треугольником называется прямоугольник, стороны которого равны 3, 4, 5.

Причем, большая сторона является гипотенузой.

Такие треугольники часто используются для составления простых задач в геометрии. Поэтому, запомните: если две стороны треугольника равны 3, то третья обязательно будет 5. Это упростит расчеты.

Виды треугольников по сторонам:

равносторонние;

равнобедренные;
разносторонние.

Равносторонний треугольник – это треугольник, у которого все стороны равны. Все углы такого треугольника равны 60 0 , то есть он всегда является остроугольным.

Равнобедренный треугольник – треугольник, у которого только две стороны равны. Эти стороны называются боковыми, а третья – основанием. Кроме того, углы при основании равнобедренного треугольника равны и всегда являются острыми.

Разносторонним или произвольным треугольником называется треугольник, у которого все длины и все углы не равны между собой.

Если в задаче нет никаких уточнений по поводу фигуры, то принято считать, что речь идет о произвольном треугольнике.

Рис. 3. Виды треугольников по сторонам.

Сумма всех углов треугольника, независимо от его вида, равна 1800.

Напротив большего угла находится большая сторона. А также длина любой стороны всегда меньше суммы двух других его сторон. Эти свойства подтверждаются теоремой о неравенстве треугольника.

Существует понятие золотого треугольника. Это равнобедренный треугольник, у которого две боковые стороны пропорциональны основе и равны определенному числу. В такой фигуре углы пропорциональны соотношению 2:2:1.

Задача:

Существует ли треугольник, стороны которого равны 6 см., 3 см., 4 см.?

Решение:

Для решения данного задания нужно использовать неравенство a

Что мы узнали?

Из данного материала из курса математики 5 класса, мы узнали, что треугольники классифицируются по сторонам и величине углов. Треугольники имеют определенные свойства, которые можно использовать при решении заданий.

Пожалуй, самой основной, простой и интересной фигурой в геометрии является треугольник. В курсе средней школы изучаются его основные свойства, однако иногда знания по этой теме формируются неполными. Виды треугольников изначально определяют их свойства. Но подобное представление остается смешанным. Поэтому сейчас разберем немного подробнее эту тему.

Виды треугольников зависят от градусной меры углов. Эти фигуры бывают остро-, прямо- и тупоугольными. Если все углы не превышают значения в 90 градусов, то фигуру смело можно назвать остроугольной. Если хотя бы один угол треугольника равен 90 градусам, то вы имеете дело с прямоугольным подвидом. Соответственно, во всех остальных случаях рассматриваемую называют тупоугольной.

Существует множество задач для остроугольных подвидов. Отличительной чертой является внутреннее местонахождение точек пересечения биссектрис, медиан и высот. В других случаях это условие может не выполняться.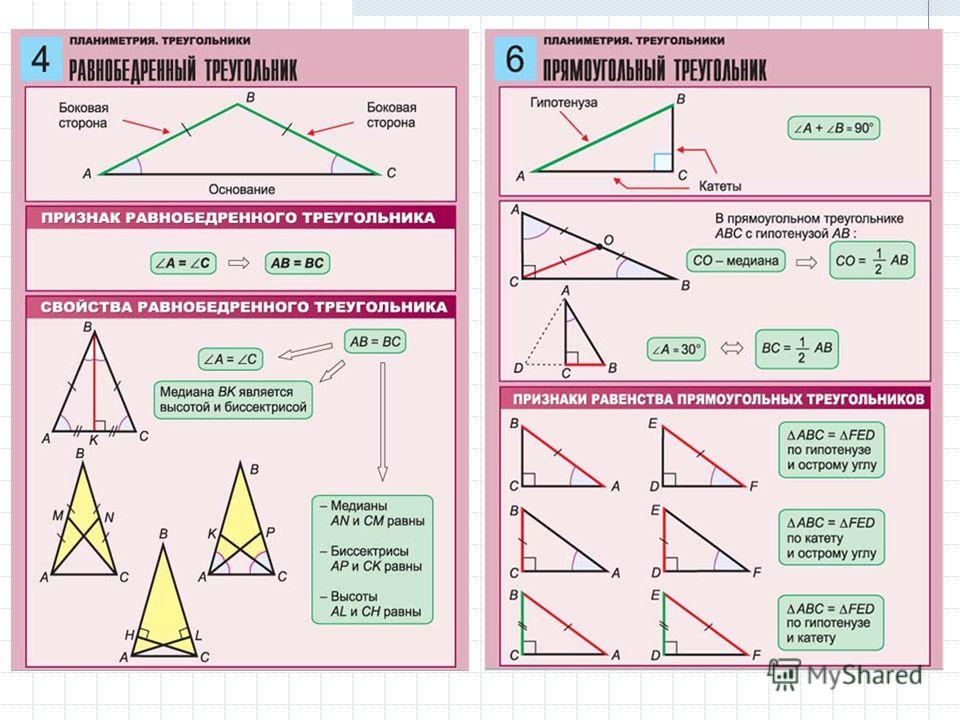 Определить тип фигуры “треугольник” нетрудно. Достаточно знать, например, косинус каждого угла. Если какие-нибудь значения меньше нуля, значит, треугольник в любом случае является тупоугольным. В случае нулевого показателя фигура обладает прямым углом. Все положительные значения гарантированно подскажут вам о том, что перед вами остроугольный вид.

Нельзя не сказать о правильном треугольнике. Это самый идеальный вид, где совпадают все точки пересечения медиан, биссектрис и высот. Центр вписанной и описанной окружности лежит также в одном месте. Для решения задач необходимо знать только одну сторону, так как вам углы изначально заданы, а две другие стороны известной. То есть фигура задается только одним параметром. Существуют Их главная особенность — равенство двух сторон и углов при основании.

Иногда встречается вопрос о том, существует ли треугольник с заданными сторонами. На самом деле вас спрашивают, подходит ли данное описание под основные виды. Например, если сумма двух сторон меньше третьей, то в реальности такой фигуры не существует вообще. Если в задании просят найти косинусы углов треугольника со сторонами 3,5,9, то здесь очевидный можно объяснить без сложных математических приемов. Предположим, вы хотите из пункта A попасть в пункт B. Расстояние по прямой равно 9 километрам. Однако вы вспомнили, что необходимо зайти в пункт C в магазин. Расстояние от А до С равно 3 километрам, а от С до В — 5. Таким образом получается, что, двигаясь через магазин, вы пройдете на один километр меньше. Но так как пункт C не расположен на прямой AB, то вам придется пройти лишнее расстояние. Здесь возникает противоречие. Это, конечно, условное объяснение. Математика знает не один способ доказательства того, что все виды треугольников подчиняются основному тождеству. Оно гласит о том, что сумма двух сторон больше длины третьей.

Любой вид обладает следующими свойствами:

1) Сумма всех углов равняется 180 градусам.

2) Всегда существует ортоцентр — точка пересечения всех трех высот.

3) Все три медианы, проведенные из вершин внутренних углов, пересекаются в одном месте.

4) Вокруг любого треугольника можно описать окружность. Также можно вписать круг так, чтобы он имел только три точки соприкосновения и не выходил за внешние стороны.

Теперь вы познакомились с основными свойствами, которыми обладают различные виды треугольников. В будущем важно понимать, с чем вы имеете дело при решении задачи.

Сегодня мы отправляемся в страну Геометрия, где познакомимся с различными видами треугольников.

Рассмотрите геометрические фигуры и найдите среди них «лишнюю» (рис. 1).

Рис. 1. Иллюстрация к примеру

Мы видим, что фигуры № 1, 2, 3, 5 — четырехугольники. Каждая из них имеет свое название (рис. 2).

Рис. 2. Четырехугольники

Значит, «лишней» фигурой является треугольник (рис. 3).

Рис. 3. Иллюстрация к примеру

Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.

Точки называются вершинами треугольника , отрезки — его сторонами . Стороны треугольника образуют в вершинах треугольника три угла.

Основными признаками треугольника являются три стороны и три угла. По величине угла треугольники бывают остроугольные, прямоугольные и тупоугольные.

Треугольник называется остроугольным, если все три угла его острые, то есть меньше 90° (рис. 4).

Рис. 4. Остроугольный треугольник

Треугольник называется прямоугольным, если один из его углов равен 90° (рис. 5).

Рис. 5. Прямоугольный треугольник

Треугольник называется тупоугольным, если один из его углов тупой, то есть больше 90° (рис. 6).

Рис. 6. Тупоугольный треугольник

По числу равных сторон треугольники бывают равносторонние, равнобедренные, разносторонние.

Равнобедренным называется треугольник, у которого две стороны равны (рис. 7).

Рис. 7.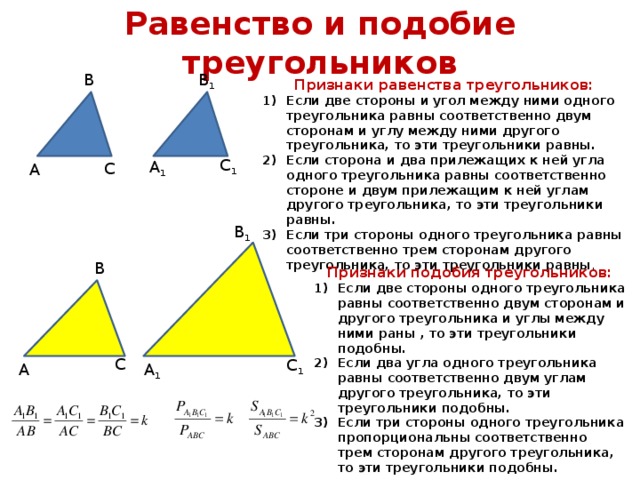 Равнобедренный треугольник

Эти стороны называются боковыми , третья сторона — основанием . В равнобедренном треугольнике углы при основании равны.

Равнобедренные треугольники бывают остроугольными и тупоугольными (рис. 8).

Рис. 8. Остроугольный и тупоугольный равнобедренные треугольники

Равносторонним называется треугольник, у которого все три стороны равны (рис. 9).

Рис. 9. Равносторонний треугольник

В равностороннем треугольнике все углы равны . Равносторонние треугольники всегда остроугольные.

Разносторонним называется треугольник, у которого все три стороны имеют разную длину (рис. 10).

Рис. 10. Разносторонний треугольник

Выполните задание. Распределите данные треугольники на три группы (рис. 11).

Рис. 11. Иллюстрация к заданию

Сначала распределим по величине углов.

Остроугольные треугольники: № 1, № 3.

Прямоугольные треугольники: № 2, № 6.

Тупоугольные треугольники: № 4, № 5.

Эти же треугольники распределим на группы по числу равных сторон.

Разносторонние треугольники: № 4, № 6.

Равнобедренные треугольники: № 2, № 3, № 5.

Равносторонний треугольник: № 1.

Рассмотрите рисунки.

Подумайте, из какого куска проволоки сделали каждый треугольник (рис. 12).

Рис. 12. Иллюстрация к заданию

Можно рассуждать так.

Первый кусок проволоки разделен на три равные части, поэтому из него можно сделать равносторонний треугольник. На рисунке он изображен третьим.

Второй кусок проволоки разделен на три разные части, поэтому из него можно сделать разносторонний треугольник. На рисунке он изображен первым.

Третий кусок проволоки разделен на три части, где две части имеют одинаковую длину, значит, из него можно сделать равнобедренный треугольник. На рисунке он изображен вторым.

Сегодня на уроке мы познакомились с различными видами треугольников.

Список литературы

М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
Нормативно-правовой документ. Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
«Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
В.Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.

Nsportal.ru ().
Prosv.ru ().
Do.gendocs.ru ().

Домашнее задание

1. Закончите фразы.

а) Треугольником называется фигура, которая состоит из …, не лежащих на одной прямой, и …, попарно соединяющих эти точки.

б) Точки называются … , отрезки — его … . Стороны треугольника образуют в вершинах треугольника ….

в) По величине угла треугольники бывают … , … , … .

г) По числу равных сторон треугольники бывают … , … , … .

2. Начертите

а) прямоугольный треугольник;

б) остроугольный треугольник;

в) тупоугольный треугольник;

г) равносторонний треугольник;

д) разносторонний треугольник;

е) равнобедренный треугольник.

3. Составьте задание по теме урока для своих товарищей.

Треугольник — определение и общие понятия

Треугольник – это такой простой многоугольник, состоящий из трех сторон и имеющий столько же углов. Его плоскости ограничиваются 3 точками и 3 отрезками, попарно соединяющими даные точки.

Все вершины любого треугольника, независимо от его разновидности, обозначаются заглавными латинскими буквами, а его стороны изображаются соответствующими обозначениями противоположных вершин, только не большими буквами, а малыми. Так, например, треугольник с вершинами обозначенными буквами А, В и С имеет стороны a, b, c.

Если рассматривать треугольник в евклидовом пространстве, то это такая геометрическая фигура, которая образовалась с помощью трех отрезков, соединяющих три точки, которые не лежат на одной прямой.

Посмотрите внимательно на рисунок, который изображен вверху. На нем точки А, В и С являются вершинами этого треугольника, а его отрезки носят названия сторон треугольника. Каждая вершина этого многоугольника образует внутри его углы.

Виды треугольников

Согласно величины, углов треугольников, они делятся на такие разновидности, как: Прямоугольные;
Остроугольные;
Тупоугольные.

К прямоугольным принадлежат такие треугольники, у которых в наличии есть один прямой угол, а остальные два имеют острые углы.

Остроугольные треугольники – это те, у которых все его углы острые.

А если у треугольника имеется один тупой угол, а два остальных угла острые, то такой треугольник относится к тупоугольным.

Каждый из вас прекрасно понимает, что не все треугольники имеют равные стороны. И соответственно тому, какую длину имеют его стороны, треугольники можно поделить на:

Равнобедренные;
Равносторонние;
Разносторонние.

Задание: Нарисуйте разные виды треугольников. Дайте им определение. Какое между ними отличие вы видите?

Основные свойства треугольников

Хотя эти простые многоугольники могут отличаться друг от друга величиной углов или сторон, но в каждом треугольнике есть основные свойства, характерны для этой фигуры.

В любом треугольнике:

Общая сумма всех его углов равняется 180º.
Если он принадлежит к равносторонним, то каждый его угол равен 60º.
Равносторонний треугольник имеет одинаковые и ровные между собой углы.
Чем меньше сторона многоугольника, тем меньший угол расположен напротив него и наоборот напротив большей стороны находиться больший угол.
Если стороны равные, то напротив них расположены равные углы, и наоборот.
Если взять треугольник и продлить его сторону, то в итоге мы образуется внешний угол. Он равен сумме внутренних углов.
В любом треугольнике его сторона, независимо от того, какую бы вы не выбрали, все равно будет меньше, чем сумма 2-х других сторон, но больше чем их разность:

1. a b – c;
2. b a – c;
3. c a – b.

Задание

В таблице приведены уже известные два угла треугольника. Зная общую сумму всех углов найдите, чему равен третий угол треугольника и занесите в таблицу:

1. Сколько градусов имеет третий угол?
2. К какому виду треугольников он относится?

Признаки равности треугольников

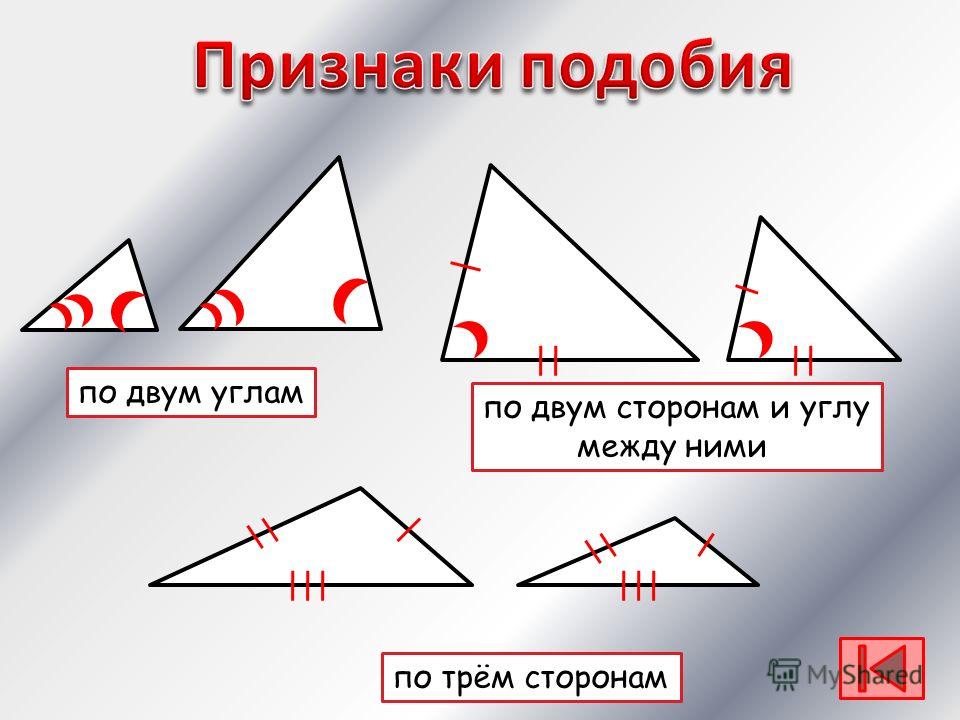
I признак

II признак

III признак

Высота, биссектриса и медиана треугольника

Высота треугольника — перпендикуляр, проведенный из вершины фигуры к его противоположной стороне, называется высотой треугольника. Все высоты треугольника пересекаются в одной точке. Точка пересечения всех 3-х высот треугольника является его ортоцентром.

Отрезок, проведенный из данной вершины и соединяющий ее на средине противоположной стороны, является медианой. Медианы, также как и высоты треугольника, имеют одну общую точку пересечения, так называемый центр тяжести треугольника или центроид.

Биссектриса треугольника — отрезок, соединяющий вершину угла и точку противоположной стороны, а также делящий этот угол пополам. Все биссектрисы треугольника пересекаются в одной точке, которую называют центром окружности, вписанной в треугольник.

Отрезок, который соединяет середины 2-х сторон треугольника, называется средней линией.

Историческая справка

Такая фигура, как треугольник, была известна еще в Древние времена. Об этой фигуре и ее свойствах упоминалось на египетских папирусах четырех тысячелетней давности. Немного позже, благодаря теореме Пифагора и формуле Герона, изучение свойства треугольника, перешло на более высокий уровень, но все же, это происходило более двух тысяч лет назад.

В XV – XVI веках стали проводить много исследований о свойствах треугольника и в итоге возникла такая наука, как планиметрия, которая получила название «Новая геометрия треугольника».

Ученый из России Н. И.Лобачевский внес огромный вклад в познание свойств треугольников. Его труды в дальнейшем нашли применение как в математике, так и физике и кибернетике.

Благодаря знаниям свойств треугольников возникла и такая наука, как тригонометрия. Она оказалась необходимой для человека в его практических потребностях, так как ее применение просто необходимо при составлении карт, измерении участков, да и при конструировании различных механизмов.

А какой самый известный треугольник вы знаете? Это конечно же Бермудский треугольник! Он получил такое название в 50-х годах из-за географического расположения точек (вершин треугольника), внутри которых, согласно существующей теории, возникали связанные с ним аномалии. Вершинами Бермудского треугольника выступают Бермудские острова, Флорида и Пуэрто-Рико.

Задание: А какие теории о Бермудском треугольнике слышали вы?

А известно ли вам, что в теории Лобачевского при сложении углов треугольника их сумма всегда имеет результат меньший, чем 180º. В геометрии Римана, сумма всех углов треугольника больше 180º, а в трудах Эвклида она равна 180 градусам.

Домашнее задание

Решите кроссворд на заданную тему

Вопросы к кроссворду:

1. Как называется перпендикуляр, который провели из вершины треугольника к прямой, расположенной на противоположной стороне?
2. Как, одним словом можно назвать сумму длин сторон треугольника?
3. Назовите треугольник, у которого две стороны равны?
4. Назовите треугольник, у которого есть угол, равный 90°?
5. Какое название носит большая, из сторон треугольника?
6. Название стороны равнобедренного треугольника?
7. Их всегда три в любом треугольнике.
8. Какое название носит треугольник, у которого один из углов превышает 90°?
9. Название отрезка, соединяющего вершину нашей фигуры со срединой противоположной стороны?
10. В простом многоугольнике АВС, заглавная буква А является …?
11. Какое название носит отрезок, делящий угол треугольника пополам.

Вопросы к теме треугольников:

1. Дайте определение.
2. Сколько высот он имеет?
3. Сколько биссектрис у треугольника?
4. Чему равна его сумма углов?
5. Какие виды этого простого многоугольника вам известны?
6. Назовите точки треугольников, которые носят название замечательных.
7. Каким прибором можно измерить величину угла?
8. Если стрелки часов показывают 21 час. Какой угол образуют часовые стрелки?
9. На какой угол поворачивается человек, если ему дана команда «налево», «кругом»?
10. Какие еще определения вам известны, которые связанные с фигурой, имеющей три угла и три стороны?

Предмети > Математика > Математика 7 класс

Как найти длину стороны прямоугольного треугольника

Все ресурсы по математике для средней школы

8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 Следующая →

Справка по математике для средней школы » Геометрия » Плоская геометрия » Треугольники » Прямоугольные треугольники » Как найти длину стороны прямоугольного треугольника

Найдите (округлив до десятых).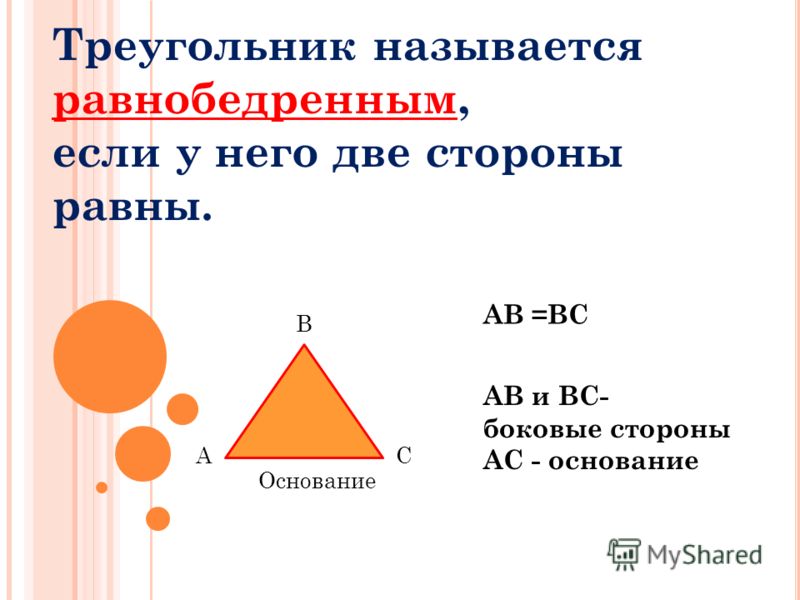 Рисунок выполнен не в масштабе.

Возможные ответы:

Правильный ответ:

Пояснение:

Мы воспользуемся теоремой Пифагора, чтобы найти недостающую длину стороны.

Сообщить об ошибке

Периметр квадратного боксерского ринга составляет футы. Когда два боксера сидят в противоположных углах между раундами, на каком расстоянии они друг от друга?

Возможные ответы:

футов

Правильный Ответ:

футов

Объяснение:

Поскольку периметр кольца равен футам, а кольцо представляет собой квадрат, найдите длину одной стороны кольца, разделив его на .

Расстояние между двумя боксерами в противоположных углах представляет собой прямую линию от одного угла до другого. Эта прямая образует гипотенузу прямоугольного треугольника, две другие стороны которого имеют длину фута (поскольку каждая из них является стороной квадрата).

Решение длины гипотенузы этого прямоугольного треугольника с помощью теоремы Пифагора дает расстояние между двумя боксерами, когда они находятся в противоположных углах.

Сообщить об ошибке

Дан прямоугольный треугольник с длиной катета 6 и длиной гипотенузы 10.

Возможные ответы:

Правильный ответ:

Объяснение:

Использование теоремы пифагорея, мы можем решить длину ноги x :

x ² + 6 ² = 10 ²

Сейчас We Solve For For For For For For For For For For For For For For For For For For For For For For For For For For

444444444444444444444444444444444444444444444444444444444444444 лет:

44444444444444444444444 гг. x ² + 36 = 100

x ² = 100 – 36

x ² = 64

x = 8

Также обратите внимание, что это пропорционально прямоугольный треугольник 3/4/5, который очень распространен. Всегда следите за отношением стороны к гипотенезе 3/5 или 4/5 или отношением стороны к стороне 3/4 в любом прямоугольном треугольнике, чтобы вы могли быстро решать такие треугольники.

Сообщить об ошибке

В прямоугольном треугольнике длина гипотенузы равна 8, а длина катета равна 7. Какова длина третьей стороны с точностью до десятых?

Возможные ответы:

3,9

2,4

3,6

1,0

Правильный ответ: 3,5

4 Объяснение:

Используя теорему Пифагора, 8 ² = 7 ² +x ² . Решение для x дает квадратный корень из 15, который равен 3,9

Сообщить об ошибке

Дан прямоугольный треугольник с длиной катета 2 и длиной гипотенузы √8, найдите длину другого катета, х .

Возможные ответы:

√8

Правильный Ответ:

Explanation:

Using Pythagorean Theorem, we can solve for the length of leg x :

x ² + 2 ² = (√8) ² = 8

Now we solve for х :

х ² + 4 = 8

x ² = 8 — 4

x ² = 4

x = 2

Отчет о ошибке

x = 2

. и . Округлив до ближайшего целого числа, какова длина гипотенузы?

Возможные ответы:

Правильный ответ:

Пояснение:

Используйте теорему Пифагора.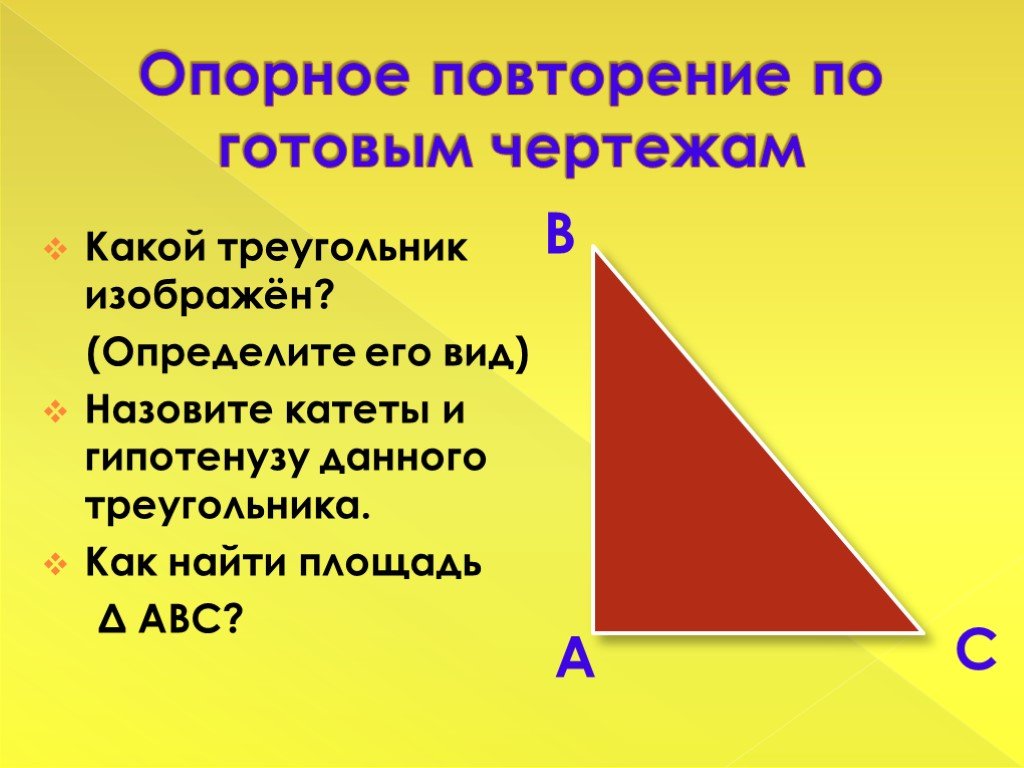 Сумма квадратов обоих катетов равна квадрату гипотенузы.

Сообщить об ошибке

Решить для .

(Рисунок выполнен не в масштабе).

Возможные ответы:

Правильный ответ:

Объяснение:

Используйте теорему Пифагора: .

Мы знаем длину одной стороны и гипотенузу.

Теперь мы можем найти недостающую сторону.

Сообщить об ошибке

Правый треугольник имеет одну сторону, равную 5, а его гипотенуза, равная 14. его третья сторона равна:

Возможные ответы:

14,87

171

13,07

171

13,07

159 171

ответ:
13. 07
Объяснение:
Теорема Пифагора дает нам a ² + b ² = c ² для прямоугольного треугольника, где c — это гипотенуза, а a и b — меньшие стороны. Здесь a равно 5, а c равно 14, поэтому b ² = 14 ² – 5 ² = 171. Следовательно, b = 171. Следовательно, b = 171. ориентировочно 13.07.
Сообщить об ошибке
Что из следующего НЕ может быть длинами сторон прямоугольного треугольника?
Возможные ответы:
12, 16, 20
5, 7, 10
5, 12, 13
8, 15, 17
14, 48, 50
Правильный ответ:
5, 7, 10
Объяснение:
Мы используем теорему Пифагора и вычисляем, что 25 + 49 не равно 100.
Все остальные варианты ответов соблюдают теорему 2
Сообщить об ошибке
Какой набор сторон может составить прямоугольный треугольник?
Возможные ответы:
6, 7, 8
10, 12, 16
4, 6, 9
9, 12, 15
Правильный ответ:
9, 12, 15
5
Пояснение:
По теореме Пифагора в прямоугольном треугольнике сумма квадратов меньших двух сторон равна квадрату наибольшей стороны. Только 9, 12 и 15 соответствуют этому правилу.
Сообщить об ошибке
← Назад 1 2 3 Далее →
Уведомление об авторских правах
Все ресурсы по математике для старших классов
8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Learn by Concept
Как найти длину стороны треугольника, если вы знаете две другие стороны
••• Gang Zhou/iStock/GettyImages
Обновлено 21 декабря 2020 г.
Автор Pharaba Witt
Нахождение измерения третьей стороны треугольника, когда известны измерения двух других сторон, работает, только если у вас есть прямоугольный треугольник или измерение хотя бы одного другого угла. Без этой информации у вас недостаточно данных для того, чтобы узнать длину третьей стороны. Прямоугольный треугольник имеет встроенный третий угол, так как один из углов должен быть равен 90 градусов.
Прямоугольный треугольник с использованием теоремы Пифагора
Начертите на бумаге треугольник, обозначив две стороны, примыкающие к прямому углу или катету, « 92
Это теорема Пифагора, используемая для решения неизвестной стороны.
Вставьте известные вам длины в уравнение. Гипотенуза всегда является самой длинной стороной в прямоугольном треугольнике. Это отличный способ проверить свою работу, потому что, если какой-либо из катетов длиннее гипотенузы, вы знаете, что допустили ошибку.
Найдите неизвестную сторону. Если вы решаете для гипотенузы, вы вводите « a » и « b », возводите оба числа в квадрат, а затем складываете числа вместе. Используйте свой калькулятор, чтобы получить квадратный корень из полученной суммы, чтобы получить ответ. Если вы решаете для одной из ног, вам нужно переместить другую ногу в ту же сторону, что и «9».0007 c » путем вычитания. Это оставляет оставшуюся ногу в покое, позволяя вам решить для нее. Это означает, что вы возводите в квадрат число « c » и известную ногу. Вычтите квадратное значение ноги из квадратного значения c . Извлеките квадратный корень из полученного числа, и вы получите ответ для неизвестного отрезка.
Использование закона синусов
Расположите треугольник так, чтобы сторона, противоположная углу, совпадала с углом. Обозначьте сторону, противоположную углу A как a , сторона напротив угла B как b и сторона против угла C как c .
Запишите уравнение в виде
\frac{a}{\sin A}= \frac{b}{\sin B} = \frac{c}{\sin C}
Это дает вам основы для решение для вашей неизвестной стороны.
Возьмите известный вам угол и с помощью калькулятора определите синус этого угла. В большинстве научных калькуляторов вы вводите значение угла, а затем нажимаете кнопку с надписью «sin». Запишите значение.
Разделите длину стороны, связанной с углом, на значение синуса этого угла. Это дает вам число, которое обычно записывается как приближение, поскольку десятичные разряды уходят на неопределенный срок. Назовите этот новый номер X для целей этого примера.
Возьмите значение другой известной стороны и разделите его на X . Это новое число равно синусу нового угла.
Введите число в калькулятор и нажмите «sin ^-1 ”, чтобы получить угол в градусах. Теперь вы можете найти угол неизвестной стороны.
Сложите два известных угла и вычтите их из 180. Сумма всех углов внутри треугольника должна составлять 180 градусов.
Рассчитайте синус нового угла, введя его в калькулятор и нажав кнопку «sin». Умножьте ответ на X, и вы получите длину неизвестной стороны.
Для примера использования теоремы Пифагора, а также нового метода решения с использованием закона косинусов, посмотрите видео ниже:

Совет: Закон синусов можно использовать, как указано, или путем инвертирования всей информации так, чтобы синус угла делился на длину стороны.
Предупреждение: Нарисуйте задачу, чтобы увидеть, что вы умножаете и делите, чтобы убедиться, что вы понимаете, как работает задача. Помните, что вы должны сделать то же самое с обеими сторонами уравнения, чтобы стороны были равны.
Похожие статьи
Каталожные номера
Учебное упражнение по тригонометрии; Д-р Дэвид П.
No related posts.