О сумме цифр, обобщённом признаке делимости и одной нерешённой задаче
Все знают, что если сумма цифр числа делится на 9, то и сумма его цифр делится на 9. А для определения, делится ли число на 11, нужно сложить его цифры, стоящие на чётных местах и отнять сумму цифр, стоящих на нечётных местах. Если результат будет делиться на 11, то и само число также будет делиться на 11.
Возникает вопрос: почему существуют признаки делимости? Иными словами, почему для ответа на вопрос, делится ли число m на число n, достаточно не выполнять деление, а провести некоторые операции с цифрами числа m? И как вывести признак делимости на произвольное n. К ответу на этот вопрос мы придём, решая одну, казалось бы, пустяковую задачку.
Задача
Возьмём какое-нибудь натуральное число, скажем, 17. Сумма его цифр равна 8. Если 17 умножить на 2, получим 34 и сумма цифр этого числа окажется равной 7. А у произведения 17*3=51 сумма цифр равна 6. Вопрос: на какое натуральное число нужно умножить 17, чтобы сумма цифр произведения была наименьшей?
Решение
Понятно, что сумма цифр, равная 1 будет только у степеней десятки, которые кратны лишь произведениям степеней двойки и пятёрки. Поэтому попробуем найти кратное 17-ти число вида 100…01 с суммой цифр, равной двум.
Поэтому попробуем найти кратное 17-ти число вида 100…01 с суммой цифр, равной двум.
17*X=100…01
Чтобы последней цифрой произведения была единица, последней цифрой неизвестного множителя должна быть тройка. Далее, т.к. 17*3=51, а предпоследняя цифра произведения равна 0, то предпоследней цифрой неизвестного множителя должна быть пятёрка.
17*53=901
Третьей с конца цифрой множителя снова должна быть тройка (чтобы произведение оканчивалось на ..001)
17*353=6001.
Далее находим, последовательно:
17*2353=40001
17*82353=1400001
17*882353=15000001
17*5882353=100000001 (!)
Весь этот процесс представлен на анимированной гиф-иллюстрации
Итак, среди чисел, кратных 17-ти наименьшая сумма цифр, равная 2, будет у числа 100000001=17*5882353.
Ответ: число 17 нужно умножить на 5882353, и тогда сумма цифр произведения будет равна 2.
Возникает вторая задача: а что было бы, если бы потребовалось найти кратное с минимальной суммой цифр для какого-нибудь другого числа? Почти сразу приходят на ум числа 3 и 9, кратные которых, вследствие соответствующих признаков делимости, не могут иметь суммы цифр, меньшие, чем 3 или 9, соответственно. Но оказывается, что и многие другие числа не имеют кратных вида 100…01.
Но оказывается, что и многие другие числа не имеют кратных вида 100…01.
К примеру, попробуем провести операции, аналогичные проведённым с числом 17, для числа 41.
Если существует такой множитель Х, что 41*Х=100…01, то последняя цифра числа Х равна 1.
41*1=41.
Далее, предпоследняя цифра числа Х должна быть равна 6
41*61=2501
41*561=23001
41*7561=310001
41*97561=4000001
И тут мы обнаруживаем, что зациклились: далее неизвестный множитель будет продолжать обрастать цифрами 6, 5, 7 и 9, а сумма цифр кратного, равная 2, достигнута не будет.
Итак, какова же минимальная сумма цифр у числа, кратного 41-му?
Вот тут мы и приходим к проблеме построения обобщённого признака делимости. Почему же для ответа на вопрос, делится ли число m на число n, достаточно не выполнять деление, а провести некоторые операции с цифрами числа m?
Как известно, если число m имеет k цифр, то его можно представить в виде суммы произведений его цифр на соответствующие степени десятки:
Далее, известно, что сумма остатков равна остатку суммы, а произведение остатков равно остатку произведения.
Этот обобщённый признак делимости называется признаком Паскаля.
Докажем теперь с помощью этого признака делимости, что не существует числа вида 100…01, которое делится на 41. Вычислим остатки от деления на 41 степеней десятки:
j |
Остаток от деления на 41 |
|
0 |
1 |
1 |
1 |
10 |
10 |
2 |
100 |
18 |
3 |
1000 |
16 |
4 |
10000 |
37 |
5 |
100000 |
1 |
6 |
1000000 |
10 |
… |
… |
… |
Заметим, что удобнее находить искомые остатки не непосредственно делением степени числа 10 на 41, а делением на 41 предыдущего остатка, умноженного на 10. И, поскольку каждый следующий остаток однозначно зависит от предыдущего, то, получив на шестом шаге единицу, мы видим, что последовательность зациклилась.
И, поскольку каждый следующий остаток однозначно зависит от предыдущего, то, получив на шестом шаге единицу, мы видим, что последовательность зациклилась.
Следовательно, признак делимости на 41 можно сформулировать следующим образом:
Чтобы проверить, делится ли число на 41, его следует справа налево разбить на грани по 5 цифр в каждой. Затем в каждой грани первую справа цифру умножить на 1, вторую цифру умножить на 10, третью – на 18, четвёртую – на 16, пятую – на 37 и все полученные произведения сложить. Если результат будет делиться на 41, тогда и только тогда само число будет делиться на 41.
Таким способом можно получать признаки делимости на любые числа.
Возвращаясь к задаче о минимальной сумме цифр кратного, мы убеждаемся, что число с двумя единицами и остальными цифрами – нулями на 41 разделиться не может.
Перебирая не более чем 5-ти значные числа с суммами цифр 3 и 4 (это можно сделать как на компьютере, так и вручную) оказывается, что среди чисел, кратных 41-му минимальную сумму цифр, равную 5, будет иметь само число 41.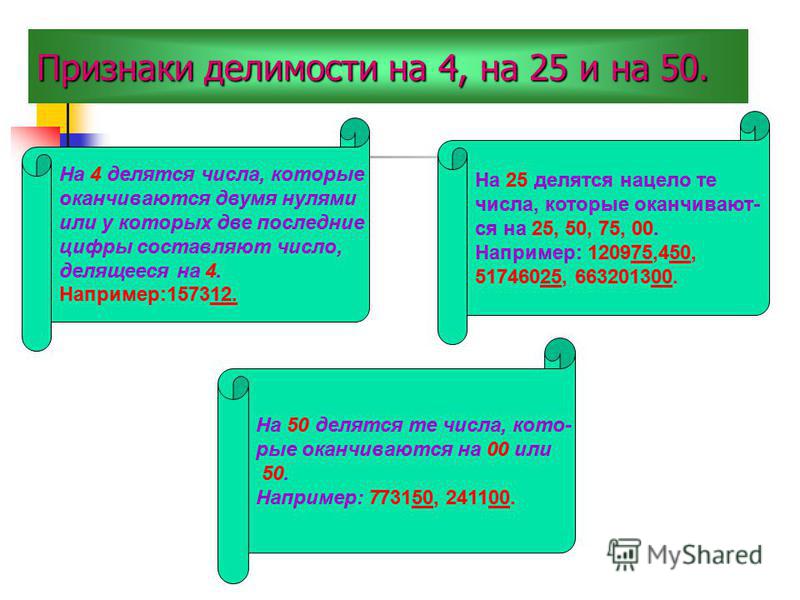
Другое интересное число, 31, замечательно тем, что, хотя на 3 не делится, никакое из его кратных не может иметь сумму цифр, меньше трёх. В первый раз минимум достигается в числе 31*322581=10000011
Собственно, вот и та самая нерешённая задача, о которой сказано в заголовке. Исследование поведения последовательности минимальных сумм цифр кратных чисел (обозначим эту функцию minmds(n) – minimal multiples’ digits sum) представляет собой открытую проблему. Мы с моим учителем, а ныне и коллегой, Сергеем Тихоновичем Кузнецовым, оптимизировали алгоритм поиска и сейчас имеются данные по 56000 чисел.
По этим данным можно построить следующую таблицу:
k |
Количество чисел в диапазоне 1-56000 с minmds(n)=k |
Минимальное n, такое, что minmds(n)=k |
1 |
65 |
1 |
2 |
15544 |
7 |
3 |
26521 |
3 |
4 |
3889 |
79 |
5 |
939 |
41 |
6 |
2485 |
33 |
7 |
143 |
239 |
8 |
23 |
2629 |
9 |
5581 |
9 |
10 |
21 |
2981 |
11 |
2 |
21649 |
12 |
89 |
813 |
13 |
0 |
? |
14 |
1 |
51139 |
15 |
4 |
13947 |
16 |
0 |
? |
17 |
0 |
? |
18 |
632 |
99 |
… |
0 |
? |
27 |
56 |
999 |
… |
0 |
? |
36 |
5 |
9999 |
Сразу возникает очевидный и интересный вопрос: для какого числа x minmds(x)=13? (И существует ли такое число вообще?) И как по числу определить его minmds, по возможности наименее прибегая к перебору? Существует ли не кратное трём число с minmds, равным 9? (На этот можно ответить при внимательном изучении прилагаемого файла 😉
Таких вопросов можно набрать множество, и решать их будет одинаково интересно как математику-профессионалу, так и учащемуся при написании работы в Малой академии наук.
Признаки делимости натуральных чисел | Образовательная социальная сеть
Государственное бюджетное общеобразовательное учреждение
ГБОУ гимназия № 11
Проект по математике
«Признаки делимости чисел»
Работу подготовила Нуруллаева Алина
6 «А» класс
Руководитель Гайлит И. В., учитель математики и информатики
Санкт-Петербург
2019
Тема проекта: «Признаки делимости натуральных чисел»
Гипотеза:
При решении задач на делимость многозначных чисел знание и применение новых признаков делимости значительно сократит время, затрачиваемое на вычисления. Признаки делимости способствуют эффективному и рациональному решению задач.
Цель:
Повторить, углубить и расширить знания по теме «Признаки делимости натуральных чисел» и научиться применять их на практике.
Задачи:
- Изучить историю возникновения признаков делимости.
- Выяснить:
- В каких сферах деятельности человека используется делимость чисел?
- Для чего нужно знать признаки делимости?
- Существуют ли другие признаки делимости отличные от тех, которые изучались на уроке?
- Есть ли универсальный признак делимости для любого числа?
- Можно ли сформулировать признак делимости на любое натуральное число?
- Поделиться новыми знаниями с одноклассниками, создать буклет-справочник «Признаки делимости натуральных чисел»
Основополагающий вопрос: Как научиться быстро и красиво вычислять?
Актуальность проблемы
При решении некоторых заданий мы столкнулись с проблемой делимости многозначных чисел. Не всегда одно натуральное число делится на другое натуральное число без остатка. Деля натуральное число, мы получаем остаток, допускаем ошибки, тем самым теряем время. Поиск делителя многозначного числа занимает много времени по двум причинам: во-первых, действие деление затратно по времени само по себе; во-вторых, делители подбираются наугад.
Не всегда одно натуральное число делится на другое натуральное число без остатка. Деля натуральное число, мы получаем остаток, допускаем ошибки, тем самым теряем время. Поиск делителя многозначного числа занимает много времени по двум причинам: во-первых, действие деление затратно по времени само по себе; во-вторых, делители подбираются наугад.
Возникает необходимость, не выполняя деление установить, делится ли одно натуральное число на другое. Вопрос: существуют ли другие признаки делимости, отличные от изученных нами на уроках? При изучении на уроках математики темы: «Признаки делимости натуральных чисел на 2, 3, 5, 9, 10» у меня возник интерес к исследованию чисел на делимость.
Мы изучаем признаки делимости в школе. Но зачем нам нужны эти признаки делимости. Если нам надо узнать делится ли одно число на другое, мы сразу начинаем делить в столбик. Но если это число большое, мы будем все это высчитывать, а потом выясним, что первое число не делится на второе?
С помощью признаков делимости, можно узнать это гораздо легче.
Делимость – это способность одного числа делиться на другое без остатка. Делитель – это число, которое делит данное число без остатка.
Признак делимости — алгоритм, позволяющий сравнительно быстро определить, является ли число кратным заранее заданному.
Признаки делимости – это правило, по которому, не производя никаких вычислений, с лёгкостью можно определить делится ли число «А» на число «Б».
Признаки делимости на 2, 3, 5, 9, 10, были известны с давних времен. Признак делимости на 2 знали древние египтяне за 2 тысячи лет до нашей эры, а признаки делимости на 2, 3, 5 были обстоятельно изложены итальянским математиком Леонардо Фибоначчи (1170-1228г.г.).
Большой вклад в изучение признаков делимости чисел внес Б. Паскаль — французский религиозный мыслитель, математик и физик, один из величайших умов 17 столетия. Родился в Клермон-Ферране (провинция Овернь) 19 июня 1623. Юный Блез очень рано проявил выдающиеся математические способности, научившись считать раньше, чем читать. Свой первый математический трактат «Опыт теории конических сечений» он написал в 24 года. Примерно в это же время он сконструировал механическую суммирующую машину, прообраз арифмометра. Работы Паскаля в области точных наук, или ранний период его творчества относится к 1640-1650 году. За эти 10 лет разносторонний ученый сделал очень много: он нашел алгоритм для нахождения признаков делимости любого целого числа на любое другое целое число, сформулировал способ вычисления биноминальных коэффициентов, изложил ряд основных положений элементарной теории вероятности, впервые точно определил и применил для доказательства метод математической индукции.
Свой первый математический трактат «Опыт теории конических сечений» он написал в 24 года. Примерно в это же время он сконструировал механическую суммирующую машину, прообраз арифмометра. Работы Паскаля в области точных наук, или ранний период его творчества относится к 1640-1650 году. За эти 10 лет разносторонний ученый сделал очень много: он нашел алгоритм для нахождения признаков делимости любого целого числа на любое другое целое число, сформулировал способ вычисления биноминальных коэффициентов, изложил ряд основных положений элементарной теории вероятности, впервые точно определил и применил для доказательства метод математической индукции.
Признак делимости Паскаля.
Натуральное число а разделится на другое натуральное число b только в том случае, если сумма произведений цифр числа а на соответствующие остатки, получаемые при делении разрядных единиц на число b, делится на это число.
В школе мы изучаем самые простые признаки делимости: на 2, 3, 4, 5, 9, 10, 25, 100.
Признаки делимости, изучаемые в школе
Если число оканчивается на 0, 2, 4, 6 или 8, то оно точно делится на 2.
- Число 52738 делится на 2, так как последняя цифра 8 делится на 2
- Число 8203 не делится на 2, так как последняя цифра 3 не делится на 2
Если сумма цифр делится на 3, то и само число кратно на 3.
- Число 52632 делится на 3, так как сумма цифр 5+2+6+3+2=18 делится на 3
- Число 106499 не делится на 3, так как сумма цифр 1+0+6+4+9+9=29 не делится на 3
Если две последние цифры числа нули или образуют число, которое делится на 4, то и само число тоже делится на 4.
- Число 76412 делится на 4, так как число 12, составленное из последних двух цифр числа, делится на 4
- Число 123802 не делится на 4, так как число 02 не делится на 4
Если число оканчивается на 0 или 5, оно делится на 5.
- Число 240 делится на 5, так как последняя цифра 0
- Число 1205 делится на 5 , так как последняя цифра 5
- Число 55434 не делится на 5, так как последняя цифра 4
Если сумма цифр делится на 9, то и кратно 9.
- Число 52632 делится на 9, так как сумма 5+2+6+3+2=18, 18 делится на 9
- Число 17835 не делится на 9, так как сумма 1+7+8+3+5=24 не делится на 9
Признак делимости на 10 очень простой. Если число оканчивается на 0, он кратно 10. Если оно оканчивается на два нуля, он кратно 100, на 3 нуля 1000 и т. д.
- Число 8200 делится на 10 , так как последняя цифра 0
- Число 537004 не делится на 10, так как последняя цифра 4
Признаки делимости, не изучаемые в школе
Если число четное и делится на 3, оно точно делится на 6.
- Число 1161 не делится на 6, так как оно не делится на 2
- Число 126954 делится на 6, так как оно делится на 2 и на 3
Число делится на 7, если из числа десятков вычесть удвоенное число единиц и получим число, кратное 7.
- Число 259 делится на 7, потому 25-(2*9) =7, а 7 делится на 7.
- Число 549 не делится на 7, потому что 54-(2*9)=36, 36 не делится на 7.
Число делится на 8, если последние 3 цифры нули или образуют число, которое делится на 8.
- Число 125000 делится на 8, так как на конце три нуля
- Число 65728 делится на 8, так как число 728, составленное из последних трех цифр числа, делится на 8
- Число 1204 не делится на 8, так как число 204, составленное из последних трех цифр числа, не делится на 8
Число делится на 11, если сумма цифр, стоящих на нечетных местах равна сумме цифр, стоящих на четных местах, либо отличается от неё на число, кратное 11.
- Число 103785 делится на 11, так как сумма цифр, занимающих нечетные места, 1+3+8=12 равна сумме цифр, занимающих четные места, 0+7+5=12.
- Число 3298 не делится на 11, так как 3+9=12, 2+8=10. Суммы цифр не равны, а разность сумм цифр 12-10=2 на 11 не делится
Число делится на 12, если оно одновременно делится и на 3, и на 4 без остатка
- Число 4250892 делится на 12, т.к. оно делится на 3 (4+2+5+0+8+9+2=30; 30:3=10) и на 4 (92:4=23)
Число делится на 13, если число десятков, сложенное с учетверенным числом единиц кратно 13
- Число 104 делится т.
 к. 10+4*3=36; 36:13=3
к. 10+4*3=36; 36:13=3
Число делится на 14, если оно одновременно делится и на 2, и на 7
- Число 765408 делится на 14, т.к. оно четное и делится на 7
Число делится на 15, если оно одновременно делится и на 3, и на 5
- Число 530505 делится на 15, т.к. оно делится и на 3, и на 5
Число делится на 16, если последние четыре цифры числа нули или образуют число, которое делится на 16
- Число 140264720048 делится на 16, т.к. последние 4 цифры 0048:16=3
Число делится на 17, если число десятков, сложенное с увеличенным в 12 раз числом единиц, кратно 17.
- Число 29053 делится на 17
- 29053→2905+36=2941→294+12=306→30+72=102→10+24=34; 34:17=2
Число делится на 18, если число четное и сумма его цифр делится на 9
- Число 840312 делится на 18, т.к. 8+4+0+3+1+2=18; 18:9=2
Число делится на 19 тогда, когда число его десятков в сумме с удвоенным числом единиц кратно 19.
- Число 551 делится на 19, так как 55+1*2=57 делится на 19
- Число 6003 не делится на 19, так как 600+3*2=606 не делится на 19
Число делится на 20, если запись числа оканчивается на 0 и предпоследняя цифра четная
- Число 6435760 делится на 20
Число делится на 21 в том и только в том случае, если оно делится одновременно и на 3, и на 7.
- 231 делится на 21, т.к. число делится и на 3, и на 7.
Число делится на 22 в том и только в том случае, если оно делится одновременно и на 2, и на 11.
- 352 делится на 22, т.к. число делится и на 2, и на 11.
число делится на 23 тогда и только тогда, когда число сотен, сложенное с утроенным числом, образованным двумя последними цифрами, делится на 23.
число делится на 23 тогда и только тогда, когда число десятков, сложенное с семикратным числом единиц, делится на 23.
Число делится на 24 в том и только в том случае, если оно делится одновременно и на 3, и на 8.
- 8136 делится на 24, т.к. число делится и на 3, и на 8.
Число делится на 25, если две последние цифры в числе равны 0 или число, образованное последними двумя цифрами делится на 25.
- Число 7150 делится на 25, так как последние две цифры образуют число 50, делящееся на 25
- Число 1292 не делится на 25, так как 92 не делится на 25
Так же есть числа, которые делятся только на себя и на 1. Это только нечетные числа и 2. Такие числа называются простыми.
Это только нечетные числа и 2. Такие числа называются простыми.
Все перечисленные признаки делимости натуральных чисел можно разделить на 4 группы:
1 группа — когда делимость чисел определяется по последней(им) цифрой (ми)- это признаки делимости на 2, на 5, на разрядную единицу, на 4, на 8, на 25, на 50.
2 группа – когда делимость чисел определяется по сумме цифр числа — это признаки делимости на 3, на 9, на7, на 37, на 11 (1 признак).
3 группа – когда делимость чисел определяется после выполнения каких-то действий над цифрами числа — это признаки делимости на 7, на 11(1 признак), на 13, на 19.
4 группа – когда для определения делимости числа используются другие признаки делимости — это признаки делимости на 6, на 15, на 12, на14.
Практическая значимость
Знание и использование выше перечисленных признаков делимости натуральных чисел значительно упрощает многие вычисления, этим самым, экономя время; исключая вычислительные ошибки, которые можно сделать при выполнении действия деления.
Собранный мной материал можно использовать на факультативных занятиях, на занятиях математического кружка. Учителя математики могут использовать его при изучении данной темы. Также рекомендую ознакомиться со своей работой тем сверстникам, которые хотят знать о математике больше, чем рядовой школьник. В результате выполнения данной работы у меня расширились знания по математике. Я узнала, что кроме известных мне признаков на 2, 3, 5, 9 и 10 существуют еще признаки делимости на 4, 6, 7, 8, 11, 12, 13, 14, 15, 19 и 25. Поняла, что в некоторых случаях без признаков делимости просто невозможно обойтись.
Познакомившись с признаками делимости чисел, считаю, что полученные знания смогу использовать в своей учебной деятельности, самостоятельно применить тот или иной признак к определенной задаче, применить изученные признаки в реальной ситуации.
Считаю, что применение признаков делимости чисел в изучении математики является эффективным. Знание их значительно ускоряет решение многих заданий. Предложенный материал «Признаки делимости чисел» можно использовать как на уроках математики, так и во внеклассных занятиях учащимися 5-9-х классов. Учителям — с целью подготовки учащихся к решению олимпиадных задач, интеллектуальным конкурсам «Марафон знаний», региональному конкурсу «Кенгуру».
Предложенный материал «Признаки делимости чисел» можно использовать как на уроках математики, так и во внеклассных занятиях учащимися 5-9-х классов. Учителям — с целью подготовки учащихся к решению олимпиадных задач, интеллектуальным конкурсам «Марафон знаний», региональному конкурсу «Кенгуру».
В дальнейшем предполагаю продолжить работу над изучением признаков делимости чисел
Для решения этих проблем ставлю следующие задачи:
· более глубокое изучение литературы по теме «признаки делимости чисел
· подбор задач, решаемых с помощью признаков делимости.
Я изложила эту работу доступным языком, чтобы каждый ученик, которому это интересно, мог взять мой реферат и самостоятельно получить дополнительные знания по признакам делимости чисел.
- Математика. Школьная энциклопедия. С.М.Никольский.- М: Большая Российская энциклопедия: Дрофа 1997-527с.
- Н.Я. Виленкин, В.И. Жохов, Математика 6 класс, Учебник для образовательных учреждений. – М.: Мнемозина, 2013 г.

- Степанов В.Г.. Основы исследовательской деятельности школьника. — Псков, 2004. С.34-38
- Энциклопедический словарь юного математика.А.П.Савин-М:Педагогика,1985-352с.
- Е.Е. Тульчинская, Тесты 5-6 классы: пособие для учащихся общеобразовательных учреждений. -М.: Мнемозина, 2008 г.
- Воробьев Н. Н. Популярные лекции по математике.– М.: Наука, 1988.– 94 с.
- Булавко И. Делимость чисел.– Квант для младших школьников, №9, 1974.
- Сергеев И.Н. Примени математику. — М.:1989.
Признаки делимости чисел — правила и примеры решений » Kupuk.net
Для быстрого решения задач и примеров по математике необходимо знать признаки делимости натуральных чисел. Это правила, которые помогают быстро понять, кратно ли большое число заданному. Существуют признаки делимости простых чисел — 2, 3, 5, 7, 11 и составных, которыми являются 6, 12. Одни признаки делимости совсем простые, другие несколько сложнее. Эти свойства с примерами будут полезны и взрослым, уже подзабывшим курс математики, и школьникам.
Дроби с кратными от 1 до 5
На единицу делится любое целое число.
Самым простым правилом является делимость на число два: если натуральное число оканчивается на четную цифру, то оно кратно двум. Если в конце стоит нечетная цифра, какими являются 1, 3, 5, 7, 9, то число на два не делится. То есть чтобы поделить многозначное число на два, в конце числа должна стоять одна из таких цифр: 2, 4, 6, 8, 0.
Пример: 6942 является четным, поскольку в конце четная цифра, поэтому оно кратно двум; число 19678456 также кратно двум, так как в конце стоит четная цифра 6. А вот число 6796345 не делится на 2, поскольку оно нечетное. Также нельзя получить ответ без остатка с такой суммы, как 398573 по этой же причине.
Деление на три имеет свое правило: нужно сложить все цифры, а затем проверить, делится ли сумма на три. Если да, то и данность разделится на три. Если нет, значит, не делится.
Например, возьмем 3576. Складываем 3+5+7+6=21. Полученную сумму 21 делим на три, получается семь. Значит, оно кратно трем без остатка. Проведем разложение шестизначного номера 353388. Оно раскладывается на три, поскольку сумма равна тридцати (3+5+3+3+8+8=30). Еще возьмем, например, 5819. Складываем: 5+8+1+9=23, полученная сумма не делится на три без остатка. Также и 2947 невозможно разделить, поскольку остаются тройки.
Складываем 3+5+7+6=21. Полученную сумму 21 делим на три, получается семь. Значит, оно кратно трем без остатка. Проведем разложение шестизначного номера 353388. Оно раскладывается на три, поскольку сумма равна тридцати (3+5+3+3+8+8=30). Еще возьмем, например, 5819. Складываем: 5+8+1+9=23, полученная сумма не делится на три без остатка. Также и 2947 невозможно разделить, поскольку остаются тройки.
Правило делимости на четыре звучит так: если две последние цифры номера кратны четырем либо оно в конце имеет два нуля, то отношение получится без остатка.
Например, 1000 делится на четыре, поскольку в конце 00. Делится также и 3824, так как в конце 24, которое кратно этому делителю. А вот 2986 не делится на четыре, так как 86 не кратно четырем, и 29087 тоже не может остаться целым, поскольку с 87 нельзя произвести расчета. Еще пример: четырехзначный номер 2648 можно разделить на этот делитель, так как 48:4=12.
Довольно простым правилом является делимость на пять. Частное получается без остатка, если в конце заданного числа стоит 5 или 0. Если оно не заканчивается одной из этих цифр, то при делении возникнет остаток.
Частное получается без остатка, если в конце заданного числа стоит 5 или 0. Если оно не заканчивается одной из этих цифр, то при делении возникнет остаток.
Проверим правило, взяв пятизначное число 45765. Оно кратно пяти без остатка, так как заканчивается на пять. Также 45030 можно разделить, поскольку в конце ноль. А вот четырехзначное число 4321 без остатка не делится.
Свойства делителей от 6 до 10
Составное шесть состоит из произведения двух последовательных чисел — 2 и 3. Теория кратности такова: число 6 составное, поэтому необходимо, чтобы одновременно действовали два правила признака делимости. Нужно, чтобы число было кратно и двум, и трем сразу.
Например, проверке подвергаются трехзначные числа 756 и 168. Они четные, поэтому делятся на два. Теперь нужно сложить 7+5+6=18, становится ясно, что сумма 18 делится на 3. Число 165 при разложении на однозначные цифры с последующим сложением превращается в 12, которое может разделиться на три. Оба числа кратны одновременно 2 и 3, значит, кратны шести.
Оба числа кратны одновременно 2 и 3, значит, кратны шести.
Определение отношения с делимостью на семь довольно сложное: число делится, если при удвоении последней цифры и полученной разности результат кратен семи или равен нулю.
Пример, трехзначное число 679 кратно 7. (Калькулятор выдал 97). Узнать можно так:
- 2*9=18.
- 67−18=49.
- 49:7=7.
Из примера видно, что удвоилось последнее число, затем получена разность, после чего — отношение-доказательство.
В классе было дано задание доказать, что число 497 делится на семь. Порядок решения:
- 2*7=14.
- 49−14=35.
- 35:7=5.
Найти признак делимости на 8 очень легко. Формулировка закона такова: последние три цифры должны быть 000 или 888. Легко можно произвести вычисления с 789000: оно делится на 8, так как оканчивается на 000. Множество 289673888 тоже кратно 8, поскольку заканчивается на 888.
Свойство при делителе 9 похоже на правило с 3. Формула делимости на 9 довольно простая: сумма цифр должна быть кратна девяти. Маленький пример: из 46980 возможно получить целое, 4+6+9+8+0= 27. Получившаяся сумма кратна 9. Еще одно задание: найти отношение с использованием признака кратности 9 при делимом 29565. Рассуждение: 2+9+5+6+5=27. Полученная сумма может разделиться на девять.
Формула делимости на 9 довольно простая: сумма цифр должна быть кратна девяти. Маленький пример: из 46980 возможно получить целое, 4+6+9+8+0= 27. Получившаяся сумма кратна 9. Еще одно задание: найти отношение с использованием признака кратности 9 при делимом 29565. Рассуждение: 2+9+5+6+5=27. Полученная сумма может разделиться на девять.
Разрядные единицы
Любое число можно разделить на разрядную единицу, если у него одинаковое или большее количество нулей в конце. Например, 5790 можно поделить на 10, так как в конце один ноль. Еще примеры:
- 4958700:100=49587.
- 374000:1000=374.
- 5781000:100=5781.
- 97430:10=9743.
Невозможно разделить 128700 на 1000, так как у разрядной единицы нулей больше, а также 237480 на 100 и другие подобные.
Делители от 11 и выше
Чтобы получилось деление на 11, необходимо сложить четные по счету номера, а затем нечетные, затем произвести вычитание. Если в процессе вычислений получился ноль или одиннадцать, то остатка не будет.
Если в процессе вычислений получился ноль или одиннадцать, то остатка не будет.
Онлайн-задание с ответом: 7535, 74019 и 50486.
Нечетные в первом случае 7 и 3, четные 5 и 5. Считаем:
- 7+3=10,
- 5+5=10,
- 10−10=0.
Четные во втором примере 4 и 1, нечетные — 7, 0, 9. Вычисление:
- 7+0+9=16.
- 4+1=5.
- 16−5=11.
В третьем примере нечетные 5, 4, 6, четные 0 и 8. Решаем:
- 5+4+6=15.
- 0+8=8.
- 15−8=7.
Ответ: в первом и втором примере десятых, сотых, тысячных и так далее не останется, а в третьем — останется.
Чтобы разделить на двузначный делитель 12, нужно произвести общие вычисления, характерные для делителей 3 и 4 одновременно. К примеру, 900 и 3432. Сначала следует разложить на слагаемые 9+0+0=9, значит, можно поделить на 3. В конце стоит два нуля — можно делить на 4. Проверка: 900:12=75. Первая часть задания решена, теперь делаем вторую: 3+4+3+2=12, 12:3=4. Таким образом проверяется кратность трем. Теперь четырем: в конце стоит 32, что указывает на кратность 4, значит, остатка не будет. Таким образом, оба примера кратны 12.
Первая часть задания решена, теперь делаем вторую: 3+4+3+2=12, 12:3=4. Таким образом проверяется кратность трем. Теперь четырем: в конце стоит 32, что указывает на кратность 4, значит, остатка не будет. Таким образом, оба примера кратны 12.
Дробь, кратная 13, разрешится без остатка, если последнюю цифру умножить на 4, после чего сложить число и последнюю цифру. Если полученная сумма кратна 13 или равно 0, то деление получится.
Например, 6942:
- 2*4=8.
- 694+8=702.
- 702:13=54.
Еще пример — 754:
- 4*4=16.
- 75+16=91.
- 91:13=7.
Признак делимости на составное число
Если делитель составной, необходимо его разложить на простые множители, которые не имеют общих кратных, кроме единицы. Пример: 15 раскладывается на 3 и 5. Любое неизвестное кратно 15, если одновременно кратно трем и пяти.
Также и с другим составным: 18 раскладывается на 2 и 9. Нельзя брать множители 3 и 6, так как они не простые, у них общее кратное 3. Например, 456 кратно трем, проверка: 4+5+6=15, также кратно 6 (при разложении на 2 и 3). Однако калькулятор выводит запятую. Если взять множители 2 и 9, будет видно, что двум — кратно, а девяти — нет, ведь сумма равна 15, которая не кратна 9.
Таблица кратных от 2 до 10
Для удобства школьникам и их родителям предлагается таблица признаков делимости чисел от 2 до 10. Она наглядно и кратко демонстрирует всю вышеизложенную теоретическую часть:
| Делимость на: | Признак числа: |
| 2 | Оканчивается четной цифрой: 0, 2, 4,6, 8 |
| 3 | Сумма цифр, их которой оно состоит, делится на 3 |
| 4 | Две последние цифры делятся на 4 |
| 5 | Окончание на 5 или 0 |
| 6 | Одновременная кратность 2 и 3 |
| 8 | Три последние цифры кратны 8 |
| 9 | Сумма цифр кратна 3 |
| 10 | Окончание равно нулю |
Вышеизложенное доказывает, что к любому натуральному числу можно подобрать простой или составной признак кратности. На практике выходит, что чем больше число, тем сложнее его признак. Часто не хочется тратить время на проверку делимости, ведь за этот промежуток уже можно выполнить само деление. Поэтому любой школьник может воспользоваться простейшими признаками делимости.
На практике выходит, что чем больше число, тем сложнее его признак. Часто не хочется тратить время на проверку делимости, ведь за этот промежуток уже можно выполнить само деление. Поэтому любой школьник может воспользоваться простейшими признаками делимости.
Признаки делимости чисел
Признаки делимости.
Подготовил ученик 6 б класса МБОУ гимназии №3
Воробьёв Александр
Руководитель: Ефремова Ольга Николаевна.
Математика – царица наук, Арифметика – царица математике!
Деление чисел издавна считалось задачей, куда более трудной, чем умножение. Поэтому делить люди научились гораздо позже, чем умножать. Учёные – математики долго занимались поиском наиболее простого способа деления чисел. Один из них – деление «уголком», которым мы пользуемся сейчас, впервые появился в Европе в 10 веке и получил название «золотого деления». На деление уголком часто затрачивается много времени, а ведь возникают ситуации, когда нужно быстро определить, делится одно число на другое или нет.
Актуальность исследования
Признаки делимости всегда интересовали ученых разных времен и народов. При изучении на уроках математики темы «Признаки делимости чисел на 2, 3, 5, 9, 10» у меня возник интерес к исследованию чисел на делимость. Было предположено, что если можно определить делимость чисел на эти числа, то должны быть признаки, по которым можно определить делимость натуральных чисел и на другие числа. В некоторых случаях, для того, чтобы узнать делится ли какое-либо натуральное число a на натуральное число b без остатка, не обязательно делить данные числа. Достаточно знать некоторые признаки делимости.
Гипотеза
Если существуют признаки делимости натуральных чисел на 2, 3, 5, 9 и 10, то существуют и другие признаки, по которым можно определить делимость натуральных чисел.
Цель исследования
Дополнить уже известные признаки делимости натуральных чисел нацело, изучаемые в школе и систематизировать эти признаки делимости.
Для достижения этой цели необходимо решить следующие задачи : Самостоятельно исследовать делимость чисел.
Изучить дополнительную литературу с целью ознакомления с другими признаками делимости.
Объединить и обобщить признаки из разных источников.
Сделать вывод.
Объект исследования – делимость натуральных чисел . Предмет исследования – признаки делимости. Методы исследования – сбор материала, обработка данных, сравнение, анализ, обобщение .
Содержание
1. Первые, кто занимался признаками делимости.
2. Леонардо Пизанский .
3. Историческая справка.
4. Блэз Паскаль .
5. Закон Паскаля .
6. Признак делимости .
7. Признаки делимости от 2 до 101.
Из истории математики
Первые люди, занимающиеся признаками деления
Леонардо Пизанский
Леонардо Фибоначчи (1170 – 1228) – это один из крупнейших Европейских средневековых математиков первой величины.
Он открыл признак делимости на, 3 и 5
2
Историческая справка
Древние египтяне за 2 тысячи лет до нашей эры уже знали признак делимости на 2.
Блез Паскаль.
Признак Паскаля — «универсальный признак делимости»:
Блез Паскаль(1623—1662) – один из самых знаменитых людей в истории человечества. Вошел в историю как выдающийся математик, физик, философ и писатель.
Натуральное число а разделится на другое натуральное число b только в том случае, если сумма произведений цифр числа а на соответствующие остатки, получаемые при делении разрядных единиц на число b, делится на это число.
Например: число 2814 делится на 7, так как 2·6+8·2+1·3+4=35 делится на 7 (Здесь 6-остаток отделения 1000 на 7, 2- остаток от деления 100 на 7 и 3- остаток от деления 10 на 7).
Признак делимости
Признак делимости — алгоритм, позволяющий сравнительно быстро определить, является ли число кратным заранее заданному.
Все рассмотренные мною в данной работе признаки делимости натуральных чисел можно разделить на 4 группы:
Делимость чисел определяется после выполнения каких-то действий над цифрами этого числа
Для определения делимости числа используются другие признаки делимости
Делимость чисел определяется по последней (им) цифре (ам)
Делимость чисел определяется по сумме цифр числа
Делимость чисел определяется
по последней (им)
цифре (ам)
Признак делимости на 2
Число делится на 2 тогда и только тогда, когда его последняя цифра делится на 2, то есть является чётной.
0,2,4,6,8 – чётные цифры.
1,3,5,7,9 – нечётные цифры .
8654 делится на 2, так как последняя цифра 4
Признак делимости на 4
Число делится на 4, когда две последние цифры нули или составляют число, делящееся на 4.
548 делится на 4,так как две последние цифры делятся на 4
Признак делимости на 5
Число делится на 5 тогда и только тогда, когда оно оканчивается на 0 или на 5.
155 делится на 5, так как последняя цифра 5
Признак делимости на 8
Число делится на 8, когда три последние цифры нули или составляют число, делящееся на 8.
111 120 делится на 8, так как три последние цифры 120
Признак делимости на 10
Число делится на 10 тогда и только тогда, когда оно оканчивается на ноль.
390 делится на 10, так как последняя цифра 0
Признак делимости на 20
Другая формулировка: число делится на 20 тогда и только тогда, когда последняя цифра числа — 0, а предпоследняя — чётная.
0,2,4,6,8 – чётные цифры.
1,3,5,7,9 – нечётные цифры
760 делится на 20, так как последняя цифра 0, а предпоследняя чётная
Признак делимости на 25
Число делится на 25 тогда и только тогда, когда две его последние цифры составляют число, которое делится на 25.
6375 делится на 25, так как две последние цифры делятся на 25
Признак делимости на 50
Число делится на 50 тогда и только тогда, когда число заканчивается 00 или 50
87550 делится на 50, так как число заканчивается на 50
Делимость чисел определяется по сумме цифр числа
Признак делимости на 3
Число делится на 3, когда сумма его цифр делится на 3.
423 делится на 3, так как сумма всех цифр делится на 3
Признак делимости на 9
Число делится на 9, когда сумма его цифр делится на 9.
486 делится на 9, так как сумма всех цифр делится на 9
9 163 627 делится на 11, так как ( 9 + 6 + 6 + 7 ) – ( 1+ 3 + 2 ) = 22 делится на 11
Признак делимости на 11
Число делится на 11 тогда и только тогда, когда модуль разности между суммой цифр, занимающих нечётные позиции, и суммой цифр, занимающих чётные места, делится на 11.
Делимость чисел определяется после выполнения каких-то действий над цифрами этого числа
Признак делимости на 7
Число делится на 7 тогда, когда утроенное число десятков, сложенное с числом единиц, делится на 7 .
154 делится на 7, так как на 7 делится 15 х 3 + 4 =49
Признак делимости на 13
Число делится на 13, когда сумма числа десятков с учетверенным числом единиц делится на 13.
104 делится на 13, так как 10+(4·4)=10+16=26 делится на 13
Признак делимости на 17
Число делится на 17 тогда:- когда модуль разности числа десятков и пятикратного числа единиц делится на 17.
221 делится на 17, так как 22 — 1 х 5 = 17 делится на 17 .
Признак делимости на 19
Число делится на 19 тогда и только тогда, когда число десятков, сложенное с удвоенным числом единиц, делится на 19.
646 делится на 19, так как 64 + 2 х 6 = 76 делится на 19
Признак делимости на 23
Число делится на 23 тогда и только тогда, когда число сотен, сложенное с утроенным числом, образованным двумя последними цифрами, делится на 23.
28842 делится на 23, так как 288 + 3 х 42 = 414 делится на 23
Признак делимости на 27
Число делится на 27 тогда и только тогда, когда при разбивании числа на группы по три цифры (начиная с единиц) сумма этих групп кратна 27.
142857 делится на 27, так как 142+857 = 999 делится на 27
Признак делимости на 29
Число делится на 29 тогда и только тогда, когда число десятков, сложенное с утроенным числом единиц, делится на 29.
261 делится на 29, так как 26 + 3 х 1 = 29 делится на 29 .
Признак делимости на 31
Число делится на 31 тогда и только тогда, когда модуль разности числа десятков и утроенного числа единиц делится на 31.
217 делится на 31, так как 21 – 3 х 7 = 0 делится на 31 .
Признак делимости на 37
Число делится на 37 тогда и только тогда, когда при разбивании числа на группы по три цифры (начиная с единиц) сумма этих групп кратна 37.
259185 делится на 37, так как 259 + 185 = 444 делится на 37
Признак делимости на 41
Число делится на 41 тогда и только тогда, когда модуль разности числа десятков и четырёхкратного числа единиц делится на 41.
369 делится на 41, так как 36 – 4 х 9 = 0 делится на 41.
Признак делимости на 59
Число делится на 59 тогда и только тогда, когда число десятков, сложенное с числом единиц, умноженное на 6, делится на 59.
767 делится на 59, так как 76 + 6 х 7 = 118 делятся на 59
Признак делимости на 79
Число делится на 79 тогда и только тогда, когда число десятков, сложенное с числом единиц, умноженное на 8, делится на 79.
711 делится на 79, так как 71 + 8 х 1 = 79 делятся на 79 .
Признак делимости на 99
Число делится на 99 тогда и только тогда, когда на 99 делится сумма чисел, образующих группы по две цифры (начиная с единиц).
12573 делится на 99, так как 1 + 25 + 73 = 99 делится на 99
Признак делимости на 101
Число делится на 101 тогда и только тогда, когда модуль алгебраической суммы чисел, образующих нечётные группы по две цифры (начиная с единиц), взятых со знаком «+», и чётных со знаком «-» делится на 101.
590547 делится на 101, так как 59 – 5 + 47 = 101 делится на 101
Для определения делимости числа используются другие признаки делимости
Признак делимости на 6
Число делится на 6 тогда, когда оно делится и на 2, и на 3.
126 делится 2, так как число делится и на 2, и на 3
Признак делимости на 12
Число делится на 12 тогда и только тогда, когда оно делится на 3 и на 4.
2304 делится на 12, так как число делится и на 3, и на 4
Признак делимости на 30
Число делится на 30 тогда и только тогда, когда оно заканчивается на 0 и сумма всех цифр делится на 3.
510 делится на 30 , так как число заканчивается 0 и делится на 3
Делимость чисел: делитель, признаки, примеры
- Делитель числа
- Признаки делимости
- Примеры
Делитель числа
Например, множество всех целых делителей числа 12:
$$ A = \{n | 12 ⋮ n,n \in \Bbb Z\} $$
$$ A = \{ \pm 1; \pm 2; \pm 3; \pm 4; \pm 6; \pm 12 \} $$
Например:
Число 105 делится на 3 и на 5. Значит, оно также делится на 15, т.е. 105 ⋮ 15
Число 231 делится на 7 и на 11. Значит, оно также делится на 77, т.е. 231 ⋮ 77
Признаки делимости
Чтобы определить делимость без самого деления, существует набор методов «экспресс-анализа», которые называют признаками делимости.
Двузначные грани числа – разбиение числа на группы по 2 цифры, считая справа налево. Например: 1|23|45|67.
Трёхзначные грани числа – разбиение числа на группы по 3 цифры, считая справа налево. Например: 1|234|567.
Знакопеременная сумма граней – каждая грань входит со знаком +/-, последняя с +.
Делитель | Признак делимости | Пример | |
2 | Число заканчивается чётной цифрой {0;2;4;6;8} | 1028 | |
3 | Сумма цифр числа делится на 3 | 1029 1+2+9 = 12 | |
4 | Число, составленное из двух последних цифр, делится на 4 | 1028 28:4 = 7 | |
5 | Число заканчивается на 0 или 5 | 1025 | |
7 | Число, полученное вычитанием удвоенной последней цифры из исходного числа с отброшенной последней цифрой, делится на 7 | 1491 149-2 = 147 147:7 = 21 | |
Знакопеременная сумма 3-значных граней числа делится на 7 | 1|491 -1+491 = 490 490:7 = 70 | ||
8 | Число, составленное из трёх последних цифр, делится на 8 | 1736 736:8 = 92 | |
9 | Сумма цифр числа делится на 9 | 1026 1+2+6 = 9 | |
10 | Число заканчивается на 0 | 1030 | |
11 | Сумма цифр на нечётных позициях и сумма цифр на нечётных позициях либо равны, либо отличаются на число, кратное 11 | 1408 (1+0)-(4+8) = -11 | |
Знакопеременная сумма цифр делится на 11 или равна 0 | -1+4+8 = 11 | ||
13 | Число, полученное добавлением учетверенной последней цифры к исходному числу с отброшенной последней цифрой, делится на 13 | 1131 113+4 $\cdot$ 1 = 117 11+4 $\cdot$ 7 = 39 39:13 = 3 | |
Знакопеременная сумма 3-значных граней числа делится на 13 | 1|131 -1+131 = 130 130:13 = 10 | ||
17 | Число, полученное добавлением последней цифры, умноженной на 12, к исходному числу с отброшенной последней цифрой, делится на 17 | 1479 147+12 $\cdot$ 9 = 255 25+12 $\cdot$ 5 = 85 85:17 = 5 | |
Число, полученное вычитанием последней цифры, умноженной на 5, к исходному числу с отброшенной последней цифрой, делится на 17 | 1479 147-5 $\cdot$ 9 = 102 10-5 $\cdot$ 2 = 0 | ||
19 | Число, полученное добавлением удвоенной последней цифры из исходного числа с отброшенной последней цифрой, делится на 19 | 1273 127+2 $\cdot$ 3 = 133 13+2 $\cdot$ 3 = 19 19:19 = 1 | |
23 | Число, полученное добавлением утроенного числа из двух последних цифр с числом сотен, делится на 23. | n последних цифр числа – нули | 21000 делится на 1000 |
Примеры
Пример 1. Число 15464*543 делится на 3. Какие цифры могут стоять на месте звёздочки?
Обозначим цифру на месте звёздочки x. Сумма всех цифр:
1+5+4+6+4+x+5+4+3 = 32+x
Сумма должна делиться на 3:
32+x
33
36
39
Ответ: {1;4;7}
Пример 2. Число 14*6* делится на 45. Какое это число?
45 = 9 $\cdot$ 5. Значит, данное число делится на 9 и на 5.
Делимость на 9 требует сумму цифр, кратную 9: 1+4+x+6+y = 9k
Делимость на 5 даёт y = 0 или y = 5.
Получаем, учитывая, что x,y – цифры:
$$ {\left\{ \begin{array}{c} y = 0 \\ 1+4+x+6+0 = 9k \end{array} \right.} \Rightarrow 11+x = 9k \Rightarrow x = 7 $$
$$ {\left\{ \begin{array}{c} y = 5 \\ 1+4+x+6+0 = 9k \end{array} \right.} \Rightarrow 16+x = 9k \Rightarrow x = 2 $$
Ответ: 14760 или 14265
Пример 3. {2020} + 8 = 10000…08 $$
{2020} + 8 = 10000…08 $$
Сумма цифр данного числа 1+8 = 9 – делится на 9.
Значит, само число также делится на 9.
Ответ: да
Рейтинг пользователей
за неделю
- за неделю
- один месяц
- три месяца
Помогай другим
Отвечай на вопросы и получай ценные призы каждую неделю
См. подробности
Головоломка— Проверить, делится ли число на 3
Вопрос задан
Изменено 3 года, 7 месяцев назад
Просмотрено 57k умножить на
Напишите код для определения, делится ли число на 3. Входные данные функции — одиночных битов, 0 или 1, а на выходе должно быть 1, если полученное число является двоичным представлением число делится на 3, иначе ноль.
Примеры:
вход "0": (0) выход 1 входы "1,0,0": (4) выход 0 входы "1,1,0,0": (6) выход 1
Это основано на вопросе интервью. Я прошу рисунок логических элементов, но, поскольку это stackoverflow, я соглашусь с любым языком кодирования. Бонусные баллы за аппаратную реализацию (verilog и т.д.).
Часть а (простая): Первый ввод — старший бит.
Часть б (немного сложнее): Первый ввод — младший бит.
Часть c (сложная): Какой из них быстрее и меньше, (a) или (b)? (Не теоретически в смысле Big-O, а практически быстрее/меньше.) Теперь возьмите более медленное/большее и сделайте его таким же быстрым/маленьким, как более быстрое/меньшее.
- головоломка
- деление
- по модулю
1
Существует довольно известный способ определить, является ли число кратным 11, путем поочередного сложения и вычитания его десятичных цифр. Если число, которое вы получите в конце, кратно 11, то число, с которого вы начали, также кратно 11:9.0005
Если число, которое вы получите в конце, кратно 11, то число, с которого вы начали, также кратно 11:9.0005
47278 4 - 7 + 2 - 7 + 8 = 0, кратное 11 (47278 = 11 * 4298) 52214 5 - 2 + 2 - 1 + 4 = 8, не кратное 11 (52214 = 11 * 4746 + 8)
Мы можем применить тот же прием к двоичным числам. Двоичное число кратно 3 тогда и только тогда, когда переменная сумма его битов также кратна 3:
4 = 100 1 - 0 + 0 = 1, не кратное 3 6 = 110 1 - 1 + 0 = 0, кратное 3 78 = 1001110 1 - 0 + 0 - 1 + 1 - 1 + 0 = 0, кратное 3 109 = 1101101 1 - 1 + 0 - 1 + 1 - 0 + 1 = 1, не кратное 3
Не имеет значения, начинаете ли вы с MSB или LSB, поэтому следующая функция Python одинаково хорошо работает в обоих случаях. Требуется итератор, который возвращает биты по одному. множитель чередуется между 1 и 2 вместо 1 и -1, чтобы избежать получения по модулю отрицательного числа.
def divisibleBy3 (итератор):
множитель = 1
аккумулятор = 0
для бита в итераторе:
аккумулятор = (аккумулятор + бит * множитель) % 3
множитель = 3 - множитель
вернуть аккумулятор == 0
0
Вот. .. кое-что новое… как проверить, делится ли двоичное число любой длины (даже тысячи цифр) на 3.
.. кое-что новое… как проверить, делится ли двоичное число любой длины (даже тысячи цифр) на 3.
-->((0))<---1- -->()<---0--->(1) ASCII-представление графа
С картинки.
- Вы начинаете с двойного круга.
- Когда вы получаете единицу или ноль, если цифра находится внутри круга, вы остаетесь в этом круге. Однако, если цифра находится на линии, то вы путешествуете по линии.
- Повторяйте второй шаг, пока не будут использованы все цифры.
- Если вы наконец окажетесь в двойном круге, то двоичное число делится на 3.
Вы также можете использовать это для генерации чисел, делящихся на 3. И я бы не подумал, что это будет сложно преобразовать в схему.
1 пример с использованием графика…
11000000000001011111111111101 делится на 3 (снова оказывается в двойном круге)
Попробуйте сами.
Вы также можете проделать аналогичные трюки для выполнения MOD 10, например, при преобразовании двоичных чисел в числа с основанием 10. (10 кругов, каждый из которых обведен дважды и представляет значения от 0 до 9результат по модулю)
(10 кругов, каждый из которых обведен дважды и представляет значения от 0 до 9результат по модулю)
РЕДАКТИРОВАТЬ: Это для цифр, идущих слева направо, хотя несложно изменить конечный автомат, чтобы принять обратный язык.
ПРИМЕЧАНИЕ: В представлении графика ASCII () обозначает один круг, а (()) обозначает двойной круг. В автоматах с конечным числом состояний они называются состояниями, а двойной кружок — это состояние принятия (состояние, означающее, что оно в конечном счете делится на 3)
3
Heh
Таблица состояний для LSB:
S I S' O 0 0 0 1 0 1 1 0 1 0 2 0 1 1 0 1 2 0 1 0 2 1 2 0
Объяснение: 0 делится на три. 0 << 1 + 0 = 0 . Повторите, используя S = (S << 1 + I) % 3 и O = 1 , если S == 0 .
Таблица состояний для MSB:
S I S' O 0 0 0 1 0 1 2 0 1 0 1 0 1 1 0 1 2 0 2 0 2 1 1 0
Объяснение: 0 делится на три.
0 >> 1 + 0 = 0 . Повторите, используя S = (S >> 1 + I) % 3 и O = 1 , если S == 0 .
S' отличается от приведенного выше, но O работает так же, поскольку S' равно 0 для тех же случаев (00 и 11). Поскольку O в обоих случаях один и тот же, O_LSB = O_MSB, поэтому, чтобы сделать MSB таким же коротким, как LSB, или наоборот, просто используйте самый короткий из обоих.
1
Вот простой способ сделать это своими руками. Так как 1 = 2 2 по модулю 3, мы получаем 1 = 2 2n по модулю 3 для каждого положительного целого числа. Кроме того, 2 = 2 2n+1 mod 3. Следовательно, можно определить, делится ли целое число на 3, подсчитав биты 1 в нечетных битовых позициях, умножив это число на 2, добавив количество битов 1 в четных битовых позициях. добавьте их к результату и проверьте, делится ли результат на 3.
Пример: 57 10 =111001 2 . 2 бита в нечетных позициях и 2 бита в четных позициях. 2*2 + 2 = 6 делится на 3. Следовательно, 57 делится на 3.
2 бита в нечетных позициях и 2 бита в четных позициях. 2*2 + 2 = 6 делится на 3. Следовательно, 57 делится на 3.
Вот еще мысль по решению вопроса в). Если инвертировать порядок битов двоичного целого числа, то все биты остаются в четных/нечетных позициях или все биты меняются. Следовательно, инвертирование порядка битов целого числа n приводит к целому числу, которое делится на 3 тогда и только тогда, когда n делится на 3. Следовательно, любое решение вопроса a) работает без изменений для вопроса b) и наоборот. Хм, может быть, это поможет выяснить, какой подход быстрее...
1
Вам нужно сделать все вычисления, используя арифметику по модулю 3. Вот так
MSB:
число=0
в то время как (! eof)
п = ввод ()
число=(число *2 + n) по модулю 3
если (число == 0)
печать делимая
LSB:
число = 0;
множитель = 1;
в то время как (! eof)
п = ввод ()
число = (число + множитель * n) по модулю 3
множитель = (множитель * 2) по модулю 3
если (число == 0)
печать делимая
Это общая идея. ..
..
Теперь ваша задача понять почему это правильно.
И да, делай уроки сам 😉
6
Идея состоит в том, что число может увеличиваться до произвольной длины, что означает, что вы не можете использовать здесь mod 3 , так как ваше число будет расти за пределы возможностей вашего целочисленного класса.
Идея состоит в том, чтобы заметить, что происходит с числом. Если вы добавляете биты вправо, на самом деле вы сдвигаете влево на один бит и добавляете новый бит.
Сдвиг влево — это то же самое, что умножение на 2, а добавление нового бита — это либо добавление 0, либо 1. Предполагая, что мы начали с 0, мы можем сделать это рекурсивно на основе модуля-3 последнего числа.
последний | ввод || следующий | пример ------------------------------------ 0 | 0 || 0 | 0 * 2 + 0 = 0 0 | 1 || 1 | 0 * 2 + 1 = 1 1 | 0 || 2 | 1 * 2 + 0 = 2 1 | 1 || 0 | 1 * 2 + 1 = 0 (= 3 по модулю 3) 2 | 0 || 1 | 2 * 2 + 0 = 1 (= 4 по модулю 3) 2 | 1 || 2 | 2 * 2 + 1 = 2 (= 5 по модулю 3)
Теперь давайте посмотрим, что произойдет, если добавить бит слева. Во-первых, обратите внимание, что:
Во-первых, обратите внимание, что:
2 2n mod 3 = 1
и
9п = 13
вход "0": (0) выход 1 входы "1,0,0": (4) выход 0 входы "1,1,0,0": (6) выход 1
, разве этот последний ввод не должен быть 12 , или я неправильно понимаю вопрос?
2
На самом деле метод LSB облегчил бы эту задачу. В C:
Метод MSB:
/*
Возвращает 1, если делится на 3, иначе 0
Примечание. Предполагается, что формат «ввода» действителен.
*/
int is_divisible_by_3_msb (char * input) {
беззнаковое значение = 0;
символ *p = ввод;
если (*p == '1') {
значение &= 1;
}
р++;
в то время как (*р) {
если (*p!= ',') {
значение <<= 1;
если (*p == '1') {
возврат &= 1;
}
}
р++;
}
вернуть (значение % 3 == 0)? 1 : 0;
}
Метод младшего бита:
/* Возвращает 1, если делится на 3, иначе 0 Примечание.Предполагается, что формат «ввода» действителен. */ int is_divisible_by_3_lsb (char * input) { беззнаковое значение = 0; беззнаковая маска = 1; символ *p = ввод; в то время как (*р) { если (*p!= ',') { если (*p == '1') { значение &= маска; } маска <<= 1; } р++; } вернуть (значение % 3 == 0)? 1 : 0; }
Лично мне трудно поверить, что один из них будет существенно отличаться от другого.
1
Я думаю, что Натан Феллман находится на правильном пути для частей a и b (за исключением того, что b нужна дополнительная часть состояния: вам нужно отслеживать, является ли ваша цифра четной или нечетной).
Я думаю трюк для части C отрицает последнее значение на каждом шаге. т.е. 0 соответствует 0, 1 соответствует 2 и 2 соответствует 1.
1
Число делится на 3, если сумма его цифр делится на 3.
Таким образом, вы можете сложить цифры и получить сумму:
- если сумма больше или равна 10, используйте тот же метод
- , если это 3, 6, 9, то оно делится на .
- если сумма отлична от 3, 6, 9, то она не делится
2
7 способов узнать, делится ли число на 7
Конфиденциальность и файлы cookie: этот сайт использует файлы cookie. Продолжая использовать этот веб-сайт, вы соглашаетесь на их использование.
Чтобы узнать больше, в том числе о том, как управлять файлами cookie, см. здесь: Политика в отношении файлов cookie
Я уверен, вы знаете, как проверить, делится ли огромное число на 3, 9, 11 или на степени двойки, такие как 2, 4 и 8; вас, вероятно, учили, как это делать в начальной школе. Однако большинство из вас, вероятно, никогда не учили, как проверить, делится ли число на 7. В этой статье мы рассмотрим семь различных способов сделать это.
7 — безусловно, наименее любимое однозначное число, когда дело доходит до делимости. Изображение: Chalkdust
Изображение: Chalkdust
Прежде чем мы начнем, давайте введем некоторые обозначения, которые мы будем использовать на протяжении всей статьи. $n$-значное число $N$ с основанием 10 — это число, цифры которого принадлежат множеству $C_{10}=\{0, 1, 2, 3, 4, 5, 6, 7, 8, 9ic_i, $, где $c_i \in C_{10}$. Обычно мы записываем это число, соединяя цифры, используя их положение, чтобы указать соответствующую степень числа 10: $c_{n-1}c_{n-2}\cdots c_1c_0$. Младшая значащая цифра $N$ — $c_0$, а старшая значащая цифра — $c_{n-1}$.
Если $p$ — натуральное число, мы говорим, что целые числа $a$ и $b$ конгруэнтны по модулю $p$, и пишем $a\equiv b\;(\textrm{mod}\; p)$ или $a\equiv_p b$, если они имеют одинаковый остаток при делении на $p$. Для $2m$ целых чисел $a_0,a_1,\dots,a_{m-1}$, $b_0,b_1,\dots,b_{m-1}$ определяем: 9k} c_{k-1}\cdots c_1c_0$.
Метод обрезки
Автором этого метода является математик Антони Жбиковски. В 1860 г. (Bulletin de l'Académie impériale des Sciences de Saint Pétersbourg) и в 1861 г. (статья Ułatwione sposoby rozpoznawania podzielności liczb ( Облегченные способы распознавания делимости чисел ), метод Политехнического дневника, Варшава) для определения, когда любое заданное целое число делится на любое другое $d$, взаимно простое с 10.
(статья Ułatwione sposoby rozpoznawania podzielności liczb ( Облегченные способы распознавания делимости чисел ), метод Политехнического дневника, Варшава) для определения, когда любое заданное целое число делится на любое другое $d$, взаимно простое с 10.
Например, если $N$ выражается в виде $N=10a+b$, то $N$ делится на 7 тогда и только тогда, когда $a-2b$ делится на 7. Доказательство следует из того, что $ N$ делится на 7 тогда и только тогда, когда $N-21b$ делится на 7.
Если $N$ является по крайней мере трехзначным числом, то замените $N$ на значение $\left\lfloor\frac{ N}{10}\right\rfloor-2\times(N\;\textrm{mod}\;10)$. После каждого шага количество цифр меньше, чем на предыдущем шаге. Следовательно, количество шагов конечно. Когда $N$ имеет длину не более 2 цифр, вы можете напрямую проверить делимость на 7, если вы знаете свою таблицу умножения на 7 до 14. Тщательная реализация этого подхода требует линейного времени, и пространственная сложность также является линейной (см. ниже). . Как правило, этот метод не дает остатка при делении $N$ на $d.$
ниже). . Как правило, этот метод не дает остатка при делении $N$ на $d.$
В общем, при разработке алгоритма, который вы хотите реализовать на практике, жизненно важно понимать его временную и пространственную сложность. Изображение: общественное достояние
В компьютерных науках временная сложность измеряет количество времени, которое требуется для выполнения алгоритма. Говорят, что алгоритм требует линейного времени, $O(n)$ времени, если время выполнения увеличивается не более чем линейно с размером входных данных, т. е. с количеством цифр $n$. Аналогично, пространственная сложность — это объем памяти, необходимый алгоритму для выполнения программы и получения результата. Например, пространство $O(n)$ означает, что количество байтов увеличивается линейно пропорционально размеру входных данных, а пространство $O(1)$ означает, что требуется фиксированное количество байтов, независимо от размера входных данных.
Мы обсудим другие подходы, которые эффективно работают в пространстве $O(1)$ (постоянная память) и которые проще реализовать; однако это происходит за счет того, что их труднее понять, и труднее доказать, что они работают. i.\] Это то же самое, что и группировка, которую мы обычно используем для больших чисел с помощью запятых, например 9i.\]
i.\] Это то же самое, что и группировка, которую мы обычно используем для больших чисел с помощью запятых, например 9i.\]
Вацлав Серпинский. Изображение: общественное достояние
Например, число $72011021110$ делится на 7, потому что $-72+11-21+110=28$ делится на 7. Этот подход можно найти в книге Teoria Liczb ( The Theory чисел ) не кем иным, как выдающимся польским математиком Вацлавом Серпинским. Его метод работает для всех трех делителей $1001=7\times11\times13$.
Этот алгоритм использует постоянную память, если число задается поразрядно из входного потока, начиная с младшей значащей цифры. Это потому, что нам просто нужно сохранить текущее значение переменной суммы, когда мы включаем каждую последующую 3-последовательность. Что делать, если цифры даны от самых значащих? Мы можем отслеживать три решения независимо друг от друга (вплоть до $+$ или $-$, которые не изменяют делимость на 7), т.е. те, которые исходят из каждой возможной длины числа по модулю 3. Когда последняя цифра (т.е. $c_0$ ) читается, то мы знаем точное количество цифр и можем вывести правильный ответ, который является одним из трех возможных решений, поэтому он по-прежнему использует постоянную память. 9i$ в определении $S_3$, а в конце проверьте, делится ли полученное число на 7. Обратите внимание, что последовательность $(1,3,2,6,4,5)$ можно заменить эквивалентной последовательностью $ (1,3,2,-1,-3,-2)$ в силу сравнения $-k\equiv_7 7-k$. Последовательность $(1,3,2,-1,-3,-2)$ также упрощает ее запоминание! Нам нужно только помнить цикл $(1,3,2)$ и иметь в виду, что мы должны менять знак после каждого полного оборота. Этот вариант алгоритма широко известен и его можно найти, например, в Википедии. 9k\times S_3$ делится на 7 и наоборот, потому что 3 и 7 взаимно просты . Таким образом, у нас есть 6 различных циклов, которые могут быть эквивалентно применены в алгоритме. Например, чтобы проверить, делится ли число 12345678 на 7, мы проверяем следующую сумму (мы выбрали цикл $(3, 2, 6, 4, 5, 1)$):
Когда последняя цифра (т.е. $c_0$ ) читается, то мы знаем точное количество цифр и можем вывести правильный ответ, который является одним из трех возможных решений, поэтому он по-прежнему использует постоянную память. 9i$ в определении $S_3$, а в конце проверьте, делится ли полученное число на 7. Обратите внимание, что последовательность $(1,3,2,6,4,5)$ можно заменить эквивалентной последовательностью $ (1,3,2,-1,-3,-2)$ в силу сравнения $-k\equiv_7 7-k$. Последовательность $(1,3,2,-1,-3,-2)$ также упрощает ее запоминание! Нам нужно только помнить цикл $(1,3,2)$ и иметь в виду, что мы должны менять знак после каждого полного оборота. Этот вариант алгоритма широко известен и его можно найти, например, в Википедии. 9k\times S_3$ делится на 7 и наоборот, потому что 3 и 7 взаимно просты . Таким образом, у нас есть 6 различных циклов, которые могут быть эквивалентно применены в алгоритме. Например, чтобы проверить, делится ли число 12345678 на 7, мы проверяем следующую сумму (мы выбрали цикл $(3, 2, 6, 4, 5, 1)$):
\[
{\color{blue}3} \times {\color{red}8} + {\color{blue}2} \times {\color{red}7} + {\color{blue}6} \times {\color{red}6} + { \color{blue}4} \times {\color{red}5} + {\color{blue}5} \times {\color{red}4} + {\color{blue}1} \times {\color {красный} 3} + {\цвет{синий}3} \times {\color{красный}2} + {\color{синий}2} \times {\color{красный}1} = {\color{оранжевый} 1}{\цвет{оранжевый}2}{\цвет{оранжевый}5};
\]
следующий ${\color{синий}3} \times {\color{оранжевый}5} + {\color{синий}2} \times {\color{оранжевый}2} + {\color{синий} 6} \times {\color{оранжевый}1} = 25$. Последняя сумма не делится на 7, следовательно, и исходное число не делится на 7. Однако число 12345683 делится на 7, потому что соответствующая сумма равна 112, что делится на 7. Обратите внимание, что каждая цифра и каждый результат после умножения могут быть заменены результатом по модулю 7, что упрощает вычисления. 9ic_{n-i-1},
Последняя сумма не делится на 7, следовательно, и исходное число не делится на 7. Однако число 12345683 делится на 7, потому что соответствующая сумма равна 112, что делится на 7. Обратите внимание, что каждая цифра и каждый результат после умножения могут быть заменены результатом по модулю 7, что упрощает вычисления. 9ic_{n-i-1},
\end{equation}
обратите внимание, что здесь мы суммируем цифры в обратном порядке. Точно так же, как мы сделали для 3, мы можем рассмотреть последовательность остатков степеней 5 при делении на 7
\[{\color{blue}(}{\color{blue}1}{\color{ синий},}{\цвет{синий} 5}{\цвет{синий},}{\цвет{синий} 4}{\цвет{синий},}{\цвет{синий} 6}{\цвет{синий} ,}{\цвет{синий} 2}{\цвет{синий},}{\цвет{синий} 3}{\цвет{синий},}{\цвет{синий} 1}{\цвет{синий},} {\ color{blue} 5}{\color{blue},}{\color{blue} 4}{\color{blue},}{\color{blue} \dots}{\color{blue})}\ ] 9i$ в определении $S_5$, а затем проверить, делится ли полученное число на 7.
Мы можем снова взять пример 12345683, которое делится на 7, но теперь мы используем сумму $S_5$ для проверить его делимость
\[
{\color{blue}1} \times {\color{red}1} + {\color{blue}5} \times {\color{red}2} + {\color{blue } 4} \times {\color{red}3} + {\color{blue}6} \times {\color{red}4} + {\color{blue}2} \times {\color{red}5 } + {\color{blue}3} \times {\color{red}6} + {\color{blue}1} \times {\color{red}8} + {\color{blue}5} \times {\ цвет {красный} 3} = {\ цвет {оранжевый} 9k\times S_5$ делится на 7 и наоборот, потому что 5 и 7 взаимно просты. Таким образом, у нас снова есть 6 различных циклов, которые могут быть эквивалентно применены в алгоритме.
Таким образом, у нас снова есть 6 различных циклов, которые могут быть эквивалентно применены в алгоритме.
Мы вычислили с двумя основными циклами
\[
C1: =(1,-2,-3,-1,2,3)\;\textrm{и}\;C2:=(1,3,2 ,-1,-3,-2).
\]
Обратите внимание, что $C1$ является противоположным $C2$ и наоборот. Мы используем $C1$ для цифр, заданных от старших значащих, и $C2$ для цифр, заданных от младших значащих. Если мы хотим эффективно реализовать этот метод на компьютере, мы можем заменить цикл $C1$ на цикл $C3:=(1,-2,4,-1,2,-4)$ и $C2$ на цикл $C4: =(1,-4,2,-1,4,-2)$.
Проверка делимости для чисел с основанием 10 — это очень хорошо, но двоичный код — это то, что нужно. Изображение: общественное достояние
Умножение на степень 2 очень естественно для компьютера, так как эту операцию можно заменить побитовым оператором сдвига влево. Предположим, что цифра 7 задана в двоичной форме, т.е. $7_{10}=111_2$ (нижний индекс указывает на основание, в котором записано число). Тогда $7_{10}\times2_{10} = 1110_2,$ и $7_{10}\times4_{10} = 11100_2,$ вам просто нужно сдвинуть биты влево. Эквивалентно, если число равно $123_{10}=1111011_2$ и мы сдвинем его влево на 3 бита, результатом будет $1111011000_2$, а его десятичная эквивалентная версия будет $123_{10}\times8_{10}=9.84_{10}$.
Тогда $7_{10}\times2_{10} = 1110_2,$ и $7_{10}\times4_{10} = 11100_2,$ вам просто нужно сдвинуть биты влево. Эквивалентно, если число равно $123_{10}=1111011_2$ и мы сдвинем его влево на 3 бита, результатом будет $1111011000_2$, а его десятичная эквивалентная версия будет $123_{10}\times8_{10}=9.84_{10}$.
Возвращаясь к делимости на степени 2, мы можем использовать более быстрый подход с компьютерным побитовым оператором И . Побитовое И двух двоичных чисел $a_1$ и $a_2$ имеет 1 цифру в $k$-м разряде, когда оба $a_1$ и $a_2$ имеют 1 в $k$-м разряде, и 0 в противном случае. Например, чтобы проверить, делится ли число на 8, нам нужно проверить три младших бита числа, поэтому $1111011000_2$ делится на 8, а $1111011010_2$ — нет. 9ic_i.
\]
Когда я попытался доказать, что метод работает, я обнаружил, что на самом деле существует шесть циклов, эквивалентных $C1$ и $C2$, которые можно использовать. Например, если использовать цифры из последовательности $(3,2,-1,-3,-2,1,3,2,-1,-3,-2)$, то обратная последовательность $(-2, -3,-1,2,3,1,-2,-3,-1,2,3)$ должны работать, когда цифры даны от старшего к младшему. При проектировании человеко-компьютерного интерфейса для людей, говорящих на европейских языках, более естественно сканировать входной поток, начиная со старшего разряда, то есть слева направо.
При проектировании человеко-компьютерного интерфейса для людей, говорящих на европейских языках, более естественно сканировать входной поток, начиная со старшего разряда, то есть слева направо.
Может быть важно рассмотреть, как число вводится в ваш алгоритм, младшая или старшая цифра первой. Изображение: Chalkdust
Все методы возведения в степень просты, поэтому можно быстро проверить, делится ли число на 7, и их легко запомнить. Более того, последние два метода могут быть эффективно реализованы на компьютере. Умножение на 2 и 4 можно заменить более быстрым побитовым оператором сдвига влево. Мы также должны помнить о смене знака каждый раз при обработке цифр (см.: циклы $C3$ и $C4$). Это проще, чем смена знака в подходе с 3-кратным возведением в степень (как в циклах $C1$ и $C2$).
Оба метода 3- и 5-возведения в степень имеют временную сложность $O(n)$ и требуют $O(1)$ места. Это связано с тем, что входное число не нужно загружать в память компьютера, а только промежуточный итог по мере вычисления сумм. Суммы $S_{-2}$ и $S_{-4}$ эквивалентны суммам $S_5$ и $S_3$ соответственно. Сумму $S_3$ можно найти в Википедии, так как она относительно известна. Там же можно найти открытие 12-летнего нигерийского мальчика Чики Офили, получившего награду «TruLittle Hero Awards» в 2019 году.. Он заметил, что для проверки числа вроде 2345 на делимость на 7 нам просто нужно убрать последнюю цифру, умножить ее на 5 и прибавить к тому, что осталось, и повторить:
Суммы $S_{-2}$ и $S_{-4}$ эквивалентны суммам $S_5$ и $S_3$ соответственно. Сумму $S_3$ можно найти в Википедии, так как она относительно известна. Там же можно найти открытие 12-летнего нигерийского мальчика Чики Офили, получившего награду «TruLittle Hero Awards» в 2019 году.. Он заметил, что для проверки числа вроде 2345 на делимость на 7 нам просто нужно убрать последнюю цифру, умножить ее на 5 и прибавить к тому, что осталось, и повторить:
\begin{align*}
&{\ color{blue}2}{\color{blue}3}{\color{blue}4}+{\color{blue}5}\times{\color{red}5}=259,\\
&{\ color{blue}2}{\color{blue}5}+{\color{blue}9}\times{\color{red}5}=70,\\
&{\color{blue}7}+{ \color{blue}0}\times{\color{red}5}=7,
\end{align*}
и для 22442:
\begin{align*}
&{\ color{blue}2}{\color{blue}2}{\color{blue}4}{\color{blue}4}+{\color{blue}2}\times{\color{red }5}=2254,\\
&{\color{blue}2}{\color{blue}2}{\color{blue}5}+{\color{blue}4}\times{\color{red }5}=245,\\
&{\color{синий}2}{\color{синий}4}+{\color{синий}5}\times{\color{красный}5}=49.
\end{align*}
Если введенное число делится на 7, то последнее число после достаточного повторения этого шага будет 7 или 49. Обратите внимание, что вместо умножения на 5 вы можете умножить на $-$2. Отсюда следует, что этот метод эквивалентен методу обрезки А. Жбиковского. 9{n\;(\textrm{mod}\;3)}\equiv_7\begin{cases}
1&\textrm{if}\;n\equiv_3 0\\
2&\textrm{if}\;n\equiv_3 1 \\
4&\textrm{if}\;n\equiv_3 2\\
\end{cases}
\]
Резюме
Мы можем видеть, что существует множество возможных методов определения, делится ли число на 7. Хотелось бы узнать, существует ли алгоритм, работающий с временной сложностью $O(1)$. Поскольку мы можем очень быстро проверить, делится ли число на 2, 5 или 10, мы можем задаться вопросом, возможен ли аналогичный быстрый алгоритм для других делителей, таких как 3 или 7. Такие алгоритмы существуют, если входные числа заданы в базе 3 или 7 соответственно.
Пусть $M(n)$ обозначает стоимость умножения двух $n$-битных чисел. Тривиальная нижняя граница для $M(n)$ является линейной, потому что вы должны прочитать все биты, прежде чем сможете умножать числа. В марте 2019 года Харви и ван дер Хувен разработали алгоритм с $M(n) = O(n\log n)$, установив безусловную верхнюю границу $O(n\log n)$. Обратите внимание, что деление чисел стоит столько же времени, сколько и умножение. Также обратите внимание, что умножение/деление на постоянное число требует линейного времени.
Тривиальная нижняя граница для $M(n)$ является линейной, потому что вы должны прочитать все биты, прежде чем сможете умножать числа. В марте 2019 года Харви и ван дер Хувен разработали алгоритм с $M(n) = O(n\log n)$, установив безусловную верхнюю границу $O(n\log n)$. Обратите внимание, что деление чисел стоит столько же времени, сколько и умножение. Также обратите внимание, что умножение/деление на постоянное число требует линейного времени.
В замечательной книге «Искусство программирования, том 2: получисловые алгоритмы» Дональд Кнут показал, что количество шагов, необходимых для преобразования $n$-значного десятичного числа в двоичное, составляет $O(M(n)\log n) $. Далее он отметил, что аналогичным образом Шёнхаге заметил, что мы можем преобразовать, в обратном порядке, то есть из двоичного в десятичный за $O(M(n)\log n)$ шагов.
Однако проверка делимости не такая сложная задача, как преобразование основания в основание (или мы показываем лучшую верхнюю границу для преобразования основания). Как правило, чтобы проверить, делится ли число на другое число, мы обычно делим делимое на делитель и проверяем остаток, но в некоторых случаях, показанных в этой статье, когда мы фиксируем конкретный делитель, мы можем проверить делимость за линейное время или даже за постоянное время без каких-либо операций деления. Тогда может быть открытым вопрос, существует ли какой-либо сублинейный алгоритм или алгоритм с постоянным временем, когда делитель является постоянным и не делит базу.
Как правило, чтобы проверить, делится ли число на другое число, мы обычно делим делимое на делитель и проверяем остаток, но в некоторых случаях, показанных в этой статье, когда мы фиксируем конкретный делитель, мы можем проверить делимость за линейное время или даже за постоянное время без каких-либо операций деления. Тогда может быть открытым вопрос, существует ли какой-либо сублинейный алгоритм или алгоритм с постоянным временем, когда делитель является постоянным и не делит базу.
Вы можете найти версию этой статьи на польском языке в ежемесячном научно-популярном журнале Delta, издаваемом Варшавским университетом. Я хотел бы поблагодарить редактора Delta, Томаша Казану, за обсуждения и советы, которые помогли упростить некоторые рассуждения в этом тексте.
Больше из Chalkdust
Прочитайте выпуск 15 прямо сейчас!
Squid Game, скрытые гармонии и DnD ждут вас в нашем новом выпуске! Плюс все ваши любимые головоломки и столбцы.
В разговоре с Сэмми Баззардом
Эллен разговаривает с математиком и ученым об Аттенборо, Арктане и Антарктиде
Выжить на мосту в игре Squid Game
E Адриан Хенле, Ник Ганцлер, Франсуа-Ксавье Кудер и Кори Саймон объединяются для смертельного испытания
Уважаемый Дирихле, выпуск 15
Свадьбы, праздники и сомы попадают в почтовый ящик профа в этом выпуске.

Случайно математические песни
Goran Newsum всегда должен быть кем -то, кто вам действительно любит
Примеры теста на раздел
| 1. Формула (Предыдущий пример) |
2. Примеры (Признак делимости от 2 до 10)
1. Проверить, делится ли 84 на 2 или нет?
Решение:
Правило деления на 2 : Последняя цифра четная, тогда число делится на 2.
Последняя цифра числа 84 — 4, которое делится на 2.
`:.` 84 делится на 2.
2. Проверить, делится ли 85 на 2 или нет?
Решение:
Правило деления 2 : Последняя цифра четная, тогда число делится на 2.
Последняя цифра числа 85 равна 5, что не делится на 2. не делится на 2.
3. Проверить, делится ли 192 на 3 или нет?
Решение:
Правило деления на 3 : Сумма цифр делится на 3, тогда число также делится на 3.
Сумма цифр числа 192 равна `1+9+2=12`, что делится на 3.
`:.` 192 делится на 3.
4. Проверить, делится ли 193 на 3 или нет?
Решение:
Правило деления 3 : Сумма цифр делится на 3, тогда число также делится на 3.
Сумма цифр числа 193 равна `1+9+3=13`, который не делится на 3,
`:.` 193 не делится на 3.
5. Проверить, делится ли 324 на 4 или нет?
Решение:
Правило деления 4 : Последние две цифры делятся на 4, тогда число также делится на 4. .` 324 делится на 4.
6. Проверить, делится ли 322 на 4 или нет?
Решение:
Правило деления на 4 : Последние две цифры делятся на 4, тогда число также делится на 4.
Последние 2 цифры числа 322 - 22, что не делится на 4.
`:.` 322 не делится на 4.
7. Проверить, делится ли 220 на 5 или нет?
Решение:
Правило деления 5 : Последняя цифра 0 или 5, тогда число также делится на 5.
Последняя цифра 220 равна 0.
`:.` 220 делится на 5.
8. Проверить, делится ли 221 на 5 или нет?
Решение:
Правило деления 5 : Последняя цифра 0 или 5, тогда число также делится на 5.
Последняя цифра числа 221 1.
`:.` 221 не делится на 5.
9. Проверить, делится ли 1734 на 6 или нет?
Решение:
Правило деления 6 : Если число делится на 2 и 3, то оно также делится на 6.
Последняя цифра числа 1734 - 4, которое делится на 2.
`:. ` 1734 делится на 2.
Сумма цифр 1734 равна `1+7+3+4=15`, что делится на 3.
`:.` 1734 делится на 3.
1734 делится на 2 и 3.
`:. ` 1734 делится на 6.
` 1734 делится на 6.
10. Проверить, делится ли 1732 на 6 или нет?
Решение:
Правило деления 6 : Если число делится на 2 и 3, то число также делится на 6.
Последняя цифра числа 1732 - 2, которое делится на 2.
`:. ` 1732 делится на 2.
Сумма цифр 1732 равна `1+7+3+2=13`, что не делится на 3.
`:.` 1732 не делится на 3.
Следовательно, 1732 также не делится на 6.
11. Проверить, делится ли 329 на 7 или нет?
Решение:
Правило деления 7 : Умножьте на 2 последнюю цифру и вычтите ее из остального числа.
Если ответ делится на 7, то число также делится на 7.
(Примените это правило к ответу еще раз, если необходимо)
Проверка 329 делится или нет на 7
`32color{red}{9}=>32 - color{red}{9} xx 2 = 32 -18 = 14`
Здесь 14 делится на 7.
`:.` 329 делится на 7.
12. Проверить, является ли 328 делится на 7 или нет?
Решение:
Правило деления 7 : Умножьте на 2 последнюю цифру и вычтите ее из остального числа.
Если ответ делится на 7, то число также делится на 7.
(При необходимости примените это правило к ответу еще раз)
Проверка 328 делится на 7 или не делится на
`32color{red}{8}=>32 - color{red}{8} xx 2 = 32 -16 = 16`
Здесь 16 не делится на 7.
`:.` 328 не делится на 7.
13. Проверить, делится ли 2568 на 8 или нет?
Решение:
Правило деления 8 : Последние три цифры делятся на 8, тогда число также делится на 8. .` 2568 делится на 8.
14. Проверить, делится ли 3568 на 8 или нет?
Решение:
Правило деления 8 : Последние три цифры делятся на 8, тогда число также делится на 8.
Последние 3 цифры числа 3568 это 568, которое делится на 8. .` 3568 делится на 8.
15. Проверить, делится ли 3564 на 8 или нет?
Решение:
Правило деления 8 : Последние три цифры делятся на 8, тогда число также делится на 8.0489 `:. ` 3564 не делится на 8.
` 3564 не делится на 8.
16. Проверить, делится ли 162 на 9 или нет?
Решение:
Правило деления 9 : Сумма цифр делится на 9, тогда число также делится на 9.
Сумма цифр числа 162 равна `1+6+2=9`, который делится на 9.
`:.` 162 делится на 9.
17. Проверить, делится ли 163 на 9 или нет?
Решение:
Правило деления 9: Сумма цифр делится на 9, тогда число также делится на 9.
Сумма цифр числа 163 равна `1+6+3=10`, что не делится на 9.
`:.` 163 не делится на 9.
18. Проверить, делится ли 430 на 10 или нет?
Решение:
Правило деления 10 : Последняя цифра 0, тогда число также делится на 10.
Последняя цифра 430 равна 0.
`:.` 430 делится на 10. 19. Проверить, делится ли 431 на 10 или нет?
Решение:
Правило деления 10 : Последняя цифра 0, тогда число также делится на 10.
Последняя цифра 431 равна 1.
`:.` 431 не делится на 105.
Этот материал предназначен для краткого изложения. Используйте свой учебник для подробного объяснения.
Любая ошибка, улучшение, отзыв
| 1. Формула (Предыдущий пример) | 3. Примеры (Проверка на делимость от 11 до 20) (Следующий пример) |
Правила делимости – MathsTips.com
Допустим, у нас есть число 512. Если нас спросят, делится ли 512 на 2 или нет, мы можем сказать, что оно делится на 2, поскольку оно есть четное число, и мы знаем, что все четные числа делятся на 2.
Утверждение «Все четные числа делятся на 2» известно как правило делимости для 2 . По этому правилу мы могли бы сказать, что 512 делится на 2 без фактического деления в большую сторону. Следовательно, правила делимости облегчают нам определение того, делится ли определенное число на другое число или нет.
Например: 12 можно разделить точно и без остатка на 3, потому что . Однако 12 нельзя разделить без остатка на 5.
Однако 12 нельзя разделить без остатка на 5.
Когда мы говорим, что одно число точно и без остатка делится на другое число, мы имеем в виду, что при делении на мы получим целое число, а не дробь.
Примечание:
- Следует отметить, что в дальнейшем в этой статье всякий раз, когда мы используем слово «делимый» , мы подразумеваем «точно и без остатка делимый» .
- Следует также отметить, что правила делимости помогают нам только определить, делится ли определенное число на другое число или нет, и они не не помогают нам получить значение частного, т.е. нам целое число, которое мы получаем, когда оно «точно и без остатка делится» на . Если мы хотим узнать значение частного при делении на, нам придется, как обычно, выполнить деление в длинное число.
Вообще говоря, целое число делит другое целое число «точно и равномерно» тогда и только тогда, когда вы можете найти такое целое число n, что
Например, 12 можно разделить на 3, потому что
Точно так же, как мы говорили о правиле делимости на 2, у нас есть разные правила делимости для чисел 2, 3, 4, 5, 6, 7, 8, 9, 10 и 11. Для небольших чисел вроде 12 можно сказать, делится оно на 3 или нет, посчитав в уме. Однако, когда числа большие, мы используем следующие правила делимости:
Для небольших чисел вроде 12 можно сказать, делится оно на 3 или нет, посчитав в уме. Однако, когда числа большие, мы используем следующие правила делимости:
Делится на 2, если его последняя цифра является четным числом или нулем, т. е. когда число является четным числом.
Например, 120, 24, 38 и т. д. являются четными числами и, следовательно, все они делятся на 2.
Правило делимости на 3:Число делится на 3, если сумма его цифр делится на 3 на 3.
Например: 192. 1+9+2=12. Это число делится на 3. Таким образом, 192 делится на 3.
Число делится на 9, если сумма его цифр делится на 9.
Например: 4725. 4+7+2+5=18. Это число делится на 9. Значит, 4725 делится на 9..
Правило делимости на 4:Число делится на 4, если число, представленное его двумя последними цифрами, делится на 4.
Например, 8920 делится на 4, потому что 20 делится на 4.
2 Опять же, 764 делится на 4, потому что 64 делится на 4.
Правило делимости на 5:Число делится на 5, если его последняя цифра 5 или 0.
Например, 150, 165. 200 и т. д. все делятся на 5,
Правило делимости на 6:Число делится на 6, если оно делится и на 2, и на 3. Таким образом, четное число, которое делится на 3, делится и на 6.
Например, 522 — четное число. Следовательно, оно делится на 2. Кроме того, 5+2+2=9, которое делится на 3. Таким образом, 522 делится на 3.
522 ius делится на 2 и на 3 оба
522 делятся на 6.
Правило делимости для 7:Правило делимости для 7 немного сложное. Давайте рассмотрим следующие два примера, чтобы понять, как работает это правило.
Пример 1: Проверить, делится ли 657 на 7.
Решение:
Шаг 1: Удаляем последнюю цифру, которая равна 7. Шаг становится равным 65.
Шаг становится равным 65.
Шаг 3: Проверяем, делится ли эта окончательная разность на 7 или нет. 51 не делится на 7. Итак, мы можем заключить, что 657 не делится на 7.
В Пример 1 мы имели дело с трехзначным числом. Итак, это было относительно легко. Теперь рассмотрим пятизначное число.
Пример 2: Проверить, делится ли 69118 на 7.
Решение:
Шаг 1: Удаляем последнюю цифру, которая равна 8. Шаг 9:11
0
Удваиваем удаленное число и вычитаем его из оставшейся части числа. равно 16. Из 69 вычитаем 16.11. Ответ: 6911-16=6895 6895 — все равно большое число. Проверка того, делится ли 6895 на 7 или нет на фактическое деление, приведет к длинному делению. Весь смысл Правил делимости состоит в том, чтобы избежать таких длинных делений.
Итак, мы повторяем процесс для 6895.
Шаг 1: Удаляем последнюю цифру, которая равна 5. Число становится 689.
Шаг 2: Удваиваем удаленное число и вычитаем его из оставшаяся часть числа. равно 10. Из 689 вычитаем 10.. Ответ: 689-10=679
Повторяем процесс для 679.
Шаг 1: Убираем последнюю цифру, которая равна 9. Число становится 67.
Шаг 2: Удваиваем удаленное число и вычесть его из оставшейся части числа. равно 18. Вычитаем 18 из 67. Ответ: 67-18=49
Шаг 3: Проверяем, делится ли эта окончательная разность на 7 или нет. 49 делится на 7. Итак, мы можем заключить, что 69118 делится на 7.
Правило делимости на 8:Число делится на 8, если число, представленное тремя его последними цифрами, делится на 8.
Например, 587320 делится на 8, потому что 320 делится на 8.
5
Точно так же 24120 делится на 8. [120 делится на 8]
[120 делится на 8]
Правило делимости для 9 очень похоже на правило для 3. Число делится на 9, если сумма его цифры делятся на 9.
Например, 3141 делится на 9, потому что сумма его цифр равна (3+1+4+1)=9, что делится на 9.
Аналогично, 1917 делится на 9. [ 1+9+1 +7=18, что делится на 9]
Правило делимости на 10:Правило делимости на 10 очень простое. Любое число, последняя цифра которого равна нулю, делится на 10.
Например, 230, 680, 1900 и т. д. все делятся на 10.
Правило делимости для 11:Допустим, нам нужно проверить, делится ли число 75236 на 11 или нет.
Складываем цифры в нечетных местах.
Цифра на первом месте (начиная слева) 7
Цифра на третьем месте 2
Цифра на пятом месте 6
Таким образом, сумма нечетных цифр = 7+2+6=15
Аналогично, сумма четных цифр=5+3=8
Разность нечетной суммы и четной суммы=15-8=7, которая не делится на 11
Значит, число 75236 не делится на 11
Теперь возьмем число 94567
Здесь нечетная сумма=9+5+7=21 и четная сумма=4+6=10
Итак, разница нечетной суммы и четной суммы=21 -10=11, что делится на 11.
Итак, 94567 делится на 11.
Примечание:
- Если разность нечетной суммы и четной суммы не делится на 11, то число также не делится на 11.
- Если разница нечетной суммы и четной суммы делится на 11 или если она равна 0, то число делится на 11.
Это полный урок с инструкциями и упражнениями о понятии делимости и общих правилах делимости, предназначенный для 5-го или 6-го класса. Во-первых, в нем кратко рассматриваются понятия множителя, делителя и числа, делящегося на другое. Затем даются «легкие» правила делимости на 2, 5, 10, 100 и 1000. Остальная часть урока посвящена правилам делимости на 3, 9, 6, 4 и 8 и содержит множество упражнений, в том числе забавные лабиринты и головоломки с загадочными числами.
1. Ответ. В каждом случае объясните, почему или почему бы и нет. а. Является ли 8 коэффициентом 100? б. Является ли 7 коэффициентом 3500? c. Является ли число 9 делителем 50?
2. Ответ. В каждом случае объясните почему или почему нет (обоснуйте свой ответ). а. Делится ли 283 на 13? б. Делится ли 13 × 2809 на 13? c. 3 × 3 × 3 × 3 × 3 делится на 2? д. e. 2 × 758 × 5 делится на 10? ф. Делится ли 2 × 15 × 2 × 7 на 4?
3. Отметьте знаком «x», если число делится на 2, 5, 10, 100 или 1000.
4. Делятся ли эти числа на 3? Если да, выполните деление в большую сторону и разделить число на 3. а. 539 б. 43 719 с. 9 032 5. Изменить одну из цифр в номере 238 882 6.
7. Делятся ли эти числа на 9? Если да, выполните длинное деление и разделите число на 9. а. б. 576 с. 44 082
8. Отметьте "x", если число делится на 2, 3, 5, 6 или 9.
9. а. Составьте список из пяти последовательных чисел б. Составьте список из пяти последовательных чисел, которые
10. Отметьте "x", если число делится на 2, 3, 4, 5, 6 или 9.
11. Отметьте "x", если число делится на 2, 3, 4, 5, 6, 8 или 9..
12.
13. а. Что такое остаток от деления 687 на 7? б. Что такое остаток от деления 688 на 7? с. Какой остаток при делении 689 на 7? а. Что такое остаток от деления 1882 на 11? б. Что такое остаток от деления 1886 на 11? с. Что такое
остаток от деления 1890 на 11? 15. а. Найдите число, которое делится на 6 без остатка и находится в диапазоне от 90 до 100. б. Найдите число, которое оставляет в остатке 1 при делении на 6 и находится между 90 и 100.
16. Лабиринты!
Найдите свой путь от слева до правое боковое перемещение вправо, влево,
вверх или вниз (не
17.
Этот урок взят из книги Марии Миллер Math Mammoth Multiplication & Division 3 и размещен на сайте www.HomeschoolMath.net с разрешения автора. Авторское право © Мария Миллер. Mammoth Mammoth Умножение и деление 3 Учебник для самообучения для 5-го класса, который охватывает многозначное умножение, деление в большую сторону, решение задач, простые уравнения, отношения, делимость и разложение на множители. Скачать (7,40 $) . => Узнайте больше и посмотрите бесплатные образцы! Смотрите другие актуальные книги Mammoth Mammoth Меню уроков математики | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Правила делимости — узнайте, как разделить на число
Правила делимости
Правила делимости — это «советы и приемы» для распознавания, делится ли одно число на другое.
Содержание
Приведенные ниже приемы помогут вам найти множители чисел и определить, является ли число простым.
Делимость на 2 Правило
Делится ли на 2?
Пожалуй, самое известное правило делимости.
Любое число , даже , делится на 2.
Это легко определить, взглянув на последнюю цифру — если она заканчивается на 2, 4, 6, 8 или 0, то она четная и, следовательно, делится на 2.
Нечетное Числа заканчиваются на 1, 3, 5, 7 или 9, и не делится на 2.
Примеры чисел делится на 2:
2 8
5 0
759 2
Примеры чисел , не , делящихся на 2:
37
245
6829
Делится ли на 3 Правило
5 9000
Если сумма цифр числа кратна 3, то это число делится на 3.
Примеры чисел делится на 3:
51 (5 + 1 = 6 )
147 (1 + 4 + 7 = 12 )
4392 (4 + 3 + 9 + 2 = 18 )
Примеры чисел не делящихся на 3:
73 (7 + 3 = 10)
431 (4 + 3 + 1 = 8)
6332 ( )
Делимость на 4 Правило
Делится ли на 4?
Если последние две цифры числа делятся на 4, то и все число делится на 4.
Примеры чисел делится на 4:
7 16
97 48
573 24
Примеры не Дивизируемые на 4: 118 Дивизируемые на 4: 118 .
Делимость на 5 Правило
Делится ли на 5?
Еще один легко заметить.
Если число оканчивается на 5 или 0, то это число делится на 5.
Examples of numbers divisible by 5:
7 5
24 0
896 5
Examples of numbers not divisible by 5:
87
649
5551
Делимость на 6 Правило
Делится ли на 6?
Знаешь, делится ли на 2 и на 3?
Если число делится на 2 И делится на 3, то это число делится на 6.
Примеры чисел делится на 6:
7 2 (7 + 2 = 9 )
17 4 (1 + 7 + 4 = 12 )
532 8 (5 + 3 + 2 + 8 = 18 )
Примеры чисел не делятся на 6:
86 (8 + 6 = 14, делится на 2, но не на 3) 369 (3 + 6 + 9 = 18, делится на 3, но не на 2) 6794 (6 + 7 + 9 + 4 = 26, делится на 2, но не на 3)
Делимость на 8 Правило
Делится ли на 8?
Если последние три цифры числа делятся на 8, то это целое число делится на 8.
Примеры чисел, делится на 8:
5 216
65 408
997 65 408 997 9 . 552 Примеры чисел не делящихся на 8: 45964 88698 157942 Как узнать число, которое делится на 3 и 8? Нет легкого места, но либо попробуйте использовать метод автобусной остановки, либо попробуйте разделить его пополам, еще раз пополам, а затем еще раз пополам. напр. 216. Половина этого 108, половина этого 54. Половина 54 равна 27, поэтому 216 делится на 8. Делимость на 9 Правило
Делится ли на 9?
Если сумма цифр числа кратна 9, то это число делится на 9.
Примеры чисел, делящихся на 9:
72 (7 + 2 = 9 )
486 ( 4 + 8 + 6 = 18 )
5985 ( 5 + 9 + 8 + 5 = 27 )
Примеры чисел , а не , делящихся на 9:
93 (9 + 3 = 12)
674 (6 + 7 + 4 = 17)
+ 8 941002 (1 + 49 = 8) 22 )
Делимость на 10 Правило
Делится ли на 10?
Вероятно, самый простой для обнаружения…
Если число оканчивается на 0, то оно делится на 10. 0002 382 0
0002 382 0
8483 0
Примеры чисел Не Раздел 10:
105
4108
1025
, и это следует, if a y Numb делится на 100 (например, 2300). Если оно заканчивается на три 0, то оно делится на 1000 (например, 71000) и т. д.
Делимость на 11 Правило
Делится ли оно на 11?
Это сложно понять, но проще на примерах.
Если это двузначное число с одинаковыми цифрами, то это число делится на 11.
Если число состоит из трех или более цифр, просуммируйте чередующиеся числа и найдите разницу – если эта разница делится на 11, то число, с которого вы начали, делится на 11
Примеры чисел, делящихся на 11:
55 (обе цифры одинаковые)
176 ((1 + 6) – (7) = 0 и ноль делится на 11)
638 ((6 + 8) – (3) = 11)
6292 ( (6 + 9) – (2 + 2) = 11 )
45441 ( (4 + 4 + 1) – (5 + 4) = 0 )
Примеры чисел не делится на 11:
177 ( (1 + 7) – (7) = 1 )
8552 ( (8 + 5) – (5 + 2) = 6 )
74611 ( (7 + 6 + 1) – (4 + 1) = 9 )
Делится ли ноль на какое-либо число?
Ноль делится на любое число (кроме самого себя), поэтому на все приведенные выше вопросы ответ «Да».
Нравится? Подробнее читайте ниже…
Обо мне
Меня зовут Никола Бхалерао, я частный репетитор из Уорика. С 2013 года провожу индивидуальные занятия для детей и взрослых. Я специализируюсь на репетиторстве по математике, но обслуживаю разные запросы, от 11+ до различных компьютерных навыков, включая обучение на веб-сайте.
Я работаю в области вычислительной техники, имею степень в области информатики Университета Уорика. Я много лет работал программистом, в последнее время в игровой индустрии. Оба моих сына были у меня репетиторами для 11+ (они ходили в местную гимназию). Я прошла обучение преподаванию математики в средней школе и полностью проверена CRB.
Я эксперт по WordPress, потратив много лет на создание множества веб-сайтов вместе с другим моим бизнесом, веб-дизайном Smiling Panda. Хотя я больше не работаю активно над веб-сайтами для других, я предлагаю помощь в понимании / обновлении / создании собственного веб-сайта WordPress.
Прочтите здесь дополнительную информацию о программе для вашего ребенка или для вас или другого взрослого .
"Никола оказала мне большую поддержку, помогая мне заполнить пробелы, оставшиеся после моего школьного образования. Это имело решающее значение для повышения моей уверенности в математике"
"Моя дочь стала более уверенной в себе, особенно в математике в уме. Ее успехи были видны в школьных заданиях. Никола проявляла к ней большую эмпатию"
"Мне не хватало уверенности в математике. Никола была фантастической учителем и действительно помогла улучшить мою технику и подход к математическим задачам. Она терпеливая, понимающая и дружелюбная"
"Любая работа, которую мы делали дома, обычно заканчивалась тем, что мы оба разочаровывались. Он не хотел поднимать руку и спросите в школе. За короткое время он приобрел гораздо больше уверенности»
"Она была очень дружелюбна и профессиональна. После нескольких занятий я почувствовал себя намного увереннее в своих способностях и прошел тесты на числовое мышление. Она очень понятно объясняет"
Она очень понятно объясняет"
"Я уже заметил большую разницу в его отношении и подходе к своему школьному домашнему заданию; он обрел готовность попробовать его, а не просто предполагать, что он не может это сделать!»
"Никола была терпеливым репетитором, всегда помогала ответить на любые вопросы, которые у меня были. Я всегда находил математику довольно страшным предметом, но благодаря репетиторству Николы я научился доверять этому предмету"
"Мы были впечатлены ее профессионализмом, терпением и преподаванием. Она работала на уровне и в темпе, который подходил нашим детям. Оба получили результаты 11+, которыми мы очень гордимся."
"Никола оказала мне большую поддержку, помогая мне заполнить пробелы, оставшиеся после моего школьного образования. Это сыграло решающую роль в повышении моей уверенности в математике"
"Моя дочь приобрела большую уверенность, особенно с ней математика в уме. Ее успехи были показаны в ее школьной работе. Никола проявляла к ней большое сочувствие»
"Мне не хватало уверенности в математике. Никола была фантастическим учителем и действительно помогла улучшить мою технику и подход к математическим задачам. Она терпеливая, понимающая и дружелюбная"
Никола была фантастическим учителем и действительно помогла улучшить мою технику и подход к математическим задачам. Она терпеливая, понимающая и дружелюбная"
"Любая работа, которую мы делали дома, обычно заканчивалась мы оба расстраивались. Он не хотел поднимать руку и спрашивать в школе. За короткое время он приобрел гораздо больше уверенности"
"Она была очень дружелюбна и профессиональна. После нескольких занятий я почувствовал себя намного увереннее в моих способностях и прошла тесты на числовое мышление. Она очень ясно объясняет вещи»
"Я уже заметил большую разницу в его отношении и подходе к выполнению школьных домашних заданий; он обрел готовность попробовать, а не просто предполагать, что не может этого сделать!"
"Никола была терпеливым репетитором, всегда помогала в ответах на любые вопросы, которые у меня были. Я всегда находил математику довольно страшным предметом, но благодаря репетиторству Николы я научился доверять этому предмету"
"Мы были впечатлены ее профессионализм, терпение и обучение.

 к. 10+4*3=36; 36:13=3
к. 10+4*3=36; 36:13=3
 n$
n$ Предполагается, что формат «ввода» действителен.
*/
int is_divisible_by_3_lsb (char * input) {
беззнаковое значение = 0;
беззнаковая маска = 1;
символ *p = ввод;
в то время как (*р) {
если (*p!= ',') {
если (*p == '1') {
значение &= маска;
}
маска <<= 1;
}
р++;
}
вернуть (значение % 3 == 0)? 1 : 0;
}
Предполагается, что формат «ввода» действителен.
*/
int is_divisible_by_3_lsb (char * input) {
беззнаковое значение = 0;
беззнаковая маска = 1;
символ *p = ввод;
в то время как (*р) {
если (*p!= ',') {
если (*p == '1') {
значение &= маска;
}
маска <<= 1;
}
р++;
}
вернуть (значение % 3 == 0)? 1 : 0;
}


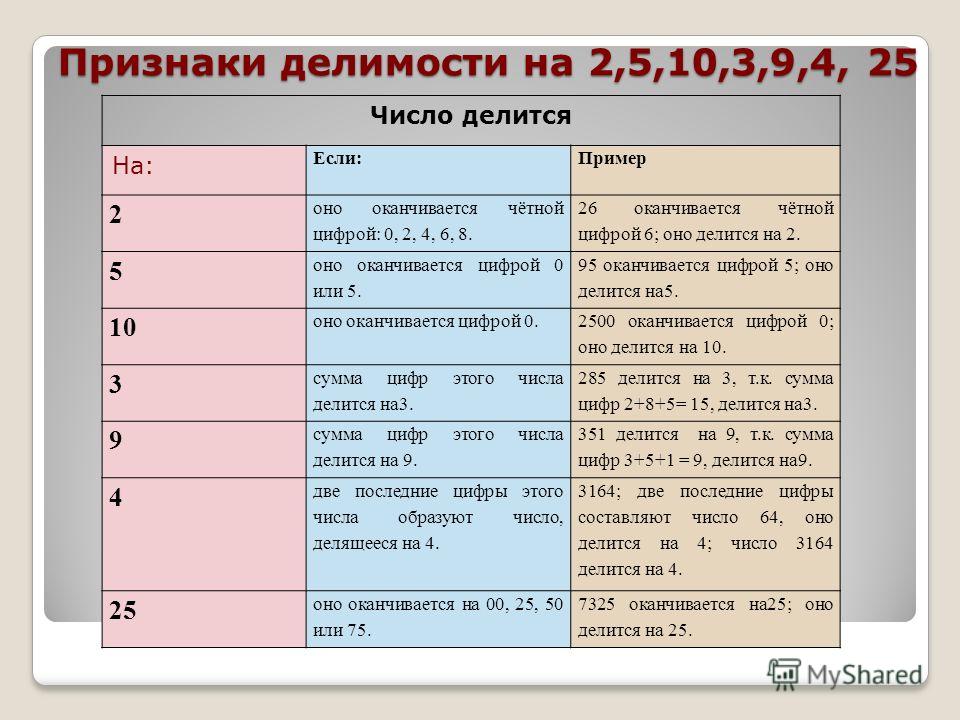
 Делится ли 9896 на 7?
Делится ли 9896 на 7?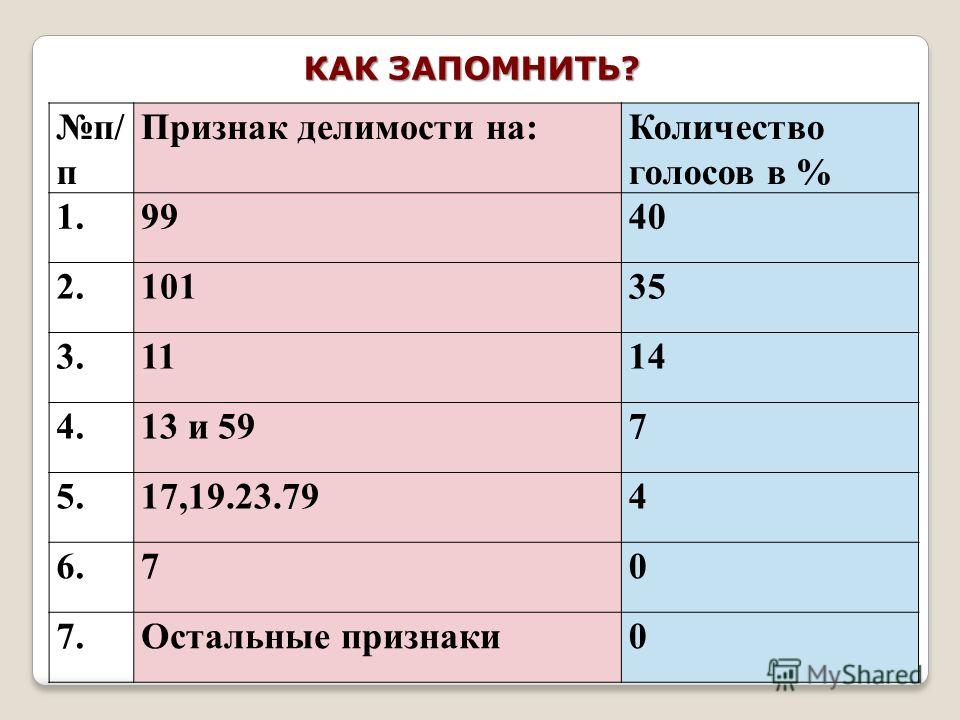 Чтобы проверить,
93 025 делится на 3,
Чтобы проверить,
93 025 делится на 3, 
 888
888 Тогда 100 − 4
= 96 тоже делится на 4.
Тогда 100 − 4
= 96 тоже делится на 4. 

 Заполните узоры. Обратите внимание на закономерности в остатках !
Заполните узоры. Обратите внимание на закономерности в остатках ! Мы знаем, что 686 делится на 7 без остатка.
Мы знаем, что 686 делится на 7 без остатка.

 Также доступен в виде печатной копии.
Также доступен в виде печатной копии.