«Окружность. Длина окружности», 5-й класс
«Окружность. Длина окружности», 5-й класс- Никитич Татьяна Николаевна, учитель математики
Разделы: Математика
Класс: 5
Оборудование:
- Игрушечные автомобили с различным диаметром колеса;
- мерки – тесьма или нить.
- линейки.
- листы бумаги с таблицей вида:
Группа С S d
Все перечисленное раздать по количеству подгрупп.
План оформления доски:
| Задача 1. | Окружность | Таблица | Задача 2. |
Таблица:
| Группа № | С (длина окружности) | S (путь) | d (диаметр колеса) |
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
Т.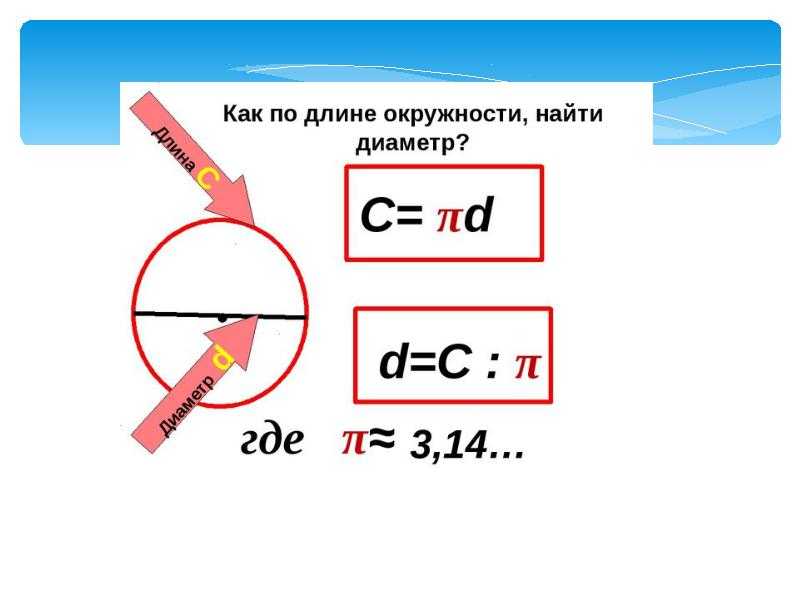 Н. Н. |
Цель: повторить понятие окружности, ее диаметра; получить формулу длины окружности и научить применять ее при решении задач, число π.
1. Анализ заданий
| Дети | |
| – На доске изображена геометрическая фигура. Как она называется? | – Окружность. |
| – Дайте определение окружности. | Окружность – это замкнутая линия, все точки которой равноудалены от одной, называемой центром окружности. |
| – Что мы называем ее радиусом? | – Радиус – это расстояние от центра до любой точки окружности.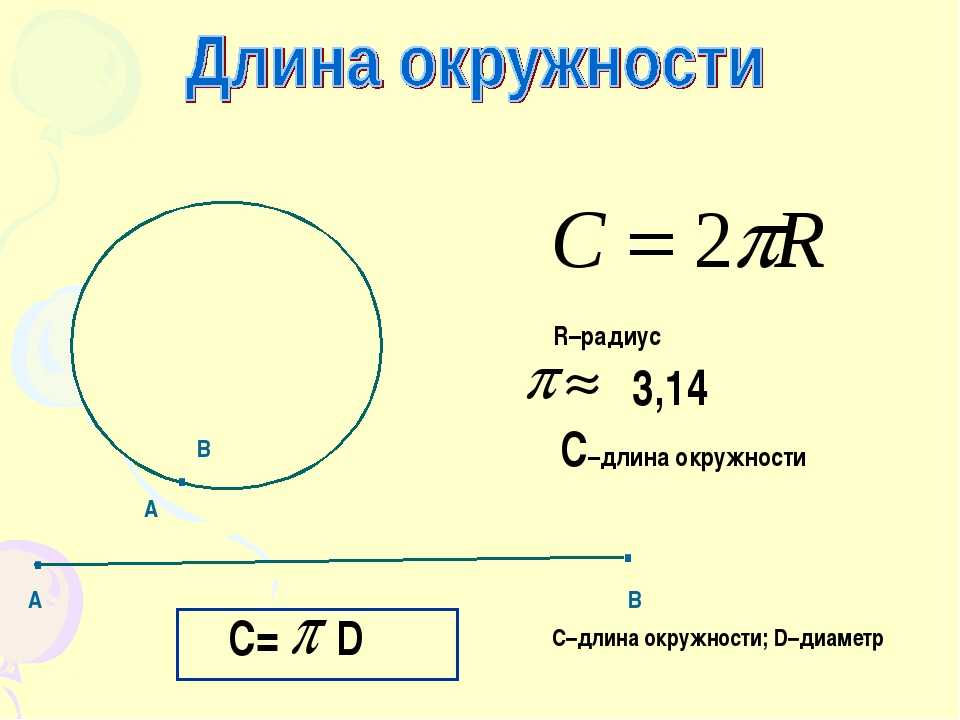 |
| – Что мы называем ее диаметром? | – Диаметр – это отрезок, соединяющий 2 точки окружности и проходящий через центр. |
| – Каким соотношением связаны между собой диаметр и радиус? | – d=2r |
| – Что мы знаем о размере всех d, всех r одной окружности? | – Они равны между собой. |
| –Нам трудно представить свою жизнь без окружности, ведь она является математической моделью многих окружающих нас предметов. Приведите примеры. | – Баранка, обруч, колесо и тд. |
2. Постановка проблемы
| Учитель | Дети |
| –На каждом столе автомашины, моделью каких их частей является окружность? | – Руль, колесо, обода фар и тд. |
| Вашему вниманию предлагается следующая задача (задача 1): Какой путь пройдет ваш автомобиль, если его правое колесо сделает 200 оборотов?Какие варианты решения? |
– Измерить длину окружности, проходящей по поверхности колеса и умножить ее на 200. |
| – Молодцы, но для того, чтобы не забыть измеренные величины, я прошу вас записать их в таблицу, лежащую перед вами. А чтобы иметь возможность обобщить эти результаты, я буду заполнять сводную таблицу на доске. |
(проводятся измерения, вычисления, заполняются таблицы и сводная таблица на доске (графы С и S)). |
| – Почему получили различные длины окружностей? | – Различные размеры колес. |
| – От чего зависит размер? | – От диаметра. |
| – Молодцы. В Республике Беларусь есть город Жодино. Он известен тем, что там расположен завод, выпускающий карьерные самосвалы марки «БелАз», грузоподъемностью 720 тонн (грузоподъемность Жигулей 440 кг). Внимание вопрос: какой путь пройдет такой самосвал, если правое переднее колесо делает 200 оборотов (диаметр колеса 3,7 метров)? (Задача 2 на доске была закрыта) |
– Не знаем как найти длину окружности, чтобы умножить ее на количество оборотов. |
| – Но нам дан диаметр. | – Но неизвестна формула, связывающая диаметр и длину окружности. |
| – Значит, для решения задачи нам нужно установить связь между диаметром и длиной окружности.Значит, тема сегодняшнего урока… | – Нахождение длины окружности, если известен ее диаметр. |
3.
 Выход из проблемной ситуации
Выход из проблемной ситуации| Учитель | Дети |
| – Измерьте диаметр колес вашего автомобиля. Занесите его в таблицу. | |
| – У каждого автомобиля самая большая длина окружности колеса? | – У того, у кого диаметр больше |
| – Какой вывод можно сделать? | – Чем больше диаметр, тем больше длина окружности. |
| – Посчитайте чему равно отношение С к d? | – Во всех случаях С/d=3 |
| – Оказывается, что если посчитать точнее, то С/d=3, 1/7=3,14159265 C/d=π, C=πd D=2r, C=2 πr |
– π=C/d=3,14 |
| – Как связаны между собой d и с? | – Прямопропорционально. |
| – Мы получили формулы, которые связывают длину окружности с диаметром, теперь мы можем вернуться к нашей задаче. S=C*n C=π*d=3,14*3,7=11,618 метров S=2323,6 метров. Значит, чтобы найти длину любой окружности надо знать радиус и знать формулу: C=2πr |
– Каждая группа считает самостоятельно |
4. Закрепление пройденного
Найти длину окружности, изображенной на рисунке 12, №№ 850, 851, 852.
Домашнее задание: №№ 868, 869, 873(а,б), 866.
5. Итог урока
чему научились сегодня на уроке? (Находить длину любой окружности, зная ее диаметр по формуле: С=π*d.
6. Список литературы
- Г.В. Дорофеев, Л.Г. Петерсон «Математика. 5 класс» — М.:Баласс, 1999.
- Е.Л. Мельникова «Проблемный урок или как открывать знания с учениками» — М., 2002.
3 способа как просто и правильно определить длину окружности велосипедного колеса для настройки велокомпьютера
Для настройки велокомпьютера в него нужно внести длину окружности велосипедного колеса. Это основная настройка, в зависимости от которой рассчитывается большинство показателей.
Рассмотрим как ее найти.
Первый и самый простой способ найти длину окружности колеса велосипеда
Посмотреть на размер покрышки, написанный на ней сбоку, и выбрать в таблице к велокомпьютеру длину окружности колеса.
Обычно такие таблицы идут в комплекте с компьютером, но если ее нет, то приведем здесь один из вариантов.
Уточнить совместимость разных маркировок и размеров покрышек можно в таблице взаимозаменяемости, а здесь приведем только схему с пояснениями какие цифры, что обозначают в различных видах маркировки размеров покрышек.
Второй способ измерить длину окружности колеса
Лучше всего его делать вдвоем – один сидит на велосипеде, а второй замеряет. При сидячем велосипедисте измерения будут более точными, так как учитывается сжатие покрышки при реальной поездке, да и ставить метки на асфальте удобнее. Не забудьте, что колеса должны быть накачены до того давления, на котором потом будите кататься.
При сидячем велосипедисте измерения будут более точными, так как учитывается сжатие покрышки при реальной поездке, да и ставить метки на асфальте удобнее. Не забудьте, что колеса должны быть накачены до того давления, на котором потом будите кататься.
- Ставим велосипед вертикально и хозяин садится на него.
- В месте соприкосновения колеса с дорогой мелом рисуем линию на боку покрышки и дороге. Они, естественно, должны совпадать.
- Проезжаем на велосипеде по прямой так, чтобы колесо сделало один полный оборот.
- Там где линия на колесе снова коснулась земли, ставим вторую метку.
- Измеряем расстояние между двумя метками – это и есть длина окружности колеса.
- Для повышения точности расчетов можно сделать 2-3 замера и взять среднее или проехать не один, а три оборота колеса и разделить полученное расстояние на 3.
Можно обмотать колесо швейным сантиметром, ниткой, бечевкой и измерить ее. Правда реальный опыт показывает, что это сделать менее удобно.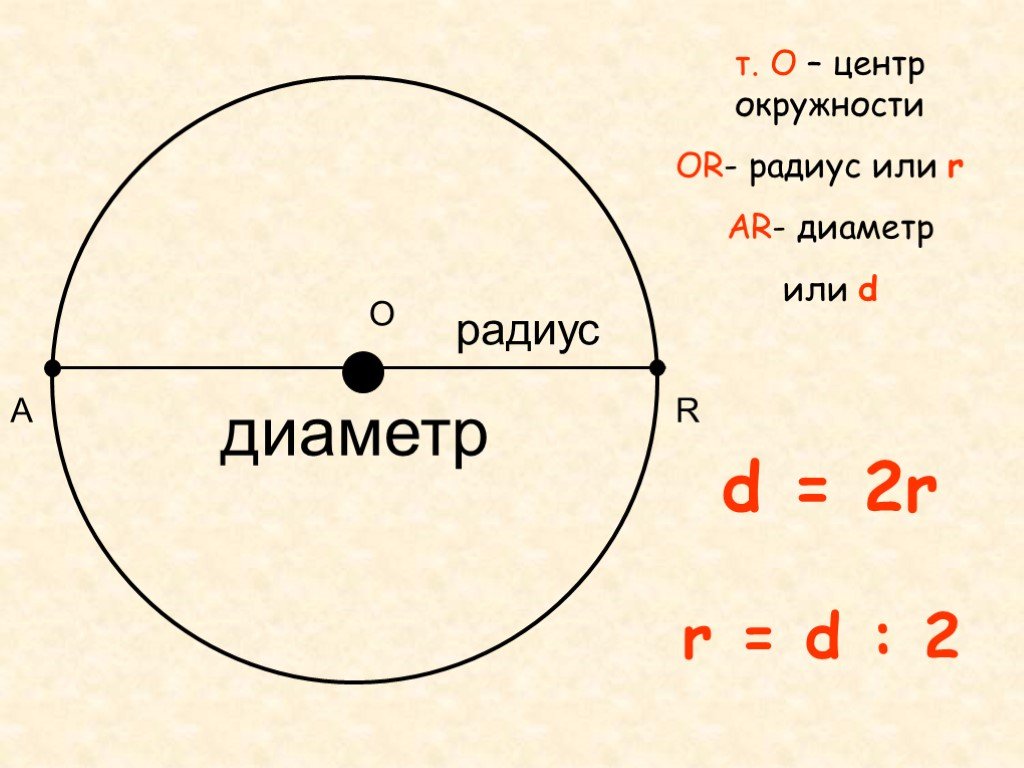 Нитка должна лежать точно по верху покрышки, а не вилять по ее поверхности, что в теории легко, а на практике не очень. И, второе, при таком способе не учитывается прогиб покрышки.
Нитка должна лежать точно по верху покрышки, а не вилять по ее поверхности, что в теории легко, а на практике не очень. И, второе, при таком способе не учитывается прогиб покрышки.
Третий способ вычислить длину окружности колеса определив его радиус
Далее, для тех, кто помнит математику.
Измерить радиус колеса от центра втулки. до наружного края покрышки (или до земли). Делать это нужно на стоящем велосипеде.
Лучше мерить вертикально до земли – так не будет погрешности на изгиб из-за того, что втулка значительно шире колеса.
Напоминаю — меряем именно от центра втулки, а не от ее краев, измеряя радиус покрышки по ее наружнему краю.
Точно измерив радиус колеса в мм и, вспомнив школьный курс математики, рассчитываем длину окружности по формуле: l = 2πR (или πD)
Длина окружности колеса (в мм) = 2 * 3,1415 (что есть число «Пи») * измеренный радиус (в мм)
Что можно получить дополнительно.
Через известный радиус, умножив его на 2, получаем диаметр покрышки в мм. Для перевода диаметра из мм в дюймы делим его на 25,4 (1 дюйм = 25,4 мм) и получаем размер колеса и его покрышки в дюймах. Результат вычислений можно округлить до стандартных дюймовых размеров колес, а длину окружности колеса выбрать из таблицы, приведенной в первом способе в начале статьи.
Для перевода диаметра из мм в дюймы делим его на 25,4 (1 дюйм = 25,4 мм) и получаем размер колеса и его покрышки в дюймах. Результат вычислений можно округлить до стандартных дюймовых размеров колес, а длину окружности колеса выбрать из таблицы, приведенной в первом способе в начале статьи.
Ну вот и все. Вычислив нужное значение заносим его в велокомпьютер.
Что еще можно почитать о велосипедных колесах и ободах:
- Велосипедные обода
- Как измерить ширину обода велосипедного колеса
- Как определить диаметр колеса велосипеда
- Ободная лента (флиппер) — что это такое и для чего нужна
Определение окружности с помощью калькулятора — открытый справочник по математике
Определение окружности с помощью калькулятора — открытый справочник по математикеОткрытый справочник по математике
Главная Контакт О Тематический указатель
Линия, образующая замкнутый контур, каждая точка которого находится на фиксированном расстоянии от центральной точки.
Попробуйте это Перетащите оранжевую точку. Круг можно перемещать, перетаскивая центральную точку и изменить размер, перетащив точку на круге.
Окружность — это тип линии. Представьте себе прямую отрезок линии, изогнутый до тех пор, пока его концы не соединятся. Затем расположите эту петлю так, чтобы она стала точно круглой, то есть все точки вдоль этой линии находились на одинаковом расстоянии от центральной точки.
Есть разница между кругом и диском. Окружность — это линия, поэтому, например, у нее нет площади — так же, как у линии нет площади. Однако диск представляет собой круглую часть самолет который имеет круглую форму. Если вы нарисуете на бумаге круг и вырежете его, круглая часть будет диском.
Свойства круга
| Центр | Точка внутри круга. Все точки на окружности равноудалены (одинаковое расстояние) от центральной точки. |
| Радиус | Радиус — это расстояние от центра до любой точки окружности. Это половина диаметра.
См. Радиус круга. Это половина диаметра.
См. Радиус круга. |
| Диаметр | Расстояние по окружности. Длина любого хорда, проходящая через центр. Это в два раза больше радиуса. См. Диаметр круга. |
| Окружность | Длина окружности — это расстояние по окружности. Видеть Окружность круга. |
| Зона | Строго говоря, круг — это линия, поэтому он не имеет площади. Обычно имеется в виду площадь области, заключенной в круг. См. Площадь, обведенная кругом. |
| Хорд | Отрезок, соединяющий любые две точки окружности. Видеть Определение аккорда |
| Тангенс | Линия, проходящая через окружность и касающаяся ее только в одной точке. См. определение касательной |
| Сеанс | Линия, пересекающая окружность в двух точках.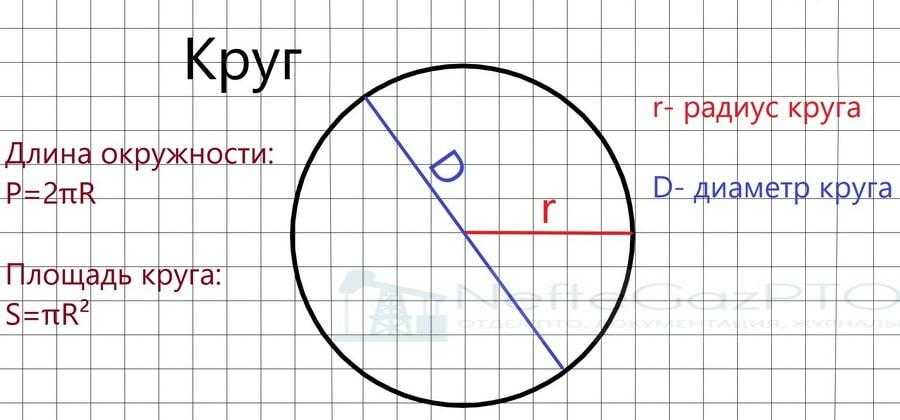 См. определение секущей См. определение секущей |
Калькулятор
| Радиус | очистить | |
| Диаметр | очистить | |
| Зона | очистить | |
| Окружность | очистить | |
Используйте калькулятор выше, чтобы рассчитать свойства круга.
Введите любое отдельное значение, и остальные три будут рассчитаны. Например: введите радиус и нажмите «Рассчитать». Будут рассчитаны площадь, диаметр и окружность.
Точно так же, если вы введете область, радиус, необходимый для получения этой области, будет рассчитан вместе с диаметром и окружностью.
Пи
В любом круге, если разделить длину окружности (расстояние по кругу) на его диаметр (расстояние по кругу), вы всегда получаете одно и то же число. Это число называется Пи и примерно равно 3,142. См. Определение числа пи.
Это число называется Пи и примерно равно 3,142. См. Определение числа пи.Отношение к эллипсу
На самом деле круг — это частный случай эллипса. В эллипсе, если вы сделаете большую и малую оси одинаковой длины, в результате получится круг с обоими фокусами в центре. См. определение эллипсаКруг как коническое сечение
Вы можете определить круг как форму, созданную, когда плоскость проходит через конус под прямым углом к оси конуса. Подробнее об этом см. Конические сечения — круг.
Круг как локус
Круг — это локус всех точек на фиксированном расстоянии от данной (центральной) точки. Это определение предполагает, что плоскость состоит из бесконечного числа точек, и мы выбираем только те, которые которые находятся на фиксированном расстоянии от центра. (См. определение локуса.)
Уравнения окружности
В координатной геометрии круг можно описать с помощью системы уравнений.
Подробнее об этом см.
Уравнения окружностей и эллипсов.
Другие темы кружка
Общий
- Определение круга
- Радиус окружности
- Диаметр круга
- Длина окружности
- Части круга (схема)
- Определение полукруга
- Тангенс
- Секущая
- Аккорд
- Теорема о пересекающихся хордах
- Теорема о пересекающихся секущих длинах
- Теорема о пересекающихся секущих углах
- Площадь круга
- Концентрические окружности
- Кольцо
- Площадь кольца
- Сектор круга
- Площадь сектора круга
- Сегмент круга
- Площадь сегмента окружности (данный центральный угол)
- Площадь сегмента круга (данная высота сегмента)
Уравнения окружности
- Основное уравнение окружности (центр в начале координат)
- Общее уравнение окружности (центр в любом месте)
- Параметрическое уравнение окружности
Уголки по окружности
- Угол вписанный
- Центральный уголок
- Теорема о центральном угле
Дуги
- Дуга
- Длина дуги
- Измеритель угла дуги
- Смежные дуги
- Большая/малая дуги
- Перехваченная дуга
- Сектор круга
- Радиус дуги или сегмента при заданной высоте/ширине
- Стрела — высота дуги или сегмента
(C) 2011 Copyright Math Open Reference.
Все права защищены
частей круга — определение, формулы, примеры
Есть много частей круга , которые делают его кругом. Круг представляет собой двумерную форму и измеряется с точки зрения его радиуса. Слово «круг» происходит от греческого слова «киркос», означающего «кольцо» или «обруч». К частям круга относятся радиус, диаметр, длина окружности и так далее. Давайте узнаем о круге и его частях подробно.
| 1. | Определение круга |
| 2. | Из каких частей состоит круг? |
| 3. | Часто задаваемые вопросы о частях круга |
Определение круга
Окружность можно определить как двухмерную фигуру, образованную набором точек, смежных друг с другом и равноудаленных от фиксированной точки. Неподвижная точка на этой изогнутой плоской фигуре называется центром окружности, общее расстояние между точками от центра называется радиусом, а линия, пересекающая центр окружности, начинающаяся из одной точки в другую, называется диаметр. Круг имеет две основные области, а именно: внутреннюю часть круга и внешнюю часть круга. Внутренняя часть круга состоит из области внутри круга, а внешняя часть круга — это область вне круга.
Круг имеет две основные области, а именно: внутреннюю часть круга и внешнюю часть круга. Внутренняя часть круга состоит из области внутри круга, а внешняя часть круга — это область вне круга.
Из каких частей состоит круг?
Круг — это замкнутая фигура с изогнутой границей, состоящая из множества частей, представляющих свойства и характеристики круга.
Круг и его части
Различные части круга перечислены ниже:
- Окружность
- Радиус
- Диаметр
- Аккорд
- Касательная
- Секущая
- Арка
- Сегмент
- Сектор
Давайте подробно обсудим каждую из частей.
Окружность круга
Окружность круга является его границей. Другими словами, когда мы измеряем границу или расстояние вокруг круга, эта мера называется окружностью и выражается в единицах длины, таких как сантиметры, метры или километры. Окружность круга состоит из трех наиболее важных элементов, а именно центра, диаметра и радиуса.
Поскольку мы не можем использовать линейку (шкалу) для измерения расстояния до этой изогнутой фигуры, мы применяем формулу, в которой используются радиус, диаметр и значение числа Пи (π). Формулы для длины окружности даются следующим образом:
- Когда радиус дан: Длина окружности по формуле = 2πr
- Если задан диаметр: длина окружности по формуле = π × D
Где,
- r = радиус окружности.
- D = диаметр окружности.
- π = Пи со значением, приближенным к 3,14159 или 22/7.
Радиус окружности
Радиус окружности — это длина отрезка, соединяющего центр окружности с любой точкой окружности. У круга может быть много радиусов (форма множественного числа радиуса), и они измеряются одинаково. Обычно радиус окружности обозначают буквой «r».
Для вычисления радиуса круга, когда известны диаметр, площадь круга и длина окружности, мы используем следующие формулы:
- Радиус окружности = Диаметр / 2.
 Диаметр в два раза больше длины радиуса, а также является самой длинной хордой окружности. Когда диаметр известен, мы используем эту формулу.
Диаметр в два раза больше длины радиуса, а также является самой длинной хордой окружности. Когда диаметр известен, мы используем эту формулу. - Радиус окружности = Окружность / 2π — Окружность — это периметр круга, и когда длина окружности задана, мы используем эту формулу.
- Радиус круга = √(Площадь/π) – Площадь круга – это пространство внутри круга. Следовательно, когда дана площадь круга, мы используем эту формулу.
Диаметр окружности
Диаметр окружности — это отрезок, проходящий через центр окружности и концы которого лежат на окружности окружности. Диаметр также известен как самая длинная хорда круга и в два раза больше длины радиуса. Диаметр измеряется от одного конца круга до точки на другом конце круга, проходящей через центр. Диаметр обозначается буквой D. Может быть бесконечное количество диаметров, где длина каждого диаметра окружности равна длине.
Чтобы вычислить диаметр круга, когда известны радиус, площадь круга и длина окружности, мы используем следующие формулы:
- Диаметр = длина окружности/π (используется, когда дана длина окружности)
- Диаметр = Радиус × 2 (используется, когда указан радиус)
- Диаметр = 2√(Площадь/π) (используется, когда дана площадь круга)
Хорда окружности
Хорда окружности — это отрезок, соединяющий две точки на окружности окружности.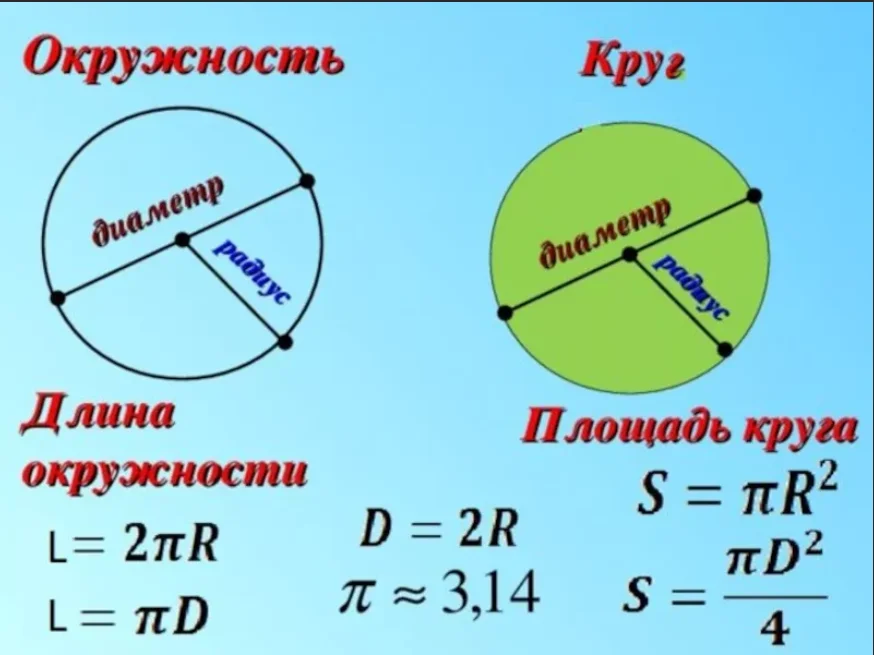 Хорда делит круг на две области, известные как сегмент круга, который можно назвать второстепенным сегментом и большим сегментом в зависимости от области, охватываемой хордой. В круге, когда хорда бесконечно продолжена в обе стороны, она становится секущей. На приведенном ниже рисунке PQ представлен хордой окружности с центром O в центре.
Хорда делит круг на две области, известные как сегмент круга, который можно назвать второстепенным сегментом и большим сегментом в зависимости от области, охватываемой хордой. В круге, когда хорда бесконечно продолжена в обе стороны, она становится секущей. На приведенном ниже рисунке PQ представлен хордой окружности с центром O в центре.
Чтобы вычислить хорду окружности, мы используем две основные формулы:
- Длина хорды = 2 × √(r 2 − d 2 ) (используя перпендикулярное расстояние от центра)
- Длина хорды = 2 × r × sin(c/2) (с использованием тригонометрии)
Где,
- r — радиус окружности
- c — угол, образуемый в центре хордой .
- d — расстояние по перпендикуляру от хорды до центра окружности.
Касательная окружности
Касательная окружности определяется как прямая линия, которая касается кривой окружности только в одной точке и не входит внутрь окружности.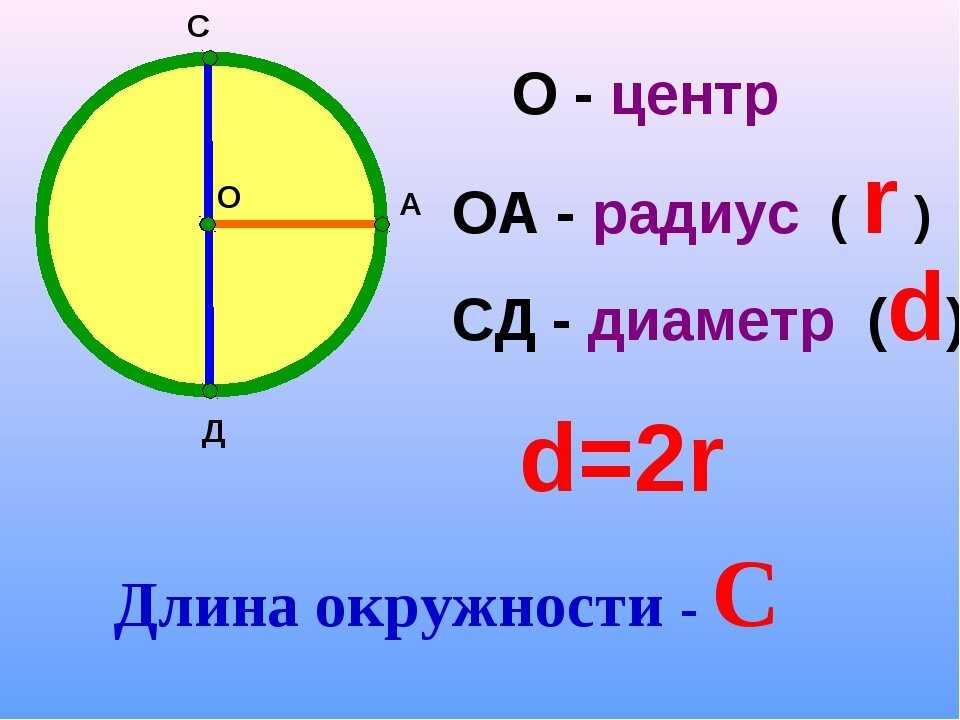 Касательная касается радиуса окружности под прямым углом. Два основных аспекта, которые следует помнить в касательной, — это наклон (м) и точка на линии. Общее уравнение или формула касательной к окружности:
Касательная касается радиуса окружности под прямым углом. Два основных аспекта, которые следует помнить в касательной, — это наклон (м) и точка на линии. Общее уравнение или формула касательной к окружности:
- Уравнение касательной к окружности x 2 + y 2 = a 2 для линии y = mx + c задается уравнением y = mx ± a √[1+ m 2 ]
- ТАНГАНСТВА КРУГКА Уравнения x 2 + Y 2 = A 2 AT (A 1 , B 1) IS XA 1 + YB 1 is is 1 + YB 1 is 9036. Это означает, что уравнение касательной выражается как xa 1 + yb 1 = a 2 , где a 1 и b 1 — координаты, в которых проведена касательная.
Секущая окружности
Секущая окружности — это линия, пересекающая окружность и пересекающая окружность в двух различных точках. Разница между хордой и секущей заключается в том, что хорда — это отрезок, концы которого находятся на окружности окружности, тогда как секущая проходит через окружность, образуя хорду или диаметр окружности.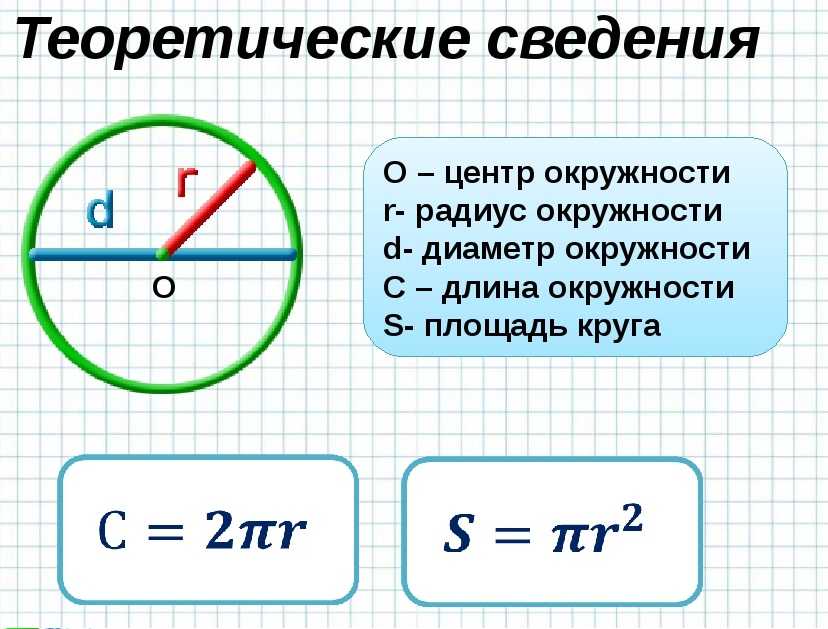
В круге используются три теоремы о секущих, которые приведены ниже:
- Теорема 1: Когда две секущие пересекаются во внешней точке, произведение одной целой секущей и ее внешней части равно произведению другой целой секущей и ее внешней части.
- Теорема 2: Две секущие могут пересекаться внутри или вне круга.
- Теорема 3: Если секущая и касательная проведены к окружности из общей внешней точки, то произведение длины всей секущей и ее внешней секущей равно квадрату длины касательной.
На приведенном ниже рисунке показаны секущая PQ и хорда AB.
Дуга окружности
Дуга окружности представляет собой изогнутую часть или часть окружности окружности. Другими словами, изогнутая часть объекта математически называется дугой. Дуга окружности имеет две дуги, а именно малую дугу и большую дугу. Чтобы найти меру этих дуг, нам нужно найти длину дуги вместе с углом, подвешенным на дуге любых двух точек. Для расчета длины дуги мы используем различные формулы, основанные на единицах измерения центрального угла (градусы или радианы). Для круга формула длины дуги равна θ, умноженному на радиус круга. Формулы:
Для круга формула длины дуги равна θ, умноженному на радиус круга. Формулы:
- Длина дуги = θ × r (используется для радиан)
- Длина дуги = θ × (π/180) × r (используется для градусов)
Где,
- L = длина дуги
- θ = центральный угол дуги
- r = радиус окружности
Сегмент окружности
Сегмент окружности — это область, ограниченная дугой и хордой окружности. Сегменты бывают двух типов — малый сегмент и большой сегмент. Малый сегмент образован малой дугой, а большой сегмент образован большой дугой окружности. Чтобы вычислить отрезок круга, мы рассматриваем площадь отрезка, состоящего из сектора (дуга + 2 радиуса) и треугольника. Следовательно, формула площади сегмента может быть выражена следующим образом
- Площадь сегмента круга = площадь сектора — площадь треугольника
Примечание: Чтобы найти площадь большого сегмента круга, мы просто вычитаем соответствующую площадь меньшего сегмента из общей площади круга.
Сектор круга
Сектор круга представляет собой круговую часть круга, состоящую из дуги с двумя радиусами, делящими круг на меньший сектор и большой сектор. Большая часть круга называется большим сектором, тогда как меньшая часть круга называется малым сектором. 2 радиуса встречаются в части окружности круга, известной как дуга, образуя сектор круга. Формулы для расчета сектора круга:
- Площадь сектора (A) = (θ/360°) × πr 2 (когда задан угол)
- Длина секции (l) = (θπr)/180 (если указана длина)
- Площадь сектора круга = (l × r)/2 (если заданы длина и радиус)
- Периметр сектора круга = 2 Радиус + ((θ/360) × 2πr )
Где,
- r = радиус окружности.
- l = длина дуги.
- θ = угол в градусах.
- π = Пи со значением, приближенным к 3,14159 или 22/7.
☛ Похожие темы
- Окружность к диаметру
- Полукруг
- 3D-фигуры
Часто задаваемые вопросы о частях круга
Из каких частей состоит круг?
Части окружности включают окружность, радиус, диаметр, хорду, касательную, секущую, дугу, сегмент и сектор. Каждая из этих частей круга играет важную роль в формировании круга.
Каждая из этих частей круга играет важную роль в формировании круга.
Какая часть круга самая длинная?
Самая длинная часть круга — это диаметр, т. е. расстояние от одного конца круга до другого конца круга. Отрезок, проходящий через центр, соединяющий две точки окружности, считается самой длинной частью. Следует отметить, что диаметр является самой длинной хордой окружности.
Каковы 4 основные части круга?
Четыре основные части круга: радиус, диаметр, центр и окружность. Центр окружности – это точка, равноудаленная от всех сторон окружности. Радиус — это длина линии от центра окружности до любой точки кривой окружности. Диаметр – это отрезок, который пересекает центр круга от одного конца круга до другого конца. Окружность круга — это граница или расстояние, которое завершает круг.
На сколько частей делится отрезок окружности?
Сегмент круга делится на две части — малый сегмент и большой сегмент. Меньшая часть сегмента круга называется малым сегментом, тогда как большая часть сегмента круга называется большим сегментом.

 Диаметр в два раза больше длины радиуса, а также является самой длинной хордой окружности. Когда диаметр известен, мы используем эту формулу.
Диаметр в два раза больше длины радиуса, а также является самой длинной хордой окружности. Когда диаметр известен, мы используем эту формулу.