Как найти площадь четырехугольника — Wiki How To Русский
‘).insertAfter(«#intro»),$(‘
‘).insertBefore( «.youmightalsolike»),$(‘
‘).insertBefore(«#quiz_container»),$(‘
‘).insertBefore(«#newsletter_block_main»),ja(!0),c=document.getElementsByClassName(«scrolltomarker»),a=0;a
В этой статье:
Квадрат, прямоугольник и другие параллелограммы
Трапеция
Дельтоид
Четырехугольник произвольной формы
Показать еще 1…
Показать меньше…
Дополнительные статьи
Источники
Вам дана задача, в которой требуется найти площадь четырехугольника, а вы даже не знаете, что такое четырехугольник? Не волнуйтесь, эта статья вам поможет! Четырехугольник — это любая фигура с четырьмя сторонами. Для вычисления площади четырехугольника нужно определить тип четырехугольника, который вам дан, и воспользоваться соответствующей формулой.
Шаги
1
Определение параллелограмма. Параллелограмм — это четырехугольник, у которого противоположные стороны равны и параллельны друг другу. Квадраты, прямоугольники и ромбы — это параллелограммы.
- Квадрат — это параллелограмм, у которого все стороны равны и пересекаются под прямым углом.
- Прямоугольник — это параллелограмм, у которого все стороны пересекаются под прямым углом.
- Ромб — это параллелограмм, у которого все стороны равны.
2
Площадь прямоугольника. Чтобы вычислить площадь прямоугольника, нужно знать его ширину (короткая сторона; представьте ее как высоту) и длину (длинная сторона; представьте ее как сторону, к которой проведена высота). Площадь прямоугольника равна произведению длины на ширину.
- ‘Площадь = длина х высота , или S = a х h.
- Пример: если длина прямоугольника равна 10 см, а ширина равна 5 см, то площадь этого прямоугольника: S = 10 х 5 = 50 квадратных сантиметров.

- Не забывайте, что площадь измеряется в квадратных единицах (квадратных метрах, квадратных сантиметрах и так далее).
3
Площадь квадрата. Квадрат — это частный случай прямоугольника, поэтому используйте ту же формулу, что и для нахождения площади прямоугольника. Но в квадрате все стороны равны, поэтому площадь квадрата равна любой из его сторон, возведенной в квадрат (то есть умноженной саму на себя).[1] X Источник информации
- Площадь = сторона х сторона, или S = a2.
- Пример: если сторона квадрата равна 4 см (a = 4), то площадь этого квадрата: S = a
4
Площадь ромба равна произведению его диагоналей, разделенной на два. Диагонали — это отрезки, соединяющие противоположные вершины ромба.
 [2]
X
Источник информации
[2]
X
Источник информации - Площадь = (диагональ1 х диагональ2)/2, или S = (d1 × d2)/2
- Пример: если диагонали ромба равны 6 см и 8 см, то площадь этого ромба: S = (6 х 8)/2 = 24 квадратных сантиметров.
5
Площадь ромба также можно найти, если умножить его сторону на высоту, опущенную на эту сторону. Но не путайте высоту со смежной стороной. Высота — это прямая, опущенная из любой вершины ромба на противоположную сторону, и пересекающая противоположную сторону под прямым углом.
- Пример: если длина ромба равна 10 см, а его высота равна 3 см, то площадь такого ромба равна 10 х 3 = 30 квадратных сантиметров.
6
Формулы для вычисления площадей ромба и прямоугольника применимы к квадратам, так как квадрат — это частный случай как прямоугольника, так и ромба.

- Площадь = сторона х высоту, или S = a × h
- Площадь = (диагональ1 × диагональ2)/2, или S = (d1 × d2)/2
- Пример: если сторона квадрата равна 4 см, то его площадь равна 4 х 4 = 16 квадратных сантиметров.
- Пример: диагонали квадрата равны по 10 см. Вы можете найти площадь этого квадрата по формуле: (10 х 10)/2 = 100/2 =
Реклама
1
Определение трапеции. Трапеция — это четырехугольник, у которого две противоположные стороны параллельны друг другу. Каждая из четырех сторон трапеции может быть разной длины.
- Есть два способа вычисления площади трапеции (в зависимости от данных значений).
2
Найдите высоту трапеции. Высота трапеции — отрезок, соединяющий параллельные стороны (основания) и пересекающий их под прямым углом (высота не равна боковым сторонам).
 Вот как найти высоту трапеции:[3]
X
Источник информации
Вот как найти высоту трапеции:[3]
X
Источник информации - Из точки пересечения меньшего основания и боковой стороны проведите перпендикуляр к большему основанию. Этот перпендикуляр и есть высота трапеции.
- Чтобы вычислить высоту, используйте тригонометрию. Например, если вы знаете боковую сторону и прилегающий к ней угол, то высота равна произведению боковой стороны на синус прилегающего угла.
3
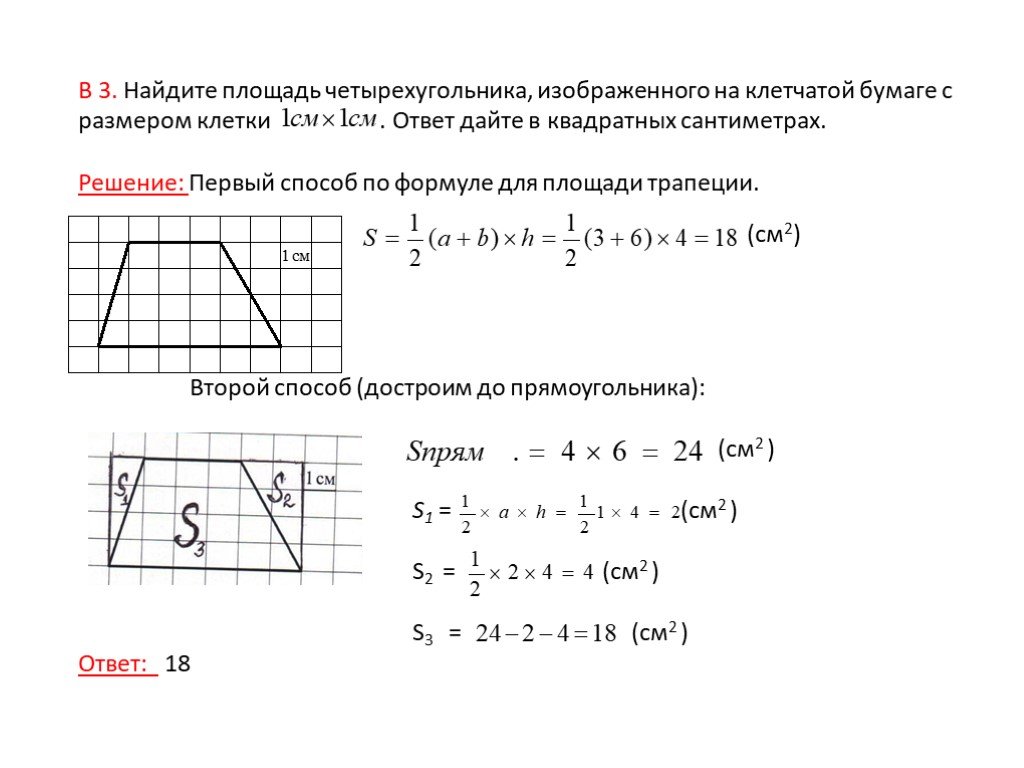
Найдите площадь трапеции, используя высоту. Если вы знаете высоту трапеции и оба основания, используйте следующую формулу для вычисления площади трапеции:
- Площадь = (основание1 + основание2)/2 × высота, или S = (a+b)/2 × h
- Пример: если высота трапеции равна 2 см, а основания трапеции равны 7 см и 11 см, то площадь этой трапеции: S = (a+b)/2 * h = (7 + 11)/2 * 2 = 18 квадратных сантиметров.
- Если высота трапеции равна 10, а основания трапеции равны 7 и 9, то площадь этой трапеции: S = (a+b)/2 * h = (7 + 9)/2 * 10 = (16/2) * 10 = 8 * 10 = 80.

4
Найдите площадь трапеции, используя среднюю линию. Средняя линия — это отрезок, параллельный основаниям и делящий боковые стороны пополам. Средняя линия равна среднему значению от обоих оснований (a и b): средняя линия = (a+b)/2.
- Площадь = средняя линия х высота, или S = m × h
- По сути, здесь вы используете формулу для нахождения площади трапеции по двум основаниям, но вместо (a+b)/2 подставлена m (средняя линия).
- Пример: если средняя линия трапеции равна 9 см, то площадь этой трапеции: S = m*h = 9 х 2 = 18 квадратных сантиметров (вы получили тот же ответ, что и в предыдущем шаге).
Реклама
1
Определение дельтоида. Дельтоид — это четырехугольник с двумя парами сторон одинаковой длины.
- Есть два способа вычисления площади дельтоида (в зависимости от данных значений).

- Есть два способа вычисления площади дельтоида (в зависимости от данных значений).
2
Найдите площадь дельтоида, используя формулу для нахождения площади ромба (с использованием диагоналей), так как ромб — это частный случай дельтоида, у которого все стороны равны. Напомним, что диагональ — отрезок, соединяющий противоположные вершины.
- Площадь = (диагональ1 х диагональ2)/2, или S = (d1 × d2)/2
- Пример: если диагонали дельтоида равны 19 см и 5 см, то площадь этого дельтоида: S = (19 х 5)/2 = 47,5 квадратных сантиметров.
- Если вы не знаете длины диагоналей и не можете их измерить, используйте тригонометрию, чтобы вычислить их. Прочтите эту статью, чтобы узнать больше информации.
3
Найдите площадь дельтоида, используя неравные стороны и угол между ними. Если вы знаете неравные стороны и угол между этими сторонами (θ), то площадь дельтоида вычисляется с помощью тригонометрии по формуле:[4] X Источник информации
- Площадь = (сторона1 х сторона2) х sin (угол), или S = (a × b) × sin(θ), где θ — угол между неравными сторонами.

- Пример: Если стороны дельтоида равны 4 см и 6 см, а угол между ними равен 120 градусам, то площадь дельтоида равна (6 х 4) х sin120 = 24 х 0,866 = 20,78 квадратных сантиметров.
- Обратите внимание, что вы должны использовать две неравные стороны и угол между ними; если вы используете две равные стороны и угол между ними, вы получите неправильный ответ.
Реклама
- Площадь = (сторона1 х сторона2) х sin (угол), или S = (a × b) × sin(θ), где θ — угол между неравными сторонами.
1
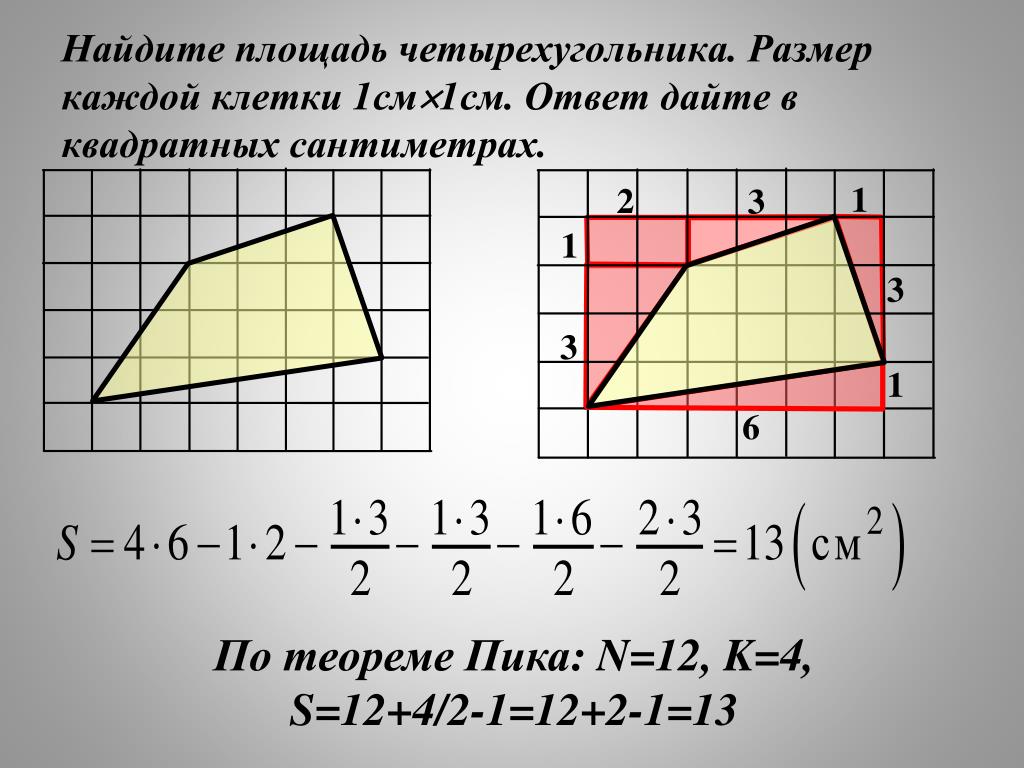
Если вам дан четырехугольник произвольной формы, то даже для таких четырехугольников существуют формулы для вычисления их площадей. Обратите внимание, что такие формулы требуют знания тригонометрии.- Во-первых, найдите длины всех четырех сторон. Обозначим их через a, b, c, d (а напротив с, а b напротив d).
- Пример: дан четырехугольник произвольной формы со сторонами 12 см, 9 см, 5 см и 14 см.
2
Найдите угол А между сторонами а и d и угол С между сторонами b и с (вы можете найти любые два противолежащих угла).

- Пример: в нашем четырехугольнике А = 80 градусов и C = 110 градусов.
3
Представьте, что существует отрезок, соединяющий вершины, образованные сторонами а и b и сторонами с и d.
- Площадь = 0,5 х сторона1 х сторона4 х sin(угол между стороной1 и стороной4) + 0,5 х сторона2 х сторона3 х sin(угол между стороной2 и стороной3), или
- Площадь = 0,5 a × d × sin A + 0,5 × b × c × sin C
- Пример: вы нашли стороны и углы, поэтому просто подставьте их в формулу.
- = 0,5 (12 × 14) × sin (80) + 0,5 × (9 × 5) × sin (110)
- = 84 × sin (80) + 22,5 × sin (110)
- = 84 × 0,984 + 22,5 × 0,939
- = 82,66 + 21,13 = 103,79 квадратных сантиметров.

- Обратите внимание, что если вы пытаетесь найти площадь параллелограмма (у которого противоположные углы равны), то формула примет вид: площадь = 0.5*(ad + bc) * sin A
Реклама
Источники
Об этой статье
На других языках
Как найти площадь четырехугольника — Wiki How Русский
Вам дана задача, в которой требуется найти площадь четырехугольника, а вы даже не знаете, что такое четырехугольник? Не волнуйтесь, эта статья вам поможет! Четырехугольник — это любая фигура с четырьмя сторонами. Для вычисления площади четырехугольника нужно определить тип четырехугольника, который вам дан, и воспользоваться соответствующей формулой.
Эту страницу просматривали 428 904 раза.
Реклама
Площадь четырехугольника — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Уроки повторения в 10 классе
Учитель: Векслер Е. В.
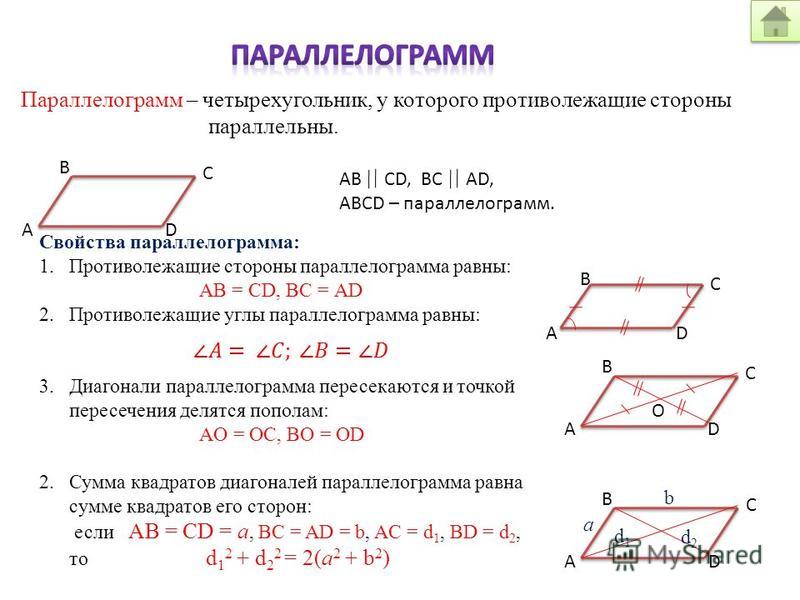
Параллелограмм – это четырехугольник,
противоположные стороны которого попарно параллельны.
Любые две противоположные стороны можно назвать
основаниями.
В параллелограмме противоположные стороны равны,
диагонали точкой пересечения делятся пополам,
противоположные углы попарно равны.
Прямоугольник – это параллелограмм, у которого
все углы прямые.
В прямоугольнике все диагонали равны.
В прямоугольнике квадрат диагонали равен сумме
квадратов двух смежных сторон.
В
А
С
D
Ромб – это параллелограмм, у которого все стороны
равны.
Диагонали ромба пересекаются под прямым углом.
Диагонали ромба являются биссектрисами его углов.
В
А
С
D
Трапеция – это четырехугольник у которого
противоположные стороны параллельны.
Параллельные стороны называются основаниями, две
другие боковыми сторонами.
основание
основание
Трапеция, у которой боковые стороны равны,
называется равнобедренной.
У равнобедренной трапеции углы при основании
равны.
Площадь произвольного
четырехугольника
d1 d 2
S
sin
2
диагонали
где d иd
1
2 четырехугольника
∟α – угол между
диагоналями
Площадь параллелограмма
b
S b h a b sin
где a, b – стороны
параллелограмма
α – один из углов
h — высота
h
a
α
Площадь квадрата
2
d
2
S a
2
Где a – сторона
d – диагональ
квадрата
d
a
Площадь ромба
d1 d 2
2
S
a sin
2
Где d иd
1
2
диагонали ромба
a – сторона ромба
α – угол
α
а
Площадь трапеции
BC AD
S
BH
2
B
А
C
D
H
Дано : ABCD — параллелограмм
Задача 1
AB=5, AD=8, ∟A=60°
B
C
Найти: площадь ABCD
Решение
A
D
S=AB·AD·sin A
S 5 8 sin 60
3
40
20 3
2
Дано: ABCD – ромб
Задача 2
AB=13, AC=24
B
Найти: площадь ромба
О
C
A
Решение
AO=½AC ( по cв-ву ромба)
АО=12
D
Треугольник АВО – прямоугольный
( по св-ву ромба)
По т.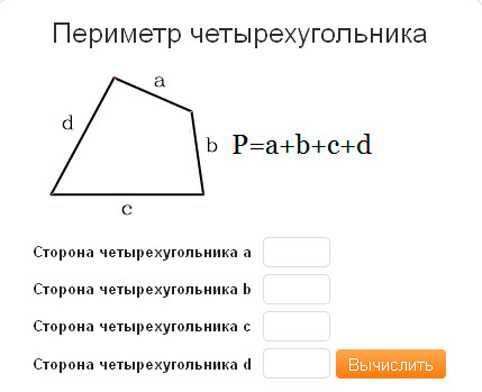 Пифагора ВО² = АВ²- АО²
Пифагора ВО² = АВ²- АО²
ВО² = 169 – 144 = 25
ВО=5
АС ВD АС 2 ВО
S
АС ВО 24 5 120
2
2
Дано: ABCD – трапеция
Задача 3
BE ┴ AD, BE=4, AD=10, BC=6
C
B
Найти: площадь ABCD
Решение
A
D
E
BC AD
S
BE
2
6 10
S
4 32
2
Задача 4
Дано:
ABCD – параллелограмм
BE=5, BF=4, ∟D=150°
B
C
F
Найти: площадь ABCD
Решение
По свойству параллелограмма
A
E
D
∟В=∟D=150°
∟A=∟C= ½ (360°- 2∟D)
∟A=30°
∆ АВЕ прямоугольный , т. к. ВЕ┴АD, катет ВЕ лежит против
угла А значит AB= 2 BE АВ= 10
По свойству параллелограмма АВ=CD= 10 , BF высота
тогда S= CD·BF= 10 · 4= 40
Найти площадь
параллелограмма
Задача 5
B
6
10
A
C
Н
D
Найти площадь
трапеции
Задача 6
B
7
C
17
A
23
D
English Русский Правила
Калькулятор площади четырехугольника
Создано Krishna Nelaturu
Отредактировано Adena Benn и Wojciech Sas, PhD
Последнее обновление: 30 декабря 2022 г.
- Что такое четырехугольник?
- Формула площади четырехугольника и вычисление площади неправильного четырехугольника
- Площадь распространенных типов четырехугольника
- Как использовать этот калькулятор площади четырехугольника
- Другие связанные калькуляторы
- Часто задаваемые вопросы
Наш калькулятор площади четырехугольника поможет вам определить площадь любого четырехугольника с различными известными параметрами. В этой статье кратко обсуждаются четырехугольники и различные доступные формулы площади четырехугольника . Итак, присоединяйтесь к нам ниже, чтобы узнать, как найти площадь четырехугольника.
Что такое четырехугольник?
В: Как определить четырехугольник?
А: «Четыре точки, соединенные прямыми линиями».
В: А что если очков коллинеарно ?
A: «Точки не должны лежать на одной прямой.»
В: Но что, если линии не образуют замкнутую фигуру ?
A: Четырехугольник — это замкнутая фигура (многоугольник) с четырьмя сторонами .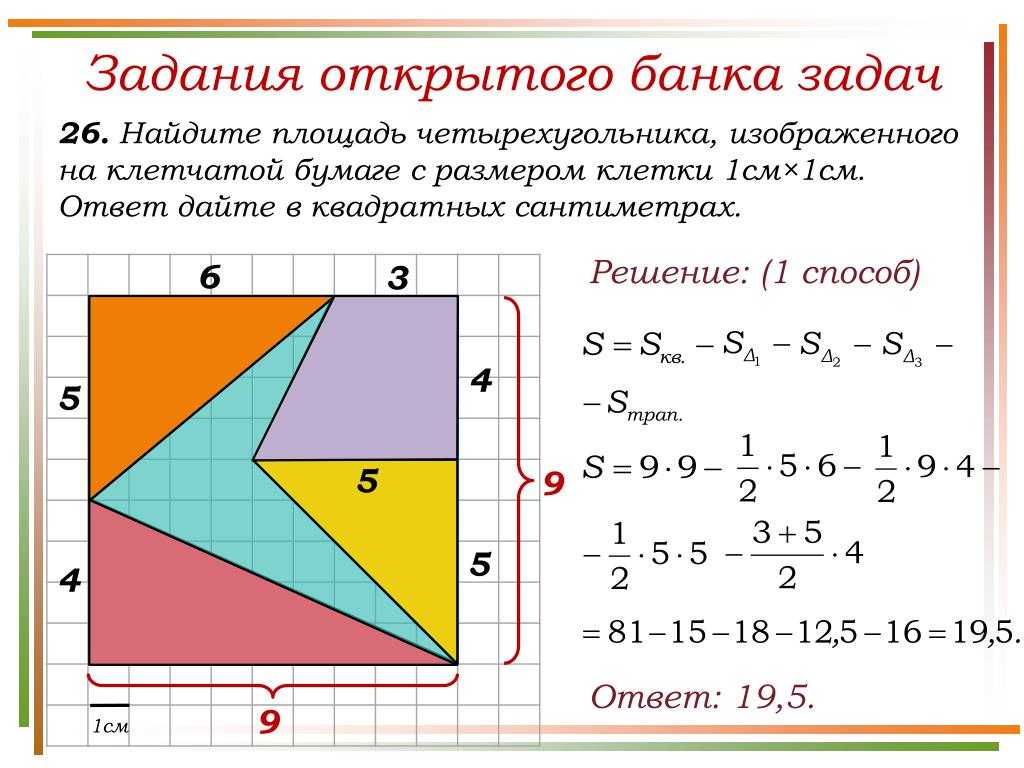
Четырехугольники можно увидеть повсюду, от бассейнов и футбольных полей до зданий и мостов. Распознавание геометрии конструкции значительно упростит расчеты. Существует много типов четырехугольников, таких как прямоугольники и трапеции. Чтобы быстро оценить площадь последнего, вы можете обратиться к калькулятору трапеций Omni. Давайте сначала научимся вычислять площадь неправильного четырехугольника.
Формула площади четырехугольника и вычисление площади неправильного четырехугольника
Существуют различные методы расчета площади неправильного четырехугольника на основе известных параметров:
- Из четыре стороны и два противоположных угла :
A = √((s-a)(s-b)(s-c)(s-d) — a∙b∙c∙d∙ cos 2 (δ∙γ))
где:
- A — Площадь четырехугольника;
- s — полупериметр четырехугольника, равный 0,5 ∙ (a + b + c + d) ;
- a, b, c, d — Четыре стороны четырехугольника; и
- δ, γ — Любые два противоположных угла четырехугольника.

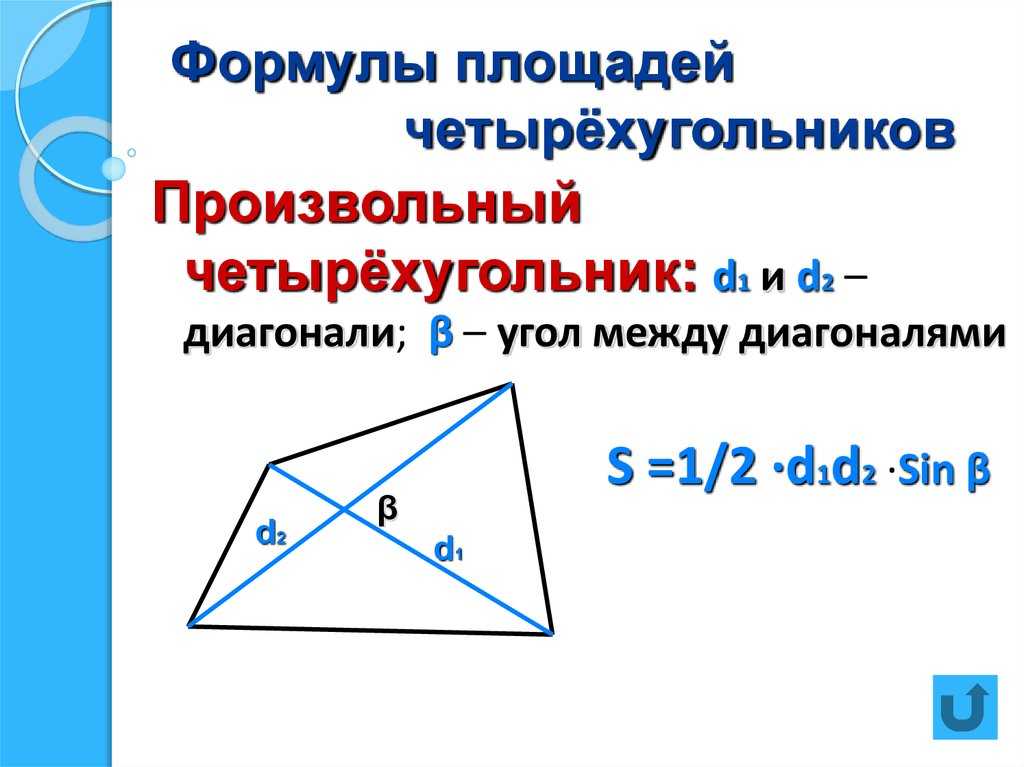
- Из его диагоналей и угла между ними:
A = 0,5 ∙ e ∙ f ∙ sin(α)
где:
- e, f — длины двух диагоналей четырехугольника; и
- α — Угол между двумя диагоналями . Между двумя диагоналями есть два уникальных угла: α и (π-α) . Поскольку sin(π-α) = sin(α) , формула площади четырехугольника дает один и тот же результат для обоих углов.
- От бимедианы и угол между:
A = m ∙ k ∙ sin(θ)
где:
- m, k — длины двух бимедианов четырехугольника; и
- θ — Угол между двумя бимедианами .
 Опять же, поскольку sin(π-θ) = sin(θ) , мы можем использовать эту формулу для вычисления площади четырехугольника независимо от нашего выбора угла.
Опять же, поскольку sin(π-θ) = sin(θ) , мы можем использовать эту формулу для вычисления площади четырехугольника независимо от нашего выбора угла.
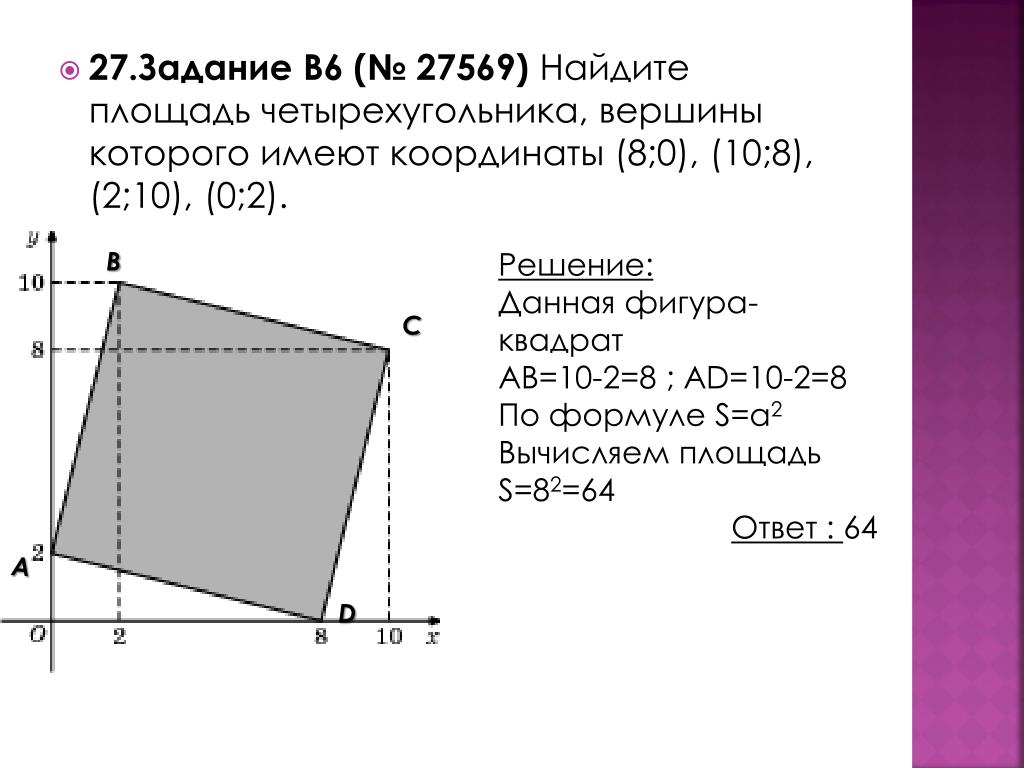
- Из декартовых координат вершин четырехугольника :
A = 0.5 ∙ (x 1 y 2 — y 1 x 2 + x 2 y 3 — y 2 x 3 + x 3 y 4 — у 3 х 4 + х 4 у 1 — у 4 х 1 )
where (x 1 , y 1 ), (x 2 , y 2 ), (x 3 , y 3 ), (x 4 , y 4 ) — это координаты четырех вершин четырехугольника.
Площадь распространенных типов четырехугольника
Мы видели, как найти площадь четырехугольника неправильной формы.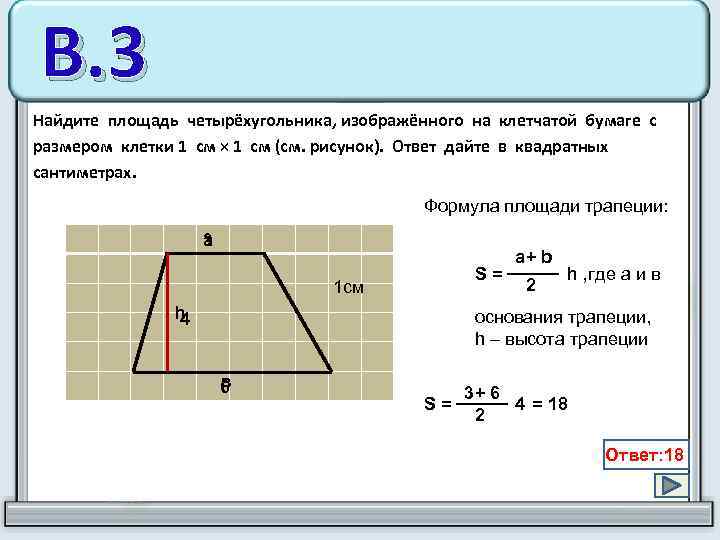 Для четырехугольников, таких как квадраты и прямоугольники, существуют другие более простые формулы площади:
Для четырехугольников, таких как квадраты и прямоугольники, существуют другие более простые формулы площади:
- Прямоугольники : Четырехугольник, у которого противоположные стороны равны по длине, а все углы прямые.
Его площадь определяется как:
A = b ∙ a
где:
- b — длина прямоугольника ; и
- a — Ширина прямоугольника .
- Квадрат : Четырехугольник со всеми сторонами одинаковой длины, и все его углы прямые.
Его площадь определяется как:
A = a 2
, где a — длина стороны квадрата, равная .
- Параллелограмм : Четырехугольник, у которого противоположные стороны равны по длине и параллельны друг другу, а противоположные углы равны.

Формула площади параллелограмма:
A = b ∙ h
где:
- b — основание параллелограмма ; и
- h — Высота параллелограмма (перпендикулярное расстояние между основанием и его противоположной стороной).
- Ромб : Четырехугольник, четыре стороны которого равны по длине.
Его площадь определяется как:
A = 0,5 ∙ d 1 ∙ d 2
где d 1 , d 2 — диагонали ромба .
- Трапеция : Трапеция (или трапеция) – это четырехугольник, по крайней мере, с одной парой параллельных сторон.
Площадь трапеции:
A = 0,5 ∙ h ∙ (a + b)
где:
- a, b — длины параллельные стороны трапеции; и
- h — Высота трапеции .

- Воздушный змей : Воздушный змей – это четырехугольник, в котором две пары смежных сторон равны по длине.
Его площадь определяется по формуле:
A = 0,5 ∙ d 1 ∙ d 2
, где d 1 , d 77’s 2 2 2 2 0023 диагонали .
Как использовать этот калькулятор площади четырехугольника
Наш калькулятор площади четырехугольника является мощным инструментом, способным вычислить площадь любого четырехугольника по различным известным параметрам:
- Выберите тип из четырехугольника . Выберите
unknownдля неправильных четырехугольников. - Для неправильных четырехугольников можно выбрать, какие параметры являются
заданными. - Введите параметры в соответствующие поля с правильными единицами измерения.

- Эта площадь четырехугольника калькулятор мгновенно рассчитает ответ для вас.
Вот некоторые другие калькуляторы четырехугольников для изучения:
- Четырехугольник; и
- Периметр четырехугольника.
Часто задаваемые вопросы
Какова площадь квадрата со стороной 5 см?
25 см 2 . Чтобы вычислить это, выполните следующие действия:
- Умножьте на сторону квадрата, чтобы получить
A = 5 × 5 = 25. - Проверьте свой результат с помощью нашего калькулятора площади четырехугольника.
Чему равна сумма всех углов четырехугольника?
Сумма всех углов четырехугольника равна 360° или 2π радиан . Думайте о четырехугольнике как о слиянии двух треугольников, имеющих общую сторону (диагональ).
Кришна Нелатуру
четырехсторонний тип
Угол α
Диагональный E
Диагональный F
Проверьте 23 Аналогичные 2D Геометрические калькуляторы 📏
Область прямоугольной матуистии000 000 2 9000. 29000 2 9000.29000 2 9000.29000 2 9000.29000 2 9000.29000 2 9000.29000 2 9000.29000 2 9000.2.29000 2 9000.2.29000 2 9000.2.29000 2 9000.2.29000 2 9000.2.2.
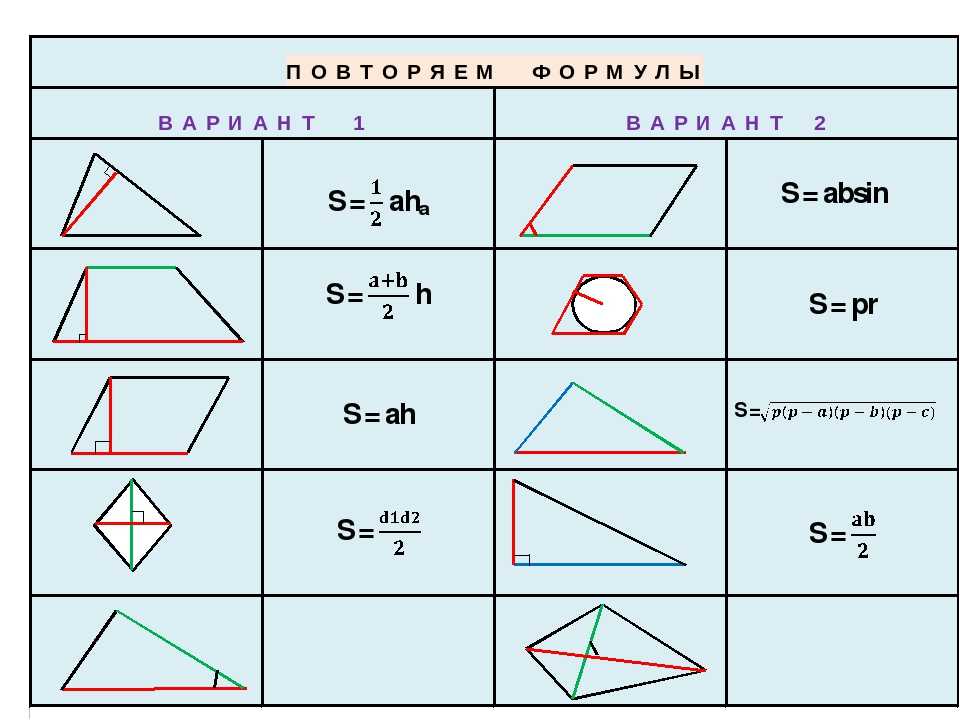
Введение
29000 2 9000.29000 2 9000.29000 2 9000.29000 2 9000.29000 2 9000.29000 2 9000.29000 2 9000.2.29000 2 9000.2.29000 2 9000.2.29000 2 9000.2.29000 2 9000.2.2.
Введение
Что такое площадь четырехугольника?
Что такое четырехугольники?
Как назвать четырехугольники
Как вычислить площадь прямоугольника, квадрата, параллелограмма и трапеции
Площадь четырехугольника рабочий лист
Распространенные заблуждения
Практика четырехугольных вопросов
Площадь четырехугольника GCSE вопросы
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Еженедельные онлайн-уроки повторения математики GCSE теперь доступны
Узнать больше
Введение
Что такое площадь четырехугольника?
Что такое четырехугольники?
Как назвать четырехугольники
Как вычислить площадь прямоугольника, квадрата, параллелограмма и трапеции
Площадь четырехугольника рабочий лист
Распространенные заблуждения
Практика четырехугольных вопросов
Площадь четырехугольника GCSE вопросы
Контрольный список обучения
Следующие уроки
Все еще застряли?
Здесь мы узнаем о площади четырехугольника , в том числе о том, как найти площадь прямоугольника, квадрата, параллелограмма и трапеции. Вы также научитесь находить площади сложных фигур, состоящих из нескольких четырехугольников, и находить недостающие длины по заданной площади.
Вы также научитесь находить площади сложных фигур, состоящих из нескольких четырехугольников, и находить недостающие длины по заданной площади.
Есть также область четырехугольных рабочих листов, основанных на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные указания о том, что делать дальше, если вы все еще застряли.
Какова площадь четырехугольника?
Площадь четырехугольника является мерой того, сколько места внутри двумерной четырехсторонней формы.
Чтобы найти площадь фигуры, мы можем либо подсчитать количество единичных квадратов внутри фигуры, либо использовать соответствующую формулу площади для этой фигуры. 92
\конец{выровнено}\]
Что такое площадь?
Что такое четырехугольники?
Четырехугольник представляет собой замкнутую двумерную фигуру с 4 прямыми сторонами и 4 вершинами.
Правильные четырехугольники имеют стороны одинаковой длины и внутренние углы одинакового размера.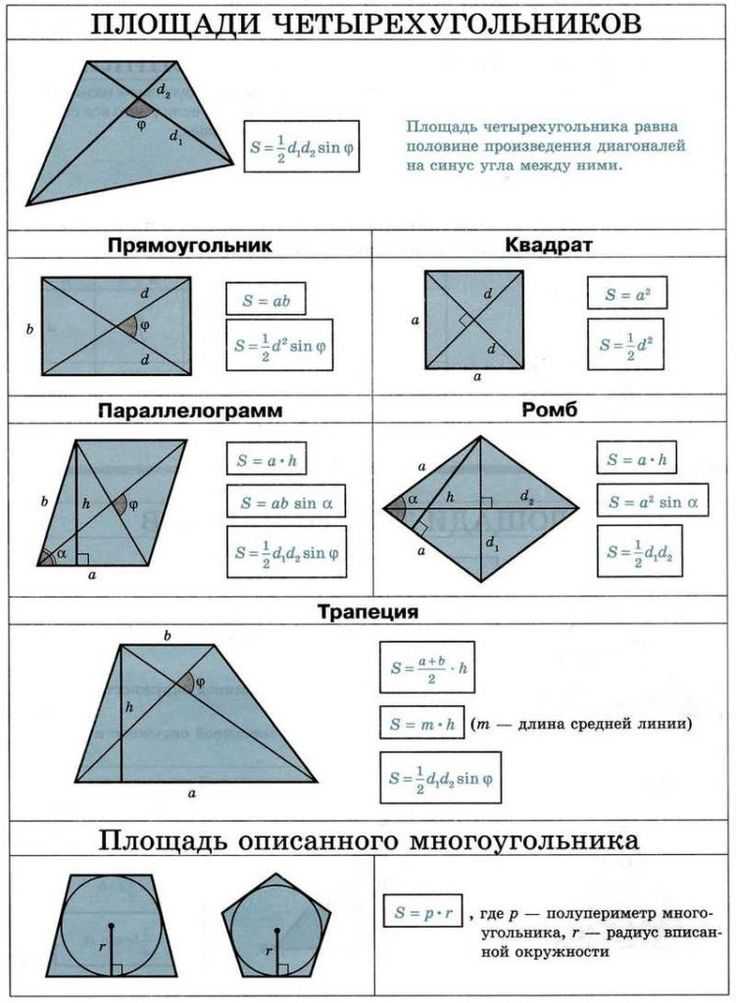
Неправильные четырехугольники имеют стороны разной длины и внутренние углы разной величины.
Существует несколько различных типов четырехугольников:
Квадрат :
Квадрат представляет собой замкнутую двумерную фигуру с четырьмя прямыми сторонами одинаковой длины и четырьмя прямыми углами (90°).
Прямоугольник :
Прямоугольник представляет собой замкнутую двумерную форму с четырьмя прямыми сторонами и четырьмя прямыми углами (90°). Он имеет две пары параллельных сторон, которые равны.
Параллелограмм :
Параллелограмм равен закрытая двухмерная форма с четырьмя прямыми сторонами. Противоположные стороны параллелограмма имеют одинаковую длину и параллельны.
Ромб :
Ромб представляет собой замкнутую двумерную форму с четырьмя равными прямыми сторонами.
Трапеция :
Трапеция представляет собой замкнутую двумерную форму с четырьмя прямыми сторонами и только одной парой параллельных сторон.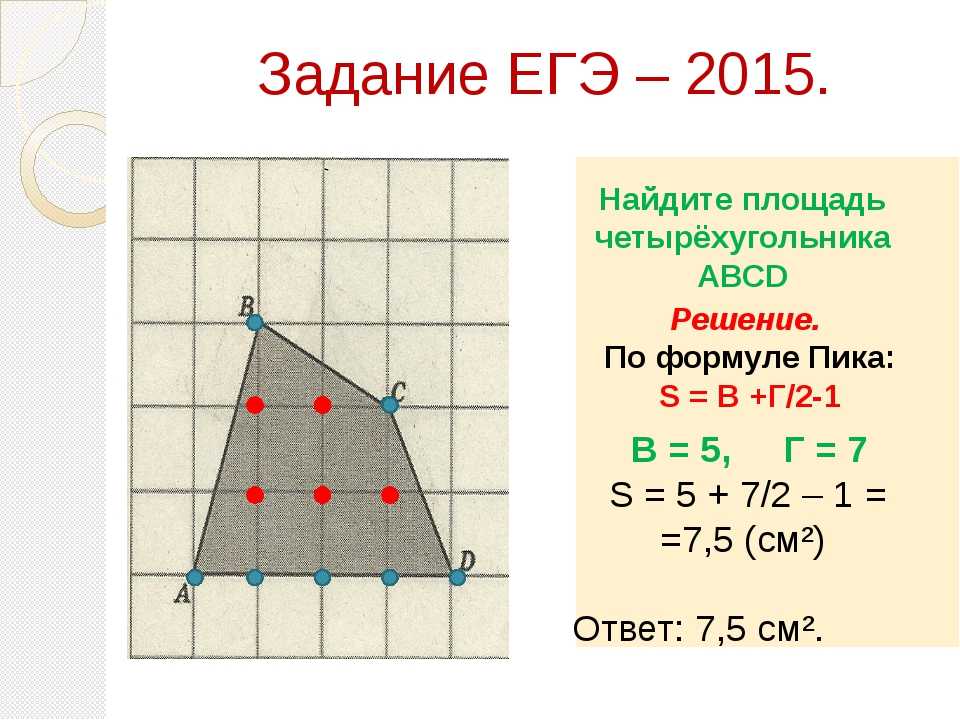
Воздушный змей :
Воздушный змей — это закрытая двухмерная форма с четырьмя прямыми сторонами. Он имеет две пары смежных сторон (стороны, которые находятся рядом друг с другом), которые равны друг другу.
Что такое четырехугольники?
Как называть четырехугольники
Мы обычно называем четырехугольники, присваивая буквы каждой из их вершин.
Это четырехугольник ABCD:
Как вычислить площадь прямоугольника, квадрата, параллелограмма и трапеции
Мы можем использовать формулы для вычисления площади следующих фигур:
Площадь прямоугольника/квадрата:
\[\text {Площадь прямоугольника/квадрата = основание × высота}\]
Площадь a параллелограмм:
\[\text {Площадь параллелограмма = основание × высота} \]
Чтобы вычислить площадь прямоугольника, квадрата или параллелограмма :
- Подставьте значения в формула.
 (Убедитесь, что единицы измерения одинаковы для всех измерений, например, для всех см) .
(Убедитесь, что единицы измерения одинаковы для всех измерений, например, для всех см) . - Выполните расчет.
- Добавьте правильные единицы измерения .
Площадь трапеции:
Трапеция имеет форму трапеции, то есть имеет только одну пару параллельных сторон. Чтобы вычислить площадь трапеции, нам нужно использовать следующую формулу.
\[\text { Площадь трапеции }=\frac{1}{2}(a+b) h \]
Чтобы вычислить площадь трапеции :
- Подставьте значения в формулу.
- Выполните расчет.
- Добавьте правильные единицы измерения.
Мы можем использовать следующую формулу для расчета площади ромба и площади воздушного змея :
\[\text { Площадь ромба или воздушного змея }=\frac{1 }{2} \times d_{1} \times d_{2} \]
Где d 1 и d 2 — длины диагоналей.
Площадь четырехугольника
Получите бесплатную площадь четырехугольника из 20+ вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
ИксПлощадь четырехугольника
Получите бесплатную площадь четырехугольника из 20+ вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Площадь четырехугольника примеры
Пример 1: площадь квадрата
Найдите площадь четырехугольника:
- Здесь высота равна 8. Поскольку это квадрат, основание также равно 8.
\begin{align} \text { Площадь }&=\text { основание } \times \text { высота } \\\\ \text {Площадь}&=8 \times 8 \end{align}
2 Выполните расчет.
\[Площадь = 64\]
3 Добавьте правильные единицы измерения.
Размеры этого квадрата указаны в см, поэтому площадь будет измеряться в см 92\]
Пример 2: площадь прямоугольника, разные единицы
Найдите площадь прямоугольника:
Подставьте значения в формулу.
Здесь основание 11м, а высота 400см.
Обратите внимание, что размер основания указан в метрах, а размер высоты — в сантиметрах.
Здесь проще всего заменить 400 см на 4 м, чтобы оба измерения были в метрах. (Вы также можете изменить 11 м на 1100 см.
\begin{align} \text { Площадь }&=\text { основание } \times \text { высота } \\\\ \text { Площадь }&=11 \times 4 \end{выровнено} 92\]
Пример 3: площадь параллелограмма
Вычислите площадь параллелограмма:
Подставьте значения в формулу.
\begin{выровнено} \text { Площадь }&=\text { основание } \times \text { высота } \\\\ \text {Площадь}&=12 \times 8 \end{align}
Выполните вычисления.
\[Площадь = 96\]
Добавьте правильные единицы измерения.
Размеры этого параллелограмма даны в миллиметрах, поэтому площадь будет в миллиметрах 92\]
Пример 4: площадь трапеции
Найдите площадь следующей трапеции:
Подставьте значения в формулу.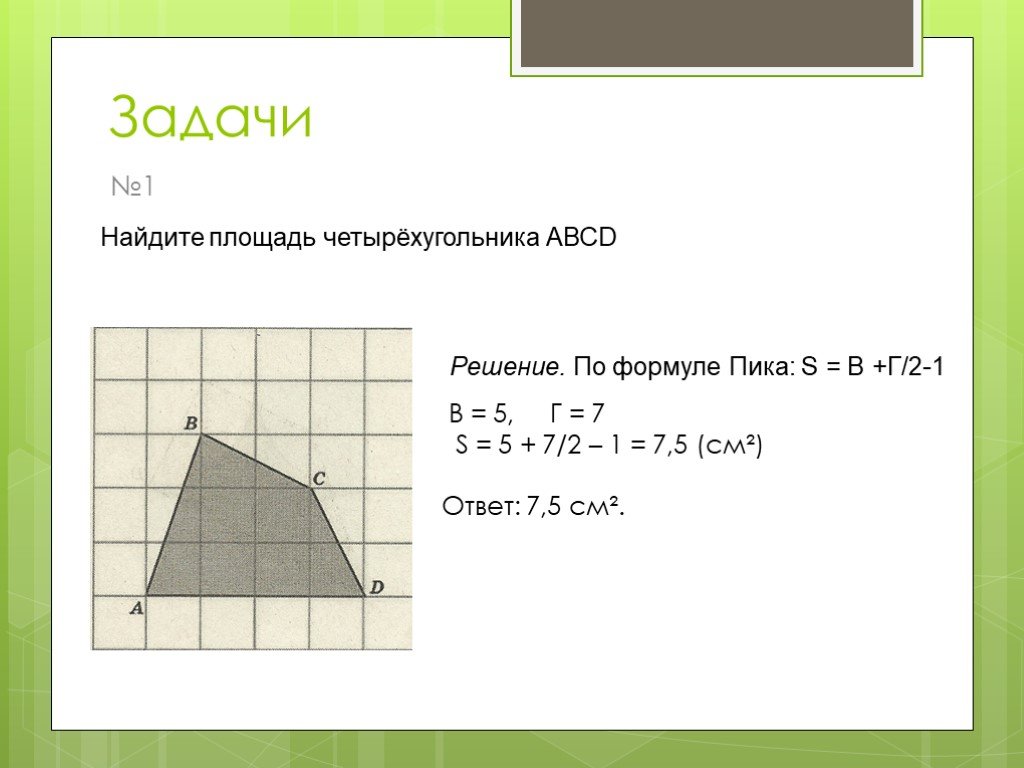
Здесь a = 9, b = 13 и h = 5
\begin{align} \text { Площадь }&=\frac{1}{2}(a+b) h \\\\ \text { Площадь }&=\frac{1}{2} \times(9+13) \times 5 \end{align}
Выполните вычисления.
Не забудьте применить BIDMAS при работе.
\begin{выровнено} \text { Площадь }&=\frac{1}{2} \times(92\]
Пример 5: площадь трапеции
Найдите площадь следующей трапеции:
Подставьте значения в формулу.
Здесь a = 5, b = 6 и h = 4
\begin{align} \text { Площадь }&=\frac{1}{2}(a+b) h \\\\ \text { Площадь }&=\frac{1}{2} \times(5+6) \times 4 \end{align}
Выполните вычисления.
\begin{выровнено} \text { Площадь }&=\frac{1}{2} \times(5+6) \times 4 \\\\ \text { Площадь }&=\frac{1}{2} \times 11 \times 4 \\\\ \текст {Площадь}&=22 \end{выровнено} 92\]
Как вычислить площадь сложных фигур с четырехугольниками
Иногда фигура состоит из двух или более четырехугольников, соединенных вместе.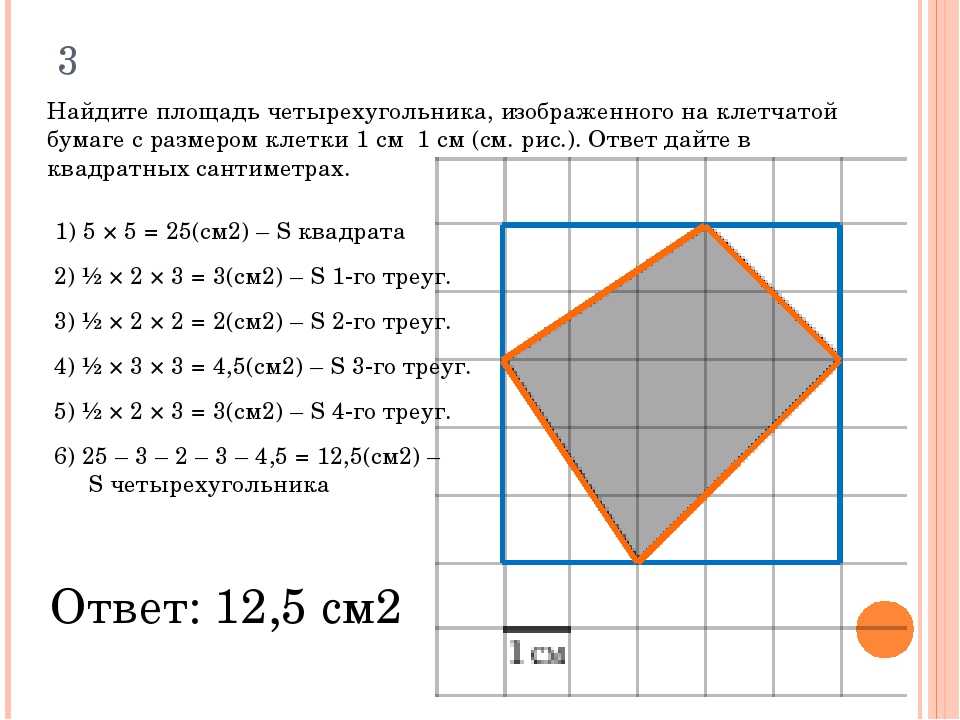 Мы можем вычислить площадь этих фигур, разбив их на отдельные четырехугольники.
Мы можем вычислить площадь этих фигур, разбив их на отдельные четырехугольники.
- Нарисуйте линии, чтобы разделить фигуру на четырехугольники (этот шаг не всегда необходим). Обозначьте четырехугольники A, B, C,…
- Рассмотрим каждый четырехугольник по отдельности
а) проведите необходимые измерения.
б) рассчитать площадь, используя методы, указанные выше. - Добавьте или вычтите соответствующие площади, чтобы найти общую площадь.
- Добавьте правильные единицы измерения.
Пример 6: составная фигура, состоящая из двух четырехугольников
Найдите общую площадь фигуры, показанной ниже:
Нарисуйте линии, чтобы разделить фигуру на четырехугольники, если это необходимо. Обозначьте четырехугольники A, B, C,…
Эта фигура уже разделена на два четырехугольника. Обозначьте их буквами А и В.
Рассмотрите каждый четырехугольник по отдельности и:
а) проведите необходимые измерения.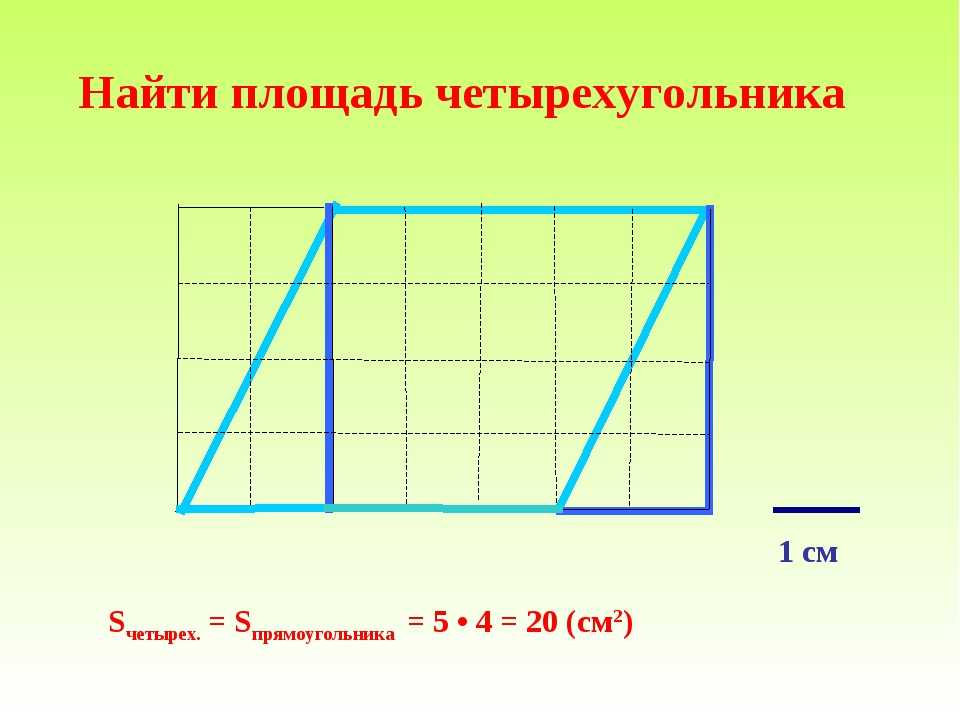 {2}
\end{выровнено}
{2}
\end{выровнено}
Добавить или вычесть области .
Сложите площади вместе:
\[18 + 10 = 28\]
Сложите единицы измерения.
Общая площадь = 28 см 2
Пример 7: составная фигура, состоящая из трех четырехугольников
Найдите общую площадь фигуры, показанной ниже:
Нарисуйте линии, чтобы разделить фигуру на четырехугольники, если это необходимо. Обозначьте четырехугольники A, B, C,…
Разделите фигуру на четырехугольники и обозначьте их A, B и C. Это можно сделать двумя разными способами — какой из них вам подойдет.
Рассмотрите каждый четырехугольник по отдельности и:
а) проведите необходимые измерения.
б) вычислить площадь, используя методы, указанные выше .
Использование первого способа расщепления:
Кваровнопочечный A :
A) Основание четырехстороннего A составляет 7 млн. {2}
\end{выровнено} 9{2}
\end{aligned}
{2}
\end{выровнено} 9{2}
\end{aligned}
Добавьте или вычтите области.
Сложите площади вместе:
\[140 + 90 + 160 = 390\]
Сложите единицы измерения.
Общая площадь = 390 м 2
Пример 8: вычитание площадей
Найдите заштрихованную площадь:
Нарисуйте линии, чтобы разделить фигуру на четырехугольники, если необходимо. Обозначьте четырехугольники A, B, C,…
Фигура уже разделена на два четырехугольника. Обозначьте их буквами А и В (А — большая трапеция, В — маленькая трапеция).
Рассмотрите каждый четырехугольник по отдельности и:
а) проведите необходимые измерения.
б) вычислить площадь, используя методы, указанные выше .
Четырехугольник A:
a ) Здесь a = 12, b = 18 и h = 20.
b )
} \text { Площадь } &=\frac{1}{2} \times(12+18) \times 20 \\\\ \text { Площадь } &=\frac{1}{2} \times 30 \times 20 \\\\ \text { Площадь } &=300 \mathrm{~см}^{2} \end{выровнено} 9{2} \end{aligned}
Добавьте или вычтите области.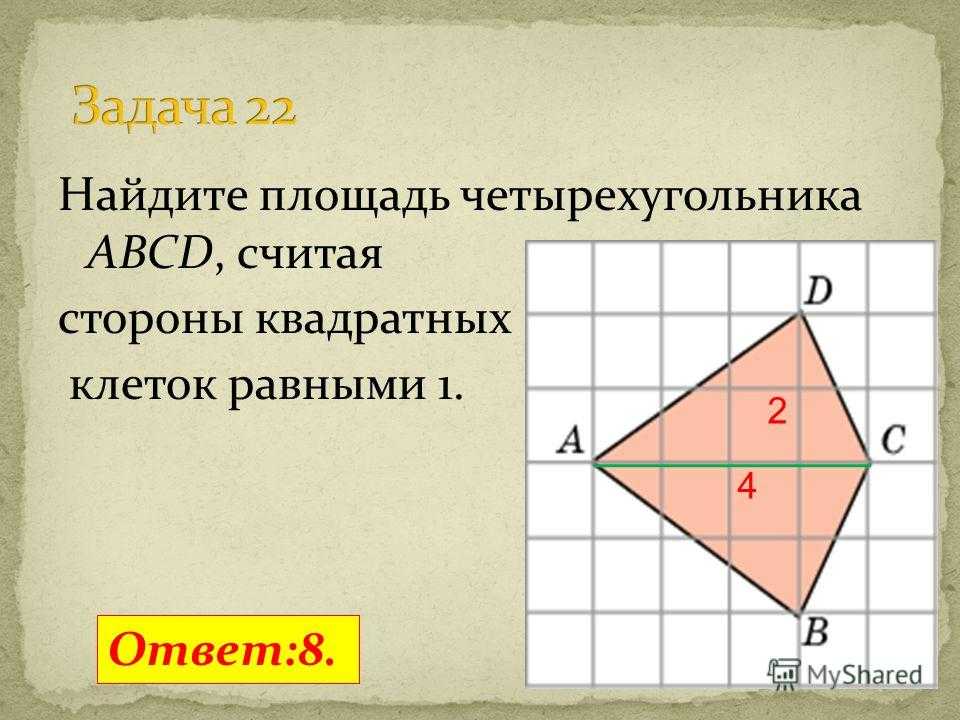
На этот раз нам нужно вычесть области, так как незатененная область удаляется из затененной области.
\[300 – 60 = 240\]
Добавьте единицы измерения.
Заштрихованная площадь = 240 см 2
Как найти недостающую длину
Иногда нам дают площадь четырехугольника, а затем нам нужно вычислить неизвестную длину.
- Подставьте известные вам значения в формулу.
- Решите уравнение .
Пример 9: недостающая длина прямоугольника
Определите высоту прямоугольника:
Подставьте известные значения в формулу.
Здесь площадь равна 40, а основание равно 10.
\begin{align} \text { Площадь }&=\text { основание } \times \text { высота } \\\\ 40&=10 \раз ч \end{align}
Решите уравнение.
Чтобы решить это уравнение нужно разделить на 10:
\[4 = h\]
Высота прямоугольника 4см.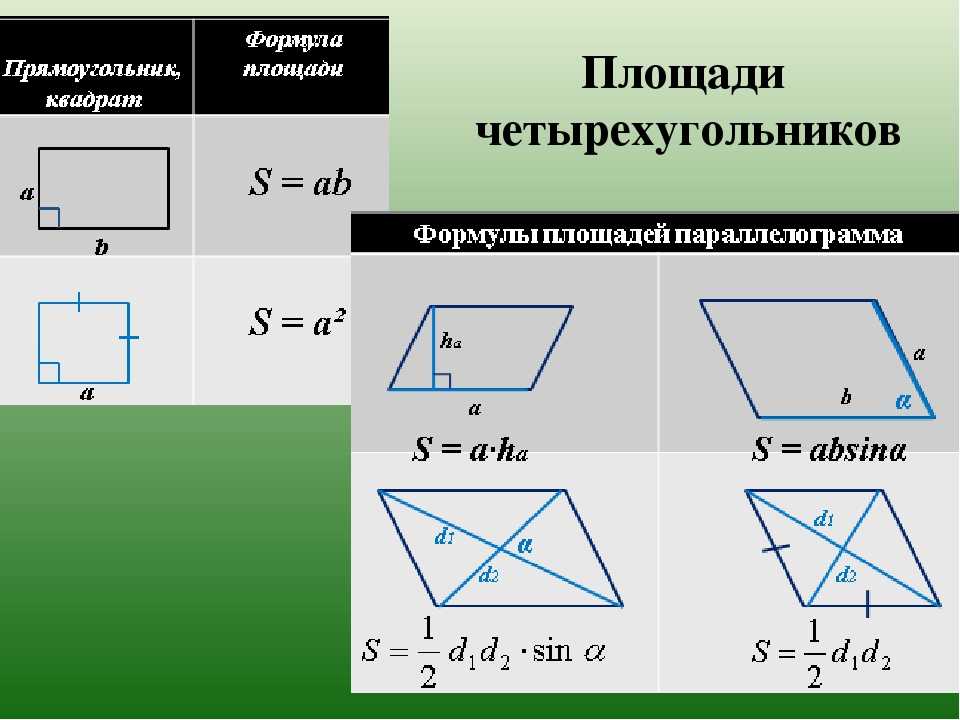
Пример 10: недостающая длина трапеции
Найдите высоту следующей трапеции, если ее площадь равна 56 см 2 :
Подставьте известные значения в формулу.
Здесь a = 6, b = 10 и площадь равна 56.
\begin{align} \text { Площадь }&=\frac{1}{2}(a+b) h \\\\ 56&=\frac{1}{2} \times(6+10) \times h \end{выровнено}
Решите уравнение.
\begin{выровнено} 56&=\frac{1}{2} \times(6+10) \times h \\\\ 56&=\frac{1}{2} \times 16 \times h \\\\ 56&=8 \раз ч \\\\ 7&=ч \end{align}
Высота трапеции 7см.
Общие заблуждения
- Расчет периметра вместо области
- Высота параллелограммы
с использованием неправильного измерения для высоты. 9{2}
(1)
\begin{align} \text { Площадь }&=\text { основание } \times \text { высота } \\\\ 60&=5 \раз ч \end{выровнено}
(1)
H = 12см
(1)
Контрольный список обучения
Вы узнали, как:
- Рассчитайте область квадратного, прямоугольного, параллелиграмма и trapezium
- .



 [2]
X
Источник информации
[2]
X
Источник информации 
 Вот как найти высоту трапеции:[3]
X
Источник информации
Вот как найти высоту трапеции:[3]
X
Источник информации 


 Опять же, поскольку sin(π-θ) = sin(θ) , мы можем использовать эту формулу для вычисления площади четырехугольника независимо от нашего выбора угла.
Опять же, поскольку sin(π-θ) = sin(θ) , мы можем использовать эту формулу для вычисления площади четырехугольника независимо от нашего выбора угла.


 (Убедитесь, что единицы измерения одинаковы для всех измерений, например, для всех см) .
(Убедитесь, что единицы измерения одинаковы для всех измерений, например, для всех см) .