Как найти тангенс угла наклона прямой на графике
Как найти угловой коэффициент (тангенс угла наклона) прямой
wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 27 человек(а).
Количество просмотров этой статьи: 95 670.
Если вы умеете вычислять угловые коэффициенты (тангенс угла наклона) прямых, то на основании этих коэффициентов можно узнать другие параметры. Например, выяснить, параллельны ли прямые или же перпендикулярны, найти их точку пересечения и многие другие величины. Вычисление углового коэффициента — довольно простая задача. Прочитайте эту статью, чтобы узнать, как это сделать.
Линейная функция
Линейная функция — функция вида График линейной функции — прямая.
Для построения графика линейной функции достаточно двух точек — потому что через две несовпадающие точки всегда можно провести прямую, причем единственную.
Угловой коэффициент прямой
Величина k в формуле линейной функции называется угловым коэффициентом прямой
Если , линейная функция возрастает. Чем больше х, тем больше у, то есть график идет вправо и вверх.
Если , линейная функция убывает. Чем больше х, тем меньше у, то есть график идет вправо и вниз.
Угловой коэффициент k равен тангенсу угла наклона графика линейной функции к положительному направлению оси Х.
Пусть Чем больше k, тем круче вверх идет график функции.
А что же будет, если ? Мы получим горизонтальную прямую На рисунке показан график функции
Заметим, что прямая (также изображенная на рисунке) не является графиком функции в нашем обычном, школьном смысле слова. В самом деле — мы помним, что функция — это соответствие между двумя множествами, причем каждому элементу множества Х соответствует один и только один элемент множества Y.
Для прямой это не выполняется: значению соответствует бесконечно много значений у.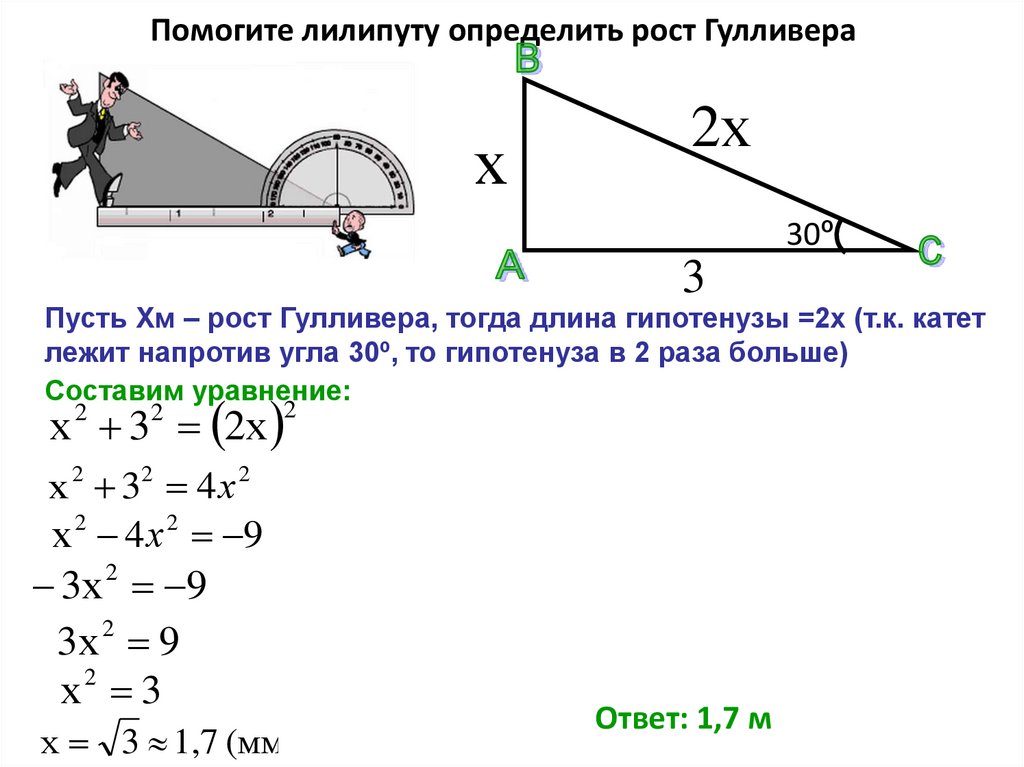
Если прямые параллельны.
При этом, чем больше b, тем выше расположен на координатной плоскости график функции.
Например, прямые и параллельны. Их угловые коэффициенты равны.
Если прямые перпендикулярны. Например, прямые и пересекаются под прямым углом. Произведение их угловых коэффициентов равно — 1.
Построение графика линейной функции
График линейной функции построить легко — достаточно двух точек.
Оказывается, что привычный нам вид уравнения прямой — не единственно возможный.
Уравнение прямой можно записать также в виде
Построим, например, прямую, заданную уравнением
При получаем, что
При получаем, что
Значит, наша прямая проходит через точки и
Выразив у из уравнения , получим уравнение прямой вида
Если вы поступаете в вуз на специальность, связанную с математикой, — уже на первом курсе вы познакомитесь и с другими видами уравнения прямой.
Зачем изучать линейную функцию?
Дело в том, что многие зависимости в природе и технике описываются формулой виде
Например, закон Ома для участка цепи: Напряжение U прямо пропорционально силе тока I.
Формула для равномерного прямолинейного движения: . Пройденное расстояние S прямо пропорционально времени.
Закон теплового расширения , который вам встретится в одной из задач под номером 10 варианта Профильного ЕГЭ по математике — тоже линейная функция. И таких примеров можно привести очень много.
Обратите внимание, что в формулу линейной функции аргумент х входит в первой степени. Мы просто умножаем х на угловой коэффициент k и прибавляем b.
Если в формулу функции входит аргумент в любой другой степени — например, в квадрате или в кубе, если мы делим на х, если в формуле присутствует или , или показательные или логарифмические выражения, зависящие от х, — график функции уже не будет прямой линией.
Уравнение прямой с угловым коэффициентом: теория, примеры, решение задач
Продолжение темы уравнение прямой на плоскости основывается на изучении прямой линии из уроков алгебры. Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом.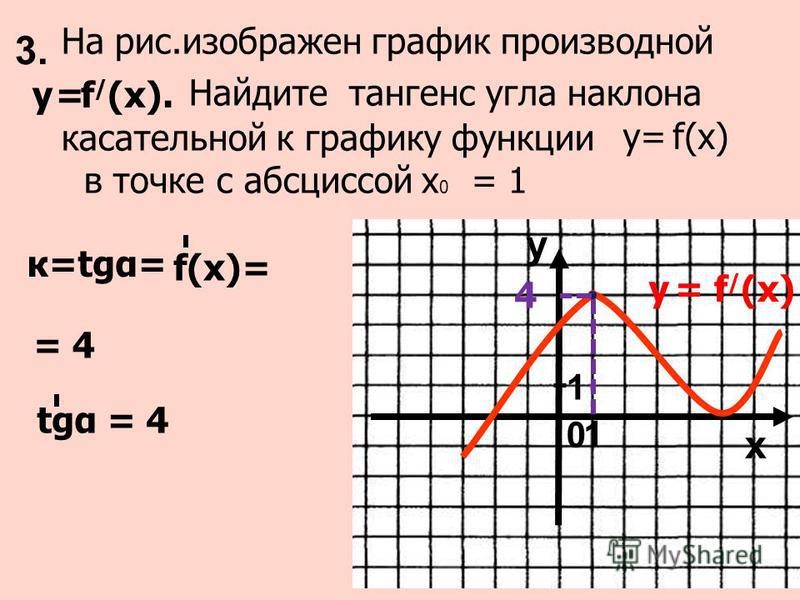
Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.
Угол наклона прямой и угловой коэффициент прямой
Перед записью такого уравнения необходимо дать определение угла наклона прямой к оси О х с их угловым коэффициентом. Допустим, что задана декартова система координат О х на плоскости.
Угол наклона прямой к оси О х , расположенный в декартовой системе координат О х у на плоскости, это угол, который отсчитывается от положительного направления О х к прямой против часовой стрелки.
Когда прямая параллельна О х или происходит совпадение в ней, угол наклона равен 0 . Тогда угол наклона заданной прямой α определен на промежутке [ 0 , π ) .
Угловой коэффициент прямой – это тангенс угла наклона заданной прямой.
Стандартное обозначение буквой k . Из определения получим, что k = t g α . Когда прямая параллельна Ох, говорят, что угловой коэффициент не существует, так как он обращается в бесконечность.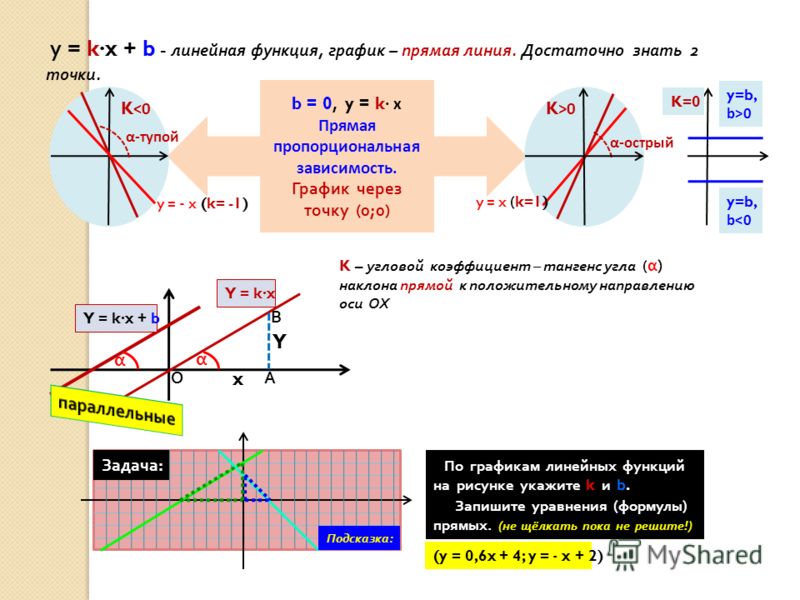
Угловой коэффициент положительный, когда график функции возрастает и наоборот. На рисунке показаны различные вариации расположения прямого угла относительно системы координат со значением коэффициента.
Для нахождения данного угла необходимо применить определение об угловом коэффициенте и произвести вычисление тангенса угла наклона в плоскости.
Посчитать угловой коэффициент прямой при угле наклона равном 120 ° .
Из условия имеем, что α = 120 ° . По определению необходимо вычислить угловой коэффициент. Найдем его из формулы k = t g α = 120 = — 3 .
Ответ: k = — 3 .
Если известен угловой коэффициент, а необходимо найти угол наклона к оси абсцисс, тогда следует учитывать значение углового коэффициента. Если k > 0 , тогда угол прямой острый и находится по формуле α = a r c t g k . Если k < 0 , тогда угол тупой, что дает право определить его по формуле α = π — a r c t g k .
Определить угол наклона заданной прямой к О х при угловом коэффициенте равном 3 .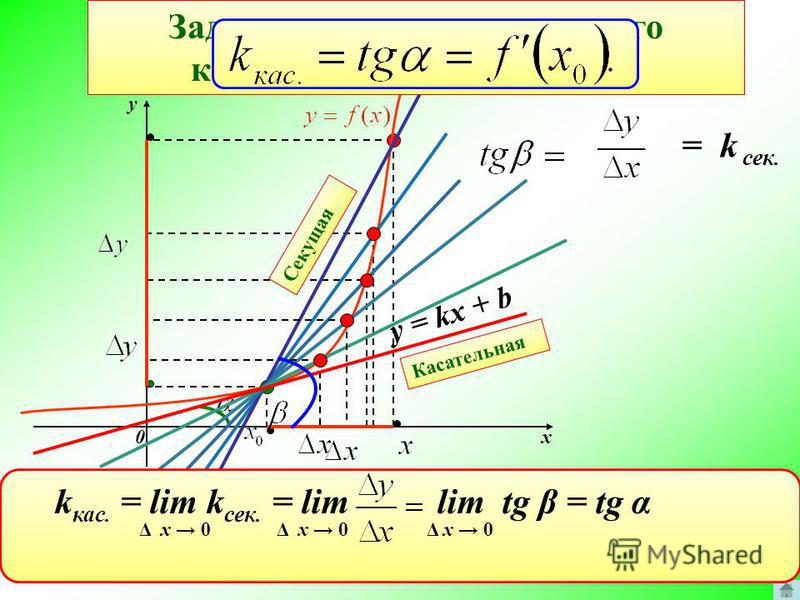
Из условия имеем, что угловой коэффициент положительный, а это значит, что угол наклона к О х меньше 90 градусов. Вычисления производятся по формуле α = a r c t g k = a r c t g 3 .
Ответ: α = a r c t g 3 .
Найти угол наклона прямой к оси О х , если угловой коэффициент = — 1 3 .
Если принять за обозначение углового коэффициента букву k , тогда α является углом наклона к заданной прямой по положительному направлению О х . Отсюда k = — 1 3 < 0 , тогда необходимо применить формулу α = π — a r c t g k При подстановке получим выражение:
α = π — a r c t g — 1 3 = π — a r c t g 1 3 = π — π 6 = 5 π 6 .
Ответ: 5 π 6 .
Уравнение с угловым коэффициентом
Уравнение вида y = k · x + b , где k является угловым коэффициентом, а b некоторым действительным числом, называют уравнением прямой с угловым коэффициентом. Уравнение характерно для любой прямой, непараллельной оси О у .
Если подробно рассмотреть прямую на плоскости в фиксированной системе координат, которая задана уравнением с угловым коэффициентом, который имеет вид y = k · x + b .
В данном случае значит, что уравнению соответствуют координаты любой точки прямой. Если подставить координаты точки М , M 1 ( x 1 , y 1 ) , в уравнение y = k · x + b , тогда в этом случае прямая будет проходить через эту точку, иначе точка не принадлежит прямой.
Задана прямая с угловым коэффициентом y = 1 3 x — 1 . Вычислить, принадлежат ли точки M 1 ( 3 , 0 ) и M 2 ( 2 , — 2 ) заданной прямой.
Необходимо подставить координаты точки M 1 ( 3 , 0 ) в заданное уравнение, тогда получим 0 = 1 3 · 3 — 1 ⇔ 0 = 0 . Равенство верно, значит точка принадлежит прямой.
Если подставим координаты точки M 2 ( 2 , — 2 ) , тогда получим неверное равенство вида — 2 = 1 3 · 2 — 1 ⇔ — 2 = — 1 3 . Можно сделать вывод, что точка М 2 не принадлежит прямой.
Ответ: М 1 принадлежит прямой, а М 2 нет.
Известно, что прямая определена уравнением y = k · x + b , проходящим через M 1 ( 0 , b ) , при подстановке получили равенство вида b = k · 0 + b ⇔ b = b . Отсюда можно сделать вывод, что уравнение прямой с угловым коэффициентом y = k · x + b на плоскости определяет прямую, которая проходит через точку 0 , b .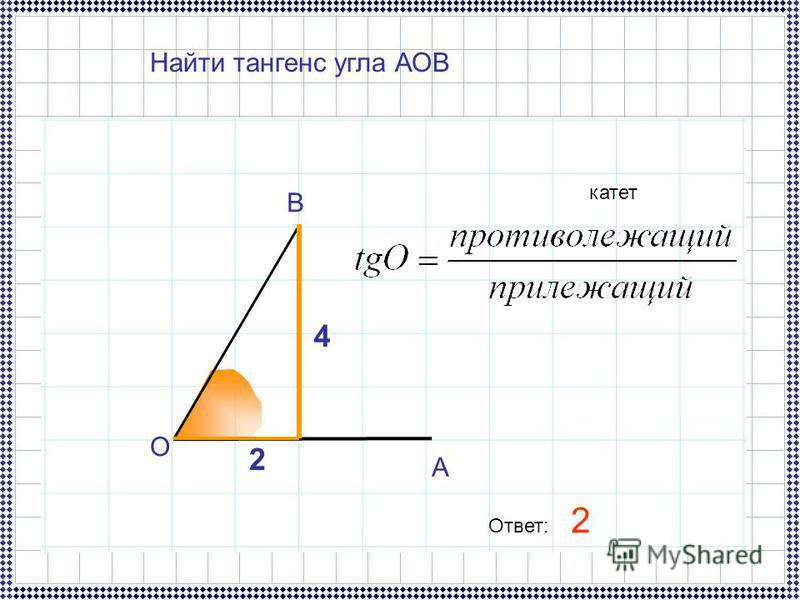
Она образует угол α с положительным направлением оси О х , где k = t g α .
Рассмотрим на примере прямую, определенную при помощи углового коэффициента, заданного по виду y = 3 · x — 1 . Получим, что прямая пройдет через точку с координатой 0 , — 1 с наклоном в α = a r c t g 3 = π 3 радиан по положительному направлению оси О х . Отсюда видно, что коэффициент равен 3 .
Уравнение прямой с угловым коэффициентом, проходящей через заданную точку
Необходимо решить задачу, где необходимо получить уравнение прямой с заданным угловым коэффициентом, проходящим через точку M 1 ( x 1 , y 1 ) .
Равенство y 1 = k · x + b можно считать справедливым, так как прямая проходит через точку M 1 ( x 1 , y 1 ) . Чтобы убрать число b, необходимо из левой и правой частей вычесть уравнение с угловым коэффициентом. Из этого следует, что y — y 1 = k · ( x — x 1 ) . Данное равенство называют уравнением прямой с заданным угловым коэффициентом k, проходящая через координаты точки M 1 ( x 1 , y 1 ) .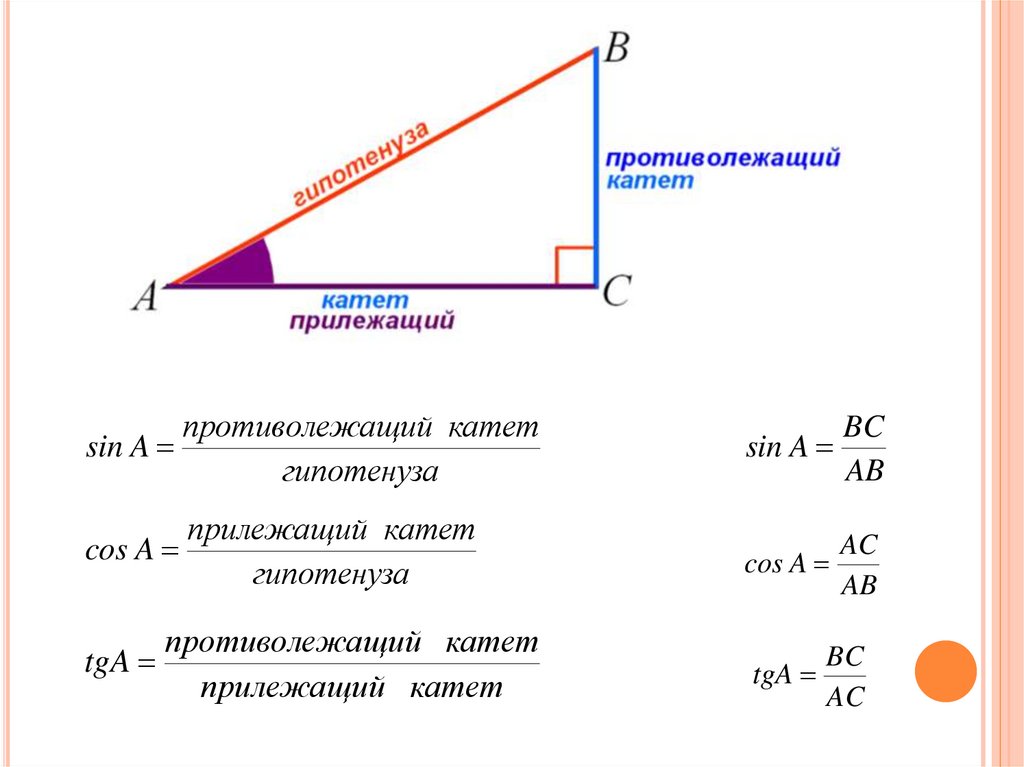
Составьте уравнение прямой, проходящей через точку М 1 с координатами ( 4 , — 1 ) , с угловым коэффициентом равным — 2 .
Решение
По условию имеем, что x 1 = 4 , y 1 = — 1 , k = — 2 . Отсюда уравнение прямой запишется таким образом y — y 1 = k · ( x — x 1 ) ⇔ y — ( — 1 ) = — 2 · ( x — 4 ) ⇔ y = — 2 x + 7 .
Ответ: y = — 2 x + 7 .
Написать уравнение прямой с угловым коэффициентом, которое проходит через точку М 1 с координатами ( 3 , 5 ) , параллельную прямой y = 2 x — 2 .
По условию имеем, что параллельные прямые имеют совпадающие углы наклона, отсюда значит, что угловые коэффициенты являются равными. Чтобы найти угловой коэффициент из данного уравнения, необходимо вспомнить его основную формулу y = 2 x — 2 , отсюда следует, что k = 2 . Составляем уравнение с угловым коэффициентом и получаем:
y — y 1 = k · ( x — x 1 ) ⇔ y — 5 = 2 · ( x — 3 ) ⇔ y = 2 x — 1
Ответ: y = 2 x — 1 .
Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно
Такое уравнение не всегда применимо для решения задач, так как имеет не совсем удобную запись.
Для этого необходимо представлять в другом виде. Например, уравнение вида y = k · x + b не позволяет записать координаты направляющего вектора прямой или координаты нормального вектора. Для этого нужно научиться представлять уравнениями другого вида.
Можем получить каноническое уравнение прямой на плоскости, используя уравнение прямой с угловым коэффициентом. Получаем x — x 1 a x = y — y 1 a y . Необходимо слагаемое b перенести в левую часть и поделить на выражение полученного неравенства. Тогда получим уравнение вида y = k · x + b ⇔ y — b = k · x ⇔ k · x k = y — b k ⇔ x 1 = y — b k .
Уравнение прямой с угловым коэффициентом стало каноническим уравнением данной прямой.
Привести уравнение прямой с угловым коэффициентом y = — 3 x + 12 к каноническому виду.
Вычислим и представим в виде канонического уравнения прямой. Получим уравнение вида:
y = — 3 x + 12 ⇔ — 3 x = y — 12 ⇔ — 3 x — 3 = y — 12 — 3 ⇔ x 1 = y — 12 — 3
Ответ: x 1 = y — 12 — 3 .
Общее уравнение прямой проще всего получить из y = k · x + b , но для этого необходимо произвести преобразования: y = k · x + b ⇔ k · x — y + b = 0 .
Производится переход из общего уравнения прямой к уравнениям другого вида.
Дано уравнение прямой вида y = 1 7 x — 2 . Выяснить, является ли вектор с координатами a → = ( — 1 , 7 ) нормальным вектором прямой?
Для решения необходимо перейти к другому виду данного уравнения, для этого запишем:
y = 1 7 x — 2 ⇔ 1 7 x — y — 2 = 0
Коэффициенты перед переменными являются координатами нормального вектора прямой. Запишем это так n → = 1 7 , — 1 , отсюда 1 7 x — y — 2 = 0 . Понятно, что вектор a → = ( — 1 , 7 ) коллинеарен вектору n → = 1 7 , — 1 , так как имеем справедливое соотношение a → = — 7 · n → . Отсюда следует, что исходный вектор a → = — 1 , 7 — нормальный вектор прямой 1 7 x — y — 2 = 0 , значит, считается нормальным вектором для прямой y = 1 7 x — 2 .
Ответ: Является
Решим задачу обратную данной.
Необходимо перейти от общего вида уравнения A x + B y + C = 0 , где B ≠ 0 , к уравнению с угловым коэффициентом. для этого решаем уравнение относительно у.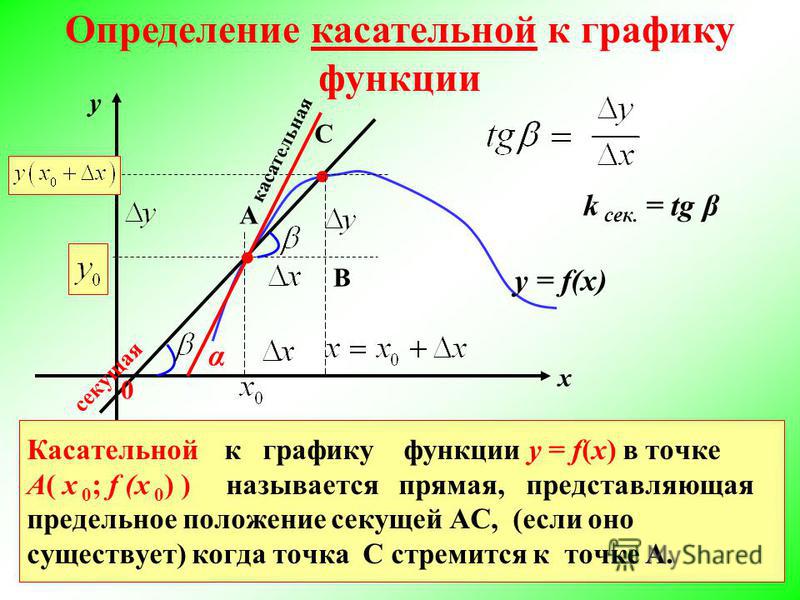
Получим A x + B y + C = 0 ⇔ — A B · x — C B .
Результат и является уравннием с угловым коэффициентом, который равняется — A B .
Задано уравнение прямой вида 2 3 x — 4 y + 1 = 0 . Получить уравнение данной прямой с угловым коэффициентом.
Исходя из условия, необходимо решить относительно у, тогда получим уравнение вида:
2 3 x — 4 y + 1 = 0 ⇔ 4 y = 2 3 x + 1 ⇔ y = 1 4 · 2 3 x + 1 ⇔ y = 1 6 x + 1 4 .
Ответ: y = 1 6 x + 1 4 .
Аналогичным образом решается уравнение вида x a + y b = 1 , которое называют уравнение прямой в отрезках, или каноническое вида x — x 1 a x = y — y 1 a y . Нужно решить его относительно у, только тогда получим уравнение с угловым коэффициентом:
x a + y b = 1 ⇔ y b = 1 — x a ⇔ y = — b a · x + b .
Каноническое уравнение можно привести к виду с угловым коэффициентом. Для этого:
x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ ⇔ a x · y = a y · x — a y · x 1 + a x · y 1 ⇔ y = a y a x · x — a y a x · x 1 + y 1
Имеется прямая, заданная уравнением x 2 + y — 3 = 1 .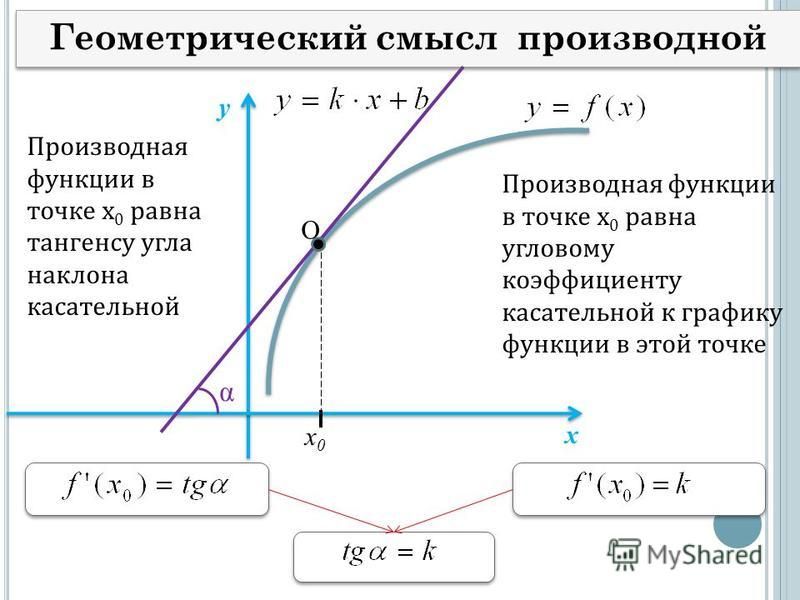
Привести к виду уравнения с угловым коэффициентом.
Исходя из условия, необходимо преобразовать, тогда получим уравнение вида _formula_. Обе части уравнения следует умножить на — 3 для того, чтобы получить необходимо уравнение с угловым коэффициентом. Преобразуя, получим:
y — 3 = 1 — x 2 ⇔ — 3 · y — 3 = — 3 · 1 — x 2 ⇔ y = 3 2 x — 3 .
Ответ: y = 3 2 x — 3 .
Уравнение прямой вида x — 2 2 = y + 1 5 привести к виду с угловым коэффициентом.
Необходимо выражение x — 2 2 = y + 1 5 вычислить как пропорцию. Получим, что 5 · ( x — 2 ) = 2 · ( y + 1 ) . Теперь необходимо полностью его разрешить, для этого:
5 · ( x — 2 ) = 2 · ( y + 1 ) ⇔ 5 x — 10 = 2 y + 2 ⇔ 2 y = 5 x — 12 ⇔ y = 5 2 x
Ответ: y = 5 2 x — 6 .
Для решения таких заданий следует приводит параметрические уравнения прямой вида x = x 1 + a x · λ y = y 1 + a y · λ к каноническому уравнению прямой, только после этого можно переходить к уравнению с угловым коэффициентом.
Найти угловой коэффициент прямой, если она задана параметрическими уравнениями x = λ y = — 1 + 2 · λ .
Необходимо выполнить переход от параметрического вида к угловому коэффициенту. Для этого найдем каноническое уравнение из заданного параметрического:
x = λ y = — 1 + 2 · λ ⇔ λ = x λ = y + 1 2 ⇔ x 1 = y + 1 2 .
Теперь необходимо разрешить данное равенство относительно y , чтобы получить уравнение прямой с угловым коэффициентом. для этого запишем таким образом:
x 1 = y + 1 2 ⇔ 2 · x = 1 · ( y + 1 ) ⇔ y = 2 x — 1
Отсюда следует, что угловой коэффициент прямой равен 2 . Это записывается как k = 2 .
Как найти тангенс угла наклона касательной?
Как найти тангенс угла наклона касательной?
Значение производной в точке касания как тангенс угла наклона (страница 2) f ′ ( x 0 ) = t g α , где – угол наклона касательной. Значит, верна формула: f ′ ( x 0 ) = t g α = k .
Как найти коэффициент угла наклона?
Если известен угловой коэффициент, а необходимо найти угол наклона к оси абсцисс, тогда следует учитывать значение углового коэффициента.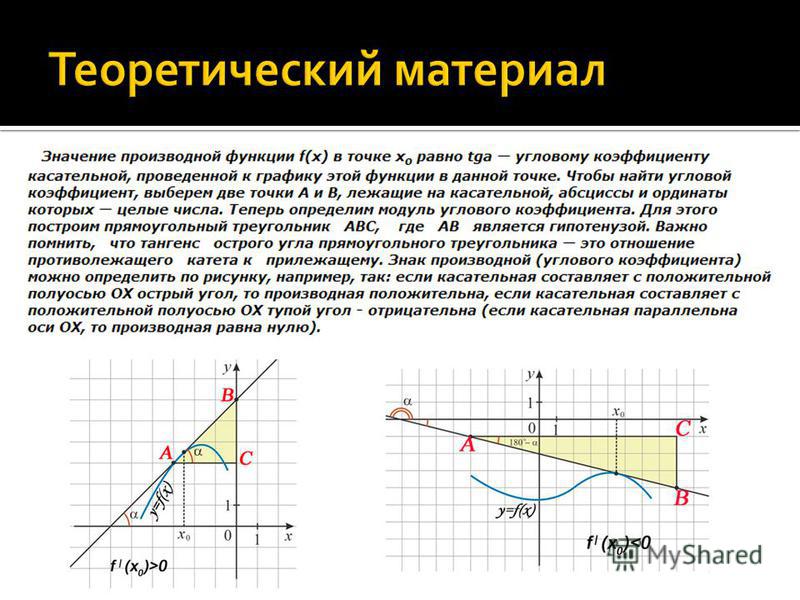
Если k > 0 , тогда угол прямой острый и находится по формуле α = a r c t g k . Если k 0 , тогда угол тупой, что дает право определить его по формуле α = π – a r c t g k .
Как определить коэффициент прямой?
Угловой коэффициент прямой равен тангенсу угла наклона прямой. Это угол между данной прямой и осью ох. Он лежит в пределах от 0 до 180 градусов. То есть, если мы приведём уравнение прямой к виду y = kx + b, то далее всегда сможем определить коэффициент k (угловой коэффициент).
Как определить наклон?
Для определения наклона используются две любые точки на прямой. При этом вычисляется частное от деления длины отрезка, полученного при проецировании этих двух точек на ось Ординат (OY), на длину отрезка, образованного проекциями этих же двух точек на ось Абсцисс (OX).
Как называется коэффициент k?
При этом k — угловой коэффициент, b — свободный коэффициент. Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.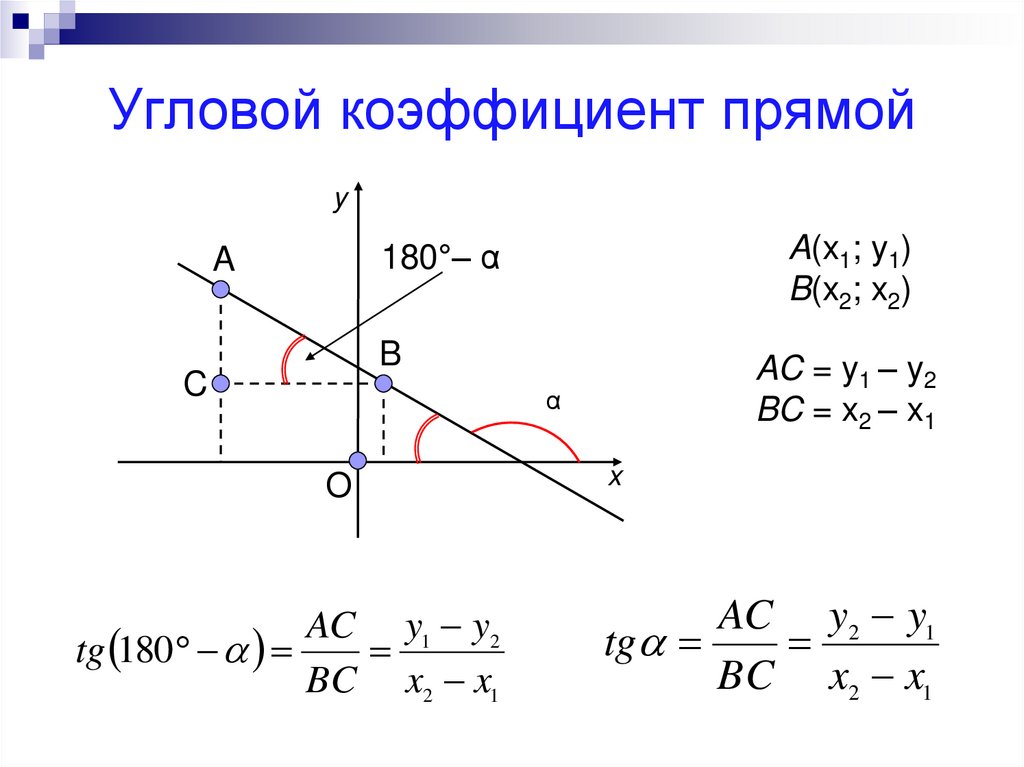
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Что значит составить уравнение прямой?
Каждая точка имеет свои координаты по осям абсцисс и ординат. Уравнение, которое описывает зависимость координат каждой точки прямой в декартовой системе Oxy O x y , называется уравнением прямой на плоскости. Фактически, уравнение прямой на плоскости – это уравнение с двумя переменными, которые обозначаются как x и y .
Как найти координаты направляющего вектора прямой?
Чтобы вычислить координаты направляющего вектора, нам нужно взять числа из знаменателя канонического уравнения прямой. Приведем пример задачи. В прямоугольной системе координат задана прямая, которую можно описать уравнением x−14=y+12−3 x — 1 4 = y + 1 2 — 3 .
Как найти вектор нормали к прямой?
Если известно уравнение прямой, а необходимо найти координаты нормального вектора, тогда необходимо из уравнения Ax+By+C=0 A x + B y + C = 0 выявить коэффициенты, которые и соответствуют координатам нормального вектора заданной прямой.
Что такое направляющий вектор прямой?
Направляющий вектор прямой — это любой ненулевой вектор, лежащий на данной прямой или на параллельной ей прямой.
Чем можно задать плоскость?
Положение плоскости в пространстве определяется тремя точками, не лежащими на одной прямой, прямой и точкой, взятой вне прямой, двумя пересекающимися прямыми и двумя параллельными прямыми. Соответственно плоскость на чертеже (рис. 3.
Как задать плоскость на эпюре?
В соответствии с этим на эпюре плоскость может быть задана:
- проекциями трёх точек, не лежащих на одной прямой (Рисунок 3.
Угол наклона и наклон линии
Пусть прямая l пересекает ось x в точке A. Угол между положительной осью x и линией l, измеренный в направлении против часовой стрелки, называется углом наклона прямая л.
На приведенном выше рисунке, если θ – это угол прямой линии l, то мы имеем следующие важные моменты.
(i) 0° ≤ θ ≤ 180°
(ii) Для горизонтальных линий θ = 0° или 180° и для вертикальных линий θ = 90°
(iii) Если прямая линия изначально лежит вдоль оси х и начинает вращаться вокруг неподвижной точки А на оси х против часовой стрелки и, наконец, совпадает с осью х, то угол наклона прямой линии в начальном положении равно 0°, а линии в конечном положении равно 0°.
(iv) Линии, перпендикулярные оси x, называются вертикальными линиями.
(v) Линии, перпендикулярные оси Y, называются горизонтальными линиями.
(vi) Другие линии, которые не перпендикулярны ни оси x, ни оси y, называются наклонными линиями.
Угол наклона и наклон линии – приложение
Основное применение угла наклона прямой линии – определение уклона.
Если θ – угол наклона прямой линии l, то tanθ называется наклоном градиента линии и обозначается буквой «m».
Следовательно, наклон прямой равен
м = tan θ
для 0° ≤ θ ≤ 180°
Найдем наклон прямой по приведенной выше формуле
(i) Для горизонтальных линий угол наклона равен 0° или 180°.
То есть
θ = 0° или 180°
Следовательно, наклон прямой линии равен
м = tan0° или tan 180° = 0
(ii) Для вертикальных линий угол наклона равен 90°.
То есть
θ = 90°
Следовательно, наклон прямой равен
м = tan90° = Не определено
(iii) Для наклонных линий, если θ имеет острую форму, наклон положительный. Если же θ тупой, то наклон отрицательный.
Наклон линии — положительный или отрицательный, нулевой или неопределенный
Когда мы смотрим на прямую линию визуально, мы можем легко определить знак наклона.
Чтобы узнать знак наклона прямой, всегда нужно смотреть на прямую слева направо.
Это иллюстрируют приведенные ниже рисунки.
Решенные задачи
Задача 1 :
Найдите угол наклона прямой, наклон которой равен 1/√3.
Решение :
Пусть θ — угол наклона линии.
Тогда наклон линии составляет
M = tanθ
Дано: наклон = 1/√3
Затем,
1/√3 = tanθ
θ = 30 °
Итак, угол угла наклон 30°.
Задача 2 :
Если угол наклона прямой равен 45°, найдите ее наклон.
Решение :
Пусть θ — угол наклона линии.
Тогда, наклон линии,
M = TANθ
Дано: θ = 45 °
Затем,
M = TAN 45 °
M = 1
Итак, склон — 1.
Итак, склон — 1.
Задача 3 :
Если угол наклона прямой равен 30°, найдите ее наклон.
Решение :
Затем, наклон линии,
м = tanθ
Дано: θ = 30°
Тогда
м = tan30°
м = 1/√3
Итак, уклон равен √3
.
Задача 4 :
Найдите угол наклона прямой, наклон которой равен √3.
Решение :
Пусть θ — угол наклона линии.
Затем, наклон линии,
м = tanθ
Дано: Уклон = √3
Тогда,
√3 = tanθ
θ = 60°
Итак, угол наклона равен 60°.
Задача 5 :
Найдите угол наклона прямой, уравнение которой y = x + 32.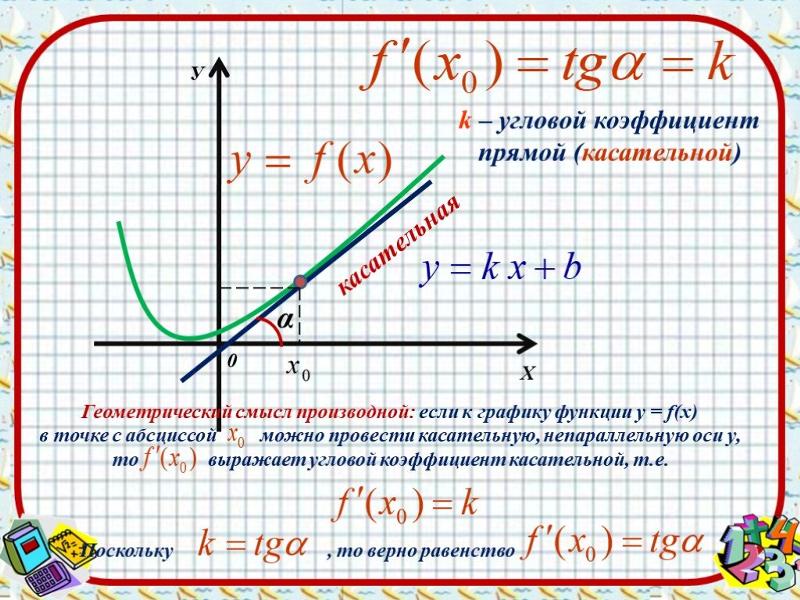
Решение :
Пусть θ — угол наклона линии.
Данное уравнение находится в форме пересечения наклона.
То есть
y = mx + b
Сравнивая
y = x + 32
и
y = mx + b,
получаем наклон 1. m = 9.0004
Мы знаем, что наклон линии равенм = tanθ
Тогда
1 = tanθ
θ = 45°
Итак, угол наклона равен 45°.
Пожалуйста, отправьте свой отзыв на [email protected]
Мы всегда ценим ваши отзывы.
©Все права защищены. onlinemath5all.com
Градиент (или наклон) линии и наклон
Применение: Дорожный знак, указывающий на крутой уклон.
Уклон дороги «15%» эквивалентен «m = 0,15».
Градиент (также известный как наклон ) линии определяется как
`»градиент»=текст(вертикальный подъем)/текст(горизонтальный ход`
На следующей диаграмме градиент линии AB задается как: `a/b`
baBAОткрыть изображение на новой странице Стороны треугольника a, b, c.
В общем, для линии, соединяющей точки ( x 1 , у 1
`(х_1, у_1)
`(x_2,y_1)
`(x_2,y_2)
`y_2-y_1
`x_2-x_1
`»наклон» = (y_2-y_1)/(x_2-x_1)`
Наклон линии, соединяющей точки ( x 1 , y 1 ) и ( x 2 , 2 y 2).
Теперь мы можем написать формулу наклона линии.
Градиент линии Формула
Из приведенной выше диаграммы видно, что градиент (обычно пишется м ) определяется как:
`м=(у_2-у_1)/(х_2-х_1`
Интерактивный график — наклон линии
Вы можете изучить концепцию наклона линии на следующем интерактивном графике (это не фиксированное изображение).
Перетащите в любую точку A ( x 1 , y 1 ) или точку B ( x 2 , y 2 ), чтобы исследовать, как работает формула градиента.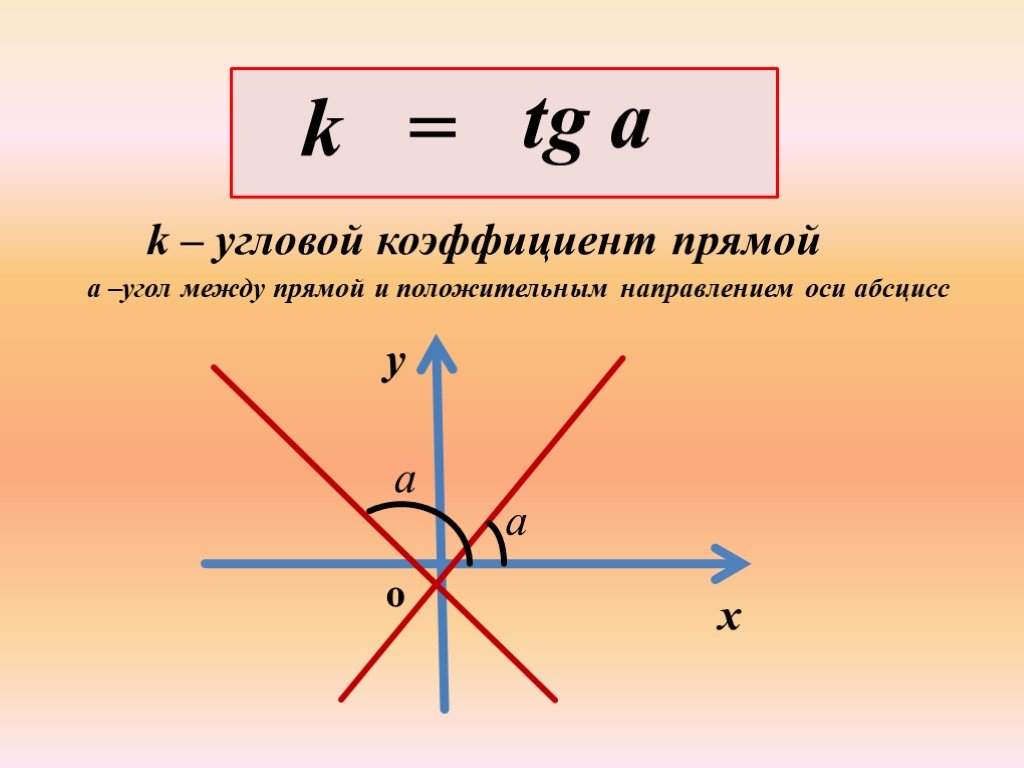
Обратите внимание, что происходит со знаком (плюс или минус) наклона, когда точка B находится выше или ниже точки A.
Наклон `= (y_2 — y_1)/(x_2 — x_1)`
`=(BC)/(AC)`
Copyright © www.intmath.com
Вы можете перемещать график вверх-вниз, влево-вправо, если, удерживая нажатой клавишу «Shift», перетаскивать график.
Если вы заблудитесь, вы всегда можете обновить страницу.
Пример
Найдите наклон линии, соединяющей точки (−4, −1) и (2, −5).
Ответить
Это задействованные точки:
123-1-2-3-4-51-1-2-3-4-5-6xy(−4, −1)(2, −5)Открыть изображение на новой страницеЛиния, соединяющая точки (−4, −1) и (2, −5).
Итак, наклон равен:
`м=(у_2-у_1)/(х_2-х_1`
`=(-5-(-1))/(2-(-4)`
`=(-4)/6`
`=-2/3`
Обратите внимание, что наклон отрицательный .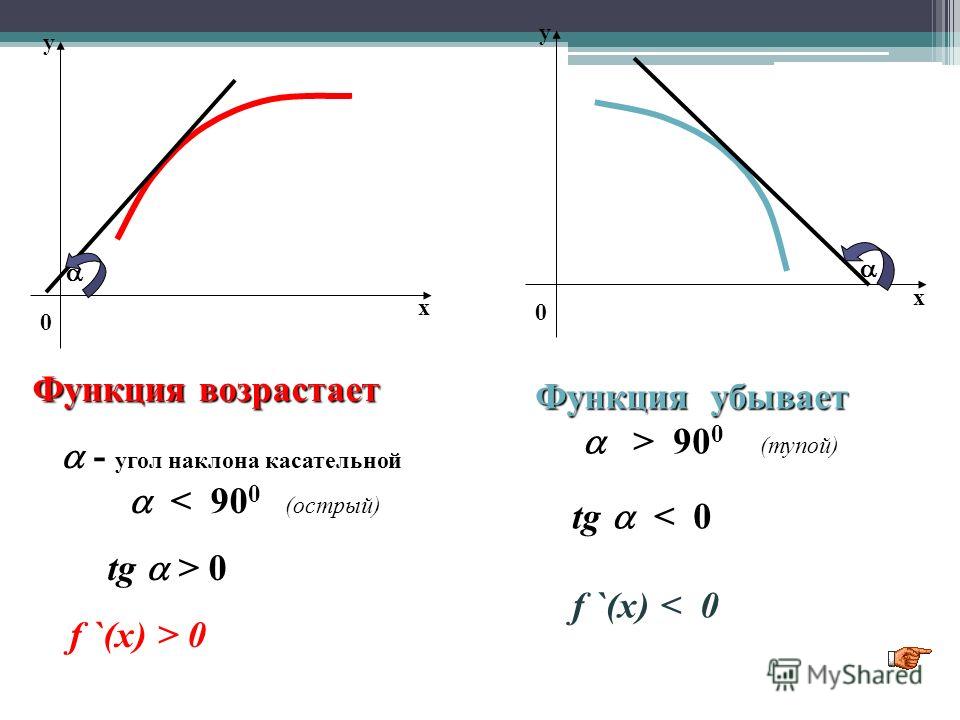
Линия идет «вниз по склону», когда мы движемся слева направо.
Положительные и отрицательные наклоны
В общем, положительный наклон указывает значение зависимой переменной (обычно y ) увеличивается по мере движения слева направо:
xy`»наклон » m » положительный»`
Линия имеет положительный наклон .
Зависимая переменная на приведенном выше графике — это значение y , а независимая переменная — x .
Отрицательный наклон означает, что значение зависимой переменной (обычно y ) равно уменьшению при движении слева направо:
xy`»наклон » m «отрицательный»`
Линия имеет отрицательный наклон .
Наклон
У нас есть линия с уклоном м и угол, который линия образует с x — ось α. xy`альфа`
`»уклон «м»»`
Угол α наклон линии с уклоном м .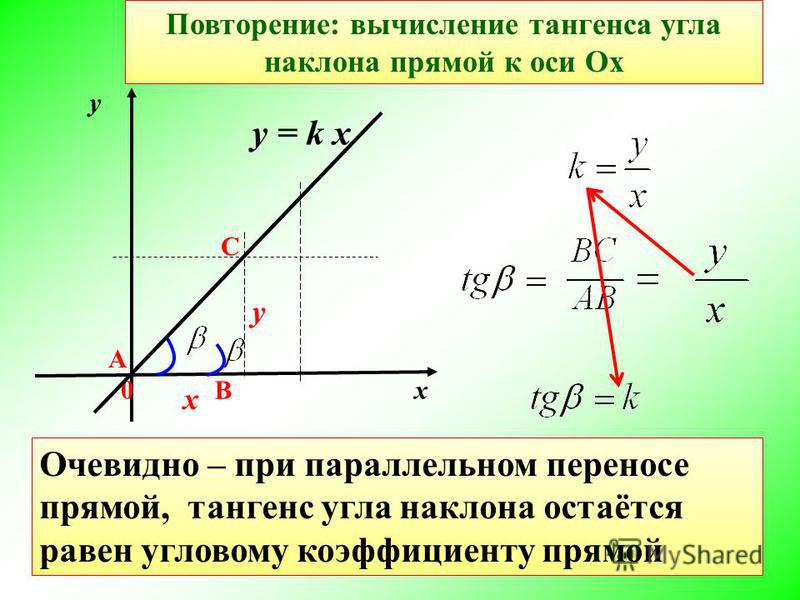
Из тригонометрии мы помним, что тангенс угла α определяется как:
`tan\ alpha=текст(напротив)/текст(смежный)`
Теперь, поскольку наклон также определяется как противоположный/примыкающий, мы имеем:
напротив соседнего`альфа`
`tan alpha = «напротив»/»смежный» = m`
Диаграмма, иллюстрирующая тангенс α = м .
Это дает нам результат:
тан α = м
Затем мы можем найти угол α , используя
α = арктангенс м
(то есть α
= тангенс -1 м )
Этот угол α называется наклоном линии.
9@`ПРИМЕЧАНИЕ: Размер угла α (по определению) только между «0°» и «180°».
Упражнение 2
Найдите наклон линии с наклоном α = 137°.