Модуль егэ. Неравенства с модулем примеры решения. Решение неравенств содержащих знак модуля.
- Альфашкола
- Статьи
- Решение неравенств с модулем
Что такое модуль \(|x-a|\)?
Давайте дадим определение:
И если мы нарисуем картинку, то получим:
То есть главным моментом будет то, что модуль всегда является числом положительным.
Пример 1. Найдите значение \(\left|6+6x\right|\le \:12\).
Решение :
\(\left|6+6x\right|\le \:12\)
Неравенство с модулем, где модуль меньше или равно какого либо значения \(|a|\le \:b\) является системой , то есть объединение двух интервалов, раскрывается по схеме :
\(\begin{equation*} \begin{cases} a,\;a\le \:b \\a,\; a\ge \:-b \end{cases} \end{equation*}\)
\(\begin{equation*} \begin{cases} 3+2x\le \:7 \\ 3+2x\ge \:-7 \end{cases} \end{equation*}\)
\(\begin{equation*} \begin{cases} 6x\le \:6 \\ 6x\ge \:-18\end{cases} \end{equation*}\)
\(\begin{equation*} \begin{cases} x\le \:1 \\ x\ge \:-3\end{cases} \end{equation*}\)
\(-3\le \:x\le \:1\)
Ответ: \(\left[-3,\:1\right]\).
Пример 2. Найдите значение \(\left|5x-9\right|<\:6\).
Решение :
\(\left|5x-9\right|<\:6\)
\(\begin{equation*} \begin{cases} 5x-9<6 \\ 5x-9>-6\end{cases} \end{equation*}\)
\(\begin{equation*} \begin{cases} 5x<15 \\ 5x>3\end{cases} \end{equation*}\)
\(\begin{equation*} \begin{cases} x<3\\ x>\frac{3}{5}\end{cases} \end{equation*}\)
\(\begin{equation*} \begin{cases} x<3\\ x>0,6\end{cases} \end{equation*}\)
\(0,6<x<3\)
Ответ: \(\left(0,6;\:3\right)\).
Неравенство с модулем, где модуль больше или равно \(|x|\geq a \) решается по формуле и является совокупностью двух интервалов:
\(\left[ \begin{gathered} x \le \: -a \\ x \geq a \\ \end{gathered} \right.\)
Пример 3. Найдите значение \(\left|x-15\right|\ge \:\:3\).
Решение :
\(\left|x-15\right|\ge \:\:3\)
\(\left[ \begin{gathered} x-15\le \:-3\\ x-15\ge \:3 \\ \end{gathered} \right.
\)
\(\left[ \begin{gathered} x\le \:12\\ x\ge \:18 \\ \end{gathered} \right.\)
Ответ: \((-\infty \:,\:12]\cup \:[18,\:\infty \:)\).
Пример 4. Найдите значение \(4\left|x+10\right|\ge \:16\).
Решение :
\(4\left|x+10\right|\ge \:16\)
\(\left[ \begin{gathered} x+10\le \:-4\\ x+10\ge \:4\\ \end{gathered} \right.\)
\(\left[ \begin{gathered} x\le \:-14\\ x\ge \:-6\\ \end{gathered} \right.\)
Ответ: \(\:(-\infty \:,\:-14]\cup \:[-6,\:\infty \:)\).
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Ринат Фарагатович Шаймарданов
Репетитор по математике
Стаж (лет)
Образование:
Уфимский авиационный институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Вера Петровна Любчак
Репетитор по математике
Стаж (лет)
Образование:
Университет штата Аризона
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Сергей Александрович Москвин
Репетитор по математике
Стаж (лет)
Образование:
Костромской государственный университет им.
Н.А. Некрасова
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Предметы
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по обществознанию
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Репетитор для подготовки к ОГЭ по физике
- Подготовка к олимпиадам по физике
- Репетитор по грамматике русского языка
- Подготовка к олимпиадам по английскому языку
- Репетитор по грамматике английского языка
- Репетитор для подготовки к ВПР по английскому языку
- Репетитор для подготовки к ВПР по обществознанию
- Репетитор по географии для подготовки к ЕГЭ
- Репетитор по географии для подготовки к ОГЭ
- Scratch
Похожие статьи
- Первообразная
- РУДН: Прикладная информатика (учебный план, проходной балл)
- ЕГЭ по математике, профильный уровень.
Задачи по планиметрии - ЕГЭ по математике, профильный уровень. Показательные уравнения
- Тренируемся решать задачи с прикладным содержанием
- Задачи на исследование функций
- Почему не стоит пользоваться маминой косметикой
- Как использовать материнский капитал на образование: полная инструкция для родителей
Задачи по планиметрииНажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Текст с ошибкой:
Расскажите, что не так
Функция абсолютного значения, функция модуля
|x| всегда положительно, независимо от того, начали ли мы с +x или -x.
|г| всегда положительно, независимо от того, начали ли мы с +y или -y.
Складывая или вычитая их без абсолютных значений, вы получаете один из четырех возможных результатов:
(+x) + (+y) или (+x) + (-y) или (-x) + (+ y) или (-x) + (-y)
Поскольку оба имеют один и тот же знак (xy>0), первое утверждение всегда верно, оно верно даже для x>y во втором утверждении. Но второе утверждение, |x| — |у| = |х — у| тогда xy<0 кажется ложным.
Сначала рассмотрим сложение… В наших примерах мы будем использовать x=3 и y=10:
Оба отрицательные: -3 + (-10) = -13.
Оба положительны: 3 + 10 = 13.
Итак, пока оба числа имеют одинаковый знак (именно это и означает: xy>0 ), ответ будет ±13. Как только вы поместите это в абсолютное значение, оба результата будут положительными 13 и |x| + |у| = |х+у|
Значение |-3| + |-10| = 3 + 10 = 13 (отдельные значения абс) и
| (-3) + (-10)| = |-13| = 13 (объединено в один абс) (13 = 13, так что работает)
|x| + |у| = | х + у | если оба числа имеют одинаковый знак (xy>0)
Здесь оба числа положительны:
|3| + |10| = 3 + 10 = 13 и | 3+10 | = |13| = 13 (13 = 13, поэтому работает)
С другой стороны, если одно положительное, а другое отрицательное, вы, по сути, вычитаете.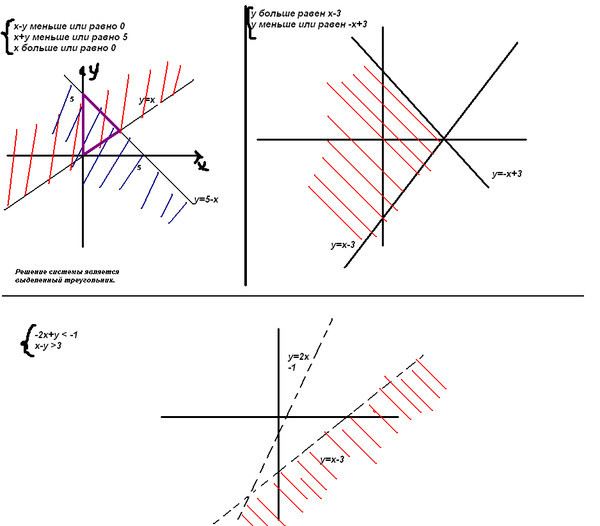
Например, -3+10 = 7 или 3 + (-10) = -7
С разными знаками вы получите либо +7, либо -7 в зависимости от порядка выполнения вычитания. Если вы поместите любой из этих результатов в абсолютное значение, вы получите ПОЗИТИВНОЕ 7.
Все четыре случая с вычитанием, когда x Оба положительных: |3| — |10| = 3 — 10 = -7 и вместе внутри | 3 — 10 | = | -7 | = 7 (-7≠7 поэтому не работает!) Оба отрицательные: |-3| — |-10| = 3 — 10 = -7 и вместе внутри |-3 — (-10) | = | 7| = 7 (-7≠7, так что не работает!) Различные знаки (xy<0): «3» отрицательная и «10» положительная: |-3| — |10| = 3 — 10 = -7 и вместе внутри |-3 — 10 | = | -13 | = 13 (-7≠13, поэтому не работает!) «10» отрицательная и «3» положительная: | 3| — | -10 | = 3 — 10 = -7 и вместе внутри |3 — (-10)| = |3 + 10 | = 13 (-7≠13, так что не работает!) Второй, |x| — |у| = |х — у| когда xy<0 не работает ни в одном из четырех случаев, а x (обратите внимание: |x| – |y| может дать отрицательный результат (когда |x| < |y|), тогда как | x – y | всегда будет положительным) Но, если мы требуем, чтобы x > y, то теперь x = 10 и y = 3, то мы имеем это: Оба положения: |10| — |3| = 10 — 3 = 7 и | 10 — 3 | = | 7 | = 7 (7 = 7, так что работает) Оба отрицательные: |-10| — |-3| = 10 — 3 = 7 и |-10 — (-3) | = | -10 + 3 | = | -7 | = 7 (7 = 7, так что работает) «10» отрицательная и «3» положительная: |-10| — |3| = 10 — 3 = 7 и |-10 — (+3) | = |-13 | = 13 (7≠13, поэтому НЕ РАБОТАЕТ!) «10» плюс и «3» минус: |10| — | -=3 | = 10 — 3 = 7 и |10 — (-3) | = |10 + 3 | = |13| = 13 (7≠13, поэтому НЕ РАБОТАЕТ!) Таким образом, во втором утверждении исходной задачи, вероятно, должно быть сказано xy>0 И x>y. Я нашел это в Интернете — верное утверждение: |x-y|>|x|-|y| для ху<0. Это НЕРАВЕНСТВО верно, УРАВНЕНИЕ во второй строке неверно. Определите интервалы, на которых функция 𝑓 от 𝑥 равна 𝑥 плюс три умноженных на абсолютное значение 𝑥 плюс три увеличивается и уменьшается. Помните, мы можем вычислить интервалы возрастания и убывания функции, думая о ее производной. В частности, если мы можем найти производную этой функции на каком-то интервале, и значение этой производной положительно (больше нуля), то сама функция должна возрастать на этом интервале. Точно так же, если производная отрицательна, если она меньше нуля на каком-то интервале, то функция должна убывать на этом интервале. И, конечно же, нам нужно быть немного осторожными здесь. Эта функция является произведением линейной функции и модуля линейной функции. Так как же вычислить его производную? Начнем с того, что напомним себе, что делает функция модуля. Отсюда следует, что для значений 𝑥 меньше отрицательной тройки значение 𝑥 плюс три отрицательно. Таким образом, когда 𝑥 меньше минус трех, выход функции, абсолютное значение 𝑥 плюс три, будет отрицательным 𝑥 плюс три. Но когда 𝑥 больше или равно минус трем, значение 𝑥 плюс три положительно. Поэтому, когда 𝑥 больше или равно минус трем, абсолютное значение просто выводит 𝑥 плюс три. Это означает, что нам разрешено думать о функции абсолютного значения как о кусочно-определенной функции. И, в свою очередь, это также означает, что мы можем переписать 𝑓 из 𝑥, используя кусочную запись, как показано. Когда 𝑥 меньше минус трех, функция является произведением 𝑥 плюс три и минус 𝑥 плюс три. А когда 𝑥 больше или равно минус трем, мы получаем 𝑥 плюс три раза 𝑥 плюс три. Итак, 𝑥 плюс три в квадрате и минус 𝑥 плюс три в квадрате — это многочлены. Это означает, что они дифференцируемы во всей своей области определения, которая, конечно же, является набором действительных чисел. Таким образом, мы можем использовать общее правило мощности, чтобы дифференцировать отрицательное 𝑥 плюс три в квадрате на интервале 𝑥 меньше, чем отрицательное три, и дифференцировать 𝑥 плюс три в квадрате на интервале 𝑥 больше или равно отрицательному трем. Обобщенное степенное правило дифференцирования является специальной версией цепного правила. В нем говорится, что мы можем дифференцировать 𝑛-ю степень 𝑓 числа 𝑥, умножив 𝑛 на 𝑓 числа 𝑥 в степени 𝑛 минус единица на производную от внутренней функции, поэтому 𝑓 простое число 𝑥. Другими словами, производная отрицательного 𝑥 плюс три в квадрате равна удвоенному отрицательному 𝑥 плюс трем в первой степени, умноженной на производную 𝑥 плюс три, что равно единице. Аналогичным образом, производная от 𝑥 плюс три в квадрате равна удвоенному 𝑥 плюс три в первой степени, умноженной на производную от 𝑥 плюс три, что равно единице. И тогда мы можем упростить каждую часть этого выражения, как показано. Теперь стоит отметить, что этот процесс работает, потому что сама функция непрерывна при 𝑥 равно минус трем. Но также существуют и левые, и правые производные, и фактически они равны нулю, а 𝑥 равно минус трем. Теперь рассмотрим знак производной на каждом интервале. Когда 𝑥 меньше минус трех, мы получаем отрицательное число, умноженное на отрицательное, что, конечно же, является положительным. Затем, когда 𝑥 больше или равно отрицательному трем, мы получаем положительное, умноженное на неотрицательное, что дает неотрицательное. Он больше или равен нулю. Поэтому мы можем сказать, что производная положительна для всех действительных значений 𝑥, за исключением случаев, когда 𝑥 равно отрицательному трем.
Видео с вопросами: Нахождение интервалов, в которых функции абсолютного значения возрастают и убывают
Стенограмма видео
Эта функция специально принимает значения 𝑥, затем прибавляет к этому значению три, а затем убеждается, что результат положительный. Например, предположим, что 𝑥 равно минус пять. Минус пять плюс три минус два. И тогда модуль или абсолютное значение этого положительное два.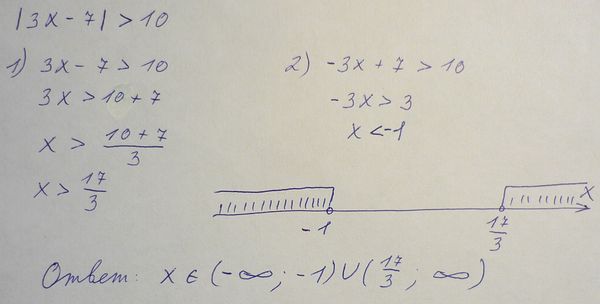
И мы, конечно, можем упростить каждую часть этой функции, как показано на рисунке. Затем, чтобы найти производную 𝑓 от 𝑥, мы будем дифференцировать каждую часть функции.
Мы можем переписать это, конечно, как отрицательное два раза 𝑥 плюс три в первой степени, умноженные на один.