Составьте уравнение касательной к графику функции y f x в точке x0: Составьте уравнение касательной к графику функции y=x^3+2x в точке с абсциссой x0=-1

Содержание

Уравнение касательной к графику функции

Похожие презентации:

Уравнение касательной к графику функции

Уравнение касательной к графику функции. 10 класс

Касательная к графику функции

Касательная к графику функции. (10 класс)

Производная функции

Функции и их свойства. Предел последовательности и функции. Производная функции и дифференциал

Касательная. Уравнение касательной

Производная функции

Уравнение касательной к
графику функции
10 класс
МБОУ Каменно-Балковская СОШ
учитель: Пономарева Ю.В.
Верно ли определение?
Касательная – это прямая,
имеющая с данной кривой
одну общую точку.
Пуст ь дана y x 2 и две прямые x 1 и y 2 x 1 ,
имеющая с данной параболой одну общую т очку М
(1;1).
x 1
На данном уроке:
1. выясним, что же такое касательная к
графику функции в точке, как составить
уравнение касательной;

рассмотрим основные задачи на
составление уравнения касательной.
Для этого:
вспомним общий вид уравнения прямой
условия параллельности прямых
определение производной
правила дифференцирования
Формулы дифференцирования
Определение производной
Пусть функция y f (x) определена в
некотором интервале, содержащем внутри
себя точку x0 . Дадим аргументу x
приращение такое, чтобы не выйти из этого
интервала. Найдем соответствующее
приращение y функции и составим
y
отношение x .Если существует предел
отношения при x 0 , то указанный предел
называют производной функции
y f (x)
‘
в точке x0 и обозначают f ( x0 ) .
y
lim
f ‘ ( x0 )
x 0 x
Правила дифференцирования
1. Производная суммы равна сумме производных.
f x g x ‘ f ‘ x g ‘ x
2. Постоянный множитель можно вынести за знак
производной.
‘
‘
kf x kf x
3. Производная произведения двух функций равна сумме

двух слагаемых; первое слагаемое есть произведение
производной первой функции на вторую функцию, а второе
слагаемое есть произведение первой функции на
производную второй функции.

f x g x f ‘ x g x f x g ‘ x
‘
4. Производная частного
f x
f ‘ x g x f x g ‘ x
2
x
g
x
g
‘
Основные формулы
дифференцирования
f (x)
С
1
x
x
x
‘
f ( x)
‘
f (x)
f ( x)
0
sin x
cos x
1
2
x
cos x
sin x
1
2 x
x
1
tgx
ctgx
1
cos 2 x
1
2
sin x
Две прямые параллельны тогда и
только тогда, когда их угловые
коэффициенты равны
Параллельны ли прямые:
a ) y 2 x 1;
б) y 2 x 2;
в) y 3 x 1.
Пусть дан график функции y=f(x). На нем выбрана точка
M(a;f(a)), в этой точке к графику функции проведена касательная
(мы предполагаем, что она существует). Найти угловой
коэффициент касательной.
y f x , M a; f a
k сек
y
x
k кас lim kcек
x 0
k кас
y
lim
x 0 x
Геометрический смысл
производной
Если к графику функции y = f (x) в точке
x a можно провести касательную,
непараллельную оси у, то f ‘ (a)
выражает угловой коэффициент
касательной
kкас
y
f (a x) f (a)
‘
lim
lim
f a
x 0 x
x a
(a x) a
Геометрический смысл
производной
Производная в точке
x x0 равна
угловому коэффициенту
касательной к
графику функции
y = f(x) в этой точке.

.
Т.е.
f ( x0 ) tg
‘
Причем, если :
1. f ‘ ( x0 ) tg 0, то острый
2. f ‘ ( x0 ) tg 0, то развернутый
3. f ‘ ( x0 ) tg 0, то тупой

Вывод уравнения касательной
y kx m, M a; f a
Пусть прямая задана уравнением:
k f ‘ (a)
f a ka m
m f a ka
y kx f a ka
y f a f
‘
a x a
уравнение касательной к
графику функции
y f (x)
Составить уравнение касательной:
к графику функции
M 1;1
f (1) 12 1
f ‘ ( x) 2 x
f ‘ (1) 2 1 2
y f (a ) f ‘ (a )( x a )
y 1 2 ( x 1)
y 1 2x 2
y 2x 1
f ( x) x
2
в точке
Составить уравнение касательной:
к графику функции
f (0) tg 0 0
1
f ( x)
cos 2 x
1
‘
f ( 0)
1
2
cos 0
y f (a ) f ‘ (a )( x a )
‘
y 0 1 ( x 0)
y x
y tgx
в точке M 0;0
Алгоритм нахождения уравнения
касательной к графику функции
y=f(x).
1. Обозначим абсциссу точки касания буквой
x=a.
2.

Вычислим f (a ) .
3. Найдем f ‘ ( x) и f ‘ (a) .
4. Подставим найденные числа a , в формулу
y f a f a x a .
‘
Составить уравнение касательной к
1
графику функции y в точке x 1 .
x
1
f ( x)
x
1) a 1
2) f (a) f (1) 1
1
‘
3) f ( x) 2
x
1
f (a ) f (1) 2 1
1
‘
‘
4) y 1 ( x 1)
y 2 x
Ответ
y 2 x
:
x3
К графику функции y 3
провести касательную так,
чтобы она была параллельна прямой y 4 x 5 .
kкас 4, k кас f ‘ ( x) f ‘ ( x) 4
x
f ( x)
3
‘
1
3 x 2 x 2
3
f ‘ (a) a 2 a 2 4,
3
‘
.
1) a1 2, a2 2
3
(
2
)
8
2
8 , f (a )
2) f (a1 )
2
3
3
3 3
3
3) f ‘ (a1 ) f ‘ (a2 ) 4
16
16
4) y 4 x
, y 4x
3
3
,
Ответьте на вопросы:
1. Что называется касательной к графику
функции в точке?
2. В чем заключается геометрический
смысл производной?
3.

Сформулируйте алгоритм нахождения
уравнения касательной?

English Русский Правила

Конспект занятия решения ключевых задач по теме «Уравнение касательной к графику функции»

Теоретический материал для самостоятельного изучения

Ход занятия:

I. Мотивационно-ориентировочная часть

1. Актуализация опорных знаний.

— Как вы понимаете термин «касательная»?

— Что такое угловой коэффициент касательной?

— Как влияет угловой коэффициент прямых на взаимное расположение прямых?

— Расставьте этапы алгоритма составления уравнения касательной в правильном порядке.

2. Постановка цели занятия.

Повторение.

Геометрический смысл производной

Производная функции в конкретной точке равна тангенсу угла наклона касательной к графику функции в этой точке, или угловому коэффициенту этой касательной:

f′(x0)= tgφ=k
Касательная — это прямая

, которая касается графика функции в одной точке и все точки которой находятся на наименьшем расстоянии от графика функции.

Поэтому касательная проходит касательно графика функции под определённым углом и не могут проходить через точку касания несколько касательных под разными углами. Уравнения касательной и уравнения нормали к графику функции составляются с помощью производной.
Уравнение касательной

Уравнение касательной к графику функции f(x) в точке x0: y=f′(x0)⋅(x−x0)+f(x0).

Уравнение касательной выводится из уравнения прямой.

Выведем уравнение касательной, а затем — уравнение нормали к графику функции.

Вспомним уравнение прямой с угловым коэффициентом:

y = kx + b

В нём k — угловой коэффициент.

Отсюда получаем следующую запись:

y — y0 = k(x — x0 ).

Значение производной f ‘(x0 ) функции y = f(x) в точке x0 равно угловому коэффициенту k = tgφ касательной к графику функции, проведённой через точку M0 (x0 ,

y0 ), где y0 = f(x0 ). В этом состоит геометрический смысл производной.

Таким образом, можем заменить k на f ‘(x0 ) и получить следующее уравнение касательной к графику функции:

y — y0 = f ‘(x0 )(x — x0 ).

Алгоритм действий для нахождения уравнения касательной

Алгоритм	Пример №1: f(x)=x2 −2x+3, x0=3
1. Вычислим f(x0)	f(x0)=f(3)=32−2⋅3+3=6
2. Найдем формулу производной функции f′(x)	f′(x)=(x2−2x+3)′=2x−2
3. Вычислим f′(x0)	f′(x0)=f′(3)=2⋅3−2=4
4. Подставим x0, f(x0) и f′(x0) в формулу уравнения касательной y=f′(x0)⋅(x−x0)+f(x0) Пример №2	y=f′(x0)⋅(x−x0)+f(x0) =4(x−3)+6= 4x−12+6= =4x−6

Закрепление знаний при решении задач

Переходим к примерам. Для решений потребуется таблица производных.

Решаем задачи вместе

Пример 1. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение.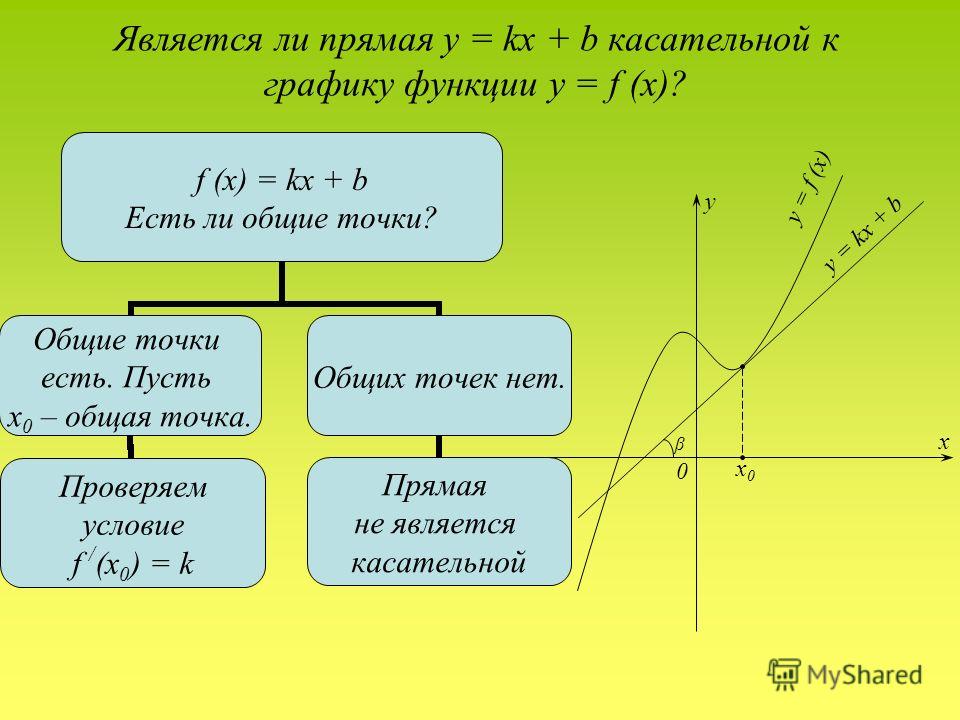 Найдём ординату точки касания:

Найдём производную функции:

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Теперь у нас есть всё, что требуется подставить в приведённую в теоретической справке запись, чтобы получить уравнение касательной. Получаем

В этом примере нам повезло: угловой коэффициент оказался равным нулю, поэтому отдельно приводить уравнение к общему виду не понадобилось. Теперь можем составить и уравнение нормали:

На рисунке ниже: график функции бордового цвета, касательная зелёного цвета, нормаль оранжевого цвета.

Следующий пример — тоже не сложный: функция, как и в предыдущем, также представляет собой многочлен, но угловой коэффициен не будет равен нулю, поэтому добавится ещё один шаг — приведение уравнения к общему виду.

Пример 2. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Найдём производную функции:

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Подставляем все полученные данные в «формулу-болванку» и получаем уравнение касательной:

Приводим уравнение к общему виду (все буквы и числа, отличные от нуля, собираем в левой части, а в правой оставляем ноль):

Составляем уравнение нормали:

Пример 3. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Найдём производную функции:

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Находим уравнение касательной:

Перед тем, как привести уравнение к общему виду, нужно его немного «причесать»: умножить почленно на 4. Делаем это и приводим уравнение к общему виду:

Составляем уравнение нормали:

Домашнее задание: повторить теоретический материал §48, стр. 253 (учебник: Алгебра. 10-11 класс. Ш.А. Алимов) рассмотреть решение задач №1,2,3, составить краткий конспект занятия.

2.3: Касательная плоскость к поверхности

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 2252

Майкл Коррал
Колледж Скулкрафт

В предыдущем разделе мы упоминали, что частные производные $\dfrac{∂f}{∂x}$ и $\dfrac{∂f}{∂y}$ можно рассматривать как скорость изменения функция $z = f (x, y)$ в положительных направлениях $x$ и $y$ соответственно. Напомним, что производная $\dfrac{dy}{dx}$ функции $y = f (x)$ имеет геометрический смысл, а именно как наклон касательной к графику $f\ ) в точке \((x, f (x))$ в $\mathbb{R}^2$. 3\), и пусть $P = (a,b,c)$ — точка на $S$. Пусть $T$ — плоскость, содержащая точку $P$, а $Q = (x, y, z)$ — точка общего положения на поверхности $S$. Если (острый) угол между вектором $\vec{PQ}$ и плоскостью $T$ стремится к нулю, когда точка $Q$ приближается к $P$ по поверхности $S$ , то мы называем $T$ 93\) определяют плоскость, то две касательные к поверхности $z = f (x, y)$ в направлениях $x$ и $y$, описанные на рис. 2.3.1, содержатся в касательная плоскость в этой точке, , если касательная плоскость существует в этой точке . Существование этих двух касательных линий само по себе не гарантирует существования касательной плоскости. Возможно, что если мы возьмем след поверхности в плоскости $x − y = 0$ (которая образует угол 45◦ с положительной осью $x$), результирующая кривая в этой плоскости может иметь касательную линию, которая не находится в плоскости, определяемой двумя другими касательными линиями, или она может вообще не иметь касательную линию в этой точке. К счастью, оказывается, что если $\dfrac{∂f}{∂x}$ и $\dfrac{∂f}{∂y}$ существуют в области вокруг точки $(a,b) $ и непрерывны в $(a,b)$, то касательная плоскость к поверхности $z = f (x, y)$ будет существовать в точке $(a,b, f (a, б))$. В этом тексте эти условия всегда будут выполняться.

Предположим, что нам нужно уравнение касательной плоскости $T$ к поверхности $z = f (x, y)$ в точке $(a,b, f (a,b))$ . Пусть $L_x$ и $L_y$ касательные к следам поверхности в плоскостях $y = b$ и $x = a$ соответственно (как на рис. 2.3.2) , и предположим, что условия существования $T$ действительно выполнены. Тогда уравнение для $T$ равно

\[A(x−a)+B(y−b)+C(z−f(a,b)) = 0 \label{Eq2.4}\]

, где $n = (A,B,C)$ — вектор нормали к плоскости $T$. Так как $T$ содержит прямые $L_x$ и $L_y$, то нам нужны только векторы $v_x$ и $v_y$, которые параллельны $L_x \text{и } L_y$ соответственно, а затем пусть $n = v_x × v_y$.

Рисунок 2.3.2: Касательная плоскость

Поскольку наклон $L_x$ равен $\dfrac{∂f}{∂x} (a,b)$, то вектор $v_x = (1,0, \dfrac{∂f}{∂x} (a,b))$ параллелен $L_x$ (поскольку $v_x$ лежит в плоскости $xz$ и лежит на прямой с наклоном $\dfrac{\dfrac{∂f}{∂x}(a,b)}{1} = \dfrac{∂f}{∂x} (a,b)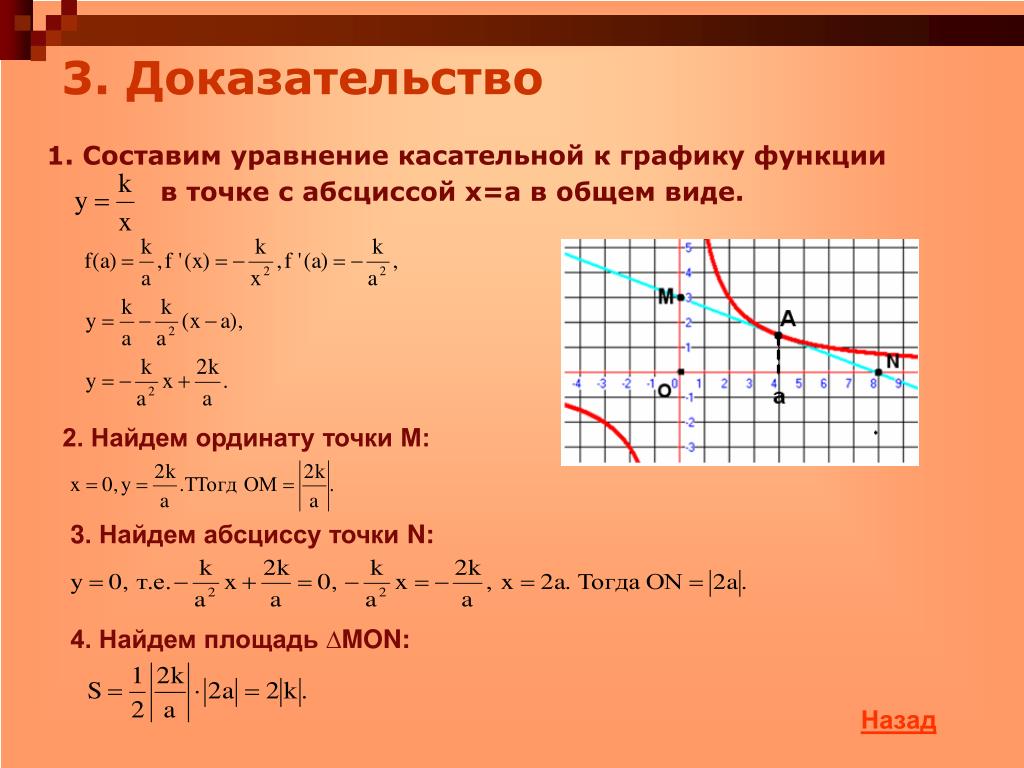$. 2\) в точке (1,2,5). 92\), имеем $\dfrac{∂f}{∂x} = 2x$ и $\dfrac{∂f}{∂y} = 2y$, поэтому уравнение касательной плоскости в точке $(1,2,5)$ равно

\[\nonumber 2(1)(x−1)+2(2)(y−2)− z +5 = 0 \text{ , или }\ ]

\[\номер 2x+4y− z −5 = 0\]

Аналогичным образом можно показать, что если поверхность неявно определяется уравнением вида $F(x, y, z) = 0$, то касательная плоскость к поверхности в точке $ (a,b,c)$ задается уравнением

\[\dfrac{∂F}{∂x}(a,b,c)(x− a)+ \dfrac{∂F}{∂y}(a,b,c)(y−b)+ \ dfrac{∂F}{∂z}(a,b,c)(z − c) = 0 \label{Eq2.7}\] 92 −9\), имеем $\dfrac{∂F}{∂x} = 2x$, $\dfrac{∂F}{∂y} = 2y$ и $\dfrac{∂F }{∂z} = 2z$, поэтому уравнение касательной плоскости в точке (2,2,−1) равно

\[\nonumber 2(2)(x−2)+2(2)(y− 2)+2(−1)(z +1) = 0 \text{, or}\]

\[\nonumber 2x+2y− z −9 = 0\]

Эта страница под названием 2.3: Касательная плоскость к поверхности распространяется в соответствии с лицензией GNU Free Documentation License 1. 3, автором, ремиксом и/или куратором которой является Майкл Коррал.

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или Страница
Автор
Майкл Коррал
Лицензия
ГНУ ФДЛ
Показать страницу TOC
нет
Теги
1. касательная плоскость

исчисление — Найдите уравнение, касательное к графику y=f(x) в точке, где x=-3, если f(-3)=2 и f'(-3)=5 [застрял]

$\begingroup$

Задача: найти уравнение, касающееся графика y=f(x) в точке где x=-3, если f(-3)=2 и f'(-3)=5

Что я пробовал: Я попытался решить это так, как находятся «нормальные» касательные уравнения, когда задача дает точку и уравнение (y = Mx + b). подойдет для решения для точки, используя Y-Y1=m(x-x1))

Где x1 =-3 [Как указано в задаче] [Единственное приведенное уравнение:] Y=f(x) [плагин «-3» приводит к] f(-3)) = Y

Задача устанавливает, что f(-3)=2 Таким образом, мы нашли y=2 & x1=-3

Если бы я попытался подставить это, чтобы «вывести» (как в обычной задаче, где требуется найти касательную, а точка задана и решена через пересечение наклона, а затем через вывод):

y=f( х)

у’=f'(х) f'(-3) = 2 //Как я мог это вывести?, здесь, вероятно, моя ошибка, хотя я не знаю, как подойти к этому по-другому.

[Тогда проблемы устанавливает «и f'(-3)=5» так что по задаче f'(-3)=5 НЕ 2, значит я что-то не так сделал и явно не решается таким образом]

Я действительно застрял здесь. Как найти уравнение?

исчисление
производные
касательная

$\endgroup$

$\begingroup$

Касательная имеет наклон $f'(-3)=5$ и проходит через точку $(-3,f(-3))=(-3,2)$. Возьмите $y=Mx+b$ и подставьте $M=f'(-3)=5$, и тангенс станет $y=5x+b$. Теперь замена $(-3,2)$ дает $b=2-5(-3)=17$. Итак, тангенс равен $y=5x+17$.

Наклон этой касательной будет равен $\frac{dy}{dx}=5$, что совпадает с наклоном кривой $f(x)$ в точке $(-3,2)$.

$\endgroup$

$\begingroup$

Вам говорят градиент и точку на линии. Это не вопрос исчисления (за исключением того, что вам нужно интерпретировать производную как указание на градиент в точке). Это просто вопрос «замени и реши $c$».

У вас уже есть метод, требуемый в вашем вопросе: подставьте $y_1=2$, $x_1=-3$ и $m=5$.

Вам определенно не нужно «выводить» $y=f(x)$, даже если бы вы могли. То, как вы пытались это сделать, просто ошибочно копирует значение из $f(x)$, что почти наверняка будет неправильным (было бы полной случайностью, если бы это сработало для данной производной).

Уравнение касательной к графику функции

Конспект занятия решения ключевых задач по теме «Уравнение касательной к графику функции»

2.3: Касательная плоскость к поверхности

исчисление — Найдите уравнение, касательное к графику y=f(x) в точке, где x=-3, если f(-3)=2 и f'(-3)=5 [застрял]

Добавить комментарий Отменить ответ