6.2.2. Точка максимума и минимума
Точка х=х1 называется точкой максимума функции у=f(x), если для всех точек некоторого интервала, содержащего точку х1, будет выполняться равенство при любых достаточно малых или .
Точка х=х2 называется точкой минимума функции у=f(x), если для всех точек некоторого интервала, содержащего точку х2, будет выполняться неравенство , где или .
Точка максимума и минимума называются точками экстремума функции. Рассмотрим методы нахождения экстремумов.
6.2.3. Необходимое условие экстремума
Теорема.
Если дифференцируемая функция у=f(x) имеет в точке х=х0 экстремум,
то её производная в точке обращается в
нуль, то есть ,
или не существует.
Пусть для определённости точка х0 является точкой максимума. Тогда из определения максимума следует, что или . Составим и оценим знаки отношения приращений , а именно: , если и , если .
По условию теоремы функция дифференцируема в точке х0, значит существует предел , и он не зависит от того, как стремится к нулю. Беря пределы от обеих приведённых выше неравенств, получаем с одной стороны , если >0, с другой , если <0. но так как есть определённое число, то два последних неравенства совместимы, только если .
Аналогичным образом теорема доказывается для случая, когда х0 – точка минимума.
Точки,
в которых производная обращается в нуль
или не существует, называются критическими
точками первого рода или точками подозрительными
на экстремум. Условия существования
критических точек, в которых производная
равна нулю, описываются условием теоремы
Ролля, которую мы приведём без
доказательств.
Геометрически это значит, что найдётся хотя бы одна точка a<c<b, в которой касательная параллельна оси Ох.
Для того, чтобы найти точку экстремума функции у=f(x) необходимо найти её производную, приравнять её нулю и решить полученное уравнение. Корни этого уравнения, а также точки разрыва производной будут критическими точками.
Пример 6.1. Найти критические точки функции у=2х3-6х2+1.
Р
ешение.
Найдём производную .
Решим уравнение 6х2-12х=0,
его корни х1=0,
х2=2 – критические точки.
Пример 6.2. Найти критические точки функции у=х3.
Решение. — критическая точка.
Легко увидеть (рис.6.3.), что х=0 для функции у=х3 не является точкой экстремума. Так что имеющееся условие экстремума (или ) является лишь необходимым, но недостаточным.
6.2.4. Достаточные признаки существования экстремума
Первый достаточный признак экстремума формулируется на основе изменения знака первой производной при переходе через критическую точку. О втором признаке экстремума речь пойдёт ниже в § 6.4.
Теорема
(первый признак экстремума): Если х0 –
критическая точка функции у=f(x) и в некоторой окрестности точки х0,
переходя через неё слева направо,
производная меняет знак на противоположный, то х0 является точкой экстремума.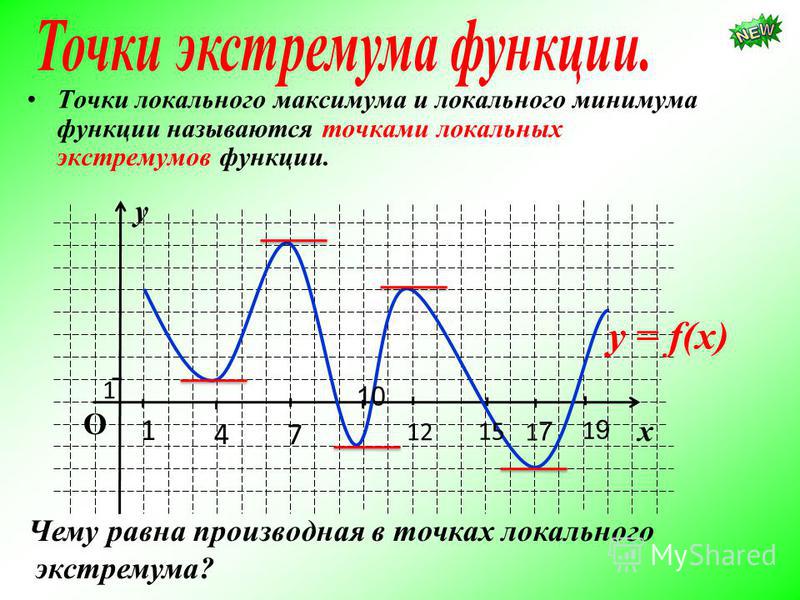
Причём,
если знак производной меняется с «+» на
«-», то х0 – точка максимума, а f(x0) – максимум функции, а если производная
меняет знак с «-» на «+», то х0 – точка минимума, а
Рассмотренный экстремум носит локальный (местный) характер и касается некоторой малой окрестности критической точки.
Точки экстремума и точки разрыва делят область определения функции на интервалы монотонности.
Пример 6.3. В примере 6.1. мы нашли критические точки х1=0 и х2=2.
Выясним,
действительно ли в этих точках функция у=2х3-6х2+1 имеет экстремум. Подставим в её производную
значения х,
взятые слева и справа от точки х1=0 в достаточно близкой окрестности,
например, х=-1и х=1.
2
Как найти максимумы и минимумы функции?
Каковы максимумы и минимумы?
Максимумы функции f(x) — это все точки на графике функции, являющиеся «локальными максимумами».
Точка, в которой x=a является локальным максимумом, если при небольшом смещении влево (точки с xa) значение f(x) уменьшается на . Мы можем визуализировать это как наш график, имеющий пик «холма» в точке x = a.
Аналогично, минимумы f(x) — это точки, для которых при небольшом смещении влево или вправо значение f(x) увеличивает . Мы называем эти точки «локальными минимумами» и можем визуализировать их как дно «впадины» на нашем графике.
Одно сходство между максимумами и минимумами нашей функции заключается в том, что градиент нашего графика всегда равен 0 во всех этих точках; в самом верху пиков и в самом низу впадин наклон нашего графика равен , полностью плоский .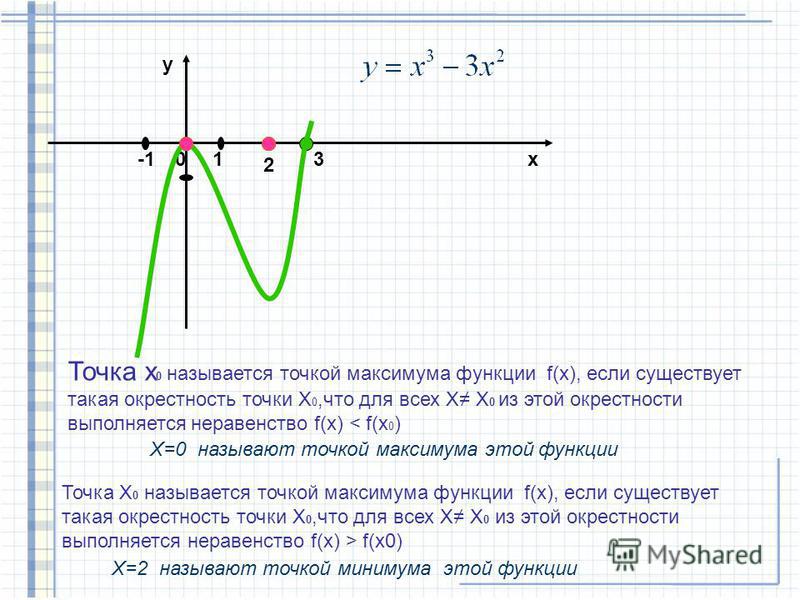
Это означает, что наша производная f ‘(x) равна равно нулю в этих точках.
Как их найти?
1) Имея f(x), мы дифференцируем один раз, чтобы найти f ‘(x).
2) Установите f ‘(x)=0 и найдите x. Используя наше приведенное выше наблюдение, значения x, которые мы находим, являются «координатами x» наших максимумов и минимумов.
3) Подставьте эти значения x обратно в f(x). Это дает соответствующие «y-координаты» наших максимумов и минимумов.
Какие из этих точек максимальные, а какие минимальные?
Здесь мы можем применить простой тест. Предположим, мы нашли стационарную точку (a,b):
1) Продифференцируем f ‘(x) еще раз, чтобы получить f »(x), вторую производную s .
2) Вычислить f »(a):
— Если f »(a)<0, то (a,b) является локальным максимумом .
— Если f »(a)>0, то (a,b) является локальным минимумом .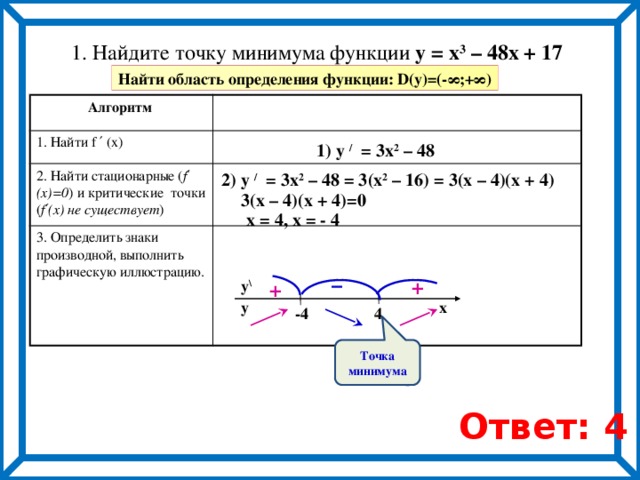
Чтобы понять, почему это работает, представьте, что вы постепенно приближаетесь к нашей точке (a,b), отображая наклон нашего графика по мере движения.
Если наша точка является локальным максимумом , мы можем, что этот наклон начинается с положительного , уменьшается до нуля в точке, затем становится отрицательным по мере того, как мы движемся через точку и за ней. Наш наклон f ‘(x) равен , уменьшаясь на на всем протяжении этого движения, поэтому мы должны иметь f »(a)<0.
Точное обратное верно, если (a,b) является локальным минимумом . Наш наклон равен , увеличивая за одно и то же движение, поэтому здесь мы имеем f »(a)>0.
Пример:
Найдите максимум и минимум f(x)=x 3 +x 2 3 .
1) Найдите f ‘(x).
— Используя правила дифференцирования, находим f'(x)=3x 2 +2x.
2) Теперь давайте установим f ‘(x) = 0: 3x 2 +2x = 0
x (3x +2) = 0 (факторизация)
x = 0 или x = -2/3
3) Подставьте эти значения обратно, чтобы мы могли найти наши «y-координаты»: f(0)=(0) 3 +(0) 2 =0
f(-2/3)=(-2/3) 3 +(-2/3) 2 =4/27
точки (0,0) и (-2/3,4/27) .
4) Наконец, мы используем наш тест: подставляя x=-2/3)
2>0, поэтому (0,0) является локальным минимумом функции f(x).
-2<0, поэтому (-2/3,4/27) равно локальный максимум f(x).
Минимальных и максимальных значений Часть I Одним из наиболее важных применений исчисления является определение минимума и максимума. Давайте используем для нашего первого примера уравнение 2X 2 -5X -7 = 0 Это квадратное уравнение с одной переменной. То есть это уравнение формы: С уравнениями этого типа мы знаем что, когда член «а» положительный, график кривой будет «вогнутым вверх» (U-образный) и, следовательно, уравнение будет иметь минимальное значение, но не максимальное значение (хорошо — технически, максимальное значение — бесконечность). Глядя на график мы видим, что точка минимума примерно X = 1,5 и Y = -10. Есть ли способ определения точки минимума Посмотрите на график. Если бы значения уклона были рассчитаны для точек на левой стороне
кривой, вы могли видеть, что наклон всегда будет отрицательным , но он становится
«менее отрицательное» — чем ближе кривая приближается к минимуму (внизу). Так что логично думать, что наклон равен нулю в этой «нижней» точке
и поэтому производная тоже равна нулю в этой точке. В этом примере мы знали , что получаем минимальное значение, потому что
мы изобразили это на графике. Кроме того, мы заявили, что «правило» для квадратных уравнений такое
что, когда член «а» положительный, кривая будет «вогнутой». В этом примере, взяв производную от производной , мы имеют положительное значение 4, и поэтому мы знаем, что это минимум. Для уравнений типа aX 2 + bX + c =0 удобным инструментом является Калькулятор квадратных уравнений. Это не только вычисляет корни уравнения, он также покажет производную и точку, в которой существует максимум или минимум. Второй пример, который мы рассмотрим, очень похож на предыдущий, за исключением что он «вогнут вниз», а не «вогнут вверх». Если вы думаете, что понимаете концепции, представленные до сих пор, а затем перейти к части II Хорошо, давайте рассмотрим это уравнение:  |
ценности. Это находит применение в производстве, финансах, машиностроении и
множество других отраслей.
Прежде чем мы рассмотрим реальный пример, мы должны научиться вычислять
такие ценности.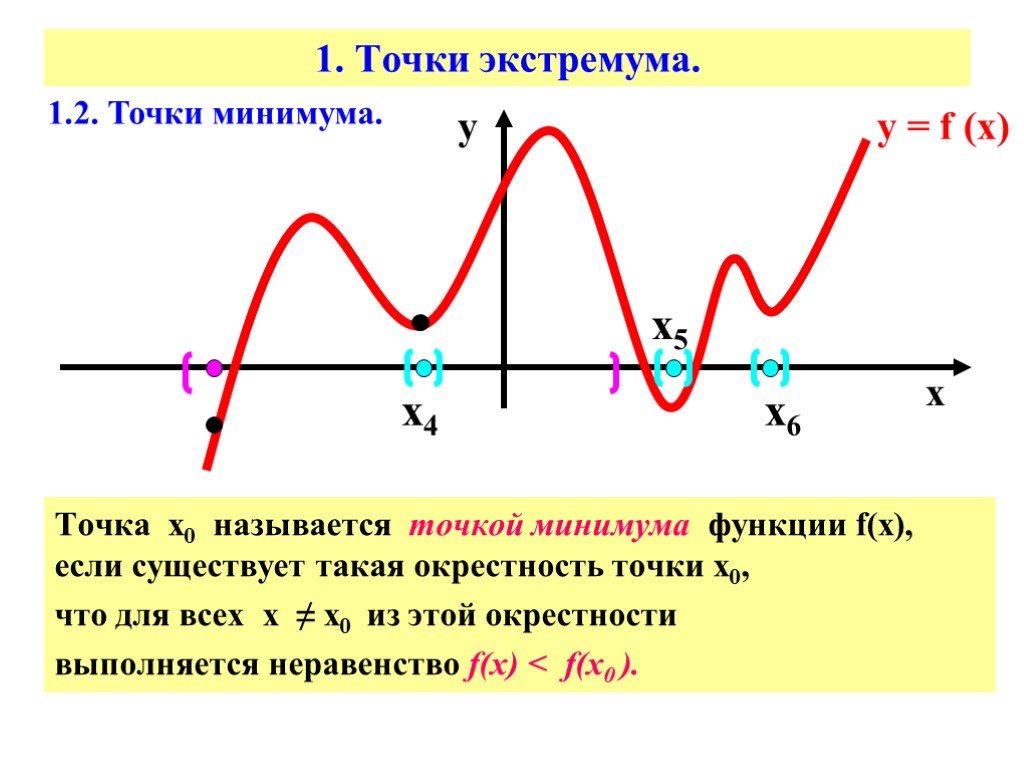
Если бы наклон был рассчитан вдоль правой стороны кривой, значение
будет ли всегда положительным , и значения наклона будут тем больше, чем дальше
вдали от «дна» точки были.
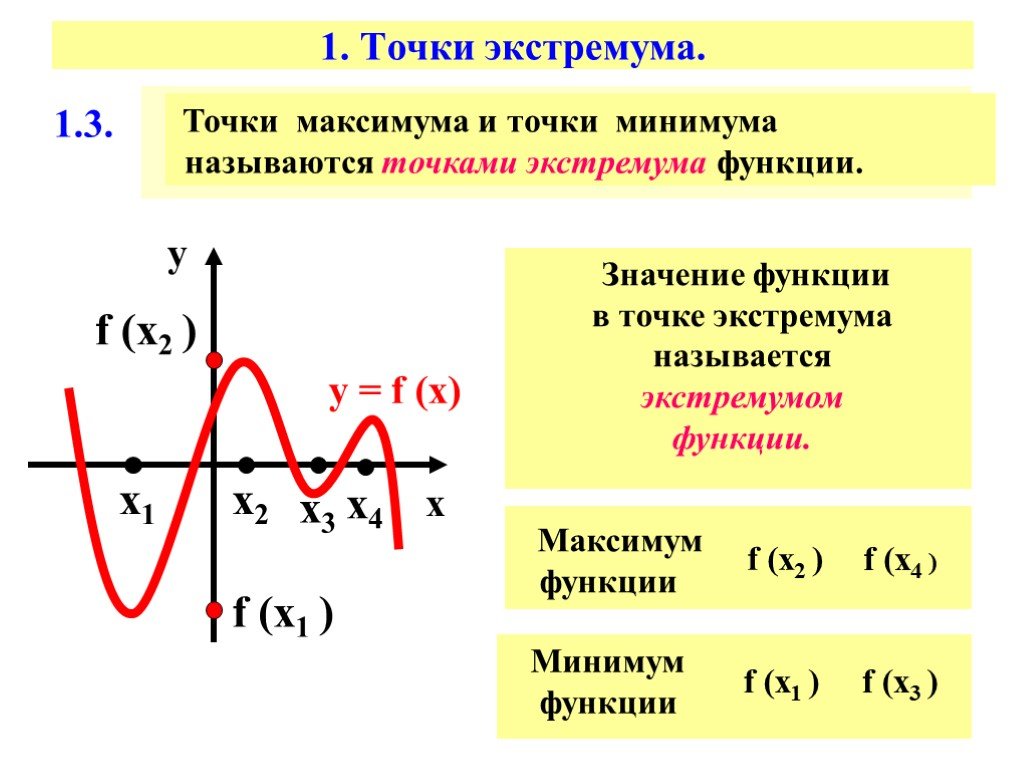Есть еще
третий способ определения того, является ли точка максимальным или минимальным значением.