Синус развернутого угла: Синус тупого угла | Треугольники

{\circ}$. Подробнее о смежных углах читайте по ссылке →

Два плоских угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.

Вертикальные углы равны. Подробнее о вертикальных углах читайте по ссылке →

Прилежащие углы — два плоских угла, которые имеют общую вершину и одну общую сторону, но их внутренние области не пересекаются.

Центральный угол — угол с вершиной в центре окружности.

Центральный угол равен градусной мере дуги, заключённой между сторонами этого угла.

Вписанный угол — плоский угол, вершина которого лежит на окружности и стороны пересекают эту окружность.

Вписанный угол равен половине градусной меры дуги, ограниченной его сторонами. Все вписанные углы, опирающиеся на одну и ту же дугу, равны.

Виды плоских углоов, в зависимости от меры

1. Нулевой угол

   — угол градусной меры $0^{\circ}$. {\circ}$.

Читать дальше: что такое прямой угол.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Элементарная математика

Сканави М.И. Элементарная математика. 2-е изд., перераб. и доп., М.: 1974г. — 592с. Книга представляет собой повторительный курс элементарной математики и рассчитана на тех, кто хочет пополнить, укрепить и систематизировать свои знания. Как и в первом издании, содержание ориентировано на программы вступительных экзаменов в технические вузы и, в особенности, на программы подготовительных отделений при высших учебных заведениях, для учащихся которых, как мы надеемся, книга окажется полезной. (Книга включает в себя Ч1 — Арифметика, алгебра и элементарные функции и Ч2 — Геометрия. Каждый раздел включает в себя теоретическую часть и большое количество задач с решениями.) Оглавление ВВЕДЕНИЕ Часть первая. АРИФМЕТИКА, АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА 2. Простые и составные числа. Признаки делимости. 3. Наибольший общий делитель и наименьшее общее кратное. 4. Целые числа. Рациональные числа. 5. Десятичные дроби. Представление рациональных чисел десятичными дробями. 6. Иррациональные числа. Действительные числа. 7. Действия с приближенными числами. 8. Числовая ось. Координаты точки на плоскости. § 2. Степени и корни 9. Степени с натуральными показателями. 10. Степени с целыми показателями. 11. Корни. 12. Степени с рациональными показателями. Степени с действительными показателями. 13. Алгоритм извлечения квадратного корня. § 3. Комплексные числа 14. Основные понятия и определения. 15. Рациональные действия с комплексными числами. 16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа. 17. Действия с комплексными числами, заданными в тригонометрической форме. Формула Муавра. 18. Извлечение корня из комплексного числа. Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ 19. Алгебраические выражения. Одночлены и многочлены. 20. Формулы сокращенного умножения. 21. Бином Ньютона. 22. Разложение многочлена на множители. 23. Дробные алгебраические выражения. § 2. Иррациональные алгебраические выражения 24. Радикалы из алгебраических выражений. 25. Освобождение от иррациональности в знаменателе дроби. Глава III. ЛОГАРИФМЫ 26. Определение и свойства логарифмов. 27. Логарифмы по различным основаниям. Модуль перехода. § 2. Десятичные логарифмы 28. Характеристика и мантисса десятичного логарифма. 29. Применение десятичных логарифмов к вычислениям. Глава IV. ФУНКЦИИ И ГРАФИКИ 30. Величина. Числовые множества. 31. Определение функции. 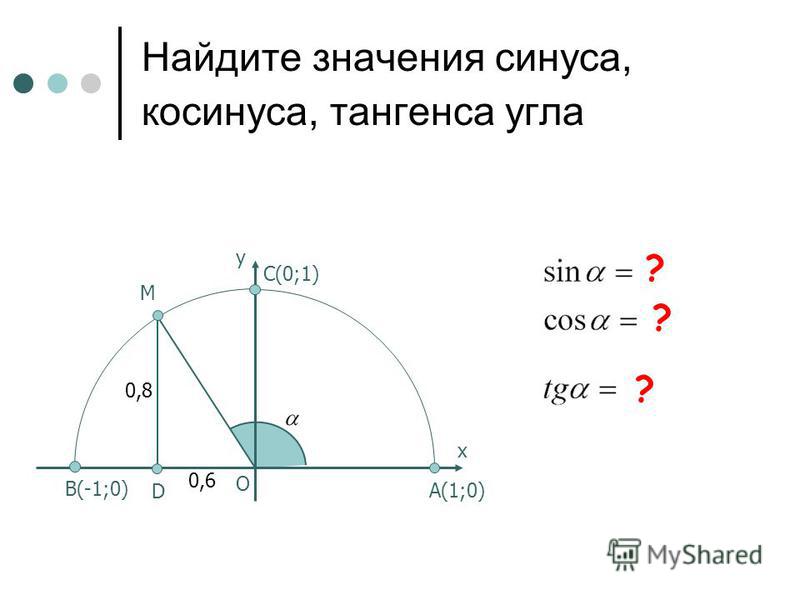n. 41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени. 42. Показательная функция. 43. Логарифмическая функция. § 3. Преобразование графиков 44. Параллельный сдвиг графика. 45. График квадратного трех члена. 46. График дробно-линейной функции. 47. Преобразование симметрии. Сжатие и растяжение графика. 48. Построение графиков функций. 49. Сложение графиков. § 4. Некоторые сведения о рациональных функциях 50. Целые и дробные рациональные функции. Деление многочленов. 51. Схема Горнера. Теорема Безу. 52. Нули многочлена. Разложение многочлена на множители. Глава V. УРАВНЕНИЯ 53. Уравнение. Корни уравнения. 54. Равносильные уравнения. 55. Системы уравнений. 56. Графическое решение уравнений. §. 2. Алгебраические уравнения с одной неизвестной 57. Число и кратность корней. 58. Уравнения первой степени (линейные уравнения). 59. Уравнения второй степени (квадратные уравнения). 60. Формулы Виета. Разложение квадратного трехчлена на множители. 61. Исследование квадратного уравнения. 62. Уравнения высших степеней. Целые корни. 63. Двучленные уравнения. 64. Уравнения, сводящиеся к квадратным. 65. Возвратные уравнения. § 3. Системы алгебраических уравнений 66. Линейные системы. 67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными. 68. Системы, состоящие из уравнения второй степени и линейного уравнения. 69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней. § 4. Иррациональные, показательные и логарифмические уравнения 70. Иррациональные уравнения. 71. Показательные уравнения. 72. Логарифмические уравнения. 73. Разные уравнения. Системы уравнений. Глава VI. НЕРАВЕНСТВА 74. Свойства неравенств. Действия над неравенствами. 75. Алгебраические неравенства. § 2. Решение неравенств 76. Множество решений нераве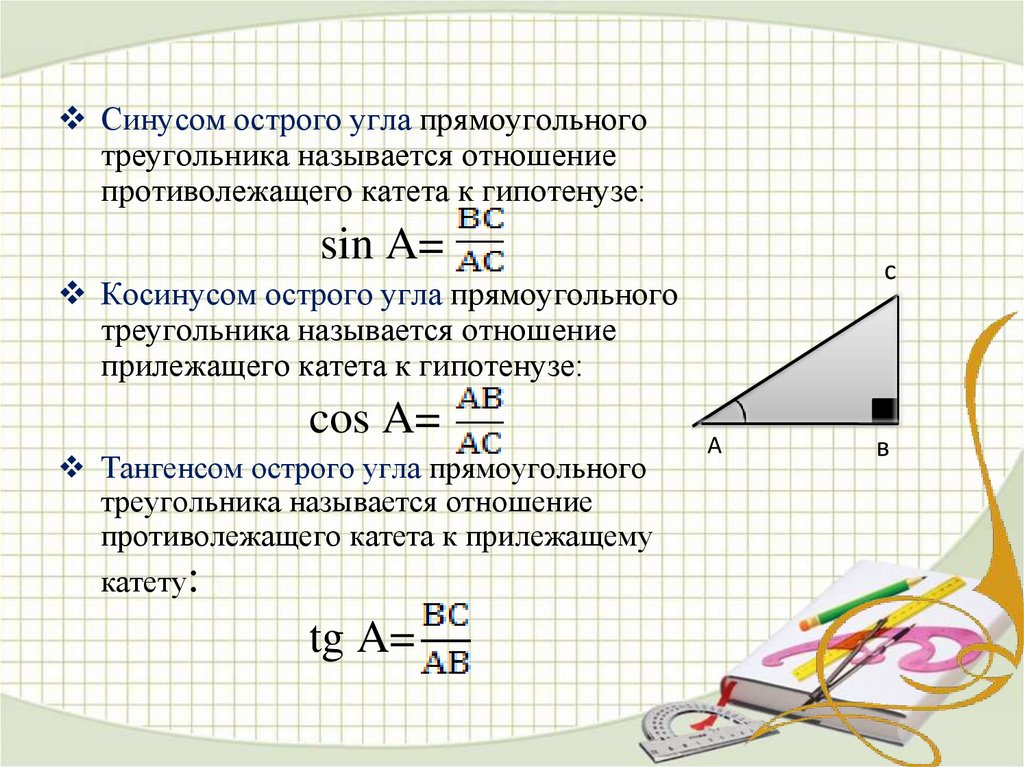нства. Равносильные неравенства. 77. Графическое решение неравенств. 79. Квадратные неравенства. 80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х. 81. Иррациональные, показательные и логарифмические неравенства. 82. Неравенства с двумя неизвестными. Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ 83. Числовая последовательность. 84. Предел числовой последовательности. 85. Бесконечно малые. Правила предельного перехода. § 2. Арифметическая прогрессия 86. Арифметическая прогрессия. Формула общего члена. 87. Свойства арифметической прогрессии. 88. Формула для суммы n членов арифметической прогрессии. § 3. Геометрическая прогрессия 89. Геометрическая прогрессия. Формула общего члена. 90. Свойства геометрической прогрессии. 91. Формулы для суммы n членов геометрической прогрессии. 92. Бесконечно убывающая геометрическая прогрессия. Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ) 93. Вектор, проекция вектора. 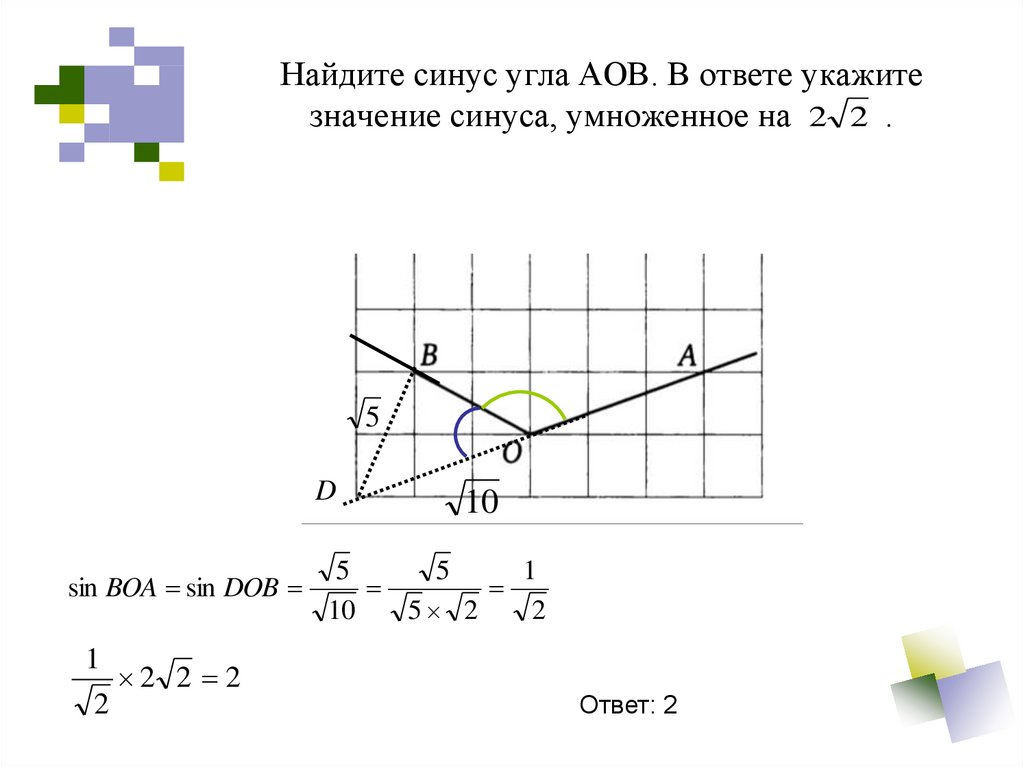94. Положительные углы и дуги, меньшие 360°. 95. Углы и дуги, большие 360°. 96. Отрицательные углы. Сложение и вычитание углов. § 2. Тригонометрические функции произвольного угла 97. Определение основных тригонометрических функций. 98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi. § 3. Соотношения между тригонометрическими функциями одного и того же угла 99. Основные тригонометрические тождества. 100. Вычисление значений тригонометрических функций по значению одной из них. 101. Значения тригонометрических функций некоторых углов. § 4. Четность, нечетность и периодичность тригонометрических функций 102. Четность и нечетность. 103. Понятие периодической функции. 104. Периодичность тригонометрических функций. § 5. Формулы приведения 105. Зависимость между тригонометрическими функциями дополнительных углов. 106. Формулы приведения. Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ § 1. Тригонометрические функции числового аргумента 108. Области определения и области изменения значений тригонометрических функций. 109. Некоторые неравенства и их следствия. § 2. Графики тригонометрических функций 110. Первоначальные сведения о таблицах тригонометрических функций. 111. Основные графики. 112. Примеры построения графиков некоторых других тригонометрических функций. 113. Дальнейшие примеры построения графиков функций. Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ 114. Расстояние между двумя точками на плоскости. 115. Косинус суммы и разности двух аргументов. 116. Синус суммы и разности двух аргументов. 117. Тангенс суммы и разности двух аргументов. 118. О формулах сложения для нескольких аргументов. § 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a 119. Тригонометрические функции двойного аргумента. 120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n. 121. Тригонометрические функции половинного аргумента. 122. Выражение основных тригонометрических функций аргумента а через tg(a/2). § 3. Преобразование в сумму выражений вида sina•cosb, cosa•cosb и sinа•sinb § 4. Преобразование в произведение сумм вида § 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента 127. Преобразование в произведение выражения a•sina + b•cosa. 128. Преобразование в произведение выражений a•sina+b и a•cosa+b 129. Преобразование в произведение выражения a•tga+b. Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ 130. Функция у = arcsin x (арксинус). 131. Функция y = arccos x (арккосинус). 132. Функция y = arctg x (арктангенс). 133. Функция y = arcctg x (арккотангенс). 134. Пример. § 2. Операции над обратными тригонометрическими функциями 135. Тригонометрические операции. 136. Операции сложения (вычитания). § 3. Обратные тригонометрические операции над тригонометрическими функциями 137. Функция у = arcsin (sin x). 138. Функция y = arctg (tg x). Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА 139. Уравнение sin х = а. 140. Уравнение cos х = a. 141. Уравнение tg x = a. 142. Уравнение ctg x = a. 143. Некоторые дополнения. § 2. Способ приведения к одной функции одного и того же аргумента 145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента. 146. Способ разложения на множители. 147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t. § 3. Некоторые частные приемы решения тригонометрических уравнений и систем 148. Введение вспомогательного аргумента. 149. Преобразование произведения в сумму или разность. 150. Переход к функциям удвоенного аргумента. 151. Решение уравнения типа… 152. Применение подстановок sinx ± соsx = y. § 4. Решение тригонометрических неравенств 154. Простейшие тригонометрические неравенства. 155. Примеры тригонометрических неравенств, сводящихся к простейшим. Часть вторая. ГЕОМЕТРИЯ 156. Точка. Прямая. Луч. Отрезок. 157. Плоскость. Фигуры и тела. 160. Равенство фигур. Движение. 161. Равенство тел. § 2. Измерение геометрических величин 162. Сложение отрезков. Длина отрезка. 163. Общая мера двух отрезков. 164. Сравнительная длина отрезков и ломаных. 165. Измерение углов. 166. Радианная мера угла. 167. Измерение площадей. 168. Площадь прямоугольника. Объем прямоугольного параллелепипеда. Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ 169. Перпендикуляр и наклонные. 170. Свойство перпендикуляра, проведенного к отрезку в его середине. 171. Параллельные прямые. 172. Углы, образованные двумя параллельными прямыми и секущей. 173. Углы с параллельными или перпендикулярными сторонами. § 2. Геометрические места точек. Окружность 174. Геометрическое место точек. 175. Свойство биссектрисы угла. 176. Окружность. 177. Взаимное расположение прямой и окружности. Касательная и секущая. 178. Хорда и диаметр. Сектор и сегмент. 179. Взаимное расположение двух окружностей. § 3. Основные задачи на построение 181. Деление отрезка пополам. Построение перпендикуляров. 182. Построение углов. 183. Другие задачи на построение. Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ 184. Стороны и углы треугольника. 185. Биссектрисы треугольника. Вписанная окружность. 186. Оси симметрии сторон треугольника. Описанная окружность. 187. Медианы и выcоты треугольника. 188. Равенство треугольников. 189. Построение треугольников. 190. Равнобедренные треугольники. 191. Прямоугольные треугольники. § 2. Параллелограммы 192. Четырехугольники. 193. Параллелограмм и его свойства. 194. Прямоугольник. § 3. Трапеция 196. Трапеция. 197. Средняя линия треугольника. 198. Средняя линия трапеции. 199. Деление отрезка на равные части. § 4. Площади треугольников и четырехугольников 200. Площадь параллелограмма. 201. Площадь треугольника. 202. Площадь трапеции. Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР 203. Пропорциональные отрезки. 204. Свойства биссектрис внутреннего и внешнего углов треугольника. § 2. Подобное преобразование фигур (гомотетия) 205. Определение гомотетичных фигур. 206. Свойства преобразования подобия. § 3. Общее подобное соответствие фигур 207. Подобные фигуры. 208. Периметры и площади подобных треугольников. 209. Применение подобия к решению задач на построение. Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ 210. Углы с вершиной на окружности. 211. Углы с вершиной внутри и вне круга. 212. Угол, под которым виден данный отрезок. 213. Четырехугольники, вписанные в окружность. 214. Пропорциональные отрезки в круге. 215. Задачи на построение. § 2. Метрические соотношения в треугольнике 216. Пропорциональные отрезки в прямоугольном треугольнике. Теорема Пифагора. 218. Теорема синусов. Формула Герона. 217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов. 218. Теорема синусов. Формула Герона. 219. Радиусы вписанной и описанной окружностей. § 3. Решение треугольников 220. Таблицы функций. 221. Решение треугольников. Сводка основных формул. 222. Решение прямоугольных треугольников. 223. Решение косоугольных треугольников. Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА 224. Выпуклые многоугольники. 225. Правильные многоугольники. 226. Соотношения между стороной, радиусом и апофемой. 227. Периметр и площадь правильного n-угольника. 228. Удвоение числа сторон правильного многоугольника. § 2. Длина окружности. Площадь круга и его частей 229. Длина окружности. 230. Площадь круга и его частей. Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ 231. Взаимное расположение двух прямых в пространстве. 232. Взаимное расположение прямой линии и плоскости. 233. Взаимное расположение двух плоскостей. 234. Свойства параллельных прямых и плоскостей. 235. Построения в стереометрии. § 2. Перпендикулярность прямых и плоскостей 236. Перпендикуляр к плоскости. 237. Перпендикуляр и наклонные. 238. Угол между прямой и плоскостью. 239. Связь между перпендикулярностью и параллельностью прямых и плоскостей. 240. Общий перпендикуляр двух скрещивающихся прямых. § 3. Двугранные и многогранные углы 241. Двугранный угол. 242. Взаимно перпендикулярные плоскости. 243. Трехгранные углы. 244. Многогранные углы. § 4. Многогранники 245. Многогранники. 246. Правильные многогранники. Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА 247. Цилиндры и призмы. 248. Параллелепипеды. 249. Объемы призм и цилиндров. 250. Площадь боковой поверхности призмы. 251. Площадь поверхности цилиндра. § 2. Пирамида. Конус 252. Свойства пирамиды и конуса. 253. Объем пирамиды и конуса. 254. Площадь боковой поверхности правильной пирамиды и конуса. 255. Усеченный конус и усеченная пирамида. § 3. Шаровая поверхность. Шар 256. Шар и шаровая поверхность. 257. Объем шара и его частей. 258. Площадь поверхности шара и ее частей. 259. Понятие телесного угла. Ответы к упражнениям Приложения

тригонометрия — Какая интуиция стоит за грехом тупого угла?

Задать вопрос

спросил 8 лет, 7 месяцев назад

Изменено 1 год, 5 месяцев назад

Просмотрено 11 тысяч раз

$\begingroup$

Определение греха угла является противоположным / гипотенузой. Очевидно, это определение легко использовать для острых углов прямоугольного треугольника, но трудно понять, как оно применимо к тупым углам.

Я знаю, что существуют тригонометрические тождества и концепции единичных окружностей, которые позволяют вычислить грех тупого угла, но я ищу более интуитивное объяснение того, что именно означает грех тупого угла.

• тригонометрия

$\endgroup$

2

$\begingroup$

«Определение синуса и угла противоположно/гипотенуза» — это работает только для прямоугольного треугольника и является началом определения функции синуса.

Чтобы расширить определение, нарисуйте единичный круг с центром в начале координат. Измерьте угол против часовой стрелки от положительной оси $x$ и возьмите точку $(x,y)$ на окружности. Синус угла (эквивалентный противолежащему/гипотенузе в первом квадранте, с гипотенузой, равной $1$) равен $y$, а косинус угла равен $x$. Вы можете пройти по кругу более одного раза, чтобы увидеть, что функции являются периодическими. 97}{5040}+\dots$$

$\endgroup$

$\begingroup$

В треугольнике $ABC$ в качестве примера возьмем угол $A$. Когда $A$ является острым, определение $\sin(A)$ – это отношение высоты $BH/AB$, где $BH$ – высота между $B$ и стороной $AC$ (мы также можем сделать где $CH$ — высота между $C$ и стороной $AB$).

в этом случае $\sin(A)=BH/AB$

когда $A=\pi/2$, в треугольнике $AB’C’$ аналогично представим $\sin(A )$ высота от $B’$ до стороны $AC’$, но на самом деле $AC’=0$ и $AB’=B’H’$, поэтому $\sin(A)=AB’/B ‘Ч’=1$

когда $A$ противоположна, то делаем то же самое в треугольнике $AB»C»$: $\sin(A)$ высота от $B»$ до стороны $AC»$, которая равно $BH»/AB»$. Это также $\sin$ угла $B»AH»$. Тогда $\sin(A)=\sin(180°-A)$.

$\endgroup$

$\begingroup$

Один из способов представить это — взять синус дополнительного угла. \circ — x) = \sin(x)$.

Я считаю, что это хорошая геометрическая интерпретация, но с чисто «интуитивной» точки зрения вы должны думать о $\sin(x)$ в терминах единичного круга.

$\endgroup$

0

$\begingroup$

Воспользуемся определением наклона или касательной конечной линии для каждого угла…. Для конечной линии острого угла наклон равен y/x…. Для конечной линии тупого угла наклон также равен y/x…..(хотя знак отрицательный)…. Теперь мы умножаем каждый наклон на x, чтобы получить значения sin для двух углов (в единичной окружности) как y и -y, которые равны по абсолютным значениям…..

$\endgroup$

2

Синус, косинус и тангенс для любого угла (острого, тупого и обратного) – BRILLIANT MATHS

Урок 7 – Синус, косинус и тангенс для любого угла (острого, тупого и обратного)

5 Цели

К концу урока учащиеся должны уметь:

• Продемонстрировать четкое понимание синуса, косинуса и тангенса дополнительных и дополнительных углов.
• Решите основные тригонометрические уравнения.
• Знать и использовать обратные величины тригонометрических отношений.

Основные тригонометрические отношения и их обратные величины друг друга, образуя четыре квадранта. В каждом из этих квадрантов мы используем соглашение о знаках, используемое при построении графиков.

Угол, если он положительный, всегда измеряется против часовой стрелки от OX, а угол образуется путем поворота линии (например, OP) против часовой стрелки. Длину ОП удобно сделать равной 1 единице. Рассмотрим диаграмму ниже.

В первом квадранте,

 

Во втором квадранте,

С помощью калькулятора можно найти синус, косинус и тангенс для углов любой величины.

 

Тригонометрические соотношения специальных углов

Соотношения для 30 ⁰ и 60 ⁰

Из C проведите перпендикуляр CD, который делит пополам основание AB и угол ACB.

 

Отношения для 45 ⁰

На рисунке ниже показан прямоугольный равнобедренный треугольник ABC с равными сторонами, каждая из которых имеет длину 1 единицу. Равные углы равны по 45 ⁰ . Now,

AC ² = AB ² + BC ²

AC ² = 1 ² + 1 ²

AC ² = 2

 

Синус и косинус тупых углов

До сих пор мы использовали синус, косинус и тангенс только в прямоугольных треугольниках. Для углов больше 90ᵒ мы увидим, что существует тесная связь между тригонометрическими отношениями и окружностями.

Посмотрите на кружок внизу.

Круг имеет радиус 1 единицу с центром (0, 0). Точка P с координатами (x, y) движется по окружности.

Угол, который OP образует с положительной осью x при повороте против часовой стрелки, равен θ.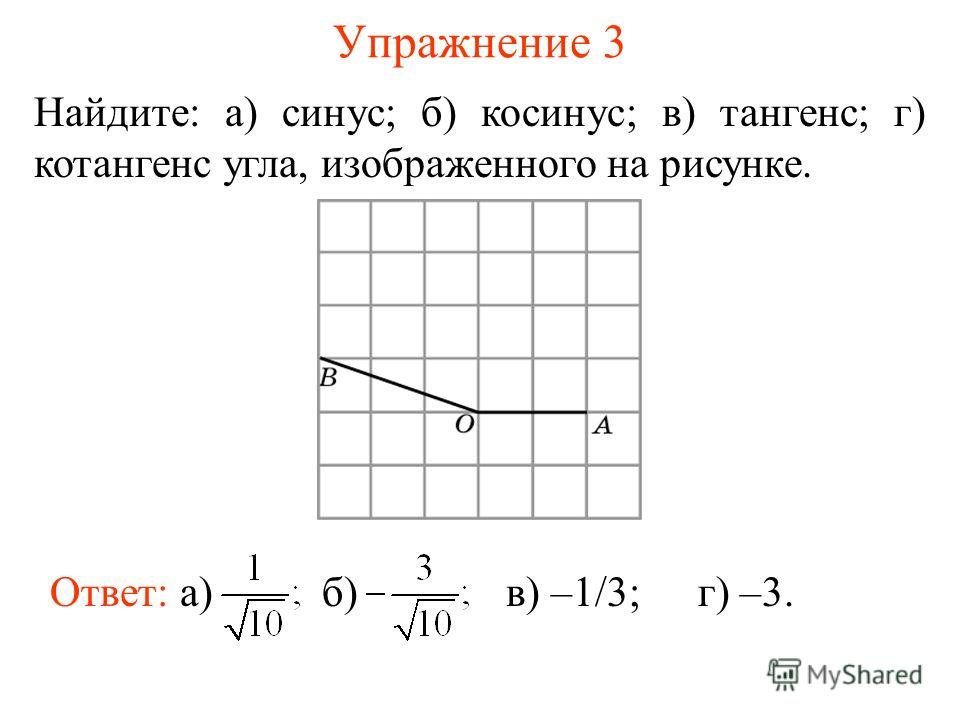

С помощью калькулятора можно построить график зависимости y = sin x для любого диапазона углов. На приведенном ниже графике показано y = sin x для x от 0ᵒ до 180ᵒ. Кривая над осью x имеет симметрию относительно x = 9.0ᵒ

Эти два результата особенно важны для использования с тупыми углами (90ᵒ < x < 180ᵒ).

 

Пример 1

Если sin 18ᵒ = 0,309, укажите другой угол, синус которого равен 0,309.

Решение

SIN θᵒ = SIN (180 — θ) ᵒ = SIN 162ᵒ

SIN 162ᵒ = 0,309 AS SIN 18 ⁰

ПРИМЕЧА ⁰

 

 

Дополнительные углы

Дополнительные углы – это углы, сумма которых равна 90 0^{. Рассмотрим треугольник ABC, показанный ниже.}

Пример 3

SIN 26 = COS 64 = 0,4384

COS 70 = SIN 20 = 0,3420

СВОРЕСА СЛАДА A обычно пишется как sin ² А. Таким образом, sin ² А = (sin А) ² и аналогично для остальных тригонометрических соотношений.

, который является cos ² a = (cos a) ² и tan ² a = (tan a) ²

Пример 4

Найдите значение COS 2 2 2

37

Раствор

Cos 37 = 0,7986, cos ² 37 = (cos 37) ² = (0,7989 29010)0110 = 0,6378

Основные тригонометрические идентичности и их взаимные. + cos ² A = 1, что можно доказать, рассмотрев прямоугольный треугольник.

 

Пример 6

Угол А является острым и 5SIN ² A — 2 = COS ² A. Найдите угол A.

Раствор

С Сневой ² A = 1

Cos ² A = 1 – sin ² A

Подставим Cos ² A = 1 – sin ² A  в полученное уравнение.

No related posts.