Внешний угол при вершине треугольника
Очередная задача про равнобедренный треугольник:
В треугольнике АВС АС=ВС. Внешний угол при вершине В равен 122 градуса. Найдите угол. Ответ дайте в градусах. Можно мне все подробно?
Постараюсь объяснить как можно подробнее. Почему я сразу сказал, что задача про равнобедренный треугольник? У обычных треугольников все стороны разной длинны. Их даже так и называют — разносторонние. Берем картинку со страницы про виды треугольников, отрезаем ненужное и начинаем разукрашивать. Геометрия — это та же детская разукрашка, только проще. В задаче обычно всегда говорится, что именно и как вы должны разукрашивать. Разукрасим нашу картинку с видами треугольников по размерам сторон синенькими буквами вершин равнобедренного треугольника.
| Виды треугольников |
Теперь нужно разобраться, что такое внешний угол при вершине треугольника.
И так, открываем «умную» книжку и начинаем копаться в математической грязи. В книжке написано буквально следующее:
Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине.
По умолчанию предполагается, что мы уже должны знать, что такое смежный угол. Не знаю, как вы, а я уже давно забыл, что это за фигня такая — «смежный угол». Ведь все нормальные люди пользуются нормальными углами. Хорошо, что к определению внешнего угла треугольника картинка прилагается, которая проясняет, как именно он выглядит.
| Внешний угол |
Я никогда не пойму, зачем к треугольнику лепить внешний угол, если у него уже есть обычные, внутренние, углы.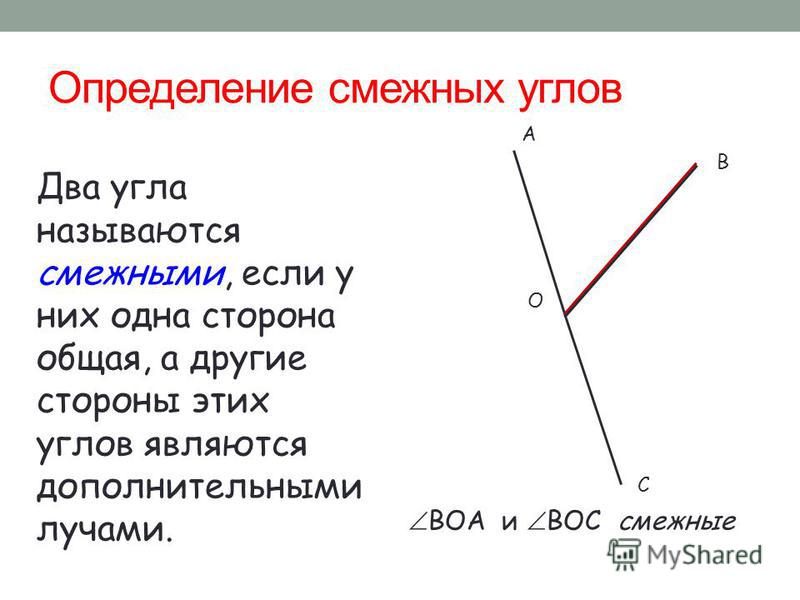
Я так понимаю, что одни дураки когда-то учили других, а те тупо повторяют действия учителей. Своими мозгами пользоваться их так никто и не научил. Кстати, величайшим достижением современного образования можно считать отсутствие в учебной программе научной теории о трех китах и Земле, которая на них держится. И это только потому, что данная теория не относится к математике. А ведь если в учебной программе что-то записано, то учить это обязательно для получения хорошей оценки.
Ладно, по возмущался и хватит. Вернемся к наше задаче. Читаем внимательно: Внешний угол при вершине В равен 122 градуса
| Внешний угол при вершине |
Кажется, я догадываюсь, откуда в математике могли появиться внешние углы.
Когда европейцы увидели пирамиды древнего Египта, они были потрясены увиденным. Им захотелось измерить эти грандиозные сооружения. Вот только внутренний угол пирамиды измерить не представляется возможным. Можно измерить внешний угол и высчитать внутренний. Математики увидели, что делают другие, и записали в свою Математическую Библию определение внешнего угла треугольника. Вот с тех пор это Священное Писание переписывается из учебника в учебник.
«смежные и вертикальные углы». Видеоурок «Смежные и вертикальные углы
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы АОВ и ВОС смежные.
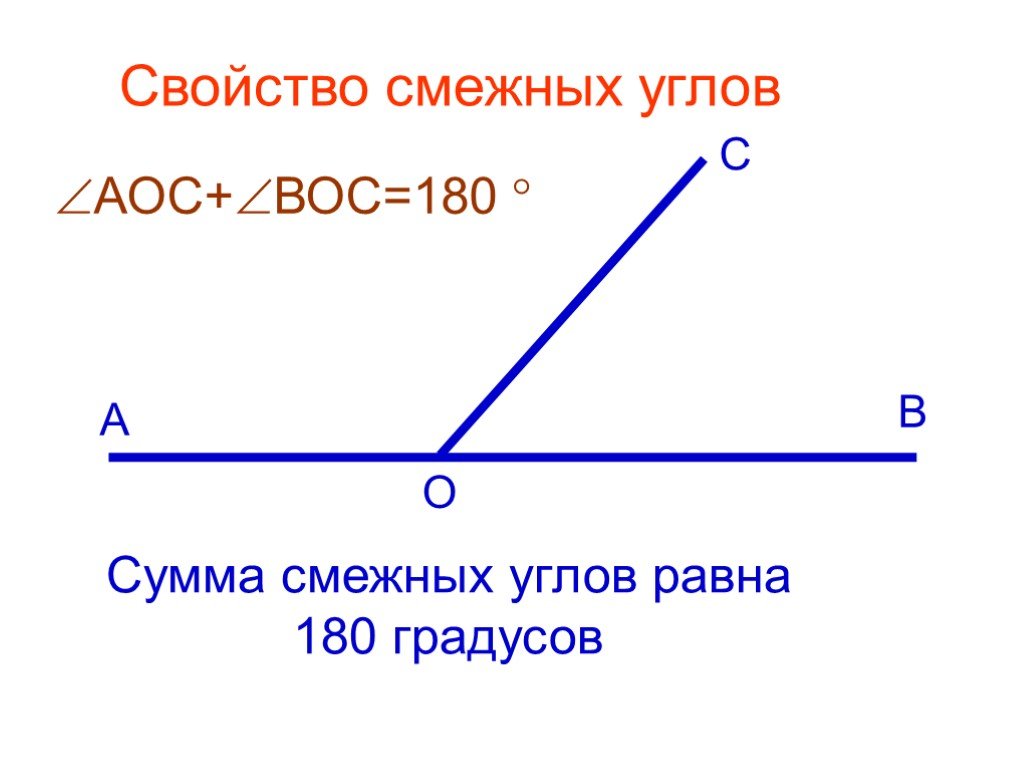
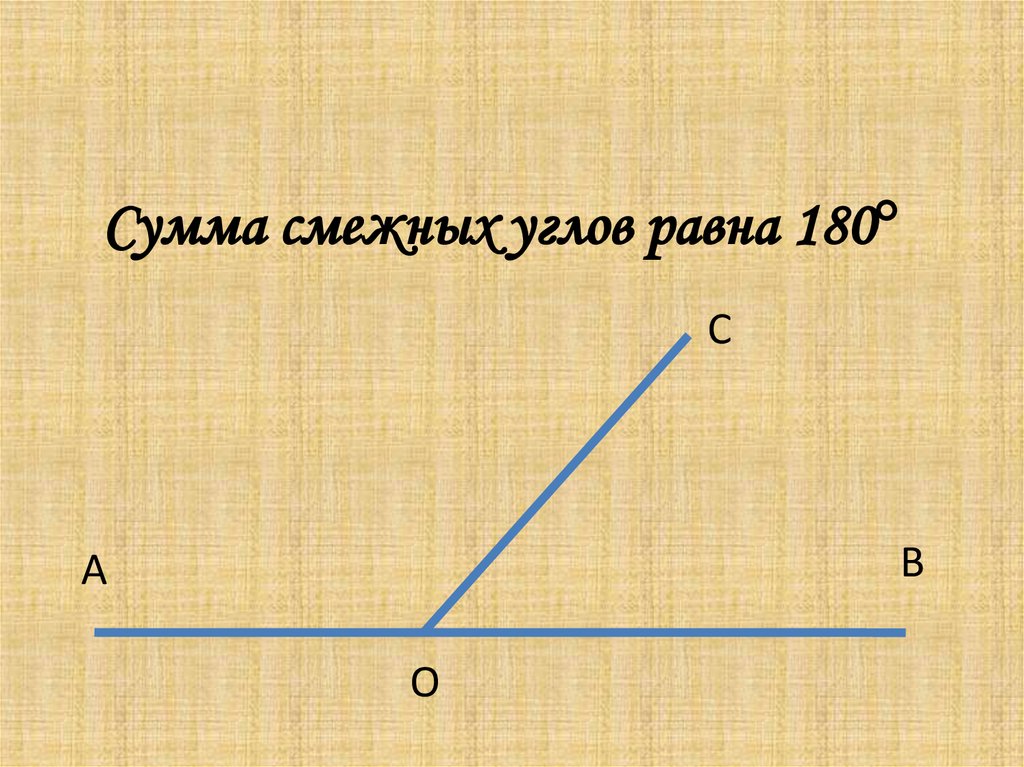
Сумма смежных углов равна 180°
Теорема 1. Сумма смежных углов равна 180°.
Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180° .
Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.
Вертикальные углы равны
Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого.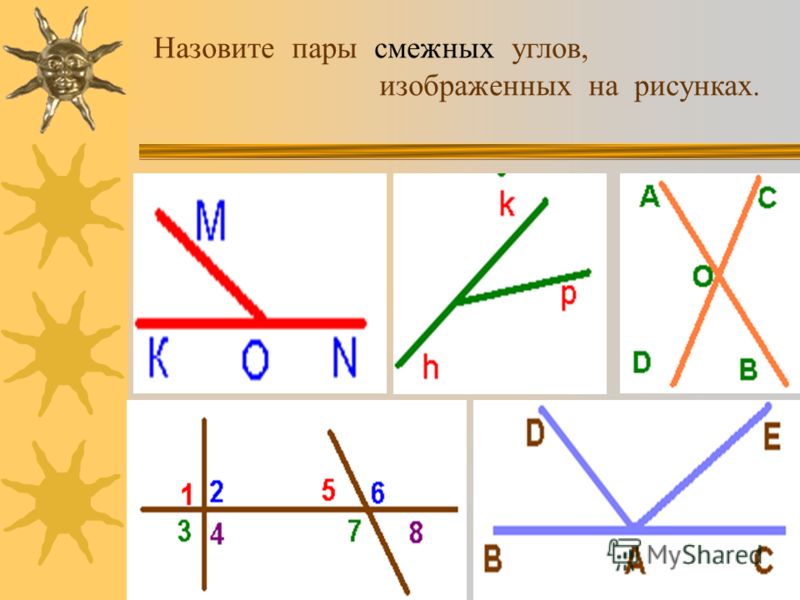
Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2).
Теорема 2. Вертикальные углы равны.
Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1 ∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.
Отсюда заключаем, что ∠ АОВ = ∠ COD.
Следствие 1. Угол, смежный с прямым углом, есть прямой угол.
Рассмотрим две пересекающиеся прямые АС и BD (рис.3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.
Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.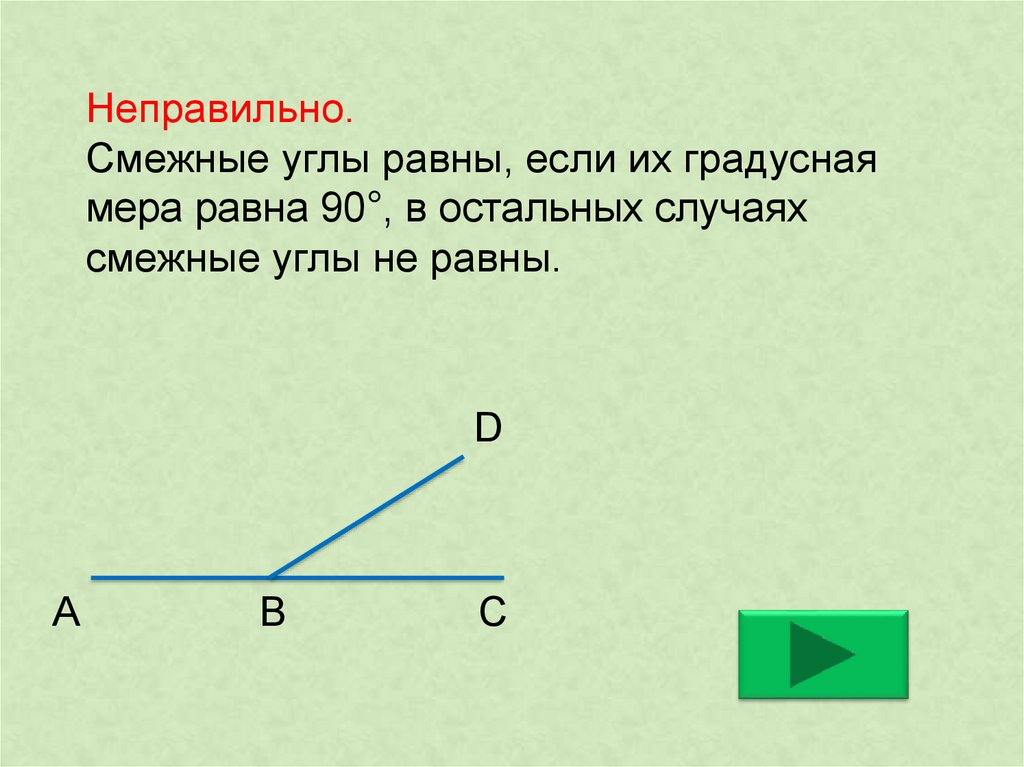
АН — перпендикуляр к прямой
Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.
Чертежный угольник
Справедлива следующая теорема.
Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис.5).
Замечание. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.
Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то».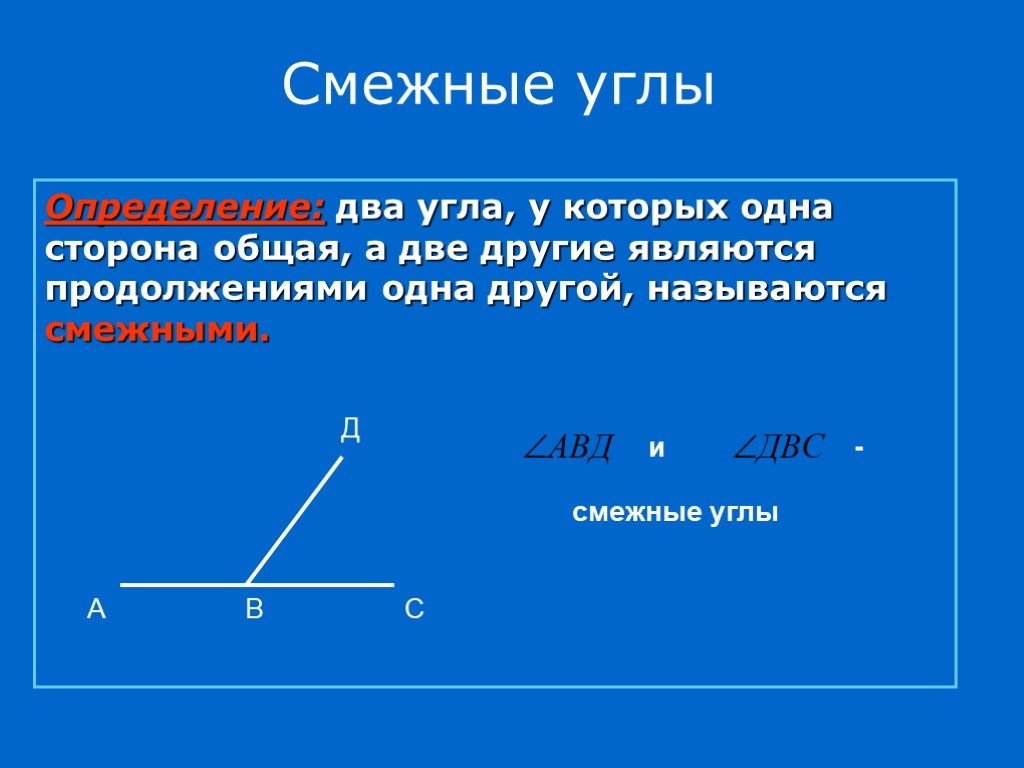
Пример 1. Один из смежных углов равен 44°. Чему равен другой?
Решение. Обозначим градусную меру другого угла через x , тогда согласно теореме 1.
44° + х = 180°.
Решая полученное уравнение, находим, что х = 136°. Следовательно, другой угол равен 136°.
Пример 2. Пусть на рисунке 21 угол COD равен 45°. Чему равны углы АОВ и АОС?
Решение. Углы COD и АОВ вертикальные, следовательно, по теореме 1.2 они равны, т. е. ∠ АОВ = 45°. Угол АОС смежный с углом COD, значит, по теореме 1.
∠ АОС = 180° — ∠ COD = 180° — 45° = 135°.
Пример 3. Найти смежные углы, если один из них в 3 раза больше другого.
Решение. Обозначим градусную меру меньшего угла через х. Тогда градусная мера большего угла будет Зх. Так как сумма смежных углов равна 180° (теорема 1), то х + Зх = 180°, откуда х = 45°.
Пример 4. Сумма двух вертикальных углов равна 100°. Найти величину каждого из четырех углов.
Решение. Пусть условию задачи отвечает рисунок 2. Вертикальные углы COD к АОВ равны (теорема 2), значит, равны и их градусные меры. Поэтому ∠ COD = ∠ АОВ = 50° (их сумма по условию 100°). Угол BOD (также и угол
АОС) смежный с углом COD, и, значит, по теореме 1
∠ BOD = ∠ АОС = 180° — 50° = 130°.
Г Л А В А I.
ОСНОВНЫЕ ПОНЯТИЯ.
§11. СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ.
1. Смежные углы.
Если мы продолжим сторону какого-нибудь угла за его вершину, то получим два угла (черт. 72): / А ВС и / СВD, у которых одна сторона ВС общая, а две другие АВи ВD составляют прямую линию.
Два угла, у которых одна сторона общая, а две другие составляют прямую линию, называются смежными углами.
Смежные углы можно получить и таким образом: если из какой-нибудь точки прямой проведём луч (не лежащий на данной прямой), то получим смежные углы.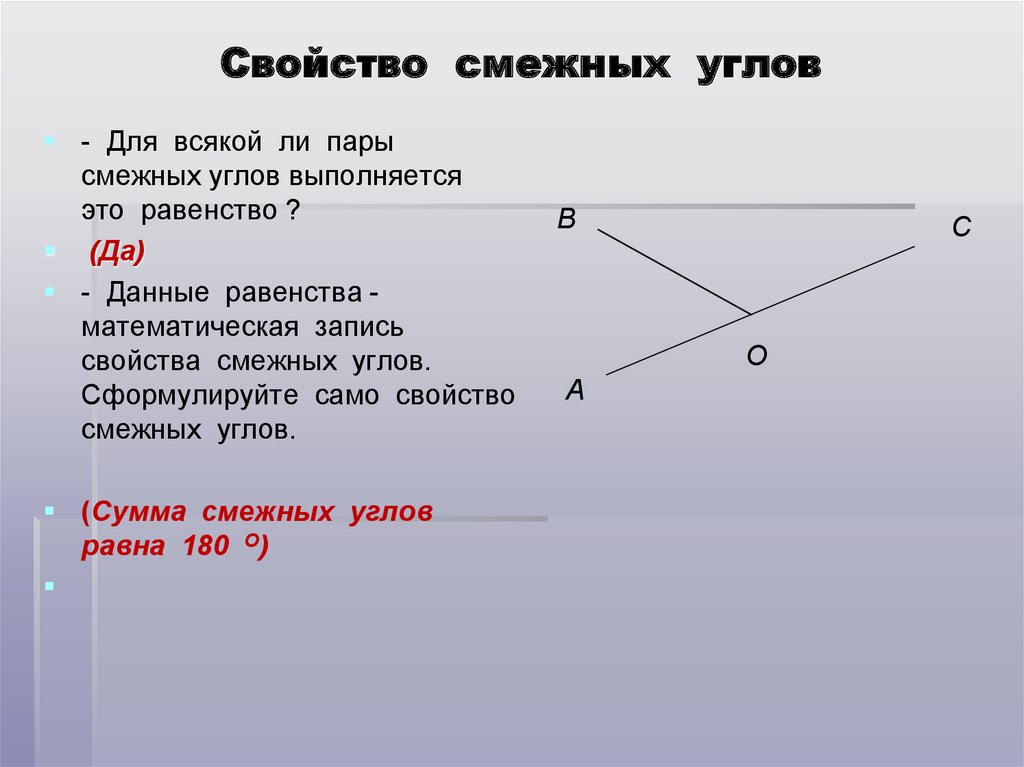
Например, / АDF и / FDВ — углы смежные (черт. 73).
Смежные углы могут иметь самые разнообразные положения (черт. 74).
Смежные углы в сумме составляют развёрнутый угол, поэтому сумма двух смежных углов равна 2d.
Отсюда прямой угол можно определить как угол, равный своему смежному углу.
Зная величину одного из смежных углов, мы можем найти величину другого смежного с ним угла.
Например, если один из смежных углов равен 3 / 5 d , то второй угол будет равен:
2d — 3 / 5 d = l 2 / 5 d .
2. Вертикальные углы.Если мы продолжим стороны угла за его вершину, то получим вертикальные углы. На чертеже 75 углы EOF и АОС- вертикальные; углы АОЕ и СОF — также вертикальные.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.
Пусть / 1 = 7 / 8 d (черт. 76). Смежный с ним / 2 будет равен 2d — 7 / 8 d , т.
е. 1 1 / 8 d .
Таким же образом можно вычислить, чему равны / 3 и / 4.
/ 3 = 2d — 1 1 / 8 d = 7 / 8 d ; / 4 = 2d — 7 / 8 d = 1 1 / 8 d (черт. 77).
Мы видим, что / 1 = / 3 и / 2 = / 4.
Можно решить ещё несколько таких же задач, и каждый раз будет получаться один и тот же результат: вертикальные углы равны между собой.
Однако, чтобы убедиться в том, что вертикальные углы всегда равны между собой, недостаточно рассмотреть отдельные числовые примеры, так как выводы, сделанные на основе частных примеров, иногда могут быть и ошибочными.
Убедиться в справедливости свойства вертикальных углов необходимо путём рассуждения, путём доказательства.
Доказательство можно провести следующим образом (черт. 78):
/ a + / c = 2d ;
/ b + / c = 2d ;
(так как сумма смежных углов равна 2d ).
/ a + / c = / b + / c
(так как и левая часть этого равенства равна 2d , и правая его часть тоже равна 2d ).
В это равенство входит один и тот же угол с .
Если мы от равных величин отнимем поровну, то и останется поровну. В результате получится: / a = / b , т. е. вертикальные углы равны между собой.
При рассмотрении вопроса о вертикальных углах мы сначала объяснили, какие углы называются вертикальными, т. е. дали определение вертикальных углов.
Затем мы высказали суждение (утверждение) о равенстве вертикальных углов и в справедливости этого суждения убедились путём доказательства. Такие суждения, справедливость которых надо доказывать, называются теоремами . Таким образом, в данном параграфе мы дали определение вертикальных углов, а также высказали и доказали теорему об их свойстве.
В дальнейшем при изучении геометрии нам постоянно придётся встречаться с определениями и доказательствами теорем.
3. Сумма углов, имеющих общую вершину.
На чертеже 79 / 1, / 2, / 3 и / 4 расположены по одну сторону прямой и имеют общую вершину на этой прямой. В сумме эти углы составляют развёрнутый угол, т. е.
/ 1+ / 2+/ 3+ / 4 = 2d .
На чертеже 80 / 1, / 2, / 3, / 4 и / 5 имеют общую вершину. В сумме эти углы составляют полный угол, т. е. / 1 + / 2 + / 3 + / 4 + / 5 = 4d .
Упражнения.
1. Один из смежных углов равен 0,72 d. Вычислить угол, составленный биссектрисами этих смежных углов.
2. Доказать, что биссектрисы двух смежных углов образуют прямой угол.
3. Доказать, что если два угла равны, то равны и их смежные углы.
4. Сколько пар смежных углов на чертеже 81?
5. Может ли пара смежных углов состоять из двух острых углов? из двух тупых углов? из прямого и тупого угла? из прямого и острого угла?
6.
Если один из смежных углов прямой, то что можно сказать о величине смежного с ним угла?
7. Если при пересечении двух прямых линий один угол прямой, то что можно сказать о величине остальных трёх углов?
Геометрия — это весьма многогранная наука. Она развивает логику, воображение и интеллект. Конечно, из-за своей сложности и огромного количества теорем и аксиом, она не всегда нравится школьникам. Кроме этого, существует необходимость постоянно доказывать свои выводы, используя общепринятые стандарты и правила.
Смежные и вертикальные углы — это неотъемлемая составляющая геометрии. Наверняка многие школьники просто обожают их по той причине, что их свойства понятны и просты в доказательстве.
Образование углов
Любой угол образуется путем пересечения двух прямых или проведения двух лучей из одной точки. Они могут называться либо одной буквой, либо тремя, которые последовательно обозначают точки построения угла.
Углы измеряются в градусах и могут (в зависимости от их значения) по-разному называться.
Так, существует прямой угол, острый, тупой и развернутый. Каждому из названий соответствует определенная градусная мера или ее промежуток.
Острым называется угол, мера которого не превышает 90 градусов.
Тупым является угол, превышающий 90 градусов.
Угол называется прямым в том случае, когда его градусная мера равна 90.
В том случае, когда он образован одной сплошной прямой, и его градусная мера равна 180, его называют развернутым.
Углы, имеющие общую сторону, вторая сторона которых продолжает друг друга, называются смежными. Они могут быть как острыми, так и тупыми. Пересечение линией образует смежные углы. Свойства их следующие:
- Сумма таких углов будет равна 180 градусам (существует теорема, доказывающая это). Поэтому можно легко вычислить один из них, если известен другой.
- Из первого пункта следует, что смежные углы не могут быть образованы двумя тупыми или двумя острыми углами.
Благодаря этим свойствам, можно всегда вычислить градусную меру угла, имея значение другого угла или, по крайней мере, отношение между ними.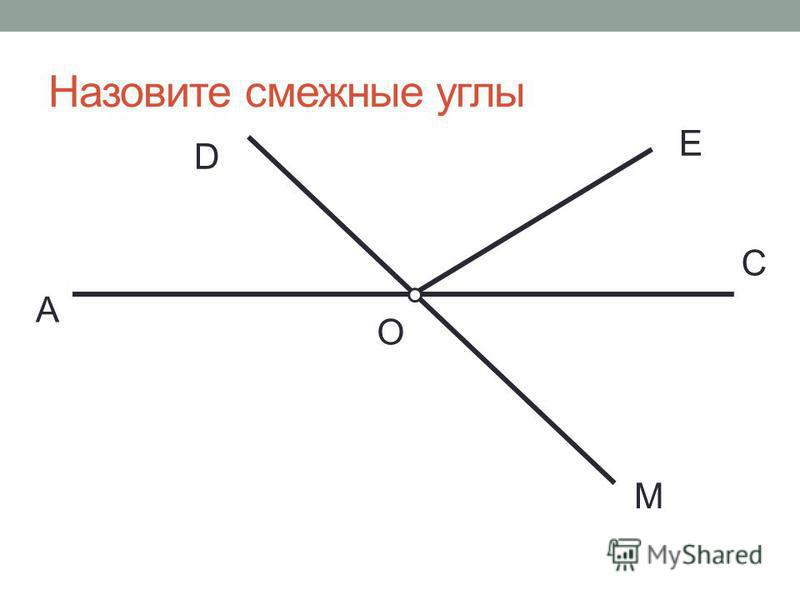
Вертикальные углы
Углы, стороны которых являются продолжением друг друга, называются вертикальными. В качестве такой пары могут выступать любые их разновидности. Вертикальные углы всегда равны между собой.
Они образуются при пересечении прямых. Совместно с ними всегда присутствуют и смежные углы. Угол может быть одновременно смежным для одного и вертикальным для другого.
При пересечении произвольной линией также рассматривают еще несколько видов углов. Такая линия называется секущей, она и образует соответственные, односторонние и накрест лежащие углы. Они равны между собой. Их можно рассматривать в свете свойств, которые имеют вертикальные и смежные углы.
Таким образом, тема углов представляется довольно простой и понятной. Все их свойства легко запомнить и доказать. Решение задач не представляется сложным до тех пор, пока углам соответствует числовое значение. Уже дальше, когда начнется изучение sin и cos, придется запоминать множество сложных формул, их выводов и следствий.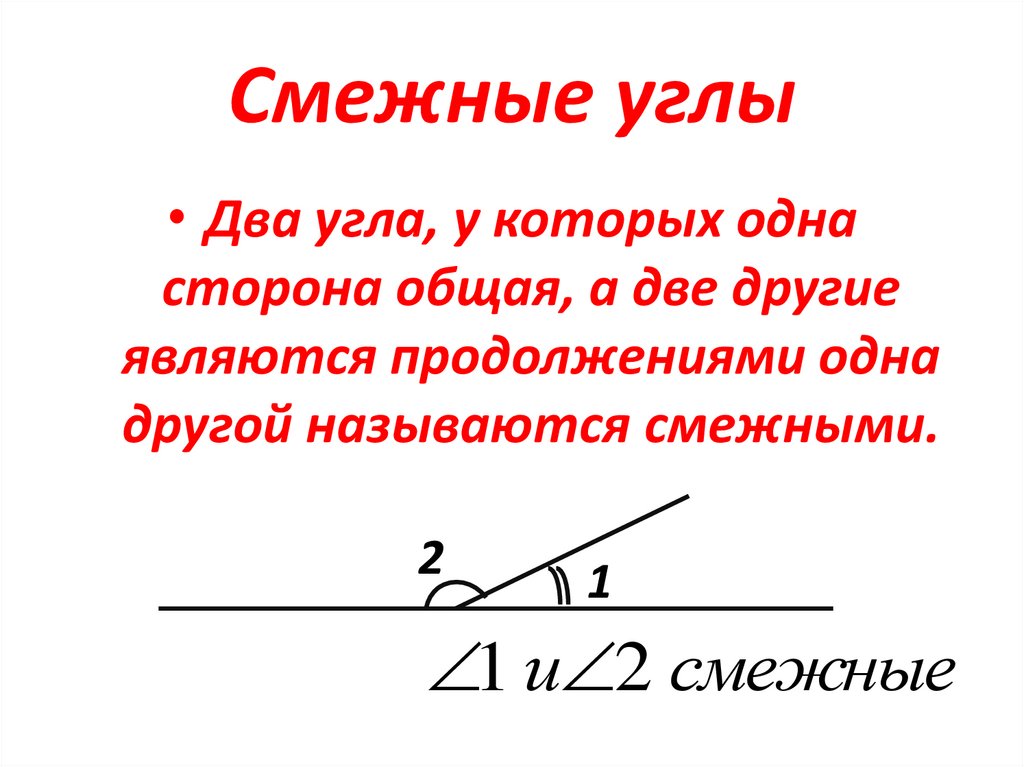
А до того времени можно просто наслаждаться легкими задачками, в которых необходимо найти смежные углы.
§ 1 Смежные углы. Определение, свойство
Рассмотрим развернутый угол АОВ, величина которого равна 180°. Проведем из вершины угла О луч ОС. Этот луч разделил развернутый угол на два угла АОС и ВОС. Такие углы называются смежными.
Определение: два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными.
Так как лучи ОА и ОВ образуют развернутый угол, то ∠АОС + ∠ВОС = ∠АОВ = 180°.
Значит, сумма смежных углов равна 180°. Запомним это важное свойство.
§ 2 Вертикальные углы. Определение, свойство
Предположим, что ученику предложили построить угол, равный данному углу АОВ, только с помощью линейки и карандаша. Он поступил так: построил лучи ОС и ОD, как продолжение соответственно лучам ОВ и ОА, и заявил, что угол СОD= углу АОВ. Прав ли он? Докажем, что он прав.
Чтобы установить равенство углов СОD и АОВ, т.
е. углов 1 и 2, докажем, что их градусные меры равны. Угол 1 и угол DОВ смежные, значит, их сумма равна 180° (∠1 + ∠DОВ = 180°). Аналогично, угол 2 и угол ДОВ смежные, значит, и их сумма равна 180° (∠2 + ∠DОВ = 180°).
Из полученных равенств выразим угол 1 и угол 2, получаем:
∠1 = 180° — ∠DOВ,
∠2 = 180° — ∠DOВ.
Таким образом, градусные меры углов 1 и 2, т.е. углов СОD и АОВ равны. Ученик оказался прав. Эти углы называются вертикальными.
Определение: два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
Запомним важное свойство вертикальных углов: вертикальные углы равны.
§ 3 Перпендикулярные прямые
В жизни вы не раз встречались с четырьмя неразвернутыми углами, которые образуются при пересечении прямых. Выясним, какими углами окажутся все эти углы, если один из них будет прямым. Как называют в этом случае пересекающиеся прямые?
Построим прямой угол АОВ. Проведем лучи ОС и ОD, как продолжение лучам ОА и ОВ соответственно, получим две пересекающиеся прямые АС и ВD и четыре угла АОВ, АОD, СОD, СОВ.
Угол АОВ равен углу ДОС как вертикальные. Так как угол АОВ = 90°, то и угол СОD= 90°, то есть прямой, тогда смежные углы СОВ и АОD также прямые (т.к. сумма смежных углов равна 180°). Таким образом, при пересечении двух прямых образовались четыре прямых угла. Эти прямые называются перпендикулярными.
Определение: две пересекающие прямые называются перпендикулярными(или взаимно перпендикулярными), если они образуют четыре прямых угла.
О таких прямых также говорят, что они пересекаются под прямым углом. На чертеже прямой угол отмечают квадратом.
Перпендикулярность прямых записывается так: АС⊥ВD, читается: «прямая АС перпендикулярна к прямой ВD».
Отметим важное утверждение: две прямые, перпендикулярные к третьей, не пересекаются.
Для проведения перпендикулярных прямых используют чертежный угольник и линейку.
В геодезии для построения прямых углов используют прибор теодолит.
§ 4 Решение задачи по теме урока
Рассмотрим задачу.
Задача: Один из смежных углов на 16° больше другого.
Найти величину каждого угла.
Пусть меньший угол СОВ = х градусов, тогда угол АОС = х + 16°. Углы АОС и ВОС — смежные, значит, их сумма равна 180°.
Получаем: х + х + 16° = 180°
Решая это уравнение, находим неизвестное: х = 82°. Значит, угол СОВ = 82°, а угол АОС = 82° + 16° = 98°.
Ответ: угол ВОС = 82°, угол АОС = 98°.
Список использованной литературы:
- Геометрия. 7-9 классы: учеб. для общеобразоват. организаций / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 2013. – 383 с. : ил.
- Гаврилова Н.Ф. Поурочные разработки по геометрии 7 класс. — М.: «ВАКО», 2004, 288с. – (В помощь школьному учителю)
- Белицкая О.В. Геометрия. 7 класс. Ч.1. Тесты. – Саратов: Лицей, 2014. – 64 с.
Тема урока: «Смежные и вертикальные углы.»
Цель урока: познакомить с понятием «смежные и вертикальные углы
Задачи:
Учебные – закрепить понятие угла, правила измерения и построения углов; на основе выделенных признаков научить объединять углы по группам; научить вести исследование с опорой на алгоритм действий, анализировать полученные данные и делать выводы; закрепить полученные на уроке знания в ходе решения задач.
Развивающие – используя возможности мультимедийной презентации и электронного учебника повысить интерес к изучаемому предмету; развивать геометрическую интуицию, умение контролировать внимание на всех этапах урока.
Воспитательные –воспитать любовь к Родине, любовь к матери, воспитать аккуратность, прилежание.
Оборудование: компьютер, мультимедийный проектор, электронный учебник, учебник «Геометрия 7-9 класс, автор Л.С.Атанасян», карточки-задания, карточки для проведения рефлексии, таблицы «Вертикальные и смежные углы».
ХОД УРОКА
Организационный момент (Слайд 1 )
А.П.Чехов говорил: «Нужно стремиться к тому,
чтобы каждый видел и знал больше,
чем видел и знал его отец и дед»
Мы начинаем урок геометрии. У всех на столе: учебник, тетрадь, карандаш, ручка, линейка, транспортир.
(Эмоциональный настрой на урок.
Стихотворение Евгения Винокурова. )
(Слайды 2)
О Петр, ведь ты построил город
Не для умерших – для живых?
Тяжелый дождь бежит за ворот
Окаменевших часовых.
Недвижимы аллеи парков.
Прямы проспекты, как стрела.
Сильней божественных монархов
Здесь геометрия была.
(Слайд 3)
Гуляют каменные финны.
Курятся трубки из бород.
Вот и построили Афины
Средь топей северных болот!
Налево львы. И львы направо.
А у заставы инвалид,
Штык держит вертикально прямо.
Как геометрия велит.
II. Подготовка к восприятию темы
Сегодня мы продолжаем наше путешествие по стране «Геометрия» и поговорим об углах. А вот о каких углах сегодня пойдет речь, мы постараемся выяснить в ходе нашего урока. Для этого мы вытащим из тайников памяти кое-что ценное и восхитимся глубокими знаниями, которые пригодятся нам сегодня на уроке.
(Слайд 4 – план урока ). Для разминки я предлагаю провести «Мозговой штурм». Да, я совсем забыла сказать, что на уроке можно ошибаться, сомневаться, консультироваться. Но при этом, вы должны дать себе установку (Слайд 5) «понять и быть тем первым, который увидит ход решения и даст правильный ответ» . Каждый правильный ответ вы будите отмечать в листке контроля. Это мне поможет выставить оценки за урок. Тот кто наберет больше баллов, тот и получит лучше оценку. Никто без поощрения не останется. Итак, мы начинаем.
III. Актуализация знаний учащихся. «Мозговой штурм» (Слайд 6)
– Давайте вспомним, о какой фигуре шла речь на прошлом уроке? (На прошлом уроке мы говорили об угле)
Какая фигура называется углом? (Геометрическая фигура, которая состоит из двух лучей, исходящих из одной точки, называется угол)
— Что такое вершина и стороны угла? (Общая точка называется вершиной угла, а лучи сторонами)
— )
С помощью какого инструмента измеряют углы?(Углы измеряют с помощью транспортира)
(Слайд 7 )
— Какие это углы?
Угол, градусная мера которого меньше 90 0 , называется острым)
(Угол, градусная мера которого больше 90, но меньше 180 0 , называется тупым)
Какие углы называются прямыми?(Угол называется прямым, если он равен 90 0 )
-Как выглядит прямой угол.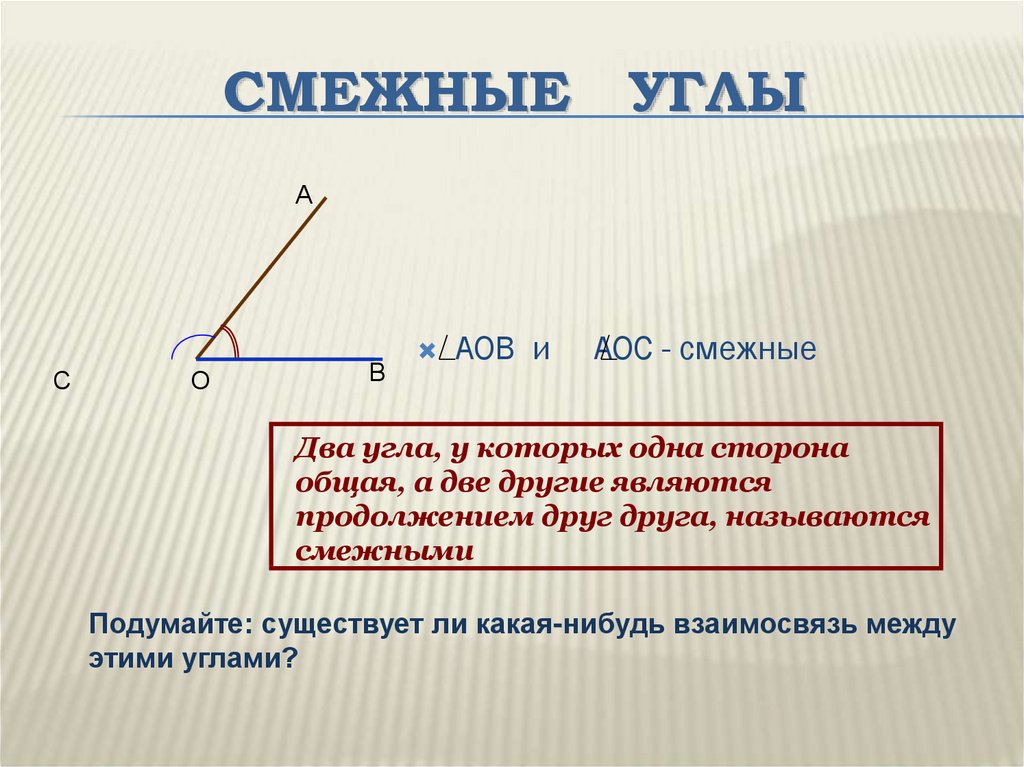
Угол называется развернутым, если он равен 180 0)
(Слайд 8)
А сейчас мы решим несколько задач на вычисление градусной меры угла. Каждый выбирает себе задание по силам. Для 1 уровня- это задача на рисунке 1. Её решение мы разберем на доске, для 2 уровня задача на рисунке 2. Её я предлагаю решить самостоятельно. Те кто выберет самостоятельное решение, каждый получит плюс в карточку учета, если ответ будет верным. Кто выбирает задачу на рисунке 2, работают самостоятельно. Кто выбирает задачу на рисунке 1 и желает ее решить у доски.
Сколько углов мы видим на рисунке?(На рисунке 3 угла)
-Н азови и покажи их? (угол АОС, угол АОВ, угол ВОС )
Что мы можем сказать о градусной мере угла ВОС?(
Запишем это и найдем градусную меру угла ВОС. Запишем ответ.
Проверим наши ответы. Кто работал самостоятельно оцените свою работу, если ответы сошлись, то поставьте плюс в карточку учета.
Итак подведем итог.
(Слайд 9)
По какому признаку мы делим углы? (Углы разделяются в зависимость от величины)
Какие это углы?(О).
IV. Практическая работа исследовательского характера
– А сейчас познакомимся со второй группой углов и попробуем выяснить, по какому признаку можно ее выделить. Перед вами карточки с изображением углов. Ваша задача – выполнить следующие действия для карточки № 1.
(Слайд 10 – алгоритм действий ).
-Какой вывод сделали? (Сумма углов равна 180 градусов )
(Слайд 11)
Как бы вы назвали эти углы?(Смежные )
По какому признаку мы выделили этот вид углов? (Этот вид углов мы выделили по взаимному расположению)
Давайте запишем определение
(Слайд 12 )
Постройте острый, прямой и тупой углы. Продолжите одну из сторон и укажите получившиеся смежные углы.
3 ученика у доски, остальные в тетради.
Для любого угла можно построить ему смежный угол? (Да)
-Повторите алгоритм действия для карточки №2.
(Слайд 13)
-Какой вывод можно сделать?.(Углы равны )
(Слайд 14)
Как бы вы назвали данный вид углов?(Вертикальные )
-Запишем определение.
(Слайд 15)
Посмотрите на правило построения вертикальных углов и выполните построение в тетради.
(Слайд 16)
-Посмотрите на чертежи и назовите вертикальные углы
(Слайд 17)
-Вернёмся к схеме, которую мы рассматривали в начале урока, и подведем итог.
(Слайд 18)
-По каким признакам мы делим углы? (Углы делятся по величине угла и по их взаимному расположению )
Какие углы по величине градусной меры мы знаем?(По величине градусной меры углы бывают: острые, тупые, прямые, развернутые)
Какие углы по взаимному расположению мы изучили сегодня? (По взаимному расположению углы бывают: смежные и вертикальные).
Не забывайте отмечать свои верные ответы в карточке учета.
-Как же теперь мы сформулировали тему нашего сегодняшнего урока(«Смежные и вертикальные углы» ).
Правильно. «Смежные и вертикальные углы». Посмотрите, как в Санкт-Петербурге это хорошо видно.
(Слайд 19)
V . Физкукльтминутка.
Вы устали? Давайте отдохнём.
(Слайд 20)
1.Голова идет по кругу.
2.Руки в стороны.(Развернутый угол, прямой угол).
3.Руки с соседом. (Смежные углы).
4.Спиной к соседу.(Вертикальные углы).
V I . Работа по отработке ЗУН. Практикум
А теперь посмотрим на практике, как вы усвоили тему сегодняшнего урока.
1.Устная работа
(Слайд 21).
Запишите ответы на вопросы в тетрадь. Проверьте свои ответы. Отметьте верные ответы в карточке учета.
2.Решение задач.
А сейчас мы вновь разделимся на группы. Каждая группа выбирает себе задание по силам.
1уровень- выполняет тест на доске.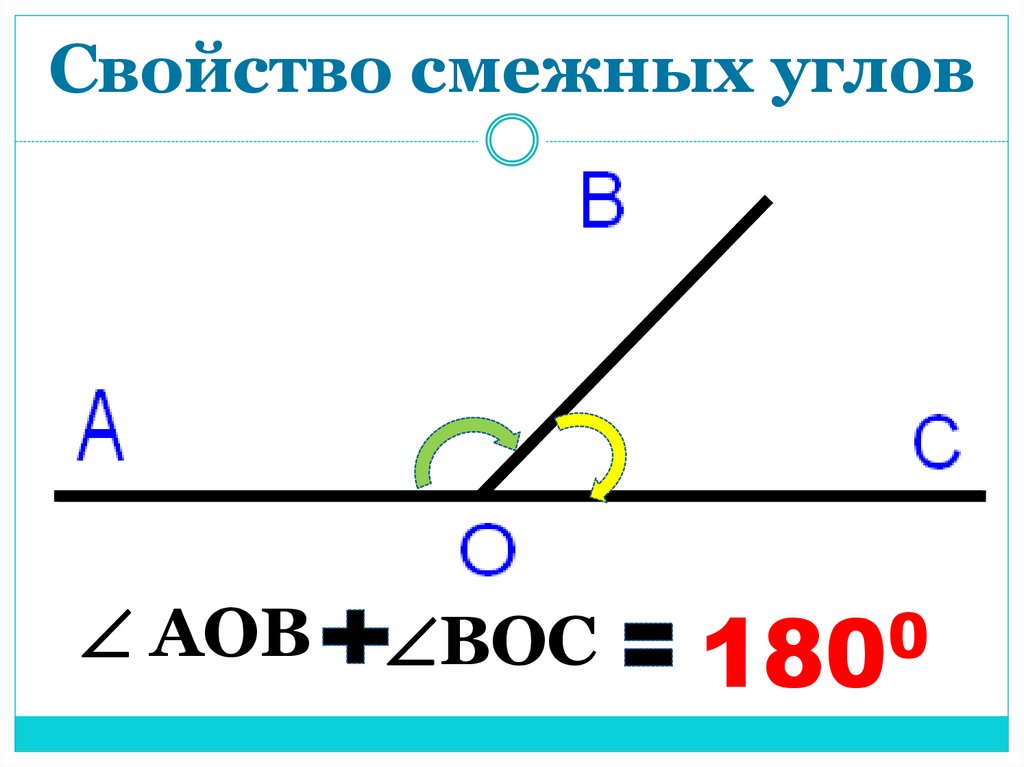
(Слайды 22, 23, 24)
2 уровень- самостоятельно решает задачи из учебника на стр. 24 №58(а, б) и №66(а). Проверить ответы можно на обратной стороне карточки, которая лежит у вас на парте.
3 уровень- выполняет тест из электронного учебного.(работа на компьютерах )
Каждый из вас может получить ещё 3 плюса.
Отметьте верные ответы в карточке учета.
Какую установку мы давали себе на урок?
(Слайд 25)
Подсчитаем плюсы. Кто набрал 10 плюсов? Вы получаете оценку «5». Кто набрал 7 плюсов? Вы получаете оценку «4». Остальные, я думаю, подучат эту тему дома и на следующем уроке получат хорошие оценки.
VI. Итоговая рефлексия
– Подошло к концу наше путешествие.
О какой фигуре мы говорили на уроке?
Что нового вы сегодня узнали на уроке?
Где в жизни мы видели смежные и вертикальные углы?
(Слайд 26)
(Слайд 27)
Если вы все поняли прикрепите цветочки с углами красного цвета к нашей корзинке, если вас, что-то заставило задуматься – жёлтого цвета и если остались вопросы – синего.
Этот букет мы подарим нашим мамам, бабушкам, сестрам в воскресенье на день матери.
VII. Запись домашнего задания.
А сейчас запишем домашнее задание
(Слайд 28)
1.п. 11 ,вопросы 17,18.
2.Решить задачи: 1 уровень-№42,45,46 из рабочей тетради
2 уровень- № 64, № 61 (а, б) из учебника
3. Творческое задание: сочините сказку о смежных и вертикальных углах.
– Спасибо всем за урок!
(Слайд 29 )
1)– Давайте вспомним, о какой фигуре шла речь на прошлом уроке? (Об угле)
— Назовите единицу измерения углов?(За единицу измерения углов принимают градус )
– Что называется градусной мерой угла?(Положительное число, которое показывает, сколько раз градус и его части укладывается в данном угле )
– По какому признаку мы разделим углы на группы? (В зависимости от величины угла)
— Какие это углы? (Острый, тупой, прямой, развернутый)
– Какие углы называются острыми? (Угол градусная мера которого меньше 90 0 )
Выберите его изображение из предложенных вам вариантов углов.
Какие углы называются тупыми? (Угол градусная мера которого больше 90, но меньше 180 0 )
Покажите изображение тупого угла.
Какие углы называются прямыми?(Угол в 90 0)
-Как выглядит прямой угол.
Какие углы называются развернутыми?( (Угол градусная мера которого равна 180 0)
-Как построить развернутый угол? (Провести прямую, отметить вершину, подписать стороны )
2)-Что мы можем сказать о градусной мере угла ВОС?(Его градусная мера равна разности градусных мер углов АОС и АОВ)
Почему?(Луч ОВ делит угол АОС на два угла: АОВ и ВОС)
— Сколько получим?(49 0 )
— Что мы скажем про угол СОN?(Его градусная мера равна 180 0 минус градусная мера угла АОС и минус градусная мера угла BON )
— Почему 180 0 минус?(Потому что угол АОВ- развернутый угол и его градусная мера равна 180 0 )
Сколько получаем?(94 0 )
Итак подведем итог.
Углы, в зависимости от величины угла, делятся: на какие?(Острые, тупые, прямые и развернутые ).
3)Углы, в зависимости от величины угла, делятся: (на острые, тупые, прямые и развернутые ). В зависимости от их взаимного расположения на (смежные и вертикальные).
Нанесение этикеток на смежные стороны ящика
Итак, вы приняли решение о необходимости маркировки двух смежных сторон транспортировочных ящиков и (очевидно!) решили, что аппликатор для печати этикеток от ID Technology — это решение, которое вам нужно. необходимость.
Вы обнаружите, что существует несколько типов аппликаторов, доступных для автоматического нанесения этикеток на ящики, давайте взглянем на некоторые из них… две отдельные этикетки или обернуть одну этикетку вокруг угла так, чтобы она была видна с обеих сторон.
Несмотря на то, что ID Technology позволяет аппликаторам хорошо работать в любой ситуации, использование только одной этикетки в углах очень часто является самым простым и экономичным способом.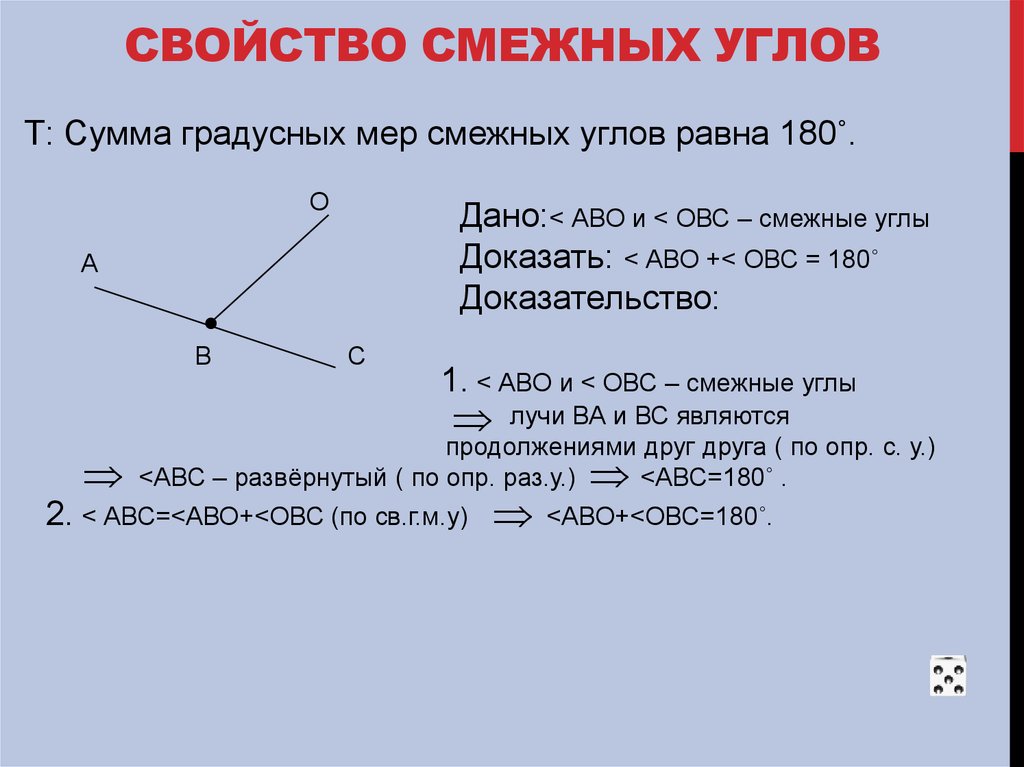
.
Утрамбовка и вторичная протирка
Это простой метод нанесения, который состоит из аппликатора для набивки и станции вторичной протирки.
Аппликатор трамбовки размещает этикетку на стороне коробки, обращенной к этикетировщику, и щетка, установленная на пневматическом цилиндре, приводится в действие, чтобы стирать этикетку с передней или задней стороны.
Этот метод лучше всего подходит для приложений с задней стороны коробки — существуют некоторые ограничения длины этикетки, возникающие при намотке этикетки на переднюю сторону коробки.
Высокоскоростная салфетка и вторичная салфетка
Аппликатор высокоскоростной салфеткиВ этом методе используется вакуумный ленточный аппликатор ID Technology в сочетании со станцией вторичной салфетки. Он предназначен для нанесения этикетки на сторону футляра, обращенную к этикетировщику, а затем оборачивает ее вокруг тренировочной кромки.
Этикетка помещается на вакуумную ленту, где она всегда находится под полным контролем.
Когда футляр проходит мимо аппликатора, он соприкасается с этикеткой, а ролик на краю узла аппликатора обеспечивает хорошую адгезию.
Освобождаясь от аппликатора, вторичная протирочная станция (с пневматическим приводом) протирает заднюю часть этикетки вокруг корпуса.
Этот метод нанесения может обеспечить более высокую производительность, чем стандартный, потому что, как только этикетка соприкасается с корпусом, может начаться следующий цикл печати, что исключает потерю времени в цикле.
Обратите внимание, что скорость конвейера должна быть выше скорости ленты, и необходима точная подача продукта, чтобы лицевая сторона коробки находилась на постоянном расстоянии от аппликатора.
Поворотная салфетка и дополнительная салфетка
Аппликатор поворотной салфетки выполняет ту же задачу, что и высокоскоростная салфетка, но использует веерную вакуумную решетку, а не ремни.
Подобно высокоскоростному аппликатору, поворотный аппликатор использует валик для протирания этикетки вдоль стороны коробки, обращенной к этикетке, а оставшаяся часть этикетки наносится на заднюю поверхность коробки по мере ее удаления.
Как и в случае с высокоскоростной салфеткой, важно, чтобы футляр предъявлялся аппликатору последовательно, чтобы можно было получить хорошие результаты.
Вращающаяся салфетка не дает преимущества в скорости вакуумной ленточной салфетки, но все же может быть приемлемым вариантом дело.
После того, как передняя поверхность корпуса удовлетворит этикетку, узел решетки отодвигается назад – ролик, установленный на конце сетки, при движении вытирает этикетку о переднюю поверхность.
Ролик следует за ящиком и протирает этикетку по лицевой стороне ящика, примыкающей к этикетировщику.
После извлечения из футляра решетка в сборе возвращается в исходное положение, и можно распечатать следующую этикетку и представить ее продуктам.
Угловой аппликатор Этот метод обеспечивает хороший контроль над этикеткой, но обратите внимание, что ящики, подлежащие маркировке, должны быть достаточно тяжелыми, чтобы их можно было толкать в сборе, а конвейер должен иметь ремни с высоким коэффициентом трения – дополнительный метод привода для ящиков.
, такие как приводной верхний ремень, тоже могут помочь.
Опыт показал, что скорость конвейера выше 80 футов/мин приводит к слишком быстрому возврату узла вакуумной решетки, поэтому в этой системе существует ограничение скорости конвейера.
Подбивка и протирание поворотным рычагом
Аппликатор поворотного рычага ID Technology — это простой способ нанесения этикетки на переднюю (или заднюю) поверхность упаковки.
С помощью этого аппликатора можно прижать этикетку к передней стороне коробки и с помощью кисти или валика протереть ее вдоль стороны, обращенной к этикетировщику.
Поворотный аппликатор удобен, если есть продукты, для которых требуется просто наклеить этикетку на переднюю сторону коробки.
При использовании аппликатора с поворотным рычагом важно, чтобы ящики стояли на конвейере прямо, а синхронизация была правильной, чтобы этикетка находилась в надлежащем контакте с продуктом во время нанесения.
Использование двух этикеток
В качестве альтернативы обертыванию этикетки вокруг угла корпуса можно также наклеить отдельную этикетку на прилегающие поверхности корпуса.
В этом коротком видеоролике показано, как работает наш аппликатор для двойной трамбовки с поворотным рычагом. При необходимости можно настроить применение 2 меток или только одной.
Требуется более высокая производительность, чем может обеспечить одна этикетировочная машина? Используйте пару этикетировочных машин с аппликаторами – просто установите что-нибудь, чтобы повернуть коробку на 90 градусов между двумя машинами.
Нанесение этикетки на две стороны корпуса кажется простым, но, как видите, существует множество возможных способов добиться этого.
С чего начать? Лучше всего договориться о том, чтобы местный эксперт по этикетированию ID Technology посетил ваше предприятие и вместе с вами предложил идеальное решение для ВАШЕГО применения. Позвоните мне по телефону 603-598-1553 x237, чтобы начать.
терминология — Существуют ли названия для различных типов смежности в квадратной сетке?
Это может немного зависеть от контекста, а также от того, можете ли вы заранее определить используемые фразы или вам нужно использовать что-то, что сразу всем понятно.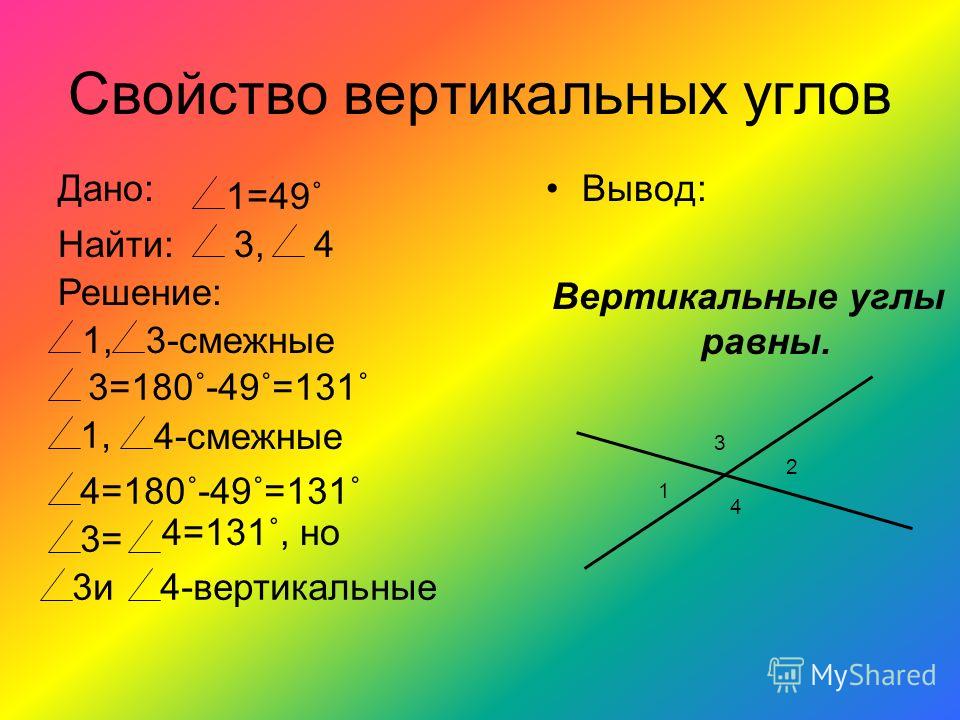
Если мы подумаем, скажем, о написании правил игры, самым простым будет случай, когда все части игры заботятся только об одном виде смежности. Тогда вы могли бы упомянуть в самом начале правил, что, когда вы говорите «смежный», вы имеете в виду что-то, лежащее в четырех ортогонально соседних квадратах, и позже в определителе не будет необходимости. Это также было бы хорошим местом для размещения описательного изображения. (Или восемь квадратов, смежных ортогонально или по диагонали, или, реже, только квадраты, смежные по диагонали.)
Если у вас разные случаи, то фразы «ортогонально смежные», «диагонально смежные» и «ортогонально или диагонально смежные», вероятно, будут самыми простыми для понимания фразами.
Если вы в основном имеете в виду все восемь смежных квадратов, то вы можете избежать неудобной длинной фразы, просто сказав «соседние» в этом случае и зарезервировав квалификаторы для исключительных случаев. Это также может потребовать некоторых вводных пояснений.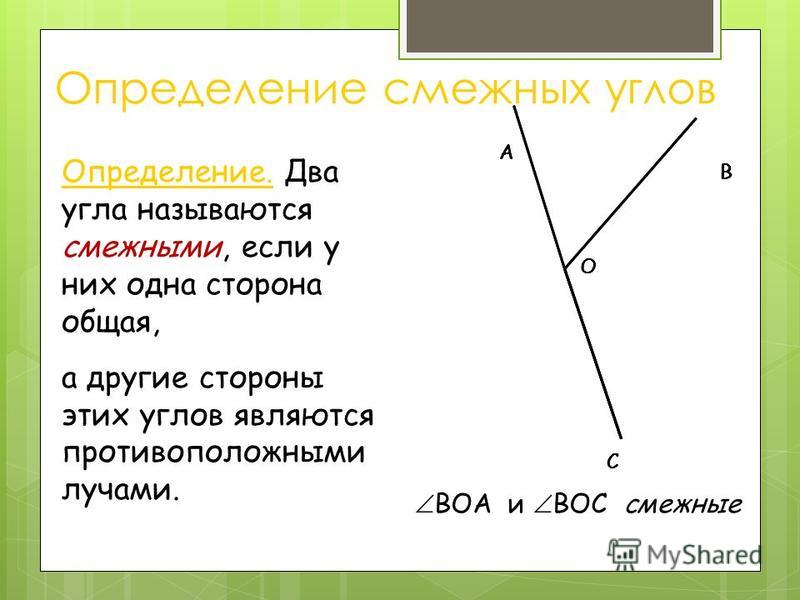
(Например, вики Freeciv, кажется, в основном используют этот обычай, хотя я не проверял, есть ли у них правильное определение. Это компьютерная игра, а не настольная, но концепции те же.)
Вы также можете использовать «восемь окружающих/соседних квадратов» и «четыре окружающих/соседних/соединенных» квадрата, если вам нужен только один из двух случаев с четырьмя рассматриваемыми квадратами. Для этого также может потребоваться определение где-то в правилах, но оно должно быть достаточно четким.
Людям с технически ориентированным умом могут понравиться фразы «8-соединенные квадраты» или «8-окрестность» и аналогичные «4-соединенные квадраты» или «4-окрестности», где последние два всегда означают четыре ортогонально соединенных квадрата. Но они обычно записываются числом в виде цифры, и это может быть связано с риском опечатки или, по крайней мере, с подозрением на опечатку больше, чем выписанные слова.
В случае «один шаг поперек и один по диагонали» ход конем кажется довольно распространенным, его используют даже игроки в го.