Как определить угловой коэффициент прямой: Угловой коэффициент прямой — задачи с решениями

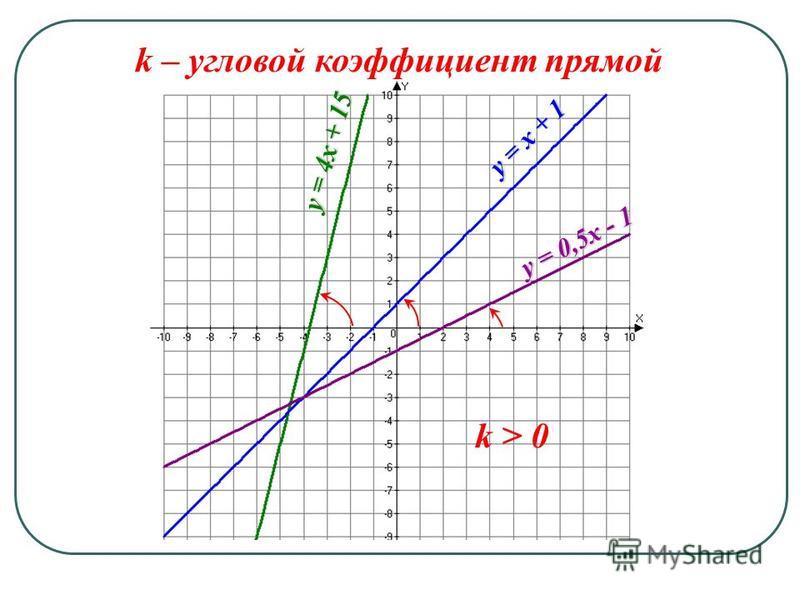
Угловой коэффициент прямой на плоскости

Термин и определение

число k в уравнении y = kx + b, численно равен тангенсу угла наклона прямой к оси Ox

Научные статьи на тему «Угловой коэффициент прямой на плоскости»

Возможны следующие варианты задания уравнения прямой на плоскости: Общее уравнение прямой; Уравнение…
с угловым коэффициентом; Через параметрические уравнения; Каноническое уравнение; С помощью двух точек…
Для того чтобы выразить координаты направляющего вектора из параметрических уравнений, нужно выписать коэффициенты…
Координаты направляющего вектора из уравнения с угловым коэффициентом Уравнение с угловым коэффициентом…
Уравнение с угловым коэффициентом, приведённое к каноническому, выглядит так: $\frac{x}{1}=\frac{y-b}

Статья от экспертов

Показано, что полиномиальное векторное поле n-й степени на плоскости имеет не более 2n + 1 (2n + 2) инвариантных прямых при n четном (нечетном) и n ≥ 3, если оно имеет особую точку, которой инцидентны n + 1 инвариантных прямых и n параллельных между собой инвариантных прямых с определенным угловым коэффициентом.

Научный журнал

Creative Commons

Это уравнение прямой с угловым коэффициентом….
Возможны четыре варианта зависимости наклона прямой от величины углового коэффициента: когда угловой…
коэффициент положителен, направляющий вектор прямой идёт снизу вверх; когда угловой коэффициент отрицателен…
, направляющий вектор прямой идёт сверху вниз; когда угловой коэффициент

равен нулю, описываемая им прямая…
Чем больше абсолютное значение углового коэффициента, тем круче наклонен график прямой.

Статья от экспертов

Цель работы: разрешение противоречия между требованиями по обеспечению точности и устойчивости при выборе величины коэффициента передачи по углу рыскания в системе угловой стабилизации беспилотного летательного аппарата охранного мониторинга. Метод: комплексный теоретико-прикладной синтез на основе эвристического метода в классе беспоисковых самонастраивающихся систем, реализующих прямое адаптивное управление. Результаты: разработан алгоритм управления, который при больших отклонениях от нуле…

Научный журнал

Creative Commons

Повышай знания с онлайн-тренажером от Автор24!

• 📝 Напиши термин
• ✍️ Выбери определение из предложенных или загрузи свое
• 🤝 Тренажер от Автор24 поможет тебе выучить термины, с помощью удобных и приятных карточек

Угловой коэффициент прямой. Уравнение прямой, проходящей через данную точку с данным угловым коэффициентом.

Угловым коэффициентом прямой называется тангенс угла наклона прямой, образованный ею с положительным направлением оси OX.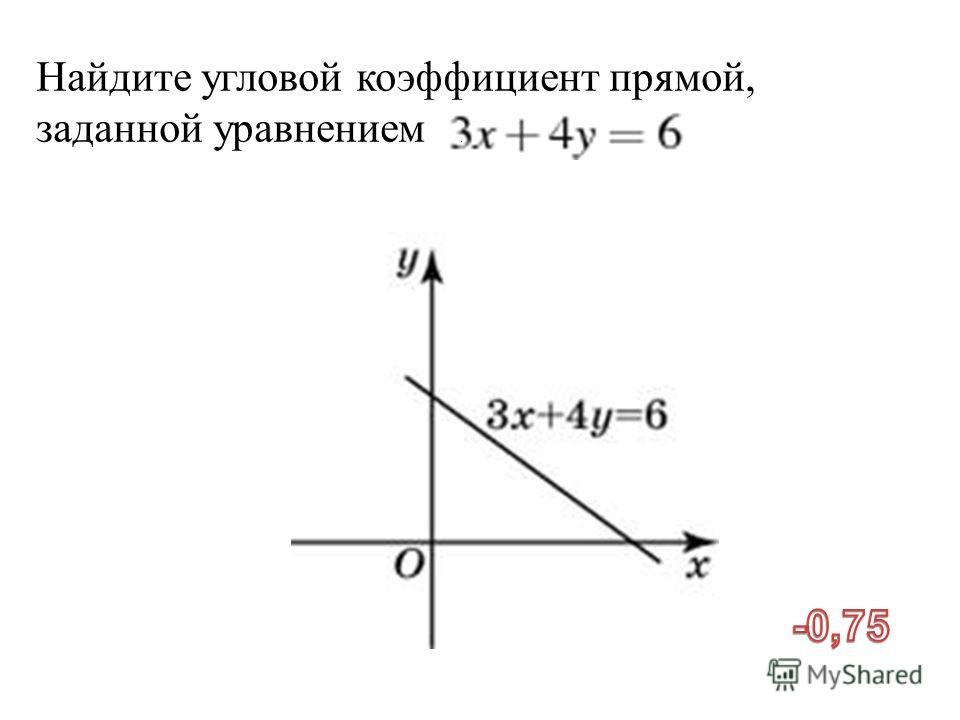

k= α, a≠ 90⁰

Пусть на прямой даны две точки М₁(х_1, y₁), M₂ (х_2, y₂).

Найдем угловой коэффициент этой прямой. Из

∆М₁M₂С получим

т.е.

– формула углового коэффициента прямой по координатам.

Заменим точку М₂(x, y) на произвольную точку M(x, y) и подставим ее координаты в формулу (1).

Получим:

Из формулы (2) следует

y ‒ y₁= k × (x ‒ x₁)

– уравнение прямой проходящей через данную точку с данным угловым коэффициентом.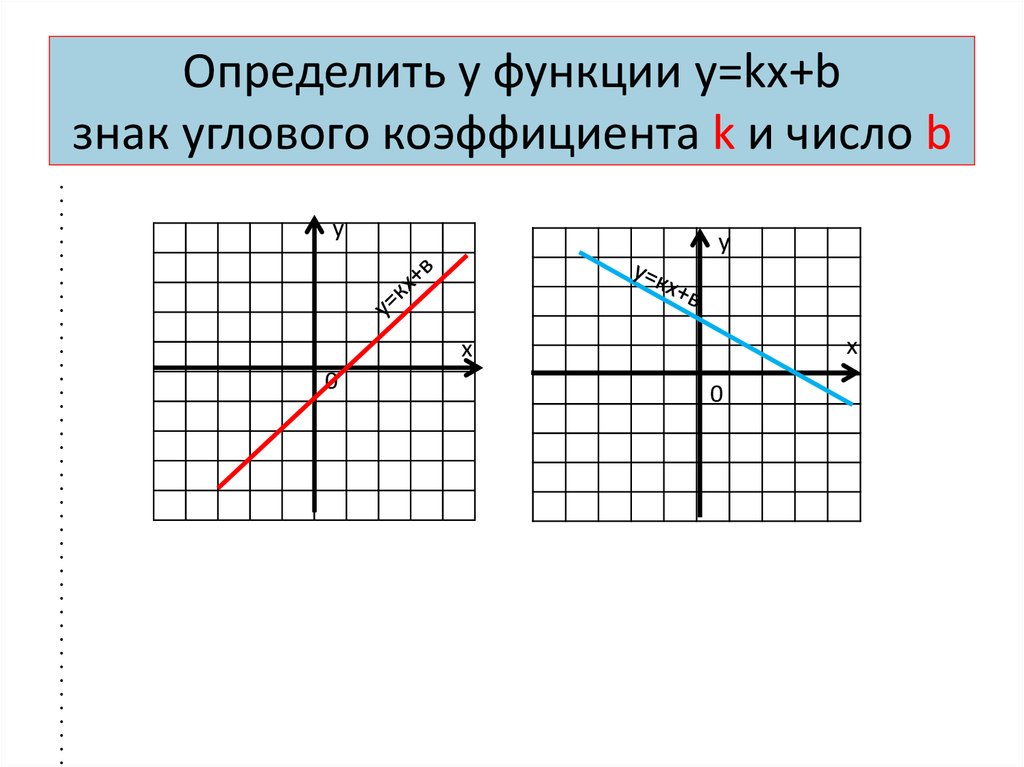

Уравнение прямой, проходящей через данную точку с данным нормальным вектором (нормалью).

Нормальным вектором прямой(нормалью)

называется любой вектор перпендикулярный данной прямой.

Обозначается = (a, b).

Пусть на прямой дана точка М₁ (x_1,y₁) и дан нормальный вектор прямой = (a, b).

Пусть М (x_, y) произвольная точка прямой.

Тогда вектор перпендикулярен вектору. Следовательно, их скалярное произведение×= 0.

Запишем это равенство в координатной форме.

Так как =(а; b) и = (x –x₁; y –y₁), то равенство ×= 0, согласно формуле, × = x₁× x₂+ y₁× y₂, в координатной форме примет вид:

a· ( x–x₁) + b· (y–y₁) = 0

– уравнение прямой, проходящей через данную точку с данным нормальным вектором.

Общее уравнение прямой.

Раскроем скобки в уравнении a·(x‒x₁)+ b·(y‒y₁)=0.

Следовательно, ax ‒ ax₁+ by ‒ by₁ = 0 или ax + by +(‒ ax₁‒ by₁) = 0.

Обозначим ‒ ax₁ — by

1=с,

тогда получим общее уравнение прямой:

ax + by + с = 0

– общее уравнение прямой.

Выразим из общего уравнения прямойyчерез x:

Следовательно,

‒ формула углового коэффициента по координатам нормального вектора.

Вопрос 2. Формула угла между прямыми.

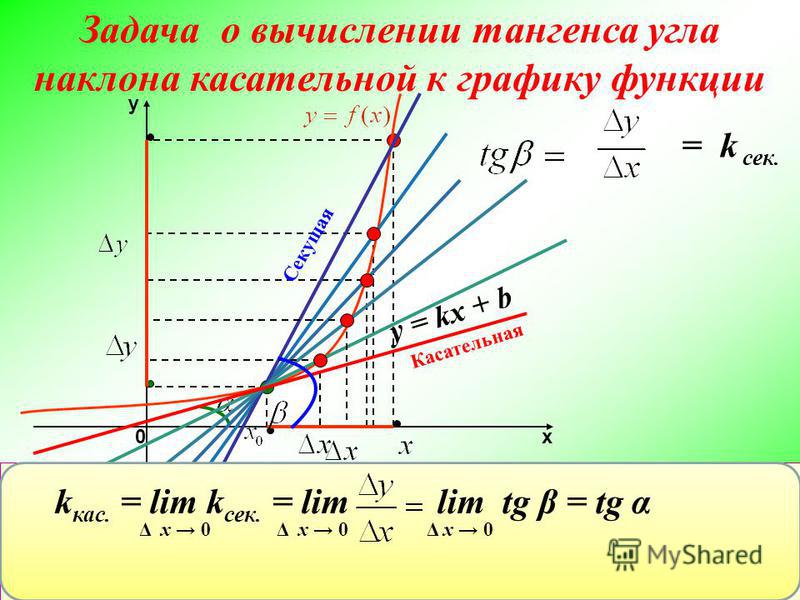
Угол между прямыми: ; равен углу между их нормальными векторами, т. е.

() =().

Воспользовавшись формулой скалярного произведения векторов, получим:

Тогда

Если прямые заданные уравнениями:

; ,

тогда

Следовательно,

По формулам (1) или (2) находят угол между прямыми.

Вопрос 3. Условия параллельности и перпендикулярности прямых.

Если , то = 0. Следовательно,  = 0 и =0.

Получим:

‒ условие параллельности прямых.

Если , то  = и ‒ не существует, то есть = 0. Следовательно,

‒ условие перпендикулярности прямых.

Пример:

Даны уравнения сторон треугольника

,

,

.

Найти:

1) Длину │CD│ и уравнение высоты CD.

2) Систему неравенств определяющих треугольник.

3) B.

Решение:

Найдем координаты вершин треугольника.

A (– 4; 8)

.

B (5; – 4)

C (10; 6)

1) Найдем уравнение высоты CD.

CD AB

;

.

│· 4

–уравнение высоты CD.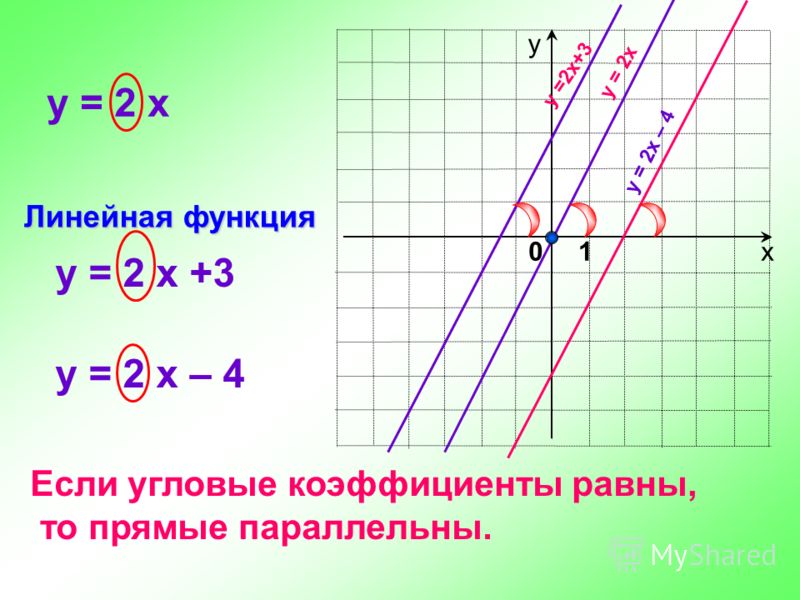

D (2; 0)

Найдемдлину │CD│.

2) Найдем систему неравенств определяющих треугольник.

,

,

.

или – уравнениеAB.

–уравнение BC.

или – уравнениеAC.

–система неравенств определяющих ∆ABC.

3) Найдем B.

или

Вопрос 4. Формула расстояния от точки до прямой.

;

││= d‒ расстояние от точки до прямой.

Тогда формула расстояния от точки до прямой примет вид:

ЛЕКЦИЯ № 14

Вопрос 1. Условия параллельности и перпендикулярности прямых и плоскостей в пространстве.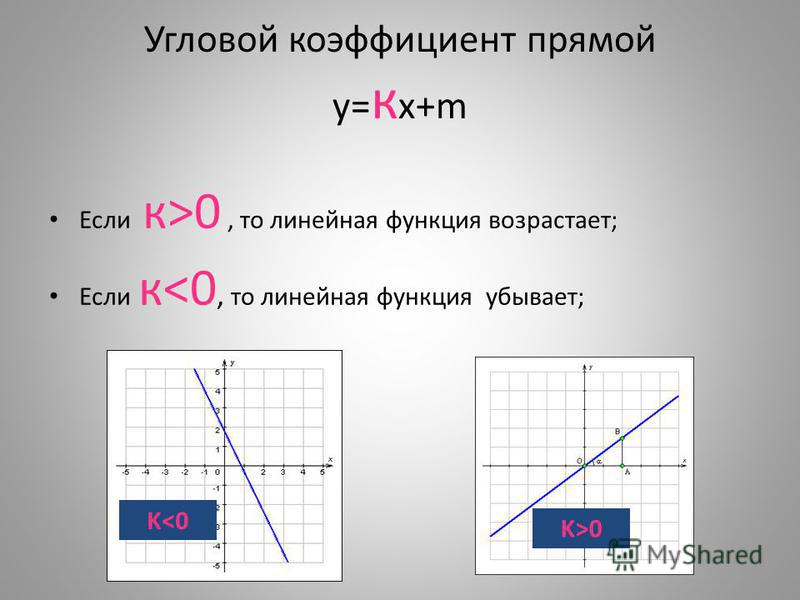

1) Условие параллельности прямой и плоскости в пространстве.

Пусть дана плоскость () и дан направляющий вектор прямой ().

Если , то вектор. Следовательно, их скалярное произведение= 0.

В координатном виде получим:

– условие параллельности прямой и плоскости.

2) Условие перпендикулярности прямой и плоскости в пространстве.

Если , то коллинеарен, тогда по признаку коллинеарности их координаты пропорциональны. Следовательно, получим:

– условие перпендикулярности прямой и плоскости.

Вопрос 2. Уравнение плоскости, проходящей через данную точку, перпендикулярно данному вектору.

Пусть дана плоскость  и вектор = (A, B, C) , пусть точка () ϵ и точка произвольная точка плоскости.

Так как , то и , лежащему в плоскости. Тогда их скалярное произведение = 0.

Запишем это равенство в координатной форме. Получим:

– уравнение плоскости с нормалью.

Вопрос 3. Общее уравнения плоскости. Условия параллельности и перпендикулярности плоскостей.

Раскроем скобки в уравнении , получим

Обозначим:

Получим:

– общее уравнения плоскости.

Пример:

Построить плоскость по ее уравнению .

При A (3; 0; 0)

При B (0; 2; 0)

При C (0; 0; 6)

Вопрос 4. Расстояние от точки до плоскости.

– формула для нахождения расстояния от точки () до плоскости.

Если плоскость , токоллинеарен. Тогда по признаку коллинеарности векторы пропорциональны.

Если (,,) и, то

– условие параллельности плоскостей.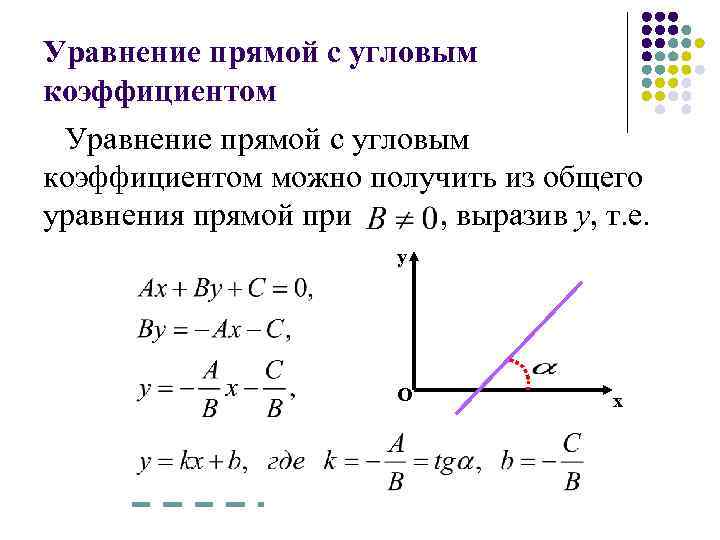

Если , то и. Тогда= 0.

Следовательно,

– условие перпендикулярности плоскостей.

Примеры:

1)

, т. к. ;k = – 5.

2)

=>

ЛЕКЦИЯ № 15

Вопрос 1. Кривые второго порядка.

К кривым второго порядка относятся: окружность, эллипс, гипербола, парабола.

Кривыми второго порядка называются линии, уравнение которых могут быть записаны в виде , где некоторые действительные числа, называемыекоэффициентами уравнения, и, по крайней мере, один из коэффициентов или.

1) ОКРУЖНОСТЬЮ называется множество точек плоскости, равноудаленных от одной точки, называемой центром окружности.

а) Окружность с центром в начале координат.

По теореме Пифагора

б) Окружность с центром в произвольной точке A₁ (x₀, y₀).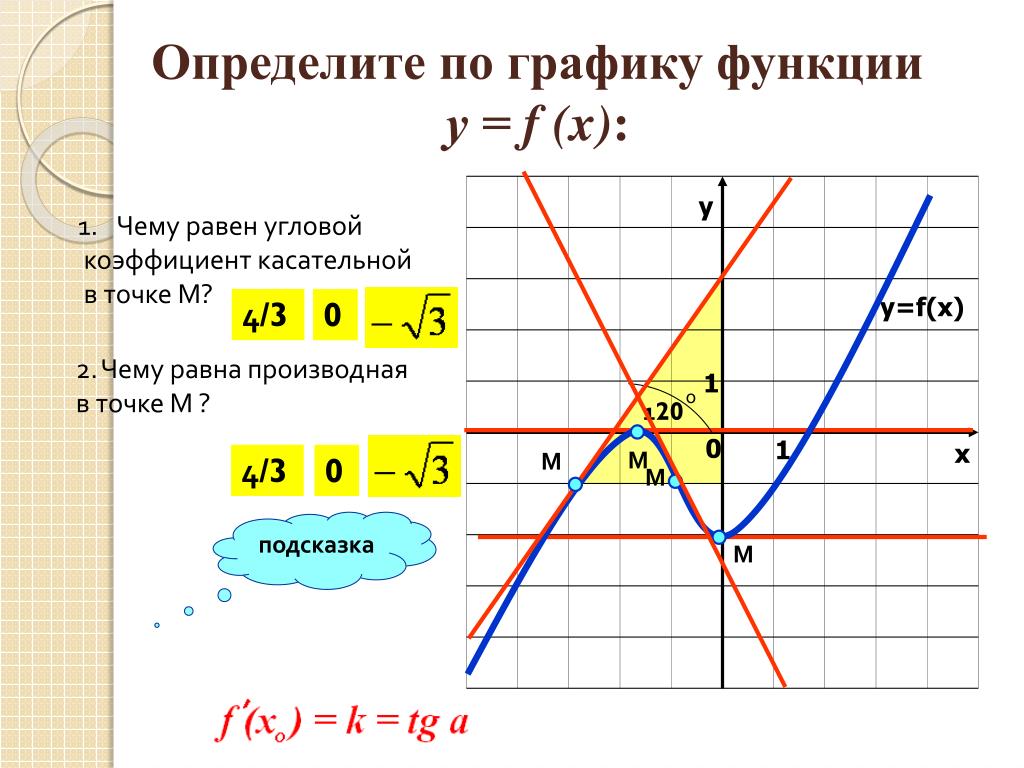

По теореме Пифагора получим уравнение окружности с центром в произвольной точке:

2) ЭЛЛИПСОМ называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, причем большая, чем расстояние между фокусами.

Из определения эллипса следует:

– расстояние между точками.

Введем обозначения – большая ось эллипса;

–малая ось эллипса,

–расстояние между фокусами,

где .

Тогда получим координаты вершин и фокусов эллипса:

(‒a; 0) (a; 0)

(0; b) (0; ‒b)

(‒c; 0) (c; 0)

Подставив полученные координаты в формулу , и воспользовавшись формулой расстояния между точками, и выполнив необходимые преобразования, получимканоническое уравнение эллипса с центром в начале координат:

Эксцентриситетом эллипса называется отношение половины расстояния до фокуса к половине большой оси, обозначается :

< 1;

У эллипса 0 << 1.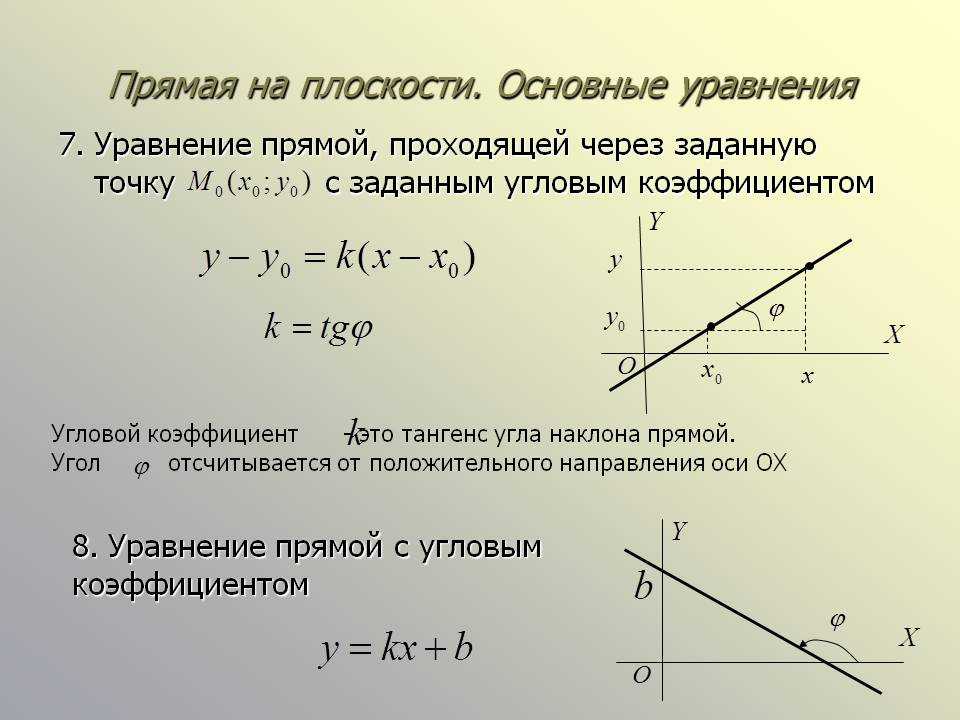

У окружности = 0, поэтому эксцентриситет .

3) ГИПЕРБОЛОЙ называется множество точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, причем меньшая, чем расстояние между фокусами.

Из определения следует

Введем обозначения – действительная ось гиперболы;

–мнимая ось гиперболы;

–расстояние между фокусами,

где .

Тогда получим координаты вершин и фокусов гиперболы:

(-a; 0) (a; 0)

(0; b) (0; -b)

(-c; 0) (c; 0)

Преобразовав формулу , получим (каноническое) уравнение гиперболы:

Эксцентриситет гиперболы: > 1.

Уравнения асимптот гиперболы (PL) и (NK):

.

4) ПАРАБОЛОЙ называется множество точек плоскости, равноудаленных от данной точки, называемой фокусом, и от данной прямой, называемой директрисой.

1. Пусть‒ произвольная точка параболы.

Из определения следует, что расстояние

Обозначим расстояние – параметр параболы.

Тогда ось OYделит пополам, ,

Подставив в формулу координаты точек и, воспользовавшись формулой расстояния между двумя точками,

, получим:

Откуда получим уравнение параболы с вершиной в начале координат (ветви вправо):

Аналогично выводятся уравнения параболы в остальных трех случаях.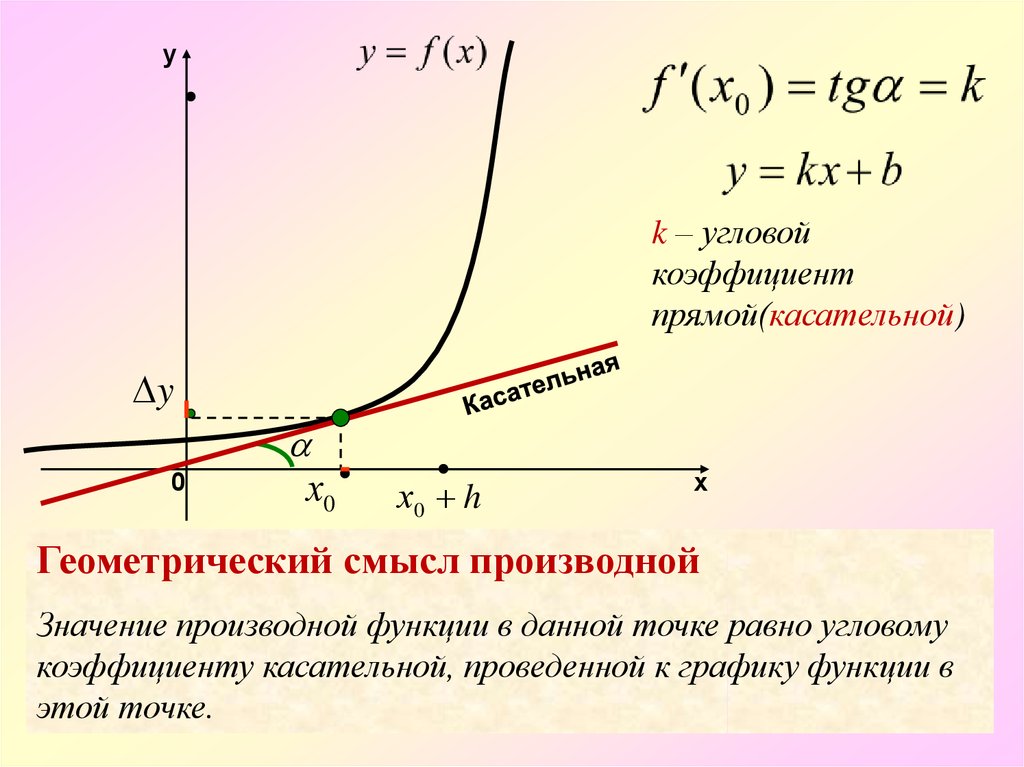

2. Уравнение параболы с вершиной в начале координат (ветви влево).

–фокус

–уравнение директрисы.

3. Уравнение параболы с вершиной в начале координат (ветви вверх).

–фокус

–уравнение директрисы.

4. Уравнение параболы с вершиной в начале координат (ветви вниз).

–фокус

–уравнение директрисы.

Наклон (градиент) прямой линии

Наклон (также называемый градиентом) линии показывает насколько она крутая.

Вычислить

Для расчета уклона:

Разделить изменение высоты на изменение горизонтального расстояния

Наклон =  Изменение по Y Изменение по X

Поиграйте (перетащите точки):

изображения/geom-line-equn. js?mode=slope

Примеры:

Наклон этой линии = 3 3 = 1 Итак, Наклон равен 1

 

		Наклон этой линии = 4 2 = 2
Линия круче, поэтому наклон больше.

 

		Наклон этой линии = 3 5 = 0,6
Линия менее крутая, поэтому и уклон меньше.

 

Положительный или отрицательный?

Двигаясь слева направо, велосипедист должен P проехать по положительному склону P Наклон:

   

При измерении линии:

• Начиная слева и пересекая вправо, положительно
  (но переходя влево отрицательно).
• Верх положительный , нижний отрицательный

 

Уклон = −4 2 = −2

Эта линия идет на вниз на по мере вашего движения, поэтому она имеет отрицательный наклон.

Прямо через

Уклон = 0 5 = 0

Линия, которая проходит прямо (по горизонтали), имеет нулевой наклон.

Прямо вверх и вниз

Уклон = 3 0 = не определено

Последнее немного сложно.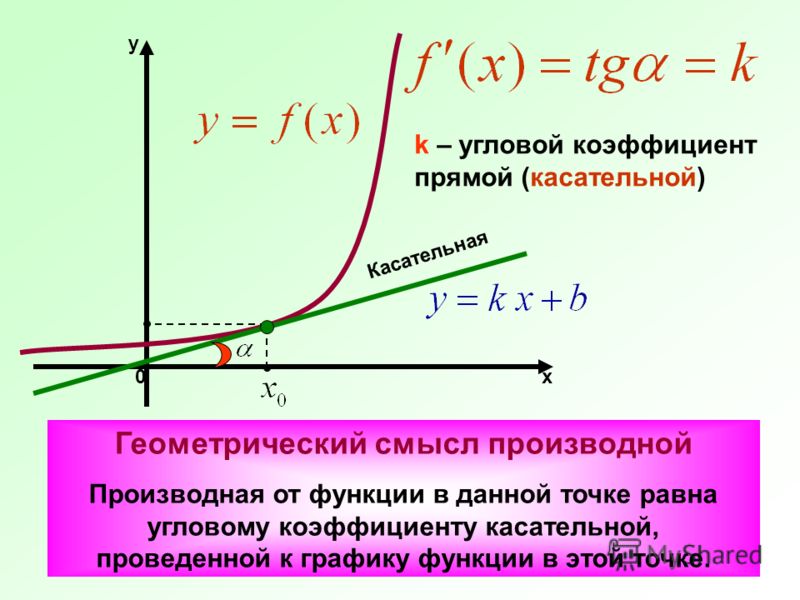 .. вы не можете делить на ноль,
, поэтому наклон линии «прямо вверх и вниз» (вертикально) «не определен».

Вставай и беги

Иногда изменение по горизонтали называют «бегом», а изменение по вертикали — «подъемом» или «падением»:

Это просто разные слова, расчеты не меняются.

 

2068, 2069, 2070, 2071, 2072, 5316, 5317, 5318, 5319, 5320

Наклон – определение, типы, примеры

Наклон линии – это мера крутизны и направления линии. Нахождение наклона линий на координатной плоскости может помочь предсказать, параллельны ли линии, перпендикулярны или нет, без фактического использования компаса.

Наклон любой линии можно рассчитать, используя любые две различные точки, лежащие на линии. Формула наклона линии вычисляет отношение «вертикального изменения» к «горизонтальному изменению» между двумя различными точками на линии. В этой статье мы разберемся с методом нахождения уклона и его применениями.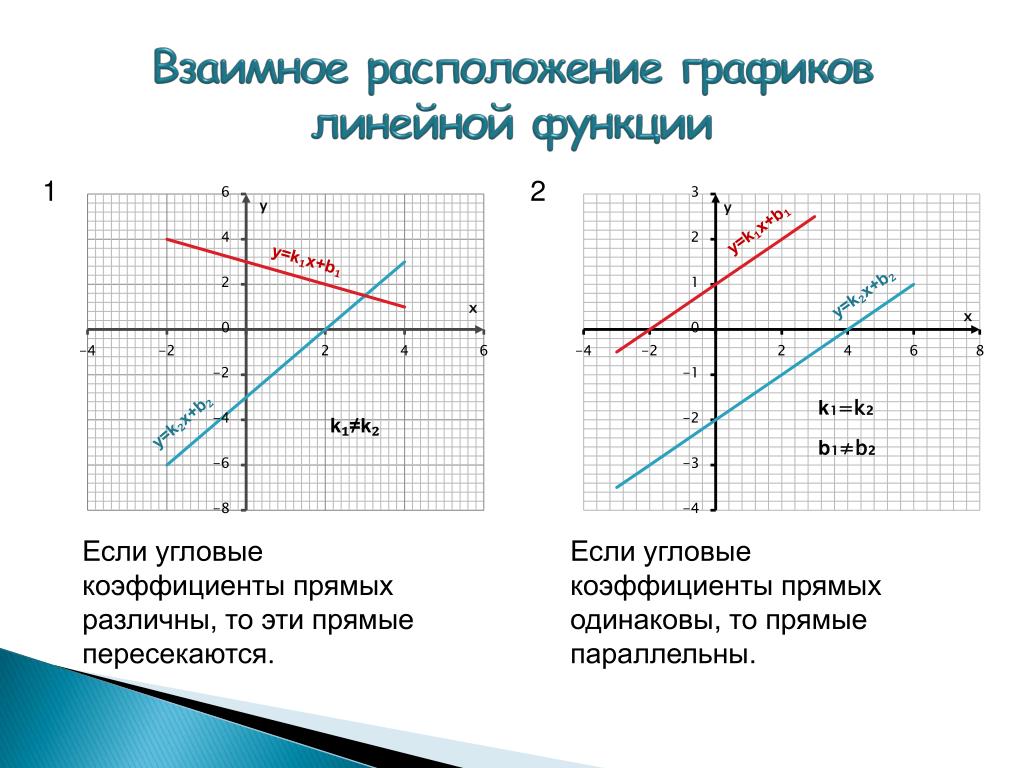

1.	Что такое уклон?
2.	Наклон линии
3.	Формула наклона линии
4.	Как найти уклон?
5.	Типы уклонов
6.	Наклон перпендикулярных линий
7.	Наклон параллельных линий
8.	Часто задаваемые вопросы о склоне

Что такое уклон?

Наклон линии определяется как изменение координаты y относительно изменения координаты x этой линии . Чистое изменение координаты y равно Δy, а чистое изменение координаты x равно Δx. Таким образом, изменение координаты y по отношению к изменению координаты x можно записать как

м = Δy/Δx
где м — уклон

Обратите внимание, что тангенс θ = Δy/Δx

Мы также называем этот тангенс θ наклоном линии.

Наклон линии

Наклон линии представляет собой отношение подъема к пробегу или подъема, деленное на пробег. Он описывает крутизну линии в координатной плоскости. Вычисление наклона линии аналогично нахождению наклона между двумя разными точками. В общем, чтобы найти наклон линии, нам нужно иметь значения любых двух разных координат на линии.

Наклон между двумя точками

Наклон линии можно рассчитать, используя две точки, лежащие на прямой. Зная координаты двух точек, мы можем применить формулу наклона линии. Пусть координаты этих двух точек будут
. Р ₁ = (х ₁ , у ₁ )
P ₂ = (x ₂ , y ₂ )

Как мы обсуждали в предыдущих разделах, наклон представляет собой «изменение координаты y по отношению к изменению координаты x этой линии». Итак, подставляя значения Δy и Δx в уравнение наклона, мы знаем, что:
Δу = у ₂ — у ₁
Δx = x ₂ — x ₁

Следовательно, используя эти значения в соотношении, мы получаем: — x ₁ )

где m — наклон, а θ — угол, образуемый линией с положительной осью x.

Формула наклона линии

Наклон линии можно рассчитать по уравнению линии. Общий наклон формулы линии задается как

y = mx + b

где

• м — уклон, такой, что m = tan θ = Δy/Δx
• θ — угол, образуемый линией с положительной осью x
• Δy — чистое изменение по оси Y
• Δx — чистое изменение по оси x

Наклон линии Пример

Вспомним определение наклона линии и попробуем решить приведенный ниже пример.

Пример: Уравнение линии с наклоном 1, которая проходит через точку (-1, -5) ?

Решение:

Мы знаем, что если уклон равен 1, то значение м будет равно 1 в общем уравнении y = mx + b. Итак, подставляем значение м в 1, и получаем,

y = x + b

Теперь у нас уже есть значение одной точки на прямой. Итак, подставляем значение точки (-1, -5) в уравнение y = x + b, и получаем,

b = -4

Отсюда, подставляя значения m и b в общем уравнении, мы получаем наше окончательное уравнение как y = x — 4.

Уравнение: y = x — 4

Как найти уклон?

Наклон линии можно найти разными способами. Первый метод определения значения уклона заключается в использовании уравнения, которое задается следующим образом: где m — наклон линии.

Кроме того, изменение x равно запустить и изменение y составляет рост или падение . Таким образом, мы также можем определить наклон как m = подъем/спуск

Нахождение наклона на графике

Один из методов нахождения наклона линии на графике заключается в прямом применении формулы с учетом координат двух лежащих точек. на линии. Допустим, значения координат двух точек не заданы. Итак, у нас есть еще один способ найти наклон линии. В этом методе мы пытаемся найти тангенс угла, образованного линией с осью x. Следовательно, мы находим наклон, как указано ниже.

Наклон линии имеет только одно значение. Таким образом, наклоны, найденные методами 1 и 2, будут равны.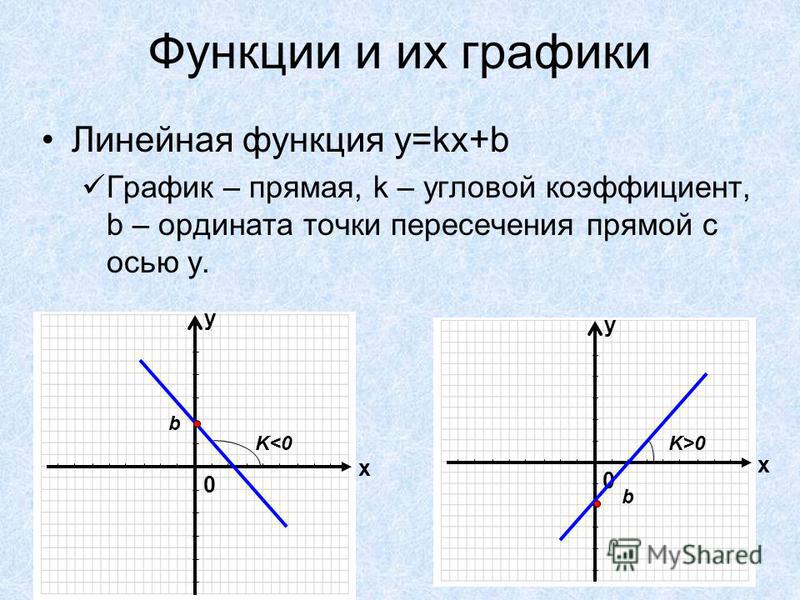 В дополнение к этому, скажем, нам дано уравнение прямой линии. Общее уравнение линии может быть дано как

y = mx + b

Значение уклона дано как м; , следовательно, значение м дает наклон любой прямой.

Следующие шаги можно выполнить, чтобы найти наклон прямой, такой, что координаты двух точек, лежащих на прямой, равны: (2, 4), (1, 2)

• Шаг 1: Запишите координаты двух точек, лежащих на прямой, (x ₂ , y ₂ ), (x ₁ , y ₁ ). Здесь координаты даны как (2, 4), (1, 2).
• Шаг 2: Примените формулу наклона линии, m = (y ₂ — y ₁ )/(x ₂ — x ₁ ) = (4 — 2)/(2 — 1) = 2,
• Шаг 3: Следовательно, наклон данной линии = 2.

Типы уклонов

Мы можем классифицировать наклон по различным типам в зависимости от отношения между двумя переменными x и y и, таким образом, от значения градиента или наклона полученной линии.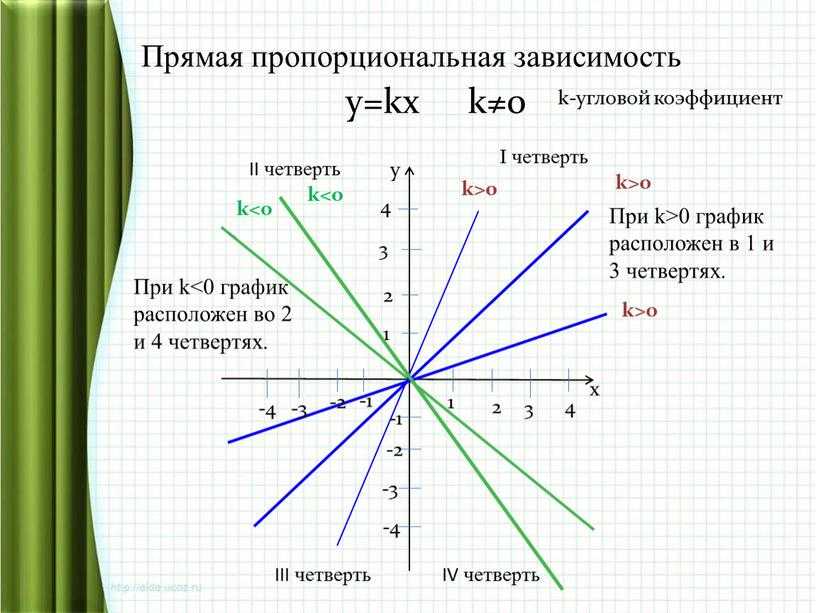 Существует 4 различных типа уклонов, обозначенных как:

• Положительный уклон
• Отрицательный наклон
• Нулевой наклон
• Неопределенный уклон

Положительный наклон

Графически положительный наклон указывает на то, что при движении слева направо в координатной плоскости линия поднимается, что также означает, что при увеличении x увеличивается и y.

Отрицательный наклон

Графически отрицательный наклон указывает на то, что при движении слева направо в координатной плоскости линия падает, что также означает, что при увеличении x уменьшается y.

Нулевой наклон

Для линии с нулевым наклоном подъем равен нулю, и, таким образом, применяя формулу превышения подъема, мы получаем наклон линии равным нулю.

Неопределенный уклон

Для линии с неопределенным уклоном значение длины равно нулю. Наклон вертикальной линии не определен.

Наклон горизонтальной линии

Мы знаем, что горизонтальная линия — это прямая линия, параллельная оси x или проведенная слева направо или справа налево в координатной плоскости. Следовательно, чистое изменение координаты y горизонтальной линии равно нулю. Наклон горизонтальной линии можно определить как

Наклон горизонтальной линии, m = Δy/Δx = ноль

Наклон вертикальной линии

Мы знаем, что вертикальная линия — это прямая линия, параллельная оси Y или рисуется сверху вниз или снизу вверх в координатной плоскости. Следовательно, чистое изменение координат x вертикальной линии равно нулю. Наклон вертикальной линии можно определить как

Наклон вертикальной линии, м = Δy/Δx = не определено

Наклон перпендикулярных линий

Набор перпендикулярных линий всегда имеет между собой угол 90º. Предположим, что у нас есть две перпендикулярные линии l ₁ и l ₂ в координатной плоскости, наклоненные под углами θ ₁ и θ ₂ соответственно с осью x, так что данные углы следуют внешнему углу теорема как, θ ₂ = θ ₁ + 90º.

Следовательно, их наклоны можно представить как
м ₁ = тангенс θ ₁
м ₂ = загар (θ ₁ + 90º) = — раскладушка θ ₁
⇒ м ₁ × м ₂ = -1

Таким образом, произведение наклонов двух перпендикулярных прямых равно -1.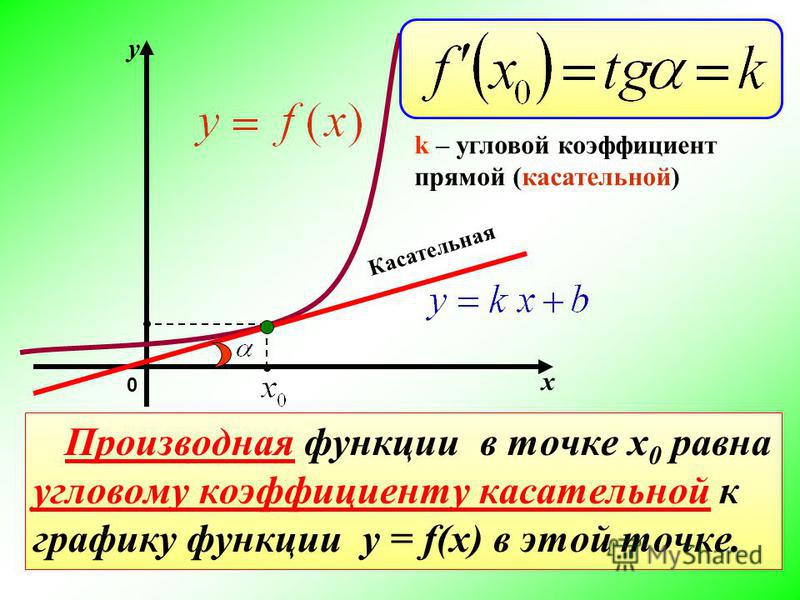

Наклон параллельных линий

Набор параллельных линий всегда имеет одинаковый угол наклона. Предположим, у нас есть две параллельные линии l ₁ и l ₂ в координатной плоскости, наклоненные под углом θ ₁ и θ ₂ соответственно с осью x, так что θ ₂ = θ ₁ .

Таким образом, их наклоны можно представить как
⇒ m ₁ = m ₂

Таким образом, наклоны двух параллельных прямых равны.

Важные примечания по наклону:

• Наклон линии — это мера тангенса угла, образуемого линией с осью x.
• Наклон постоянен на протяжении всей прямой.
• Форма пересечения наклона прямой линии может быть задана как y = mx + b
• Наклон обозначается буквой m и определяется выражением m = tan θ = (y ₂ — y ₁ )/(x ₂ — x ₁ )

Сложный вопрос:

Прямая имеет уравнение y = 2x — 7.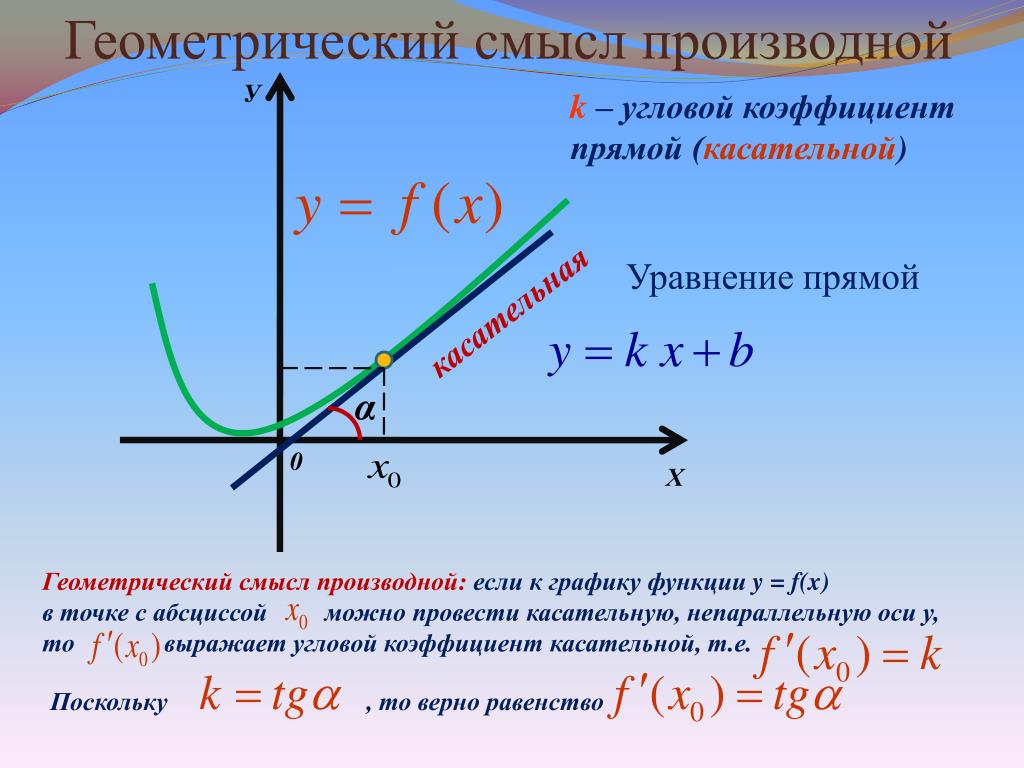 Найдите уравнение прямой, которая перпендикулярна данной прямой и проходит через начало координат.

☛ Похожие темы:

• Линейное уравнение
• Квадратное уравнение
• Кубическое уравнение

Часто задаваемые вопросы о склоне

Что такое наклон линии?

Наклон линии, также известный как градиент, определяется как значение крутизны или направление линии в координатной плоскости. Уклон можно вычислить разными способами, зная уравнение прямой или координаты точек, лежащих на прямой.

По какой формуле можно найти наклон линии?

Мы можем вычислить наклон линии напрямую, используя формулу наклона линии, зная координаты двух точек, лежащих на линии. Формула дается как,
Уклон = m = tan θ = (y ₂ — y ₁ )/(x ₂ — x ₁ )

Как рассчитать уклон?

Наклон определяется путем измерения тангенса угла, образованного линией с осью x. Существуют различные методы определения наклона линии. Выражение, которое можно использовать для определения наклона, имеет вид tan θ или (y ₂ — y ₁ )/(x ₂ — x ₁ ), где θ — угол, который линия образует с положительной осью x, и (x ₁ , y ₁ ) и (x ₂ , y ₂ ) — координаты двух точек, лежащих на прямой.

Какие существуют 4 типа склонов?

Существует 4 различных типа наклона: положительный наклон, отрицательный наклон, нулевой наклон и неопределенный наклон.

Что такое неопределенный уклон?

Любой уклон с углом 90º с осью x, будет иметь неопределенное значение тангенса 90º. Следовательно, такие линии будут иметь неопределенное значение наклона.

Как выглядит склон?

Наклон есть не что иное, как мера тангенса угла, составленного с осью x. Следовательно, это всего лишь мера угла.

Какие 3 способа найти уклон?

Способы определения уклона: форма точечного уклона, форма пересечения наклона и стандартная форма.