Как отмечать координаты точек на координатной прямой. Координатная прямая (числовая прямая), координатный луч. Виды точек на координатной прямой
На данном уроке мы познакомимся с понятием координатной прямой, выведем ее основные характеристики и свойства. Сформулируем и научимся решать основные задачи. Решим несколько примеров на сочетание этих задач.
Из курса геометрии мы знаем, что такое прямая, но что нужно сделать с обычной прямой, чтобы она стала координатной?
1) Выбрать точку начала отсчета;
2) Выбрать направление;
3) Выбрать масштаб;
На рисунке 1 изображена обычная прямая, а на рисунке 2 — координатная.
Координатной прямой называется такая прямая l , на которой выбрана начальная точка О — начало отсчета, масштаб — единичный отрезок, то есть такой отрезок, длина которого считается равной единице, и положительное направление.
Координатную прямую также называют координатной осью или осью Х.
Выясним, зачем нужна координатная прямая, для этого определим ее основное свойство.
Координатная прямая устанавливает взаимооднозначное соответствие между множеством всех чисел и множеством всех точек на этой прямой. Приведем примеры:
Заданы два числа: (знак «+», модуль равен трем) и (знак «-», модуль равен трем).Изобразим эти числа на координатной прямой:
Здесь число называется координатой А, число — координатой В.
Говорят также, что образом числа есть точка С с координатой , а образом числа есть точка D с координатой :
Итак, поскольку основное свойство координатной прямой — это установление взаимооднозначного соответствия между точками и числами, то возникает две основные задачи: указать точку по заданному числу, мы это уже сделали выше, и указать число по заданной точке. Рассмотрим пример второй задачи:
Пусть дана точка М:
Чтобы определить по данной точке число нужно в первую очередь определить расстояние от начал отсчета до точки. В данном случае расстояние равно двум. Теперь нужно определить знак числа, то есть в каком луче прямой лежит точка М.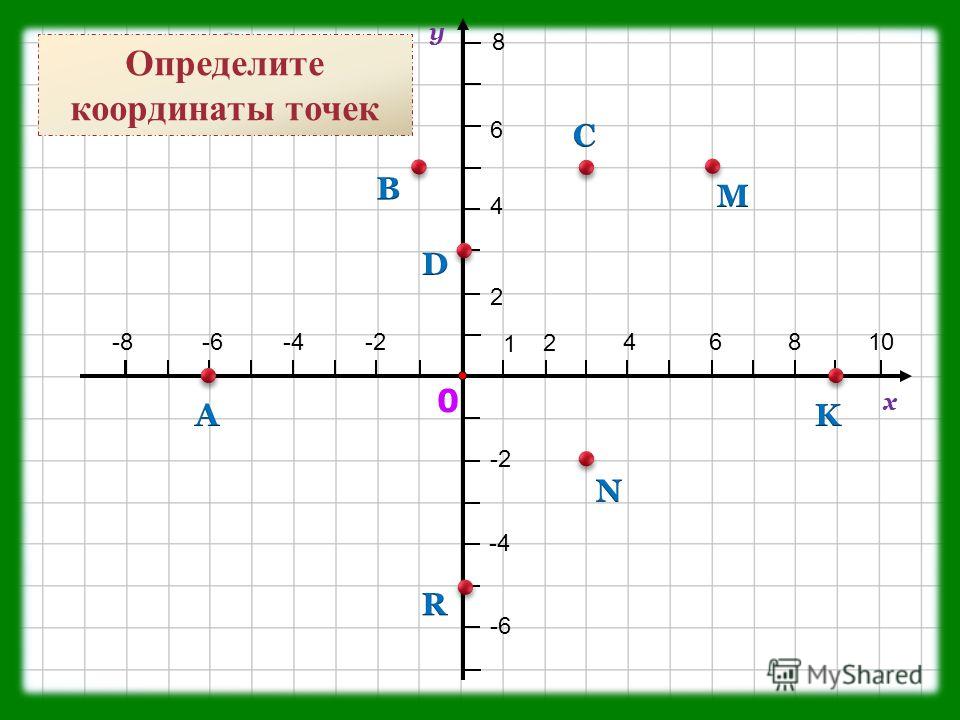
В данном случае точка лежит справа от начала отсчета, в положительном луче, значит число будет иметь знак «+».
Возьмем еще одну точку и по ней определим число:
Расстояние от начала отсчета до точки аналогично предыдущему примеру равно двум, но в данном случае точка лежит слева от начала отсчета, на отрицательном луче, значит точка N характеризует число
Все типовые задачи, связанные с координатной прямой, так или иначе связаны с ее основным свойством и двумя основными задачами, которые мы сформулировали и решили.
К типовым задачам относятся:
—уметь расставлять точки и их координаты ;
—понимать сравнение чисел :
выражение означает, что точка С с координатой 4 лежит правее точки М с координатой 2:
И наоборот, если нам задано расположение точек на координатной прямой, мы должны понимать, что их координаты связаны определенным соотношением:
Пусть заданы точки М(х М) и N(x N):
Мы видим, что точка М лежит правее точки n, значит, их координаты соотносятся как
—Определение расстояния между точками .
Мы знаем, что расстояние между точками Х и А равно модулю числа . пусть даны две точки:
Тогда расстояние между ними будет равно:
Еще одно очень важная задача — это
Рассмотрим луч, который лежит на координатной оси, не включает свое начало, но включает все остальные точки:
Итак, у нас задано множество точек, расположенных на координатной оси. Опишем множество чисел, которое характеризуется данным множеством точек. Таких чисел и точек бесчисленное множество, поэтому данная запись выглядит так:
Сделаем пояснение: при втором варианте записи если ставят круглую скобку «(» значит крайнее число — в данном случае число 3, не включается в множество, если же поставить квадратную скобку «[», то крайнее число включается в множество.
Итак, мы записали аналитически числовое множество, которое характеризует заданное множество точек. аналитическая запись, как мы сказали, выполняется или в виде неравенства, или в виде промежутка.
Задано множество точек:
В данном случае точка а=3 входит в множество. Опишем аналитически множество чисел:
Обратим внимание, что после или перед знаком бесконечности всегда ставят круглую скобку, так как бесконечности мы никогда не достигнем, а около числа может стоять как круглая скобка, так и квадратная, в зависимости от условий поставленной задачи.
Рассмотрим пример обратной задачи.
Дана координатная прямая. Изобразить на ней множество точек, соответствующих числовому множеству и :
Координатная прямая устанавливает взаимооднозначное соответствие между любой точкой и числом, а значит и между числовыми множествами и множествами точек. Мы рассмотрели лучи, направленные как в положительном, так и в отрицательном направлении, включающие свою вершину и не включающие ее. Теперь рассмотрим отрезки.
Пример 10:
Задано множество чисел . Изобразить соответствующее множество точек
Пример 11:
Задано множество чисел .
Иногда чтобы показать, что концы отрезка не включаются в множество, рисуют стрелки:
Пример 12:
Дано числовое множество . Построить его геометрическую модель:
Найти наименьшее число из промежутка :
Найти наибольшее число из промежутка , если оно существует:
Мы может отнять от восьми сколь угодно малое число и сказать, что результат и будет наибольшим числом, но тут же найдем число еще меньше, и результат вычитания увеличится, так что найти наибольшее число в данном промежутке невозможно.
Обратим внимание на тот факт, что ни к одному числу на координатной прямой нельзя подобрать ближайшее число, потому что всегда найдется число еще ближе.
Сколько натуральных чисел содержится в заданном промежутке?
Из промежутка выделим следующие натуральные числа: 4, 5, 6, 7 — четыре натуральных числа.
Напомним, что натуральные числа — это числа, применяемые для счета.
Возьмем другое множество.
Пример 13:
Задано множество чисел
Построить его геометрическую модель:
Данная статья посвящена разбору таких понятий, как координатный луч и координатная прямая. Мы остановимся на каждом понятии и подробно рассмотрим примеры. Благодаря этой статье вы сможете освежить свои знания или ознакомиться с темой без помощи преподавателя.
Для того, чтобы определить понятие координатного луча, следует иметь представление о том, что такое луч.
Определение 1
Луч — это геометрическая фигура, которая имеет начало отсчета координатного луча и направление движения. Прямую обычно изображают горизонтально, указывая направление направо.
На примере мы видим, что O является началом луча.
Пример 1
Координатный луч изображается по той же схеме, но существенно отличается. Мы ставим точку отсчета и отмеряем единичный отрезок.
Пример 2
Определение 2
Единичный отрезок — это расстояние от 0 до точки, выбранной для измерения.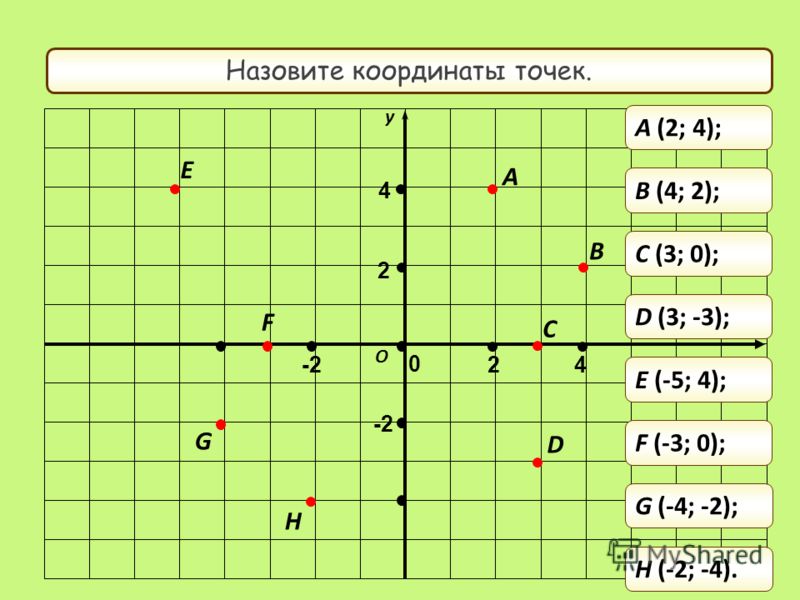
Пример 3
От конца единичного отрезка нужно отложить несколько штрихов и сделать разметку.
Благодаря манипуляциям, которые мы проделали с лучом, он стал координатным. Подпишите штрихи натуральными числами в последовательности от 1 — например, 2 , 3 , 4 , 5 …
Пример 4
Определение 3
– это шкала, которая может длиться до бесконечности.
Зачастую его изображают лучом с началом в точке O , и откладывают единственный единичный отрезок. Пример указан на рисунке.
Пример 5
Мы в любом случае сможем продолжить шкалу до того числа, которое нам необходимо. Вы можете записывать числа как удобно – под лучом или над ним.
Пример 6
Для отображений координат луча могут использоваться как заглавные, как и строчные буквы.
Принцип изображения координатной прямой практически не отличается от изображения луча. Все просто — прочертите луч и дополните до прямой, придав положительное направление, которое указывается стрелочкой.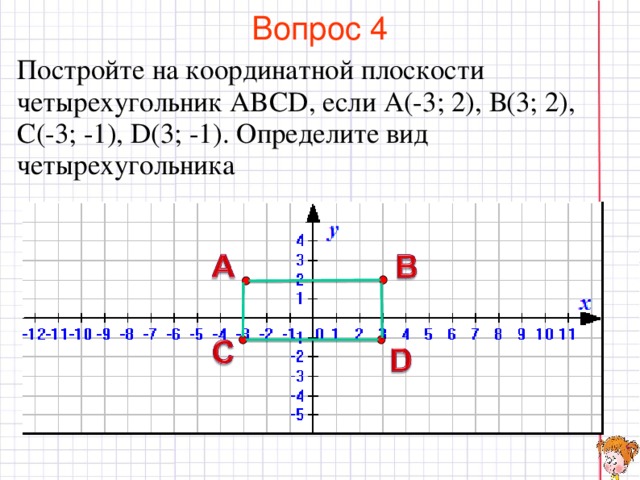
Пример 7
Проведите луч в противоположную сторону, дополнив его до прямой
Пример 8
Отложите единичные отрезки по примеру, указанному выше
С левой стороны запишите натуральные числа 1 , 2 , 3 , 4 , 5 … с противоположным знаком. Обратите внимание на пример.
Пример 9
Вы можете отметить только начало отсчета и единичные отрезки. Смотрите на примере, как это будет выглядеть.
Пример 10
Определение 4
– это прямая, которая изображается с определенной точкой отсчета, которая принимается за 0 , единичным отрезком и заданным направлением движения.
Соответствие между точками координатной прямой и действительными числами
Координатная прямая может содержать множество точек. Они напрямую связаны с действительными числами. Это можно определить, как взаимно однозначное соответствие.
Определение 5
Каждой точке на координатной прямой соответствует единственное действительное число, а каждому действительному числу соответствует единственная точка на координатной прямой.
Для того, чтобы лучше понять правило, следует отметить точку на координатной прямой и посмотреть, какое натуральное число соответствует отметке. Если эта точка совпадает с началом отсчета, она будет отмечена нулем. Если точка не совпадает с началом отсчета, мы откладываем нужное количество единичных отрезков до тех пор, пока не достигнем указанной отметки. Число, записанное под ней, и будет соответствовать данной точке. На примере, указанном внизу, мы покажем вам это правило наглядно.
Пример 11
Если мы не можем найти точку, откладывая единичные отрезки, следует отмечать также точки, составляющие одну десятую, сотую или тысячную долю единичного отрезка. На примере можно подробно рассмотреть данное правило.
Отложив несколько подобных отрезков, мы сможем получить не только целое, но и дробное число – как положительное, так и отрицательное.
Отмеченные отрезки помогут нам отыскать на координатной прямой необходимую точку. Это могут быть как целые, так и дробные числа.
Однако на прямой существуют точки, которые очень сложно найти с помощью единичных отрезков. Этим точкам соответствуют десятичные дроби. Для того, чтобы искать подобную точку, придётся откладывать единичный отрезок, десятую, сотую, тысячную, десятитысячную и другие его доли. Одной точке координатной прямой отвечает иррациональное число π (= 3 , 141592 . . .) .
Множество действительных чисел включается в себя все числа, которые можно записать в виде дроби. Это позволяет выявить правило.
Определение 6
Каждой точке координатной прямой соответствует конкретное действительное число. Разные точки определяют разные действительные числа.
Это соответствие однозначно –каждой точке соответствует определенное действительное число. Но это работает также и в обратном направлении. Мы также можем указать определенную точку на координатной прямой, которая будет относиться конкретному действительному числу. Если число не является целым, то нам необходимо отметить несколько единичных отрезков, а также десятых, сотых долей в заданном направлении.
Например, числу 400350 отвечает точка на координатной прямой, в которую из начала отсчета можно попасть, отложив в положительном направлении 400 единичных отрезков, 3 отрезка, составляющих десятую долю единичного, и 5 отрезков – тысячную долю.
Координатная прямая.
Возьмем обычную прямую. Назовем ее прямая x (рис.1). Выберем на этой прямой точку отсчета O, а также стрелкой укажем положительное направление этой прямой (рис. 2). Таким образом, справа от точки O у нас будут положительные числа, а слева – отрицательные. Выберем масштаб, то есть размер отрезка прямой, равный единице. У нас получилась координатная прямая (рис. 3). Каждому числу соответствует определенная единственная точка на этой прямой. Причем это число называют координатой этой точки. Поэтому прямая и называется координатной. А точка отсчета O называется началом координат.
К примеру, на рис. 4 точка B находится на расстоянии 2 правее начала координат. Точка D находится на расстоянии 4 левее начала координат.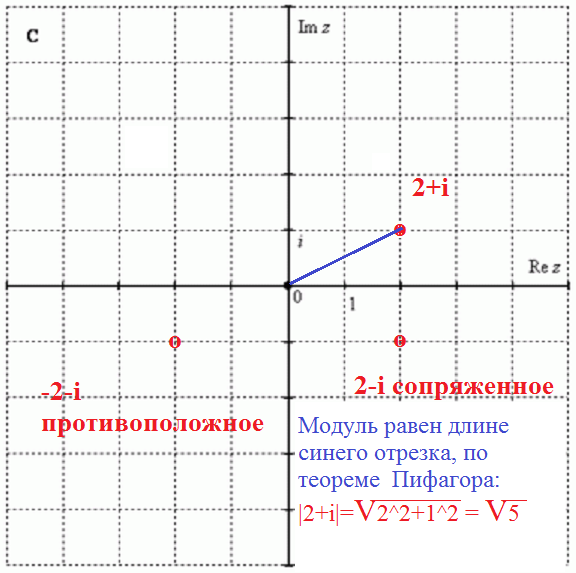
Зная координаты двух точек координатной прямой, мы всегда можем вычислить расстояние между ними. Допустим, у нас две точки A и B с координатами a и b соответственно. Тогда расстояние между ними будет |a — b|. Запись |a — b| читается как «a минус b по модулю» или «модуль разности чисел a и b».
Что такое модуль?
Алгебраически модуль числа x – это неотрицательное число. Обозначается как |x|. Причем если x > 0, то |x| = x. Если x
Геометрически модуль числа x – это расстояние между точкой и началом координат. А если есть две точки с координатами x1 и x2, то |x1 — x2| — это расстояние между этими точками.
Модуль также называют абсолютной величиной .
О чем еще мы можем сказать, когда речь идет о координатной прямой? Конечно о числовых промежутках.
Виды числовых промежутков.
Допустим у нас два числа a и b. Причем b > a (b больше a). На координатной прямой это означает, что точка b находится правее точки a. Заменим в нашем неравенстве b на переменную x. То есть x > a. Тогда x – это все числа, которые больше числа a. На координатной прямой это соответственно все точки правее точки a. Эта часть линии заштрихована (рис. 6). Такое множество точек называют открытым лучом , а данный числовой промежуток обозначают (a; +∞), где знак +∞ читается как «плюс бесконечность». Обратите внимание, что сама точка a не входит в данный промежуток и обозначается светлым кружком.
Рассмотрим также случай, когда x ≥ a. Тогда x – это все числа, которые больше или равны a. На координатной прямой это все точки правее а, а также сама точка a (на рис. 7 точка a уже обозначается темным кружком).
Такое множество точек называют замкнутым лучом (или просто лучом), а данный числовой промежуток обозначают .
Координатную прямую также называют координатной осью . Или просто осью x.
Утверждать, что вы знаете математику, невозможно, если вы не умеете строить графики, изображать неравенства на координатной прямой, работать с осями координат. Визуальная составляющая в науке жизненно необходима, ведь без наглядных примеров в формулах и вычислениях порой можно сильно запутаться. В данной статье мы посмотрим, как работать с осями координат, и научимся строить простейшие графики функций.
Применение
Координатная прямая — это основа простейших видов графиков, с которыми сталкивается школьник на своем учебном пути. Она используется практически в каждой математической теме: при расчёте скорости и времени, проецировании размеров объектов и вычислении их площади, в тригонометрии при работе с синусами и косинусами.
Главная ценность такой прямой — это наглядность.
Поскольку математика — это наука, в которой требуется высокий уровень абстрактности мышления, графики помогают в представлении объекта в реальном мире. Как он себя ведет? В какой точке пространства будет находиться через несколько секунд, минут, часов? Что можно сказать о нём в сопоставлении с другими объектами? Какой скоростью он обладает в случайно выбранный момент времени? Как охарактеризовать его движение?
А про скорость речь идёт неспроста — именно её зачастую отображают графики функции. А ещё они могут отображать изменение температуры или давления внутри объекта, его размеров, ориентации относительно горизонта. Таким образом, построить координатную прямую зачастую требуется и в физике.
Одномерный график
Существует понятие многомерности. В достаточно всего одного числа, чтобы определить местоположение точки. Это как раз и есть случай с применением координатной прямой. Если пространство двухмерное, то потребуется два числа. Графики такого типа используются гораздо чаще, и чуть дальше в статье мы их обязательно рассмотрим.
Что можно увидеть с помощью точек на оси, если она всего одна? Можно увидеть размер объекта, его положение в пространстве относительно некоторого «нуля», т. е. точки, выбранной в качестве начала отсчёта.
Изменение параметров с течением времени увидеть не удастся, так как все показания будут отображаться для одного конкретного момента. Однако с чего-то надо начинать! Итак, приступим.
Как построить координатную ось
Для начала требуется провести горизонтальную линию — это и будет наша ось. С правой стороны «заострим» её, чтобы она была похожа на стрелку. Таким образом мы обозначим направление, в котором числа будут увеличиваться. В сторону уменьшения стрелка обычно не ставится. Традиционно ось направлена вправо, поэтому мы просто последуем данному правилу.
Поставим нулевую отметку, которая будет отображать начало координат. Это то самое место, от которого ведется отсчёт, будь то размер, вес, скорость или что угодно другое. Кроме нуля, мы обязательно должны обозначить так называемую цену деления, т.
е. ввести стандарт единицы, в соответствии с которой будем откладывать на оси те или иные величины. Это обязательно нужно делать, чтобы уметь находить длину отрезка на координатной прямой.
Через равное расстояние друг от друга поставим точки или «зарубки» на линии, а под ними напишем соответственно 1,2,3 и так далее. И вот, всё готово. Но с получившимся графиком надо ещё научиться работать.
Виды точек на координатной прямой
С первого взгляда на предложенные в учебниках рисунки становится понятно: точки на оси могут быть закрашенные или не закрашенные. Вы думаете, это случайность? Вовсе нет! «Сплошная» точка используется при нестрогом неравенстве — том, которое читается как «больше или равно». Если же нужно строго ограничить интервал (например, «икс» может принимать значения от нуля до единицы, но не включает её), мы воспользуемся «полой» точкой, то есть, по сути, маленьким кружком на оси. Надо заметить, что ученики не очень любят строгие неравенства, потому что с ними сложнее работать.
В зависимости от того, какие точки вы используете на графике, будут называться и построенные интервалы. Если неравенство с двух сторон нестрогое, то мы получим отрезок. Если с одной стороны он окажется «открыт», то называться будет полуинтервалом. Наконец, если часть прямой ограничена с двух сторон полыми точками, она будет называться интервалом.
Плоскость
При построении двух прямых на мы уже можем рассматривать графики функций. Скажем, горизонтальная линия будет осью времени, а вертикальная — расстоянием. И вот уже мы в состоянии определить, какое расстояние преодолеет объект через минуту или час пути. Таким образом, работа с плоскостью даёт возможность следить за изменением состояния объекта. Это гораздо интереснее, чем исследование статичного состояния.
Простейший график на такой плоскости — прямая, она отражает функцию Y(X) = aX + b. Линия изгибается? Это означает, что объект меняет свои характеристики в процессе исследования.
Представьте, вы стоите на крыше здания и держите в вытянутой руке камень.
Когда вы отпустите его, он полетит вниз, начав своё движение с нулевой скорости. Но уже через секунду он будет преодолевать 36 километров в час. Камень продолжит ускоряться и дальше, и чтобы нарисовать его движение на графике, вам потребуется замерить его скорость в несколько моментов времени, выставив точки на оси в соответствующих местах.
Отметки на горизонтальной координатной прямой по умолчанию получают название X1, X2,X3, а на вертикальной — Y1, Y2,Y3 соответственно. Проецируя их на плоскость и находя пересечения, мы находим фрагменты результирующего рисунка. Соединив их одной линией, мы получим график функции. В случае с падающим камнем квадратичная функция будет иметь вид: Y(X) = aX * X + bX + c.
Масштаб
Конечно, не обязательно выставлять рядом с делениями на прямой целочисленные значения. Если вы рассматриваете движение улитки, которая ползет со скоростью 0,03 метра в минуту, выставьте в качестве значений на координатной прямой дроби. В данном случае задайте цену деления как 0,01 метра.
Особенно удобно выполнять такие чертежи в тетради в клетку — здесь сразу видно, хватит ли места на листе для вашего графика, не выйдете ли вы за поля. Свои силы рассчитать несложно, ведь ширина клетки в такой тетради — 0,5 сантиметра. Понадобилось — уменьшили рисунок. От изменения масштаба графика он не потеряет и не изменит своих свойств.
Координаты точки и отрезка
Когда на уроке дается математическая задача, в ней могут содержаться параметры различных геометрических фигур как в виде длин сторон, периметра, площади, так и в виде координат. В этом случае может потребоваться как построить фигуру, так и получить какие-то данные, связанные с ней. Возникает вопрос: как найти на координатной прямой требуемую информацию? И как построить фигуру?
Например, речь идёт о точке. Тогда в условии задачи будет фигурировать заглавная буква, а в скобках будут стоять несколько цифр, чаще всего две (это значит, считать мы будем в двухмерном пространстве). Если в скобках три числа, записанные через точку с запятой или через запятую, то это трехмерное пространство.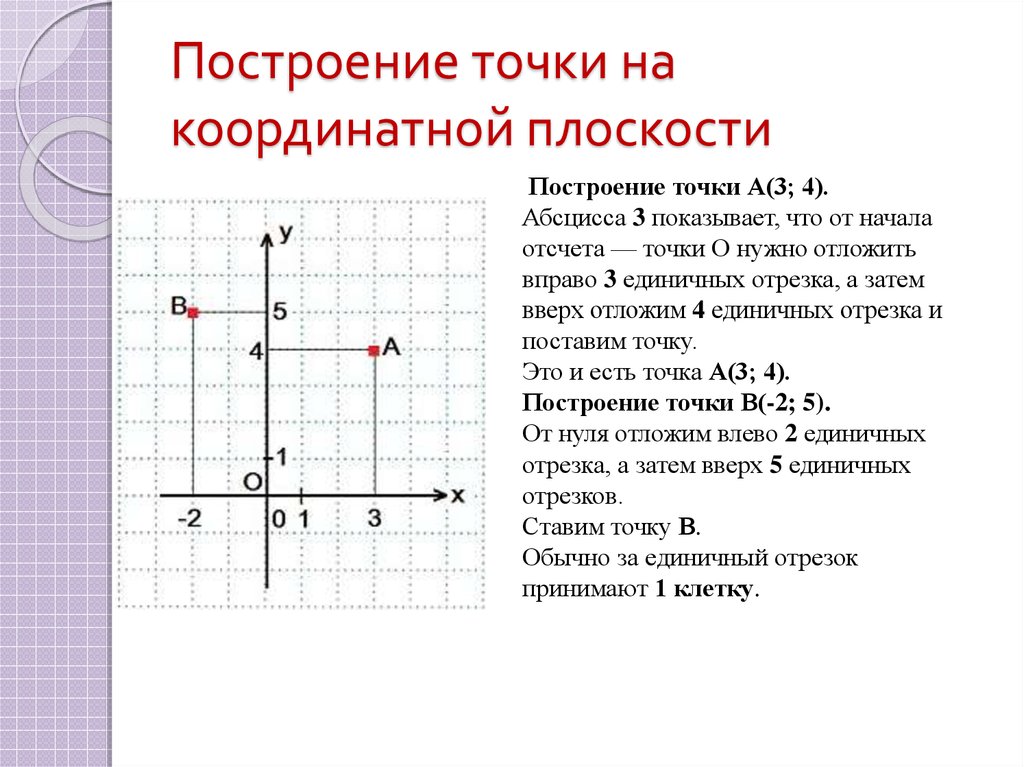
Каждое из значений — это координата на соответствующей оси: сначала по горизонтальной (X), затем — по вертикальной (Y).
Помните, как построить отрезок? Вы проходили это на геометрии. Если есть две точки, то между ними можно провести прямую. Их-то координаты и указываются в скобках, если в задаче фигурирует отрезок. Например: A(15, 13) — B(1, 4). Чтобы построить такую прямую, нужно на координатной плоскости найти и отметить точки, а затем их соединить. Вот и всё!
А любые многоугольники, как вы знаете, можно нарисовать с помощью отрезков. Задача решена.
Расчёты
Допустим, есть некоторый объект, положение которого по оси X характеризуется двумя числами: начинается он в точке с координатой (-3) и заканчивается в (+2). Если мы хотим узнать длину этого предмета, то должны вычесть из большего числа меньшее. Обратите внимание, что отрицательное число поглощает знак вычитания, потому что «минус на минус даёт плюс». Итак, мы складываем (2+3) и получаем 5. Это и есть требуемый результат.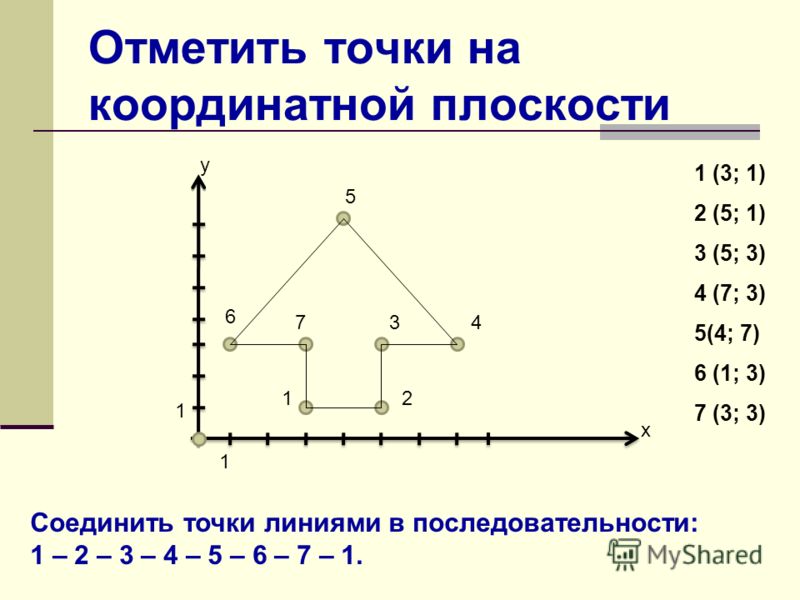
Другой пример: нам дана конечная точка и длина объекта, но не дана начальная (и требуется её найти). Пусть положение известной точки будет (6), а размер изучаемого предмета — (4). Вычитая длину из конечной координаты, мы получим ответ. Итого: (6 — 4) = 2.
Отрицательные числа
Нередко требуется на практике работать с отрицательными значениями. В этом случае мы будем уходить по оси координат влево. Например, объект высотой 3 сантиметра плавает в воде. На треть он погружен в жидкость, на две трети находится на воздухе. Тогда, выбрав в качестве оси поверхность воды, мы с помощью простейших арифметических вычислений получаем два числа: верхняя точка объекта имеет координату (+2), а нижняя — (-1) сантиметр.
Нетрудно заметить, что в случае с плоскостью у нас образуется четыре четверти координатной прямой. Каждая из них имеет свой номер. В первой (верхней правой) части будут располагаться точки, имеющие две положительные координаты, во второй — слева сверху — значения по оси «икс» будут отрицательные, а по «игрек» — положительные.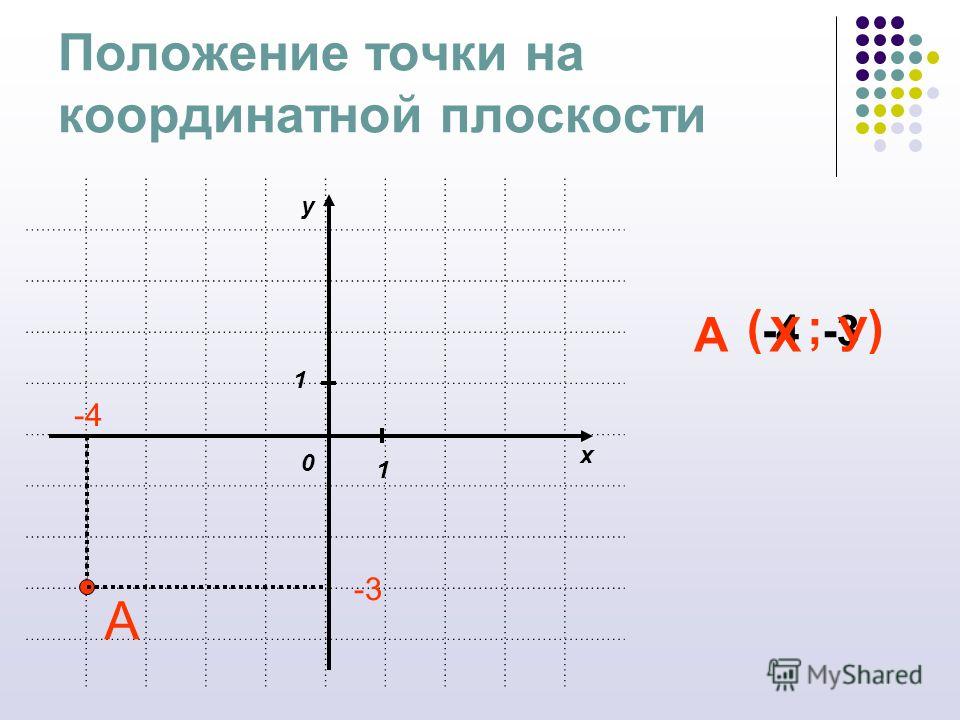
Третья и четвертая отсчитываются дальше против часовой стрелки.
Важное свойство
Вы знаете, что прямую можно представить как бесконечное множество точек. Мы можем просмотреть сколь угодно внимательно любое количество значений в каждую сторону оси, но не встретим повторяющихся. Это кажется наивным и понятным, но проистекает то утверждение из важного факта: каждому числу соответствует одна и только одна точка на координатной прямой.
Заключение
Помните, что любые оси, фигуры и по возможности графики необходимо строить по линейке. Единицы измерений были придуманы человеком не случайно — допустив погрешность при черчении, вы рискуете увидеть уже не то изображение, которое должно было получиться.
Будьте внимательны и аккуратны в построении графиков и вычислениях. Как и любая наука, изучаемая в школе, математика любит точность. Приложите немного старания, и хорошие оценки не заставят себя долго ждать.
Так единичный отрезок и его десятая, сотая и так далее доли позволяют нам попасть в точки координатной прямой, которым будут соответствовать конечные десятичные дроби (как в предыдущем примере).
Однако на координатной прямой существуют точки, в которые мы не можем попасть, но к которым мы можем подойти сколь угодно близко, использую все меньшие и меньшие до бесконечно малой доли единичного отрезка. Этим точкам соответствуют бесконечные периодические и непериодические десятичные дроби. Приведем несколько примеров. Одной из таких точек на координатной прямой соответствует число 3,711711711…=3,(711)
. Чтобы подойти к этой точке нужно отложить 3
единичных отрезка, 7
его десятых долей, 1
сотую долю, 1
тысячную, 7
десятитысячных долей, 1
стотысячную, 1
миллионную долю единичного отрезка и так далее. А еще одной точке координатной прямой отвечает пи (π=3,141592…
).
Так как элементами множества действительных чисел являются все числа, которые можно записать в виде конечных и бесконечных десятичных дробей, то вся вышеизложенная в этом пункте информация позволяет утверждать, что каждой точке координатной прямой мы поставили в соответствие конкретное действительное число, при этом понятно, что разным точкам соответствуют разные действительные числа.
Также достаточно очевидно, что это соответствие является взаимно однозначным. То есть, мы можем указанной точке на координатной прямой поставить в соответствие действительное число, но мы также можем по данному действительному числу указать конкретную точку на координатной прямой, которой отвечает данное действительное число. Для этого нам придется отложить от начала отсчета в нужном направлении определенное количество единичных отрезков, а также десятых, сотых и так далее долей единичного отрезка. Например, числу 703,405 отвечает точка на координатной прямой, в которую из начала отсчета можно попасть, отложив в положительном направлении 703 единичных отрезка, 4 отрезка, составляющих десятую долю единичного, и 5 отрезков, составляющих тысячную долю единичного.
Итак, каждой точке на координатной прямой отвечает действительное число, и каждое действительное число имеет свое место в виде точки на координатной прямой. Вот почему координатную прямую очень часто называют числовой прямой .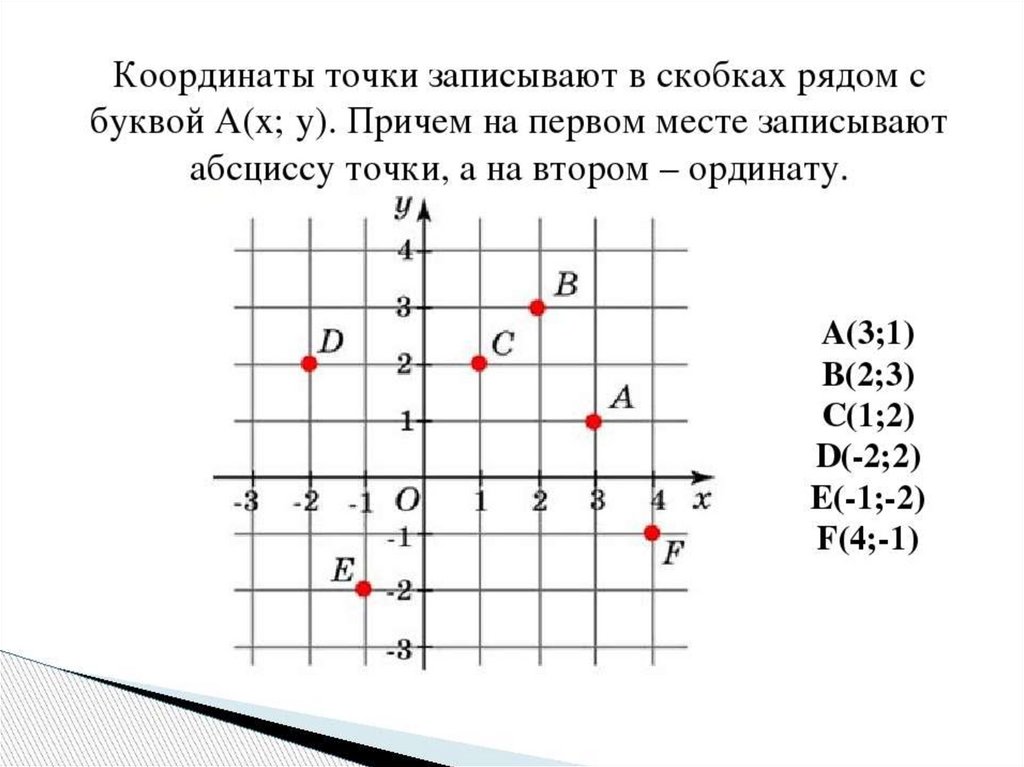
Координаты точек на координатной прямой
Число, соответствующее точке на координатной прямой, называется координатой этой точки .
В предыдущем пункте мы сказали, что каждому действительному числу соответствует единственная точка на координатной прямой, поэтому, координата точки однозначно определяет положение этой точки на координатной прямой. Иными словами, координата точки однозначно задает эту точку на координатной прямой. С другой стороны каждой точке на координатной прямой соответствует единственное действительное число – координата этой точки.
Осталось сказать лишь о принятых обозначениях. Координату точки записывают в круглых скобках справа от буквы, которой обозначена точка. Например, если точка М имеет координату -6 , то можно записать М(-6) , а запись вида означает, что точка М на координатной прямой имеет координату .
Список литературы.
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика: учебник для 5 кл. общеобразовательных учреждений.
- Виленкин Н.Я. и др. Математика. 6 класс: учебник для общеобразовательных учреждений.
- Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 8 кл. общеобразовательных учреждений.
Сырники с зеленью, сыром и чесноком жареные
Сырники с зеленью, сыром и чесноком жареные
№ 1428 Математика 6 класс Виленкин. Помогите отметить точки на координатной плоскости – Рамблер/класс
№ 1428 Математика 6 класс Виленкин. Помогите отметить точки на координатной плоскости – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Отметьте на координатной плоскости точки А (-2; 4), В (-4;-5),
С(8; 0), D (-4; 4).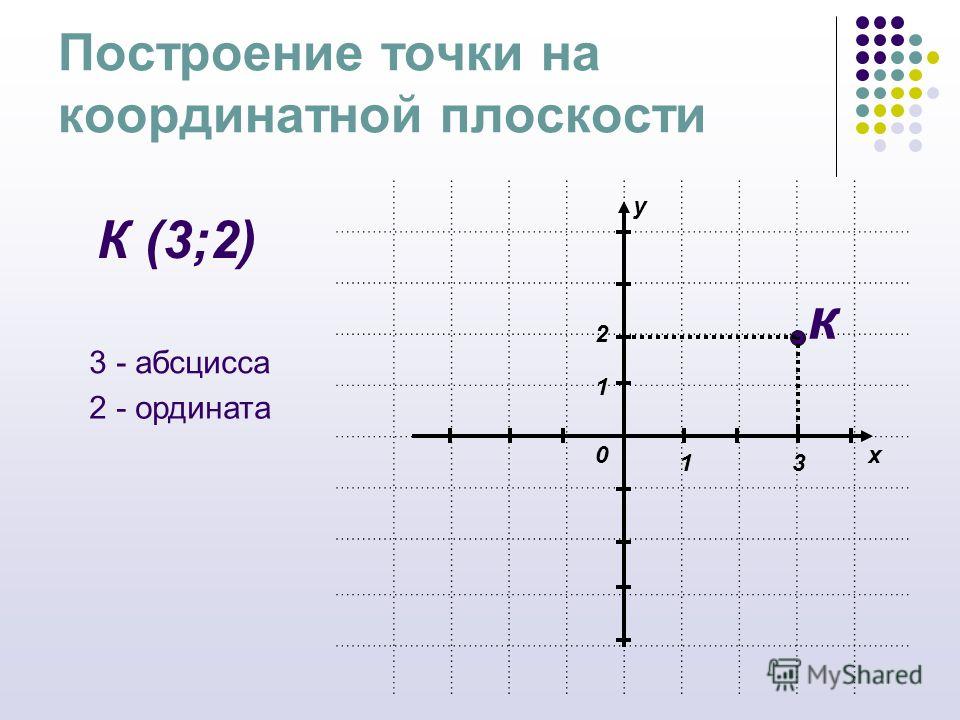
Найдите координаты точки пересечения прямых АВ и СD.
ответы
Точка пересечения прямх АВ и СDимеет координаты приблизительно равные (-2,2; 3,3).
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Психология
3 класс
5 класс
Репетитор
похожие вопросы 5
Приветик! Кто решил? № 411 Математика 6 класс Виленкин.
Выполните вычисления с помощью микрокалькулятора и резуль-
тат округлите до тысячных:
3,281 ∙ 0,57 + 4,356 ∙ 0,278 — 13,758 (Подробнее…)
ГДЗМатематика6 классВиленкин Н.Я.
678. Изобразите этот круг, проведите диаметр, радиус и укажите их длины. 6 класс Мордкович математика ГДЗ
678.
Площадь круга равна:
а) 28,26 см2; б) 113,04 см2; в) 0,5024 дм2; г) 78,5 см2.
Изобразите этот круг, (Подробнее…)
ГДЗМордкович А.Г.Алгебра6 класс
Помогите установить соответствие между неравенствами. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№17. Под руководством Ященко И.В.
Здравствуйте! Помогите установить соответствие между неравенствами и их решениями: (Подробнее…)
ЕГЭЭкзаменыМатематикаЯщенко И.В.
Помогите выбрать утверждения. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№18. Под руководством Ященко И.В.
Здравствуйте! Перед волейбольным турниром измерили рост игроков волейбольной команды города N. Оказалось, что рост каждого из (Подробнее…)
ЕГЭЭкзаменыМатематикаЯщенко И.В.
11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.
11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
точек графика в системе координат
> … Математика > Введение в графики > Точки графика в системе координат
Этот урок знакомит нас с системой координат. Есть много примеров систем координат, как показано выше. Стандартный способ представления систем координат находится на Декартова система координат . В декартовой координатной плоскости все основано на двух числовых линиях: одной горизонтальной (она лежит ровно, как горизонт), а другой вертикальной (идет вверх и вниз). Горизонтальная ось обозначена как ось x, а вертикальная — как ось y. Когда мы описываем место на плоскости, мы описываем его с помощью x и y подобно тому, как мы обозначаем ячейки в Excel или точки на карте. Пара чисел (x, y), представляющая точку, называется координатой, а x и y — парой координат. Точно так же, как x предшествует y в алфавите, x всегда предшествует y в координатной точке. Главное помнить, что значение x — это число, соответствующее горизонтальной оси, а значение y — число, соответствующее вертикальной оси.
Следующее видео покажет, как это работает на изображении декартовой плоскости.
Отображение точек в системе координат
Источник видео (04:48 мин.) | Расшифровка
Теперь, когда мы знаем, как читать координаты, мы научимся наносить точку в декартовой системе координат.
Практика построения точек в декартовой системе координат
Источник видео (02:19 мин.) | Стенограмма
Система координат — это любая система, в которой мы можем описать местоположение с помощью координат, как показано во введении к уроку. Декартова плоскость — это особая система координат с осями x и y.
Помните, что ось X — это горизонтальная линия, а ось Y — вертикальная линия. Кроме того, мы помечаем местоположение или точку координатой, которая сначала имеет метку x, а затем метку y: (x, y).
Словарь
Ось (произносится со звуком «есть», как в слове «история») = единственное число для одной оси. (Пример: одна ось горизонтальна.)
Оси (произносится со звуком «ээз», как в слове «заморозить») = множественное число для более чем одной оси. (Пример: для системы координат необходимы обе оси.)
Дополнительные ресурсы
- Академия Хана: введение в координатную плоскость (06:47 мин.; расшифровка)
- Академия Хана: построение точки (упорядоченная пара) (02:07 мин.; расшифровка)
- Академия Хана: точки на плоскости Примеры координатной плоскости (06:49 мин; расшифровка)
Практические задачи
1. Используйте следующий график декартовой системы координат, чтобы ответить на этот вопрос.
Для каждой из следующих пар координат укажите букву соответствующей точки на графике.
- \(\влево ( 3,0 \вправо )\) (
Решение
x
Решение: Ответ: D
Детали:
Помните, что каждая точка записывается в виде \((x,y)\), где координата x записывается первой, а координата y написано второе. Мы начнем с координаты x \(({\color{Red}3},0)\). Чтобы найти положение точки \(({\color{Red}3},0)\) мы находим вертикальную линию, которая пересекает \({\color{Red}3}\) на оси x.Далее мы смотрим на нашу координату y \((3,{\color{Red}0})\). Поскольку координата y представляет собой \({\color{Red}0}\), мы находим горизонтальную линию, которая пересекает ось y в точке \({\color{Red}0}\).
Место пересечения этих двух линий является точкой \((3,0)\), поэтому ответ будет D .
) - \(\влево(4, 3\вправо)\) (
Решение
x
Решение:
)
Ответ: C - \(\влево ( 3,-4 \вправо )\) (
Решение
x
Решение: Ответ: B
Детали:
Каждая точка записывается в виде (x,y), где координата x записывается первой, а координата y — второй. Мы начнем с координаты x \(({\color{Red}3},−4)\). Чтобы найти положение точки \(({\color{Red}3},−4)\) мы находим вертикальную линию, которая пересекает ось x в точке 3.Далее мы смотрим на нашу координату y \((3,{\color{Red}−4})\). Поскольку координата y представляет собой \({\color{Red}−4}\), мы находим горизонтальную линию, которая пересекает ось y в точке \({\color{Red}−4}\).
Место, где пересекаются эти две прямые, является точкой \((3,−4)\), поэтому ответ будет B .
) - \(\влево ( 4,-3 \вправо )\) (
Решение
x
Решение:
)
Ответ: F
2. Используйте следующий график декартовой системы координат, чтобы ответить на этот вопрос.
Для каждой из следующих букв укажите соответствующую пару координат.
- А (
Решение
x
Решение:
)
\((2,5)\) - С (
Решение
x
Решение:
)
\((-2,5)\) - Б (
Решение
x
Решение:
)
\((2,-5)\) - Э (
Решение
x
Решение:
)
\((-2,0)\)
Нужна дополнительная помощь?
- Изучите другие уроки математики в Ресурсном центре.
- Посетите онлайн-ресурсы для обучения в Ресурсном центре.
- Свяжитесь со своим инструктором.
- Если вам все еще нужна помощь, назначьте репетитора.
Знать, как нанести точку на плоскости, если известны ее координаты
- Автор Прия_Сингх
- Последнее изменение 23-11-2022
Построение точки на плоскости, если ее координаты заданы: Координатная плоскость — это двумерная плоскость, образованная пересечением вертикальной линии, известной как ось \(y-\), и горизонтальной линии, известной как \(x -\)ось. Это перпендикулярные линии, которые пересекают друг друга в точке, известной как начало координат.
Плоскость называется декартовой плоскостью, а линии известны как оси координат. Оси координат делят плоскость на четыре части, называемые квадрантами. В этой статье мы узнаем, как построить точку на декартовой плоскости.
Координатная плоскость
Координатная плоскость представляет собой двумерную поверхность, разделенную двумя линиями, пересекающимися друг с другом под прямым углом. Горизонтальная линия называется осью \(x-\), а вертикальная линия называется осью \(y-\). Эти две оси пересекаются в точке, называемой началом координат.
Числа на координатной сетке используются для определения местоположения точек. Координатную плоскость можно использовать для построения точек, линий и многого другого. Он действует как карта и дает точные указания из одной точки в другую.
Что такое точка на координатной плоскости?
Каждая точка на координатной плоскости представлена упорядоченной парой \((x, y),\), записанной в скобках, соответствующей координате \(x-\) и координате \(y-\). Эти координаты могут быть положительными, нулевыми или отрицательными, в зависимости от положения точки в соответствующих квадрантах.
Как найти точки на координатной плоскости?
Чтобы найти точку на координатной плоскости, необходимо выполнить следующие шаги:
- Во-первых, вам нужно найти точку.
- Затем вам нужно найти квадрант, глядя на символы его координат \(x\) и \(y\).
- Координата \(x-\) или абсцисса точки затем определяется путем считывания количества единиц справа/слева от начала координат по оси \(x-\).
- Наконец, вам нужно найти координату \(y-\) или точку, считывая количество единиц выше или ниже начала координат вдоль оси \(y-\), параллельной ей.
Пример: Теперь посмотрите на приведенную ниже диаграмму:
- Сначала обратите внимание на красную точку на графике координат.
- Размещается во втором квадранте.
- Здесь точка удалена на \(3\) единиц от начала координат по отрицательной оси \(x-\).
- И точка находится на расстоянии \(2\) единиц от начала координат параллельно положительной оси \(y-\).
Следовательно, точка на данном графике имеет координаты \((-3, 2).\)
Квадрант
Квадрантом можно назвать область или часть декартовой плоскости, полученную, когда две оси пересекают друг друга под прямым углом. Используется для определения положения точки на плоскости.
Четыре квадранта: Оси \(x-\) и \(y-\) делят плоскость на четыре квадранта графика:
- Верхний правый угол плоскости является первым квадрантом. В этом квадранте обе координаты \(x\) и \(y-\) будут положительными.
- Верхний левый угол плоскости — второй квадрант. В этом квадранте координата \(x-\)отрицательна, а координата \(y-\) положительна.
- Нижний левый угол плоскости — третий квадрант. В этом квадранте координаты \(x\) и \(y-\) отрицательны.
- Правый нижний угол плоскости — четвертый квадрант. В этом квадранте координата \(x-\) положительна, а координата \(y-\) отрицательна.
Квадранты на координатной плоскости
Квадрант можно определить как область или часть декартовой плоскости или координатной плоскости, полученной при перпендикулярном пересечении двух осей.
- Первый квадрант равен \(x>0, y>0\)
- Второй квадрант равен \(x<0, y>0\)
- Третий квадрант равен \(x<0, y<0\)
- Четвертый квадрант: \(x>0, y<0\)
Как записывать точки координат?
Координаты всегда пишутся в скобках, а два числа разделяются запятой. Координаты — это упорядоченные пары чисел; первое число показывает точку на оси \(x-\), называемую абсциссой, а второе — точку на оси \(y-\), называемую ординатой.
Нанесение точки на координатную плоскость: Мы увидим, как начертить точку на координатной плоскости на примере:
Пример: Нанесем точку \(P=(5, 6.)\) на Нанесите точку на координатную плоскость, вы должны выполнить следующие шаги:
- Вы должны нарисовать две перпендикулярные линии, ось \(x-\) и ось \(y-\).
- От исходной точки вы должны переместиться на 5 единиц вправо по положительной оси \(x-\).
- Теперь вам нужно переместиться на \(6\) единиц вверх, параллельно положительной оси \(y-\)
- Здесь вы отмечаете точку пересечения и отмечаете ее как \((5, 6).\)
Обратите внимание, что точка \(P\) находится в первом квадранте. Кроме того, это называется положительной координатной плоскостью, так как значение обеих координат для любой точки в этом квадранте будет положительным.
Использование точки на координатной плоскости
Вы можете использовать координатную плоскость
а) Чтобы найти или нанести точку и нарисовать отрезок, треугольник, четырехугольник и другие геометрические фигуры. Их отражение относительно осей \(x-\) и \(y-\) и начала координат также может быть локализовано.
б) Графики алгебраических уравнений можно рисовать на координатной плоскости.
в) В более крупном масштабе понятие координатной плоскости можно применять для рисования карт стран, континентов и всего мира. Он имеет огромное применение в географии.
Решенные примеры
Q.1. Найдите точки \((5,0),(0,5),(2,5),(5,2),(-3,5),(-3,-5),(5,- 3)\) и \(\left( {6,1} \right)\).
Ответ: Беря \({\rm{1}}\,{\rm{см = 1}}\,{\rm{единица,}}\), мы проводим ось \(x-\) и \(y- \)ось. Точки показывают положение точек на данной диаграмме.
Q. 2. Нанесите следующие точки на декартовой плоскости (используйте шкалу: \(x — {\rm{ось}} = 1\;{\rm{см}}\) и \(y — {\rm{ось} } = 1\;{\rm{см}}\) )
| \(х\) | \(-3\) | \(0\) | \(-1 \) | \(4\) | \(2\) 9{{\rm{th}}}}\) квадрант. Q.3. Найдите координаты \((3, 5)\) и \((5, -4)\) в декартовой системе координат. Q.4. Найдите заданную точку на координатной плоскости: \((-9, 4)\) Q.5. Найдите заданную точку на координатной плоскости: \((7, -8)\) РезюмеВ данной статье мы рассмотрели координатные плоскости и точку на координатной плоскости с примерами. Затем мы поговорили о том, как найти или локализовать точку на координатной плоскости. Мы рассмотрели, как написать точку на координатной плоскости, а затем использовали изображение точки на координатной плоскости. Наконец, мы предоставили решенные примеры вместе с несколькими часто задаваемыми вопросами. Изучите концепции декартовой системы Часто задаваемые вопросы (FAQ) Q.1. Как изображается точка на плоскости? Q.2. Как найти точку на координатной плоскости? Q.3. Каково расстояние между двумя точками? Q.4. Как изобразить точку с рациональными координатами на координатной плоскости? Q.5. Как вы наносите упорядоченные пары на координатную плоскость? |