Как перевести углы в градусы? – Обзоры Вики
Чтобы преобразовать радианы в градусы, умножьте радиан на 180 / π. Таким образом, формула имеет вид: Угол в радианах x 180 / π = Угол в градусах.
Отсюда, что такое 1 степень 54? [Проверено экспертами] 1 градус 54′ = 114 ‘ Как ? — школьные Знания.
Кроме того, как вы конвертируете 1 в радианы? 1 радиан примерно равен 57.2958°. Рассмотрим полукруг с радианами, равными 180°. Если вы хотите преобразовать градус или угол в радианы, просто умножьте угол на а затем разделите его на 180.
Как перевести градусы в радианы в минуту? Чтобы преобразовать градусы в радианы, сначала преобразуйте количество градусов, минут и секунд в десятичную форму. Разделите количество минут на 60 и прибавьте к количеству градусов.. Так, например, 12 ° 28 ′ равно 12 + 28/60, что равно 12. 467 °. Затем умножьте на π и разделите на 180, чтобы получить угол в радианах.
467 °. Затем умножьте на π и разделите на 180, чтобы получить угол в радианах.
Как найти угол в один градус?
1° = (π)/180 радиан. Это дает нам формулу для преобразования градусов в радианы и наоборот. Таким образом, чтобы преобразовать градусы в радианы, используйте эту формулу = Градусная мера × (π/180°). 1° = (π)/180 радиан = 0.017453 радиан.
Как вы конвертируете десятичные градусы в градусы, минуты, секунды в Excel? Просто изменить текст в скобках ([Lat/Long Cell]), чтобы указать на ячейку DD, которую вы хотите преобразовать в DMS. Если вы хотите другое количество знаков после запятой для секунд, добавьте нужное количество нулей после запятой в части «0», а также установите «00.00» для количества знаков.
Как перевести десятичные градусы в градусы минуты секунды на калькуляторе?
com/embed/eKJjaHz479o» frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″>Также Почему пи 180 градусов? Таким образом, пи радианы составляют полукруг. То, что он совпадает на 180 градусов, это только потому, что кто-то решил, что 360 — это хорошее количество частей, на которые можно разрезать круг. (Очевидно, вавилонская математика была источником этого соглашения: каков периметр единичного круга? Единичный круг означает круг с радиусом в 1 единицу.
Какой угол в радианах равен 270?
Объяснение: если 1 градус равен π180 радиан, то 270 градусов будут равны 270, умноженным на π180 радиан.
Что такое 30 градусов в радианах? Градусы в радианы диаграмма
| Угол в градусах | Угол в радианах |
|---|---|
| 0° | 0 |
| 30° | π / 6 = 0.524 рад |
| 45° | π / 4 = 0.785 рад |
| 60° | π / 3 = 1.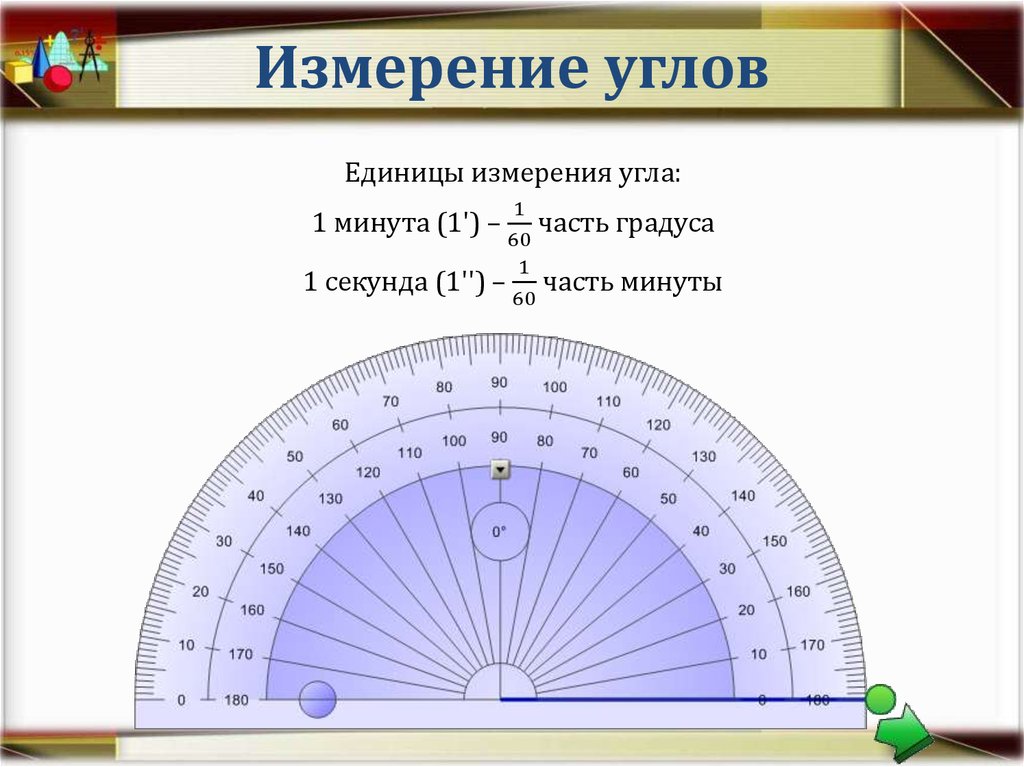 047 рад 047 рад |
Чему равен радиан 40 мин 20?
Следовательно, 40 ° 20 ′ равно (121/540) π радиан.
Как перевести градусы во время?
Преобразование градусов в градусы-минуты-секунды может быть выполнено с помощью коэффициента преобразования 60. Это связано с тем, что: 1 градус = 60 минут (60′) 1 минута = 60 секунд (60 дюймов)
Сколько градусов в 60 минутах? Отвечать: Один градус делится на 60 угловых минут. и одна минута разделена на 60 угловых секунд. Использование градусов-минут-секунд также признано как обозначение DMS. В часах, чтобы полностью завершить 24 часа, часам требуется полные 360∘ вращение дважды.
Сколько длится угловая секунда? Угловая секунда (обозначается символом «) — это угловая единица измерения, равная 1/3600 градуса или 1/60 угловой минуты. В радиане также 206,264.5 дюйма, так что 1 дюйм = 4.848 × 10–6 радиан.
Как найти степень по физике?
Образец вопроса
- Примените теорему Пифагора, чтобы найти величину.
 Подставьте числа, чтобы получить 5.1.
Подставьте числа, чтобы получить 5.1. - Примените уравнение тета = загар – 1 (y/x), чтобы найти угол. Подставьте числа, чтобы получить загар – 1 (5.0/1.0) = 79 градусов.
Как перевести загар в 40 градусов? Значение тангенса 40 градусов равно 0.8390996. . .. Тангенс 40 градусов в радианах записывается как тангенс (40° × π/180°), т. е. тангенс (2π/9) или тангенс (0.698131…).
Как получить градусы на калькуляторе?
Как получить символ градуса на TI 84 Plus CE? Введите количество градусов и нажмите [2nd] [APPS] [1]. для вставки символа градуса.
Как вы получаете дипломы на TI 84 Plus CE?
Как вы вводите символ градуса в Excel? Метод №1: Используйте библиотеку символов, чтобы получить символ градуса
- В ячейке введите «180» (без кавычек).

- Затем перейдите на вкладку «Вставка» и щелкните значок «Символ» (крайний справа). …
- В раскрывающемся списке вверху выберите шрифт Symbol. …
- Прокрутите вниз и выберите символ градуса.
- Щелкните Вставить.
Как преобразовать числа в градусы в Excel?
Функция Excel ГРАДУСЫ преобразует углы (выраженные в радианах) в градусы. Например, формула =ГРАДУСЫ (PI()) возвращает 180. angle — угол в радианах, который вы хотите преобразовать в градусы.
…
Преобразование градусов в радианы вручную.
| Формула | Степени |
|---|---|
| = PI () | 180 |
| = 90 * PI () / 180 | 90 |
| = 45 * PI () / 180 | 45 |
| = 30 * PI () / 180 | 30 |
Как переводить из радиан в градусы. Как перевести радианы в градусы
Люди в математической науке довольно часто сталкиваются с такой задачей, как перевод градусов в радианы или наоборот. Выполнить данную задачу довольно просто и для этого не нужно иметь глубокие познания в различных прикладных науках или математике. Итак, для начала необходимо разобраться с этими величинами измерения. Градус и радиан – это основные единицы, которыми измеряются плоские углы в математике и физике. Ещё данные единицы используют в картографии для определения координат в любой точке земного шара.
Выполнить данную задачу довольно просто и для этого не нужно иметь глубокие познания в различных прикладных науках или математике. Итак, для начала необходимо разобраться с этими величинами измерения. Градус и радиан – это основные единицы, которыми измеряются плоские углы в математике и физике. Ещё данные единицы используют в картографии для определения координат в любой точке земного шара.
Эти величины измерения обозначаются следующим образом:
- рад – радиан
- градус — º
Как перевести градусы в радианы
Для начала, чтобы стала понятной формула перевода градусов в радианы, нужно научиться переводить угол в радианы и радианы в угол:
- 1 рад = (180/π)ºπ 57,295779513, где известно, что π = 3,14
- 1° = (π/180) рад π 0,017453293 рад
По вышеизложенным формулам сразу же становиться ясно, что π рад = 180°, именно из них и берут своё начало понятные всем и простые формулы для перевода величин измерения. Сейчас рассмотрим основные формулы, которые используются при переводе:
1. Градусы в радианы
Градусы в радианы
Zº=Z рад × (180/π), где Zº — угол в градусах, а Z рад – угол в радианах, π = 3,14
2. Радианы в градусы
Z рад = Z° × (π/180)
Теперь рассмотрим пример, чтобы стало понятней, как пользоваться вышеприведёнными формулами на практике. Для этого возьмём два угла 20º и 100º:
1. Перевод градусов в радианы
- 20º = 20 рад × (π/180) π 0,35 рад
- 100º = 100 рад × (180/π) π 1, 7453 рад
2. Перевод радиан в градусы
- 20 рад = 20º × (180/π) π 1146,15, где π = 3,14
- 100 рад = 100° × (180/π) π 5729, 577, где π = 3,14
Рассмотрев формулы для перевода величин измерения, становиться понятно, что справиться с поставленой задачей довольно просто. Для тех людей, которые самостоятельно не хотят проводить расчеты, в интернете существует множество сайтов, на которых с помощью он-лайн калькуляторов можно перевести градусы в радианы или наоборот, их использование значительно облегчит вам выполнение различных задач по тригонометрии.
Необходимость в измерении углов появилась у людей с тех пор, как цивилизация достигла минимального технического уровня. Всем известна феноменальная точность соблюдения наклона и ориентации по странам света, обеспеченная строителями египетских пирамид. Современную градусную меру углов, как сейчас считается, изобрели древние аккадцы.
Что такое градусы?
Градус — общепринятая единица измерения углов. В полной окружности 360 градусов. Причина выбора именно этого числа неизвестна. Вероятно, аккадцы разделили окружность на сектора, используя угол равностороннего треугольника, а затем полученные сегменты снова разделили на 60 частей согласно своей системе счисления. Градус тоже делится на 60 минут, а минуты — на 60 секунд. Общепринятыми обозначениями являются:
° — угловые градусы
’ — минуты,
’’ — секунды.
За тысячелетия градусная мера углов прочно вошла во многие сферы человеческой деятельности. Она и сейчас незаменима во всех областях науки и техники — от картографии до расчета орбит искусственных спутников Земли.
Что такое радианы?
Архимеду приписывается открытие постоянства соотношения длины окружности и ее диаметра. Мы называем его числом π. Оно иррационально, то есть не может быть выражено в виде обычной или периодической дроби. Чаще всего используется значение числа π с точностью до двух знаков после запятой — 3,14. Длина окружности L с радиусом R легко вычисляется по формуле: L=2πR.
Окружность радиуса R=1 имеет длину 2π. Это соотношение используется в геометрии как формулировка радианной меры угла.
По определению, радиан — угол с вершиной в центре окружности, опирающийся на дугу с длиной, равной радиусу окружности. Международное обозначение радиана — rad, отечественное — рад. Размерности он не имеет.
Дуга окружности с радиусом R с угловой величиной α радиан, имеет длину α * R.
Зачем понадобилось вводить новую единицу измерения угла?
Развитие науки и техники привело к появлению тригонометрии и математического анализа, необходимых для точных расчетов механических и оптических устройств. Одной из его задач является измерение длины кривой линии. Самый распространенный случай — определение длины дуги окружности. Использование для этой цели градусной меры углов крайне неудобно. Идея сопоставить длину дуги с радиусом окружности возникала у многих математиков, но сам термин «радиан» был введен в научный обиход только во второй половине XIX века. Сейчас все тригонометрические функции в математическом анализе по умолчанию используют радианную меру угла.
Одной из его задач является измерение длины кривой линии. Самый распространенный случай — определение длины дуги окружности. Использование для этой цели градусной меры углов крайне неудобно. Идея сопоставить длину дуги с радиусом окружности возникала у многих математиков, но сам термин «радиан» был введен в научный обиход только во второй половине XIX века. Сейчас все тригонометрические функции в математическом анализе по умолчанию используют радианную меру угла.
Как переводить градусы в радианы
Из формулы длины окружности вытекает, что в нее укладывается 2π радиусов. Отсюда вытекает, что: 1⁰=2π/360= π/180 рад.
И простая формула перевода из радианов в градусы: 1 рад = 180/π.
Пусть мы имеем угол в N градусов. Тогда формула для перевода из градусов в радианы будет такой: α(радиан) = N/(180/π) = N*π/180.
Остались вопросы?
Ответы на них можно найти , где подробно разъяснены понятия длины окружности, радианной меры углов и на конкретных примерах показан перевод градусов в радианы. Знания упомянутого крайне важны для понимания математики, без которой невозможно существование современной цивилизации.
Знания упомянутого крайне важны для понимания математики, без которой невозможно существование современной цивилизации.
Градусная мера угла. Радианная мера угла. Перевод градусов в радианы и обратно.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
И для тех, кто «очень даже…»)
В предыдущем уроке мы освоили отсчёт углов на тригонометрическом круге. Узнали, как отсчитывать положительные и отрицательные углы. Осознали, как нарисовать угол больше 360 градусов. Пришла пора разобраться с измерением углов. Особенно с числом «Пи», которое так и норовит запутать нас в хитрых заданиях, да…
Стандартные задания по тригонометрии с числом «Пи» решаются неплохо. Зрительная память выручает. А вот любое отклонение от шаблона — валит наповал! Чтобы не свалиться — понимать надо. Что мы с успехом сейчас и сделаем. В смысле — всё поймём!
Итак, в чём считаются углы? В школьном курсе тригонометрии используются две меры: градусная мера угла и радианная мера угла .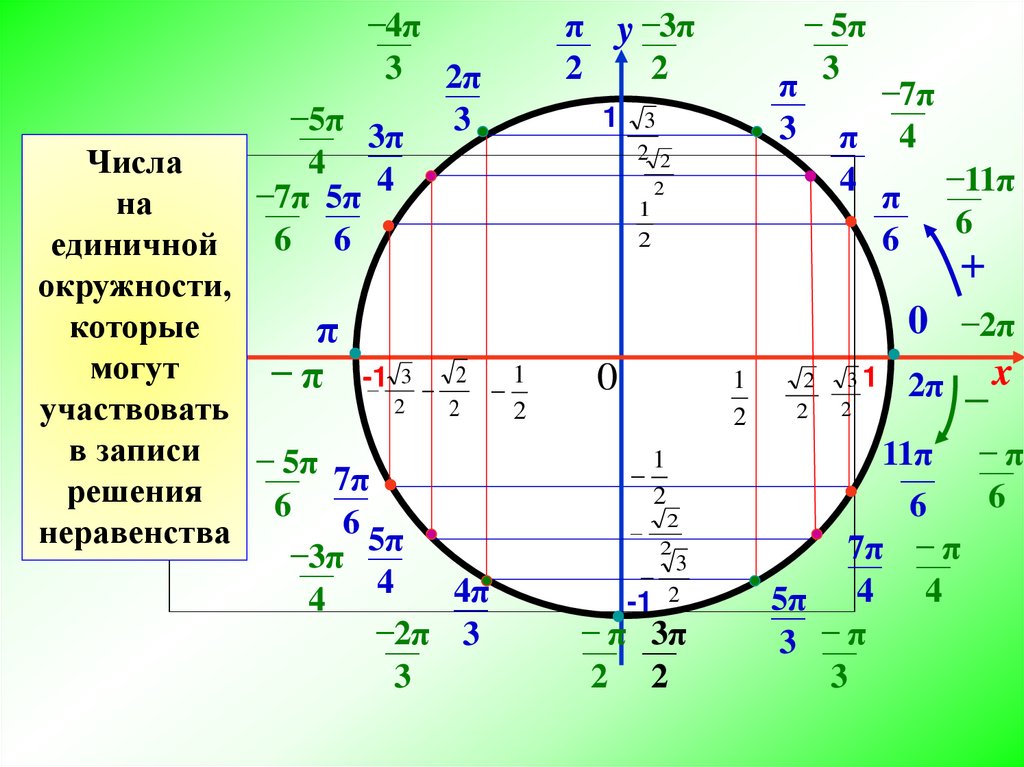 Разберём эти меры. Без этого в тригонометрии — никуда.
Разберём эти меры. Без этого в тригонометрии — никуда.
Градусная мера угла.
К градусам мы как-то привыкли. Геометрию худо-бедно проходили… Да и в жизни частенько встречаемся с фразой «повернул на 180 градусов», например. Градус, короче, штука простая…
Да? Ответьте мне тогда, что такое градус? Что, не получается с ходу? То-то…
Градусы придумали в Древнем Вавилоне. Давненько это было… Веков 40 назад… И придумали просто. Взяли и разбили окружность на 360 равных частей. 1 градус — это 1/360 часть окружности. И всё. Могли разбить на 100 частей. Или на 1000. Но разбили на 360. Кстати, почему именно на 360? Чем 360 лучше 100? 100, вроде, как-то ровнее… Попробуйте ответить на этот вопрос. Или слабо против Древнего Вавилона?
Где-то в то же время, в Древнем Египте мучились другим вопросом. Во сколько раз длина окружности больше длины её диаметра? И так измеряли, и этак… Всё получалось немного больше трёх. Но как-то лохмато получалось, неровно.
Это и есть число «Пи». Вот уж лохматое, так лохматое. После запятой — бесконечное число цифр без всякого порядка… Такие числа называются иррациональными. Это, кстати, и означает, что из равных кусочков окружности диаметр ровно не сложить. Никогда.
Для практического применения принято запоминать всего две цифры после запятой. Запоминаем:
Раз уж мы поняли, что длина окружности больше диаметра в «Пи» раз, имеет смысл запомнить формулу длины окружности:
Где L — длина окружности, а d — её диаметр.
В геометрии пригодится.
Для общего образования добавлю, что число «Пи» сидит не только в геометрии… В самых различных разделах математики, а особенно в теории вероятности, это число возникает постоянно! Само по себе.
Но вернёмся к градусам. Вы сообразили, почему в Древнем Вавилоне круг разбили на 360 равных частей? А не на 100, к примеру? Нет? Ну ладно. Выскажу версию. У древних вавилонян не спросишь… Для строительства, или, скажем, астрономии, круг удобно делить на равные части. А теперь прикиньте, на какие числа делится нацело 100, и на какие — 360? И в каком варианте этих делителей нацело — больше? Людям такое деление очень удобно. Но…
Как выяснилось много позже Древнего Вавилона, не всем нравятся градусы. Высшей математике они не нравятся… Высшая математика — дама серьёзная, по законам природы устроена. И эта дама заявляет: «Вы сегодня на 360 частей круг разбили, завтра на 100 разобьёте, послезавтра на 245… И что мне делать? Нет уж…» Пришлось послушаться. Природу не обманешь…
Пришлось ввести меру угла, не зависящую от человеческих придумок. Знакомьтесь — радиан!
Радианная мера угла.
Что такое радиан? В основе определения радиана — всё равно окружность. Угол в 1 радиан, это угол, который вырезает из окружности дугу, длина которой (L ) равна длине радиуса (R ). Смотрим картинки.
Угол в 1 радиан, это угол, который вырезает из окружности дугу, длина которой (L ) равна длине радиуса (R ). Смотрим картинки.
Маленький такой угол, почти и нет его… Наводим курсор на картинку (или коснёмся картинки на планшете) и видим примерно один радиан . L = R
Чувствуете разницу?
Один радиан много больше одного градуса. А во сколько раз?
Смотрим следующую картинку. На которой я нарисовал полукруг. Развёрнутый угол размером, естественно, в 180°.
А теперь я нарежу этот полукруг радианами! Наводим курсор на картинку и видим, что в 180° укладывается 3 с хвостиком радиана.
Кто угадает, чему равен этот хвостик!?
Да! Этот хвостик — 0,1415926…. Здравствуй, число «Пи», мы тебя ещё не забыли!
Действительно, в 180° градусах укладывается 3,1415926… радиан. Как вы сами понимаете, всё время писать 3,1415926… неудобно. Поэтому вместо этого бесконечного числа всегда пишут просто:
А вот в Интернете число
писать неудобно. .. Поэтому я в тексте пишу его по имени — «Пи». Не запутаетесь, поди?…
.. Поэтому я в тексте пишу его по имени — «Пи». Не запутаетесь, поди?…
Вот теперь совершенно осмысленно можно записать приближённое равенство:
Или точное равенство:
Определим, сколько градусов в одном радиане. Как? Легко! Если в 3,14 радианах 180° градусов, то в 1 радиане в 3,14 раз меньше! То есть, мы делим первое уравнение (формула — это тоже уравнение!) на 3,14:
Это соотношение полезно запомнить В одном радиане примерно 60°. В тригонометрии очень часто приходится прикидывать, оценивать ситуацию. Вот тут это знание очень помогает.
Но главное умение этой темы — перевод градусов в радианы и обратно.
Если угол задан в радианах с числом «Пи», всё очень просто. Мы знаем, что «Пи» радиан = 180°. Вот и подставляем вместо «Пи» радиан — 180°. Получаем угол в градусах. Сокращаем, что сокращается, и ответ готов. Например, нам нужно выяснить, сколько градусов в угле «Пи»/2 радиан ? Вот и пишем:
Или, более экзотическое выражение:
Легко, верно?
Обратный перевод чуть сложнее. Но не сильно. Если угол дан в градусах, мы должны сообразить, чему равен один градус в радианах, и умножить это число на количество градусов. Чему равен 1° в радианах?
Но не сильно. Если угол дан в градусах, мы должны сообразить, чему равен один градус в радианах, и умножить это число на количество градусов. Чему равен 1° в радианах?
Смотрим на формулу и соображаем, что если 180° = «Пи» радиан, то 1° в 180 раз меньше. Или, другими словами, делим уравнение (формула — это тоже уравнение!) на 180. Представлять «Пи» как 3,14 никакой нужды нет, его всё равно всегда буквой пишут. Получаем, что один градус равен:
Вот и всё. Умножаем число градусов на это значение и получаем угол в радианах. Например:
Или, аналогично:
Как видите, в неспешной беседе с лирическими отступлениями выяснилось, что радианы — это очень просто. Да и перевод без проблем… И «Пи» — вполне терпимая штука… Так откуда путаница!?
Вскрою тайну. Дело в том, что в тригонометрических функциях значок градусов — пишется. Всегда. Например, sin35°. Это синус 35 градусов . А значок радианов (рад ) — не пишется! Он подразумевается. То ли лень математиков обуяла, то ли ещё что… Но решили не писать. Если внутри синуса — котангенса нет никаких значков, то угол —
То ли лень математиков обуяла, то ли ещё что… Но решили не писать. Если внутри синуса — котангенса нет никаких значков, то угол —
Это и приводит к непоняткам… Человек видит «Пи» и считает, что это 180°. Всегда и везде. Это, кстати, срабатывает. До поры до времени, пока примеры — стандартные. Но «Пи» — это число! Число 3,14, а никакие не градусы! Это «Пи» радиан = 180°!
Ещё раз: «Пи» — это число! 3,14. Иррациональное, но число. Такое же, как 5 или 8. Можно, к примеру, сделать примерно «Пи» шагов. Три шага и ещё маленько. Или купить «Пи» килограммов конфет. Если продавец образованный попадётся…
«Пи» — это число! Что, достал я вас этой фразой? Вы уже всё давно поняли? Ну ладно. Проверим. Скажите-ка, какое число больше?
Или, что меньше?
Это из серии слегка нестандартных вопросов, которые могут и в ступор вогнать…
Если вы тоже в ступор впали, вспоминаем заклинание: «Пи» — это число! 3,14. В самом первом синусе четко указано, что угол — в градусах ! Стало быть, заменять «Пи» на 180° — нельзя! «Пи» градусов — это примерно 3,14°. Следовательно, можно записать:
В самом первом синусе четко указано, что угол — в градусах ! Стало быть, заменять «Пи» на 180° — нельзя! «Пи» градусов — это примерно 3,14°. Следовательно, можно записать:
Во втором синусе обозначений никаких нет. Значит, там — радианы ! Вот здесь замена «Пи» на 180° вполне прокатит. Переводим радианы в градусы, как написано выше, получаем:
Осталось сравнить эти два синуса. Что. забыли, как? С помощью тригонометрического круга, конечно! Рисуем круг, рисуем примерные углы в 60° и 1,05°. Смотрим, какие синусы у этих углов. Короче, всё, как в конце темы про тригонометрический круг расписано. На круге (даже самом кривом!) будет чётко видно, что sin60° существенно больше, чем sin1,05° .
Совершенно аналогично поступим и с косинусами. На круге нарисуем углы примерно 4 градуса и 4 радиана (не забыли, чему примерно равен 1 радиан?). Круг всё и скажет! Конечно, cos4 меньше cos4°.
Потренируемся в обращении с мерами угла.
Переведите эти углы из градусной меры в радианную:
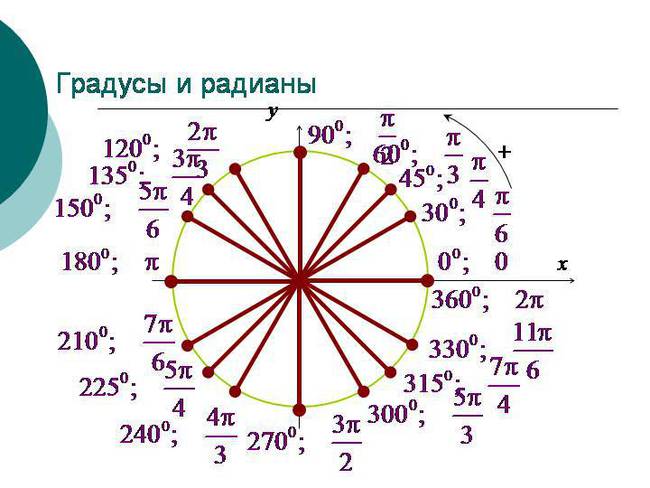
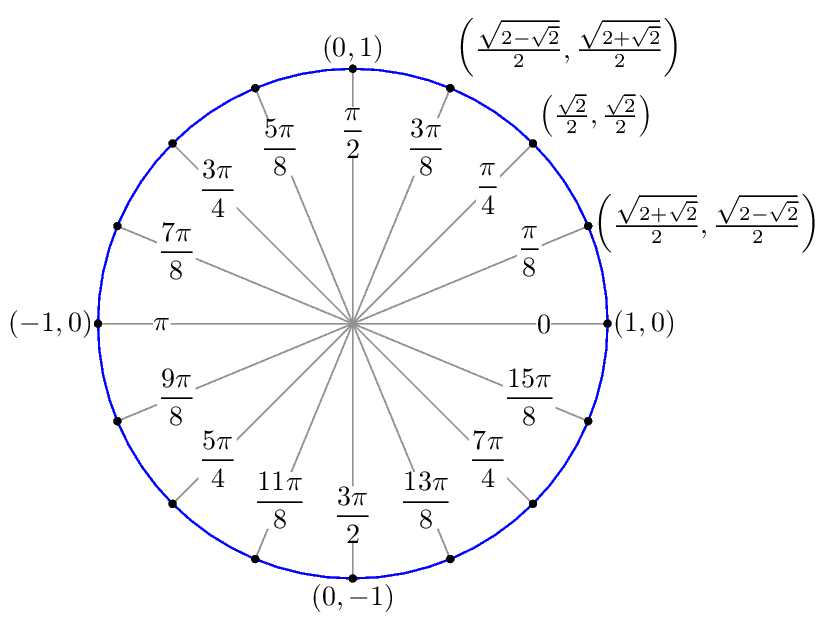
360°; 30°; 90°; 270°; 45°; 0°; 180°; 60°
У вас должны получиться такие значения в радианах (в другом порядке!)
Я, между прочим, специально выделил ответы в две строчки. Ну-ка, сообразим, что за углы в первой строчке? Хоть в градусах, хоть в радианах?
Да! Это оси системы координат! Если смотреть по тригонометрическому кругу, то подвижная сторона угла при этих значениях точно попадает на оси . Эти значения нужно знать железно. И угол 0 градусов (0 радиан) я отметил не зря. А то некоторые этот угол никак на круге найти не могут… И, соответственно, в тригонометрических функциях нуля путаются… Другое дело, что положение подвижной стороны в нуле градусов совпадает с положением в 360°, так совпадения на круге — сплошь и рядом.
Во второй строчке — тоже углы специальные… Это 30°, 45° и 60°. И что в них такого специального? Особо — ничего. Единственное отличие этих углов от всех остальных — именно про эти углы вы должны знать всё .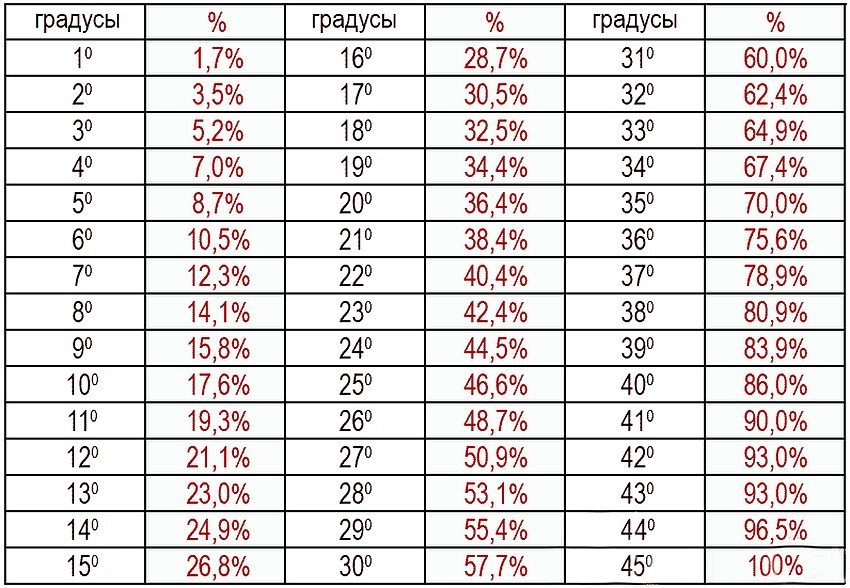 И где они располагаются, и какие у этих углов тригонометрические функции. Скажем, значение sin100° вы знать не обязаны. А sin45° — уж будьте любезны! Это обязательные знания, без которых в тригонометрии делать нечего… Но об этом подробнее — в следующем уроке.
И где они располагаются, и какие у этих углов тригонометрические функции. Скажем, значение sin100° вы знать не обязаны. А sin45° — уж будьте любезны! Это обязательные знания, без которых в тригонометрии делать нечего… Но об этом подробнее — в следующем уроке.
А пока продолжим тренировку. Переведите эти углы из радианной меры в градусную:
У вас должны получиться такие результаты (в беспорядке):
210°; 150°; 135°; 120°; 330°; 315°; 300°; 240°; 225°.
Получилось? Тогда можно считать, что перевод градусов в радианы и обратно — уже не ваша проблема.) Но перевод углов — это первый шаг к постижению тригонометрии. Там же ещё с синусами-косинусами работать надо. Да и с тангенсами, котангенсами тоже…
Второй мощный шаг — это умение определять положение любого угла на тригонометрическом круге. И в градусах, и в радианах. Про это самое умение я буду вам во всей тригонометрии занудно намекать, да…) Если вы всё знаете (или думаете, что всё знаете) про тригонометрический круг, и отсчёт углов на тригонометрическом круге, можете провериться. Решите эти несложные задания:
Решите эти несложные задания:
1. В какую четверть попадают углы:
45°, 175°, 355°, 91°, 355° ?
Легко? Продолжаем:
2. В какую четверть попадают углы:
402°, 535°, 3000°, -45°, -325°, -3000°?
Тоже без проблем? Ну, смотрите…)
3. Сможете разместить по четвертям углы:
Смогли? Ну вы даёте..)
4. На какие оси попадёт уголок:
и уголок:
Тоже легко? Хм…)
5. В какую четверть попадают углы:
И это получилось!? Ну, тогда я прям не знаю…)
6. Определить, в какую четверть попадают углы:
1, 2, 3 и 20 радианов.
Ответ дам только на последний вопрос (он слегка хитрый) последнего задания. Угол в 20 радианов попадёт в первую четверть.
Остальные ответы не дам не из жадности.) Просто, если вы не решили чего-то, сомневаетесь в результате, или на задание №4 потратили больше 10 секунд, вы слабо ориентируетесь в круге. Это будет вашей проблемой во всей тригонометрии. Лучше от неё (проблемы, а не тригонометрии!)) избавиться сразу. Это можно сделать в теме: Практическая работа с тригонометрическим кругом в разделе 555.
Это будет вашей проблемой во всей тригонометрии. Лучше от неё (проблемы, а не тригонометрии!)) избавиться сразу. Это можно сделать в теме: Практическая работа с тригонометрическим кругом в разделе 555.
Там рассказано, как просто и правильно решать такие задания. Ну и эти задания решены, разумеется. И четвёртое задание решено за 10 секунд. Да так решено, что любой сможет!
Если же вы абсолютно уверены в своих ответах и вас не интересуют простые и безотказные способы работы с радианами — можете не посещать 555. Не настаиваю.)
Хорошее понимание — достаточно веская причина, чтобы двигаться дальше!)
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Функция РАДИАНЫ (на английском RADIANS) – это одна из математических и тригонометрических функций, которая часто применяется для инженерных расчетов.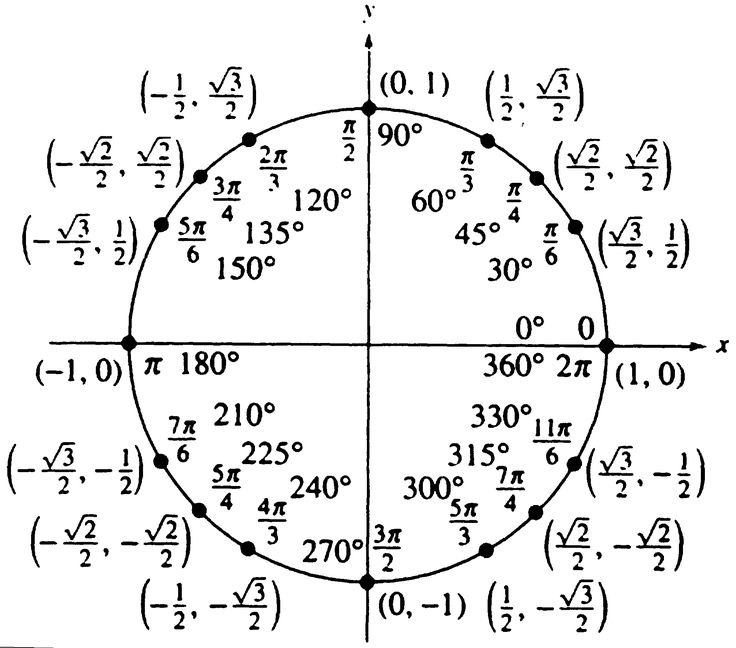 Данная функция в Excel легко преобразует градусы в радианы – угол, соответствующий дуге, а длина этой дуги равна ее радиусу.
Данная функция в Excel легко преобразует градусы в радианы – угол, соответствующий дуге, а длина этой дуги равна ее радиусу.
Как работает функция индекс в Excel?
ПРИМЕР 1. Для инженерных расчетов связанных с движением по окружности зачастую необходимо вычислять угловые скорости и переводить градусы в радианы и радианы в градусы. В Excel для этого предусмотрены специальные функции. Для упрощения математических расчетов может потребоваться выразить в одной и второй величине.
Нам необходимо найти сколько будет в Радианах 180°. Нажимаем кнопку fx возле строки формул для вызова окна выбора функций «Вставка функции» (SHIFT+F3) и в окне поиска вводим функцию «РАДИАНЫ». Выбираем высветившуюся нужную функцию, как показано на ниже рисунке.
Появляется окно, в которое нужно ввести аргументы функции. Вводим значение 180, так как нам нужно найти сколько будет радиан в 180 градусах. Жмем ОК.
В 180 градусах будет 3,1415 радиан.
Найдем радианы для угла в 90°. Откроем окно функций и введем функцию, что необходимо вычислить. Находим ее в окне мастера функций и выбираем аргумент 90.
Откроем окно функций и введем функцию, что необходимо вычислить. Находим ее в окне мастера функций и выбираем аргумент 90.
ОК. В 90 градусах будет 1,5707 радиан.
В следующих примерах рассмотрим, как конвертировать эти единицы измерения углов в обоих направлениях.
Как перевести Радианы в Градусы средствами Excel
ПРИМЕР 2. Иногда нужно единицу измерения углов rad перевести в значение gradus° . Для этого предусмотрена функция ГРАДУСЫ. Она позволяет перевести значения выраженные в радианах в градусы в десятичном исчислении.
Нам нужно найти сколько будет в градусах 4,1 радианы. Нажимаем кнопку fx для вызова окна выбора функции и в окне поиска вводим соответствующее название функции.
Появляется окно в которое нужно ввести аргументы функции. Вводим значение 4,1, так как нам следует найти сколько будет gradus° в 4,1 rad . Нажимаем ОК.
Для исходного значения 4,1 получаем ровно 235 градусов.
Таким образом выполняется перевод из радиан в градусы в Excel.
Сколько радиан в нескольких значениях градуса?
ПРИМЕР 3. Иногда нужно определить сколько радиан в сразу нескольких значениях градуса и вводить тогда каждый раз аргумент очень долго. В таком случае можно воспользоваться немного иным способом конвертирования величин для измерения углов.
Требуется найти сколько будет в Радианах 45, 67, 23, 12, 57 градусов. Нажимаем кнопку fx (SHIFT+F3) для вызова окна выбора функции и в окне поиска вводим необходимо функцию как показано ниже на рисунке. Указываем на высветившуюся функцию.
Преобразование ракурсов в различные форматы
- Преобразование ракурсов в различные форматы
Это приложение преобразует указанные вами углы (в любом формате) в любой или все форматы, указанные вами с помощью флажков в соседнем столбце.
Исходный угол:- Формат отображения:
- Шестидесятеричный формат: 123°34’56» 24-часовой угловой формат 8ч 14м 20с Радианный формат 2.
 . Если вы хотите вводить шестидесятеричные числа с символом °, вы можете отредактировать существующий номер по умолчанию, оставив ° нетронутым. Отображаемые результаты всегда будут отображаться с символом °. Первый нечисловой символ во входных данных, следующий за первым числовым символом, определяет формат угла. Числовые символы включают не только цифры, но и пробел, а также знаки + и -. Другие символы форматирования, включая пробелы, могут быть использованы или опущены по желанию. Пять форматов: 934 56
. Если вы хотите вводить шестидесятеричные числа с символом °, вы можете отредактировать существующий номер по умолчанию, оставив ° нетронутым. Отображаемые результаты всегда будут отображаться с символом °. Первый нечисловой символ во входных данных, следующий за первым числовым символом, определяет формат угла. Числовые символы включают не только цифры, но и пробел, а также знаки + и -. Другие символы форматирования, включая пробелы, могут быть использованы или опущены по желанию. Пять форматов: 934 56 Час : Ч ч 8:14:20 или 8 ч 14 мин 20 с или даже 8:14.33333 Радиан Р р 2.15692R Процент % 34,32840% Десятичный (пусто) 123.58222 Каждый из этих форматов указывает один и тот же угол.
 Каждая из них имеет свое назначение и иногда используется в астрономических расчетах.
Каждая из них имеет свое назначение и иногда используется в астрономических расчетах.- Шестидесятеричная система счисления, пожалуй, самая привычная — градусы, минуты и секунды. (См. Шестидесятеричный ниже).
- Измерение углов в часах возникло потому, что астрономы хотели знать, когда и где звезда будет находиться в определенное время. Радианная угловая мера кажется странной большинству людей, когда они впервые сталкиваются с ней. Странность этой системы в том, что часовой угол применяется только к окружностям. Высота всегда измеряется в шестидесятеричном формате. Это связано с тем, что угол склонения (возвышения) не меняется со временем, а изменяется только экваториальное (окружность) прямое восхождение. Преобразование в часовые углы и обратно требует простого умножения или деления шестидесятеричных углов на 15 [15 = 360°/24 часа]. 90 116 радианов — это естественные математические единицы измерения угла. Он основан на том факте, что окружность всегда равна 2πR, где R — ее радиус.
- Процент полного оборота часто используется в расчетах двойных звезд. Один процентный пункт равен 3,6° с.
- Десятичный формат — это просто шестидесятеричный формат, измененный на одно десятичное число. Он всегда отображается по умолчанию.
- Окончательный формат, угловых секунд , генерируется внутри для очень узких углов, таких как угловые диаметры планет и угловые расстояния между звездами. Когда углы превышают 600 угловых секунд, этот формат возвращается к шестидесятеричному формату. Не существует способа ввода углов в формате угловых секунд, кроме шестидесятеричных чисел с градусами и минутами, установленными равными нулю или малым десятичным дробям.
 Один радиан равен 180°/π.
Один радиан равен 180°/π. - Шестидесятеричный
Слово шестидесятеричное число появляется на этой странице и на странице FDO Astronomical Utility Tools. Шестидесятеричная система относится к современной версии старой финикийской системы с основанием шестьдесят.
 Мы используем это для часов, минут и секунд, а также для углов. Астрономы используют как часовые углы (где полный оборот происходит за 24 часа), так и градусы (где полный оборот составляет 360°).
Мы используем это для часов, минут и секунд, а также для углов. Астрономы используют как часовые углы (где полный оборот происходит за 24 часа), так и градусы (где полный оборот составляет 360°).- Правила задания углов
- Измерения вокруг окружности указаны в [кратных] диапазоне от 0° до 360° (см. примечание). Если ваш источник использует отрицательные углы, программа корректирует их, добавляя кратные 360°. Например, -85° становится (360+-85)° или 275°. Долготы (λ), азимуты (A) и прямые восхождения (α) составляют 90 147 окружностей и 90 148 углов. Окна угла окружности появляются первыми всякий раз, когда инструменты предоставляют поля для углов.
- Измерения вверх или вниз по возвышение диапазон от -90° до 90°. Значения вне этого диапазона логически корректируются, чтобы попасть в этот диапазон. Хотя мы могли бы выбрать любой другой диапазон, охватывающий 180°, по традиции предпочтение отдается от -90° до 90°. Широта (β), высота (a) и склонение (δ) составляют 90 147 углов возвышения и 90 148 углов.
 Блоки угла возвышения всегда являются вторыми в паре блоков.
Блоки угла возвышения всегда являются вторыми в паре блоков.
- Местоположение пользователя
Долгота и широта на поверхности Земли традиционно измеряются восток/запад и север/юг соответственно. Вы можете добавить одно из этих четырех слов (или E, W, N, S), отделенное от угла необходимым пробелом. Правильные переводы в систему 360° и -9Будет сделана система от 0° до 90°. Для тех, кто настаивает на использовании знаков, расположение в южном и западном полушариях является негативным.
- Автором этой утилиты является Les Coleman, и на нее распространяются авторские права, принадлежащие Les Coleman. На этот материал можно ссылаться и воспроизводить его при условии надлежащего указания авторства, как указано в Руководстве по надлежащему использованию Frosty Drew и связанных с ним материалов.
Случайный преобразователь | Преобразовать градусы [°] в обороты [повороты] Преобразователь длины и расстоянияПреобразователь массыСухой объем и общие измерения для приготовления пищиКонвертер площадиКонвертер объема и общего измерения для приготовления пищиПреобразователь температурыПреобразователь давления, напряжения, модуля ЮнгаПреобразователь энергии и работыПреобразователь мощностиПреобразователь силыПреобразователь силыПреобразователь времениПреобразователь линейной скорости и скоростиПреобразователь углаПреобразователь эффективности использования топлива, расхода топлива и экономии топливаПреобразователь чиселКонвертер единиц информации и Хранение данныхКурсы обмена валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияПреобразователь ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер импульсаИмпульс крутящего моментаКонвертер удельной энергии, теплоты сгорания (в расчете на массу)Конвертер удельной энергии, теплоты сгорания (в объеме) Конвертер температуры Конвертер интервала Конвертер коэффициента теплового расширенияКонвертер теплового сопротивленияТеплопровод Конвертер удельной теплоемкостиПлотность теплоты, плотность пожарной нагрузкиКонвертер плотности теплового потокаКонвертер коэффициента теплопередачиКонвертер объемного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер массового потокаКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкости Конвертер кинематической вязкости Конвертер поверхностного натяженияМодерация проницаемости, проницаемости, паропроницаемости Преобразователь скорости пропускания паровПреобразователь уровня звукаПреобразователь чувствительности микрофонаПреобразователь уровня звукового давления (SPL)Преобразователь уровня звукового давления с выбираемым эталонным давлениемПреобразователь яркостиПреобразователь силы светаПреобразователь освещенностиПреобразователь разрешения цифрового изображенияПреобразователь частоты и длины волныПреобразователь оптической силы (диоптрий) в фокусное расстояниеПреобразователь оптической силы (диоптрий) в увеличение (X)Электрический заряд КонвертерКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаОбъемный заряд De Преобразователь электрического токаПреобразователь линейной плотности токаПреобразователь поверхностной плотности токаПреобразователь напряженности электрического поляПреобразователь электрического потенциала и напряженияПреобразователь электрического сопротивленияПреобразователь удельного электрического сопротивленияПреобразователь электрической проводимостиПреобразователь электропроводностиПреобразователь емкостиПреобразователь емкостиПреобразователь индуктивностиПреобразователь реактивной мощности переменного токаПреобразователь калибров проводов в СШАПреобразование уровней в дБм, дБВ, Ватт и других единицахПреобразователь силы магнитного поля КонвертерПлотность магнитного потокаМощность поглощенной дозы излучения, Мощность общей дозы ионизирующего излучения КонвертерРадиоактивность. 1 degree [°] = 0.00277777777777778 turn [turn] From: degreeradiangradgonminutesecondsignmilrevolutioncircleturnquadrantright anglesextant To: degreeradiangradgonminutesecondsignmilrevolutioncircleturnquadrantright anglesextant Volume and Cooking MeasurementsTeaspoons, tablespoons, cups or milliliters? Какие удобнее? Нажмите или коснитесь, чтобы узнать! Обзор Типы углов Измерение углов Использование транспортира Углы в изобразительном искусстве и архитектуре Обзор Угол — геометрическая фигура, образованная двумя пересекающимися линиями с общей начальной точкой. Типы уголковУглы называются прямыми, , если они равны 90°, острыми, — если они меньше 90°, и тупыми, — если они больше 90°. Углы, равные 180°, называются прямыми , углы, равные 360°, называются полными , а углы, которые больше прямых, но меньше полных, называются рефлекторными углами. Если два угла равны друг другу по величине, они называются равными . Два угла, которые при соединении образуют 90 °, называются дополнительными . Если они образуют угол 180°, они являются дополнительными , а если их сумма равна 360°, они являются дополнительными или сопряженными. Два угла, образованные двумя пересекающимися прямыми и противоположные друг другу, не дополняющие друг друга, называются вертикальными или противоположными углами. Измерение угловОбычные и цифровые транспортиры Угол может быть измерен транспортиром или его величина может быть рассчитана по формулам путем измерения дуги окружности, образованной сторонами угла, и одной из сторон от вершины до точка пересечения с ковчегом. Как правило, углы измеряются в градусах или радианах, хотя существуют и другие единицы измерения. Углы можно измерять между прямыми линиями, а также между кривыми. В этом случае они измеряются между касательными к каждой из кривых в точке пересечения. Использование транспортира Транспортир — это специальный инструмент, предназначенный для измерения углов. Большинство транспортиров имеют круглую форму с диапазоном 360 ° или полукругом 180 °. Некоторые транспортиры имеют поворотные рычаги. Они обычно сделаны из прозрачного материала для удобства. Шкала в градусах более распространена, но также используются радианные транспортиры. Транспортиры используются в школе, а также в архитектуре, машиностроении и изготовлении инструментов. Углы в изобразительном искусстве и архитектуреКондоминиумы и лофты Pure Spirits в Торонто, Онтарио Углы использовались художниками, дизайнерами, ремесленниками и архитекторами с древних времен для создания акцентов, структур, визуальных иллюзий и других визуальных эффектов. на зрителя. Геометрические узоры с острыми углами или сочетание острых и тупых углов часто используются в мозаиках и витражах, например, в средневековой архитектуре или в исламском мозаичном искусстве. Музей турецкого и исламского искусства. Стамбул, Турция. Воспроизведено с разрешения автора. Гирих, форма исламского искусства, в которой используется мозаика, металл, дерево, бумага или ткань, является примером такого геометрического искусства. В гирихах вариации между углами образуют симметричные звезды и многоугольники. Традиционно используются пять конкретных полигональных тайлов, а их внутренние углы строго определены и состоят из комбинаций этих четырех углов: 72°, 108°, 144° и 216°. Руб-эль-Хизб и звезда Аль-Кудс В исламском искусстве и архитектуре часто используется Руб-эль-Хизб, геометрическая звездообразная фигура, образованная двумя перекрывающимися квадратами, как показано на изображениях. Она может быть сплошной или нарисованной из линий, и в этом случае ее называют звездой Аль-Кудс. Иногда его украшают дополнительными кругами, нарисованными на каждом пересечении двух квадратов. Руб-эль-Хизб используется в ряде логотипов и флагов, а также является основой для башен-близнецов Петронас в Куала-Лумпуре, Малайзия — самых высоких зданий-близнецов в мире на момент написания (весна 2013 г. Flatiron Buiding, New York Острые углы часто используются в архитектуре для украшения. Они придают зданиям динамичный и элегантный, хотя иногда и устрашающий вид, а тупые углы создают более уютный вид. Например, можно с благоговением восхищаться замками и готическими соборами, но, скорее всего, для жизни выберет дом с тупой угловой крышей. Углы также используются в архитектуре для усиления конструкций. Основываясь на нагрузках, действующих на различные части здания, архитекторы рассчитывают углы, под которыми стены, арки, крыша и другие элементы расположены друг к другу. Можно построить арку без цемента или других связующих материалов, просто основываясь на углах между камнями, из которых она состоит. Как правило, основная часть конструкции здания строится под углом 90° к земле, но есть некоторые исключения. В мире есть ряд зданий, которые намеренно или непреднамеренно наклонены к земле. Например, четыре башни минарета, окружающие Тадж-Махал, построены под небольшим углом, скошенным в сторону от основной конструкции, чтобы в случае землетрясения они не вывалились внутрь, а предотвратили повреждение основной гробницы. В некоторых случаях наклон происходит непреднамеренно, например, в Пизанской башне. Башня была построена так, чтобы стоять вертикально, под прямым углом к земле, но из-за качества почвы под ней и плохого фундамента одна ее сторона не поддерживалась так, как другая, поэтому башня постепенно начала наклоняться. с одной стороны, с увеличением наклона, пока он не был стабилизирован и частично выпрямлен в конце 20 века. Максимальный наклон составлял около 5,5 °, но в настоящее время он составляет около 4 °. Пизанская башня Суурхузен — еще один пример здания, которое непреднамеренно наклонено. В настоящее время он наклонен примерно на 5 °. Считается, что крен вызван повреждением деревянного фундамента при осушении окружающего болота. Ссылки Эта статья написана Катериной Юрием Перевести градусы в секстанты Перевести градусы в секунды Перевести градусы в обороты Перевести градусы в грады Перевести градусы в грады Перевести градусы в минуты 6 00007 9000 Перевести градусы в милыВас могут заинтересовать другие конвертеры из группы «Общие конвертеры единиц измерения»:Конвертер длины и расстояния Конвертер массы сухой объем и общие измерения приготовления пищи Площадь преобразователя Объем и общий преобразователь измерения приготовления ТЕМПЕРАТУРСКИЙ ПЕРЕВОД Давление, напряжение, конвертер модуля Янга Время. Преобразователь Преобразователь линейной скорости и скорости Преобразователь эффективности использования топлива, расхода топлива и экономии топлива Преобразователь чисел Преобразователь единиц информации и хранения данных Конвертер метрических префиксов Передаточный преобразователь Скорости обмена валюты Мужская одежда и размеры обуви Женская одежда и размеры обуви Компактный расчет. |

 Подставьте числа, чтобы получить 5.1.
Подставьте числа, чтобы получить 5.1.
 . Если вы хотите вводить шестидесятеричные числа с символом °, вы можете отредактировать существующий номер по умолчанию, оставив ° нетронутым. Отображаемые результаты всегда будут отображаться с символом °. Первый нечисловой символ во входных данных, следующий за первым числовым символом, определяет формат угла. Числовые символы включают не только цифры, но и пробел, а также знаки + и -. Другие символы форматирования, включая пробелы, могут быть использованы или опущены по желанию. Пять форматов: 934 56
. Если вы хотите вводить шестидесятеричные числа с символом °, вы можете отредактировать существующий номер по умолчанию, оставив ° нетронутым. Отображаемые результаты всегда будут отображаться с символом °. Первый нечисловой символ во входных данных, следующий за первым числовым символом, определяет формат угла. Числовые символы включают не только цифры, но и пробел, а также знаки + и -. Другие символы форматирования, включая пробелы, могут быть использованы или опущены по желанию. Пять форматов: 934 56 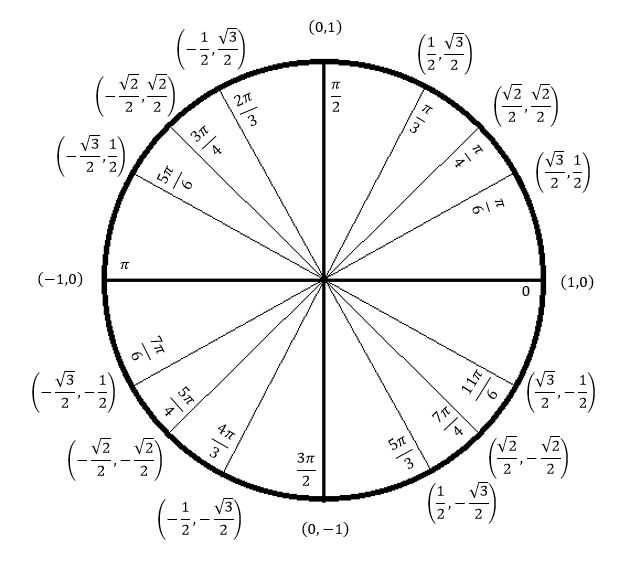 Каждая из них имеет свое назначение и иногда используется в астрономических расчетах.
Каждая из них имеет свое назначение и иногда используется в астрономических расчетах. Один радиан равен 180°/π.
Один радиан равен 180°/π. Мы используем это для часов, минут и секунд, а также для углов. Астрономы используют как часовые углы (где полный оборот происходит за 24 часа), так и градусы (где полный оборот составляет 360°).
Мы используем это для часов, минут и секунд, а также для углов. Астрономы используют как часовые углы (где полный оборот происходит за 24 часа), так и градусы (где полный оборот составляет 360°).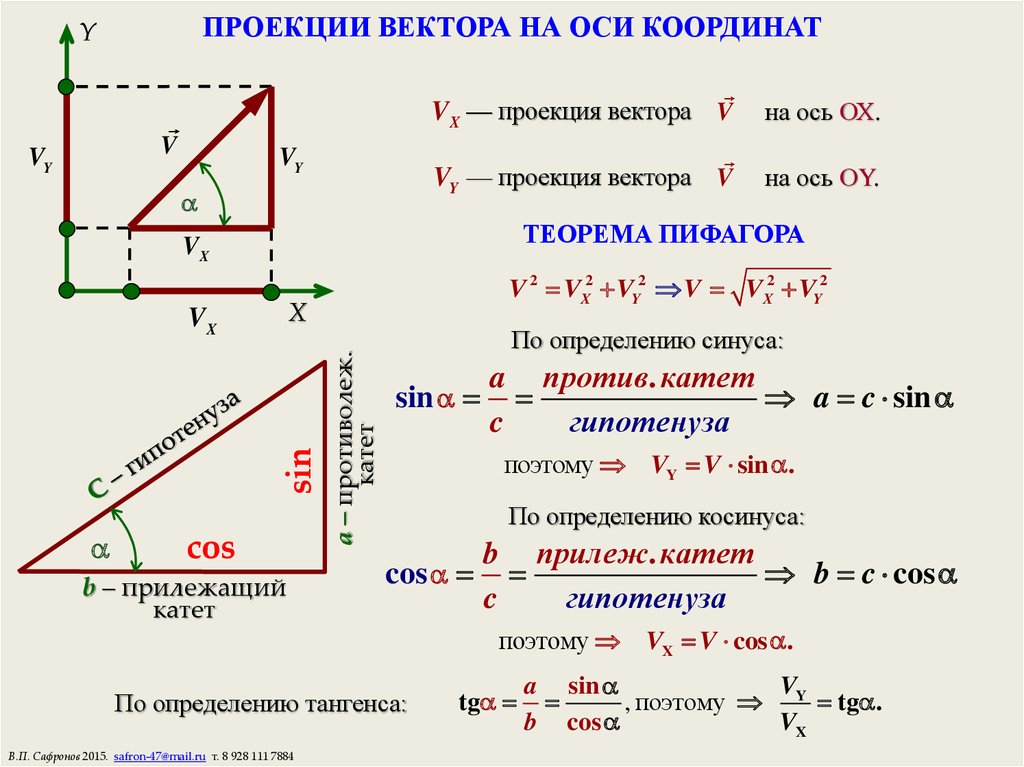 Блоки угла возвышения всегда являются вторыми в паре блоков.
Блоки угла возвышения всегда являются вторыми в паре блоков.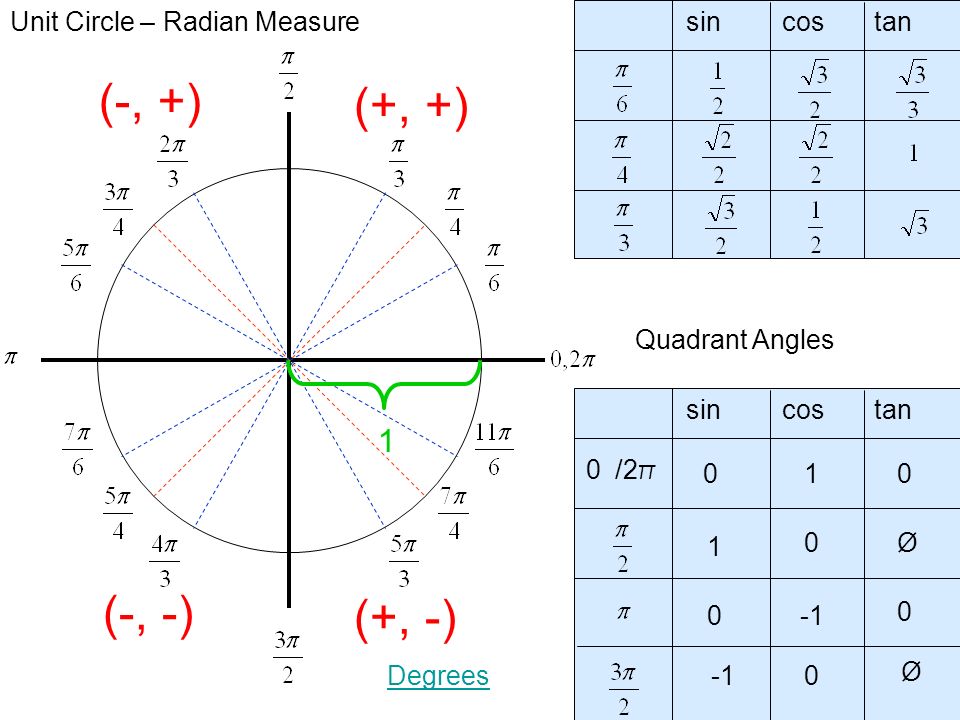 Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксовКонвертер передачи данныхКонвертер типографских и цифровых изображенийКонвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица
Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксовКонвертер передачи данныхКонвертер типографских и цифровых изображенийКонвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица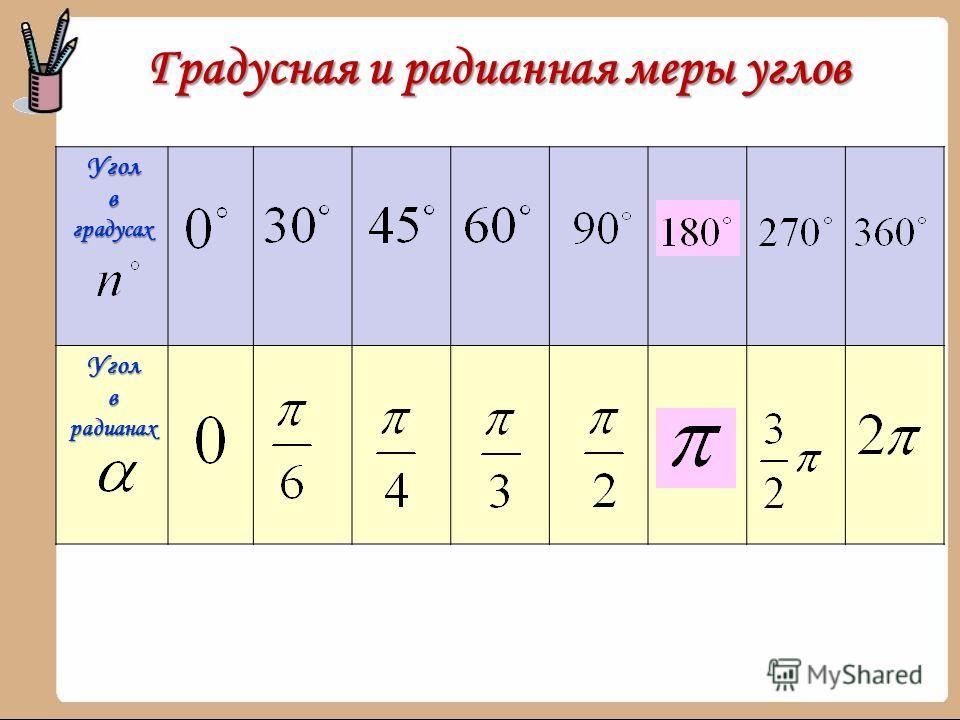 Общая точка – это вершина угла, а прямые – стороны. Углы обладают многими интересными свойствами. Например, в параллелограмме сумма всех углов равна 360°, а в треугольнике — 180°.
Общая точка – это вершина угла, а прямые – стороны. Углы обладают многими интересными свойствами. Например, в параллелограмме сумма всех углов равна 360°, а в треугольнике — 180°.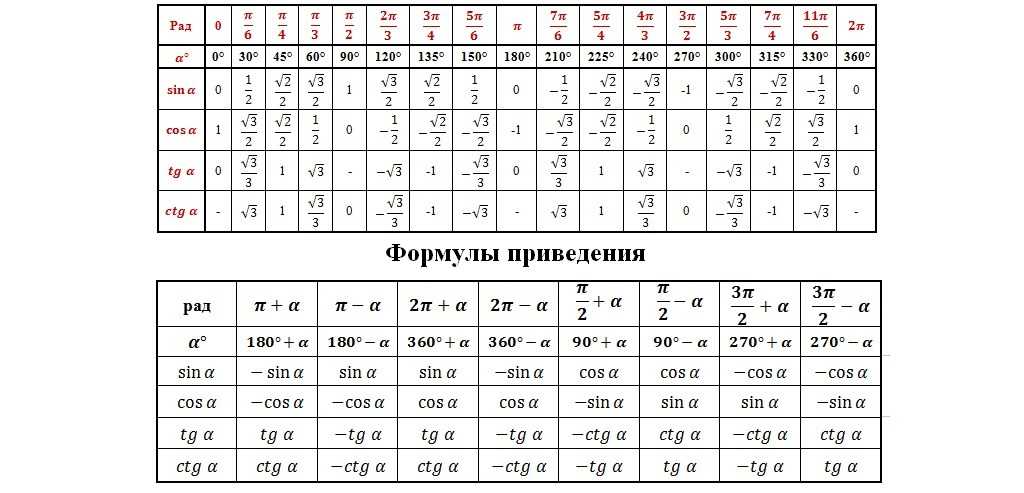 Они конгруэнтны.
Они конгруэнтны.
 Эти углы кратны 36°. Каждая плитка далее делится на симметричные узоры, чтобы усложнить дизайн. Плитки называются гирих и дают название художественной форме. Zellige — похожая форма плитки из Марокко. Формы плитки не определены так строго, как в гирихе, и части зеллидж часто более декоративны, с более круглыми узорами, но каждый художник полагается на взаимодействие углов, подобное гириху.
Эти углы кратны 36°. Каждая плитка далее делится на симметричные узоры, чтобы усложнить дизайн. Плитки называются гирих и дают название художественной форме. Zellige — похожая форма плитки из Марокко. Формы плитки не определены так строго, как в гирихе, и части зеллидж часто более декоративны, с более круглыми узорами, но каждый художник полагается на взаимодействие углов, подобное гириху. ).
). Иногда здания строятся под углом к земле в архитектурных и дизайнерских целях, например, здание Capital Gate в Абу-Даби, которое наклонено на 18 ° к западу. Комплекс Puzzling World в Ванаке, Новая Зеландия, является еще одним примером намеренно построенных наклонных конструкций. Падающая башня Ванаки стоит под углом 53° к земле.
Иногда здания строятся под углом к земле в архитектурных и дизайнерских целях, например, здание Capital Gate в Абу-Даби, которое наклонено на 18 ° к западу. Комплекс Puzzling World в Ванаке, Новая Зеландия, является еще одним примером намеренно построенных наклонных конструкций. Падающая башня Ванаки стоит под углом 53° к земле.
 у вас есть трудности с переводом единицы измерения на другой язык? Помощь доступна! Разместите свой вопрос в TCTerms и через несколько минут вы получите ответ от опытных технических переводчиков.
у вас есть трудности с переводом единицы измерения на другой язык? Помощь доступна! Разместите свой вопрос в TCTerms и через несколько минут вы получите ответ от опытных технических переводчиков.
 », то есть « умножить на десять в степени ». Электронная нотация обычно используется в калькуляторах, а также учеными, математиками и инженерами.
», то есть « умножить на десять в степени ». Электронная нотация обычно используется в калькуляторах, а также учеными, математиками и инженерами.