Модуль отрицательных чисел
- программирование
Оператор по модулю возвращает остаток от деления. Но все становится немного сложнее, когда вы добавляете в смесь отрицательные числа.
Модуль или часто называемый «mod» представляет остаток от деления. В 1801 году Гаусс опубликовал книгу по модульной арифметике. Позднее Дональд Кнут дал общепринятое математическое определение.
мод(а, п) = а - п * этаж(а / п)
Выполнение целочисленного деления, а затем его повторное умножение означает нахождение наибольшего числа, меньшего , а , которое делится на n без остатка. Вычитание этого числа из на дает остаток от деления и тем самым модуль.
Но что делает операция по модулю? Для чего это можно использовать при кодировании?
Ограничение границ
В программировании оператор по модулю ( %
mod ) часто используется для ограничения индекса границами массива или структурой данных с ограниченной длиной.
значений = [ 3, 4, 5 ] индекс = 5 value_at_index = значения[ индекс % значений.длина ]
Для приведенного выше примера это означает 5 mod 3 = 2 в соответствии с определением 5 - floor(5/3)*3 = 2 . Это означает, что независимо от того, какое значение имеет индекс , границы массива соблюдены.
Но так ли это на самом деле?
Что произойдет, если делимое или делитель подписаны и имеют отрицательное значение? Оказывается, правила по модулю отрицательных чисел действительно зависят от языка, который вы используете.
Как модуль работает в Java?
Как модуль работает в javascript?
Как работает модуль в Python?
Хотя код выглядит почти одинаково на большинстве языков, распечатка результатов показывает языки в основном из двух разных лагерей.
Только два языка занимают разную позицию: Dart и, в частности, Zig, который
различает оба случая как @rem(a,b) и @mod(a,b) и ошибки на отрицательном делителе.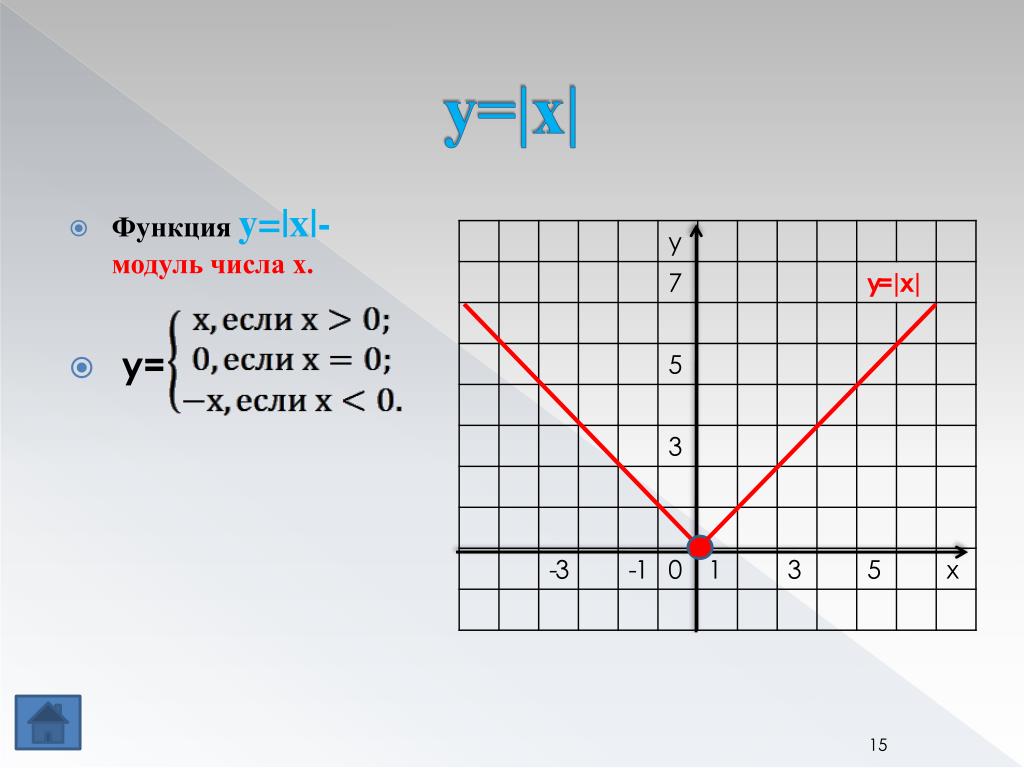
| Язык | 13 мод 3 | -13 мод 3 | 13 мод -3 | -13 мод -3 |
|---|---|---|---|---|
| С | 1 | -1 | 1 | -1 |
| С# | 1 | -1 | 1 | -1 |
| С++ | 1 | -1 | 1 | -1 |
| Эликсир | 1 | -1 | 1 | -1 |
| Эрланг | 1 | -1 | 1 | -1 |
| Перейти | 1 | -1 | 1 | -1 |
| Ява | 1 | -1 | 1 | -1 |
| Джаваскрипт | 1 | -1 | 1 | -1 |
| Котлин | 1 | -1 | 1 | -1 |
| Ним | 1 | -1 | 1 | -1 |
| PHP | 1 | -1 | 1 | -1 |
| Ржавчина | 1 | -1 | 1 | -1 |
| Скала | 1 | -1 | 1 | -1 |
| Свифт | 1 | -1 | 1 | -1 |
| Кристалл | 1 | 2 | -2 | -1 |
| Хаскелл | 1 | 2 | -2 | -1 |
| Луа | 1 | 2 | -2 | -1 |
| Питон | 1 | 2 | -2 | -1 |
| Рубин | 1 | 2 | -2 | -1 |
| Дротик | 1 | 2 | 1 | 2 |
| Зиг @рем | 1 | -1 | ошибка | ошибка |
| Зиг @мод | 1 | 2 | ошибка | ошибка |
Поэтому, если вы используете оператор по модулю для обеспечения правильных границ для доступа к коллекции, имейте в виду, что некоторые языки требуют большего внимания.
Простой и эффективный способ — проверить знак.
Интервал мод(а, б) {
с = а % б
возврат (с < 0) ? с + б : с
}
В качестве другого варианта вы также можете дважды применить модуль по модулю.
int mod(a, b) {
(((а % б) + б) % б)
}
Четное или нечетное
Еще одна ловушка, на которую следует обратить внимание, — это проверка того, является ли число нечетным или четным, с использованием оператора по модулю. Основываясь на приведенных выше выводах, вы всегда должны сравнивать с 0 .
bool is_odd(int n) {
вернуть n % 2 != 0; // может быть 1 или -1
}
Но любой, кто когда-либо заглядывал уровнем ниже C, укажет, что использование по модулю в любом случае не обязательно является лучшей реализацией для is_odd . Умножение и особенно деление — одни из самых дорогих инструкций процессора. Если вы имеете дело с числами на основе 2, часто есть более быстрый способ.
x % 2n == x & (2n - 1) // для n>0
По крайней мере, для положительного делителя операцию по модулю можно заменить простой побитовой и операция.
х % 2 == х и 1 х% 4 == х и 3 х% 8 == х & 7 ...
Что позволяет гораздо быстрее реализовать is_odd .
bool is_odd(int n) {
вернуть n & 1 != 0;
}
Вкратце
Оператор по модулю может быть невероятно полезным, но разработчики также должны знать о вышеупомянутых пограничных случаях и о том, когда его использовать или не использовать.
Более подробное обсуждение см. в статье в Википедии.
Присоединяйтесь к другим 1000 подписчиков.
Получайте уведомления о новых статьях.
Получите приоритетный доступ к вещам, которые я создаю.
Узнавайте о розыгрышах первыми.
Адрес электронной почты
Не смешное дело. Вы можете отписаться в любое время.
Я забочусь о вашей конфиденциальности.
Спасибо! Пожалуйста, проверьте свой почтовый ящик.
Извините, но что-то пошло не так.
Или подпишитесь на RSS-рассылку
Операторы псевдокода :: CC 110 Учебник
Ресурсы
- Слайды
Теперь, когда у нас есть возможность хранить числовые данные в переменных в псевдокоде, мы также должны научиться преобразовывать эти данные во что-то новое. Для этого давайте узнаем о операторах . Оператор в программировании — это специальный символ, который можно использовать в выражении для того, чтобы каким-то образом манипулировать данными. Большинство операторов являются бинарными операторами , что означает, что они выполняют операцию, которая использует два значения в качестве входных данных и производит одно значение в качестве вывода. На самом деле, в некоторых языках программирования сами операторы реализованы в виде процедур языка!
Выражение, содержащее бинарный оператор, обычно имеет следующий формат:
<выражение> <оператор> <выражение>
Как и прежде, части <выражение> могут быть любым допустимым выражением в языке, а часть <оператор> обычно представляет собой одиночный символ, но также может быть и коротким ключевым словом.
К счастью, все эти операторы уже должны быть хорошо знакомы нам из математики, так что это просто краткое обсуждение того, как их можно использовать в программировании.
Сложение и вычитание
Для начала мы можем использовать символы плюс + и минус - в качестве операторов для выполнения сложения и вычитания в псевдокоде, как и в математике. Например, мы можем добавить две переменные вместе, чтобы создать третью переменную, как показано в этом примере:
а <- 5 б <- 7 с <- а + б ДИСПЛЕЙ(с)
Когда мы запускаем этот код на нашей «ментальной модели» компьютера, мы должны получить такой результат:
Точно так же мы можем вычесть две переменные, используя символ минус - как показано здесь:
х <- 24 у <- 10 г <- х - у ДИСПЛЕЙ (г)
Этот код должен выдать следующий результат:
Умножение и деление
В псевдокоде мы используем звездочку * , иногда называемую звездочкой, для умножения двух значений.
Например, мы можем найти произведение двух значений, как показано в этом блоке псевдокода:
а <- 6 б <- 7 с <- а * б ДИСПЛЕЙ(с)
Когда мы запустим этот код, мы должны увидеть следующий результат, отображаемый пользователю:
Деление выполняется с помощью символа косой черты /. Отличный способ думать о делении в программировании как о дроби, так как он использует один и тот же символ между двумя числами. Например, если мы выполним этот код:
х <- 27 у <- 3 г <- х/у ДИСПЛЕЙ (г)
мы увидим этот вывод:
Что, если при делении получится остаток? В этом случае мы будем просто использовать десятичные значения в псевдокоде, чтобы результат был точно правильным. Например, если мы попытаемся разделить 19 долларов$ на $5$, как в этом примере:
а <- 19 б <- 5 с <- а / б ДИСПЛЕЙ(с)
Наша «мысленная модель» компьютера выдаст следующий результат:
Итак, как мы видим, все эти операторы в псевдокоде работают точно так же, как их аналоги в математике.
Несмотря на то, что мы не запускаем наш код на реальном компьютере, мы должны иметь возможность легко использовать простой калькулятор, который поможет нам выполнить эти операции, если это необходимо.
Модуль оператора
Есть еще один оператор, который обычно используется в псевдокоде — 9.0045 по модулю оператора
MOD в качестве оператора по модулю.Например, если мы хотим найти остаток после деления 19$ на 5$, мы должны использовать следующий код:
х <- 19 у <- 5 z <- x MOD у ДИСПЛЕЙ (г)
Когда мы запустим этот код, мы получим следующий вывод:
Это связано с тем, что значение $5$ впишется в значение $19$ всего $3$ раза, и тогда у нас останется значение $4$.
Математически мы говорим, что 19 долларов / 5 = (3 * 5) + 4 доллара. Поскольку $4$ — это оставшаяся часть, это итоговое значение, когда мы используем оператор по модулю.
В этом курсе нас будет интересовать только то, как работает оператор по модулю применительно к целым положительным числам. На практике его можно применить к любому числовому значению, включая десятичные значения и отрицательные числа, но в большинстве случаев эти значения бесполезны. Итак, для простоты мы будем использовать только положительные целые числа с этим оператором.
Порядок действий
Наконец, как и в математике, мы также должны знать порядок применения этих операторов, особенно если они объединены в одно выражение. К счастью, те же правила, которые мы изучили в математике, применимы и в программировании. В частности, операторы в псевдокоде применяются в следующем порядке:
- Операции в скобках разрешаются первыми слева направо.
-
*,/иMODразрешаются вторыми, двигаясь слева направо.
-
+и-разрешаются третьими, двигаясь слева направо.
В большинстве случаев лучше заключать круглые скобки всякий раз, когда мы включаем несколько операторов в одну строку, чтобы предполагаемая интерпретация была совершенно ясной. Тем не менее, давайте рассмотрим быстрый пример, чтобы увидеть порядок операций на практике.
Вот сложное выражение в псевдокоде, которое мы можем попытаться вычислить:
х <- 8 / 4 + 5 * (3 + 1) - 7 МОД 4
Глядя на наш порядок операций, первый шаг — обработка любых выражений внутри круглых скобок. Итак, сначала мы начнем с выражения (3 + 1) и оценим его как 4 .
х <- 8 / 4 + 5 * 4 - 7 MOD 4
Затем мы пойдем справа налево и выполним любые операции умножения, деления и по модулю. Это означает, что мы будем оценивать 8 / 4 , 5 * 4 и 7 MOD 4 и замените их полученными значениями:
х <- 2 + 20 - 3
Наконец, мы будем выполнять сложение и вычитание слева направо.