Как перевести в число в радианы: Как перевести число в радианы 🚩 из градусов в радианы 🚩 Математика

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21
Найти точное значение		cos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27
Найти точное значение		sin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упростить
sin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )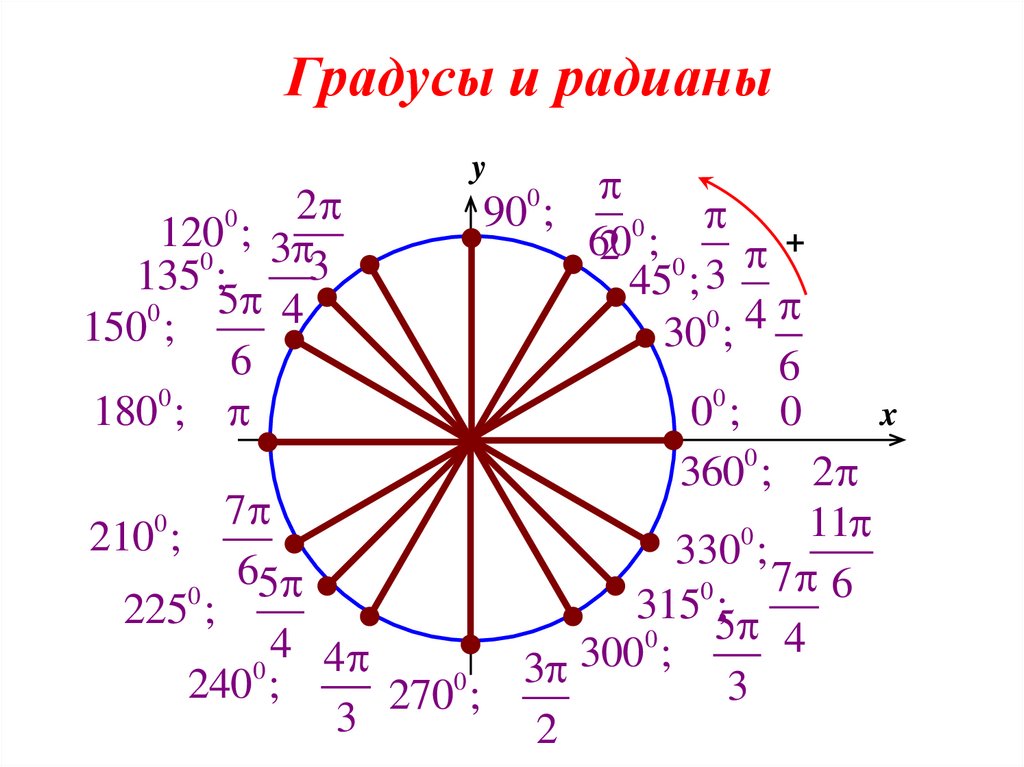
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )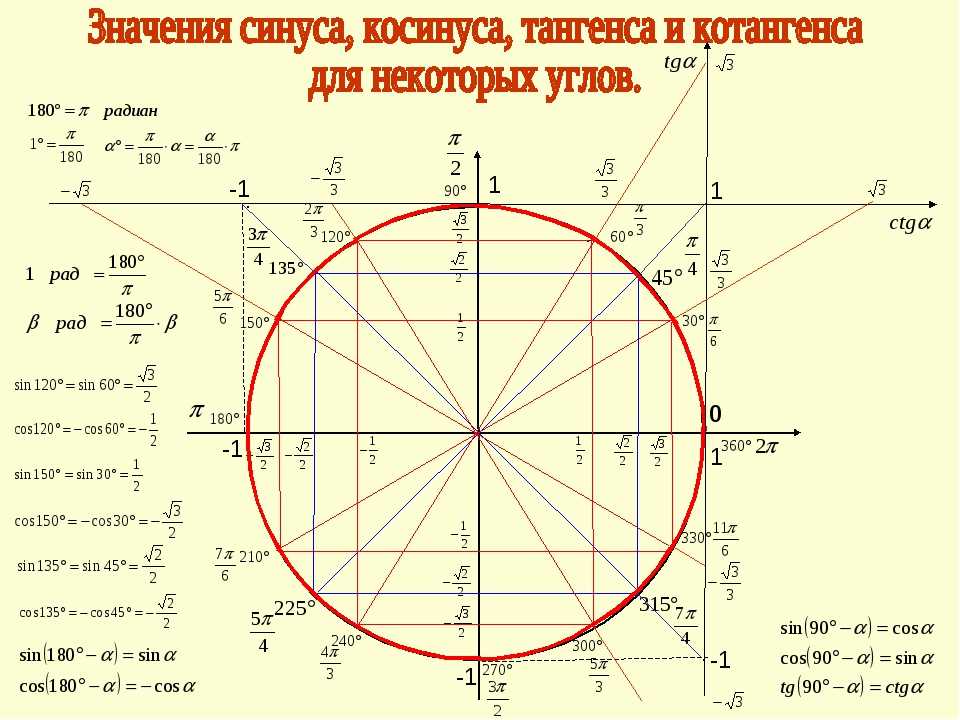
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94
Найти точное значение		arcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100
Преобразовать из градусов в радианы		88 град.

Мэтуэй | Популярные задачи

92
1 Найти точное значение грех(30)
2 Найти точное значение грех(45)
3 Найти точное значение грех(30 градусов)
4 Найти точное значение грех(60 градусов)
5 Найти точное значение загар (30 градусов)
6 Найти точное значение
угловой синус(-1)
7 Найти точное значение грех(пи/6)
8 Найти точное значение cos(pi/4)
9 Найти точное значение грех(45 градусов)
10 Найти точное значение грех(пи/3)
11 Найти точное значение арктан(-1)
12 Найти точное значение cos(45 градусов)
13 Найти точное значение cos(30 градусов)
14 Найти точное значение желтовато-коричневый(60)
15 Найти точное значение csc(45 градусов)
16 Найти точное значение загар (60 градусов)
17 Найти точное значение сек(30 градусов)
18 Найти точное значение cos(60 градусов)
19 Найти точное значение cos(150)
20 Найти точное значение грех(60)
21 Найти точное значение cos(pi/2)
22 Найти точное значение загар (45 градусов)
23 Найти точное значение arctan(- квадратный корень из 3)
24 Найти точное значение csc(60 градусов)
25 Найти точное значение сек(45 градусов)
26 Найти точное значение csc(30 градусов)
27 Найти точное значение грех(0)
28 Найти точное значение грех(120)
29 Найти точное значение соз(90)
30 Преобразовать из радианов в градусы пи/3
31 Найти точное значение желтовато-коричневый(30)
32
35 Преобразовать из радианов в градусы пи/6
36 Найти точное значение детская кроватка(30 градусов)
37 Найти точное значение арккос(-1)
38 Найти точное значение арктан(0)
39 Найти точное значение детская кроватка(60 градусов)
40 Преобразование градусов в радианы 30
41 Преобразовать из радианов в градусы (2 шт. )/3
42 Найти точное значение sin((5pi)/3)
43 Найти точное значение sin((3pi)/4)
44 Найти точное значение тан(пи/2)
45 Найти точное значение грех(300)
46 Найти точное значение соз(30)
47 Найти точное значение соз(60)
48 Найти точное значение соз(0)
49 Найти точное значение соз(135)
50 Найти точное значение cos((5pi)/3)
51 Найти точное значение cos(210)
52 Найти точное значение сек(60 градусов)
53 Найти точное значение грех(300 градусов)
54 Преобразование градусов в радианы 135
55 Преобразование градусов в радианы 150
56 Преобразовать из радианов в градусы (5 дюймов)/6
57 Преобразовать из радианов в градусы (5 дюймов)/3
58 Преобразование градусов в радианы 89 градусов
59 Преобразование градусов в радианы 60
60 Найти точное значение грех(135 градусов)
61 Найти точное значение грех(150)
62 Найти точное значение грех(240 градусов)
63 Найти точное значение детская кроватка(45 градусов)
64 Преобразовать из радианов в градусы (5 дюймов)/4
65 Найти точное значение грех(225)
66 Найти точное значение грех(240)
67 Найти точное значение cos(150 градусов)
68 Найти точное значение желтовато-коричневый(45)
69 Оценить грех(30 градусов)
70 Найти точное значение сек(0)
71 Найти точное значение cos((5pi)/6)
72 Найти точное значение КСК(30)
73 Найти точное значение arcsin(( квадратный корень из 2)/2)
74 Найти точное значение загар((5pi)/3)
75 Найти точное значение желтовато-коричневый(0)
76 Оценить грех(60 градусов)
77 Найти точное значение arctan(-( квадратный корень из 3)/3)
78 Преобразовать из радианов в градусы (3 пи)/4 
79 Найти точное значение sin((7pi)/4)
80 Найти точное значение угловой синус(-1/2)
81 Найти точное значение sin((4pi)/3)
82 Найти точное значение КСК(45)
83 Упростить арктан(квадратный корень из 3)
84 Найти точное значение грех(135)
85 Найти точное значение грех(105)
86 Найти точное значение грех(150 градусов)
87 Найти точное значение sin((2pi)/3)
88 Найти точное значение загар((2pi)/3)
89 Преобразовать из радианов в градусы пи/4
90 Найти точное значение грех(пи/2)
91 Найти точное значение сек(45)
92 Найти точное значение cos((5pi)/4)
93 Найти точное значение cos((7pi)/6)
94 Найти точное значение угловой синус(0)
95 Найти точное значение грех(120 градусов)
96 Найти точное значение желтовато-коричневый ((7pi)/6)
97 Найти точное значение соз(270)
98 Найти точное значение sin((7pi)/6)
99 Найти точное значение arcsin(-( квадратный корень из 2)/2)
100 Преобразование градусов в радианы 88 градусов

Связывание действительных чисел с точками на единичной окружности

До сих пор мы думали о входных данных тригонометрической функции как о углах с единицами градусов.

Для тригонометрии на основе треугольника (например, нахождение высоты гор и навигация), это естественно и уместно.

Однако тригонометрические функции также необходимы в ситуациях, когда в поле зрения нет треугольника!
В этих случаях используется другой подход.

В приложениях, отличных от треугольников, обычно не естественно рассматривать тригонометрические входные данные как угол — и в этом могут быть недостатки.
Например, расчетные формулы усложняются, когда требуются переводные коэффициенты. чтобы преобразовать ввод степени
в (безразмерное) действительное число.

При использовании тригонометрических функций мы часто хотим, чтобы ввод был простым вещественным числом — только то, к чему мы привыкли со знакомым функции 92\,. $ Радианная мера спешит на помощь!

Вы можете подумать, что оба подхода к тригонометрии в значительной степени зависят от углов:

  • В подходе прямоугольного треугольника синус и косинус определяются с помощью углов в прямоугольном треугольнике.
  • В методе единичного круга синус и косинус определяются с использованием углов, расположенных стандартным образом в единичном круге.

Как мы можем получить углы «вне поля зрения» и думать о входных данных как о действительных числах?

Ключом к успеху является установление связи между действительными числами (точками на реальном числовая линия) и единичный круг следующим образом:

Связывание действительных чисел с точками на единичной окружности

Представьте прямую числовую прямую как бесконечную строку:
  • черная точка на $\,0\,$ (как показано справа)
  • положительных чисел, окрашенных в зеленый цвет (бесконечно простирающихся вправо)
  • отрицательных чисел, окрашенных в красный цвет (бесконечно простирающихся влево)

Возьмите этот кусок нити и оберните его вокруг единичного круга следующим образом:
  • поставить черную точку в точке $(1,0)$ на единичной окружности
  • перенос положительных чисел против часовой стрелки (запуск)
  • перенос отрицательных чисел по часовой стрелке (начало вниз)
Конечно, зеленый и красный в конечном итоге перекроются, 90 913, поскольку они будут продолжать вращаться по кругу.
(Здесь показаны только короткие кусочки зеленой и красной «ниточки»!)

Таким образом, каждое действительное число заканчивается (связано) с уникальной точкой на единичной окружности — так называемой «конечной точкой».
Затем применяются обычные определения единичного круга:

  • косинус — первая координата (значение $x$) конечной точки
  • синус — это вторая координата (значение $y$) конечной точки
Когда вы оборачиваете «строку» прямой числовой линии вокруг единичного круга,
естественным образом появляется угол (показан справа синим цветом).

Действительное число $\,x\,$ является мерой этого угла в радианах!

Итак, какова мера угла в радианах?
Это длина дуги, образующей угол на единичной окружности !

ОПРЕДЕЛЕНИЕ радианная мера углов

Пусть $\,\theta\,$ — любой угол, отложенный стандартным образом на единичной окружности:

  • Начинаем с положительной оси $x$.
  • Положительные углы заметаются против часовой стрелки (начните с движения вверх).
  • Отрицательные углы сметаются по часовой стрелке (начните с движения вниз).

Длина (со знаком) дуги, образуемой углом на единичной окружности
, равна радианам меры угла $\,\theta\,.$ 9\circ}$$

радианная мера $\,\theta\,$
равна $\,1\,$
радианная мера $\,\theta\,$
равна $\,-2\,$
радианная мера $\,\theta\,$
равна $\,\pi\,$
радианная мера $\,\theta\,$
равна $\,-\frac{\pi}{2}\,$

Примечания к определению:

  • Числа, указанные в R адианах, являются просто R истинными числами. (Причудливый набор текста — это запоминающее устройство!)
    Запомните связь прямой числовой линии с точками на единичной окружности.
    Думайте о слове « R adian» как о мягком напоминании R о том, что вы имеете дело с реальным числом R .
  • Аббревиатура «радиан» — «рад». 9\circ = \frac{\pi}6 \text{ рад}$

    Почему название «радианная мера»?

    Вы можете подумать, что «радиан» — довольно случайное имя…
    ( … возможно, не более случайное, чем «градус», означающий $\,\frac{1}{360}\,$ оборота, или «град» означает $\,\frac{1}{400}\,$ оборота!)

    Однако название «радиан» на самом деле поучительно, наводит на размышления и имеет смысл:

    Начните с угла $\,\theta\,$ в окружности радиуса $\,r\,. $
    Предположим, угол опирается на дугу длины $\,s\,$, как показано справа.

    Мы хотим найти радианную меру $\,\theta\,.$

    С этой целью мы должны масштабировать круг до единицы измерения круга .
    Для этого разделите все длины на $\,r\,$, как показано справа.

    Поскольку мерой угла в радианах является длина дуги, которую он образует в единичной окружности,
    имеем: $$ \cssId{s107}{\text{мера в радианах}\theta = \frac{s}{r}} $$

    Теперь подумайте об интерпретации задачи деления $\displaystyle\,\frac{s}{r}\,.$

    Задача о делении $\displaystyle\,\frac{10}{2}\,$ отвечает на вопрос «Сколько 2$ в $\,10\,$?»
    Ответ: $5$

    Аналогично , задача деления $\displaystyle\,\frac{s}{r}\,$ отвечает на вопрос «Сколько $r$ в $\,s\,$?»
    Ответ: радианная мера угол!

    Радианная мера угла дает количество радиусов, необходимых для стягивания угла!

    RAD I a N
    размер:

    количество
    РАД иус В
    угол

    Это знание позволяет легко визуализировать углы, которые даны в радианах.

    No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *

    © 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа»

    Карта сайта