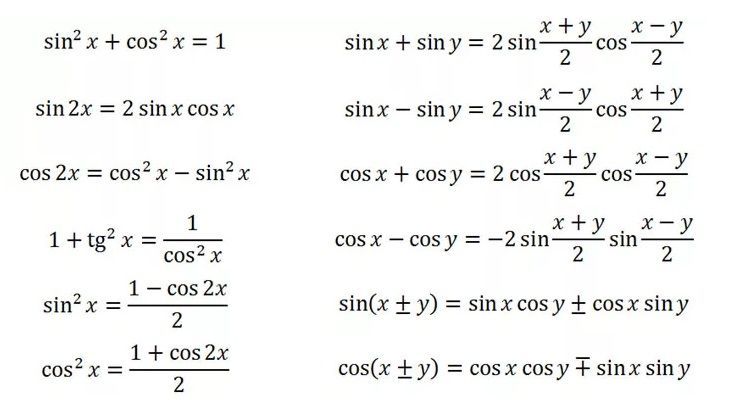Тригонометрические формулы суммы и разности двух углов:
Синус суммы \(sin(\alpha\ + \ \beta)\ = \ sin\alpha \cdot cos\beta\ + \ cos\alpha \cdot sin\beta\)
Синус разности \(sin(\alpha\ — \ \beta)\ = \ sin\alpha \cdot cos\beta\ — \ cos\alpha \cdot sin\beta\)
Косинус суммы \(cos(\alpha\ + \ \beta)\ = \ cos\alpha \cdot cos\beta\ –\ sin\alpha \cdot sin\beta\)
Косинус разности \(cos(\alpha\ –\ \beta)\ = \ cos\alpha \cdot cos\beta\ + \ sin\alpha \cdot sin\beta\)
Тангенс суммы \(\text{tg}\left( \alpha + \beta \right) = \frac{tg\ \alpha + tg\ \beta}{1 — tg\ \alpha \cdot tg\ \beta},\ \alpha,\ \beta,\ \alpha + \beta \neq \frac{\pi}{2} + \pi n,\ n \in Z\)
Тангенс разности \(\text{tg}\left( \alpha — \beta \right) = \frac{tg\ \alpha — tg\ \beta}{1 + tg\alpha \cdot tg\ \beta},\ \ \alpha,\ \beta,\ \alpha + \beta \neq \frac{\pi}{2} + \pi n,\ n \in Z\)
Пример:
Решение.
\circ})\ = \ 0,5 \cdot (0,9\ –\ 0,5)\ = \ 0,2\).
Формулы суммы и разности тригонометрических функций:
\(\sin\alpha + \sin\beta = 2\sin\frac{\alpha + \beta}{2} \cdot \cos\frac{\alpha — \beta}{2}\)
\(\sin\alpha — \sin\beta = 2\sin\frac{\alpha — \beta}{2} \cdot \cos\frac{\alpha + \beta}{2}\)
\(\cos\alpha + \cos\beta = 2\cos\frac{\alpha + \beta}{2} \cdot \cos\frac{\alpha — \beta}{2}\)
\(\cos\alpha — \cos\beta = — 2\cos\frac{\alpha + \beta}{2} \cdot \cos\frac{\alpha — \beta}{2}\)
Формул приведения много, а точнее 32. И все формулы надо знать. К счастью, существует простое мнемоническое правило, позволяющее быстро воспроизвести любую формулу приведения.
Каждая формула связывает между собой либо синус с косинусом, либо тангенс с котангенсом. Причём, первая функция либо меняется на вторую, либо нет.
1. В левой части формулы аргумент представляет собой сумму или разность одного из «основных координатных углов»: \(\frac{\pi}{2},\ \pi,\frac{3\pi}{2},\ 2\pi\ \) и острого угла α, а в правой части аргумент α.
2. В правой части знак перед функцией либо «плюс», либо «минус».
Мнемоническое правило:
Достаточно задать себе два вопроса:
1. Меняется ли функция на кофункцию?
Ответ: Если в формуле присутствуют углы \(\frac{\pi}{2}\) или \(\frac{3\pi}{2}\) — это углы вертикальной оси, киваем головой по вертикали и сами себе отвечаем: «Да», если же присутствуют углы горизонтальной оси π или 2π, то киваем головой по горизонтали и получаем ответ: «Нет».
2. Какой знак надо поставить в правой части формулы?
Ответ: Знак определяем по левой части. Смотрим, в какую четверть попадает угол, и вспоминаем, какой знак в этой четверти имеет функция, стоящая в левой части.
Пример:
\(\sin(\frac{3\pi}{2} + \alpha).\)
«Меняется функция или нет?»
\(\frac{3\pi}{2}\) — угол вертикальной оси, киваем головой по вертикали: «Да, меняется».
\circ}) = — 5 \cdot 1 = — 5\)
Основные тригонометрические формулы синуса, косинуса, тангенса и котангенса. Тригонометрия 9. Ч13
12+
6 месяцев назад
Математика от Баканчиковой295 подписчиков
Тригонометрия 9 класс. Основные тригонометрические формулы. Как получаются основные тригонометрические формулы? Какие формулы получаются из основных тригонометрических формул, и как с ними работать? Сегодня мы ответим на эти вопросы. Если Вы не видели наши предыдущие уроки по теме: «Тригонометрические функции в геометрии», то обязательно посмотрите их, тогда этот урок будет Вам очень понятен. В заключение урока мы покажем Вам 20 основных тригонометрических формул, которые нужно запомнить. Подробный план урока и ссылки на предыдущие уроки Вы можете найти в описании под видео.
00:00 Начало видео.
00:47 Тригонометрические формулы тангенса и котангенса. Как они получаются?
04:34 Умножим тангенс на котангенс. tg α * ctg α = ?
07:14 Прибавим 1 к квадрату тангенса и квадрату котангенса.
Тригонометрические функции в геометрии. Часть 5. Геометрия 9 класс. https://rutube.ru/video/9393cb6043b9878b49883195db02d251/
Как найти противо- и прилежащие катеты по углу и гипотенузе. Как найти площадь треугольника, параллелограмма и трапеции. Тригонометрические функции. Часть 6. Геометрия 9 класс. https://rutube.ru/video/01cfdff903c6c37227f510c5f4bf7984/
Как найти объем пирамиды (конуса) по боковому ребру (образующей) и углу между боковым ребром (образующей) и плоскостью основания. Тригонометрические функции. Часть 7. Геометрия 10-11 класс. https://rutube.ru/video/a246217e2de6f5960fb55a3e77b904d0/
Как найти противо- и прилежащие катеты по углу и другому катету. Как найти площадь треугольника и параллелограмма. Тригонометрические функции. Часть 8. Геометрия 9 класс. https://rutube.ru/video/5b374b4961980532582185a1803b6be0/
Тангенс и котангенс в решении задач по стереометрии. Тригонометрические функции. Часть 9. Геометрия 10-11 класс. https://rutube.ru/video/22ce4c90678e252c22f2084eb1ec14a3/
Как найти гипотенузу по катету и противолежащему или прилежащему углу.
Формула основных тригонометрических отношений
Перейти к содержимому
self s
Тригонометрические отношения: В математике тригонометрия — это область знаний, которая помогает учащимся изучать треугольники. Студент должен отметить, что треугольники состоят из прямых углов. Отсюда находятся основные тригонометрические соотношения. Существует шесть основных тригонометрических соотношений, которые вычисляются по сторонам прямоугольного треугольника.
- Формула интегрирования
- Формула тригонометрии
- Триггерные идентификаторы
- Тригонометрические соотношения
- Тригонометрические функции с формулами
- Что такое тригонометрические производные
- Высота и расстояние
- Тригонометрическая формула, включающая сумму разностей идентификаторов продуктов
- Теорема Пифагора
- Формула дифференциации
- Основные идентификаторы триггеров
Тригонометрические отношения дополнительных углов
Тригонометрические отношения Основываясь на значении отношения сторон в прямоугольном треугольнике, тригонометрические отношения определяются как значения всех тригонометрических функций.
Можно сказать, что отношения сторон по отношению к любому из его острых углов представляют собой тригонометрическое отношение этого конкретного угла.
На приведенном выше рисунке видно, что это прямоугольный треугольник, а в точке B он прямоугольный. Тригонометрические отношения вычисляются по сторонам указанного выше прямоугольного треугольника и равны шести числам. Соотношения перечислены как синус, косинус, тангенс, котангенс, косеканс и секанс. Студент сможет научиться составлять таблицу тригонометрии для этих соотношений относительно определенных углов, таких как 90°,60°, 45°,30° и 0°. Тригонометрические соотношения по отношению к углу C определены ниже:
Синус угла представлен как отношение перпендикуляра к стороне AB к гипотенузе угла AC. Косинус угла представляет собой отношение стороны, примыкающей к стороне ВС, к этому углу к гипотенузе АС. Тангенс угла представлен как отношение перпендикулярной стороны АВ к этому углу стороны, примыкающей к этому углу.
Шесть тригонометрических отношений
Косеканс угла определяется как мультипликативная величина, обратная синусу. Котангенс угла представляется как мультипликативная величина, обратная тангенсу. Сеанс угла представляется как мультипликативная величина, обратная косинусу.
Тригонометрические отношения углов в радианах
Как найти тригонометрические отношения
9004 003
Таблица тригонометрических соотношений в радианах
Идентификация триггера
Основные тригонометрические отношенияТригонометрические отношенияФормула тригонометрических отношенийТригонометрические отношения углов в радианах
Полный список тригонометрических формул и тождеств [изменено]
Тригонометрия — это изучение треугольников и связей между длинами треугольников и углами в математике.
Тригонометрия и связанные с ней уравнения имеют множество применений. Триангуляция, например, используется в географии для расчета расстояния между ориентирами; в астрономии для определения расстояния до соседних звезд; и в спутниковых навигационных системах.
Тригонометрические формулыТригонометрические формулы представляют собой набор всех тригонометрических формул, использующих тригонометрические тождества для решения задач, связанных со сторонами и углами прямоугольного треугольника. Для заданных углов эти формулы тригонометрии включают тригонометрические функции, такие как синус, косинус, тангенс, косеканс, секанс и котангенс. В следующих разделах подробно объясняются пифагорейские тождества, тождества произведения, тождества кофункций (сдвига углов), тождества суммы и разности, тождества двойного угла, тождества половинного угла и т. д.
Список тригонометрических формул Когда мы впервые знакомимся с тригонометрическими формулами, мы рассматриваем только прямоугольные треугольники.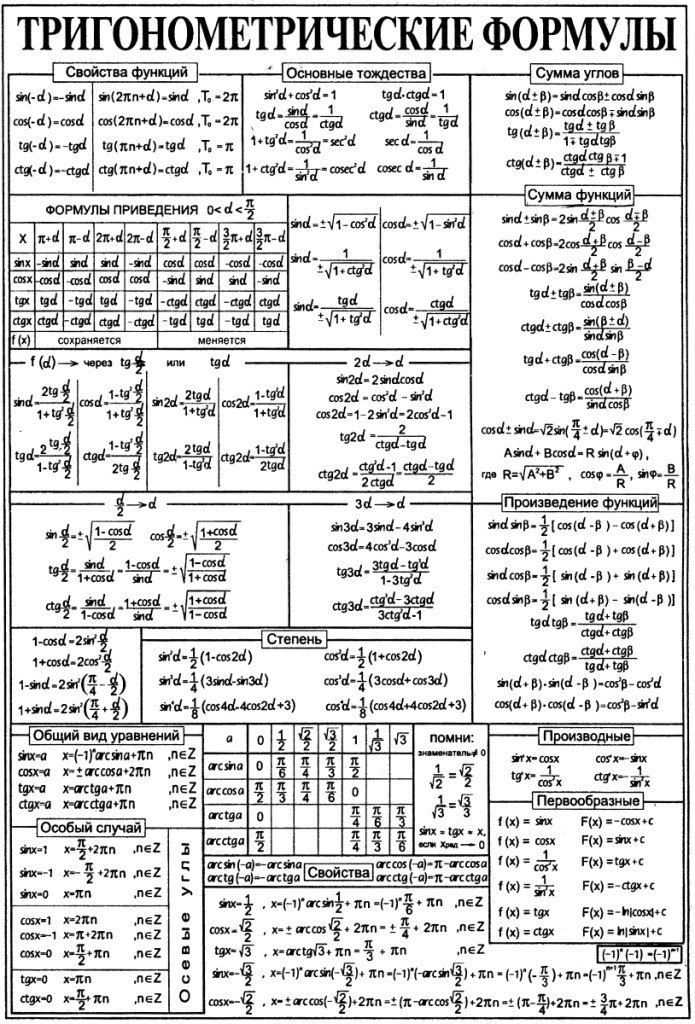
Вот список формул тригонометрии.
- Основные тригонометрические формулы
- Обратные тригонометрические формулы
- Тригонометрические тождества
- Взаимные тождества
- Периодические идентификаторы
- Совместно-функциональные личности
- Идентичности суммы и разности
- Двухугольные удостоверения
- Трёхугольные удостоверения
- Полуугольные удостоверения
- Идентификаторы продуктов
- Сумма идентификаторов продуктов
Основные тригонометрические формулы
В тригонометрии есть шесть соотношений, которые используются для нахождения элементов.
Их называют тригонометрическими функциями. Синус, косинус, секанс, косеканс, тангенс и котангенс — шесть тригонометрических функций.
Тригонометрические функции и тождества получены с использованием прямоугольного треугольника в качестве эталона:
\(sin \theta = \frac{Противоположная сторона}{Гипотенуза}\)
\(cos \theta = \frac{Смежная сторона}{Гипотенуза}\)
\(tan \theta = \frac{Противоположная сторона}{Смежная сторона}\)
\(sec \theta = \ frac{Гипотенуза}{Смежная сторона}\)
\(cosec \theta = \frac{Гипотенуза}{Противоположная сторона}\)
\(cot \theta = \frac{Смежная сторона}{Противоположная сторона }\)
Обратные тригонометрические формулыТригонометрические отношения инвертируются с помощью обратной тригонометрической формулы для получения обратных тригонометрических функций, таких как 9{-1}x\)
Тригонометрические тождества Тригонометрические тождества — это равенства, включающие тригонометрические функции, которые остаются верными для всех переменных в уравнении.
Существует несколько тригонометрических тождеств, относящихся к длине стороны и углу треугольника. Эти тождества остаются верными для прямоугольного треугольника.
Взаимные тождества\(cosec \theta = \frac{1}{sin \theta }\)
9{0} -x)=secx\) Идентичности суммы и разности Идентичности двойного угла Тройной угол 00 004 Идентификаторы половинного угла Идентичности продуктов Суммирование идентификаторов произведений Заключительные примечания Мы предоставили список всех формул тригонометрии для студентов. Эти формулы полезны для решения задач, основанных главным образом на тригонометрии. В дополнение к ним, тригонометрические тождества помогают вам разрабатывать тригонометрические формулы.