Цифры с буквенными наращениями — Гнать, дышать, держать, зависеть… — LiveJournal
В ряде случаев допускается написание порядковых числительных арабскими цифрами с наращением падежного окончания:
в 1-м ряду;
откройте 22-ю страницу;
в составе 10-го мотополка.
При этом нужно помнить следующие правила.
КАКИЕ ЧИСЛИТЕЛЬНЫЕ ЗАПИСЫВАЮТСЯ ЦИФРАМИ С НАРАЩЕНИЕМ
Цифрами с наращением записываются только порядковые числительные. Количественные числительные записываются только цифрами или словами даже в косвенных падежах.
Правильно: в 4-м квартале 2010 года, браслеты с тремя бриллиантами, браслеты с 3 бриллиантами.
Неправильно: браслеты с 3-мя бриллиантами.
КАК ПРАВИЛЬНО СОСТАВИТЬ НАРАЩЕНИЕ
Наращение должно быть:
1. Однобуквенным, если последней букве числительного предшествует гласный звук.
Правильно: 5-й (пятый, пятой), 5-я (пятая), 5-е (пятое, пятые), 5-м (пятым, пятом), 5-х (пятых)
Неправильно: 5-ый, 5-ой, 5-ая, 5-ое, 5-ые, 5-ым, 5-ом, 5-ых
2.
Двухбуквенным, если последней букве числительного предшествует согласный.
Правильно: 5-го (пятого), 5-му (пятому), 30-ми (тридцатыми)
Неправильно: 5-ого, 5-ому, 30-ыми.
КОГДА НАРАЩЕНИЕ НЕ ПИШЕТСЯ
1. С римскими цифрами: XX съезд, XXI век
2. В номерах томов, глав, страниц, иллюстраций, таблиц, приложений и т. п. — если родовое слово (том, глава и т. д.) предшествует номеру: в томе 6; главе 5; на с. 85; на рис. 8.
При этом, если родовое название элемента стоит после числительного, числительное следует писать с наращением: в 6-м томе; в 5-й главе.
3. Даты (годы и числа месяца), если слово год или название месяца следует за числом: В 1997 году; 12 декабря 1997 года. Неверно: В 1972-м году; 12-го декабря 1997-го года.
При этом, если слово год или название месяца опущено или поставлено перед числом, падежное окончание рекомендуется наращивать: в мае, числа 20-го; год 1920-й; Грянул 1917-й; Концерт перенесли с 15 мая на 22-е; 20-го же апреля.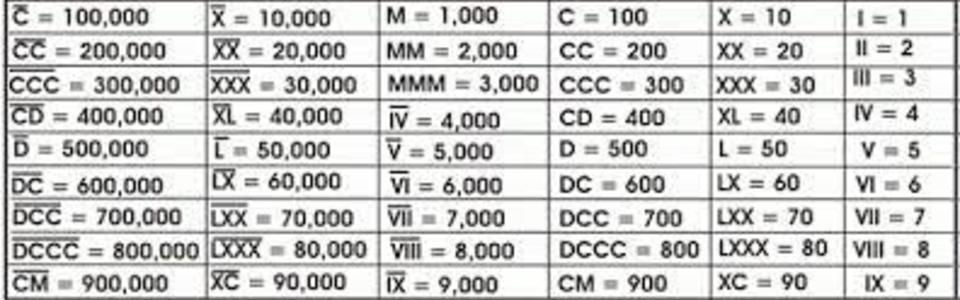
..
НАРАЩЕНИЯ ПРИ ПЕРЕЧИСЛЕНИИ
1. Если один за другим следуют два порядковых числительных через запятую или союз, то наращение пишется у обоих: 1-й, 2-й ряды; 9-е и 10-е классы.
2. Если один за другим следуют более двух порядковых числительных через запятую, точку с запятой или союз, наращение пишется только у последнего: ученики 5, 7, 9-х классов; 8, 11, 15, 18-й секторы.
3. Если подряд идут два числительных через тире, то наращение пишется:
а) только у второго, когда оно одинаковое у обоих числительных: 50—60-е годы; в 20—30-х гг.;
б) у каждого числительного, когда падежные окончания у них разные или когда предшествующие первому числительному слова управляют только им и не связаны со вторым: в 20-м—30-х секторах; в начале 70-х-80-е годы.
Пруфлинк: http://diamondsteel.ru/useful/handbook/6.html#6.2.2. (Мильчин)
Tags: грамматика
Правила публикации статей в «Археографическом ежегоднике»
Редколлегия «Археографического ежегодника» принимает к рассмотрению только оригинальные статьи или ранее не издававшиеся публикации документов, присланные файлом в формате Word, прикрепленным к электронному письму.
В письме необходимо сообщить сведения о себе: фамилия, имя и отчество полностью, ученые степень и звание, место работы (учебы) и должность, телефон и электронный адрес.
E-mail редакции: sosch@mail.ru
Статьи и публикации не должны превышать 1 п. л. (40 000 знаков с пробелами и с учетом сносок), рецензии – 0,5 п. л. (20 000 знаков), хроника – 0,25 п. л. (8 000 знаков).
Члены редколлегии знакомятся с материалами и принимают коллективное решение о публикации. Отзывы членов редколлегии и рецензентов автору не сообщаются, но направляются вопросы, замечания и предложения по тексту. В случае отрицательного решения о публикации редколлегия направляет автору мотивированный отказ.
Формат текста
При оформлении текста статьи и примечаний следует ориентироваться на нормы ГОСТ Р 7.0.11–2011.
Выравнивание основного текста – по ширине страницы
Фамилия автора, город (в скобках) – по правому краю (курсив)
Название статьи – по центру (полужирный)
Абзац – отступ 1,27 см
Междустрочный интервал – 1,5 (сверху и снизу – 0)
Шрифт – Times New Roman, размер 14
Без переносов
Буква ё ставится только в тех случаях, когда замена на е искажает смысл слова или фразы; во всех остальных случаях – только е.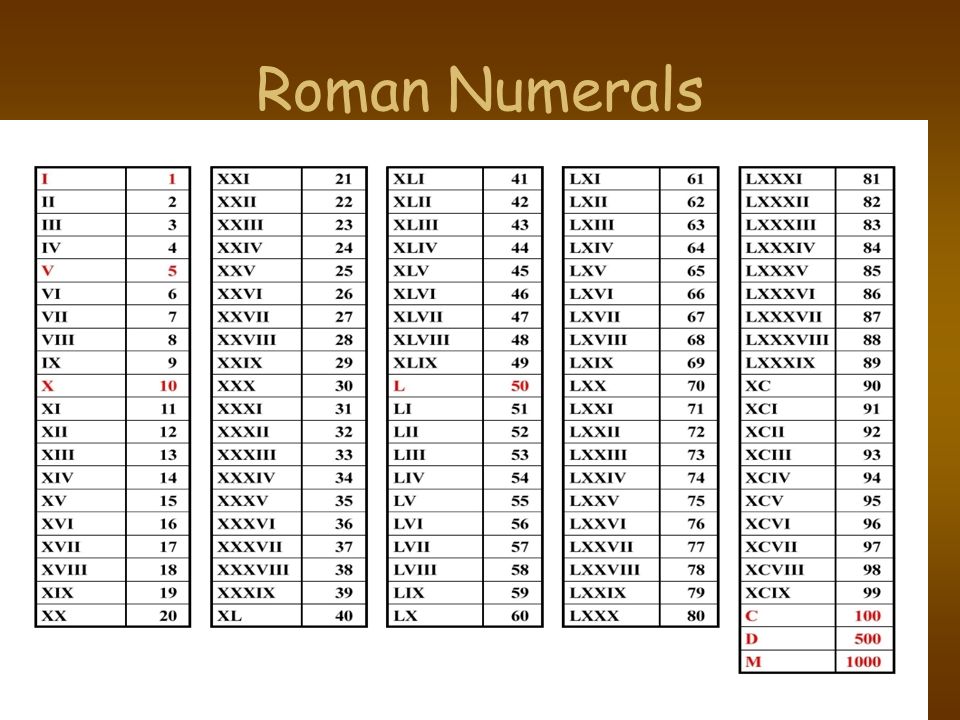
Сокращения
При первом упоминании фамилии обязательно указываются инициалы, которые разделяются пробелом и отделяются пробелом от фамилии.
Годы, обозначающие определенный период, указываются только в цифрах: 1960-е годы, 60-е годы ХХ в.
Конкретная дата дается с сокращением г. или гг.: 1861 г., 1870–1875 гг.
Век или века обозначаются римскими цифрами с сокращением в. или вв.: XVIII в., IX–XI вв.
Между цифрами ставится короткое тире (не дефис).
Допускаются сокращения: т. д., т. п., др., проч., см.
Кавычки
Кавычки только «». Если закавыченное слово (слова) находятся внутри цитаты, употребляются кавычки в кавычках: «“раз”, два, три “четыре, пять”, шесть, семь, “восемь”».
Примечания
Сноски – постраничные, автоматические, нумеруются арабскими цифрами
В конце предложения цифра сноски ставится перед точкой
Шрифт сносок: Times New Roman, размер 10
Междустрочный интервал в сносках – 1,5 (выравнивание – по ширине)
Возможны текстовые (пояснительные) сноски внизу страницы, которые обозначаются звездочкой (*)
Ф.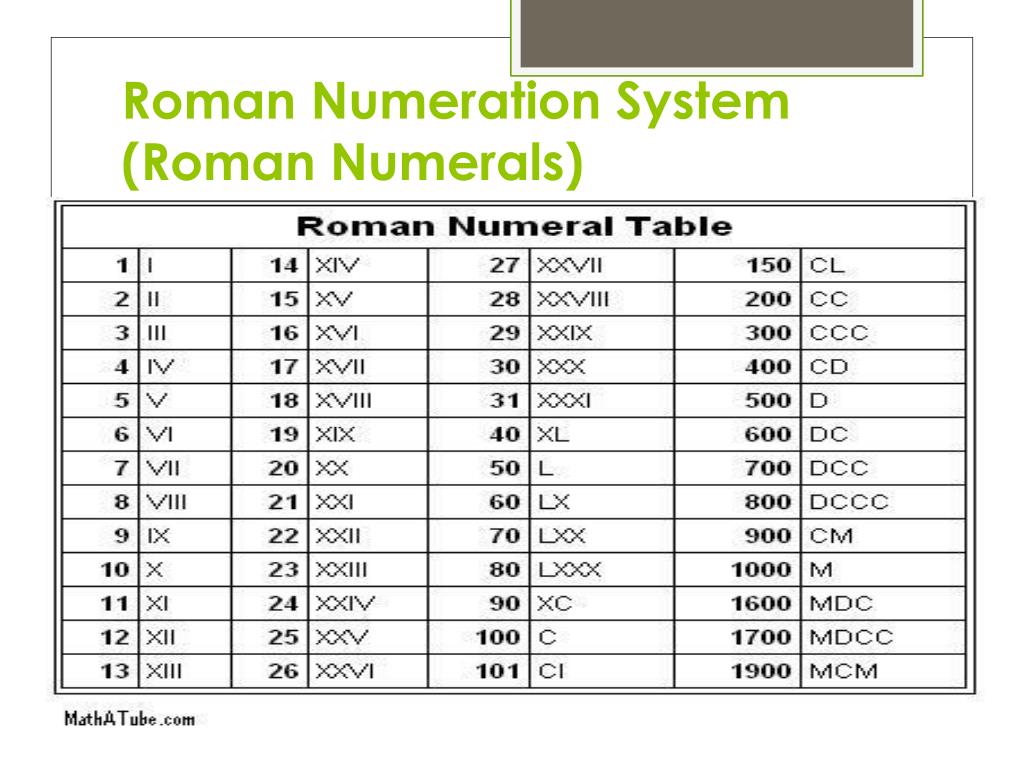
И.О. авторов в концевых сносках – курсивом. Если в сноске несколько работ одного автора, вместо Ф.И.О. – Он же (Она же).
Выходные данные: город, год (издательство не указывается, кроме случаев, когда это имеет смысловое значение). Сокращенно даются названия городов Москва, Ленинград, Петроград, Санкт-Петербург – М., Л., Пг., СПб. (остальные полностью).
Номер тома, выпуска, книги, части ставятся после выходных данных, перед указанием страниц: М., 2001. Т. 1. С. 25 (каждая позиция отделяется пробелом).
Если сноски на одну и ту же работу идут подряд, пишется: Там же (или Ibid. – для иностранных работ). При повторных упоминаниях работы указывается автор и название – полное или краткое с многоточием (без повторения выходных данных) – но не Указ. соч. или Op. cit.
Архивные сноски содержат указание на название архива (полное или краткое), номера фонда, описи, дела и листа
Несоблюдение авторами данных правил может послужить отказом в публикации статьи в ежегоднике.
Все материалы публикуются в ежегоднике бесплатно.
11th century years in numerals
| Year | Numeral | Words | ||
|---|---|---|---|---|
| 1000 | M | One thousand | ||
| 1001 | MI | Ten oh one | ||
| 1002 | MII | TEN OH TWO | ||
| 1003 | MIII | TEN OH THER | ||
| 1004 | MIV0018 | Ten oh four | ||
| 1005 | MV | Ten oh five | ||
| 1006 | MVI | Ten oh six | ||
| 1007 | MVII | Ten oh seven | ||
| 1008 | MVIII | Ten oh eight | ||
| 1009 | MIX | Ten oh nine | ||
| 1010 | MX | Ten ten | ||
| 1011 | MXI | Ten eleven | ||
| 1012 | MXII | Ten twelve | ||
| 1013 | MXIII | Ten thirteen | ||
| 1014 | MXIV | Ten fourteen | ||
| 1015 | MXV | Десять пятнадцать | ||
| 1016 | MXVI | Десять шестнадцать | ||
| 1017 | MXVII 8 | 00061018 | MXVIII | Ten eighteen |
| 1019 | MXIX | Ten nineteen | ||
| 1020 | MXX | Ten twenty | ||
| 1021 | MXXI | Ten twenty-one | ||
| 1022 | MXXII | Ten twenty-two | ||
| 1023 | MXXIII | Ten twenty-three | ||
| 1024 | MXXIV | Ten twenty-four | ||
| 1025 | MXXV | Ten twenty-five | ||
| 1026 | MXXVI | Ten twenty-six | ||
| 1027 | MXXVII | Ten twenty-seven | ||
| 1028 | MXXVIII | Ten twenty-eight | ||
| 1029 | MXXIX | Ten twenty-nine | ||
| 1030 | MXXX | Ten thirty | ||
| 1031 | MXXXI | Ten thirty-one | ||
| 1032 | MXXXII | Ten thirty-two | ||
| 1033 | MXXXIII | Ten thirty-three | ||
| 1034 | MXXXIV | Ten thirty-four | ||
| 1035 | MXXXV | Ten thirty-five | ||
| 1036 | MXXXVI | Ten thirty-six | ||
| 1037 | MXXXVII | Ten thirty-seven | ||
| 1038 | MXXXVIII | Ten thirty-eight | ||
| 1039 | MXXXIX | Ten thirty-nine | ||
| 1040 | MXL | Ten forty | ||
| 1041 | MXLI | Ten forty-one | ||
| 1042 | MXLII | Ten forty-two | ||
| 1043 | MXLIII | Ten forty-three | ||
| 1044 | MXLIV | Ten forty-four | ||
| 1045 | MXLV | Ten forty-five | ||
| 1046 | MXLVI | Ten forty-six | ||
| 1047 | MXLVII | ДЕСЯТЬ ФОТОРИДЕНИЯ | ||
| 1048 | MXLVIII | TEN FORTOT-EIGH0018 | ||
| 1050 | ML | Ten fifty | ||
| 1051 | MLI | Ten fifty-one | ||
| 1052 | MLII | Ten fifty-two | ||
| 1053 | MLIII | Ten fifty-three | ||
| 1054 | MLIV | Ten fifty-four | ||
| 1055 | MLV | Ten fifty-five | ||
| 1056 | MLVI | Ten fifty-six | ||
| 1057 | MLVII | Ten fifty-seven | ||
| 1058 | MLVIII | Ten fifty-eight | ||
| 1059 | MLIX | Ten fifty-nine | ||
| 1060 | MLX | Ten sixty | ||
| 1061 | MLXI | Ten sixty-one | ||
| 1062 | MLXII | Ten sixty-two | ||
| 1063 | MLXIII | Ten sixty-three | ||
| 1064 | MLXIV | Ten sixty-four | ||
| 1065 | MLXV | Ten sixty-five | ||
| 1066 | MLXVI | Ten sixty-six | ||
| 1067 | MLXVII | Ten sixty-seven | ||
| 1068 | MLXVIII | Ten sixty-eight | ||
| 1069 | MLXIX | Ten sixty-nine | ||
| 1070 | MLXX | Ten seventy | ||
| 1071 | MLXXI | Ten seventy-one | ||
| 1072 | MLXXII | Ten seventy-two | ||
| 1073 | MLXXIII | Ten seventy-three | ||
| 1074 | MLXXIV | Ten seventy-four | ||
| 1075 | MLXXV | Ten seventy-five | ||
| 1076 | MLXXVI | Ten seventy-six | ||
| 1077 | MLXXVII | Ten seventy-seven | ||
| 1078 | MLXXVIII | Ten seventy-eight | ||
| 1079 | MLXXIX | Ten seventy-nine | ||
| 1080 | MLXXX | Ten eighty | ||
| 1081 | MLXXXI | Ten eighty-one | ||
| 1082 | MLXXXII | Ten eighty-two | ||
| 1083 | MLXXXIII | Ten eighty-three | ||
| 1084 | MLXXXIV | Ten eighty-four | ||
| 1085 | MLXXXV | Ten eighty-five | ||
| 1086 | MLXXXVI | Ten eighty-six | ||
| 1087 | MLXXXVII | Ten eighty-seven | ||
| 1088 | MLXXXVIII | Ten eighty-eight | ||
| 1089 | MLXXXIX | Ten eighty-nine | ||
| 1090 | MXC | Ten ninety | ||
| 1091 | MXCI | Ten ninety-one | ||
| 1092 | MXCII | Десять девять-двух | ||
| 1093 | MXCIII | Ten Neinety-Three | 109417 1094949494944944949494494944949449494494944949449494494944949449494494949н. 0017 Ten ninety-four | |
| 1095 | MXCV | Ten ninety-five | ||
| 1096 | MXCVI | Ten ninety-six | ||
| 1097 | MXCVII | Ten ninety-seven | ||
| 1098 | MXCVIII | Десять девять-восьми | ||
| 1099 | MXCIX | Десять девян-девяти |
000000 Хинди-2-й.0001
Результаты обучения
- Познакомьтесь с эволюцией системы счета, которую мы используем каждый день
- Запись чисел римскими цифрами
- Преобразование между индийско-арабскими и римскими цифрами
Эволюция системы
Целые числа и разрядность
Напомним, что целых чисел начинаются с [латекс]0[/латекс] и продолжаются.
[латекс]0,1,2,3,4,5\точки[/латекс]
Каждое разрядное значение 9{2}=10\ast 10=100[/latex], [latex]1[/latex], за которым следуют 2 нуля, и так далее.
Это хороший способ быстро увидеть значение заданной степени числа десять. Теперь мы можем расширить эту идею, чтобы помещать значения в целые числа, которые действуют как счетчики количества степеней десятки.
Вызов разрядов целых чисел.
… тысяч сотен десятков единиц.
Каждое из этих значений может быть представлено в виде возрастающей степени десяти.
… 10 3 + 10 2 {0} = 2000 + 400 + 50 + 3 = 2453[/латекс].
Наша собственная система счисления, состоящая из десяти символов {0,1,2,3,4,5,6,7,8,9}, называется индуистской арабской системой . Это десятичная (десятичная) система с основанием, поскольку разрядные значения увеличиваются в десятичной степени. Кроме того, эта система является позиционной, что означает, что положение символа влияет на значение этого символа в числе. Например, положение символа 3 в числе 435 681 дает ему значение, намного большее, чем значение символа 8 в том же числе. Позже мы более подробно изучим базовые системы.
Развитие этих десяти символов и их использование в позиционной системе пришло к нам прежде всего из Индии. [1]
Рис. 10. Аль-Бируни
Только в пятнадцатом веке символы, с которыми мы знакомы сегодня, впервые сформировались в Европе. Однако история этих чисел и их развития насчитывает сотни лет. Одним из важных источников информации по этой теме является писатель аль-Бируни, фотография которого показана на рис. 10. [2] Аль-Бируни, родившийся в современном Узбекистане, несколько раз посещал Индию и делал индийская система счисления. Когда мы смотрим на происхождение чисел, с которыми столкнулся аль-Бируни, мы должны вернуться в третий век до нашей эры, чтобы исследовать их происхождение. Именно тогда использовались цифры Брахми.
Числительные Брахми были более сложными, чем те, которые используются в нашей собственной современной системе. У них были отдельные символы для чисел от 1 до 9, а также отдельные символы для 10, 100, 1000,…, а также для 20, 30, 40,… и другие для 200, 300, 400, …, 900.
Брахми символы 1, 2 и 3 показаны ниже. [3]
Эти цифры использовались вплоть до четвертого века н.э. с изменениями в зависимости от времени и географического положения. Например, в первом веке нашей эры один конкретный набор цифр Брахми принял следующую форму: [4]
Начиная с четвертого века, вы можете проследить несколько различных путей, по которым числа Брахми шли, чтобы добраться до разных точек и воплощений. Один из этих путей привел к нашей нынешней системе счисления и прошел через то, что называется цифрами Гупта. Цифры Гупта были популярны во времена правления династии Гупта и распространялись по всей империи, когда они завоевывали земли в период с четвертого по шестой век. Они имеют следующий вид: [5]
Вопрос о том, как числа попали в форму Гупта, вызывает серьезные споры. Было предложено множество возможных гипотез, большинство из которых сводится к двум основным типам. [6] Гипотеза первого типа утверждает, что числительные произошли от начальных букв названий чисел.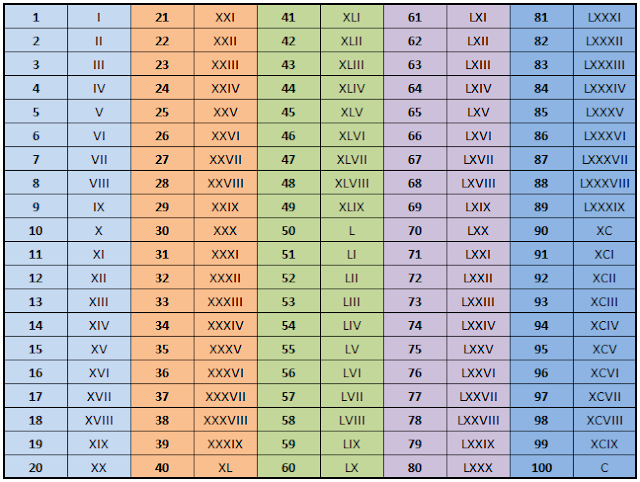
Это не редкость. . . греческие цифры развивались таким образом. Второй тип гипотезы утверждает, что они произошли от какой-то более ранней системы счисления. Однако предлагаются и другие гипотезы, одна из которых принадлежит исследователю Ифре. Его теория состоит в том, что изначально было девять цифр, каждая из которых была представлена соответствующим количеством вертикальных линий. Один из возможных вариантов: [7]
Поскольку для написания этих символов требовалось много времени, они в конечном итоге превратились в курсивные символы, которые можно было писать быстрее. Если мы сравним их с числами Гупта выше, мы можем попытаться увидеть, как мог происходить этот эволюционный процесс, но наше воображение было бы практически всем, на что нам пришлось бы полагаться, поскольку мы не знаем точно, как разворачивался этот процесс.
Числа Гупта со временем превратились в другую форму чисел, называемую цифрами Нагари, и они продолжали развиваться до одиннадцатого века, когда они выглядели следующим образом: [8]
Обратите внимание, что к этому времени появился символ 0! Однако у майя в Америке задолго до этого был символ нуля, как мы увидим позже в этой главе.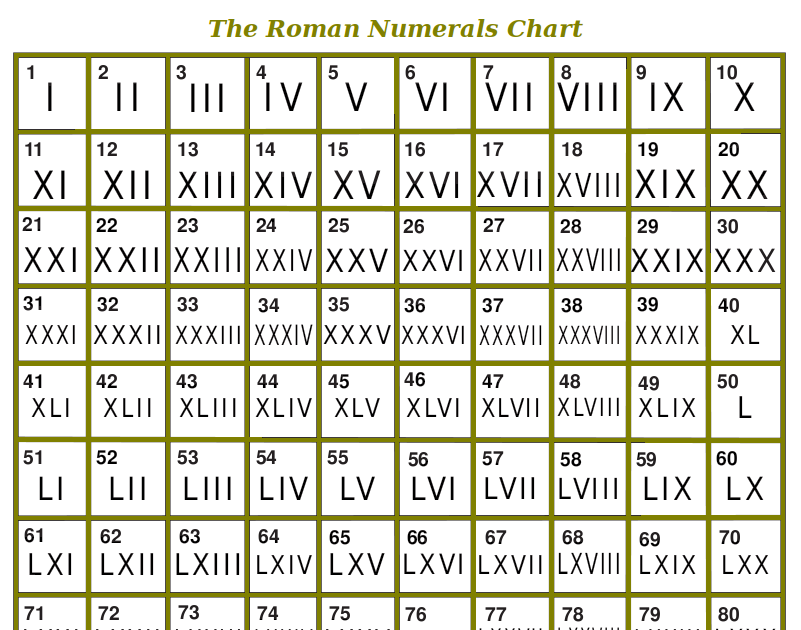
Эти цифры были приняты арабами, скорее всего, в восьмом веке во время исламских вторжений в северную часть Индии. [9] Считается, что арабы сыграли важную роль в их распространении в другие части мира, включая Испанию (см. ниже).
Другие примеры вариаций до одиннадцатого века включают: [10]
Рис. 11. Девангари, восьмой век
Рис. 12. Западно-Арабский Гобар, десятый век
числительные по мере их развития и, в конечном итоге, дошли до пятнадцатого века в Европе.
Рис. 14.
Подробнее о разрядном значении
Наша современная система счисления – позиционная . То есть любая цифра может появиться в любой позиции, и позиция, в которой она появляется, говорит нам, каково ее действительное значение в степенях десяти. По этой причине мы должны использовать нули в качестве заполнителей. 9{0}[/латекс].
Числовая система, представленная римскими цифрами , возникла в Древнем Риме ( 753 г.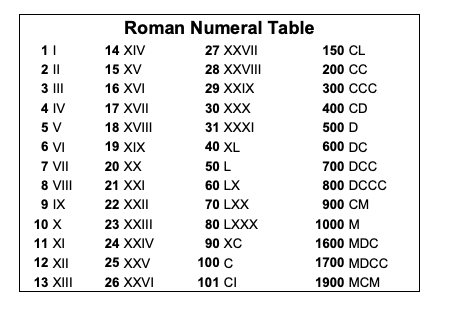
.1301–1500)). Числа в этой системе представлены комбинациями букв латинского алфавита. Римские цифры, используемые сегодня, основаны на семи символах:
| Символ 9.0836 | я | х | л | С | Д | М | |
| Значение | 1 | 5 | 10 | 50 | 100 | 500 | 1000 |
Использование римских цифр продолжалось еще долго после заката Римской империи. Начиная с 14 века римские цифры в большинстве контекстов стали заменяться более удобными индийско-арабскими цифрами; однако этот процесс был постепенным, и использование римских цифр в некоторых второстепенных приложениях сохраняется и по сей день.
Числа от 1 до 10 обычно обозначаются римскими цифрами следующим образом:
I, II, III, IV, V, VI, VII, VIII, IX, X .
Числа образуются путем объединения символов и сложения значений, поэтому II равно двум (две единицы), а XIII равно тринадцати (десять и три единицы).
Символы располагаются слева направо в порядке их значения, начиная с самого большого. Однако в некоторых конкретных случаях, чтобы избежать последовательного повторения четырех символов (например, IIII или XXXX), используется вычитательная запись: как в этой таблице:
| Число | 4 | 9 | 40 | 90 | 400 | 900 |
| Римская цифра | IV | IX | XL | ХС | компакт-диск | см |
Итого:
- I, поставленный перед V или X, означает, что на единицу меньше, поэтому четыре — это IV (на единицу меньше пяти), а девять — IX (на единицу меньше десяти)
- X, помещенный перед L или C, означает, что на десять меньше, поэтому сорок — это XL (десять меньше пятидесяти), а девяносто — XC (десять меньше ста)
- C, помещенная перед D или M, означает, что на сотню меньше, поэтому четыреста — это CD (сто меньше пятисот), а девятьсот — CM (сто меньше тысячи)
Пример
Напишите индийско-арабское число для [латекс]MCMIV[/латекс].
Показать решение
Попробуйте
Современное использование
К 11 веку индийско-арабские цифры были завезены в Европу из Аль-Андалуса через арабских торговцев и трактаты по арифметике. Однако римские цифры оказались очень устойчивыми, оставаясь широко используемыми на Западе вплоть до 14 и 15 веков, даже в бухгалтерском учете и других деловых записях (где фактические расчеты производились с использованием счетов). Замена их более удобными «арабскими» эквивалентами происходила довольно постепенно, и римские цифры до сих пор используются в определенных контекстах. Несколько примеров их текущего использования:
Испанский реал с использованием «IIII» вместо IV
- Имена монархов и пап, напр. Елизавета II Соединенного Королевства, Папа Бенедикт XVI. Их называют царственными номерами; например II произносится как «второй». Эта традиция спорадически зародилась в Европе в Средние века, получив широкое распространение в Англии только во время правления Генриха VIII.
Раньше монарх был известен не по цифре, а по эпитету, например, Эдуард Исповедник. Некоторые монархи (например, Карл IV в Испании и Людовик XIV во Франции), кажется, предпочитали использовать IIII вместо IV на своих монетах (см. Изображение выше). - Суффиксы поколений, особенно в США, для людей, носящих одно и то же имя из поколения в поколение, например Уильям Ховард Тафт IV.
- Во Французском республиканском календаре, инициированном во время Французской революции, годы нумеровались римскими цифрами – от года I (1792 г.), когда этот календарь был введен, до года XIV (1805 г.), когда от него отказались.
- Год производства фильмов, телепередач и других произведений искусства в рамках самого произведения. Было высказано предположение (возможно, в шутку) BBC News, что изначально это было сделано «в попытке скрыть возраст фильмов или телевизионных программ». [23] Вне ссылок на работу будут использоваться обычные индийско-арабские цифры.
- Часовые метки на часах. В этом контексте 4 обычно пишут IIII.
- Год постройки фасадов и краеугольных камней.
- Нумерация страниц предисловий и введения книг, а иногда и приложений.
- Номера томов и глав книги, а также несколько актов в пьесе (например, Акт III, Сцена 2).
- Продолжения некоторых фильмов, видеоигр и других произведений (как в Рокки II ).
- Контуры, в которых числа используются для отображения иерархических отношений.
- Повторяющееся грандиозное событие, например:
- Летние и зимние Олимпийские игры (например, XXI Зимние Олимпийские игры; Игры XXX Олимпиады)
- Суперкубок, ежегодный чемпионат Национальной футбольной лиги (например, Суперкубок XXXVII; Суперкубок 50 является разовым исключением [24] )
- WrestleMania, ежегодное мероприятие WWE по профессиональному рестлингу (например, WrestleMania XXX). Это использование также было непоследовательным.
Раньше монарх был известен не по цифре, а по эпитету, например, Эдуард Исповедник. Некоторые монархи (например, Карл IV в Испании и Людовик XIV во Франции), кажется, предпочитали использовать IIII вместо IV на своих монетах (см. Изображение выше).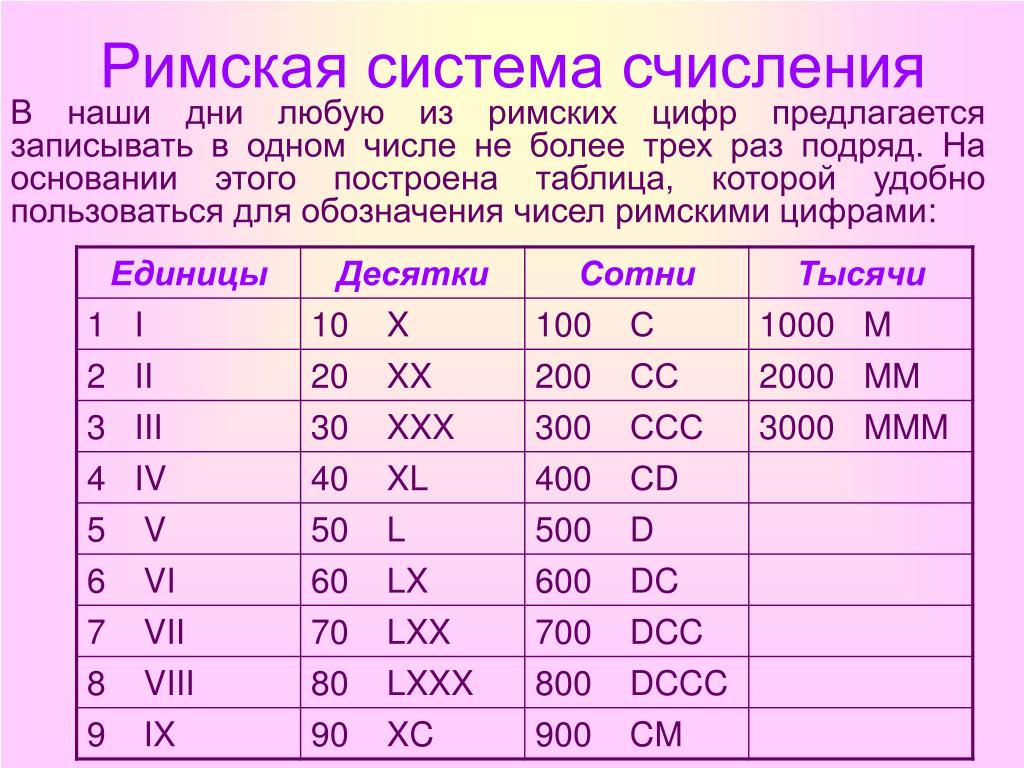
В этом контексте 4 обычно пишут IIII.- http://www-groups.
