График линейной функции | ЮКлэва
Чтобы понять то, что здесь будет написано, тебе нужно хорошо знать, что такое линейная функция.
Начнем с небольшой проверки:
- Как выглядит линейная функция в общем виде (формула)?
- Почему она называется линейной?
- Как влияет коэффициент при \( \displaystyle x\) на график линейной функции?
Если хоть один вопрос вызвал затруднения, прочти тему «Линейная функция».
Приступим к покорению линий и графиков!
График линейной функции — коротко о главном
График линейной функции – прямая линия. Прямую можно провести через две точки.
Чтобы построить график линейной функции вида y=kx+b, нужно:
- вычислить координаты любых двух точек (взять любые два значения аргумента x и вычислить соответствующие два значения y,
- для каждой пары ( x;y ) найти точку в системе координат, и провести прямую через эти две точки.

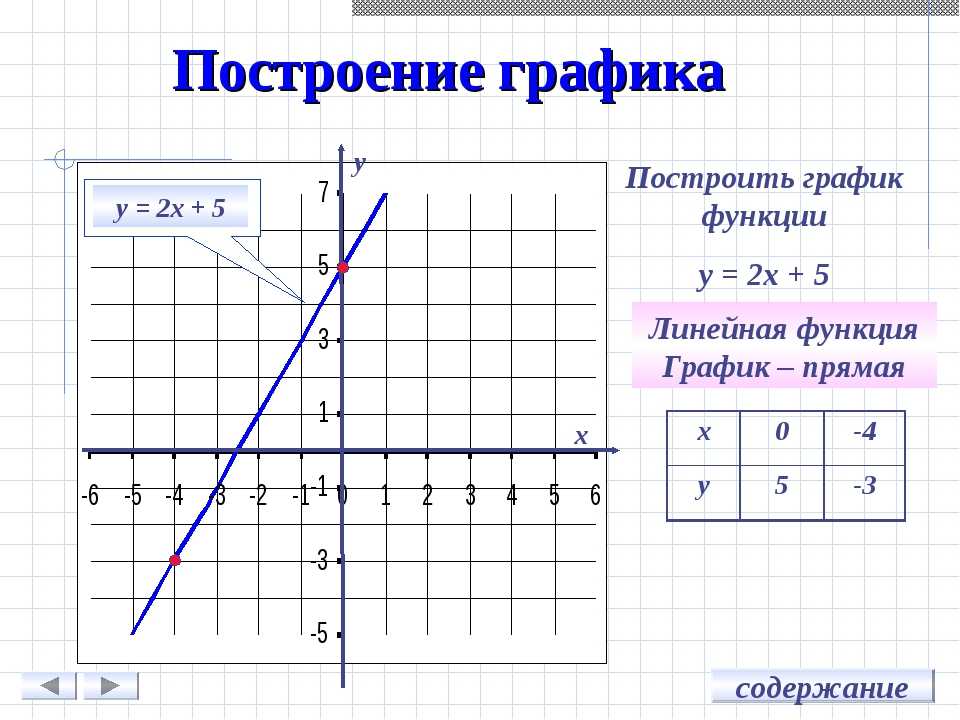
Рассмотрим пример для функции \( y=2x+1\):
Проще всего найти функцию, если аргумент: \( x=0:y\left( 0 \right)=2\cdot 0+1=1\).
Итак, первая точка имеет координаты \( \left( 0;1 \right)\).
Теперь возьмем любое другое число в качестве \( x\), например, \( x=1:y\left( 1 \right)=2\cdot 1+1=3\).
Вторая точка имеет координаты \( \left( 1;3 \right)\).
Угловой коэффициент \( \displaystyle k\) – это тангенс угла наклона прямой.
Для его нахождения выберем две точки \( \displaystyle A\) и \( \displaystyle B\) на графике и построим прямоугольный треугольник с гипотенузой \( \displaystyle AB\)
\( \displaystyle k=tg\alpha =\frac{BC}{AC}=\frac{2}{1}=2\)
Построение графика линейной функции
Итак, ты уже умеешь обращаться с линейной функцией, анализировать ее график и строить его по точкам.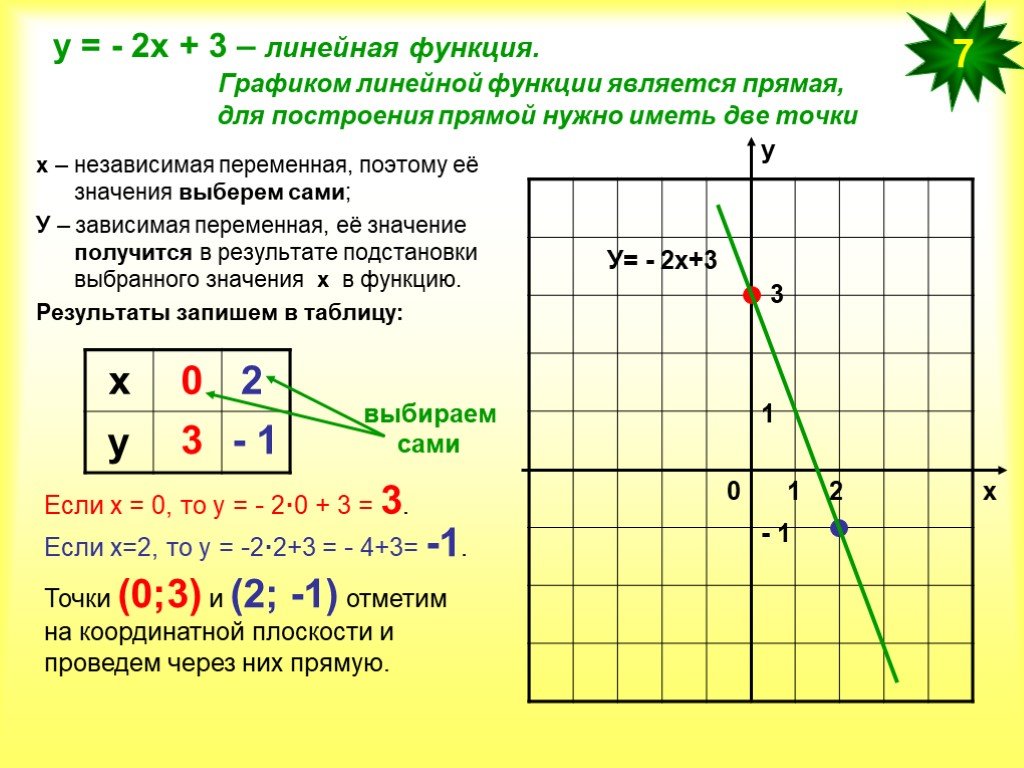 Кстати, сколько нужно точек, чтобы построить график линейной функции?
Кстати, сколько нужно точек, чтобы построить график линейной функции?
Скажу сразу, эта тема настолько простая, что много нового ты здесь не выучишь. Но ты научишься не теряться во всяких нестандартных ситуациях.
Итак, дамы и господа, линейная функция:
\( \displaystyle y=kx+b\)
Построение графика линейной функции: ты берешь два каких-либо икса, (например, \( \displaystyle 0\) и \( \displaystyle 1\)), подставляешь их в формулу, находишь соответствующие игреки.
Затем отмечаешь эти две точки на координатной плоскости, прикладываешь линейку, и график готов. Просто и быстро, и ничего выдумывать не надо.
Но бывает, что функция задана по-другому, например, неявно. Сейчас разберем, как быстро справляться с такими ситуациями.
Пример неявно заданной линейной функции
Постройте график уравнения \( \displaystyle 2y+3x=6\).
Ну а что тут сложного? Чтобы произвести построение графика линейной функции выражаем y и строим по точкам.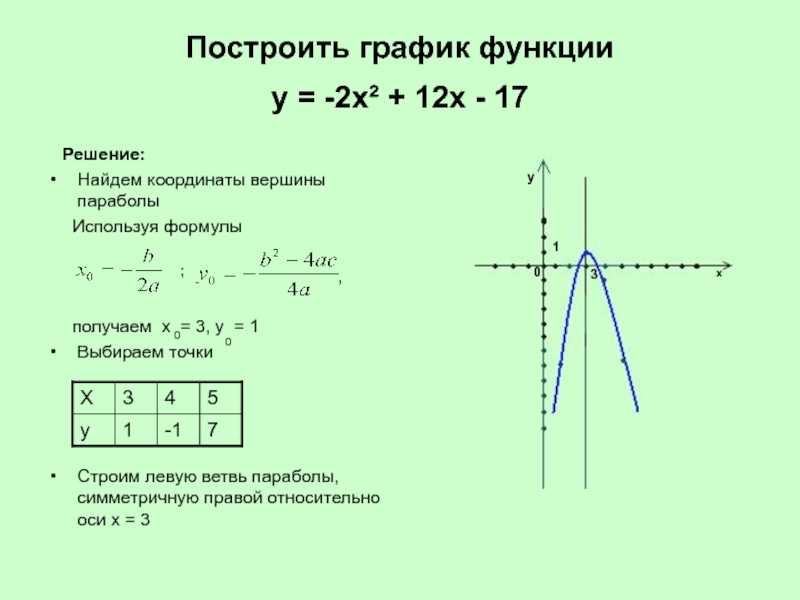
Это да, но можно сделать проще и интересней!
Выясним, в какой точке эта прямая будет пересекать ось \( \displaystyle Ox\).
Что характерно для этой точке? Правильно, \( \displaystyle y=0\). Так и пишем:
\( \displaystyle 2\cdot 0+3x=6\text{ }\Rightarrow \text{ }x=2\)
А теперь проделаем то же самое с другой осью: в какой точке график пересекает ось \( \displaystyle Oy\)?
\( \displaystyle x=0\text{ }\Rightarrow \text{ }2y+3\cdot 0=6\text{ }\Rightarrow \text{ }y=3\)
Бум! Вот и они – две точки графика. Осталось только приложить линейку:
Согласись, это было быстро и просто!
А теперь сам:
\( \displaystyle 4x-5y=3\)
Ладно, а как еще можно задать функцию?
Ну, например словесно:
Прямая проходит через точку \( \displaystyle A\left( 2;3 \right)\), а ее угловой коэффициент равен \( \displaystyle 0,75\).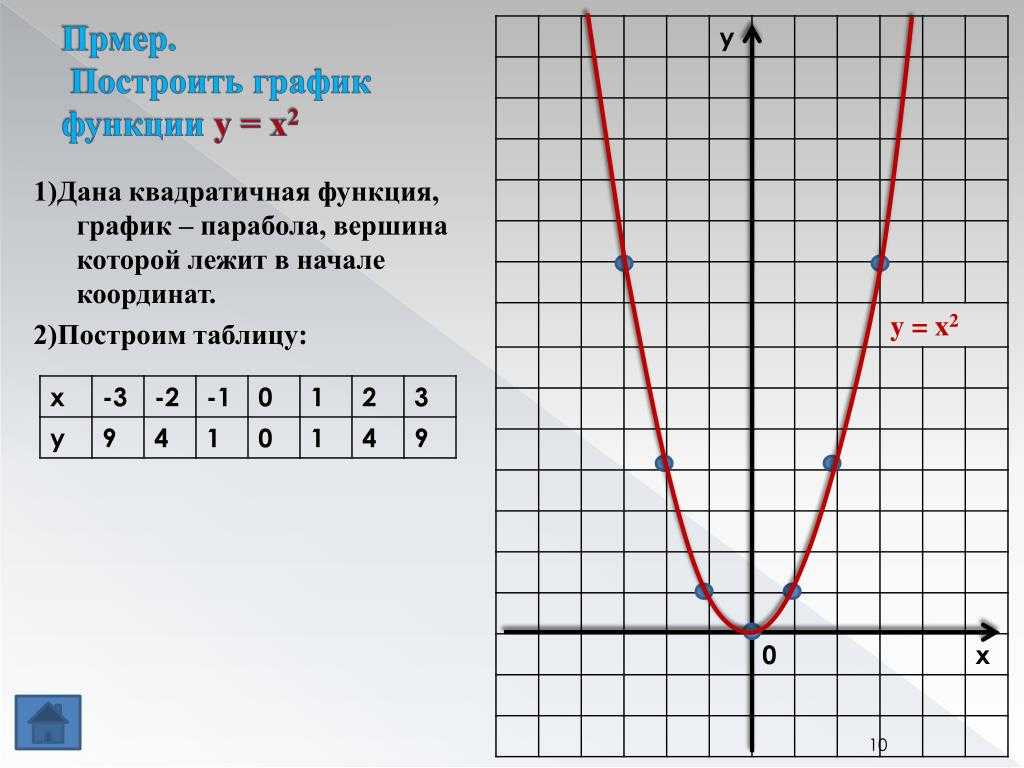
Ну что же, вспоминаем: что такое угловой коэффициент?
Что такое угловой коэффициент
Это, с одной стороны, коэффициент при \( \displaystyle x\), а с другой – это тангенс угла между прямой и осью \( \displaystyle Ox\).
Вот это мы и используем когда делаем построение графика линейной функции: ставим точку \( \displaystyle A\), и рисуем прямоугольный треугольник так, что один его катет параллелен оси \( \displaystyle Ox\), а другой – перпендикулярен.
При этом второй катет должен быть ровно в \( \displaystyle 0,75\) раз больше первого.
Очень удобно в этом случае, чтобы первый катет был равен \( \displaystyle 4\), тогда второй будет равен \( \displaystyle 3\):
4 примера построения графика линейных функций
Пример №1
Прямая, уравнение которой имеет вид \( y=-2x+b\) (\( b\) неизвестно), проходит через точку \( M\left( 1;2 \right)\).
Справился?
Должно получиться вот так:
Пример №2
Произведи построение графика линейной функции и найди уравнение прямой, проходящей через точку \( A\left( 3;1 \right)\) и параллельной прямой \( y=-1,5x+1\).
Строить график прямой \( y=-1,5x+1\) нельзя.
О, это что-то новенькое. Про параллельность прямых мы еще не учили.
Но как обычно, все просто. Нарисуем несколько параллельных прямых на координатной плоскости:
Что у них общего? Вообще, какие параметры важны для графиков? Конечно же, коэффициенты \( k\) и \( b\).
И сразу становится ясно: раз \( k\) отвечает за наклон, а наклон у них одинаковый (это же параллельные прямые, а ось \( Ox\) – секущая), значит, у них одинаковый коэффициент \( k\)!
Вернемся к задаче. Напомню условие:
Произведи построение графика линейной функции и найди уравнение прямой, проходящей через точку \( A\left( 3;1 \right)\) и параллельной прямой \( y=-1,5x+1\). {2}}-1}{x+1}=\frac{\left( x-1 \right)\left( x+1 \right)}{x+1}=x-1\)
{2}}-1}{x+1}=\frac{\left( x-1 \right)\left( x+1 \right)}{x+1}=x-1\)
Вот и все!
А, нет, не все… еще ведь ОДЗ: на ноль делить нельзя, бла бла бла…
Ладно, ничего сложного здесь нет: \( x+1\ne 0\text{ }\Rightarrow \text{ }x\ne -1\).
Это и есть все отличие от обычной прямой: просто надо будет выколоть из графика одну точку: \( y=x-5\).
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
Элементарные функции и их графики (ЕГЭ 18. Задача с параметром)
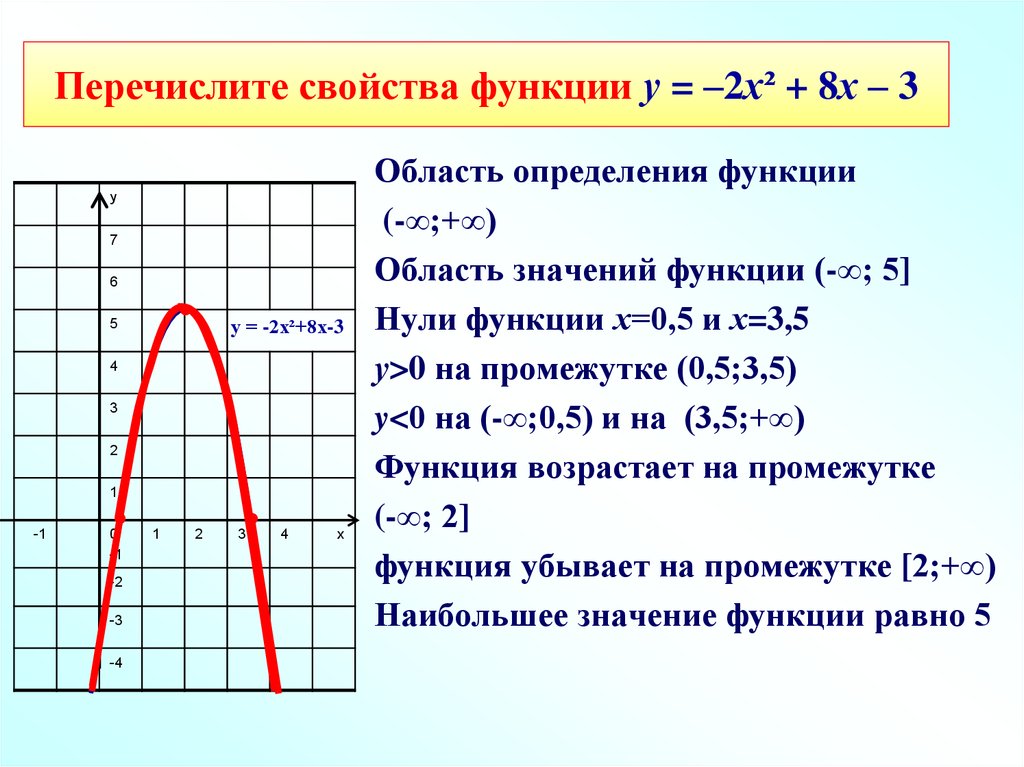
Задачи с параметром из ЕГЭ зачастую предполагают исследование функций или хотя бы знание их свойств.
Чтобы научиться исследовать функции, для начала лучше всего научиться строить их графики.
На этом уроке мы рассмотрим основные элементарные функции, научимся строить их графики и узнаем, как на них влияют разные параметры (коэффициенты в функциях).
Мы рассмотрим:
- степенную функцию (линейную, квадратичную, обратную зависимость, корни),
- тригонометрические и обратные тригонометрические,
- показательную и
- логарифмическую функции.
Преобразования графиков функций (ЕГЭ 18. Задачи с параметром)
Научились строить график какой-то функции? А что, если я теперь поменяю один из коэффициентов? Или «заключу» часть функции в модуль?
Можно ли не строить для этого новый график, а просто передвинуть/растянуть старый?
Можно! И на этом уроке мы научимся производить такие трансформации.
Благодаря таким трансформациям мы станем понимать, как выглядят графики функций при всех значениях параметра и научимся решать задачи из ЕГЭ на эту тему.
Как построить график линейной функции? | 7 класс
Содержание
Вспомним, что такое график функции:
Графиком функции называется множество точек плоскости, абсциссы которых равны значениям аргумента $x$, а ординаты – соответствующим значениям функции $y$.
Как мы уже выяснили, график линейной функции представляет из себя прямую линию.
Для его построения нет необходимости находить координаты более двух точек. То есть, чтобы построить график линейной функции, достаточно подставить в заданную формулу всего два значения $x$
Значит, нужно:
- Подставить в функцию 2 любых значения $x$ и получить соответствующие значения $y$.
- Мы получили координаты 2 точек. Отметим их на координатной плоскости.
- Проведём через эти 2 точки прямую линию.
Построим график функции $y=2x+1$
Для удобства состоим таблицу значений $x$ и $y$.
| Переменная | Значение 1 | Значение 2 |
|---|---|---|
| $x$ | ||
| $y$ |
Какие $x$ взять? Удобно брать небольшие числа, например $0$ и $1$
| Переменная | Значение 1 | Значение 2 |
|---|---|---|
| $x$ | $\color{#3D68EB}0$ | $\color{#ED7858}1$ |
| $y$ |
Теперь нужно посчитать $y$. Подставляем по очереди 2 значения $x$ в нашу функцию:
Подставляем по очереди 2 значения $x$ в нашу функцию:
$x=\color{#3D68EB}0$
$y=2x+1$
$y=2 \cdot 0 + 1 = \color{#253f8d}1$
$x=\color{#ED7858}1$
$y=2x+1$
$y=2 \cdot 1 + 1 = \color{#eb3d3d}3$
Вписываем полученные значения в таблицу и отмечаем точки:
| Переменная | Значение 1 | Значение 2 |
|---|---|---|
| $x$ | $\color{#3D68EB}0$ | $\color{#ED7858}1$ |
| $y$ | $\color{#253f8d}1$ | $\color{#eb3d3d}3$ |
Проводим через эти точки прямую линию. График готов.
{
"questions": [{
"widgets": {
"graph": {
"type": "graph",
"func": "line",
"settings": { "cells": 12 },
"answer": {
"k": 2,
"b": 1
}
}
},
"content": "Постройте график функции $y=2x+1$[[graph]]"
}, {
"widgets": {
"graph": {
"type": "graph",
"func": "line",
"settings": { "cells": 12 },
"answer": {
"k": 2,
"b": 2
}
}
},
"content": "Постройте график функции $y=2x+2$[[graph]]"
}, {
"widgets": {
"graph": {
"type": "graph",
"func": "line",
"settings": { "cells": 12 },
"answer": {
"k": 1,
"b": 1
}
}
},
"content": "Постройте график функции $y=x+1$[[graph]]"
}]
}
Доведите навык до совершенства с помощью тренажёра построения графиков линейной функции.
5
Оценить урок
Поделиться уроком →
Что можно улучшить?
Изложение материала
Непонятное объяснение
Урок неполный, не хватает информации
Урок перегружен, слишком много информации
Тесты плохого качества
Тестов недостаточно
Тестов слишком много
Тесты слишком легкие
Тесты слишком сложные
Изображения
Изображения плохого качества
Изображений недостаточно
Изображений слишком много
Другое
Войдите, чтобы оценивать уроки
Что нужно исправить?
Спасибо, что помогаете нам стать лучше!
Следующий урок
Коэффициенты k и b
GraphPad Prism 9 Руководство по подгонке кривой
Prism предлагает анализ функции графика, но фактически не анализирует никаких данных. Вместо этого он генерирует кривые из уравнения, которое вы выбираете, и параметров, которые вы вводите.
Вместо этого он генерирует кривые из уравнения, которое вы выбираете, и параметров, которые вы вводите.
Как: Построить график функции
1. Начните с любой таблицы данных или графика, нажмите «Анализ», откройте папку «Создать кривую» и выберите «Построить график функции».
2. На первой вкладке (Функция) выберите уравнение, начальное и конечное значения X и количество кривых, которые вы хотите построить.
3. На второй вкладке (Опции) выберите, хотите ли вы построить первую производную, вторую производную или интеграл функции. «Кривая» на самом деле представляет собой набор координат X и Y, которые определяют серию точек, которые соединяются, образуя кривую. Вы можете выбрать количество сегментов линии, которые будут определять кривую. Нет особых причин менять значение по умолчанию (150), если только вы не хотите отображать только часть кривой на некоторых графиках, и в этом случае вам следует увеличить это значение.
4. На третьей вкладке (Значения параметров) введите значения параметров (или щелкните значок рыболовного крючка, чтобы просмотреть анализ крючка или информацию о константах).
Советы по построению графика функции
Построение семейства кривых
Если вы решите построить более одной кривой (выбор на первой вкладке), остальная часть диалогового окна работает немного иначе.
Вы хотите, чтобы один параметр в уравнении менялся от кривой к кривой. Не определяйте это в уравнении. Вместо этого определите значения на третьей вкладке.
Вы также захотите пометить столбцы вычисляемой таблицы. Есть два способа сделать это. В нижней части второй вкладки (Параметры) укажите, хотите ли вы маркировать каждую кривую вручную (введите метки в верхней части третьей вкладки) или хотите, чтобы каждый столбец был маркирован с использованием значения одного из параметров. Последнее обычно имеет больше смысла и проще.
Если вам нужно сделать что-то более сложное, помните, что вы можете написать уравнение, чтобы некоторые строки применялись только к определенным наборам данных. Поместите перед строкой, которая относится только к столбцу A и т. д.
д.
В верхней части третьей вкладки перечислены все кривые, которые вы создадите. Выберите одну или несколько из этих кривых (или нажмите «выбрать все»), а затем введите значения параметров ниже. Часто вы захотите сначала нажать «выбрать все» и ввести большинство параметров. Затем щелкните по одной кривой за раз и введите значение параметра, которое варьируется между кривыми.
Построение каждой кривой на отдельном графике
По умолчанию Prism создает график, содержащий все кривые на одном графике. Если вы хотите, чтобы каждая кривая была на своем графике, перейдите в таблицу результатов, найдите раскрывающееся меню «Создать» на панели инструментов (выглядит как зеленый знак «плюс») и выберите «Новый график существующих данных…». В появившемся диалоговом окне выберите создание одного графика для каждого набора данных (в данном контексте набор данных — это кривая).
Если вы планируете увеличить и построить только часть кривой
Кривая определяется по умолчанию как 150 сегментов линии. Это создает гладкую кривую. Но если вы затем измените диапазон значений X, показанных на графике, будет видна только часть этих сегментов линии, и кривая может показаться грубой. Чтобы устранить эту проблему, вернитесь в диалоговое окно параметров на вкладку «Параметры» и увеличьте количество сегментов линии до гораздо большего значения.
Это создает гладкую кривую. Но если вы затем измените диапазон значений X, показанных на графике, будет видна только часть этих сегментов линии, и кривая может показаться грубой. Чтобы устранить эту проблему, вернитесь в диалоговое окно параметров на вкладку «Параметры» и увеличьте количество сегментов линии до гораздо большего значения.
Объединение двух кривых на одном графике
График ниже объединяет две построенные функции на одном графике. В первый раз, когда я построил график функции, я выбрал распределение Гаусса с X в диапазоне от -3 до 3. Я установил среднее значение на 0,0, стандартное отклонение на 1,0 и амплитуду на 100,0 (произвольно, так как я скрыл эту ось) . Затем я повторил этот анализ, но на этот раз установил диапазон X от 1,3 до 3,0. Я поместил обе кривые на один график (Изменить.. Добавить наборы данных — помните, что кривая, созданная в результате этого анализа, является «набором данных» для Prism). Для более короткой кривой я решил создать заливку области.
R Графика — Построение
❮ Предыдущая Далее ❯
Plot
Функция plot() используется для рисования точек (маркеров) на диаграмме.
Функция принимает параметры для указания точек на диаграмме.
Параметр 1 указывает точки на оси x .
Параметр 2 указывает точки на оси Y .
В самом простом случае вы можете использовать функцию plot() для построения двух чисел относительно друг друга:
Пример
Нарисуйте одну точку на диаграмме в позиции (1) и позиции (3):
plot(1, 3)
Результат:
Попробуйте сами »
Чтобы нарисовать больше точек, используйте векторы :
Пример
Нарисуйте две точки на диаграмме, одну в позиции (1, 3) и одну в позиции (8, 10):
plot(c(1, 8), c(3, 10))
Результат:
Попробуйте сами »
Несколько точек
Вы можете нанести столько точек, сколько хотите, просто убедитесь, что у вас одинаковое количество точек по обеим осям:
Пример
plot(c(1, 2, 3, 4, 5), c(3, 7, 8, 9, 12))
Результат:
Попробуйте сами »
Для лучшей организации, когда у вас много значений, лучше использовать переменные:
Пример
x <- c(1, 2, 3, 4, 5)
y <- c(3, 7, 8, 9, 12)
plot(x, y)
Результат:
Попробуйте сами »
Последовательности точек
Если вы хотите рисовать точки последовательно, на обеих осях x и ось Y , используйте оператор : :
Пример
plot(1:10)
Результат:
Попробуйте сами »
9 0014 Нарисуйте линию
График () Функция также принимает параметр типа со значением l для рисования линии, соединяющей все точки в
диаграмма:
Пример
plot(1:10, type="l")
Результат:
Попробуйте сами »
Метки графиков
Функция plot() также принимает другие параметры,
например, основной , xlab и ylab если вы хотите настроить график с основным заголовком и различными метками для
оси X и Y:
Пример
plot(1:10, main="Мой график", xlab="Ось X", ylab="Ось Y")
Результат:
Попробуйте О себе »
Внешний вид графика
Существует множество других параметров, которые можно использовать для изменения внешнего вида точек.
Цвета
Используйте col=" color " , чтобы добавить цвет к
баллы:
Пример
plot(1:10, col="red")
Результат:
Попробуйте сами »
Размер
Использование cex= номер 9 0051 изменить размер
точек ( 1 по умолчанию, а 0,5 означает на 50% меньше, и 2 означает увеличение на 100 %):
Пример
plot(1:10, cex=2)
Результат:
Попробуйте сами »
Форма точки
Используйте pch со значением от 0 до 25, чтобы изменить формат формы точки:
Пример
plot(1:10, pch=25, cex=2) 900 03
Результат:
Попробуйте сами »
Значения параметра pch находятся в диапазоне от 0 до 25, что означает, что мы можем выбрать до 26 различных типов
формы точек:
❮ Предыдущая Следующий ❯
ВЫБОР ЦВЕТА
Лучшие учебники
Учебник по HTMLУчебник по CSS
Учебник по JavaScript
Учебник How To
Учебник по SQL
Учебник по Python
Учебник по W3.
 CSS
CSS Учебник по Bootstrap
Учебник по PHP
Учебник по Java
Учебник по C++
Учебник по jQuery
9000 3
Основные каталожные номера
Справочник по HTMLСправочник по CSS
Справочник по JavaScript
Справочник по SQL
Справочник по Python
Справочник по W3.CSS
Справочник по Bootstrap
Справочник по PHP
Цвета HTML
Справочник по Java
Справочник по Angular
Справочник по jQuery
Основные примеры
Примеры HTMLПримеры CSS
Примеры JavaScript
Примеры инструкций
Примеры SQL
Примеры Python
Примеры W3.CSS
Примеры Bootstrap
Примеры PHP
Примеры Java
Примеры XML
Примеры jQuery
ФОРУМ | О
W3Schools оптимизирован для обучения и обучения. Примеры могут быть упрощены для улучшения чтения и обучения.
Учебники, ссылки и примеры постоянно пересматриваются, чтобы избежать ошибок, но мы не можем гарантировать полную правильность всего содержания.