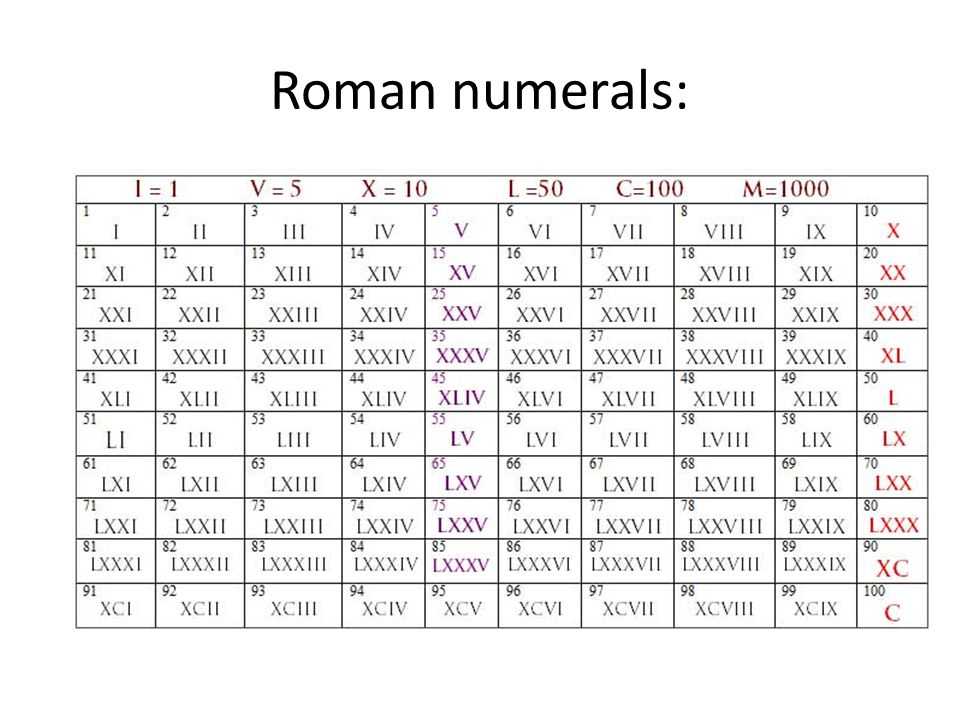
XL век до н. э.
Толкование
- XL век до н. э.
4-е тысячелетие до н. э. XLII век до н. э. — XLI век до н. э. —
XL век до н. э. — XXXIX век до н. э. — XXXVIII век до н. э.4009 4008 4007 4006 4005 4004 4003 4002 4001 4000 3999 3998 3997 3996 3995 3994 3993 3992 3991 3990 3989 3988 3987 3986 3985 3984 3983 3982 3981 3980 3979 3978 3977 3976 3975 3974 3973 3972 3971 3970 3969 3968 3967 3966 3965 3964 3963 3962 3961 3960 3959 3958 3957 3956 3955 3954 3953 3952 3951 3950 3949 3948 3947 3946 3945 3944 3943 3942 3941 3940 3939 3938 3937 3936 3935 3934 3933 3932 3931 3930 3929 3928 3927 3926 3925 3924 3923 3922 3921 3920 3919 3918 3917 3916 3915 3914 3913 3912 3911 3910 3909 3908 3907 3906 3905 3904 3903 3902 3901 3900 3899 3898 3897 3896 3895 3894 3893 3892 3891 3890 Хронологическая таблица XL век до нашей эры — промежуток времени между 1 января 4000 года до н.
 э. и 31 декабря 3901 года до н. э..
э. и 31 декабря 3901 года до н. э..События
- Возникновение цивилизации в области Плодородного полумесяца (в Месопотамии, в районе современного Ирака).
- Возникновение первых шумерских поселений в Междуречье.
- Возникновение культуры Лянчжу в Китае
- Возникновение культуры Накада в Египте.
- Возникновение культуры Ранний Дзёмон на Японских островах.
- Основана первая Корейская цивилизация. Согласно легенде, основатель — сын бога и медведицы, превратившейся в женщину.
- Использование плуга.
- Одомашнивание лошади.
- Поселенцы эпохи неолита начинают располагать свои поселения в наиболее пригодных для защиты местах, вблизи рек, на возвышенностях, в болотах. Для дополнительной защиты они также зачастую окружают их деревянными стенами, земляными насыпями и рвами.
- В разветвленной системе пещер на юге Армении, в районе границы с Ираном, обнаружены глиняные горшки и чаны, которые были изготовлены в XL веке до н.
 э. Их наличие свидетельствует о том, что уже в медном веке люди занимались виноделием.
э. Их наличие свидетельствует о том, что уже в медном веке люди занимались виноделием.
Мифология
- Согласно Беде Достопочтенному мир был сотворён 18 марта 3952 года до н. э.
- XL век до н. э. рассматривается некоторыми христианами, приверженцами Младоземельного креационизма, как период возникновения первобытной человеческой цивилизации.
- Согласно Корейским легендам, бог погоды Хванун сошёл на землю и распространил среди людей гармонию, мир и процветание. Тигр и медведица пришли к нему и попросили превратить их в людей. Бог дал им чеснок и полынь и приказал укрыться в тёмной пещере. Оба должны были прожить 100 дней питаясь только этими растениями и не видеть дневного света, чтобы стать людьми. Оба согласились и какое-то время у них всё получалось. Однако, тигр больше не смог переносить растительную пищу и бросился наружу навстречу солнцу и мясу. Даже несмотря на то, что медведица видела как легко сдался Тигр, она вытерпела до конца. Наконец сто дней прошли и медведица превратилась в прекрасную женщину.
 Бог назвал её Юэнг-Ньэо [熊女, медведица] и они поженились. У них родился сын, которого они назвали Дан-Гун [壇君]. Дан-Гун стал первым императором Кореи.
Бог назвал её Юэнг-Ньэо [熊女, медведица] и они поженились. У них родился сын, которого они назвали Дан-Гун [壇君]. Дан-Гун стал первым императором Кореи.
См. также
Это незавершённый список века. Вы можете помочь проекту, исправив и дополнив его.
Wikimedia Foundation. 2010.
Игры ⚽ Нужно сделать НИР?
- Языки Франции
- VIVA World Cup
Полезное
Как вычислять с римскими цифрами? Способы из книги о средневековой науке
Фрагменты новых книг
© Издательство «Альпина нон-фикшн»
В издательстве «Альпина нон-фикшн» выходит книга историка-медиевиста Себа Фалька «Светлые века». ТАСС публикует отрывок об арифметических операциях с римскими цифрами
Еще в эпоху Возрождения о Средних веках сложилось предубеждение как о времени темном. В «Светлых веках: Путешествии в мир средневековой науки» Себ Фальк его оспаривает. Проводником в этом путешествии служит упомянутый в отрывке английский монах Джон Вествик. Через его биографию Фальк показывает интеллектуальный ландшафт тех времен — как выясняется, совсем не пустынный.
В «Светлых веках: Путешествии в мир средневековой науки» Себ Фальк его оспаривает. Проводником в этом путешествии служит упомянутый в отрывке английский монах Джон Вествик. Через его биографию Фальк показывает интеллектуальный ландшафт тех времен — как выясняется, совсем не пустынный.
В 1396 году монахи Сент-Олбанса наконец исправили несправедливость длиной в две сотни лет, учиненную Джеффри Горэмом. Когда Джон Вествик родился, поместье Уэствик принадлежало графу Оксфорду, фавориту Ричарда II, но в 1388 году Безжалостный парламент осудил графа Роберта за измену и конфисковал его владения. Восемь лет спустя аббат Сент-Олбанса сговорился о покупке Уэствик-Горэма за 900 марок. Чтобы собрать такую внушительную сумму, пришлось скидываться, и хронист аббатства записал имена монахов и других благодетелей, которые внесли свою лепту. Он аккуратно отметил, какую сумму выделил каждый, — с помощью римских цифр:
«Предмет: получено в порядке дарения от братии и прочих как вспомоществование для покупки владения Уэствик, как то: в дар от владыки Николаса из Редклифа, архидьякона, XL марок. В дар от господина Роджера Хенрида, ризничего, VI фунтов XIII шиллингов IIII пенса. В дар от Томаса Сайдона, слуги аббата, VI фунтов XIII шиллингов IIII пенса…»
В дар от господина Роджера Хенрида, ризничего, VI фунтов XIII шиллингов IIII пенса. В дар от Томаса Сайдона, слуги аббата, VI фунтов XIII шиллингов IIII пенса…»
Список содержит имена 15 жертвователей и завершается следующими строками:
«В дар от Роберта Транча XI шиллингов & VIII пенсов. Итого: L фунтов II шиллинга VIII пенсов».
Здесь римские цифры используются вперемешку с чем-то довольно близким к позиционной системе счисления: фунтами, шиллингами и пенсами. (Вавилонская позиционная система счисления сложилась на базе единиц такого же типа, приспособившись к измеряемой величине.) В шиллинге было 12 пенсов, а в фунте — 20 шиллингов. Задача усложнялась тем, что деньги считали еще и в марках: одна марка составляла 2/3 фунта, или 13 шиллингов 4 пенса. Николас из Редклифа пожертвовал 40 марок, да и Роджер Хенрид и Томас Сайдон вряд ли намеревались внести в копилку непонятные 6 фунтов, 13 шиллингов и 4 пенса, а скорее всего, выделили круглую сумму в 10 марок. Хронист аббатства суммировал все эти марки, фунты, шиллинги и пенсы и пришел к верному результату (записав его римскими цифрами): 50 фунтов 2 шиллинга и 8 пенсов.
Хронист аббатства суммировал все эти марки, фунты, шиллинги и пенсы и пришел к верному результату (записав его римскими цифрами): 50 фунтов 2 шиллинга и 8 пенсов.
Если такие вычисления кажутся вам каким-то арифметическим подвигом, учтите, что до денежных реформ 1960-х и 1970-х годов школьникам всей бывшей Британской империи приходилось учиться складывать и вычитать двенадцатые и двадцатые доли фунтов, шиллингов и пенсов. (Чуть ли не весь остальной мир перешел на десятичную денежную систему еще в XIX веке.) Если немного попрактиковаться, сложению и вычитанию римских чисел тоже нетрудно научиться. Для начала можно представить себе X, десятку, как единицу — I, перечеркнутую линией, обозначающей, что перед нами сумма десяти таких единиц. V (пятерка) — это десятка (X), разделенная пополам горизонтально. Элементарное сложение, например VII + XVIII, нетрудно выполнить, записав все цифры рядом и переставив их для удобства местами: VIIXVIII превращается в XVVIIIII, а отсюда легко прийти к верному результату: XXV.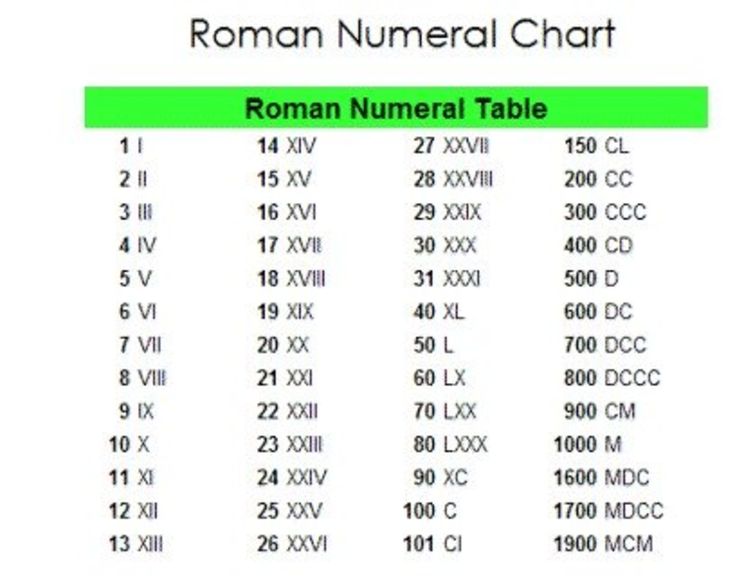
На эту тему
На самом деле подобные примеры можно решать и в уме. Для вычислений посложнее римские цифры переводили в более гибкий формат. В своем знаменитом трактате «Об исчислении времен» живший в VIII веке монах из Нортумбрии Беда Достопочтенный — выдающийся энциклопедист — знакомит читателя с двумя способами сделать это: греческая алфавитная система и метод, который он называл «очень полезным и простым умением счета на пальцах».
Как Беда и другие монахи считали на пальцах в десятичной системе? Вытяните руки перед собой, ладонями от лица. Начинать следует слева, с трех крайних пальцев левой руки. Эти три пальца, выпрямленные или полностью либо частично согнутые, показывают единицы от 1 до 9. Вот почему целые числа назывались digiti, что на латыни означает «пальцы»; отсюда и название цифровых технологий (digital). Степени десяти отсчитывали, по-разному сгибая и скрещивая большой и указательный пальцы (латинское слово «десять» — articuli — означает «костяшки»).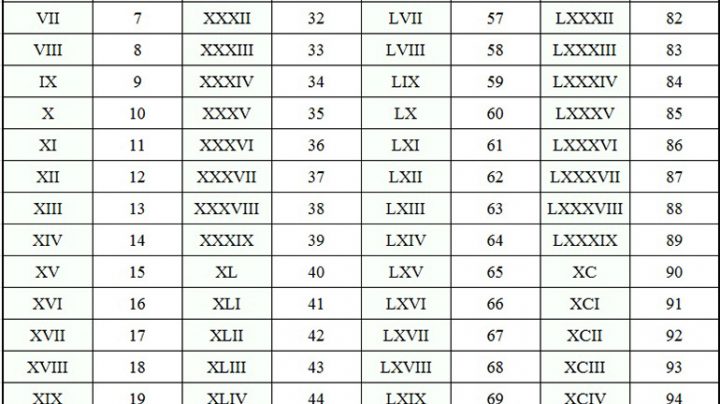 За сотни отвечали большой и указательный пальцы правой руки, а за тысячи — средний, безымянный и мизинец. Таким образом, пальцами можно было показать любое число от 0 до 9999. Пальцам присваивалось конкретное разрядное значение — тысячам, сотням, десяткам и единицам было выделено определенное место, поэтому сложение и вычитание больших чисел трудности не представляли, более того, этим способом можно было даже решать простейшие примеры на умножение.
За сотни отвечали большой и указательный пальцы правой руки, а за тысячи — средний, безымянный и мизинец. Таким образом, пальцами можно было показать любое число от 0 до 9999. Пальцам присваивалось конкретное разрядное значение — тысячам, сотням, десяткам и единицам было выделено определенное место, поэтому сложение и вычитание больших чисел трудности не представляли, более того, этим способом можно было даже решать простейшие примеры на умножение.
Самые маленькие числа откладывали на пальцах левой руки, и тому было две причины. Во-первых, в этом случае человек, который стоит к вам лицом, читает число как полагается, то есть слева направо. Жестовая арифметика служила не только для счета, но и для коммуникации. Жесты использовали на рынках, где шум и языковой барьер могли помешать разговору, или в монастырях, где нужно было соблюдать тишину. Беда даже предлагал использовать их в качестве алфавитно-цифрового кода, позволяющего передавать тайные сообщения. Во-вторых, если вы в своих вычислениях не выходите за сотню, правая рука остается свободной, и ею можно делать заметки, куда-то указывать или что-то в ней держать.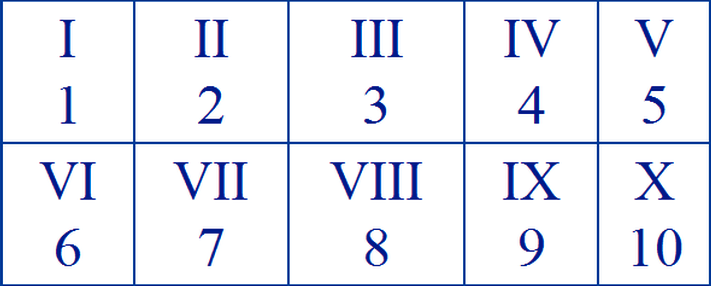 Изумительно практичная система Беды пришла прямиком из классных комнат, где монахи учились использовать руки для запоминания музыкальной грамоты и определения дат или дней солнечного и лунного циклов.
Изумительно практичная система Беды пришла прямиком из классных комнат, где монахи учились использовать руки для запоминания музыкальной грамоты и определения дат или дней солнечного и лунного циклов.
Для простых вычислений было вполне достаточно пальцев, а вот для сложных использовали calculi — камешки или фишки. Джон Вествик учился работать с числами и наверняка мастерски пользовался абаком — счетной доской. Размещение камешков на расчерченной линиями доске представляло собой разложение числа на разряды. Некоторые разновидности абаков позволяли добавить промежуточную позицию для пяти единиц, пяти десятков, пяти сотен и так далее, и тогда фишек для счета требовалось меньше. В других разновидностях сами фишки были пронумерованы цифрами от 1 до 9, и тогда абак был просто рамкой, разделяющей разряды единиц, десятков, сотен и так далее. Монахи рисовали такие рамки в книгах и манускриптах, расчерчивая их на столбцы, которые часто стилизовали под колоннады своей обители, и раскладывали там счетные фишки. В промежутки между колонками они вписывали свои вычисления.
В промежутки между колонками они вписывали свои вычисления.
На эту тему
Абаками активно пользовались вплоть до Нового времени, несмотря на широкое распространение других, более совершенных техник счета. В сочинении «Жемчужина философии», популярнейшем учебнике, написанном картезианским монахом Грегором Рейшем и выдержавшем в XVI веке 12 изданий, раздел, посвященный арифметике, начинается с гравюры, иллюстрирующей два подхода к предмету). Слева — Боэций, позднеримский теоретик свободных искусств. Еще один энциклопедист (для средневековой науки всесторонне одаренные люди не редкость), Боэций писал труды по логике, музыке и арифметике, но наибольшую известность ему принесло «Утешение философией», размышление о природе человека. Книга оставила глубокий след в веках: только на английский язык ее переводили Альфред Великий, Джеффри Чосер и Елизавета I. В этом сочинении Боэций, как многие астрономы до и после него, размышлял о необъятности Вселенной, космически малой величине Земли и холоде далеких звезд. Его присутствие на гравюре напоминает читателям, что математика — нечто большее, чем абстрактные величины.
Его присутствие на гравюре напоминает читателям, что математика — нечто большее, чем абстрактные величины.
Справа на гравюре изображена фигура равной значимости: это Пифагор. Великий греческий философ выкладывает на счетной доске числа 1241 и 82. Самая дальняя от него линия — это тысячи, следующая — сотни, и так далее, но обратите внимание: между линиями десятков и сотен выделено место для полусотен. Боэций же демонстрирует индо-арабские цифры и их преимущества для записи дробей. Между ними стоит госпожа Арифметика, ее платье украшено степенями двойки и тройки. Хотя в конечном итоге индо-арабские цифры, для операций с которыми достаточно было пера и бумаги, победили (чем они в значительной степени обязаны появлению бухгалтерского учета и сложных банковских операций), счетные доски благодаря своей бесспорной универсальности продолжали применяться и в Новое время. В умелых руках они не уступают электронным калькуляторам. В 1946 году в Токио состоялось захватывающее публичное состязание между японским абацистом и американцем, считавшим на калькуляторе.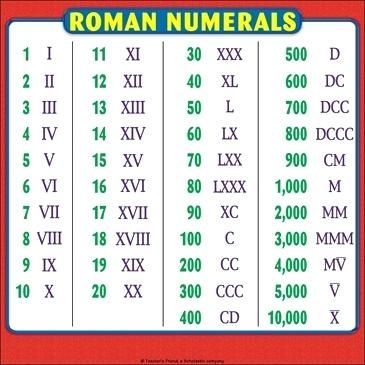 Победу одержал абацист, который в решении серии сложных математических задач продемонстрировал как невероятную скорость, так и высокую точность вычислений.
Победу одержал абацист, который в решении серии сложных математических задач продемонстрировал как невероятную скорость, так и высокую точность вычислений.
На эту тему
Менее опытным пользователям счетная доска могла пригодиться для записи промежуточных результатов вычислений. Средневековые математики знали множество способов упростить вычисления, разбивая задачу на серию операций, которые можно было произвести в уме или с помощью абака. Джон Вествик наверняка владел какими-то из них. Один способ, который называют по-разному: умножением по методу русских крестьян или египетским методом, был придуман независимо в нескольких странах, и ему вполне могли обучать и в Сент-Олбанской школе. Он сводит объемные и сложные примеры на умножение и деление к серии удвоений и делений пополам. Популярность этого метода может объяснить, почему в первых учебниках арифметики, использующей новые индо-арабские цифры, умножению и делению числа на два учили как отдельным операциям — чему-то среднему между сложением и умножением.
Красота метода удвоения и деления пополам — в том, что единственное, что вам нужно знать, — это как прибавить число к самому себе. Пусть вам нужно умножить 43 на 13. Запишите эти числа рядом и начинайте удваивать большее и делить пополам меньшее (отбрасывая остаток). Вот что у вас получится:
43 13
86 6 (отбрасываем остаток)
172 3
344 1 (отбрасываем остаток)
Когда разделить на два больше не получается, вычеркните строчки, в которых число в колонке деления четное (в нашем случае это 86; 6), и сложите числа, оставшиеся в первой колонке. У вас получится 43 х 13 = 43 + 172 + 344 = 559. Немного попрактиковавшись, можно научиться считать очень быстро — и, так как здесь используется устный счет, провернуть этот номер с римскими цифрами не труднее, чем с индо-арабскими. Метод работает, потому что основывается на том, что любое число можно разложить на степени двойки. Например, 43 х 13 = 43 х (1 + 4 + 8).
Мы оставляем только ряды с нечетными числами в колонке деления, потому что именно здесь мы «теряем» остаток, который нужно было бы прибавить в конце. Если вы умножаете на число, которое представляет собой степень двойки (например, 8), остатки не теряются: вы вычеркнете все строки, кроме последней, поскольку умножение на 8 представляет собой простую серию удвоений.
Если вы умножаете на число, которое представляет собой степень двойки (например, 8), остатки не теряются: вы вычеркнете все строки, кроме последней, поскольку умножение на 8 представляет собой простую серию удвоений.
Продолжение
То же и с делением. Скажем, вы хотите разделить 729 на 34 (или DCCXXIX на XXXIV). Просто удваивайте 34 до тех пор, пока не сможете сделать это, не переходя за 729:
XXXIV (1)
LXVIII (2)
CXXXVI (4)
CCLXXII (8)
DXLIV (16) (Удваивать 544 мы не будем, чтобы не перейти за 729.)
Теперь, начиная с нижней линии, складывайте числа (выбирая большие), чтобы подобраться как можно ближе к 729 (придется немного попрактиковаться). Когда вы это сделаете, суммируйте степени двойки, указанные рядом с вашими слагаемыми, и получите ответ. Например:
DXLIV (ряд 16) + СXXXVI (ряд 4) + XXXIV (ряд 1) = DCCXIV.
Итак, 729 / 34 = 16 + 4 + 1= 21 (остаток 15).
И снова результат можно высчитать в уме, но, если бы Джон Вествик считал с помощью абака, он обнаружил бы, что римские числа прекрасно укладываются в его колонки и расшифровать ответ несложно. А вот чтобы записать итог индо-арабскими цифрами, нужно было подумать чуть дольше.
А вот чтобы записать итог индо-арабскими цифрами, нужно было подумать чуть дольше.
Если рука набита, никакой сложности эти приемы не представляют. Овладев ими и имея счетные доски, монахи не видели необходимости отказываться от системы, которая прекрасно служила их предшественникам. Если же в силу специфики научных интересов и занятий им приходилось то и дело умножать и делить, проще было составить таблицу умножения римских чисел, а не обучаться новой арифметике с нуля. Такие справочные таблицы и счетные доски Джон Вествик всегда держал под рукой в годы учебы в Сент-Олбанской грамматической школе. Они немало ему послужили, прежде чем растущий интерес к астрономии не заставил его перейти на новые цифры и приемы умножения, принятые в индо-арабском «алгорисмусе».
Теги
Фрагменты новых книг
Цифры
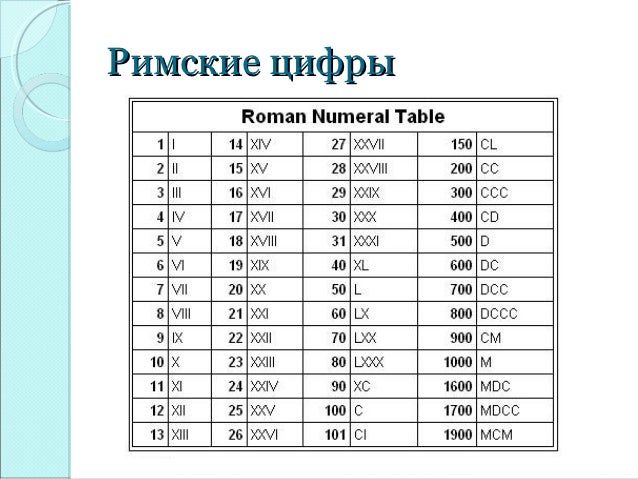
Римские цифры
В большинстве шотландских документов периода 1500-1750 гг. римские цифры или
слова используются для чисел. Лишь позднее в этот период арабский
цифры встречаются более регулярно. я для 1 на его
собственное или в конце номера будет отображаться как j. x равно 10 , L равно 50 и C равно 100 .
я для 1 на его
собственное или в конце номера будет отображаться как j. x равно 10 , L равно 50 и C равно 100 .
|
|
|
Числа как слова
Ниже приведен примерный список шотландских слов, используемых в датах и числах.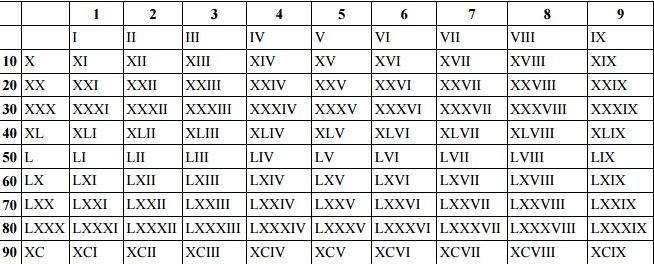 Как с
все слова, это в основном зависело от отдельного клерка, как он написал слово.
Нет ничего необычного в том, что клерки пишут одно и то же слово по-разному в
тот же документ. Приведенный ниже список является образцом и не должен восприниматься как
окончательный список.
Как с
все слова, это в основном зависело от отдельного клерка, как он написал слово.
Нет ничего необычного в том, что клерки пишут одно и то же слово по-разному в
тот же документ. Приведенный ниже список является образцом и не должен восприниматься как
окончательный список.
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Арабские цифры
Арабские цифры, записанные в шотландских документах периода 1500-1800 гг. достаточно узнаваемы (т.е. способ их написания не изменился
значительно между шестнадцатым веком и сегодняшним днем), за исключением
двух числительных: шесть и восемь.
достаточно узнаваемы (т.е. способ их написания не изменился
значительно между шестнадцатым веком и сегодняшним днем), за исключением
двух числительных: шесть и восемь.
Как видно из изображения ниже, некоторые писатели склонны преувеличивать верхний ход 6 путем удлинения и наклона по диагонали вверх.
Обратите внимание, как это соотносится с раннесовременной формой цифры восемь (т. на изображении ниже показаны 8 и 6 )
В ряду цифр может быть трудно отличить его от цифра 5 . В примере даты 1665 ниже, писатель сделал цифру 5 достаточно сложный, чтобы отличить это из предшествующих ему 6s .
Преувеличенное наклонное 6 можно спутать с буквами b , v и o . Чтобы помочь вам запомнить эту форму
раннего современного 6 , изображение ниже показывает шесть наклонных шестерок.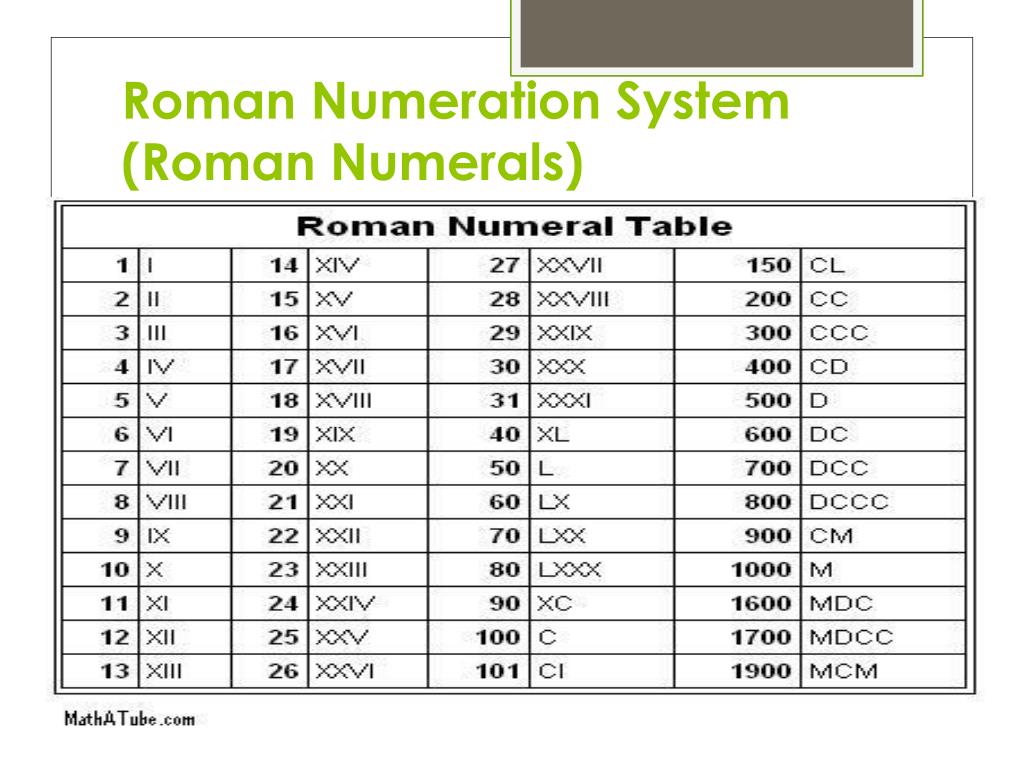
В документах семнадцатого и восемнадцатого веков число 8 часто записывается в форме, в которой верхняя петля немного смещена вправо. нижней петли, как вы можете видеть на примере ниже.
В большинстве письменных текстов это не является большой проблемой, но в строке цифры вы можете увидеть, как это можно спутать с 6 . Где цифры появляются рядом с буквами, это может быть проблемой. Сначала Ввиду того, что приведенный ниже пример можно легко спутать с иероглифами, но представляет собой сумму денег: шесть шиллингов восемь пенсов — цифра 6 , за которой следует scharfes s (представляющий Латинское слово солид , означающее шиллингов ), затем цифра 8 , затем буква d (представляющая латинское слово денариев , то есть копеек ).
Эта форма числа 8 чем-то напоминает пеликана —
верхняя петля выглядит как клюв, а нижняя — как тело пеликана.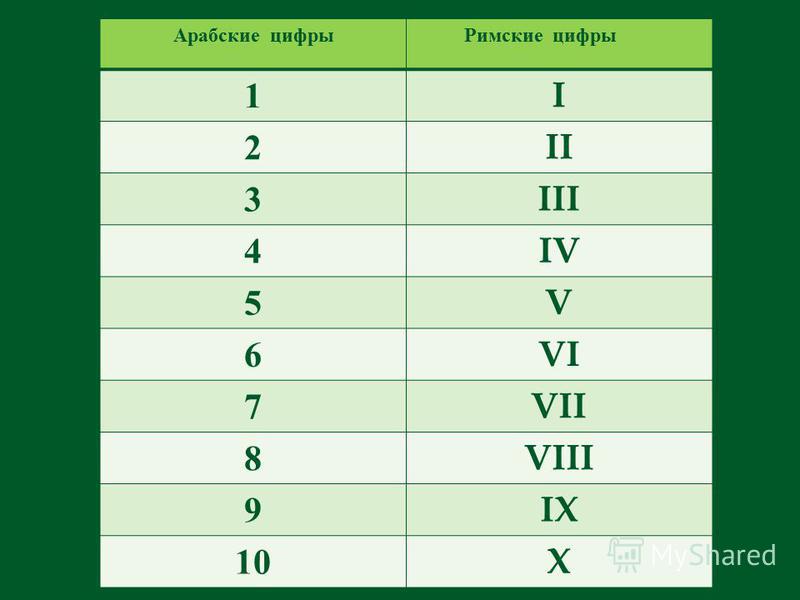 Итак, чтобы помочь вам вспомнить, что цифра, похожая на пеликана, — это 9.0007 8 , вот стая из 8 маленьких пеликанов.
Итак, чтобы помочь вам вспомнить, что цифра, похожая на пеликана, — это 9.0007 8 , вот стая из 8 маленьких пеликанов.
Финики
Деньги
Измерения
Вернуться на главную страницу Numbers.
Вы здесь: > > > > > Быстро ссылка | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Датировка
Календарные годы 1752 год был первым годом в Англии, официально
начать с 1 января. Таким образом, номер года не менялся до 25 Март, поэтому, взяв в качестве примера 1558 год, даты шли следующим образом:
Итак, если вы видите документ, датированный любым периодом между
января и 24 марта до 1752 г. Закон о календаре 1752 года внес дополнительные изменения. В 1582 году папа Григорий XIII реформировал использовавшийся тогда календарь, известный как юлианский календарь (названный в честь Юлия Цезаря). Юлианский календарь не совсем соответствовал солнечному году. Новый григорианский календарь сократил 10 дней из года в связи с корректировкой. Другие католические страны последовали и приняли григорианский календарь, но Англия, будучи протестантской, этого не сделала. Таким образом, Англия отставала от календаря нового стиля на 10 дней. К 1752 году Англия отставала от других европейских стран примерно на 11 дней. Так что в 1752 году эти дни пришлось вырезать из года, чтобы произвести корректировку. В Шотландии 1 января стало официальным начало года в 1600 г., на следующий день после 31 декабря 1599 г. Годы правленияНекоторые документы будут датированы не по календарю года, а по году царствования — как долго правящий монарх был на троне. «1 Елизавета I» означает первый год царствование Елизаветы I. Елизавета I вступила на престол 17 ноября 1558 г., поэтому 1 Елизавета I означает период между 17 ноября 1558 г. и 16 ноября 1559 г.. Остерегайтесь документов, написанных в царствование
Карла II. Хотя он вступил на престол в мае 1660 г., после
периода Содружества, он фактически рассчитал свое царствование
год, начиная с 30 января 1649 года, даты казни
своего отца Карла I. Так что документы написаны в первый же год, что
Карлу II было лет, действительно лет на троне на самом деле было бы 12 лет. Для получения дополнительной информации о датах (включая дни святых, годы царствования, религиозные праздники и сроки суды) см. C.R. Cheney and M. Jones (eds), «A Handbook дат: для студентов, изучающих британскую историю» (Кембриджский университет Press, ред. 2000 г.). ЦифрыВерх стр. Арабские цифры не использовались в Англии до XVI века, и даже после этого римские цифры продолжали использоваться. Сегодня большинство людей все еще знакомы с классические римские цифры. Однако знайте, что вы найдете несколько иначе они представлены в документах, написанных по-английски. В частности, использовался нижний регистр. «1» сама по себе, или в конце числа, обычно обозначался буквой «j».
Подсчет проводился в баллах (балл = 20),
поэтому вы часто будете сталкиваться с чем-то вроде этого: Порядковые номера представлены верхним индексом
буквы, следующие за ними, как и сегодня. xxiiij -й = 24 -й Но примечание xxij -й = «два и двадцатый», то есть 22 -й . ДеньгиВерх стр. Деньги рассчитывались в фунтах, шиллингах и пенсы. Один фунт = 20 шиллингов. Фунт был представлен либо с помощью «ли», либо £: запишите оба со знаком £ перед отданная сумма. Этот символ на самом деле представляет собой тщательно продуманную букву «L», от латинское «весы», что означает фунт. Сравните символ примерно фунт в весе, который представлен «фунт» — это происходит от такой же. Один шиллинг = 12 пенни. Шиллинг был представлена буквой «s», первоначально сокращенной от «solidos», римской монеты. Один пенни = два полпенни или четыре фартинга. Пенни был представлен буквой «d», сокращенно от «динарий», римской монеты. Полпенни = 2 фартинга. Один фартинг = четверть пенни. Фартинг был представлен «qua», сокращением от «quadrans». 4-пенсовая монета называлась крупой. Была также сумма денег, известная как метка. Марка была не реальной монетой, а суммой. Это стоило две трети фунта, то есть 13 шиллингов 4 пенса. Половина балла (одна треть фунт) составлял поэтому 6 шиллингов 8 пенсов. При расшифровке документов, в которых упоминаются суммы денег, не расширяйте аббревиатуры типа ли, об и т.д. Оставьте сокращайте их, и не забудьте транскрибировать li как «£». Они никогда не были выписаны полностью. РазмерыВерх на странице Измерения площади даны в акрах (сокращенно на «а»), руды («р») и насесты («р»). 40 окуней = 1 руда 4 руды = 1 акр Путаница возникает из-за того, что насест
также является мерой длины. ОкругаВерх стр. Список исторических английских графств и их стандарт сокращения
Когда вы видите эти сокращения, как указано выше, в документах, не расширяйте их, а оставьте сокращенными. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 э. и 31 декабря 3901 года до н. э..
э. и 31 декабря 3901 года до н. э.. э. Их наличие свидетельствует о том, что уже в медном веке люди занимались виноделием.
э. Их наличие свидетельствует о том, что уже в медном веке люди занимались виноделием.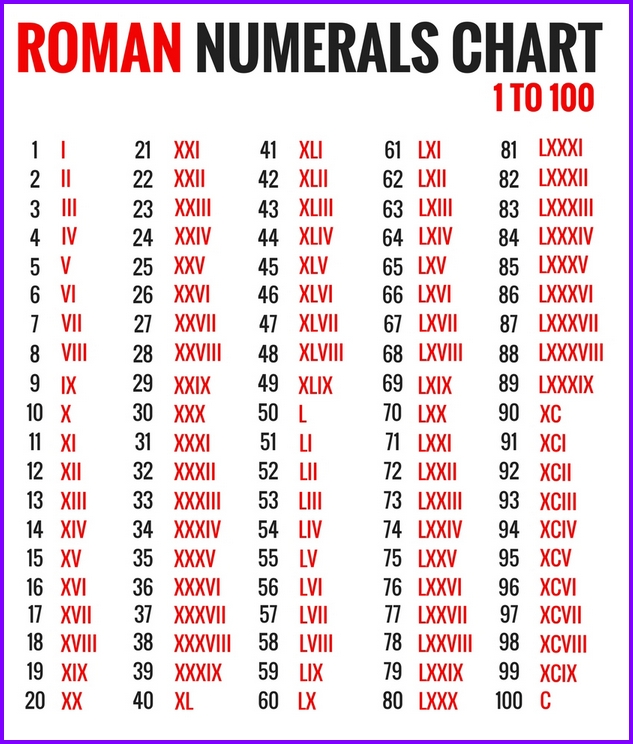 Бог назвал её Юэнг-Ньэо [熊女, медведица] и они поженились. У них родился сын, которого они назвали Дан-Гун [壇君]. Дан-Гун стал первым императором Кореи.
Бог назвал её Юэнг-Ньэо [熊女, медведица] и они поженились. У них родился сын, которого они назвали Дан-Гун [壇君]. Дан-Гун стал первым императором Кореи. До Календарного акта 1752 г.
Англия официально началась 25 марта (День леди), а не 1 января.
(хотя это было во время празднования Нового года).
До Календарного акта 1752 г.
Англия официально началась 25 марта (День леди), а не 1 января.
(хотя это было во время празднования Нового года).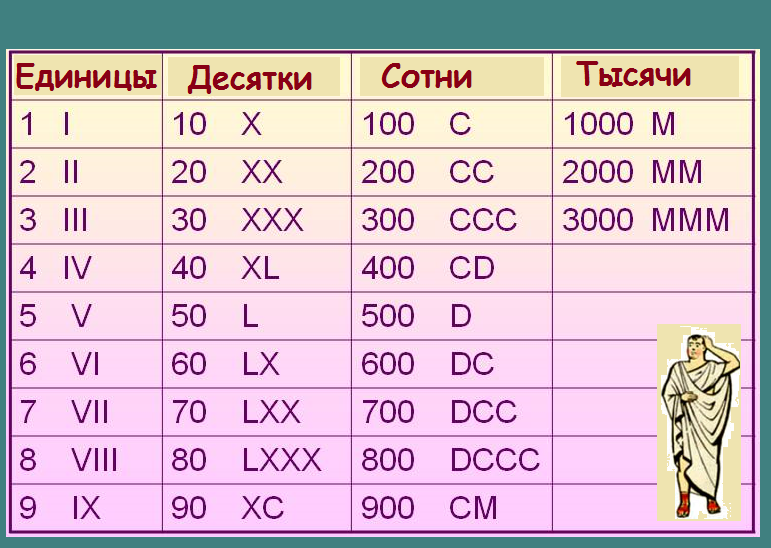 , имейте в виду, что, говоря современным языком,
нужно добавить год. В публикациях вы можете увидеть это написано
как январь 1750/51, год, как он был известен в то время /
год, каким мы его знаем сейчас. Это также известно как ОС (старый стиль) и
НС (новый стиль).
, имейте в виду, что, говоря современным языком,
нужно добавить год. В публикациях вы можете увидеть это написано
как январь 1750/51, год, как он был известен в то время /
год, каким мы его знаем сейчас. Это также известно как ОС (старый стиль) и
НС (новый стиль). Поэтому за средой, 2 сентября 1752 г., сразу же последовал четверг, 14 сентября.
Поэтому за средой, 2 сентября 1752 г., сразу же последовал четверг, 14 сентября. Карл II.
Карл II. я обычно ставили точки, если они представляли
числа).
я обычно ставили точки, если они представляли
числа).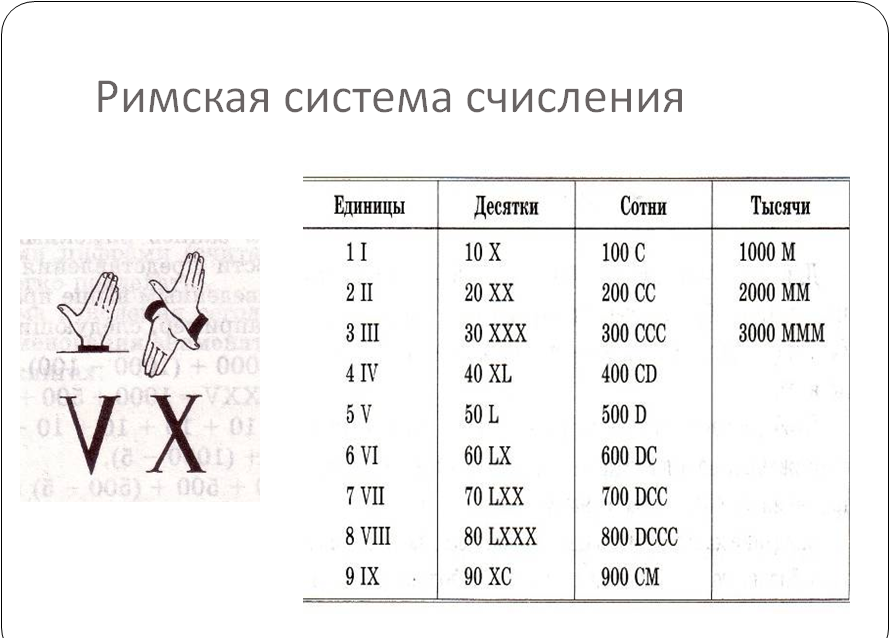
 Полпенни был
представлен «об», сокращение от «оболус», римская монета.
Полпенни был
представлен «об», сокращение от «оболус», римская монета.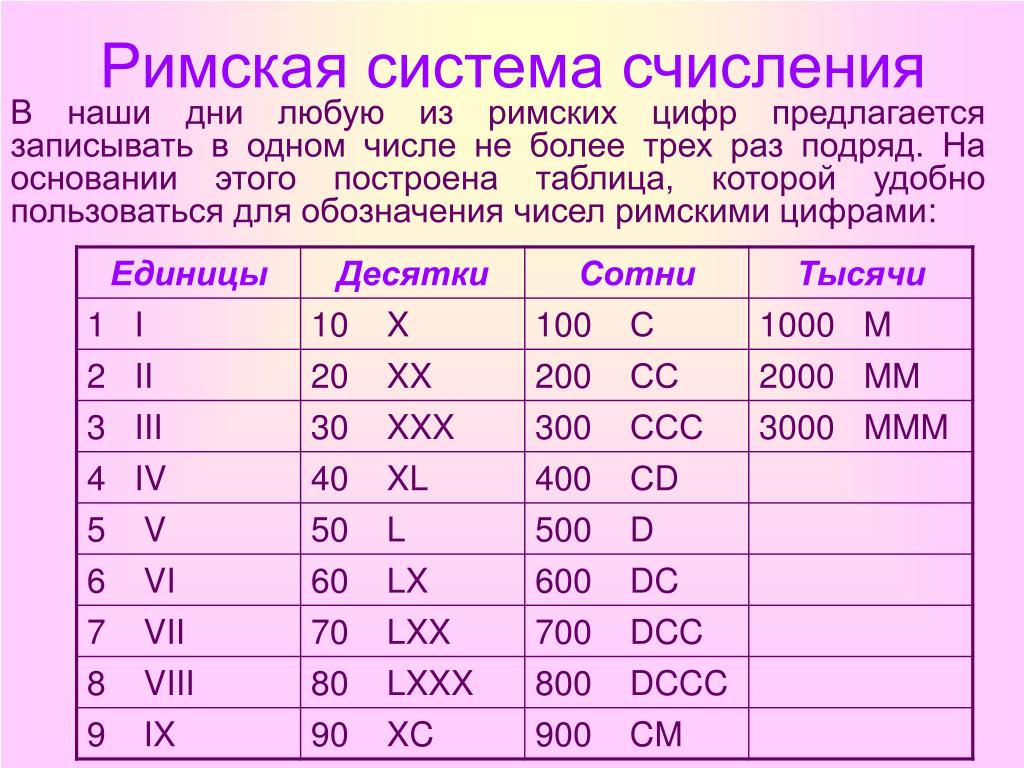 Окунь, шест и удочка — все термины
для измерения длины примерно 5 метров (5,5 ярдов).
Для получения дополнительной информации об измерении см. Colin Chapman, How
тяжелый, сколько и как долго?: гири, деньги и другие меры
использовали наши предки» (Лохин, 1995).
Окунь, шест и удочка — все термины
для измерения длины примерно 5 метров (5,5 ярдов).
Для получения дополнительной информации об измерении см. Colin Chapman, How
тяжелый, сколько и как долго?: гири, деньги и другие меры
использовали наши предки» (Лохин, 1995).