Формула периметр основания пирамиды: Периметр и апофема правильной пирамиды

Площадь поверхности правильной пирамиды формулы и калькулятор

{S_{полн} = \dfrac{1}{2}PL + S}

Найти площадь

полной поверхностибоковой поверхности

Тип пирамиды

правильнаяправильная треугольнаяправильная четырехугольнаяправильная шестиугольная

Через

периметр, площадь и апофемусторону основания и высоту

Периметр основания P

ммсмдммкмдюймы (in)футы (ft)

Апофема L

ммсмдммкмдюймы (in)футы (ft)

Площадь основания S

мм²см²дм²м²км²кв. дюймы (in²)кв. футы (ft²)

Результат в

мм²см²дм²м²км²кв. дюймы (in²)кв. футы (ft²)

Виджет

Ссылка на расчет

Сообщить об ошибке

Сохранить расчет

Печатать

На странице вы найдете онлайн-калькуляторы, которые помогут найти площадь полной и боковой поверхности правильной пирамиды, а также треугольной, четырехугольной и шестиугольной пирамиды. Кроме того приводятся формулы, по которым вы можете произвести расчет самостоятельно.

1. калькулятор площади поверхности пирамиды
2. формула площади полной поверхности правильной пирамиды через периметр, площадь и апофему
3. формула площади полной поверхности правильной пирамиды через сторону основания и высоту
4. формула площади полной поверхности правильной треугольной пирамиды через сторону основания и апофему
5. формула площади полной поверхности правильной треугольной пирамиды через сторону основания и боковую грань
6. формула площади полной поверхности правильной треугольной пирамиды через сторону основания и высоту
7. формула площади полной поверхности правильной четырехугольной пирамиды через сторону и боковую грань
8. формула площади полной поверхности правильной четырехугольной пирамиды через сторону и высоту
9. формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и апофему
10. формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и апофему
11. формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
12. формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и высоту
13. формула площади боковой поверхности правильной пирамиды через периметр и апофему
14. формула площади боковой поверхности правильной пирамиды через сторону основания и высоту
15. формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и апофему
16. формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и боковую грань
17. формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и высоту
18. формула площади боковой поверхности правильной треугольной пирамиды через периметр основания и апофему
19. формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и апофему
20. формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
21. формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и высоту
22. формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и апофему
23. формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
24. формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и высоту
25. примеры задач

Познакомьтесь с важными понятиями, которые необходимо знать для расчета площади поверхности пирамиды.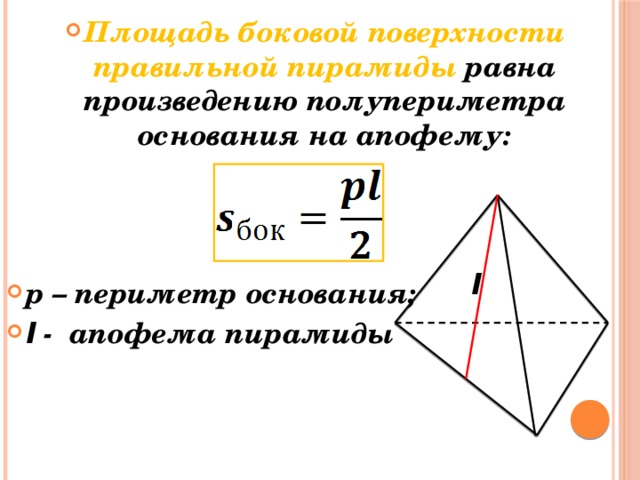

Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину.

Правильная пирамида – это пирамида, основанием которой является правильный многоугольник, а вершина фигуры проецируется в центр ее основания.

Площадь полной поверхности пирамиды — это сумма площадей боковых граней и площади основания.

Площадь боковой поверхности пирамиды — это совокупная площадь всех боковых граней пирамиды.

Апофема — перпендикуляр, опущенный из вершины пирамиды на ребро основания.

Формула площади полной поверхности правильной пирамиды через периметр, площадь и апофему

{S_{полн} = \dfrac{1}{2}PL+S}

P — периметр основания пирамиды

L — апофема пирамиды

S — площадь основания пирамиды

Формула площади полной поверхности правильной пирамиды через сторону основания и высоту

{S_{полн} = \dfrac{na}{2} {\Bigg( \dfrac{a}{2 \\tg ( \dfrac{180°}{n})} + \sqrt{h^2+ \Bigg( \dfrac{a}{2 \\tg ( \dfrac{180°}{n})} \Bigg) ^2} \Bigg)}}

a — сторона основания пирамиды

h — высота пирамиды

n — число сторон основания

Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и апофему

{S_{полн} = \dfrac{a^2 \sqrt{3}+6aL}{4}}

a — сторона основания пирамиды

L — апофема пирамиды

Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и боковую грань

{S_{полн} = \dfrac{a^2 \sqrt{3}+6a \sqrt{b^2 — \dfrac{a^2}{4}}}{4}}

a — сторона основания пирамиды

b — боковая грань пирамиды

Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и высоту

{S_{полн} = \dfrac{3a}{2} {\Bigg( \dfrac{a}{2 \tg ( 60°)} + \sqrt{h^2+ \Bigg( \dfrac{a}{2 \tg ( 60°)} \Bigg) ^2} \Bigg)}}

a — сторона основания пирамиды

h — высота пирамиды

Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань

{S_{полн} = a^2 + 2a \sqrt{b^2- \dfrac{a^2}{4}}}

a — сторона основания пирамиды

b — боковая грань пирамиды

Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и высоту

{S_{полн} = 2a {\Bigg( \dfrac{a}{2 \tg ( 45°)} + \sqrt{h^2+ \Bigg( \dfrac{a}{2 \tg ( 45°)} \Bigg) ^2} \Bigg)}}

a — сторона основания пирамиды

h — высота пирамиды

Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и апофему

{S_{полн} = a^2+2aL}

a — сторона основания пирамиды

L — апофема пирамиды

Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и апофему

{S_{полн} = \dfrac{3\sqrt{3}a^2}{2}+3aL}

a — сторона основания пирамиды

L — апофема пирамиды

Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань

{S_{полн} = \dfrac{3\sqrt{3}a^2}{2}+3a\sqrt{b^2-\dfrac{a^2}{4}}}

a — сторона основания пирамиды

b — боковая грань пирамиды

Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и высоту

{S_{полн} = 3a {\Bigg( \dfrac{a}{2 \tg ( 30°)} + \sqrt{h^2+ \Bigg( \dfrac{a}{2 \tg ( 30°)} \Bigg) ^2} \Bigg)}}

a — сторона основания пирамиды

h — высота пирамиды

Формула площади боковой поверхности правильной пирамиды через периметр и апофему

{S_{бок} = \dfrac{1}{2}PL}

P — периметр основания пирамиды

L — апофема пирамиды

Формула площади боковой поверхности правильной пирамиды через сторону основания и высоту

{S_{бок} = \dfrac{na}{2} \sqrt{h^2+ \Bigg( \dfrac{a}{2 \tg ( \dfrac{180°}{n})} \Bigg) ^2} }

a — сторона основания пирамиды

h — высота пирамиды

n — число сторон основания

Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и апофему

{S_{бок} = \dfrac{3}{2}aL}

a — сторона основания пирамиды

L — апофема пирамиды

Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и боковую грань

{S_{бок} = \dfrac{3a \sqrt{b^2 — \dfrac{a^2}{4}}}{2}}

a — сторона основания пирамиды

b — боковая грань пирамиды

Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и высоту

{S_{бок} = \dfrac{3a}{2} \sqrt{h^2+ \Bigg( \dfrac{a}{2 \tg ( 60°)} \Bigg) ^2}}

a — сторона основания пирамиды

h — высота пирамиды

Формула площади боковой поверхности правильной треугольной пирамиды через периметр основания и апофему

{S_{бок} =\dfrac{1}{2}PL}

P — периметр основания пирамиды

L — апофема пирамиды

Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и апофему

{S_{бок} = 2aL}

a — сторона основания пирамиды

L — апофема пирамиды

Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань

{S_{бок} = 2a \sqrt{b^2 — \dfrac{a^2}{4}}}

a — сторона основания пирамиды

b — боковая грань пирамиды

Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и высоту

{S_{бок} = 2a \sqrt{h^2+ \Bigg( \dfrac{a}{2 \tg ( 45°)} \Bigg) ^2}}

a — сторона основания пирамиды

h — высота пирамиды

Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и апофему

{S_{бок} = 3aL}

a — сторона основания пирамиды

L — апофема пирамиды

Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань

{S_{бок} = 3a\sqrt{b^2-\dfrac{a^2}{4}}}

a — сторона основания пирамиды

b — боковая грань пирамиды

Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и высоту

{S_{бок} = 3a \sqrt{h^2+ \Bigg( \dfrac{a}{2 \tg ( 30°)} \Bigg) ^2}}

a — сторона основания пирамиды

h — высота пирамиды

Примеры задач на нахождение площади поверхности пирамиды

Задача 1

Стороны основания правильной четырехугольной пирамиды равны 60см, боковые ребра равны 78см. 2} = 60 \: см²

Ответ: 60 см²

Проверка .

Геометрия 10-11 класс. Пирамида — math200.ru

Skip to content

Геометрия 10-11 класс. Пирамидаadmin2022-11-30T21:50:23+03:00

Скачать файл в формате pdf.

Геометрия 10-11 класс. Пирамида

Пирамидой называется многогранник, который состоит из плоского многоугольника – основания пирамиды, точки, не лежащей в плоскости основания,– вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания. Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами. Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания. Пирамида называется n-угольной, если ее основанием является n-угольник. Треугольная пирамида называется также тетраэдром.

Пирамида называется правильной, если ее основанием является правильный многоугольник, а основание высоты совпадает с центром этого многоугольника. Очевидно, у правильной пирамиды боковые ребра равны; следовательно, боковые грани – равные равнобедренные треугольники. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.

Площадь боковой поверхности правильной пирамиды вычисляется по формуле:\({S_{{\text{бок}}{\text{.пов}}}} = \frac{1}{2}p\,l\),   где p – периметр основания;   l – длина апофемы.

Объем пирамиды вычисляется по формуле:  \(V = \frac{1}{3}S\,H\),   где S – площадь основания; H – длина высоты пирамиды.

Если у пирамиды все боковые ребра равны между собой или наклонены под одним и тем же углом к плоскости основания, то основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды (эта же точка служит точкой пересечения серединных перпендикуляров к сторонам основания пирамиды).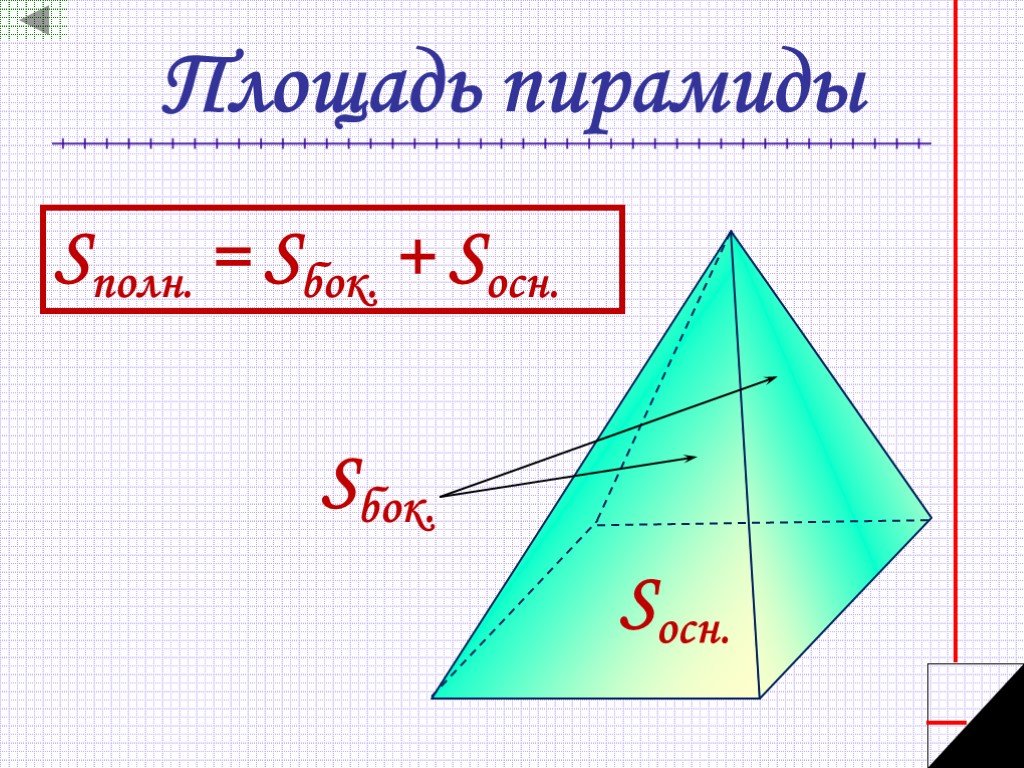

Если у пирамиды боковые грани наклонены к плоскости основания под одним и тем же углом, то основание высоты пирамиды совпадает с центром окружности, вписанной в основание (эта же точка служит точкой пересечения биссектрис углов в основании пирамиды).

Задачи для самостоятельного решения

Задача 1. Стороны основания треугольной пирамиды равны 5, 8 и 9. Высоты боковых граней, проведенных к ребрам основания равны 10. Найдите площадь боковой поверхности пирамиды. Ответ ОТВЕТ: 110.

Задача 2. Дана правильная семиугольная пирамида, ребро основания равно 8, апофема – 9. Найдите площадь боковой поверхности пирамиды. Ответ ОТВЕТ: 252.

Задача 3. Периметр основания правильной четырехугольной пирамиды – 32, апофема – 7. Найдите площадь одной боковой грани. Ответ ОТВЕТ: 28.

Задача 4. Дана треугольная пирамида DABC.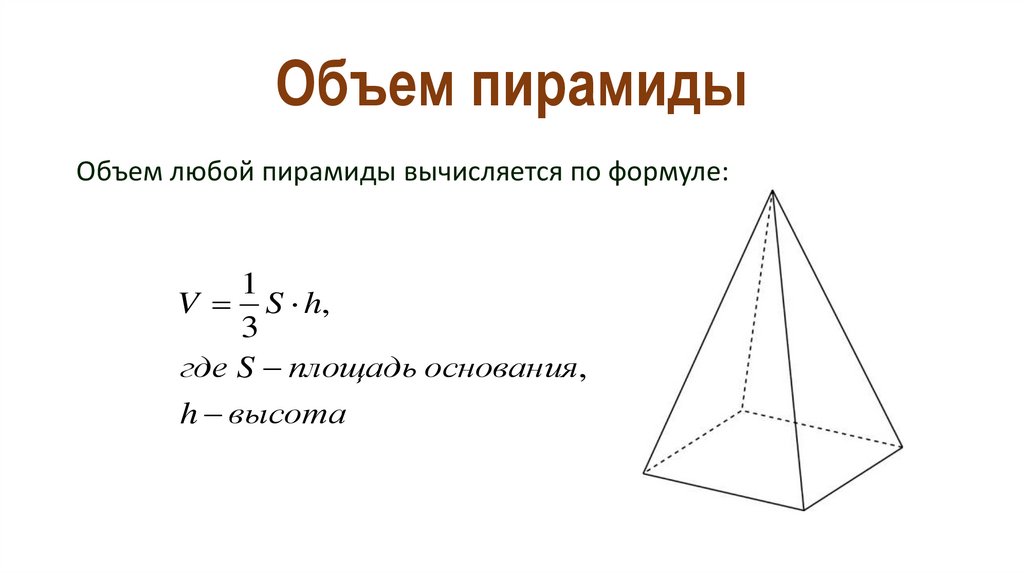 Боковые ребра DA = DB = DC = 5,  AB = AC = 8,  BC = 6. Найдите площадь боковой поверхности. Ответ ОТВЕТ: 36.

Задача 5. Дана правильная четырехугольная пирамида, её высота равна 3, площадь боковой поверхности 80. Найдите площадь полной поверхности. Ответ ОТВЕТ: 144.

Задача 6. Высоты боковых граней четырехугольной пирамиды, проведенные из вершины равны 7, две противоположные стороны основания равны 8 и 14. Найдите площадь боковой поверхности. Ответ ОТВЕТ: 154.

Задача 7. Дана правильная четырехугольная пирамида с боковыми ребрами равными 10 и высотой – \(2\sqrt 7 .\) Найдите площадь полной поверхности пирамиды. Ответ ОТВЕТ: 336.

Задача 8. Дана четырехугольная пирамида SABCD, в основании которой равнобедренная трапеция в которую можно вписать окружность с основаниями AB = 9 и CD = 4. \circ }.\) Найдите площадь полной поверхности пирамиды. Ответ ОТВЕТ: 117.

Задача 9. Дана треугольная пирамида SABC с высотой SA, равной 9. Стороны основания AB = AC = 13, BC = 10. Найдите площадь полной поверхности пирамиды. Ответ ОТВЕТ: 252.

Задача 10. Дана четырехугольная пирамида SABCD в основании, которой ромб ABCD с диагоналями AC = 16, BD = 12 которые пересекаются в точке O. Отрезок SO равный 2 является высотой пирамиды. Найдите площадь боковой поверхности. Ответ ОТВЕТ: 104.

Задача 11. Дана четырехугольная пирамида SABCD в основании, которой ромб ABCD площадь которого равна 60 и стороной 10. Диагонали ромба пересекаются в точке O. Отрезок SO равный 4 является высотой пирамиды. Найдите площадь боковой поверхности.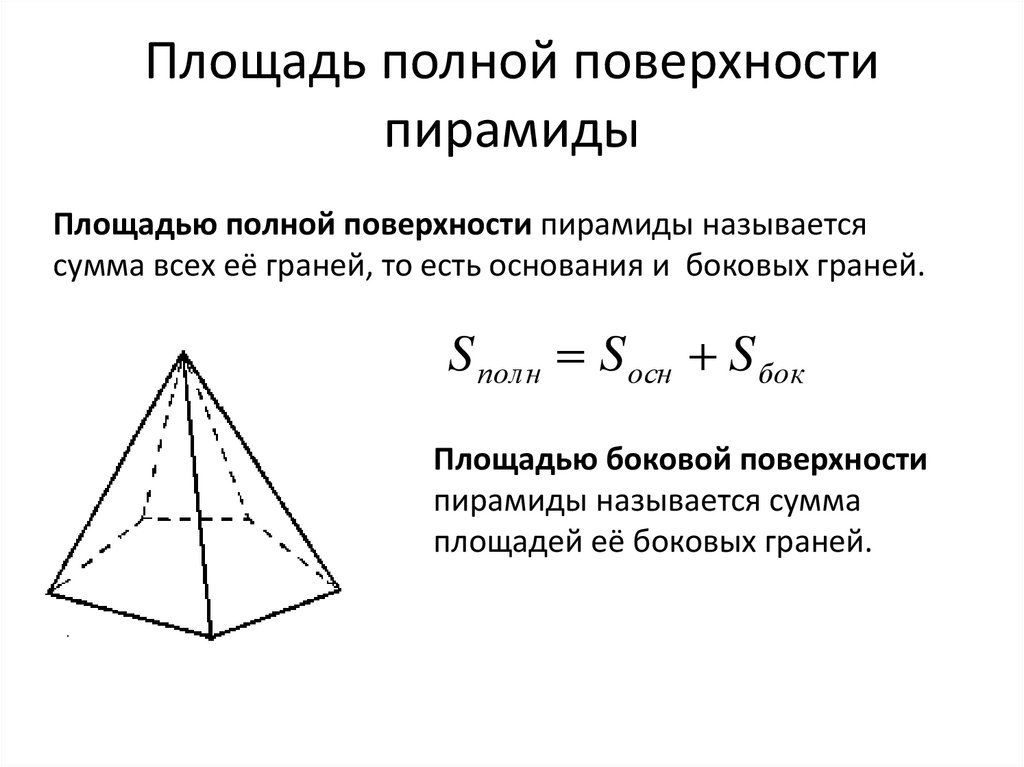 \circ }.\)  Найдите высоту пирамиды. Ответ ОТВЕТ: 5.

Реклама

Поддержать нас

пирамид

пирамид

Показать рекламу

Скрыть рекламу
О рекламе

Когда мы думаем о пирамидах, мы думаем о Великих пирамидах Египта .

На самом деле это Квадратные пирамиды , потому что их основание — Квадрат.

Части пирамиды

Пирамида получается путем соединения основания с вершиной

Основание представляет собой многоугольник (плоский с прямыми краями), а все остальные грани — треугольники. Никаких кривых!

Типы пирамид

Существует много типов пирамид, и они названы в честь формы их основания.

	Пирамида	База
Треугольный Пирамида:
Квадрат Пирамида:
Пятиугольный Пирамида:
. .. и так далее …

 

Пролетите здесь через несколько пирамид.

Правая и наклонная пирамида

Это говорит нам, где вершина (вершина) пирамиды. Когда вершина находится прямо над центром основания, это правильная пирамида , в противном случае это наклонная пирамида .

Правая пирамида	Наклонная пирамида

Правильная и неправильная пирамида

Это говорит нам о форме основания . Когда основание представляет собой правильный многоугольник, это правильная пирамида , иначе это неправильная пирамида .

Правильная пирамида	Неправильная пирамида
Основание стандартное	Основание неправильной формы

Площадь и объем

Объем пирамиды

• ¹ / ₃ × [Площадь основания] × Высота

Площадь поверхности пирамиды

Когда все боковые грани одинаковы:

• [Площадь основания] +
  1 / ₂ × периметр × [наклонная длина]

Если боковые грани разные:

• [Основная площадь] + [Боковая площадь]

 

Примечания по площади поверхности

Площадь поверхности состоит из двух частей: площадь основания ( Базовая площадь ) и площадь боковых граней ( Боковая площадь ).

Для Базовая площадь :

Это зависит от формы, существуют разные формулы для треугольника, квадрата и т. д. Формулы см. в разделе Площадь или в нашем Инструменте расчета площади

Для Боковая площадь :

Когда все боковые грани одинаковые:

• Умножьте периметр на «наклонную длину» и разделите на 2. Это потому, что боковые грани всегда являются треугольниками, а треугольник формула «база умноженная на высоту, деленная на 2»

Но когда боковые грани разные (например, в «неправильной» пирамиде), мы должны сложить площади каждого треугольника, чтобы найти общую боковую площадь.

 

 

Copyright © 2017 MathsIsFun.com

Как найти площадь боковой поверхности квадратной пирамиды

Обновлено 25 февраля 2023 г.

Клэр Гиллеспи

Математические задачи с трехмерными фигурами могут потребовать от нас найти площадь боковой поверхности квадратной пирамиды. Площадь боковой поверхности – это сумма площадей его боковых граней (боков), а площадь полной поверхности – сумма его боковых граней и основания. Таким образом, в квадратной пирамиде боковые грани — это четыре треугольника, которые образуют верхнюю и боковые части фигуры.

TL;DR (слишком длинно, не читал)

Во всех следующих вычислениях мы предполагаем, что это правильные пирамиды. Это означает, что вершина пирамиды находится прямо над центром основания. Это означает, что все боковые стороны являются равнобедренными треугольниками (или равносторонними).

Решение для площади боковой поверхности

Общая формула площади боковой поверхности правильной пирамиды:

\text{площадь боковой поверхности} = 2 \times \text{периметр основания} \times \text{высота наклона пирамиды​}

Эта формула по существу находит площадь, которая составляет каждую боковую грань, по классической формуле площади треугольника:

\text{Площадь} = \text{база} \times \text{высота}

периметр действует как совокупное основание для всех сторон, а наклонная высота пирамиды является высотой треугольников. Затем мы делим на два, чтобы учесть площадь треугольника, и получаем формулу площади поверхности.

Определение боковой поверхности

Вычислите периметр основания, умножив длину стороны пирамиды на четыре, потому что у квадрата четыре равные стороны. Найти наклонную высоту одной из боковых граней может оказаться сложнее, но в реальном мире ее часто можно измерить с помощью довольно простых инструментов.

Если сторона квадратной пирамиды – прямоугольной пирамиды с квадратным основанием – равна 6 дюймам, периметр равен:

4 х 6 = 24 \text{\ дюймов}

Боковой наклон квадратной пирамиды расстояние от вершины пирамиды до края основания, делящего пополам одну из граней треугольника. Если высота поперечного наклона составляет 8 дюймов, мы можем вычислить

24 х 8 = 192

• . Если вместо этого нам дана высота квадратной пирамиды, мы можем использовать теорему Пифагора, чтобы найти наклонную высоту. Просто будьте осторожны, чтобы использовать основание прямоугольного треугольника в пределах размеров квадратной пирамиды.

Разделите ваш ответ на два

Чтобы найти площадь боковой поверхности, мы вычисляем

Теперь мы знаем, что площадь боковой поверхности квадратной пирамиды с периметром основания 24 дюйма и высотой бокового наклона 8 дюймов составляет 96 квадратных дюймов.

• Если мы уже знаем площадь каждой из четырех боковых граней квадратной пирамиды, мы можем вычислить площадь боковой поверхности, найдя сумму площадей боковых граней. Например, если площади боковых граней составляют 10 дюймов, 10 дюймов, 7 дюймов и 7 дюймов, получится 10 + 10 + 7 + 7 = 34. Площадь боковой поверхности составляет 34 квадратных дюйма. 92

  Боковая площадь прямоугольной пирамиды

  Прямоугольная пирамида представляет другой уровень сложности при нахождении боковой площади, но мы по-прежнему можем использовать те же принципы, что и для пирамиды с квадратным основанием. Поскольку прямоугольная пирамида по-прежнему имеет треугольные стороны, мы можем использовать формулу площади треугольника, но нам нужно учитывать, что стороны прямоугольника различны. Это означает, что равными будут только треугольники напротив друг друга, а не все четыре боковые грани.

  Чтобы учесть это, мы можем вычислить боковую площадь в парах противоположных граней, поэтому мы разобьем периметр на длину (l) и ширину (w) и их боковые грани.

  A_\text{lateral} = \frac{2l \times h_{длина} + 2w \times h_{ширина}}{2}

  Применение этих взаимосвязей к другим пирамидам

  многоугольник, отличный от квадрата, эта формула для площади поперечного сечения все еще может быть применена. Будь то шестиугольная пирамида (с 6 боковыми сторонами) или пятиугольная пирамида (с 5 боковыми сторонами), можно использовать общую формулу в начале. Поскольку все пирамиды имеют треугольные грани, мы можем вычислить периметр, просуммировав стороны основания, а затем умножив периметр на высоту наклона и разделив его на два, чтобы получить площадь поперечного сечения.

  No related posts.