Как по графику найти наибольшее значение функции – Наибольшее и наименьшее значение функции

Найти наибольшее значение функции как найти по графику

а -сторона квдрата. а — 2 — ширина прямоугольника. а + 1 — длина прямоугольника. Площадь прямоугольника. Sпр = (а — 2)(а + 1). Площадь квадрата. Sкв = а?. Sкв — Sпр = 10. а? — (а — 2)(а + 1) = 10. а? — а? + 2а — а + 2 = 10. а + 2 = 10. а = 8. Sпр = (8 — 2)(8 + 1)= 6·9 = 54. Ответ: площадь прямоугольника равна 54см?.

Наибольшее и наименьшее значение функции.

С практической точки зрения наибольший интерес представляет использование производной для нахождения наибольшего и наименьшего значения функции. С чем это связано? Максимизация прибыли, минимизация издержек, определение оптимальной загрузки оборудования. Другими словами, во многих сферах жизни приходится решать задачи оптимизации каких-либо параметров. А это и есть задачи на нахождение наибольшего и наименьшего значения функции.

В этой статье мы будем говорить о нахождении наибольшего и наименьшего значений явно заданной функции одной переменной y=f(x) .

Навигация по странице.

Наибольшее и наименьшее значение функции — определения, иллюстрации.

Кратко остановимся на основных определениях.

Стационарные точки – это значения аргумента, при которых производная функции обращается в ноль.

Для чего нам стационарные точки при нахождении наибольшего и наименьшего значений? Ответ на этот вопрос дает теорема Ферма. Из этой теоремы следует, что если дифференцируемая функция имеет экстремум (локальный минимум или локальный максимум) в некоторой точке, то эта точка является стационарной. Таким образом, функция часто принимает свое наибольшее (наименьшее) значение на промежутке X в одной из стационарных точек из этого промежутка.

Также часто наибольшее и наименьшее значение функция может принимать в точках, в которых не существует первая производная этой функции, а сама функция определена.

Сразу ответим на один из самых распространенных вопросов по этой теме:»Всегда ли можно определить наибольшее (наименьшее) значение функции»? Нет, не всегда. Иногда границы промежутка X совпадают с границами области определения функции или интервал X бесконечен. А некоторые функции на бесконечности и на границах области определения могут принимать как бесконечно большие так и бесконечно малые значения. В этих случаях ничего нельзя сказать о наибольшем и наименьшем значении функции.

Для наглядности дадим графическую иллюстрацию. Посмотрите на рисунки – и многое прояснится.

На первом рисунке функция принимает наибольшее ( max y ) и наименьшее ( min y ) значения в стационарных точках, находящихся внутри отрезка [-6;6] .

Рассмотрим случай, изображенный на втором рисунке. Изменим отрезок на [1;6] . В этом примере наименьшее значение функции достигается в стационарной точке, а наибольшее — в точке с абсциссой, соответствующей правой границе интервала.

На рисунке №3 граничные точки отрезка [-3;2] являются абсциссами точек, соответствующих наибольшему и наименьшему значению функции.

На открытом интервале

На четвертом рисунке функция принимает наибольшее ( max y ) и наименьшее ( min y ) значения в стационарных точках, находящихся внутри открытого интервала (-6;6) .

На интервале [1;6) наименьшее значение функции достигается в стационарной точке, а про наибольшее значение мы ничего сказать не можем. Если бы точка x=6 была частью интервала, тогда при этом значении функция принимала бы наибольшее значение. Этот пример изображен на рисунке №5.

На рисунке №6 наименьшее значение функции достигается в правой границе интервала (-3;2] , о наибольшем значении никаких выводов сделать нельзя.

В примере, представленном на седьмом рисунке, функция принимает наибольшее значение ( max y ) в стационарной точке с абсциссой x=1 , а наименьшее значение ( min y ) достигается на правой границе интервала. На минус бесконечности значения функции асимптотически приближаются к y=3 .

Алгоритм нахождения наибольшего и наименьшего значения непрерывной функции на отрезке [a;b] .

Запишем алгоритм, позволяющий находить наибольшее и наименьшее значение функции на отрезке.

Находим область определения функции и проверяем, содержится ли в ней весь отрезок [a;b] . Находим все точки, в которых не существует первая производная и которые содержатся в отрезке [a;b] (обычно такие точки встечаются у функций с аргументом под знаком модуля и у степенных функций с дробно-рациональным показателем). Если таких точек нет, то переходим к следующему пункту. Определяем все стационарные точки, попадающие в отрезок [a;b] . Для этого, находим производную функции, приравниваем ее к нулю, решаем полученное уравнение и выбираем подходящие корни. Если стационарных точек нет или ни одна из них не попадает в отрезок, то переходим к следующему пункту. Вычисляем значения функции в отобранных стационарных точках (если такие имеются), в точках, в которых не существует первая производная (если такие имеются), а также при x=a и x=b. Из полученных значений функции выбираем наибольшее и наименьшее — они и будут искомыми наибольшим и наименьшим значениями функции соответственно.

Разберем алгоритм при решении примера на нахождение наибольшего и наименьшего значения функции на отрезке.

на отрезке [1;4] ; на отрезке [-4;-1] .

Очевидно, производная функции существует во всех точках отрезков [1;4] и [-4;-1] .

Для первого случая вычисляем значения функции на концах отрезка и в стационарной точке, то есть при x=1 , x=2 и x=4 :

Для второго случая вычисляем значения функции лишь на концах отрезка [-4;-1] (так как он не содержит ни одной стационарной точки):

Алгоритм нахождения наибольшего и наименьшего значения непрерывной функции на открытом или бесконечном интервале X.

Прежде чем ознак

poiskvstavropole.ru

Точки экстремума, наибольшее и наименьшее значение на промежутке

Экстремумы функции

Для того чтобы ввести понятие наибольшего и наименьшего значения функций, вначале познакомимся с таким понятием, как экстремумы функций. Это понятие нам будет необходимо не для самого определения значений таких функций, а для построения схемы нахождения таких промежутков для конкретно заданных функций.

Определение 1

Точка $x’$ входящая в область определения функции называется точкой экстремума, если она либо будет точкой максимума, либо будет точкой минимума для функции $f(x)$.

Определение 2

Точка $x’$ будет называться точкой максимума для введенной функции $f(x)$, если у она имеет такую окрестность, что для всех точек $x$, которые входят в эту окрестность, будет верно $f(x)\le f(x'{\rm \ })$.

Определение 3

Точка $x_0$ будет называться точкой минимума для введенной функции $f(x)$, если она имеет такую окрестность, что для всех точек $x$, которые входят в эту окрестность, будет верно $f(x)\ge f(x'{\rm \ })$.

Чтобы полностью разобраться в данном понятии, далее введем понятие критической точки функции.

Определение 4

Точка $x’$ будет называться критической точкой для данной функции $f(x)$, если выполняются два следующих условия:

1. Точка $x’$ является внутренней точкой для области определения данной функции;
2. $f’\left(x'{\rm \ }\right)=0$ или не существует.

Сформулируем без доказательства теоремы о необходимом (теорема 1) и достаточном (теорема 2) условии для существования точки экстремума.

Теорема 1

Если $y=f(x)$ имеет экстремум в точке $x_0$, то либо её производная в ней равняется нулю, либо производная в ней не существует.

Теорема 2

Пусть точка $x’$ будет критической для $y=f(x)$ и принадлежит интервалу $(a,b)$, причем на каждом интервале $\left(a,x'{\rm \ }\right)\ и\ (x'{\rm \ },b)$ производная $f'(x)$ существует и сохраняет один и тот же знак. В этом случае:

1. Если в $(a,x'{\rm \ })$ $f’\left(x\right) >0$, а в $(x'{\rm \ },b)$ $f’\left(x\right)
2. Если в $(a,x'{\rm \ })$ $f’\left(x\right)0$, то $x’$ —будет точкой минимума для этой функции.
3. Если и в $(a,x'{\rm \ })$, и в $(x'{\rm \ },b)$ производная $имеет\ один\ и\ тот\ же\ постоянный\ знак$, то $x’$ не будет точкой экстремума для этой функции.

На рисунке 1 мы можем наглядно увидеть смысл теоремы 2.

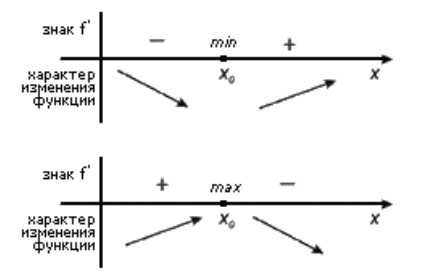
Рисунок 1.

Примеры точек экстремумов вы можете видеть на рисунке 2.

Рисунок 2.

Правило исследования на экстремум

1. Найти $D(f)$;
2. Найти $f'(x)$;
3. Найти точки, где $f’\left(x\right)=0$;
4. Найти точки, где $f'(x)$ не будет существовать;
5. Отметить на координатной прямой $D(f)$ и все найденные в 3 и 4 пункте точки;
6. Определить знак $f'(x)$ на полученных промежутках;
7. Используя теорему 2, сделать заключение по поводу всех найденных точек.

Понятие наибольшего и наименьшего значений

Определение 5

Функция $y=f(x)$, которая имеет областью определения множество $X$, имеет наибольшее значение в точке $x’\in X$, если выполняется

\[f\left(x\right)\le f(x’)\]

Определение 6

Функция $y=f(x)$, которая имеет областью определения множество $X$, имеет наименьшее значение в точке $x’\in X$, если выполняется

\[f\left(x\right)\ge f(x’)\]

Чтобы найти наименьшее и наибольшее значение заданной функции на каком либо отрезке необходимо произвести следующие действия:

1. Найти $f'(x)$;
2. Найти точки, в которых $f’\left(x\right)=0$;
3. Найти точки, в которых $f'(x)$ не будет существовать;
4. Выкинуть из точек, найденных в пунктах 2 и 3 те, которые не лежат в отрезке $[a,b]$;
5. Вычислить значения в оставшихся точках и на концах $[a,b]$;
6. Выбрать из этих значений наибольшее и наименьшее.

Примеры задач

Пример 1

Найти наибольшее и наименьшее значения на [0,6]: $f\left(x\right)=x^3-3x^2-45x+225$

Решение.

1. $f’\left(x\right)=3x^2-6x-45$;
2. $f’\left(x\right)=0$;
3. \[3x^2-6x-45=0\]
4. \[x^2-2x-15=0\]
5. \[x=5,\ x=-3\]
6. $f'(x)$ существует на всей $D(f)$;
7. $5\in \left[0,6\right]$;

8. Значения:

   \[f\left(0\right)=225\] \[f\left(5\right)=50\] \[f\left(6\right)=63\]

9. Наибольшее значение равняется $225$, наименьшее равняется $50.$

Ответ: $max=225,\ min=50$.

Пример 2

Найти наибольшее и наименьшее значения на [-1,1]:$f\left(x\right)=\frac{x^2-4x+4}{x-2}$

Решение.

\[f\left(x\right)=\frac{x^2-4x+4}{x-2}=\frac{{(x-2)}^2}{x-2}=x-2,\ x\ne 2\]

1. $f’\left(x\right)=(x-2)’=1$;

   Точек экстремума нет.

2. Значения:

   \[f\left(-1\right)=-3\] \[f\left(1\right)=-1\]

Ответ: $max=-1,\ min=-3$.

spravochnick.ru

Задания №12. Исследование функции без применения производной

Рассмотрим задачи категории В12 ЕГЭ по математике на  элементарное исследование функции. Мощный инструмент для исследования функции – это, конечно, производная. Но в отдельных случаях  (такие задачи мы сейчас и рассмотрим) вполне можно обойтись и без нее.

Несколько задач из открытого банка заданий ЕГЭ по математике:

Надеюсь, вы различаете понятия  «точка минимума», «минимум»,  «наименьшее значение функции»…

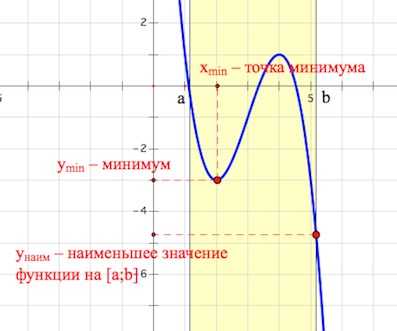
Задание 1.

Най­ди­те точку ми­ни­му­ма функ­ции .

 Решение: + показать

Задание 2.

Найдите наименьшее значение функции

Решение: + показать

Проще всего, пожалуй, будет рассуждать так:

поэтому .

Значит, наименьшее значение функции – это .

Ответ: . 

Задание 3.

Най­ди­те точку мак­си­му­ма функ­ции  .

Решение: + показать

Задание 4.

Най­ди­те  ми­ни­му­м функ­ции .

Решение: + показать

Задание 5.

Най­ди­те наи­мень­шее зна­че­ние функ­ции

Решение: + показать

Продолжение смотрите здесь.

Вы можете пройти тест по Задачам №12 (исследование функции без использования производной).

egemaximum.ru

Наибольшее и наименьшее значения функции — ПриМат

Для функции, непрерывной на отрезке по первой теореме Вейерштрасса существует точка, в которой функция принимает наибольшее значение и точка, в которой функция принимает наименьшее значение.

Функция принимает наибольшее значение на отрезке в точке , если и :
Аналогично функция принимает наименьшее значение на отрезке в точке , если и :

Примеры:

1.Найти наибольшее и наименьшее значения функции на сегменте .

Решение:

Найдем производную функции .  Найдем точки, в которых производная равна нулю:   . Значение принадлежит сегменту . Находим значения функции в полученной стационарной точке и на концах промежутка:

1. ;
2. ;
3. .

Таким образом:
;
.

2.Найти отношение радиуса основания к высоте цилиндра , если при заданном объеме площадь полной поверхности является наименьшей.

Решение:

Пусть — фиксированный объем цилиндра, площадь полной поверхности , тогда , где — площадь основания цилиндра .

Тогда . Найдем производную : . Найдем стационарные точки: . Получим: .

Вывод: цилиндр при заданном объеме имеет наименьшую площадь полной поверхности, если его высота в 2 раза больше радиуса, т.е в случае, когда осевое сечение — квадрат.

Список литературы:

Наибольшее и наименьшее значения функции

Лимит времени: 0

Информация

Тест на тему «Наибольшее и наименьшее значения функций».

Вы уже проходили тест ранее. Вы не можете запустить его снова.

Тест загружается…

Вы должны войти или зарегистрироваться для того, чтобы начать тест.

Вы должны закончить следующие тесты, чтобы начать этот:

Правильных ответов: 0 из 4

Ваше время:

Время вышло

Вы набрали 0 из 0 баллов (0)

Средний результат
Ваш результат

максимум из 7 баллов

Место	Имя	Записано	Баллы	Результат
Таблица загружается
Нет данных

Ваш результат был записан в таблицу лидеров

1. С ответом
2. С отметкой о просмотре

Таблица лучших: Наибольшее и наименьшее значения функции

максимум из 7 баллов

Место	Имя	Записано	Баллы	Результат
Таблица загружается
Нет данных

Поделиться ссылкой:

Похожее

ib.mazurok.com

No related posts.