Задачи с решением круги эйлера – описание, примеры, для дошкольников, для школьников

Содержание

Использование метода кругов Эйлера (диаграмм Эйлера–Венна) при решении задач в курсе информатики и ИКТ

Разделы: Информатика

1. Введение

В курсе Информатики и ИКТ основной и старшей школы рассматриваются такие важные темы как “Основы логики” и “Поиск информации в Интернет”. При решении определенного типа задач удобно использовать круги Эйлера (диаграммы Эйлера-Венна).

Математическая справка. Диаграммы Эйлера-Венна используются прежде всего в теории множеств как схематичное изображение всех возможных пересечений нескольких множеств. В общем случае они изображают все 2ⁿ комбинаций n свойств. Например, при n=3 диаграмма Эйлера-Венна обычно изображается в виде трех кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.

2. Представление логических связок в поисковых запросах

При изучении темы “Поиск информации в Интернет” рассматриваются примеры поисковых запросов с использованием логических связок, аналогичным по смыслу союзам “и”, “или” русского языка. Смысл логических связок становится более понятным, если проиллюстрировать их с помощью графической схемы – кругов Эйлера (диаграмм Эйлера-Венна).

Логическая связка	Пример запроса	Пояснение	Круги Эйлера
& — “И”	Париж & университет	Будут отобраны все страницы, где упоминаются оба слова: Париж и университет	Рис.1
\| — “ИЛИ”	Париж \| университет	Будут отобраны все страницы, где упоминаются слова Париж и/или университет	Рис.2

3. Связь логических операций с теорией множеств

С помощью диаграмм Эйлера-Венна можно наглядно представить связь логических операций с теорией множеств. Для демонстрации можно воспользоваться слайдами в Приложение 1.

Логические операции задаются своими таблицами истинности. В Приложении 2 подробно рассматриваются графические иллюстрации логических операций вместе с их таблицами истинности. Поясним принцип построения диаграммы в общем случае. На диаграмме – область круга с именем А отображает истинность высказывания А (в теории множеств круг А – обозначение всех элементов, входящих в данное множество). Соответственно, область вне круга отображает значение “ложь” соответствующего высказывания. Что бы понять какая область диаграммы будет отображением логической операции нужно заштриховать только те области, в которых значения логической операции на наборах A и B равны “истина”.

Например, значение импликации равно “истина” в трех случаях (00, 01 и 11). Заштрихуем последовательно: 1) область вне двух пересекающихся кругов, которая соответствует значениям А=0, В=0; 2) область, относящуюся только к кругу В (полумесяц), которая соответствует значениям А=0, В=1; 3) область, относящуюся и к кругу А и к кругу В (пересечение) – соответствует значениям А=1, В=1. Объединение этих трех областей и будет графическим представлением логической операции импликации.

4. Использование кругов Эйлера при доказательстве логических равенств (законов)

Для того, чтобы доказать логические равенства можно применить метод диаграмм Эйлера-Венна. Докажем следующее равенство ¬(АvВ) = ¬А&¬В (закон де Моргана).

Для наглядного представления левой части равенства выполним последовательно: заштрихуем оба круга (применим дизъюнкцию) серым цветом, затем для отображения инверсии заштрихуем область за пределами кругов черным цветом:

Рис.3 Рис.4

Для визуального представления правой части равенства выполним последовательно: заштрихуем область для отображения инверсии (¬А) серым цветом и аналогично область ¬В также серым цветом; затем для отображения конъюнкции нужно взять пересечение этих серых областей (результат наложения представлен черным цветом):

Рис.5 Рис.6 Рис.7

Видим, что области для отображения левой и правой части равны. Что и требовалось доказать.

5. Задачи в формате ГИА и ЕГЭ по теме: “Поиск информации в Интернет”

Задача №18 из демо-версии ГИА 2013.

В таблице приведены запросы к поисковому серверу. Для каждого запроса указан его код – соответствующая буква от А до Г. Расположите коды запросов слева направо в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.

Код	Запрос
А	(Муха & Денежка) \| Самовар
Б	Муха & Денежка & Базар & Самовар
В	Муха \| Денежка \| Самовар
Г	Муха & Денежка & Самовар

Решение:

Для каждого запроса построим диаграмму Эйлера-Венна:

Запрос А

Рис.8

Запрос Б

Рис. 9

Запрос В

Рис. 10

Запрос Г

Рис. 11

Ответ: ВАГБ.

Задача В12 из демо-версии ЕГЭ-2013.

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысяч)
Фрегат \| Эсминец	3400
Фрегат & Эсминец	900
Фрегат	2100

Какое количество страниц (в тысячах) будет найдено по запросу Эсминец?

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

Пусть

Ф – количество страниц (в тысячах) по запросу Фрегат;

Э – количество страниц (в тысячах) по запросу Эсминец;

Х – количество страниц (в тысячах) по запросу, в котором упоминается Фрегат и не упоминается Эсминец;

У – количество страниц (в тысячах) по запросу, в котором упоминается Эсминец и не упоминается Фрегат.

Построим диаграммы Эйлера-Венна для каждого запроса:

Запрос	Диаграмма Эйлера-Венна	Количество страниц
Фрегат \| Эсминец	Рис.12	3400
Фрегат & Эсминец	Рис.13	900
Фрегат	Рис.14	2100
Эсминец	Рис.15	?

Согласно диаграммам имеем:

Х+900+У = Ф+У = 2100+У = 3400. Отсюда находим У = 3400-2100 = 1300.
Э = 900+У = 900+1300= 2200.

Ответ: 2200.

6. Решение логических содержательных задач методом диаграмм Эйлера-Венна

Задача 1.

В классе 36 человек. Ученики этого класса посещают математический, физический и химический кружки, причем математический кружок посещают 18 человек, физический — 14 человек, химический — 10. Кроме того, известно, что 2 человека посещают все три кружка, 8 человек — и математический и физический, 5 и математический и химический, 3 — и физический и химический.

Сколько учеников класса не посещают никаких кружков?

Решение:

Для решения данной задачи очень удобным и наглядным является использование кругов Эйлера.

Самый большой круг – множество всех учеников класса. Внутри круга три пересекающихся множества: членов математического (М), физического (Ф), химического (Х) кружков.

Пусть МФХ – множество ребят, каждый из которых посещает все три кружка. МФ¬Х – множество ребят, каждый из которых посещает математический и физический кружки и не

посещает химический. ¬М¬ФХ — множество ребят, каждый из которых посещает химический кружок и не посещает физический и математический кружки.

Аналогично введем множества: ¬МФХ, М¬ФХ, М¬Ф¬Х, ¬МФ¬Х, ¬М¬Ф¬Х.

Известно, что все три кружка посещают 2 человека, следовательно, в область МФХ впишем число 2. Т.к. 8 человек посещают и математический и физический кружки и среди них уже есть 2 человека, посещающих все три кружка, то в область МФ¬Х впишем 6 человек (8-2). Аналогично определим количество учащихся в остальных множествах:

Круги Эйлера с названиями непересекающихся множеств:

Рис. 16

Круги Эйлера с количественной информацией:

Рис. 17

Например, количество человек, которые посещают физический кружок 2+6+1+5=14

Просуммируем количество человек по всем областям: 7+6+3+2+4+1+5=28. Следовательно, 28 человек из класса посещают кружки.

Значит, 36-28 = 8 учеников не посещают кружки.

Ответ: 8.

Задача 2.

После зимних каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников класса двое не были ни в кино. ни в театре, ни в цирке. В кино побывало 25 человек, в театре — 11, в цирке 17 человек; и в кино, и в театре — 6; и в кино и в цирке — 10; и в театре и в цирке — 4.

Сколько человек побывало и в кино, и в театре, и в цирке?

Решение:

Пусть х – количество ребят, которые побывали и в кино, и в театре, и в цирке.

Тогда можно построить следующую диаграмму и посчитать количество ребят в каждой области:

Рис.18.

В кино и театре побывало 6 чел., значит, только в кино и театре (6-х) чел.

Аналогично, только в кино и цирке (10-х) чел.

Только в театре и цирке (4-х) чел.

В кино побывало 25 чел., значит, из них только в кино были 25 — (10-х) – (6-х) – х = (9+х).

Аналогично, только в театре были (1+х) чел.

Только в цирке были (3+х) чел.

Не были в театре, кино и цирке – 2 чел.

Значит, 36-2=34 чел. побывали на мероприятиях.

С другой стороны можем просуммировать количество человек, которые были в театре, кино и цирке:

(9+х)+(1+х)+(3+х)+(10-х)+(6-х)+(4-х)+х = 34

33+х = 34.

Отсюда следует, что только один человек побывал на всех трех мероприятиях.

Ответ: 1.

Таким образом, круги Эйлера (диаграммы Эйлера-Венна) находят практическое применение при решении задач в формате ЕГЭ и ГИА и при решении содержательных логических задач.

Литература

В.Ю. Лыскова, Е.А. Ракитина. Логика в информатике. М.: Информатика и Образование, 2006. 155 с.
Л.Л. Босова. Арифметические и логические основы ЭВМ. М.: Информатика и образование, 2000. 207 с.
Л.Л. Босова, А.Ю. Босова. Учебник. Информатика и ИКТ для 8 класса: БИНОМ. Лаборатория знаний, 2012. 220 с.
Л.Л. Босова, А.Ю. Босова. Учебник. Информатика и ИКТ для 9 класса: БИНОМ. Лаборатория знаний, 2012. 244 с.
Сайт ФИПИ: http://www.fipi.ru/

6.05.2013

urok.1sept.ru

Разработка урока по тему «Решение задач с помощью кругов Эйлера»

Задачи занятия:

Образовательные:

рассмотреть решение логических задач с помощью кругов Эйлера.

Развивающие:

развитие логического мышления;

развитие поисковой, творческой, познавательной деятельности;

развитие познавательного интереса к предмету;

Воспитывающие:

формирование эстетического наслаждения от выполненной работы;

формирование навыков само- и взаимоконтроля.

Оборудование:

набор задач каждому ученику;

компьютер, проектор;

презентация.

Ход занятия:

Организационный момент.
Всё то что мы изучили раннее используем при решении задач. ( слайд 2—5)
Зачем нужны круги Эйлера? (слайд 6)

Круги Эйлера имеют прикладное назначение, то есть с их помощью на практике решаются задачи на объединение или пересечение множеств в математике, логике, менеджменте и не только.

Если говорить о видах кругов Эйлера, то можно разделить их на те, что описывают объединение

А также на те, что описывают пересечение множеств по какому-то признаку. Таким принципом руководствовался Джон Венн в своих схемах. И именно он лежит в основе многих популярных в интернете мемов. Вот вам один из примеров таких кругов Эйлера

Изучение нового материала.

Задача 1. (слайд 7,8)

Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 – в районной.

Сколько шестиклассников:

1. Являются читателями обеих библиотек;
2. Не являются читателями районной библиотеки;
3. Не являются читателями школьной библиотеки;
4. Являются читателями только районной библиотеки;
5. Являются читателями только школьной библиотеки?

Заметим, что первый вопрос является ключевым для понимания и решения данной задачи. Ведь не сразу сообразишь, как получается 20 + 25 = 45 из 35. В первом вопросе звучит подсказка к пониманию условия: есть ученики, которые посещают обе библиотеки. А если условие задачи изобразить на схеме, то ответ на первый вопрос становится очевидным.

Решение.

1. 20 + 25 – 35 = 10 (человек) – являются читателями обеих библиотек. На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы.

2. 35 – 20 = 15 (человек) – не являются читателями районной библиотеки. (На схеме левая часть левого круга)

3. 35 – 25 = 10 (человек) – не являются читателями школьной библиотеки. (На схеме правая часть правого круга)

4. 35 – 25 = 10 (человек) – являются читателями только районной библиотеки. (На схеме правая часть правого круга)

5. 35 – 20 = 15 (человек) – являются читателями только школьной библиотеки. (На схеме левая часть левого круга).

Очевидно, что 2 и 5, а также 3 и 4 – равнозначны и ответы на них совпадают

Задача №2: (слайд 9,10)

Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским – 28, французским – 42. Английским и немецким одновременно владеют 8 человек, английским и французским -10 , немецким и французским – 5, всеми тремя языками – 3.

Сколько туристов не владеют ни одним языком?

Решение:

Выразим условие задачи графически. Обозначим кругом тех, кто знает английский, другим кругом – тех, кто знает французский, и третьим кругом – тех, кто знают немецкий.

Всеми тремя языками владеют три туриста, значит, в общей части кругов вписываем число 3.

Английским и французским языками владеют 10 человек, а 3 из них владеют ещё и немецким. Значит, английским и французским владеют 10-3=7 человек.

В общую часть английского и французского кругов вписываем цифру 7.

Английским и немецким языками владеют 8 человек, а 3 из них владеют ещё и французским. Значит, английским и немецким владеют 8-3=5 человек

В общую часть английского и немецкого кругов вписываем число 5

Немецким и французским языками владеют 5 человек, а 3 из них владеют ещё и английским. Значит, немецким и французским владеют 5-3=2 человека.

В общую часть немецкого и французского кругов вписываем цифру 2.

Известно, что немецким языком владеют 30 человек, но 5+3+2=10 из них владеют и другими языками, значит, только немецкий знают 20 человек.

Английский язык знают 28 человек, но 5+3+7=15 человек владеют и другими языками, значит, только английский знают 13 человек.

Французский язык знают 42 человека, но 2+3+7=12 человек владеют и другими языками, значит, только французский знают 30 человек

По условию задачи всего 100 туристов. 20+30+13 +5+2+3+7=80 туристов знают хотя бы один язык, следовательно, 20 человек не владеют ни одним языком

Задача 3.( слайд 11,12) ( самостоятельно парами)

В трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?

Решение.

Пусть
Д – драмкружок,
Х – хор,
С – спорт.

Тогда
в круге Д – 27 ребят,
в круге Х – 32 человека,
в круге С – 22 ученика.

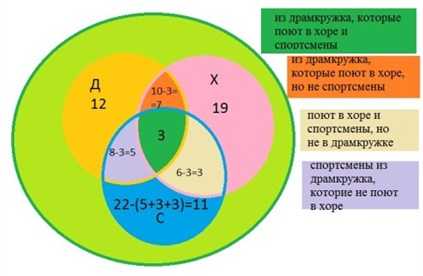
Те 10 ребят из драмкружка, которые поют в хоре, окажутся в общей части кругов Д и X. Трое из них ещё и спортсмены, они окажутся в общей части всех трёх кругов. Остальные семеро спортом не увлекаются. Аналогично, 8 – 3 = 5 спортсменов, не поющих в хоре и 6 – 3 = 3, не посещающих драмкружок.

Легко видеть, что 5 + 3 + 3 = 11 спортсменов посещают хор или драмкружок,

22 – (5 + 3 + 3) = 11 занимаются только спортом;

70 – (11 + 12 + 19 + 7 + 3 + 3 + 5) = 10 – не поют в хоре, не занимаются в драмкружке, не увлекаются спортом.

Ответ: 10 человек и 11 человек

Задача 4°

Из 100 приехавших туристов 75 знали немецкий язык и 83 знали французский. 10 человек не знали ни немецкого, ни французского. Сколько туристов знали оба эти языка?

Получим уравнение: 75+83-х=90

158-х=90

х=68

Задача 4. (слайд 16,17,18)

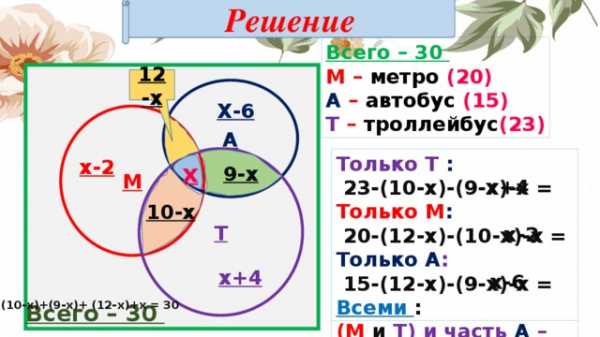
В классе 30 человек. 20 из них каждый день пользуются метро, 15 – автобусом, 23 – троллейбусом, 10 – и метро, и троллейбусом, 12 – и метро, и автобусом, 9 – и троллейбусом, и автобусом. Сколько человек ежедневно пользуется всеми тремя видами транспорта?

Решение.

1 способ. Для решения опять воспользуемся кругами Эйлера. Пусть х человек пользуется всеми тремя видами транспорта. Тогда пользуются
только метро и троллейбусом – (10 – х) человек,
только автобусом и троллейбусом – (9 – х) человек,
только метро и автобусом – (12 – х) человек.

Найдем, сколько человек пользуется одним только метро:
20 – (12 – х) – (10 – х) – х = х – 2.

Аналогично получаем: х – 6 – только автобусом и х + 4 – только троллейбусом, так как всего 30 человек, составляем уравнение:
х + (12 – х) + (9 – х) + (10 – х) + (х + 4) + (х – 2) + (х – 6) = 30,
отсюда х = 3.

2 способ. А можно эту задачу решить задачу другим способом: 20 + 15 + 23 – 10 – 12 – 9 + х = 30, 27 + х = 30, х = 3. Здесь сложили количество учеников, которые пользуются хотя бы одним видом транспорта и из полученной суммы вычли количество тех, кто пользуется двумя или тремя видами и, поэтому, вошли в сумму 2-3 раза. Таким образом, получили количество всех учеников в классе.

Ответ. 3 человека ежедневно пользуются всеми тремя видами транспорта.

Отрабатывание навыков решения задач.

Решение примеров

Урок 1: №

Урок 2: №

Д/З: Урок 1: п. 9.3, №

Урок 2: №

infourok.ru

Решение задач с помощью кругов Эйлера.

Решение задач с помощью кругов Эйлера

Выполнила учитель математики

МАОУ «Школа № 4, г. Благовещенска»

Станишевская Т. В.

-20

-32

-26+(-6)=

Сложение отрицательных чисел

-70+50=

-136

17+(-30)=

Сложение положительных чисел

80+120=

Сложение

чисел с разными знаками

-63+(-73)=

200

-61+(+73)=

-13

136

120

88+(-73)=

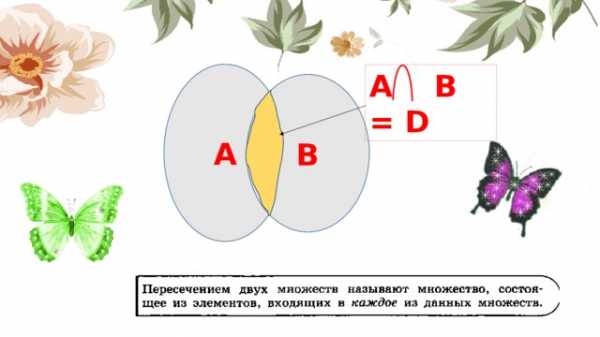
A B = C

A B = D

A B =

Зачем нужны круги Эйлера?

Вставка рисунка

Если говорить о видах кругов Эйлера, то можно разделить их на те, что описывают объединение

Решение задач с помощью кругов Эйлера

Выводы: Круги Эйлера – это геометрическая схема, которая позволяет делать более наглядными логические связи между явлениями и понятиями. А также помогает изобразить отношения между каким-либо множеством и его частью.

Убедиться в этом можно на примере задачи.

Задача. Все мои подруги выращивают в своих квартирах какие-нибудь цветы. Шестеро из них разводят кактусы, а пятеро фиалки. И только у двух есть и кактусы и фиалки. Сколько у меня подруг?

Решение задач с помощью кругов Эйлера

Задача 1 .

Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной или районной. Из них 25 человек берут книги в школьной библиотеке, 20 – в районной.

Р — районная библиотека 20

Ш – школьная библиотека 25

Всего – 35

Сколько шестиклассников:

1. Являются читателями обеих библиотек; 2. Не являются читателями районной библиотеки; 3. Не являются читателями школьной библиотеки; 4. Являются читателями только районной библиотеки; 5. Являются читателями только школьной библиотеки?

Решение

Алгоритм решения задач

1.Внимательно изучаем и кратко записываем условие задачи.

2.Определяем количество множеств и обозначаем их.

3. Выполняем рисунок. Строим пересечение множеств.

4. Записываем исходные данные в круги.

5. Выбираем условие, в котором содержится больше свойств.

6. Записываем недостающие данные в круги Эйлера (рассуждая и анализируя)

Проверяем решение задачи и записываем ответ

1. 20 + 25 – 35 = 10 (человек) – являются читателями обеих библиотек.

обе10

2. 35 – 25 = 10 (человек) – являются читателями только районной библиотеки.

3. 35 – 20 = 15 (человек) – являются читателями только школьной библиотеки.

4. 35 – 20 = 15 (человек) – не являются

читателями районной библиотеки.

5. 35 – 25 = 10 (человек) – не являются читателями школьной библиотеки.

Всего 35

Задача №2:

Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским – 28 , французским – 42 . Английским и немецким одновременно владеют 8 человек, английским и французским — 10 , немецким и французским – 5 , всеми тремя языками – 3 .

Сколько туристов не владеют ни одним языком?

Решение :

Всего – 100

Н – немецкий (30)

А – английский (28)

Ф – французский (42)

(Н и А) и часть Ф – 8

(Ф и А) и часть Н – 10

(Н и Ф) и часть А – 5

Все языки – 3

Не владеют ни одним языком?

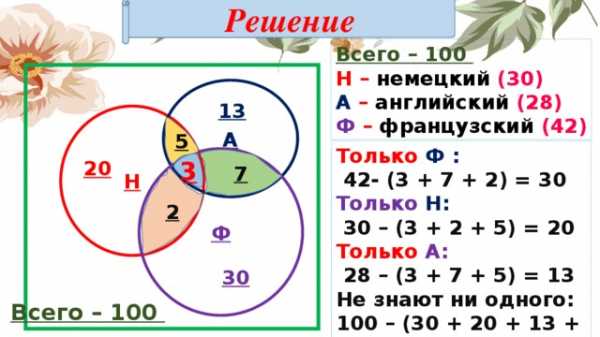
Решение

Всего – 100

Н – немецкий (30)

А – английский (28)

Ф – французский (42)

Только Ф :

42- (3 + 7 + 2) = 30

Только Н:

30 – (3 + 2 + 5) = 20

Только А:

28 – (3 + 7 + 5) = 13

Не знают ни одного:

100 – (30 + 20 + 13 + 17) = 20

(Н и А) и часть Ф – 8,

8 – 3 = 5(только Н и А)

(Ф и А) и часть Н – 10,

10 – 3 = 7 (только Ф и А)

(Н и Ф) и часть А – 5,

5 – 3 = 2 (только Н и Ф)

Все — 3

Всего – 100

Задача 3.

В трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?

Пусть Д – драмкружок, Х – хор, С – спорт.

Тогда в круге Д – 27 ребят, в круге Х – 32 человека, в круге С – 22 ученика.

Задача 4 .

В классе 30 человек. 20 из них каждый день пользуются метро, 15 – автобусом, 23 – троллейбусом, 10 – и метро, и троллейбусом, 12 – и метро, и автобусом, 9 – и троллейбусом, и автобусом. Сколько человек ежедневно пользуется всеми тремя видами транспорта?

Решение :

Всего – 30

М – метро (20)

А – автобус (15)

Т – троллейбус (23)

(М и А) и часть Т – 12

(Т и А) и часть М – 9

(М и Т) и часть А – 10

Всеми – х

Пользуются всеми тремя?

Решение

Всего – 30

М – метро (20)

А – автобус (15)

Т – троллейбус (23)

12-х

Х-6

Только Т :

(М и А) и часть Т – 12,

23-(10-х)-(9-х)-х =

12 – х (только М и А )

(Т и А) и часть М – 9,

Только М :

20-(12-х)-(10-х)-х =

9 – х (только Т и А )

(М и Т) и часть А – 10,

Только А :

15-(12-х)-(9-х)-х =

10 – х (только М и Т )

Всеми – х

Всеми :

9-х

х-2

10-х

х+4

х-2

х+4

х-6

Всеми :

(х+4)+(х-2) +( х-6) + (10-х)+(9-х)+ (12-х)+х = 30

Всего – 30

Всеми :

(х+4)+(х-2) +( х-6) + (10-х)+(9-х)+ (12-х)+х = 30

х + 4 + х – 2 + х – 6 + 10 – х + 9 – х + 12 – х + х = 30

х + 27 = 30

х = 30 – 27

х = 3

Ответ: Пользуются всеми тремя видами транспорта

3 человека

Slide title

Click to add Title

multiurok.ru

План-конспект урока (алгебра, 5 класс) по теме: Решение задач с помощью кругов Эйлера

Урок математики в 5 «Б» классе. Провела: учитель I категории Астапова Н.Г

Тема: Решение задач с помощью кругов Эйлера.

Цели:

Обучающая – познакомить учащихся со способом решения логических задач с помощью кругов Эйлера — Венна
Развивающая – способствовать развитию логического мышления, памяти, самостоятельности и инициативы при выполнении групповых и индивидуальных заданий.
Воспитывающая – способствовать формированию информационной культуры учащихся, ответственности в групповой и индивидуальной работе.

Ход урока:

1) Орг. момент.

— Какие геометрические фигуры вы знаете?

— Как вы думаете, как мы их будем сегодня использовать при решении задач?

— Такое применение геометрических фигур, в основном кругов, при решении логических задач ввел Леонардо Эйлер. Тема нашего сегодняшнего урока «Решение задач с помощью кругов Эйлера»

2) Сообщение исторического материала: сообщение делает учащийся из 6 класса.

Одним из первых, кто использовал для решения задач круги, был выдающийся немецкий математик и философ Готфрид Вильгельм Лейбниц (1646 – 1716). В его черновых набросках были обнаружены рисунки с кругами. Затем этот метод основательно развил швейцарский математик Леонард Эйлер (1707 – 1783).

Леонард Эйлер, крупнейший математик XVIII века, родился в Швейцарии. В 1727г. по приглашению Петербургской академии наук он приехал в Россию. Эйлер попал в круг выдающихся математиков, получил большие возможности для создания и издания своих трудов. Он работал с увлечением и вскоре стал, по единодушному признанию современников, первым математиком мира.

Научное наследие Эйлера поражает своим объемом и разносторонностью. В списке его трудов более 800 названий. Полное собрание сочинений ученого занимает 72 тома.

Леонард Эйлер

(1707 – 1783)

Последние 17 лет жизни Эйлера были омрачены почти полной потерей зрения. Но он продолжал творить так же интенсивно, как в молодые годы. Только теперь он уже диктовал ученикам, которые проводили за него громоздкие вычисления.

С1761 по 1768 год им были написаны знаменитые «Письма к немецкой принцессе», где Эйлер как раз и рассказывал о своем методе, об изображении множеств в виде кругов. Именно поэтому рисунки в виде кругов, обычно называют «кругами Эйлера». Эйлер отмечал, что изображение множеств в виде кругов «очень подходит для того, чтобы облегчить наши рассуждения». Понятно, что слово «круг» здесь весьма условно, множества могут изображаться на плоскости в виде произвольных фигур.

После Эйлера этот же метод разрабатывал чешский математик Бернард Больцано (1781 – 1848). Только в отличие от Эйлера он рисовал не круговые, а прямоугольные схемы. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шредер (1841 – 1902). Этот метод широко используется в его книге «Алгебра логика». Но наибольшего расцвета графические методы достигли в сочинениях английского логика Джона Венна (1843 – 1923). С наибольшей полнотой этот метод изложен им в книге «Символическая логика», изданной в Лондоне в 1881 году. В честь Венна вместо кругов Эйлера соответствующие рисунки называют иногда диаграммами Венна; в некоторых книгах их называют также диаграммами (или кругами) Эйлера – Венна.

3) Пример решения задач:

Задача 1. Все мои друзья занимаются каким-нибудь видом спорта. 16 из них увлекаются футболом, а 12 — баскетболом. И только двое увлекаются и тем и другим видом спорта. Угадайте, сколько у меня друзей?

Решение: Обратимся к кругам Эйлера:

Изобразим два множества (можно вводить обозначения их не только кругами), так как два вида спорта. В одном я буду фиксировать друзей, которые увлекаются футболом, а в другом — баскетболом. Поскольку некоторые из моих друзей увлекаются и тем и другим видом спорта, то квадраты нарисую так, чтобы у них была общая часть (пересечение). В этой общей части ставим цифру 2. В оставшейся части «футболистов» круга ставим цифру 14 (16 − 2= 14). В свободной части «баскетболистов» круга ставим цифру10 (12 − 2 = 10). А теперь рисунок сам подсказывает, что всего у меня 14 + 2 + 10 = 26 друзей.

Ответ: 26 друзей.

Задача 2. Любимые мультфильмы

Среди школьников шестого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны», «Волк и теленок». Всего в классе 38 человек. «Белоснежку и семь гномов» выбрали 21 ученик, среди которых трое назвали еще «Волк и теленок», шестеро – «Губка Боб Квадратные Штаны», а один написал все три мультфильма. Мультфильм «Волк и теленок» назвали 13 ребят, среди которых пятеро выбрали сразу два мультфильма. Сколько человек выбрали мультфильм «Губка Боб Квадратные Штаны»?

Решение

В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Получаем такой чертеж:

Учитывая условие, что среди ребят, которые назвали мультфильм «Волк и теленок» пятеро выбрали сразу два мультфильма, получаем:

21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов».
13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок».
Получаем:

38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны».
Делаем вывод, что «Губка Боб Квадратные Штаны» выбрали 8 + 2 + 1 + 6 = 17 человек.
Ответ. 17 человек выбрали мультфильм «Губка Боб Квадратные Штаны».

Задача 3. Гарри Поттер, Рон и Гермиона

На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон?

Решение

Учитывая условия задачи, чертеж будет таков:
Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона, то 11 – 4 – 2 = 5 – книг прочитал только Гарри. Следовательно,
26 – 7 – 2 – 5 – 4 = 8 – книг прочитал только Рон.
Ответ. 8 книг прочитал только Рон.

4) Работа в группах. Самостоятельное решение задач, с последующей проверкой.

1 группа: Пионерский лагерь

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке? Сколько ребят заняты только спортом?

Решение

Изобразим множества следующим образом:

70 – (6 + 8 + 10 + 3 + 13 + 6 + 5) = 19 – ребят не поют, не увлекаются спортом, не занимаются в драмкружке. Только спортом заняты 5 человек.
Ответ. 5 человек заняты только спортом.

2 группа: Экстрим

Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?

Решение

Всеми тремя спортивными снарядами владеют три человека, значит, в общей части кругов вписываем число 3. На скейтборде и на роликах умеют кататься 10 человек, а 3 из них катаются еще и на сноуборде. Следовательно, кататься только на скейтборде и на роликах умеют 10-3=7 ребят. Аналогично получаем, что только на скейтборде и на сноуборде умеют кататься 8-3=5 ребят, а только на сноуборде и на роликах 5-3=2 человека. Внесем эти данные в соответствующие части. Определим теперь, сколько человек умеют кататься только на одном спортивном снаряде. Кататься на сноуборде умеют 30 человек, но 5+3+2=10 из них владеют и другими снарядами, следовательно, только на сноуборде умеют кататься 20 ребят. Аналогично получаем, что только на скейтборде умеют кататься 13 ребят, а только на роликах – 30 ребят. По условию задачи всего 100 ребят. 20+13+30+5+7+2+3=80 – ребят умеют кататься хотя бы на одном спортивном снаряде. Следовательно, 20 человек не умеют кататься ни на одном спортивном снаряде.
Ответ. 20 человек не умеют кататься ни на одном спортивном снаряде.

3 группа: «троечники»

В классе учатся 40 человек. Из них по русскому языку имеют «тройки» 19 человек, по математике – 17 человек и по истории – 22 человека. Только по одному предмету имеют «тройки»: по русскому языку – 4 человека, по математике – 4 человека, по истории – 11 человек. Семь учеников имеют «тройки» и по математике и по истории, а 5 учеников – «тройки» по всем предметам. Сколько человек учится без «троек»? Сколько человек имеют «тройки» по двум из трех предметов?

Решение. Нарисуем круги Эйлера. Внутри большего круга, изображающего всех учеников класса, поместим три меньших круга М, Р, И, означающих соответственно математика, русский язык и история.

Дальнейшие расчеты не представляют большого труда. Так как число ребят, имеющих «тройки» по математике и истории, равно 7, то число учеников, имеющих только две «тройки» — по математике и по истории, равно 7-5=2. Тогда 17-4-5-2=6 учеников имеют две «тройки» — по математике и по русскому языку, а 22-5-2-11=4 ученика только две «тройки» — по истории и по русскому языку. В этом случае без «тройки» учится 40-22-4-6-4=4 ученика. А имеют «тройки» по двум предметам из трех 6+2+4=12 человек.

4 группа: Любители физики

Из 100 семиклассников, выполнивших практическое задание по физике, 75 сделали модели, а 65 эскиз фонтана, а 10 человек ни чего не сделали. Сколько учеников сделали модель и эскиз?

Решение: В большом круге, изображающем 100 семиклассников, поместим 2 меньших круга, изображающих учеников, выполнивших модель и эскиз фонтана. Мы видим, что 90 учеников (100-10)выполнили хотя бы одну часть задания; 15 учеников (90-75) сделали только эскиз фонтана, 75-15=50 – учеников сделали эскиз и фонтан.

Ответ: 50 учеников.

4) Итог урока.

— Чем был для вас полезен сегодняшний урок?

5) Домашнее задание: В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, ителевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?

В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?	В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?	В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?	В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?	В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?	В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?	В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?	В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?	В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?	В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?	В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?	В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?	В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?	В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?	В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?	В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?	В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?	В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?	В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?	В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?	В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?	В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?	В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?

1 группа: Пионерский лагерь

2 группа: Экстрим

3 группа: «троечники»

4 группа: Любители физики

nsportal.ru

Проект ученицы 9 класса «Круги Эйлера». Решение задач.

Проект

Тема:Круги Эйлера.

Выполнила: Нестеренко Марина

ученица 9б класса школы №367

«Школа надомного обучения

Научный руководитель:

учитель математики

Монакова Клара Захаровна

2010 г.

Оглавление.

1. Введение.

а) Исторические сведения.

б) Изображение множества чисел с помощью кругов Эйлера.

2. Решение задач с помощью кругов Эйлера.

а) Простые задачи.

б) Сложные задачи.

3. Заключение.

1. Введение.

Один из величайших математиков петербургский академик Леонард Эйлер за свою долгую жизнь (он родился в 1707 г., а умер в 1783 г.) написал более 850 научных работ. В одной из них и появились эти круги. А впервые он их использовал в письмах к немецкой принцессе. Эйлер писал тогда, что «круги очень подходят для того, чтобы облегчить наши размышления». Позднее аналогичный прием использовал ученый Венн и его назвали «диаграммы Венна». Эйлер писал тогда, что «они очень подходят для того, чтобы облегчить наши размышления». При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов и они получили название «круги Эйлера».

Этот метод даёт ещё более наглядное представление о возможном способе изображения условий, зависимости, отношений в логических задачах.

Множество всех действительных чисел Эйлер изобразил с помощью этих кругов: N-множество натуральных чисел, Z – множество целых чисел, Q – множество рациональных чисел, R – множество вех действительных чисел.

Ну а как же круги Эйлера помогают при решении задач? Для ответа возьмем несколько задач:

2. Решение задач с помощью кругов Эйлера.

1. Часть жителей нашего города умеет говорить только по-русски, часть – только по-башкирски и часть умеет говорить на обоих языках. По-башкирски говорят 85%, по-русски 75%. Сколько процентов жителей говорят на обоих языках?

Решение. Составим схему –

В кружке под буквой «Б» обозначим жителей, говорящих по-башкирски, под буквой «Р» — по-русски. В общей части кружков обозначим жителей, говорящих на обоих языках. Теперь от всех жителей (100%) отнимем кружок «Б» (85%), получим жителей, говорящих только по-русски (15%). А теперь от всех, говорящих по-русски (75%), отнимем эти 15%. Получим говорящих на обоих языках (60%).

2. Все мои подруги выращивают в своих квартирах какие-нибудь растения. Шестеро из них разводят кактусы, а пятеро — фиалки. И только у двоих есть и кактусы и фиалки. Угадайте, сколько у меня подруг?

Решение. Обратимся к кругам Эйлера:

Изобразим два круга, так как у нас два вида цветов. В одном будем фиксировать владелиц кактусов, в другом — фиалок. Поскольку у некоторых подруг есть и те, и другие цветы, то круги нарисуем так, чтобы у них была общая часть. В этой общей части ставим цифру 2 так как кактусы и фиалки у двоих. В оставшейся части «кактусового» круга ставим цифру 4 (6 − 2 = 4). В свободной части «фиалкового» круга ставим цифру 3 (5 − 2 = 3). А теперь рисунок сам подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг.

3. В футбольной команде «Спартак» 30 игроков, среди них 18 нападающих. 11 полузащитников, 17 защитников и вратари. Известно, что трое могут быть нападающими и защитниками, 10 защитниками и полузащитниками, 6 нападающими и защитниками, а 1 и нападающим, и защитником, и полузащитником. Вратари не заменимы. Сколько в команде «Спартак» вратарей?

Решение.

18+11+17-3-10-6+1=28 (игроков) на этой диаграмме. Но в команде всего 30 футболистов. Значит вратарей будет 30-28=2. Ответ: 2 вратаря.

4. В классе 30 человек. 20 из них каждый день пользуются метро, 15 — автобусом, 23 — троллейбусом, 10 — и метро, и троллейбусом, 12 — и метро, и автобусом, 9 — и троллейбусом, и автобусом. Сколько человек ежедневно пользуются всеми тремя видами транспорта?

Решение. 1 способ. Для решения опять воспользуемся кругами Эйлера:

Пусть х человек пользуется всеми тремя видами транспорта. Тогда пользуются только метро и троллейбусом — (10 − х) человек, только автобусом и троллейбусом — (9 − х) человек, только метро и автобусом — (12 − х) человек. Найдем, сколько человек пользуется одним только метро:

20 − (12 − х) − (10 − х) − х = х − 2

Аналогично получаем: х − 6 — только автобусом и х + 4 — только троллейбусом, так как всего 30 человек, составляем уравнение:

Х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30. отсюда х = 3.

2 способ. А можно эту задачу решить задачу другим способом:

20+15+23-10-12-9+х=30, 27+х=30, х=3.

5. В восьмом классе учится 40 человек. Каждый из них изучает не менее одного иностранного языка: английский, немецкий, французский. 34 человека изучают хотя бы один из двух языков: английский, немецкий. 25 человек — хотя бы один из языков: немецкий, французский. 6 человек только немецкий. Одновременно два языка — английский и немецкий — изучают на 3 человека больше, чем французский и немецкий языки. Сколько человек изучает каждый из языков и сколько изучает одновременно каждую пару языков?

Решение

хотя бы 1

А + Н = 34 Ф + Н = 25

Н = 6

А + Н = на 3 человека >, чем Ф + Н = х

одновр. одновр.

34 – х – 3 – 6 – х + х + 3 + 6 + х +25 – х – 6 – х – 3 = 40

– 2х = 40 – 34 + 3 – 25

– 2х = –10

х = 5

Ф + Н = 5 человек.

А + Н = 8 человек.

А = 34 – 8 – 6 – 5 =15 человек.

Н = 6 человек.

Ф =25 – 5 – 6 –8 = 6 человек.

Всего 40 человек.

4. В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и

холодильник и микроволновку, 19 — и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?

Решение:

Купили только холодильники: 35-(20-3)-(15-3)-3=4.

Купили только микроволновки: 36-(20-3)-(19-3)-3=0.

Купили только телевизоры: 37-(15-3)-(19-3)-3=6.

Тогда всего покупателей было: 4+17+3+16+12+6=58.

65-58=7 посетителей магазина не купили ничего.

Заключение.

В результате работы над данной темой я пришла к следующим выводам:

1) Все множества чисел связаны между собой так, что каждое следующее, более объемное, включает в себя предыдущее множество полностью;

2) Любое натуральное число является элементом любого следующего множества.

3) Применение кругов Эйлера (диаграмм Эйлера-Венна) позволяет легко решить задачи, которые обычным путем разрешимы лишь при составлении системы трех уравнений с тремя неизвестными.

nsportal.ru

План-конспект урока по информатике и икт (7 класс) на тему: Презентация к уроку «Решение задач с помощью кругов Эйлера»

Слайд 1

Решение задач с помощью кругов Эйлера 6

Слайд 2

Устная работа — Что такое множество? — Какие бывают множества? — Какое множество называют пустым? — В каком случае множество А называют подмножеством множества В? Приведите пример. — Какое множество называют пересечением множеств А и В? Проиллюстрируйте свой ответ рисунком и приведите примеры.

Слайд 3

Проверка домашнего задания № 2 на стр. 21 № 8 на стр.22 Боря Гриша Витя Егор Москва — — + — Омск + — — — Санкт-Петербург — + — — Киров — — — +

Слайд 4

Проверка домашнего задания № 11 на стр.22 Я – источник информации Мой телефон – кодирующее устройство Телефон товарища — декодирующее устройство Мобильная связь – канал связи Мой товарищ – приемник информации

Слайд 5

Леонард Эйлер Леонард Эйлер, крупнейший математик XVIII века, родился в Швейцарии. В 1727г. по приглашению Петербургской академии наук он приехал в Россию. Эйлер попал в круг выдающихся математиков, получил большие возможности для создания и издания своих трудов. Он работал с увлечением и вскоре стал, по единодушному признанию современников, первым математиком мира. Одним из первых, кто использовал для решения задач круги, был выдающийся немецкий математик и философ Готфрид Вильгельм Лейбниц (1646 – 1716). В его черновых набросках были обнаружены рисунки с кругами. Затем этот метод основательно развил швейцарский математик Леонард Эйлер (1707 – 1783). (1707 г.-1783 г.)

Слайд 6

Слайд 7

Круги ЭЙЛЕРА — геометрическая схема, с помощью которой можно изобразить соотношения между множествами.

Слайд 8

Типы кругов Эйлера

Слайд 9

Решение задач Задача 1 ( «Обитаемый остров» и «Стиляги») Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек – фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?

Слайд 10

Решение. Чертим два множества таким образом: 6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств. 15 – 6 = 9 – человек, которые смотрели только «Обитаемый остров». 11 – 6 = 5 – человек, которые смотрели только «Стиляги». Получаем: Ответ. 5 человек смотрели только «Стиляги». 6 «Обитаемый остров» «Стиляги» «обитаемый остров» «Стиляги» 9 6 5

Слайд 11

В деревне в каждой семье есть корова или лошадь, причем в 20 дворах есть коровы, в 25 – лошади, а в 15 – и коровы, и лошади. Сколько в деревне дворов? Задача №2 СПОСОБ 1 15 5+ 15 + 10 = 30 К=20 Л=25 5 10

Слайд 12

В деревне в каждой семье есть корова или лошадь, причем в 20 дворах есть коровы, в 25 – лошади, а в 15 – и коровы, и лошади. Сколько в деревне дворов? 20 + 25 К=20 Л=25 Задача №2 СПОСОБ 2 — 15 15 = 30

Слайд 13

Алгоритм решения задач с помощью кругов Эйлера Записываем краткое условие задачи. Выполняем рисунок. Записываем данные в круги Эйлера. Выбираем условие, которое содержит больше свойств. Анализируем, рассуждаем, не забывая записывать результаты в части круга. Записываем ответ.

Слайд 14

Физминутка Раз – подняться, потянуться Два – нагнуться, разогнуться Три – в ладоши, три хлопка Головою три кивка На четыре – руки шире Пять – руками помахать Шесть – на место тихо сесть

Слайд 15

Работа на уроке Ответьте на вопрос № 11 к §1.3 на стр.30

Слайд 16

Домашнее задание §1.3, №12

Слайд 17

МАТЕМАТИКА. 6 КЛАСС: УЧЕБ. ДЛЯ ОБЩЕОБРАЗОВАТ. ОРГАНИЗАЦИЙ/ [ Г.В. ДОРОФЕЕВ, И.В. ШАРЫГИН, С.Б. СУВОРОВА И ДР. ] «МАТЕМАТИЧЕСКАЯ ЭНЦИКЛОПЕДИЯ» HTTP://MINISOFT.NET.RU/ HTTP://LOGIKA.VOBRAZOVANIE.RU/INDEX.PHP?LINK=KR_E.HTML HTTP://RESHIZADACHU.UCOZ.RU/INDEX/KRUGI_EHJLERA/0-18 Литература

nsportal.ru

Использование метода кругов Эйлера (диаграмм Эйлера–Венна) при решении задач в курсе информатики и ИКТ

Разработка урока по тему «Решение задач с помощью кругов Эйлера»

Решение задач с помощью кругов Эйлера.

План-конспект урока (алгебра, 5 класс) по теме: Решение задач с помощью кругов Эйлера

Проект ученицы 9 класса «Круги Эйлера». Решение задач.

План-конспект урока по информатике и икт (7 класс) на тему: Презентация к уроку «Решение задач с помощью кругов Эйлера»

Добавить комментарий Отменить ответ